Обзор средств matlab и ToolBox'ов для приближения данных

Вид материала

Подобный материал:

1 2 3 4

Как связаны выпуклая оболочка, триангуляция Делоне и диаграмма Вороного

Мы рассмотрим этот вопрос на примере множества точек на плоскости (x_i,y_i)_i=1,2,...,k.

Определим для каждой точки высоту z_i = x_i² + y_i². Тогда точки с координатами (x_i,y_i,z_i)_i=1,2,...,k лежат на параболоиде
z(x,y) = x² + y² (на рисунке он обозначен желтым цветом).

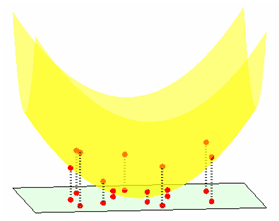
Построим для множества точек с координатами (x_i,y_i,z_i)_i=1,2,...,k выпуклую оболочку

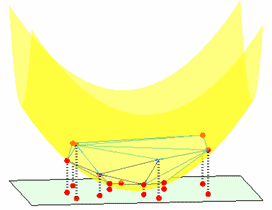
и спроектируем ее нижние грани, которые видны наблюдателю, находящемуся под плоскостью и смотрящему вверх, на плоскость, где лежат точки из исходного множества. То, что получится и будет триангуляцией Делоне

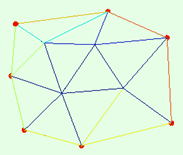
Команды, для получения этих картинок приведены ниже:

% задаем координаты точек на плоскости

x =[-0.3 -0.04 0.37 0.35 0.08 -0.34 -0.36 -0.13 0.15 0.02 -0.21]';

y =[0.29 0.38 0.25 -0.24 -0.39 -0.32 -0.02 0.08 0.05 -0.2 -0.21]';

% рисуем плоскость при помощи полигонального объекта

figure('Color','w')

patch('XData',[-0.6 0.6 0.6 -0.6], 'YData',[-0.6 -0.6 0.6 0.6], 'FaceColor','g','FaceAlpha',0.1)

% делаем оси невидимыми и устанавливаем нужный угол обзора

axis off

view(-8,12)

hold on

% рисуем точки маркерами

plot(x,y,'r.','MarkerSize',20)

% строим параболоид

[X,Y]=meshgrid(-0.6:0.05:0.6);

Z=X.2+Y.2;

hs=surf(X,Y,Z,'EdgeColor','none','FaceColor','y','FaceAlpha',0.5)

% в цикле для каждой точки рисуем линию от исходной плоскости до параболоида и отмечаем

% на нем новые точки

for k=1:length(x)

line('XData',[x(k) x(k)],'YData',[y(k) y(k)], 'ZData', [0 x(k)2+y(k)2],...

'Color','k','LineWidth',2,'LineStyle',':')

plot3(x(k),y(k),x(k)2+y(k)2,'r.','MarkerSize',20)

end

% строим выпуклую оболочку точек

kvert=convhulln([x,y,x.2+y.2])

% визуализируем выпуклую оболочку

h=trimesh(kvert,x,y,x.2+y.2)

set(h,'Marker','.','MarkerSize',20,'MarkerEdgeColor','r')

% устанавливаем нужный угол обзора (наблюдатель под плоскостью)

view(0,-90)

% удаляем параболоид

delete(hs)

Построенный выше параболоид z(x,y) = x² + y² позволяет получить диаграмму Вороного для множества точек (x_i,y_i)_i=1,2,...,k. Для этого проведем в каждой точке (x_i,y_i,z_i)_i=1,2,...,k касательную плоскость к параболоиду, на рисунке показана касательная плоскость в одной точке

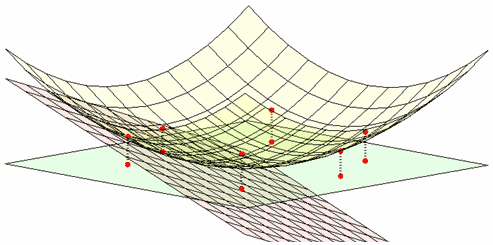
Для каждой точки (x_i,y_i,z_i)_i=1,2,...,k уравнение касательной к параболоиду плоскости будет иметь следующий вид:

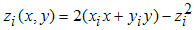
Несложно показать, что если некоторая точка (x,y) равноудалена от точек (x_i,y_i) и (x_j,y_j), то тогда z_i(x,y) = z_j(x,y), а если точка (x,y) дальше от (x_i,y_i), чем от некоторой другой точки (x_j,y_j), то тогда z_i(x,y) > z_j(x,y). Обратное тоже верно, т.е. если z_i(x,y) > z_j(x,y), то (x,y) дальше от (x_i,y_i), чем от (x_j,y_j) и из равенства z_i(x,y) = z_j(x,y) следует, что расстояния от (x,y) до (x_i,y_i) и (x_j,y_j) совпадают. Каждая плоскость z_i(x,y) делит все пространство на верхнее и нижнее полупространства. Построив объединение верхних подпространств мы получим выпуклый многогранник. Проекция его граней на исходную плоскость и даст диаграмму Вороного.

Если известна диаграмма Вороного для точек (x_i,y_i,z_i)_i=1,2,...,k, то легко получить триангуляцию Делоне. Мы берем точки, находящиеся в смежных ячейках (не забывая про бесконечные ячейки) и соединяем их отрезками.

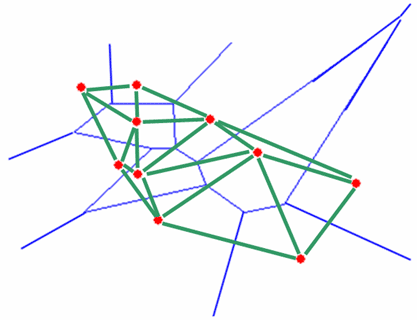
Синими линиями нарисована диаграмма Вороного для красных точек, а зелеными - триангуляция Делоне.

Если для множества точек уже построена диаграмма Вороного, то при помощи несложного алгоритма выпуклая оболочка множества точек может быть найдена за время, пропорциональное числу точек.

Нахождение площади многоугольника и пересечения четырехугольников

Нахождение ближайшей точки и симплекса, содержащего точку

Приближение разбросанных данных

Blog

Обзор средств matlab и ToolBox'ов для приближения данных