Новосибирский Государственный Технический Университет Кафедра прикладной математики курсовая

Вид материала

Содержание

3. Структуры данных, используемые для представления исходных данных и результатов задачи
4. Укрупнённый алгоритм решения задачи
5. Структура программы
6. Текст программы на языке C++
7. Набор тестов

Подобный материал:

Министерство образования и науки Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра прикладной математики

Курсовая работа по практикуму на ЭВМ:

структуры данных и алгоритмы

Факультет: прикладной математики и информатики

Группа:

Студент:

Преподаватели:

Новосибирск 2009

1. Условие

В системе двусторонних дорог за проезд каждой дороги взимается некоторая пошлина. Найти путь из города A в город B с минимальной величиной S + P, где S – сумма длин дорог пути, а P – сумма пошлин проезжаемых дорог.

2. Анализ задачи

2.1. Исходные данные задачи:

n – количество городов,

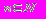
m – количество дорог,

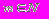
G – список дорог,

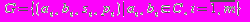
A – исходный город,

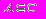
B – конечный город,

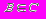
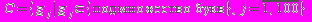
2.2. Результат:

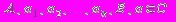- маршрут из A в B с минимальной величиной S + P; “No Way”, если маршрута нет

2.3. Решение:

Математическая модель системы двусторонних дорог – неориентированный взвешенный помеченный граф

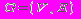с весовой функцией

, причём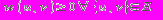

. При этом вершины соответствуют городам (метка вершины – название города), а рёбра – двусторонним дорогам. Вес ребра определяется по формуле

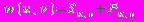, где

- длина дороги между городами u и v,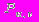

- пошлина, взимаемая за проезд по этой дороге. В случае существования нескольких дорог между одной и той же парой городов, в граф добавляется ребро с наименьшим весом (поскольку задача состоит в отыскании пути с наименьшим весом).

Для нахождения маршрута в графе с наименьшим весом, хорошим алгоритмом является алгоритм Дейкстры. Алгоритм Дейкстры решает задачу о кратчайших путях из одной вершины k для взвешенного ориентированного графа

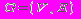, в котором все веса рёбер неотрицательны.

Основные подзадачи:

Ввод системы дорог
Нахождение кратчайшего пути

Формальная постановка задачи

Построить граф заданной системы дорог, найти кратчайший путь между двумя заданными вершинами.

Основные подзадачи:

Ввод системы дорог

2) Нахождение кратчайшего пути

3. Структуры данных, используемые для представления исходных данных и результатов задачи

3.1. Входные данные

Внешнее представление системы двусторонних дорог:

<система-дорог> ::= <количество-городов> <количество-дорог> <список-дорог>

<количество-городов> ::= <натуральное-число>

<количество-дорог> ::= <натуральное-число>

<название-города> ::= <буква>|<название-города> <буква>

<список-дорог> ::= <дорога>|<дорога> <список-дорог>

<дорога> ::= <название-города> <название-города> <расстояние> <пошлина>

<расстояние> ::= <натуральное-число>

<пошлина> ::= <натуральное-число>

Внутреннее представление системы двусторонних дорог:

Для алгоритма Дейкстры хорошим представлением графа является представление списками смежности. Список смежности даёт компактное представление для разреженных графов – тех, у которых множество рёбер много меньше множества вершин, что характерно для системы дорог. Чтобы не усложнять списки смежности, вместо названия города будем помечать вершину номером. Вершины пронумеруем с нуля. Список смежных вершин представим двусвязным закольцованным списком (такой список можно так же использовать в качестве очереди, требуемой для алгоритма Дейкстры).

list *G[100]; // Список смежности вершин

char city[100][100]; // Массив городов

3.2. Выходные данные

Внешнее представление: список вершин маршрута или текстовое сообщение «Пути нет»

Внутреннее представление:

Pr[] – массив предшественников вершин;

4. Укрупнённый алгоритм решения задачи

4.1.

{

Данные = ЧтениеДанных

Граф = ПостроитьГраф(Данные)

Если (Существует(Маршрут(Граф, А. В)))

{

Вывести Маршрут(Граф, А. В)

} иначе {

Пути нет :O

}

}

4.2. Алгоритм нахождения маршрута

{

for (каждая вершина v из V)

{

d[v] ← ∞;

Pr[v] ← -1;

}

d[s] ← 0;

Q ← V[G];

while (Q ≠ 0)

{

u ← Extract-Min(Q);

for (каждая вершина v из Adj[u])

if (d[v] > d[u] + w(u, v))

{

d[v] ← d[u] + w(u, v);

Pr[v] ← u;

}

}

ВывестиМаршрут(A, B, Pr)

}

4.3. Алгоритм вывода маршрута

{

Если (A == B)

{

Вывести(A -> )

} иначе {

Если (Pr[B] == -1)

{

Маршрута нет

} иначе {

ВывестиМаршрут(A, Pr[B], Pr)

Вывести(B -> )

}

}

}

5. Структура программы

Текст программы разбит на три модуля.

Модуль 1 содержит основную подпрограмму, осуществляющую чтение исходных данных, построение графа и выдачу результата.

Модуль 2 содержит подпрограмму поиска и вывода пути.

Модуль 3 содержит основные операции для работы с линейным списком.

5.1. Состав модуля 1:

Главная функция main:

Назначение: чтение исходных данных, построение графа, выдача результата

Прототип: int main()

Функция getCity:

Назначение: получить номер города по имени (возможно, добавив его в массив городов, если город в массиве отсутствует)

Прототип: int getCity(char city[100][100], int *cityN, char cityName[100])

Параметры: city – массив городов, cityN – количество городов (изменяемое), cityName – имя города

5.2. Состав модуля 2:

Функция printMinimalPathway:

Назначение: поиск путей в графе Алгоритмом Дейкстры, вывод минимального пути или сообщения о том, что пути нет

Прототип: void printMinimalPathway(list *G[100], int N, int weights[100][100], char city[100][100], int A, int B)

Параметры: G – список смежности, N – количество вершин, weights – массив весов, city – массив имён городов, A – исходный пункт, B – конечный

5.3. Структура программы по управлению:

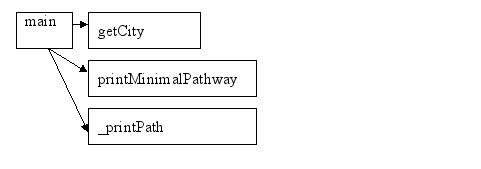
6. Текст программы на языке C++

main.cpp

#include

#include

#include "list.h"

#include "graph.h"

int getCity(char city[100][100], int *cityN, char cityName[100])

{

for (int i = 0; i < *cityN; i++)

{

if (!strcmp(city[i], cityName))

{

return i;

}

}

strcpy(city[*cityN], cityName);

int ret = *cityN;

(*cityN)++;

return ret;

}

int main()

{

char filename[16];

printf("Filename: "); gets(filename);

FILE *f = fopen(filename, "r");

if (!f)

{

perror("Error opening file");

return 1;

}

// Создание пустого графа

list *G[100];

int cityN = 0;

char city[100][100];

int weights[100][100];

int N; fscanf(f, "%d", &N);

if (N == 0)

{

printf("No way\n");

return 0;

}

int M; fscanf(f, "%d", &M);

for (int i = 0; i < N; i++)

{

G[i] = new_list();

for (int j = 0; j < N; j++)

{

weights[i][j] = 0;

}

}

// Ввод системы дорог

for (int i = 0; i < M; i++)

{

char temp[100];

fscanf(f, "%s", &temp);

int city1 = getCity(city, &cityN, temp);

fscanf(f, "%s", &temp);

int city2 = getCity(city, &cityN, temp);

int s, p;

fscanf(f, "%d %d", &s, &p);

push(G[city1], city2);

push(G[city2], city1);

if (!weights[city1][city2] || weights[city1][city2] > s + p)

{

weights[city1][city2] = weights[city2][city1] = s + p;

}

}

// Остальные данные

char _A[100], _B[100];

fscanf(f, "%s %s", &_A, &_B);

int A = getCity(city, &cityN, _A);

int B = getCity(city, &cityN, _B);

// Вычисление и вывод результата

printMinimalPathway(G, N, weights, city, A, B);

return 0;

}

graph.h

#pragma once

#include "list.h"

void printMinimalPathway(list *G[100], int N, int weights[100][100], char city[100][100], int A, int B);

graph.cpp

#include

#include "list.h"

#include "graph.h"

void _printPath(int from, int to, char city[100][100], int Pr[100])

{

if (from == to)

{

printf("%s", city[to]);

} else {

if (Pr[to] == -1)

{

printf("No way\n");

} else {

_printPath(from, Pr[to], city, Pr);

printf(" -> %s", city[to]);

}

}

}

void printMinimalPathway(list *G[100], int N, int weights[100][100], char city[100][100], int A, int B)

{

int d[100], Pr[100];

for (int i = 0; i < N; i++)

{

d[i] = 100000;

Pr[i] = -1;

}

d[A] = 0;

list *Q = new_list();

for (int i = 0; i < N; i++)

{

push(Q, i);

}

while (Q != Q->next)

{

int u = pop(Q, d);

list *cur = G[u];

while (G[u] != (cur = cur->next))

{

int v = cur->data;

if (d[v] > d[u] + weights[u][v])

{

d[v] = d[u] + weights[u][v];

Pr[v] = u;

}

}

}

_printPath(A, B, city, Pr);

}

list.h

#pragma once

struct list

{

list *next;

list *prev;

int data;

};

list *new_list();

int pop(list *, int *);

void push(list *, int);

list.cpp

#include "list.h"

#include

list *new_list()

{

list *q = new list;

q->data = 0;

q->next = q;

q->prev = q;

return q;

}

int pop(list *q, int *d)

{

if (q->prev == q)

{

printf("Queue was empty\n");

return 0;

}

float min = d[q->prev->data];

list *victim = q->prev;

list *current = q;

while (q != (current = current->next))

{

if (d[current->data] < min)

{

min = d[current->data];

victim = current;

}

}

victim->prev->next = victim->next;

victim->next->prev = victim->prev;

int data = victim->data;

delete victim;

return data;

}

void push(list *q, int data)

{

list *tmp = q->next;

q->next = new list;

q->next->prev = q;

q->next->next = tmp;

q->next->data = data;

tmp->prev = q->next;

}

7

. Набор тестов

Тест 1: Пустой граф

Входные данные: 0 0

A B

Выходные данные: No way

Т

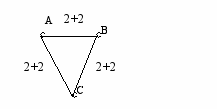ест 2: Треугольник

Входные данные: 3 3

A B 2 2

A C 2 2

B C 2 2

A C

Выходные данные: A -> C

Т

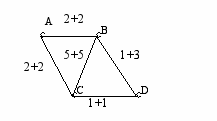ест 3: Четырёхугольник

Входные данные: 4 5

A B 2 2

A C 2 2

B C 5 5

B D 1 3

C D 1 1

B C

Выходные данные: B -> D -> C

Т

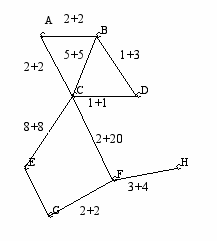ест 4: Комплексный

Входные данные: 8 10

A B 2 2

A C 2 2

B C 5 5

B D 1 3

C D 1 1

E C 8 8

C F 2 20

G E 2 2

G F 1 1

F H 3 4

G A

Выходные данные: G -> E -> C -> A

Тест 5: Тест 4 в обратную сторону

Входные данные: 8 10

A B 2 2

A C 2 2

B C 5 5

B D 1 3

C D 1 1

E C 8 8

C F 2 20

G E 2 2

G F 1 1

F H 3 4

A G

Выходные данные: A -> C -> E -> G

Т

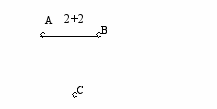ест 6: Недостижимые вершины

Входные данные: 3 1

A B 2 2

A C

Выходные данные: No way

Blog

Новосибирский Государственный Технический Университет Кафедра прикладной математики курсовая

Содержание