Geum.ru

Рабочая программа учителя математики Усмановой Р. А., Iквалификационная категория, по учебному курсу «Математика» 11 класс Базовый уровень

Вид материалаРабочая программа

Содержание


Рабочая программа
Пояснительная записка
Цели: формирование представлений
Основное содержание тем учебного курса
Контрольная работа №1,2
3. Метод координат в пространстве (12ч )
Контрольная работа №3
Контрольная работа № 4,5
Осевые сечения и сечения параллельные основанию.
Контрольная работа №8
Контрольная работа №9
Требования к уровню подготовки учеников
Алгебра уметь
Начала математического анализа
Формы организации учебного процесса
Виды организации учебного процесса
Учебно – теоретические материалы
Подобный материал:
Муниципальное общеобразовательное учреждение

средняя общеобразовательная школа села Сарлы Азнакаевского муниципального района РТ.


«Рассмотрено »

Руководитель ШМО

____________


Протокол № ___ от

«____»____________2010 г.
«Согласовано»

Заместитель директора школы по УВР МОУ СОШ с.Сарлы

______Мухаммадиева М.М.


«____»____________2010 г.
«Утверждено»

Директор МОУ СОШ с.Сарлы

__________Ахматов М.Д.


Приказ № __от «___»____2010 г.



РАБОЧАЯ ПРОГРАММА

учителя математики


Усмановой Р.А.,

I квалификационная категория,


по учебному курсу «Математика »

11 класс

Базовый уровень


Рассмотрено на заседании

педагогического совета школы

протокол № ____от «__»_______2010 г.


2010 - 2011 учебный год

Структура документа

Рабочая учебная программа включает три раздела: пояснительную записку; основное содержание с примерным распределением учебных часов по разделам курса; требования к уровню подготовки выпускников.

Пояснительная записка

Тематическое планирование по математике 11 класса (базовый уровень) составлено:

- на основе федерального компонента государственного стандарта среднего (полного) общего образования;

- примерной программы по математике основного общего образования;

-федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2010-2011 учебный год;

с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования;

- базисного учебного плана 2011 года.

Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся 11 класса средствами данного учебного предмета.

Организационно-планирующая функция предусматривает структурирование учебного материала, определение его количественных и качественных характеристик.

Данное тематическое планирование, тем самым содействует сохранению единого образовательного пространства, не сковывая творческой инициативы учителей, предоставляет широкие возможности для реализации различных подходов к построению учебного курса.

Общая характеристика учебного предмета

При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:

- систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, - -- расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач;

- расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация широты применения функций для описания и изучения реальных зависимостей;

- знакомство с основными идеями и методами математического анализа;

- изучение свойств пространственных тел, формирование умения применять полученные знания для решения практических задач.


Цели:
  • формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
  • развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
  • овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
  • воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Место предмета в базисном учебном плане

Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации для обязательного изучения математики на этапе среднего общего образования отводится 136 часов из расчета 4 часа в неделю.
Общеучебные умения, навыки и способы деятельности

В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:

- построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;

- выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;

- самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;

- проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;

- самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.

Тематическое планирование составлено к УМК А.Н.Колмогоров и другие «Алгебра и начала анализа», 10-11 класс, М. «Просвещение», 2000-2004 годов и Л.С.Атанасян и другие «Геометрия» 10-11 класс, М.: Просвещение, 2003 года на основе федерального компонента государственного стандарта общего образования с учетом авторского тематического планирования учебного материала, опубликованного в журнале «Математика в школе » №7, 2001, и в газете «Математика» №16, 2006 (приложение к газете «Первое сентября»).

Курсивом в тематическом планировании выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников. Подчеркиванием выделен материал, содержащийся в Федеральном компоненте государственных образовательных стандартов среднего (полного) общего образования, но отсутствующий в учебнике А.Н.Колмогоров и др. «Алгебра и начала анализа», 10-11 класс, М. «Просвещение», 2000-2004 годов.


Основное содержание тем учебного курса

Тематическое планирование

(5 часов в неделю, всего 170 часов)


№ п/п
Название темы
Количество часов
Контрольная работа

1
Повторение основных вопросов курса математики 10 класса
4
входная

2
Первообразная. Интеграл

22
№ 1,2

3
Метод координат в пространстве
12
№ 3

4
Обобщение понятия степени.

16
№4,5




Цилиндр, конус и шар
13
№6

5
Показательная и логарифмическая функция
22
№ 7

7
Объёмы тел
12

№ 8




Производная показательной и логарифмической функций
16
№9

8
Элементы теории вероятности
8



9
Резерв учебного времени. Итоговое повторение курса математики 10-11 класса:
42
тест

10
Итоговая контрольная работа
3
№10



Всего

170
10


1.Повторение основных вопросов курса математики 10 класса (4 ч)

Вводный контроль

2. Первообразная. Интеграл (22ч )

Первообразная, правила отыскания первообразной. Понятие криволинейной трапеции, понятие определенного интеграла. Формула Ньютона — Лейбница. Площадь криволинейной трапеции.

Контрольная работа №1,2

Знать:

Понятие первообразной, правила отыскания первообразной.

Понятие криволинейной трапеции, понятие определенного интеграла. таблицу первообразных (не­определенных интегралов) основных функций и уметь при­менять формулу Ньютона — Лейбница при вычислении определенных интегралов и площадей фигур.

Уметь:

Находить первообразную функции, применяя правила; вычислять площадь криволинейной трапеции. Применять для вычисления площадей фи­гур на плоскости и для решения геометрических и физиче­ских задач

3. Метод координат в пространстве (12ч )

Декартовы координаты в пространстве. Формула расстояния между двумя точками. Формула расстояния от точки до плоскости.

Векторы. Угол между векторами. Координаты вектора. Скалярное произведение векторов. Длина вектора в координатах, угол между векторами в координатах. Коллинеарные векторы, коллинеарность векторов в координатах.

Контрольная работа №3

Знать:

понятие прямоугольной системы координат в пространстве; понятие координат вектора в прямоугольной системе координат; понятие радиус-вектора произвольной точки пространства; формулы координат середины отрезка, длины вектора через его координаты, расстояние между двумя точками; понятие угла между векторами;

понятие скалярного произведения векторов;

формулу скалярного произведения в координатах; свойства скалярного произведения; понятие движения пространства и основные виды движения.

Уметь:

строить точки в прямоугольной системе координат по заданным её координатам и находить координаты точки в заданной системе координат; выполнять действия над векторами с заданными координатами; доказывать, что координаты точки равны соответствующим координатам её радиус-вектора, координаты любого вектора равны разностям соответствующих координат его конца и начала; решать простейшие задачи в координатах; вычислять скалярное произведение векторов и находить угол между векторами по их координатам; вычислять углы между прямыми и плоскостям; строить симметричные фигуры

4. Обобщение понятия степени. (16 ч.)

Корень п-ой степени из действительного числа. Степенная функция, свойства корня п-ой степени. Упрощение выражений, содержащих радикалы. Производная степенной функции.

Контрольная работа № 4,5

Знать: Понятие корня п-ой степени из действительного числа, понятие степенной функции, свойства корня п-ой степени, формулу производной степенной функции

Уметь: Строить график степенной функции, преобразовывать выражения, содержащие радикалы, применять свойства корней при упрощении выражений, сокращении дробей, находить производную степенной функции

5.Цилиндр, конус, шар (13ч. )

Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию.

Шар и сфера, их сечения, касательная плоскость к сфере.

Контрольная работа№6

Знать:

понятие цилиндрической поверхности, цилиндра и его элементов(боковая поверхность, основания, образующие, ось, высота, радиус; формулы для вычисления площадей боковой и полной поверхностей цилиндра; понятие конической поверхности, конуса и его элементов(боковая поверхность, основание, вершина,

образующая, ось, высота), усечённого конуса; формулы для вычисления площадей боковой и полной поверхностей конуса и усечённого конуса; понятия сферы, шара и их элементов(центр, радиус, диаметр); уравнение сферы в заданной прямоугольной системе координат; взаимное расположение сферы и плоскости; теоремы о касательной плоскости к сфере; формулу площади сферы.

Уметь:

решать задачи на вычисление боковой и полной поверхностей цилиндра; решать задачи на вычисление боковой и полной поверхностей конуса и усечённого конуса;

решать задачи на вычисление площади сферы.

6. Показательная и логарифмическая функции (22ч)

Показательная и логарифмическая функции. График показательной и логарифмической функций. Показательное и логарифмическое уравнения, неравенства. Свойства логарифмов.

Контрольная работа №7

Знать: Понятие показательной и логарифмической функции, алгоритм решения показа тельных и логарифмических уравнений и неравенств, свойства логарифмов, понятие натурального логарифма:

Уметь: Строить графики показательной и логарифмической функций, решать показательные и логарифмические уравнения и неравенства, применять свойства логарифмов при решении упражнений.

7.Объемы тел вращения (12ч)

Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.

Контрольная работа №8

Знать:

понятие объёма, основные свойства объёма; формулы нахождения объёмов призмы, в основании которой прямоугольный треугольник и прямоугольного параллелепипеда; правило нахождения прямой призмы; что такое призма, вписана и призма описана около цилиндра; формулу для вычисления объёма цилиндра; способ вычисления объёмов тел с помощью определённого интеграла, основную формулу для вычисления объёмов тел; формулу нахождения объёма наклонной призмы; формулы вычисления объёма пирамиды и усечённой пирамиды; формулы вычисления объёмов конуса и усечённого конуса; формулу объёма шара; определения шарового слоя, шарового сегмента, шарового сектора, формулы для вычисления их объёмов; формулу площади сферы.

Уметь:

объяснять, что такое объём тела, перечислять его свойства и применять эти свойства в несложных ситуациях; применять формулы нахождения объёмов призмы при решении задач; решать задачи на вычисления объёма цилиндра; воспроизводить способ вычисления объёмов тел с помощью определённого интеграла; применять формулу нахождения объёма наклонной призмы при решении задач; решать задачи на вычисление объёмов пирамиды и усечённой пирамиды; применять формулы вычисления объёмов конуса и усечённого конуса при решении задач; применять формулу объёма шара при решении задач; различать шаровой слой, сектор, сегмент и применять формулы для вычисления их объёмов в несложных задачах; применять формулу площади сферы при решении задач.

8. Производная логарифмической и показательной функции (16 ч)

Производная показательной функции, число е. Производная логарифмической функции

Контрольная работа №9

9. Элементы теории вероятности (8ч)

Табличное и графическое представление данных. Числовые характеристики рядов данных. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.

уметь

решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул; вычислять в простейших случаях вероятности событий на основе подсчета числа исходов; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: анализа реальных числовых данных, представленных в виде диаграмм, графиков; анализа информации статистического характера.

10.Итоговое повторение (42ч)

Итоговая контрольная работа №10

Цели: повторить и обобщить знания и умения, учащихся через решение задач по следующим темам: метод координат в пространстве; многогранники; тела вращения; объёмы многогранников и тел вращения. Обобщить и систематизировать знания, навыки и умения по основным темам курса математики за курс 10-11 классов:

Функция, определение, способы задания, свойства функций, сведенные в общую схему исследования функции.

Линейная функция. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.

Функция 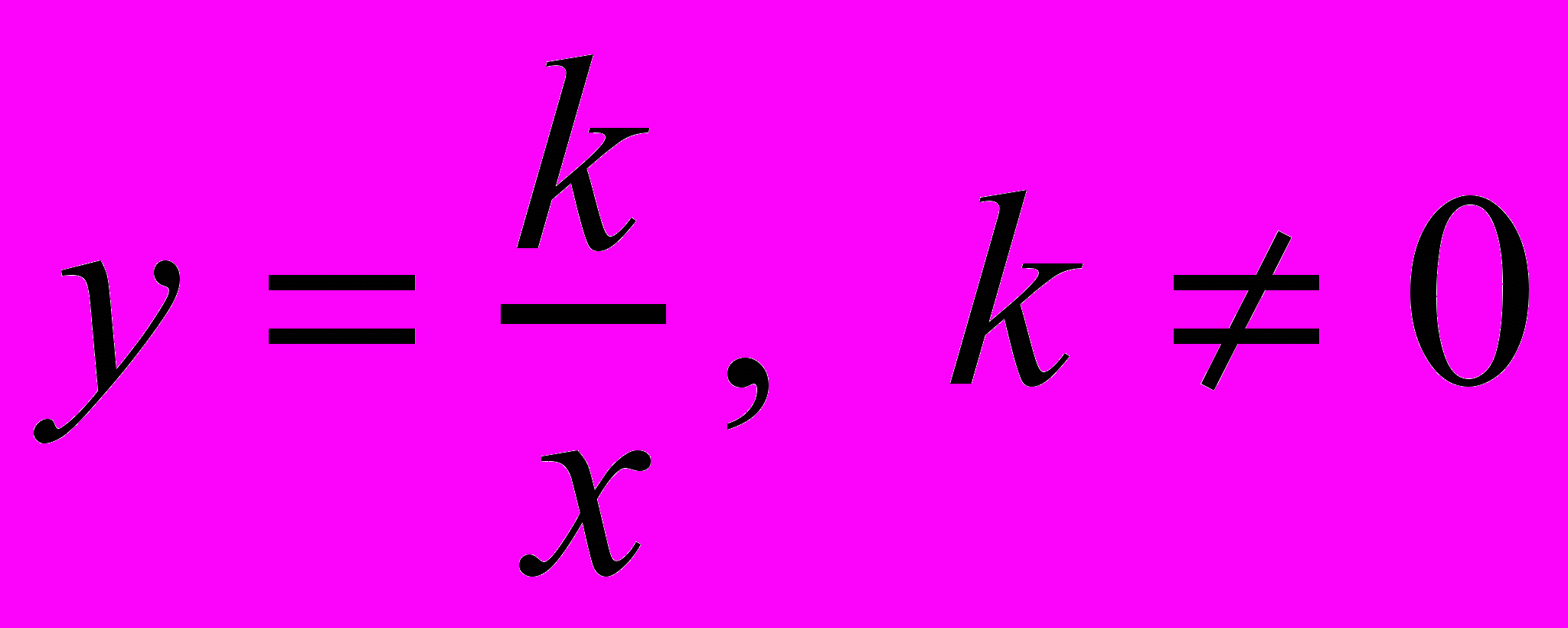. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.

Квадратичная функция 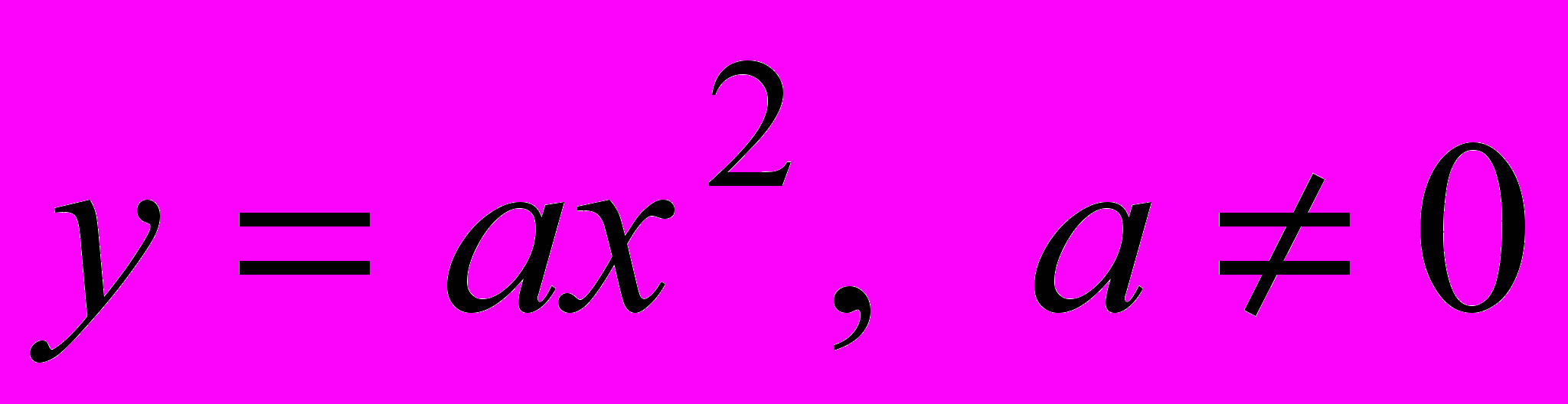и 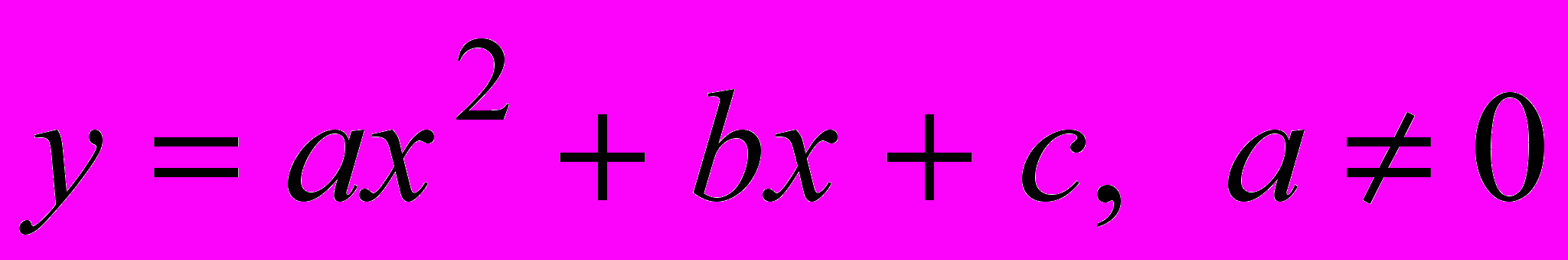. Систематизация ее свойств на основе общей схемы исследования функций. Решение задач с использованием свойств функции.

Показательная функция 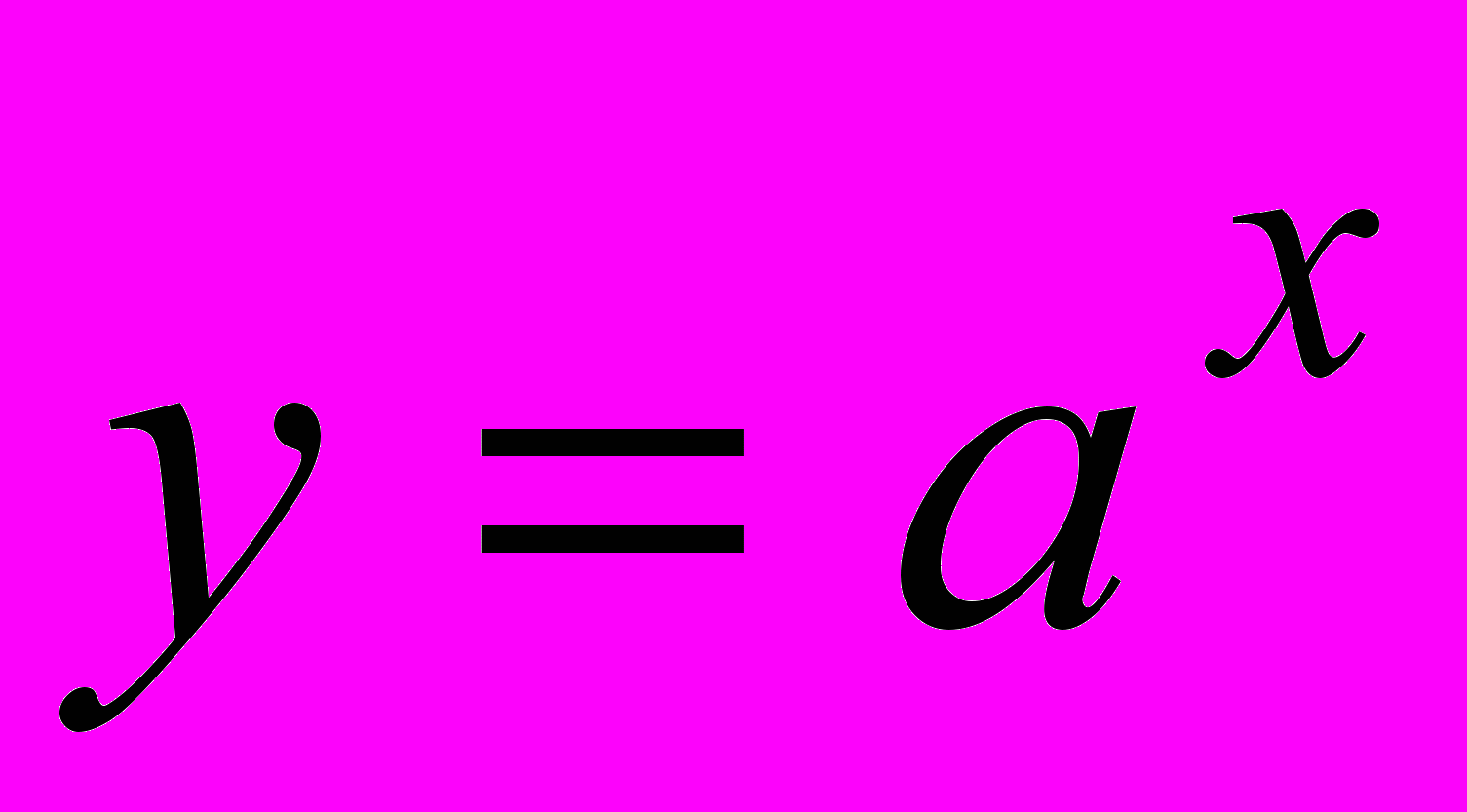, её свойства и график. Решение задач с использованием свойств функции.

Логарифмическая функция 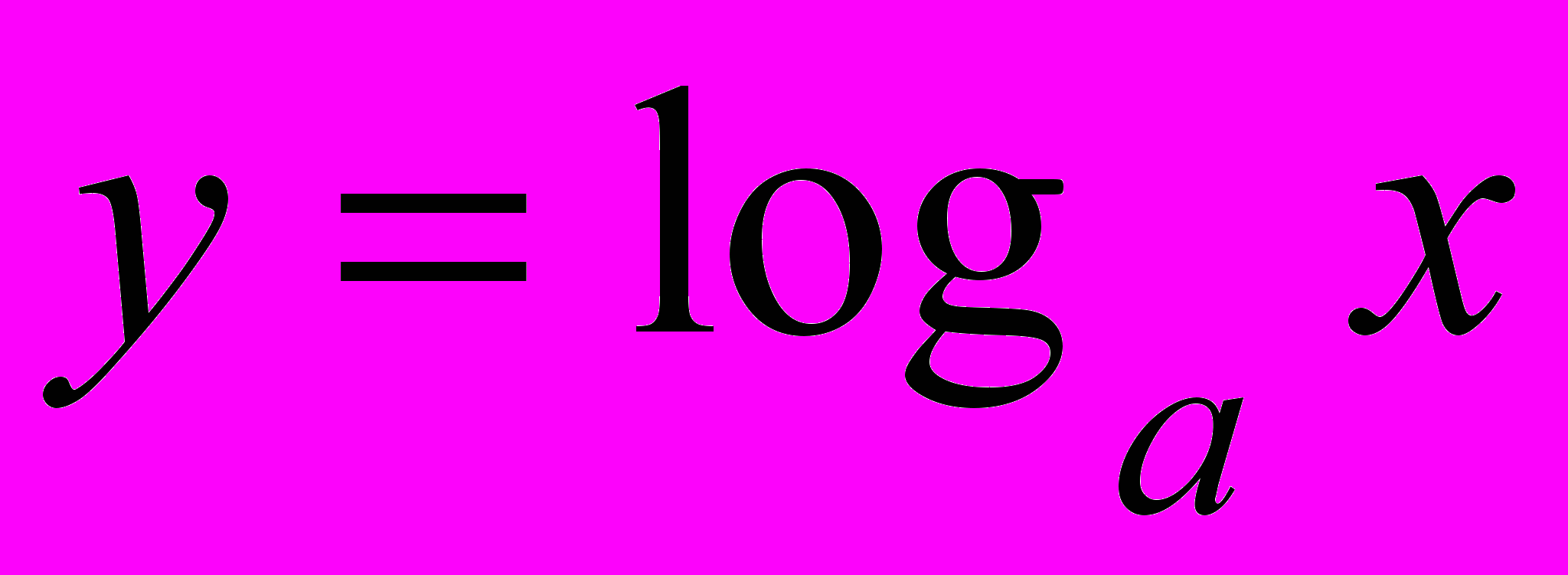, её свойства и график. Решение задач с использованием свойств функции.

Тригонометрические функции (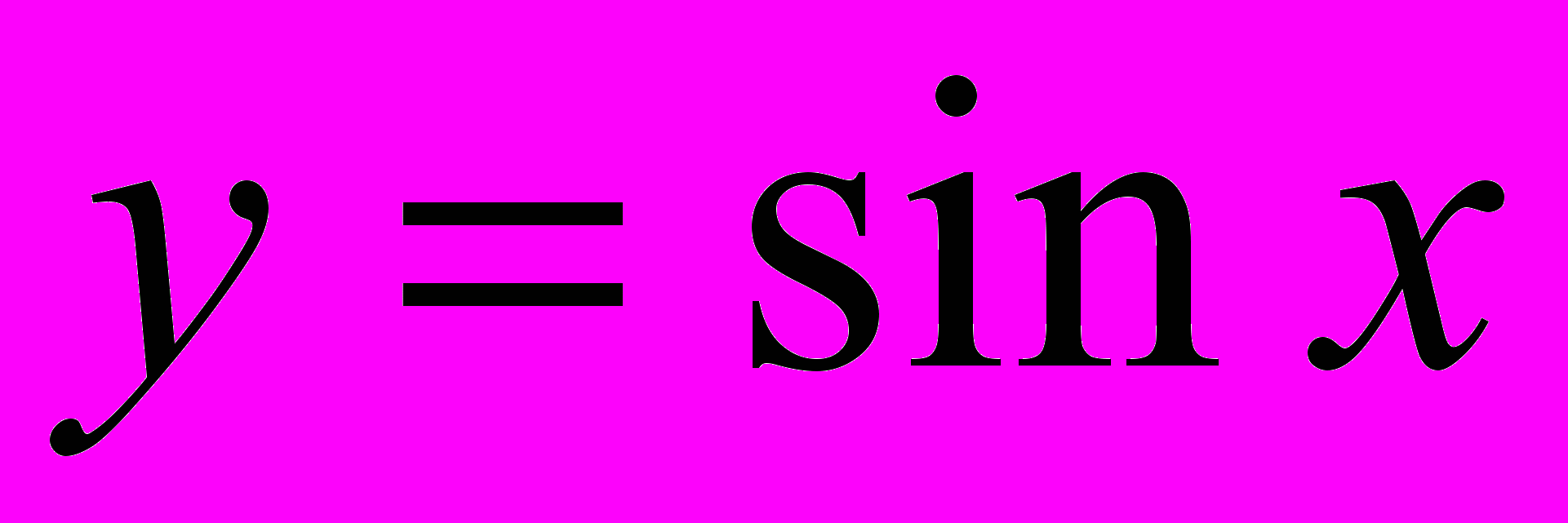, , 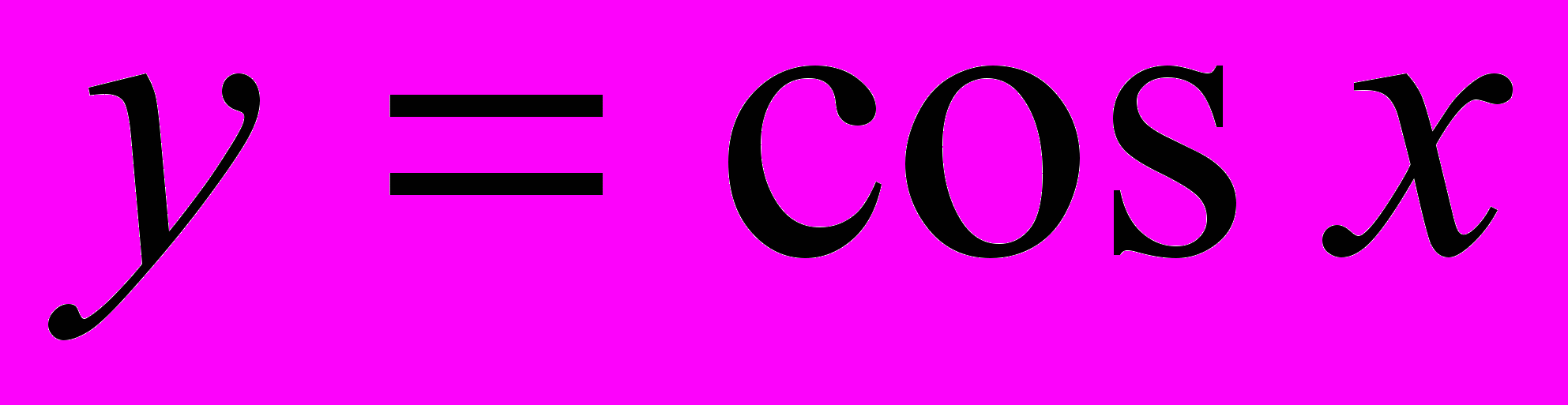, 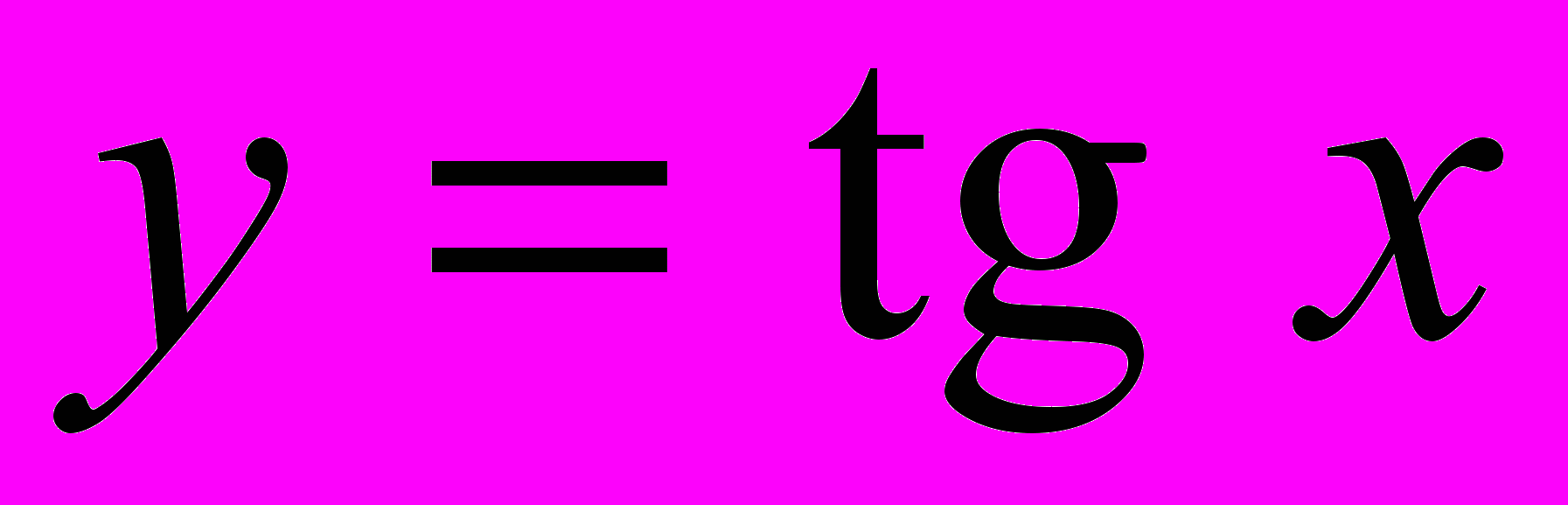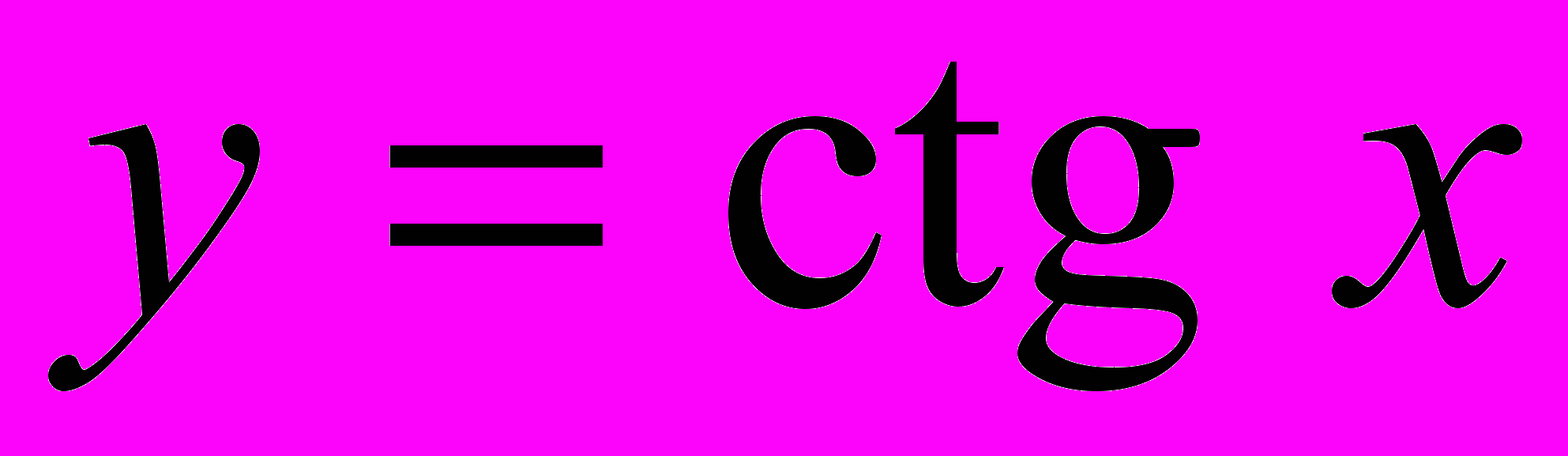), их свойства и графики. Решение задач с использованием свойств функций.

Тождественные преобразования степеней с рациональным показателем, иррациональных и логарифмических выражений.

Тождественные преобразования тригонометрических выражений.

Решение рациональных и иррациональных уравнений (в том числе содержащих модули и параметры).

Решение показательных и логарифмических уравнений и их систем (в том числе содержащих модули и параметры).

Решение тригонометрических уравнений, (в том числе содержащих модули и параметры).

Решение задач с использованием производной.

Уметь: Преобразовывать выражения, применяя основные тригонометрические формулы, решать тригонометри­ческие, уравнения, неравенства, системы, содержащие тригонометрические уравне­ния, находить производные функций, применять производную при исследовании функций, решать показательные и логарифмические , иррациональные уравнения и неравенства, решать уравнения и задачи с параметрами

Знать: Понятие равносильности уравнений, равносильности неравенств, теоремы о равносильности уравнений, методы решения уравнений, методы решения уравнений и нера­венств с модулями, понятие иррациональных уравнений и неравенств, понятие уравнений и неравенств с двумя переменными, понятие задач с параметрами.

Требования к уровню подготовки учеников


В результате изучения математики на базовом уровне ученик должен

знать/понимать
  • значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
  • значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
  • универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
  • вероятностный характер различных процессов окружающего мира;
  • значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
  • значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
  • универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;

Алгебра

уметь
  • выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
  • проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы ;
  • вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
  • практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы, используя при необходимости справочные материалы и простейшие вычислительные устройства;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
  • описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;

Начала математического анализа

уметь

  • вычислять в простейших случаях площади с использованием первообразной;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
  • решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;


ГЕОМЕТРИЯ

уметь
  • распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
  • описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
  • анализировать в простейших случаях взаимное расположение объектов в пространстве;
  • изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
  • строить простейшие сечения куба, призмы, пирамиды;
  • решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
  • использовать при решении стереометрических задач планиметрические факты и методы;
  • проводить доказательные рассуждения в ходе решения задач;
  • использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
  • исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
  • вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.


Формы организации учебного процесса:

индивидуальные, групповые, индивидуально-групповые, фронтальные, классные и внеклассные.

Формы контроля:

самостоятельная работа, контрольная работа, тесты, наблюдение, зачёт, работа по карточке.

Виды организации учебного процесса:


самостоятельные работы, контрольные работы, зачёт, лекции, практикумы.


Учебно-методическое обеспечение


Учебно – программные материалы


1) Программы для общеобразовательных школ, гимназий, лицеев с углубленным и профильным обучением: Математика. 5-11 классы. Составитель Г.М.Кузнецова, Н.Г. Миндюк. 4-е изд. М: Дрофа, 2002.

2) Вестник образования. №2, 2006.

3) Сборник нормативных документов. Математика. Федеральный компонент государственного стандарта. Федеральный базисный план. Москва. Дрофа. 2009.

4) Программно-методические материалы. Математика 5-11классы. Москва. Дрофа. 2002.

Учебно – теоретические материалы


1) А.Н.Колмогоров и др. «Алгебра и начала анализа» учебник для 10-11 классов общеобразовательных учреждений. М.: Просвещение, 2002года.

2) Методическое пособие для учителя. Алгебра 10 класс. Поурочные планы

Автор: Г.И. Григорьева. - Волгоград: Учитель, 2006.

3) Л.С. Атанасян, В.Ф. Бутузов и др. «Геометрия» учебник для 10-11 классов общеобразовательных учреждений. М.: Просвещение, 2002.

4) Книга для учителя. Изучение геометрии в 10-11 классах.

Авторы: С.М. Саакян, В.Ф. Бутузов. – М.: Просвещение, 2004.


Учебно – практические материалы


1) Алгебра и начала анализа. Дидактические материалы для 10-11 классов.

Авторы: М.И.Шабунин, М.В.Ткачева и другие. М: Мнемозина, 2003.

3) Алгебра и начала анализа 10-11 классы. Самостоятельные и контрольные работы.

Авторы: А.П.Ершова, В.В.Голобородько. М: Илекса, 2005.


Учебно – справочные материалы


1) Математический энциклопедический словарь. Москва. Советская энциклопедия,1995.

2) ЕГЭ справочник по математике. Теоретический минимум для подготовки к ЕГЭ.М:

Е-Медиа, 2003.


Учебно – наглядные материалы


1) Плакаты по темам.

2) Мультимедиотека.