Удк 681. 3 Сидоров М. Е., Трушин О. В. Школа работы на ibm pc. Часть Уфа, 1996. с

Вид материала

Содержание

Уравнение прямой, проходящей через две точки "1" и "2"
Уравнение прямой в общем виде
2. 1. 4. Построение касательных и нормалей к плоским кривым
Уравнение касательной к кривой имеет вид
Алгоритм построения касательной к кривой
2. 1. 5. Двумерные преобразования координат
Procedure i_r
Procedure mult

Подобный материал:

1 ... 11 12 13 14 15 16 17 18 ... 21

Практическое задание N 2. 6

1. Определить графическим методом корни уравнения F(X)=0, заданного в таблице задания N . Сложную функцию разбить на две, например: Y1=X-2; Y2=4*Sin(x); и определить точку пересечения кривых.

2. 1. 3. Уравнение прямой на плоскости

При решении различных задач конструирования используются графические редакторы и специальные программы автоматизированного конструирования. С помощью таких программ можно рисовать на экране различные рисунки, эскизы деталей. В программах графического редактора используются формулы из аналитической геометрии на плоскости и в пространстве. Приведем уравнения, позволяющие строить простейшие фигуры на плоскости. Пусть на плоскости задана правая прямоугольная система координат XoY.

Уравнение прямой, проходящей через две точки "1" и "2":

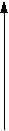y2

* (Xt, Yt)

1

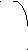
y1 alf

0 x1 x2 X

y = F(x) = D*(x-x1)+y1; или y = D*x+D1;

где D = tg(alf) = (y2-y1)/(x2-x1); D1=y1-D*x1;

Уравнение прямой в общем виде:

F(x,y) = A*x + B*y + C = 0;

где A= y2-y1; B=-(x2-x1); C= -A*x1 - B*y1;

Рассмотрим задачи, связанные с определением принадлежности точки с координатами (Xt, Yt) области, ограниченной заданной прямой Y=F(x).

При Yt > Y = F(Xt) получаем:

Yt > D*(Xt-x1)+y1; или F(x,y)= A*Xt + B*Yt + Ci > 0; где (B > 0)

- неравенства, определяющие область точек (Xt, Yt), лежащих выше прямой Y=Fi(x).

Для прямой, параллельной оси "Y" при Xt>x1 - точки лежат правее прямой x=x1.

118

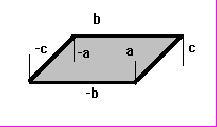
Приведем неравенства, определяющие область точек (Xt, Yt) фигур:

a) прямоугольник: |Yt| площадь S=4*a*b;

b) ромб: a*|Yt|+b*|Xt| площадь S=2*a*b;

c) параллелограмм: |Yt|

площадь S=2*b*(a+c);

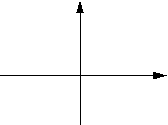
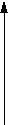
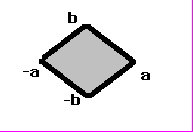
b

-a a

-b

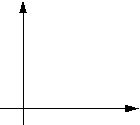
Рассмотрим область треугольника, заданного координатами трех вершин:

1 - (x1, y1), 2 - (x2, y2), 3 - (x3, y3). Площадь треугольника:

S = 0. 5*abs((x1-x2)*(y1+y2)+(x2-x3)*(y2+y3)+(x3-x1)*(y3+y1))

Пусть прямая F₁(x,y)=0 проходит через точки 1 и 2. Точка (Xt, Yt), лежащая внутри треугольника находится с той же стороны, что и точка 3, тогда неравенства для обоих точек имеют одинаковый знак, т. е. их произведение положительно:

2

1 * (Xt, Yt)

3

F₁(Xt,Yt)* F₁(x3,y3) > 0

Аналогично для других сторон треугольника, получаем:

F₂(Xt,Yt)* F₂(x1,y1) > 0

F₃(Xt,Yt)* F₃(x2,y2) > 0

Выполнение трех неравенств определяет точку в треугольнике.

Практическое задание N 2. 7

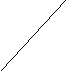
y0

x0

1. Рассчитать число попаданий при стрельбе в прямоугольник, параллелограмм, ромб, смещенные на x0, y0 и в треугольник, заданный координатами своих вершин. Фигуры находятся внутри круга радиуса R. Разброс точек равномерный по площади круга: угол f=2*Pi*Random; радиус r=R*Random. Сравнить число попаданий с теоретической вероятностью, равной отношению площади фигуры к площади круга. При визуализации стрельбы точки, попавшие в мишень, отмечать другим цветом.

2. 1. 4. Построение касательных и нормалей к плоским кривым

Для проведения касательной к кривой необходимо задать уравнение кривой в каком либо виде: Y=F(x); или F1(x, y)=0; или X=Fx(t); Y=Fy(t); и координаты точки на кривой (xi, yi).

119

Уравнение касательной к кривой имеет вид:

(x-xi)*dY/dx =(y-yi); или (x-xi)*dFy/dt = (y-yi)*dFx/dt;

где dY/dx = dF(x)/dx = - (F1(x, y)/x)/(F1(x, y)/y);

Уравнение нормали к кривой имеет вид:

(x-xi) = -(y-yi)*dY/dx; или (x-xi)*dFx/dt = -(y-yi)*dFy/dt;

Пусть уравнение кривой имеет вид: X=A*cos(t); Y=B*sin(t); - эллипс. Алгоритм построения касательной к кривой в расчетной области X_Min<=x<=X_Max , Y_Min<=y<=Y_Max следующий.

1) Находим производные dFx/dt=-A*sin(t); dFy/dt=B*cos(t).

2) В области изменения параметра "t" задаем ti и определяем координаты точки Xi, Yi и производные dXi= (dFx/dt)_i, dYi= (dFy/dt)_i в точке "ti".

3) Находим точки "1" и "2" пересечения касательной с границами расчетной области:

при dXi<>0 полагаем x1=x_Min и находим y1=(x1-xi)*dYi/dXi + yi;

если y1< y_Min, то y1=y_Min и определяем x1= (y1-yi)*dXi/dYi + xi;

если y1> y_Max, то y1=y_Max и определяем x1= (y1-yi)*dXi/dYi + xi;

аналогично, при dXi<>0 полагаем x2=x_Max и находим y2 по приведенной выше схеме с корректировкой значений y2 и x2.

При dXi=0 полагаем x1=xi и y1=y_Max и x2=xi и y2=y_Min.

4) Через точки "1" и "2" проводим прямую.

L

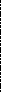
Yi

L

Xi

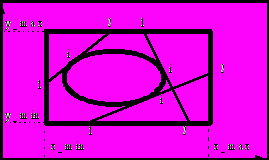
Несколько проще алгоритм построения касательной постоянной длины "2*L" к плоской кривой. В этом случае:

при dXi<>0 находим alf=arctg(dY/dx)_i; иначе alf=90⁰; и определяем:

x1 = xi + L*cos(alf); y1 = yi + L*sin(alf);

x2 = xi - L*cos(alf); y2 = yi - L*sin(alf);

При построении нормали используется уравнение нормали к кривой и приведенные выше алгоритмы.

Практическое задание N 2. 8

В заданной прямоугольной области построить серию касательных, либо нормалей к плоским кривым: эллипсу, параболе, гиперболе и т. п.

120

2. 1. 5. Двумерные преобразования координат

Преобразование координат графических объектов используется с целью модификации, зеркального отображения и перемещения объекта. Основные случаи :

- преобразование системы координат, например, из полярной в декартову,

- изображение типовых или повторяющихся деталей объекта,

- построение проекций трехмерных объектов,

- направленная деформация при синтезе новых форм,

- мультипликация и создание узоров.

Различают двумерные ( 2D ) и трехмерные ( 3D) преобразования. Рассмотрим двумерные аффинные преобразования, когда в получаемом новом изображении объекта сохраняется прямолинейность и параллельность прямых, а также деление отрезков в заданных соотношениях.

Общий вид формул двумерных аффинных преобразований:

x₁= a₁₁ x + a₁₂ y + a₁₃или в x₁ a₁₁ a₁₂ a₁₃ x

матричном y₁ = a₂₁ a₂₂ a₂₃ * y

y₁= a₂₁ x + a₂₂ y + a₂₃виде: z₁ 0 0 1 z

Здесь x, y - координаты исходного, а x₁, y₁ - преобразованного объекта.

Коэффициенты преобразований a _{I J}сохраняют в виде матрицы, расширенной до квадратной, - при для вычисления коэффициентов составного преобразования перемножают соответствующие матрицы коэффициентов типовых преобразований.

Примеры типовых преобразований и соответствующие им матрицы:

( Ф - исходная фигура, Ф₁ - преобразованная )

Y

dx Ф₁ Параллельный 1 0 dx

dy перенос 0 1 dy

Ф 0 0 1

X

Y

Ф₁ Масштабирование Sx 0 0

Sx = x₁/x; Sy = y₁/y 0 Sy 0

Ф 0 0 1

X

Y

Ф₁

Поворот относительно cos a -sin a 0

начала координат sin a cos a 0

Ф 0 0 1

a

X

121

Зеркальное отображение:

Y

Ф₁ cos(2*A) sin(2*A) 0

относительно оси Y=Х sin(2*A) - cos(2*a) 0

Ф проходящей под углом “A” 0 0 1

₀ X

Ф₁ относительно начала -1 0 0

координат 0 -1 0

0 0 1

Y

Y₁

a Ф₁

Деформация сдвига : 1 tg(a) 0

Ф X₁ в направлении X - a tg(b) 1 0

в направлении Y - b 0 0 1

b

X

Составные преобразования обычно представляют в виде комбинаций типовых преобразований. Например, поворот относительно произвольной точки ( Xc, Yc) можно представить как комбинацию трех преобразований:

- параллельный перенос, переводящий центр поворота в начало координат,

- поворот относительно начала координат,

- параллельный перенос, противоположный первоначальному.

Перемножение матриц выполняется следующим образом:

a₁₁ a₁₂ a₁₃b₁₁ b₁₂ b₁₃c₁₁ c₁₂ c₁₃

a₂₁ a₂₂ a₂₃ * b₂₁ b₂₂ b₂₃ = c₂₁ c₂₂ c₂₃

a₃₁ a₃₂ a₃₃b₃₁ b₃₂ b₃₃c₃₁ c₃₂ c₃₃

где c_I_J= a_I₁*b₁_J+ a_I₂*b₂_J+ a_I₃*b_J₃ , i= 1, 2, 3; j= 1, 2, 3.

то есть элемент матрицы “C”, расположенный в I-строке и J-столбце, равен сумме произведений элементов I -ой строки матрицы “A“ на соответствующие элементы J-го столбца матрицы B.

В приведенной ниже программе плоская фигура задается в виде линий, последовательно соединяющих координаты массива точек (xa, ya) на чертеже ( x, y - в системе координат экрана ). Эти координаты подвергаются аффинным преобразованиям, коэффициенты преобразования хранятся в двумерном массиве r. Начальному положению фигуры соответствует единичная матрица R (единицы на главной диагонали, остальные члены - нули). При очередном преобразовании коэффициенты матрицы R пересчитываются путем умножения на нее матрицы этого преобразования (А), получаемая матрица (В) снова записывается в R. Новые координаты x, y высчитываются в процедуре NEW_XY, которая вызывается непосредственно при выводе фигуры на экран процедурой PICTURE.

122

uses Graph, Crt; {------- Аффинные преобразования плоских фигур -------- }

var Gd,Gm,n,i,j,k,l,m,xc,yc,xc1,yc1: integer; {-- описание --}

{ глобальных переменных}

xa, ya: array[1..50] of real; { исходные координаты фигуры }

x, y : array[1..50] of integer; { новые координаты фигуры }

a, b, r: array[1..3, 1..3] of real; { массивы коэффициентов матриц 3*3 }

PROCEDURE I_R; {-------- присвоение матрице R значения единичной ---------}

begin

for i:=1 to 3 do begin { 1 0 0 }

for j:=1 to 3 do r[i, j]:=0; { 0 1 0 }

r[i, i]:=1; end; { 0 0 1 }

end;

PROCEDURE MULT; {---------- умножение матриц А и R: R = B = A*R ------------}

var z: real;

begin

for i:=1 to 3 do

for j:=1 to 3 do begin z:=0;

for k:=1 to 3 do z:=z+a[i,k]*r[k,j];

b[i,j]:=z end;

for i:=1 to 3 do

for j:=1 to 3 do r[i,j]:=b[i,j] end;

PROCEDURE MOVE(dx,dy:real); {----расчет матриц А и R для переноса фигуры ---}

begin { ---на dx, dy--- }

for i:=1 to 3 do begin { 1 0 dx }

for j:=1 to 3 do a[i,j]:=0; { 0 1 dy }

a[i,i]:=1 end; { 0 0 1 }

a[1,3]:=dx; a[2,3]:=dy;

MULT; end;

PROCEDURE SCALE(sx,sy:real); {-расчет матриц А и R для масштабирования ----}

begin {--фигуры: по оси Х - умножение на sx, по оси Y - на sy --}

for i:=1 to 3 do

for j:=1 to 3 do a[i,j]:=0; { sx 0 0 }

a[1,1]:=sx; { 0 sy 0 }

a[2,2]:=sy; a[3, 3]:=1; { 0 0 1 }

MULT; end;

PROCEDURE ROTATE(alfa: real); {- расчет матриц А и R для поворота фигуры--}

Blog

Удк 681. 3 Сидоров М. Е., Трушин О. В. Школа работы на ibm pc. Часть Уфа, 1996. с

Содержание