Дорог задана квадратной матрицей порядка n, элемент а
| Вид материала | Документы |
- Операции: слушать и слышать коллег, подвергая услышанное анализу, 8.68kb.
- Строительные нормы и правила российской федерации автомобильные дороги, 1207.85kb.
- Краткая информационная справка о состоянии сети автомобильных дорог Нижегородской области, 66.07kb.
- Компания «Элемент Лизинг» предоставляет финансирование на покупку любых автомобилей, 9.9kb.
- Новосибирский Государственный Технический Университет Кафедра прикладной математики, 194.71kb.
- В 1817 г шведский химик А. Арфведзон, производя анализ сравнительно редкого минерала, 29.8kb.
- Учебный элемент 11, 54.1kb.
- Лекция 3, 169.64kb.
- Документ содержит указания по конструированию и расчету нежестких дорожных одежд автомобильных, 3047.06kb.
- Контрольная работа №1 «Основные понятия языка Паскаль», 83.52kb.
1. Дано натуральное число n. Сколько различных цифр встречается в его десятичной записи?
2. Имеется n городов. Некоторые из них соединены дорогами известной длины. Вся система дорог задана квадратной матрицей порядка n, элемент аij которой равен некоторому отрицательному числу, если город i не соединен напрямую дорогой с городом j и равен длине дороги в противном случае (i, j=1,...,n).
а) Для 1-го города найти кратчайшие маршруты в остальные города.
б) В предположении, что каждый город соединен напрямую дорогой с каждым, найти кратчайший маршрут, начинающийся в 1-м городе и проходящий через все остальные города.
3. Найти такую расстановку пяти ферзей на шахматной доске, при которой каждое поле будет находиться под ударом одного из них.
4. Дано натуральное число n.
А) Выяснить, входит ли цифра 3 в запись числа n2.
б) Поменять порядок цифр числа n на обратный.
в) Переставить первую и последнюю цифры числа n.
г) Приписать по единице в начало и в конец записи числа n.
5. Алгоритм Евклида нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел основан на следующих свойствах этой величины. Пусть т и n — одно временно не равные нулю целые неотрицательные числа и пусть m≥n. Тогда, если n = 0, то НОД (n, т) = т, а если n≠0, то для чисел m, n и r, где r—остаток от деления m на n, выполняется равенство НОД (m, n) = НОД(n, r). Например, НОД(15, 6) = НОД(6, 3) = НОД(3, 0) = 3. Даны натуральные числа n, m.
а) Используя алгоритм Евклида, найти наибольший общий делитель n и m.
б) Найти наименьшее общее кратное n и m. (Как здесь может помочь алгоритм Евклида?)
6.Даны натуральное число n, действительные числа a1,...,an. В последовательности a1,...,an, определить число соседств:
а) двух положительных чисел;
б) двух чисел разного знака;
в) двух чисел одного знака, причём модуль первого числа должен быть больше модуля второго числа.
7. Дано действительное число X. Не пользуясь никакими другими арифметическими операциями, кроме умножения, сложения и вычитания, вычислить 2x4-3x3+4x2-5x+6. Разрешается использовать не более четырёх умножений и четырёх сложений и вычитаний.
8. Даны действительные числа c,d. Вычислить
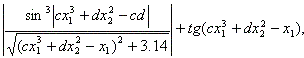
где x1 - больший, а x2 - меньший корни уравнения x2 - 3x - |cd| = 0
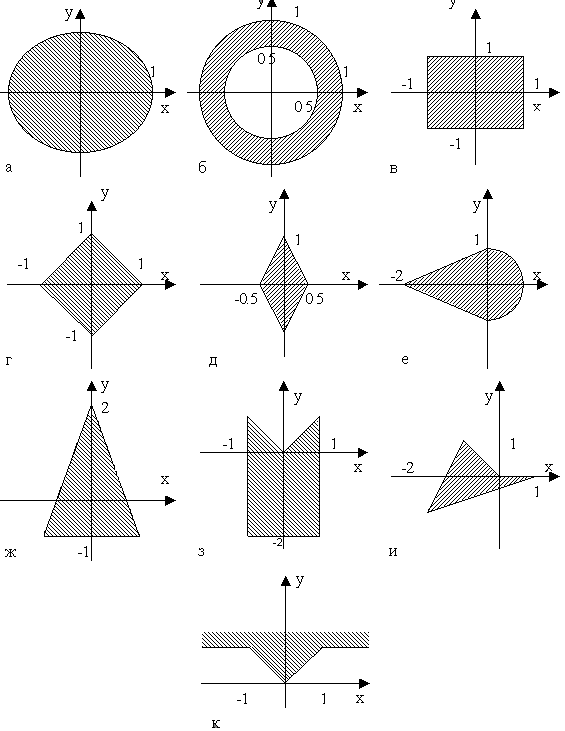
9. Даны действительные числа x, y. Определить под к), принадлежит ли точка с координатами x, y заштрихованной части плоскости
(рис.2, а - к).
10. Дано натуральные число n. Можно ли представить его в виде суммы трех квадратов натуральных чисел? Если можно, то
а) указать тройку х, у, z таких натуральных чисел, что n = x2 + y2 + z2;
б) указать все тройки х, у, z таких натуральных чисел, что n = x2 + y2 + z2.
11. Дано натуральное число n. Вычислить под г):
a)
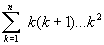 ;
;б)
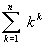 ;
;в)
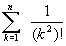 ;
;г)
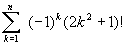 ;
; 12. Даны натуральное число m, действительные числа a1,..., a30 (числа a1,...,a30 попарно различны, m≤30). В последовательности a1,...,a30 поменять местами наибольший член и член с номером m.
