«Площади»
| Вид материала | Документы |
- ТемЫ рефератов по мерчендайзингу, 204.9kb.
- Разработка урока по теме «Понятие площади многоугольника», 32.86kb.
- Механика Жидкостей и Газов, 12.81kb.
- Блиц (матан и триг.) блиц (геометрия) Вопросы по планиметрии, 56.04kb.
- Лабораторная работа №1 Тема: «Разработка простейших программ линейных структур», 169.83kb.
- Городские тематические экскурсии, 85.03kb.
- Урок-сказка по теме "Площади и объемы". 5-й класс, 87.63kb.
- Урок геометрии в 8 классе по теме «Площади многоугольников», 52.25kb.
- Об изучении площади в начальной и средней школе, 56.34kb.
- Доклад заместителя министра лесного хозяйства, 82.14kb.
Разработка урока по алгебре и началам анализа в 10-м классе по теме: "Абсолютная величина в уравнениях"ссылка скрыта Статья отнесена к разделу: ссылка скрыта  “Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду ”. Л.Н.Толстой. Задачи: 1)учить наблюдать, рассуждать, анализировать; 2)учить задавать вопросы, учить сотрудничеству, сотворчеству; 3)учить грамотной математической речи. Ход урока:1) Мотивация учения.Посмотрите друг на друга, улыбнитесь, ведь веселому человеку легче добиться успеха. А успех нам просто необходим. Прочтите эпиграф, т.к. он тесно связан с темой нашего урока “Абсолютная величина в уравнениях”. Она выбрана не случайно. Просмотрев сборники заданий для поступающих в ВУЗы, я увидела, что эта тема встречается на вступительных экзаменах в Академию экономики и управления, в Академию путей сообщения, Техническом университете и т.д. Тема очень важная и не очень простая, поэтому будем учиться решать эту проблему вместе, будем учиться сотрудничеству, сотворчеству, учиться наблюдать, рассуждать, анализировать, делать выводы, учиться грамотной математической речи. И все это для того, чтобы получить хорошие знания. 2) Составление кластера.Сначала систематизируем теоретические знания по этой теме. 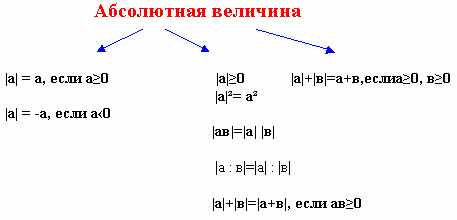 Задание: проследить во время работы на уроке, какие свойства модуля применили при решении уравнений. 3) Работа в группах.Задание №1 (индивидуальное). 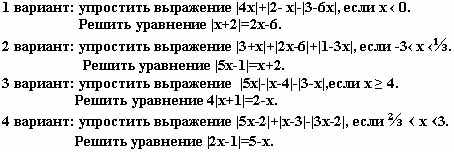 Задание № 2 (работа в группах). 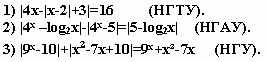 Задание: анализ, решение и проговаривание решений трех уравнений, оформление решений в тетрадях. Задание№ 3: защита решений уравнений у доски. “ Умелый вопрос-это уже добрая половина знаний”. Френсис Бекон. Во время ответов у доски учащиеся в тетрадях расставляют символы: “+” - все понятно и сомнений в решении нет; “?” - совсем непонятно, требуется дополнительное объяснение; “!” - совершено новый материал, ранее неизвестный. При защите решений у доски отвечающего ученика перебивать не разрешается. После ответа каждый ученик имеет право задать вопрос. Причем оценивается не только ответ у доски, но и качественный вопрос с места. В качестве судей выступают учитель, старшие ученики, более подготовленные ученики этого же класса. 4) Рефлексия.А теперь вернемся к кластеру, составленному в начале урока. Какие свойства, записанные в кластере, применили сегодня на уроке при решении уравнений? Составление синквейна (на выполнение задания дается 2-3 мин) Модуль Трудно, но решаемо Раскрыть, найти, проверить В свои силы надо верить Интересно! 5) Домашнее задание.Работа по подготовке к зачету с открытым текстом. Решить уравнения:  Используемая литература:
Урок – деловая игра по геометрии: "Площади многоугольников". 9-й классссылка скрыта Статья отнесена к разделу: ссылка скрыта  Цель: усвоение учащимися формул для вычисления площадей параллелограмма, треугольника, трапеции и применение полученных знаний к решению практических задач. Задачи обучения: Образовательная: проверить степень усвоения учащимися изученного материала; Воспитательная: ориентация учащихся на профессию строителя; Развивающая: практическое применение и развитие логического мышления. Оборудование: персональный компьютер, мультимедиа проектор, карточки с заданиями, магнитофон. Программное обеспечение: школьная программа на домашнем компьютере “Геометрия не для отличников”. Тип урока: комбинированный. Форма проведения: деловая игра. Ход урока.Знакомство со строительным производством, распространенная строительная профессия - столяр (используется дикторский текст, записанный на аудиокассету). Строительное производство сегодня – это механизированный процесс. Непосредственно на строительном объекте столяр устанавливает оконные и дверные блоки, производит настилку дощатых и паркетных полов, монтирует встроенную мебель и т.д. Учитель: Выполнение такой работы невозможно без знания устройства и правила эксплуатации деревообрабатывающих станков, знания технологии и организации строительного производства, умения читать чертежи. Профессия требует объемного воображения, хорошего глазомера, знания геометрии, рисования, черчения. Сегодня все ученики будут выступать в роли строителя. Требуется выполнить работу по настилке полов строящегося детского сада. Но перед тем, как приступить к данной работе, нам необходимо проверить ваши знания формул и применение их при решении задач. Графический диктант с взаимопроверкой.  - высказывание верное - высказывание верное— - высказывание неверное
 Компьютерное тестирование. 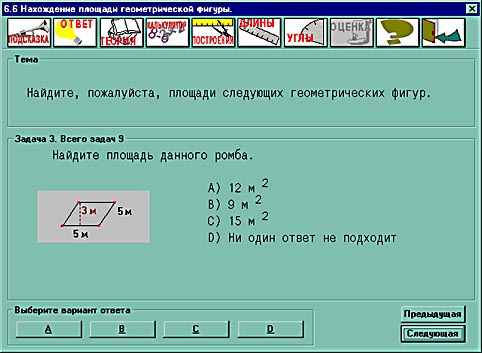  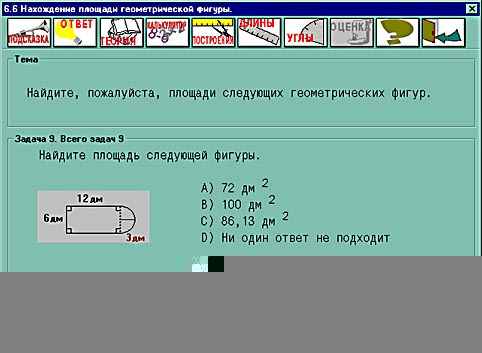 Проверка знаний учащихся по применению формул при решении задач на нахождение площади фигур. (Решение теста учащимися выполняется индивидуально). Выступления учащихся по теме: “Паркетное производство”. Групповая работа: Каждая команда приступает к практическим вычислениям. Вся работа производится двумя командами. Первая команда – столяры. Им нужно изготовить паркетные плитки указанных размеров в таком количестве, чтобы после настилки пола не осталось лишних плиток и число треугольных плиток было минимальным, а плиток в форме параллелограммов и трапеций – одинаковое количество. Вторая команда – поставщики. Им нужно доставить необходимое количество плиток на строительную площадку. Они рассчитывают это количество, сколько и каких паркетных плиток понадобится для покрытия пола. 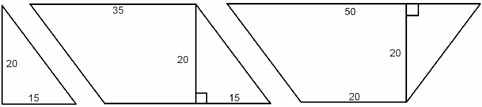 Предлагается произвести настилку паркетного пола в игровом зале размером 5,75 X 8 м. Паркетные плитки имеют форму прямоугольных треугольников, параллелограммов и равнобоких трапеций. Размеры плиток в сантиметрах указаны на рисунке. Итоги работы: слово бригаде, которая первая выполнит правильный расчет. Паркет укладывается в ряды так, что параллелограммы и трапеции чередуются, а треугольников в одном ряду всего два. Подсчеты показывают, что в одном ряду по ширине укладывается по два треугольника и по восемь параллелограммов и трапеций. Действительно, площадь одной полосы шириной 20 см и длиной 575 см будет 11500 см2. Если площадь двух треугольников 300 см2, а площадь параллелограмма или трапеции 700 см2, то в одной полосе по ширине игрового зала поместится по 8 параллелограммов и трапеций: (11500 —300):700= 16. Таких полос в длине комнаты поместится 800:20 = 40. Следовательно, для настилки пола понадобится 80 треугольников и по 320 параллелограммов и трапеций. Проверкой устанавливается: площадь игрового зала 575 X 800 = 460 000 см, площадь одной полосы 575 X 20=11500 см2, а таких полос 40, поэтому 11500X40 = 460 000 см2 — площадь паркетного пола. Подведение итогов урока. Учитель: На этом мы не заканчиваем изучение темы площади. В старших классах познакомимся с площадями объемных фигур. Домашнее задание. Составить задачу по настилке паркетного пола, используя свой набор геометрических фигур. Литература.
ссылка скрыта |
