Geum.ru

Методические указания по выполнению лабораторной работы на пэвм для самостоятельной работы студентов

Вид материалаМетодические указания

Содержание


3-й вариант.
2-й вариант.
3-й вариант.
Подобный материал:
1   2   3   4   5   6

2. Сложные проценты

Сложные проценты применяются в долгосрочных финансово-кредитных операциях (сроком более 1 года), если проценты не выплачиваются периодиче­ски сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процен­тов к сумме, которая служила базой для их определения назы­вают капитализацией процентов.


2.1. Наращение по сложным процентам с постоянной ставкой

Пусть первоначальная сумма долга равна Р, тогда через один год сумма долга с присоединенными процентами составит Р(1+i), через 2 года P(1+i)(1+i)=P(1+i)2, через п лет - P(1+i)n. Таким образом, полу­чаем формулу наращения для сложных процентов:

S = Р (1+i ) n, (11)

где S - наращенная сумма,

i - годовая ставка сложных процентов,

п - срок ссуды,

(1+ i ) n - множитель наращения.

На практике обычно используют дискретные про­центы (проценты, начисляемые за одинаковые интервалы времени: год, полугодие, квартал).


Пример 6. В кредитном договоре на сумму 1 000 000 руб. и сро­ком на 4 года зафиксирована ставка сложных процентов, равная 20% годовых. Определить наращенную сумму.

Известно:

Р = 1 000 000 руб.,

n = 4 года ,

i = 0,20 или 20% .

Найти

S = ? Решение.

1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств. Используем формулу (11):

S = Р (1+ i ) n = 1 000 000*(1+0,2)4 = 2 073 600 руб.

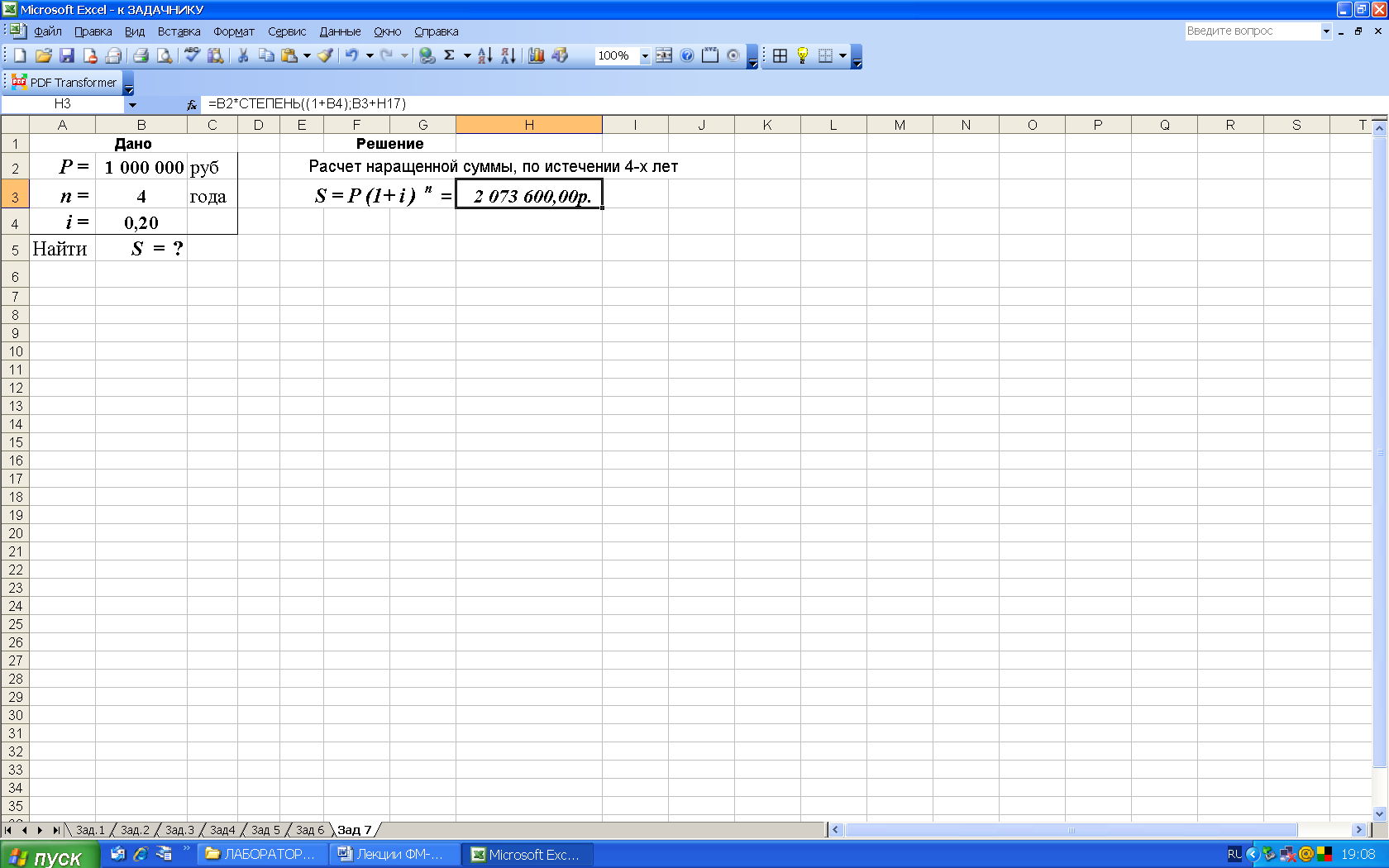
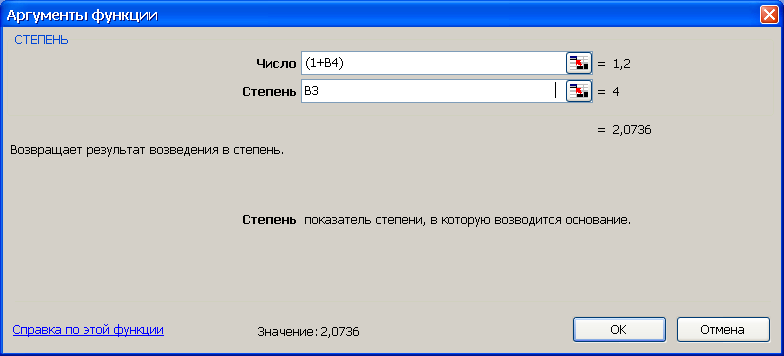
2-й вариант. Для выполнения расчетов по формулам воспользуемся функцией СТЕПЕНЬ (находится в категории Математические). Данная функция возвращает результат возведения в степень, рис.9.



а)



б)

Рис.9. Результаты расчета наращенной суммы S (рис. а) и вид диалогового окна СТЕПЕНЬ с введенными данными (рис. б). В ячейку H3 введена формула =B2*СТЕПЕНЬ((1+B4);B3)

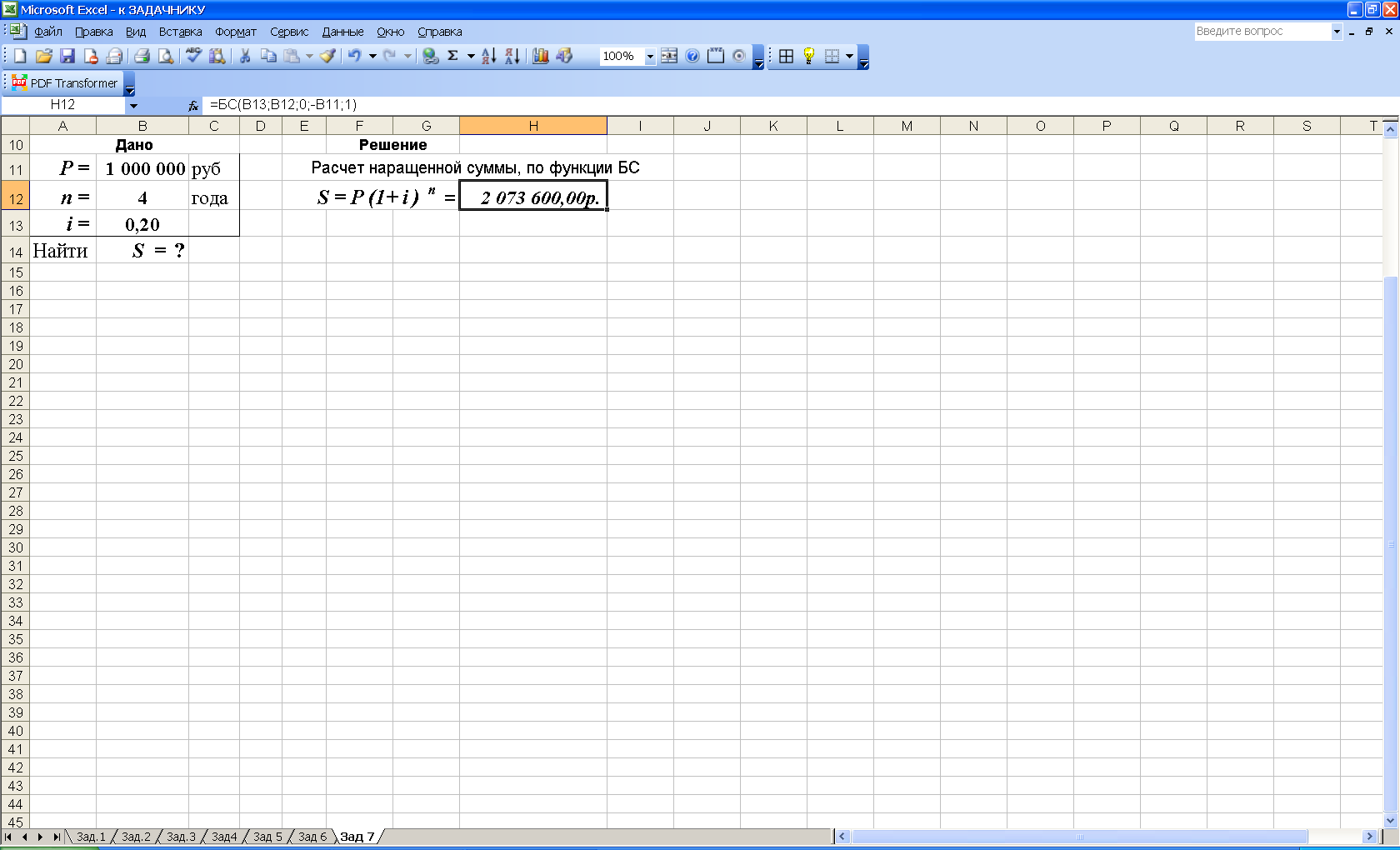
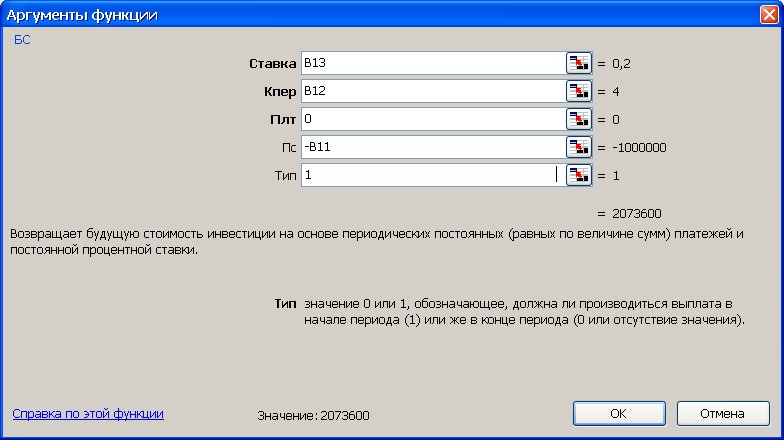
3-й вариант. Для выполнения расчетов по формулам воспользуемся функцией БС (находится в категории Финансовые). Данная функция возвращает результат возведения в степень, рис.10.

Синтаксис функции БС (ставка; кпер; плт; пс; тип). Ее аргументами являются:

ставка – процентная ставка за период;

кпер  – общее число периодов платежей по аннуитету;

плт – выплата, производимая в каждый период, ее значение неизменно в течение всего периода выплат. Обычно плт состоит из основного платежа и платежа по процентам, но не включает других налогов и сборов. Если аргумент опущен, должно быть указано значение аргумента пс.

пс  – приведенная к текущему моменту стоимость или общая сумма, которая на текущий момент равноценна ряду будущих платежей. Если аргумент пс опущен, то он полагается равным 0. В этом случае должно быть указано значение аргумента плт.

тип – число 0 или 1, обозначающее, когда должна производиться выплата (0 - в конце периода 1 - в начале периода) Если аргумент «тип» опущен, то он полагается равным 0.




а)





б)

Рис. 10. Результаты расчета наращенной суммы S по функции БС (рис. а) и вид диалогового окна БС с введенными данными (рис. б). В ячейку H12 введена формула =БС(B13;B12;0;-B11;1)


2.2. Наращение по сложным процентам при изменении ставки во времени

Если ставка сложных процентов меняется во времени, формула наращения имеет следующий вид:




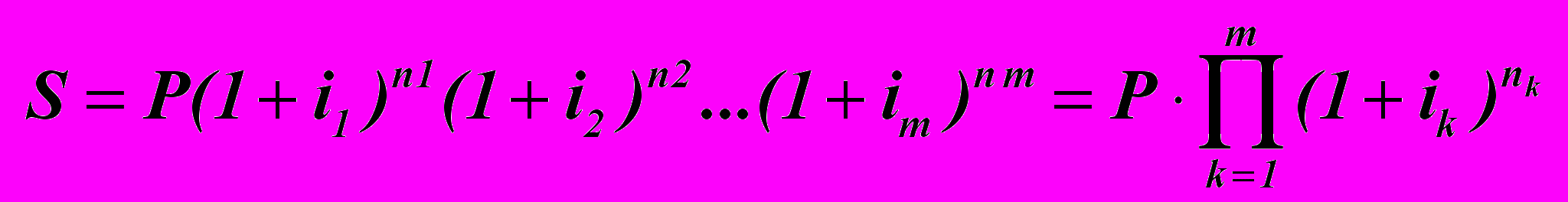
(12)


где i1, i2,..., ik - значения ставок процентов, дейст­вующих в соответствующие периоды n1, п2,..., nk времени.

Пример 7. В финансовом договоре зафиксирована переменная ставка слож­ных процентов, определяемая как 20% годовых плюс маржа 10% в первые два года, 8% - в третий год, 5% - в четвертый год. Опреде­лить величину множителя наращения за 4 года.

Известно:

i1 = 0,20 или 20% ,

Δi1 = 0,10 или 10% ,

n1 = 2 года ,

Δi2 = 0,08 или 8% ,

n2 = 1 год ,

Δi3 = 0,05 или 5% ,

n3 = 1 год .

Найти П(1+ i k )n k = ?

Решение.

1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств по формуле (12):

П(1+ik )n k = (1+0,3)2 *(1+0,28) * (1+0,25)=2,704.

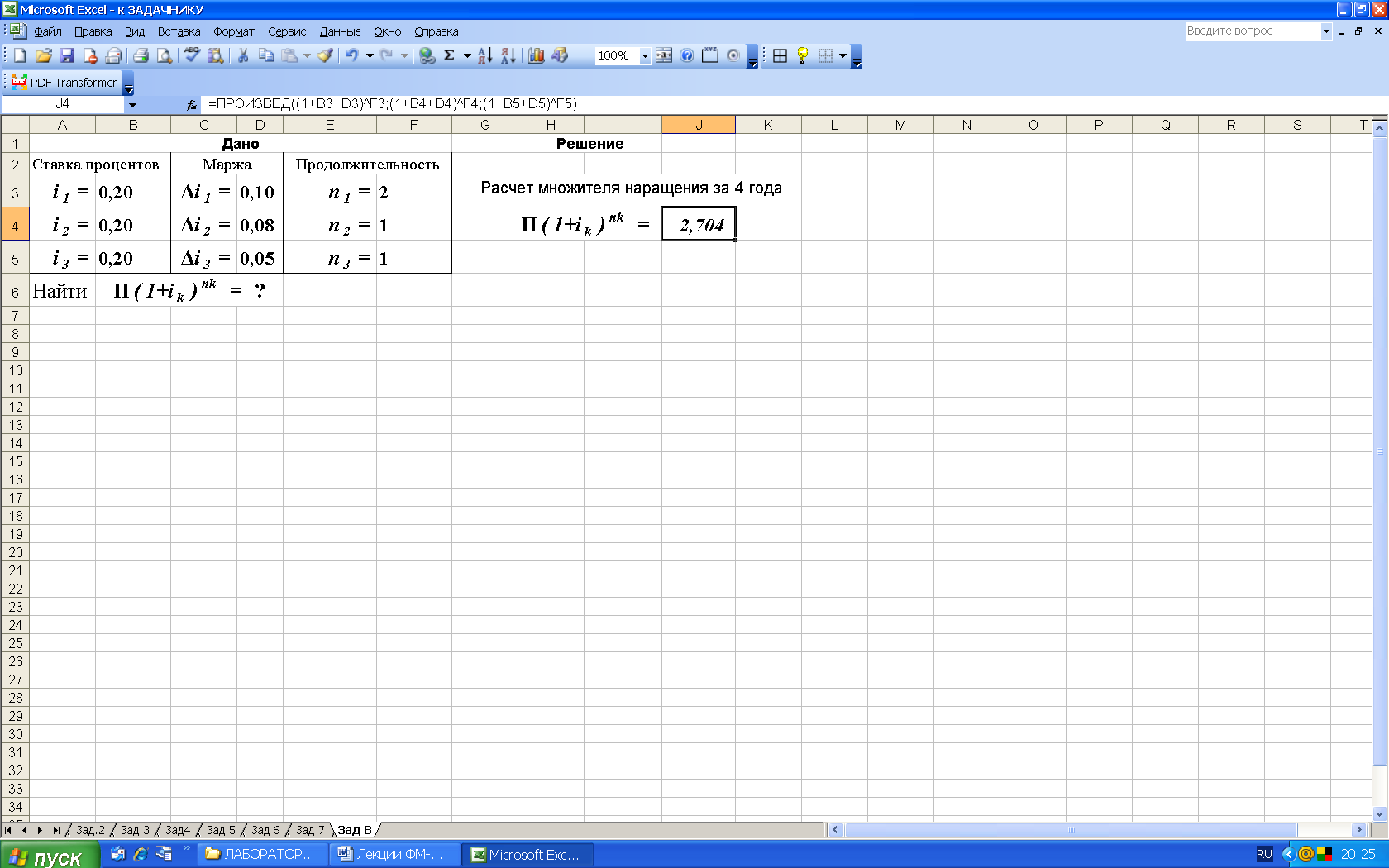
2-й вариант. Для выполнения расчетов по формулам воспользуемся функцией ПРОИЗВЕД (находится в категории Математические). Данная функция возвращает результат возведения в степень, рис.11.



а)



б)

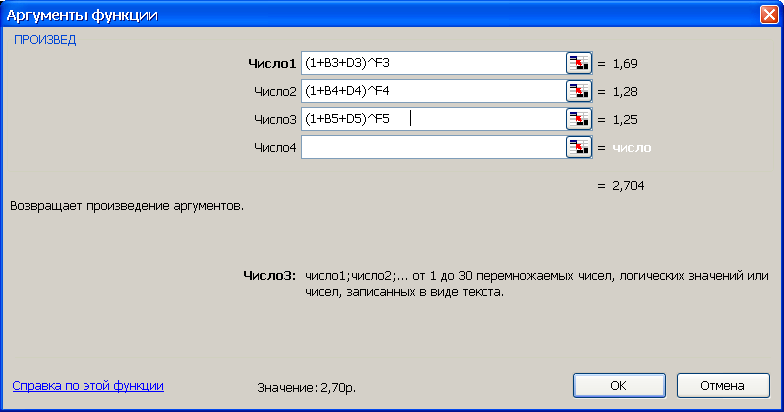
Рис. 11. Результаты расчета множителя наращения (рис. а) и вид диалогового окна ПРОИЗВЕД с введенными данными (рис. б). В ячейку J4 введена формула =ПРОИЗВЕД((1+B3+D3)F3;(1+B4+D4)F4;(1+B5+D5)F5)


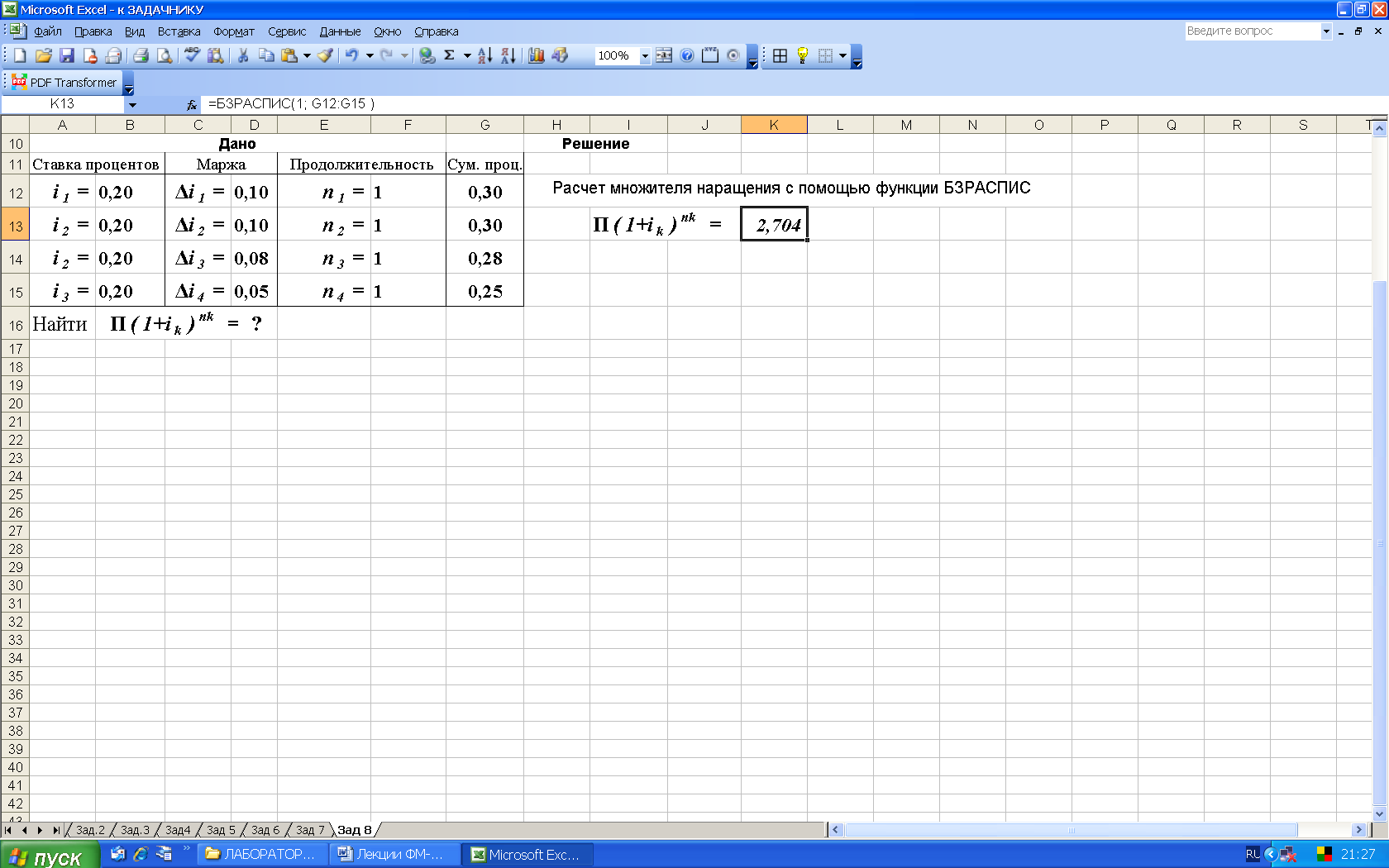
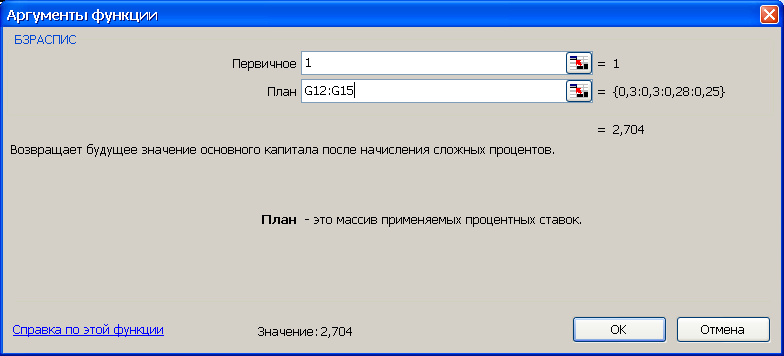
3-й вариант. Предварительно следует подготовить исходные данные по форме представленной на рис. 12а. Для выполнения расчетов следует воспользоваться функцией БЗРАСПИС (находится в категории Финансовые). Данная функция возвращает будущее значение основного капитала после начисления сложных процентов с переменной ставкой, рис.12. Поскольку здесь рассчитывается множитель наращения, то в качестве первоначальной суммы вводится 1 (см. рис 12б).



а)



б)

Рис. 12. Результаты расчета множителя наращения (рис. а) и вид диалогового окна БЗРАСПИС с введенными данными (рис. б). В ячейку J13 введена формула =БЗРАСПИС(1; G12:G15)


Синтаксис функции БЗРАСПИС (первичное; план). Аргументы функции:

первичное – действительное число, задающее первоначальную стоимость инвестиции;

план – массив значений, содержащих процентные ставки.

Напомним, что для вычисления будущей стоимости с постоянной ставкой используется функция БС.


2.3. Номинальная и эффективная ставки процентов


Номинальная ставка. Пусть годовая ставка сложных процентов равна j, а число периодов начисления в году т. При каждом начисле­нии проценты капитализируются, то есть добавляются к сумме с на­численными в предыдущем периоде процентами. Каждый раз про­центы начисляют по ставке j/m. Ставка j называется номинальной. Начисление процентов по номинальной ставке производится по фор­муле:

S=P(1+j / m ) N, (13)

где N - число периодов начисления (N=mn, может быть и дробным числом).

Пример 8. Ссуда 20 000 000 руб. предоставлена на 28 месяцев. Проценты сложные, ставка 18% годовых. Проценты начисляются ежеквартально. Вычислить наращенную сумму по истечении срока.

Известно:

P = 20 000 000 руб.,

j = 0,18 или 18% ,

n = 28 месяцев = 28/12 лет,

m = 4.

Найти S = ?

Решение.

1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств по формуле (13).

Всего за n лет имеем N = mn = 4*(28/12) = 28/3 периодов начислений при ежеквартальном (m = 4) начислении процентов в году. По формуле (13) находим: S = 20 000 000 * (1+ 0,18 / 4 ) (28/3) = 30 161 206,25 руб.

2-й вариант. Для выполнения расчетов воспользуемся функцией СТЕПЕНЬ (из категории Математические). Данная функция возвращает результат возведения в степень, рис.13.




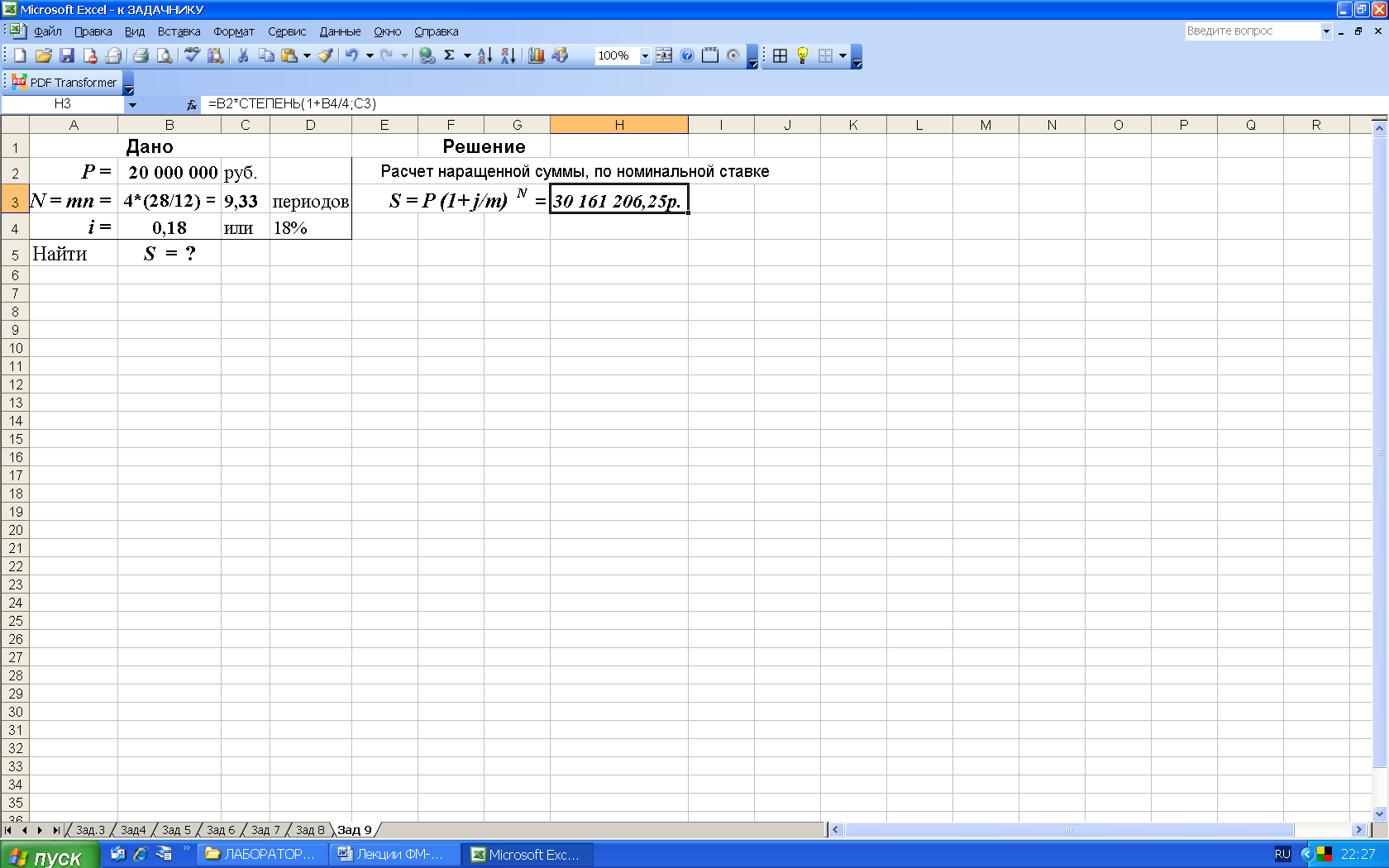
Рис. 13. Результаты расчета наращенной суммы по номинальной ставке. В ячейку H3 введена формула =B2*СТЕПЕНЬ(1+B4/4;C3)


3-й вариант. Вычисления с помощью встроенных функций Excel. Для выполнения расчетов воспользуемся функцией БС (см. категорию Финансовые). Результаты расчета приведены на рис. 14.



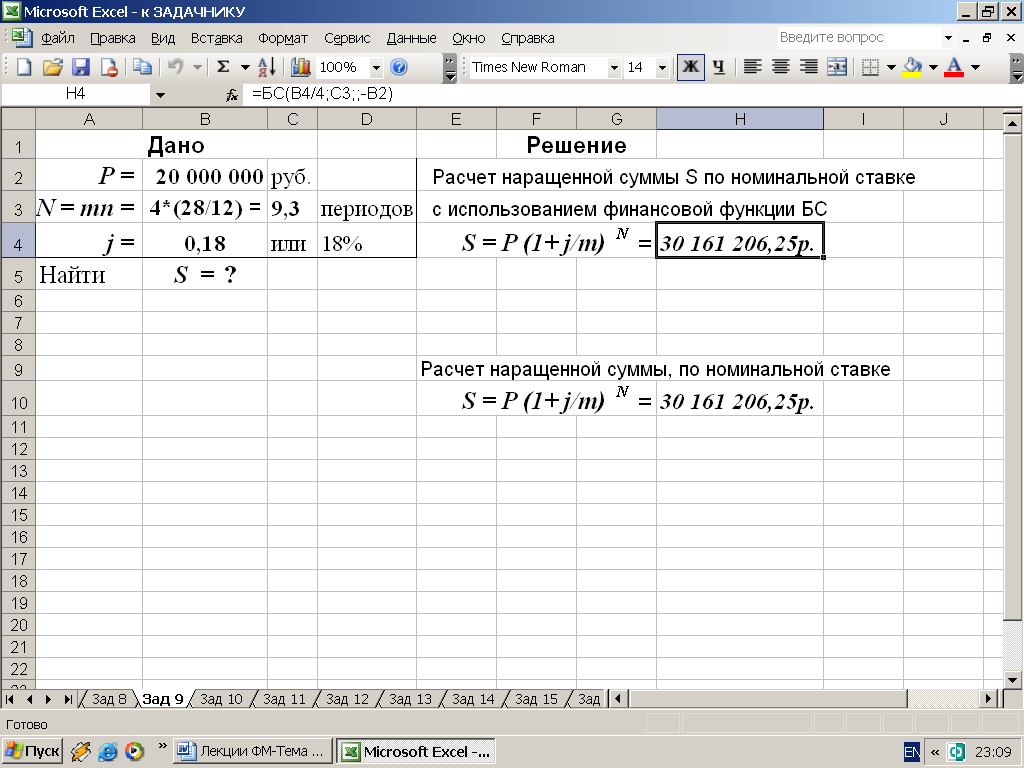
Рис. 14. Результаты расчета наращенной суммы S по номинальной ставке с использованием финансовой функции БС. В ячейку H4 введена формула =БС(B4/4;C3;;-B2).


При финансовом анализе широко используется понятие эффективной ставки. Чем выше эффективная ставка финансовой операции, тем при прочих равных условиях она выгоднее кредитору.


Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m-разовое нара­щение в год по ставке j/m.

Если проценты капитализируются т раз в год, каждый раз со ставкой j/m, то, по определению, можно записать равенство для соот­ветствующих множителей наращения:

(1+ iэ )n = (1+j/m)mn , (14)

где iэ, j - эффективная и номинальная ставки.

Связь между эффективной и номинальной ставками выражается со­отношением

iэ= (1 + j / m)m -1. (15)

Пример 9. Вычислить эффективную ставку процента, если банк начисляет проценты ежеквартально, исходя из номинальной ставки в 16% годовых.

Известно:

j = 0,16 или 16% .

Найти i э = ?

Решение.

1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств проводим по формуле (15):

i э = (1 + j / m)m -1= (1+ 0,16 /4)4 - 1 = 0,170, или 17,0%.

2-й вариант. Расчет эффективной ставки выполним в Excel по формуле (15), результаты расчета представлены на рис. 15.




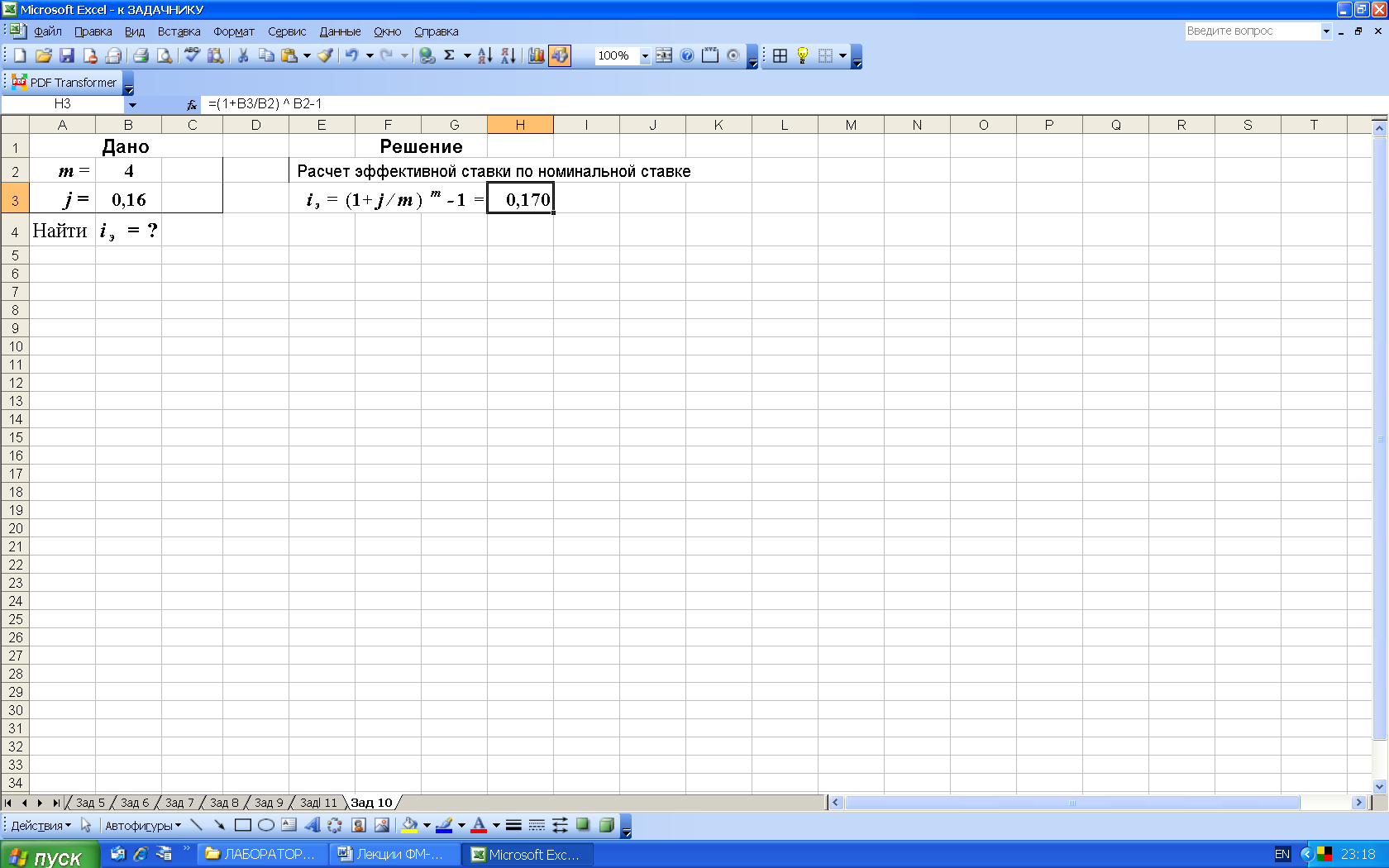
Рис. 15. Результаты расчета эффективной ставки в среде Excel. В ячейку H3 введена формула =(1+B3/B2) B2-1


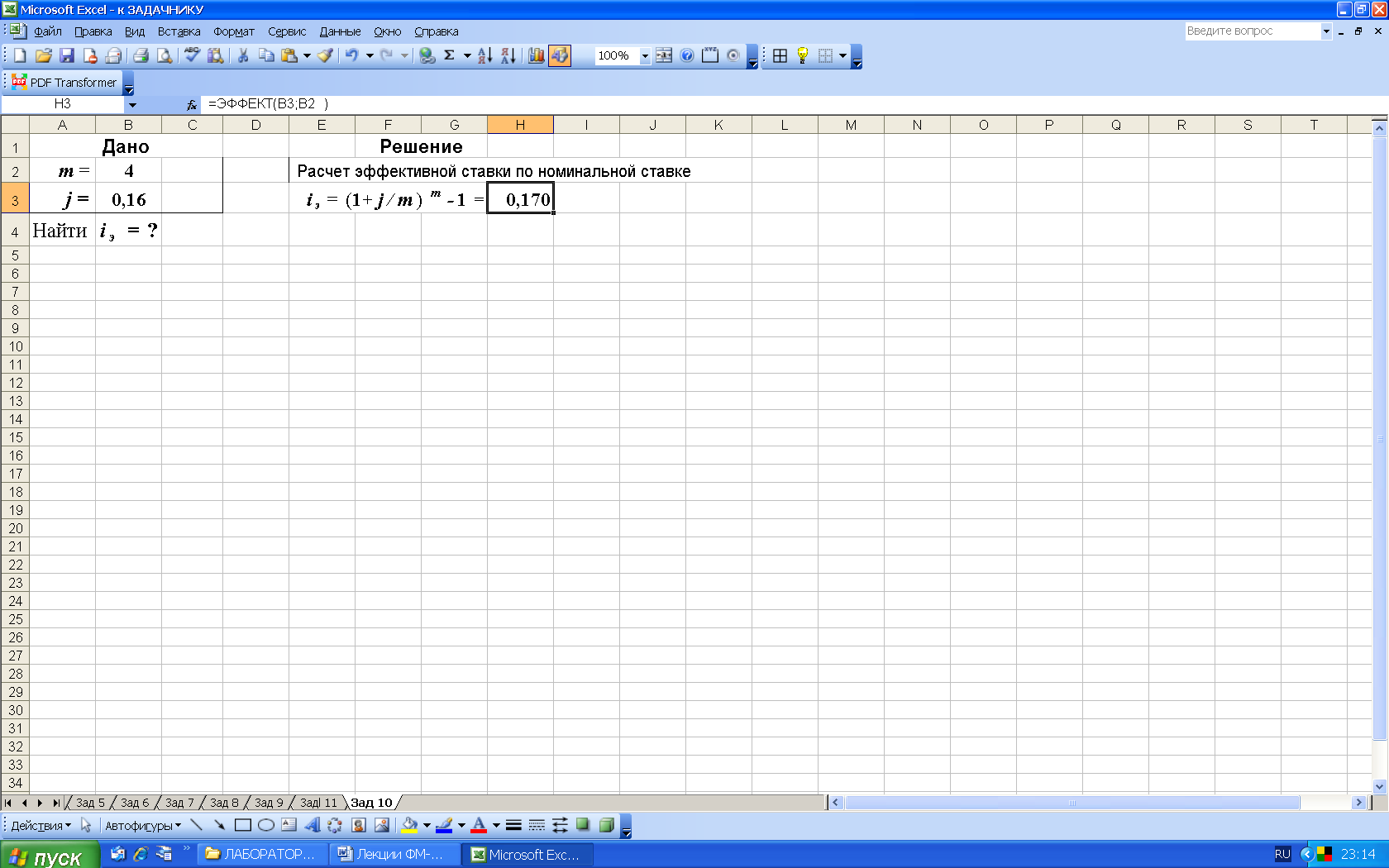
3-й вариант. Расчет эффективной ставки выполним в среде Excel с использованием функции ЭФФЕКТ (из категории Финансовые). Данная функция возвращает эффективную (фактическую) процентную ставку, при заданной номинальной процентной ставке и количестве периодов, за которые начисляются сложные проценты, рис.16.



а)



б)

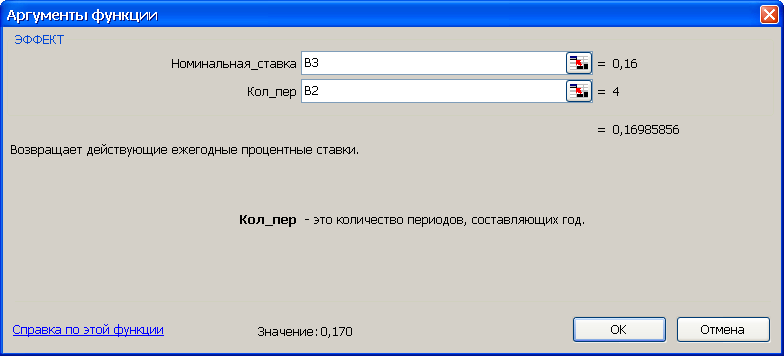
Рис. 16. Результаты расчета эффективной ставки (рис. а) и вид диалогового окна ЭФФЕКТ с введенными данными (рис. б). В ячейку H3 введена формула =ЭФФЕКТ(B3;B2)


Синтаксис функции ЭФФЕКТ (номинальная_ставка;кол_периодов). Аргументы функции:

номинальная_ставка – значение номинальной процентной ставки,

кол_периодов – количество периодов начисления.


Обратная зависимость между номинальной и эффективной ставкой выражена следующей формулой:

j = m [(1+ iэ )1/m-1]. ( 16)


Пример 10. Определить, какой должна быть номинальная став­ка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку в 12% годовых.

Известно:

iэ = 0,12 или 12% .

Найти j = ?

Решение.

1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств произведем по формуле (16):

j = m [(1+ iэ )1/m-1] = 4*[ (1+0,12) (1/4) - 1 ] = 0,11495, или 11,495%.

2-й вариант. Для выполнения расчетов по формулам в среде Excel воспользуемся математической функцией СТЕПЕНЬ, рис. 17.




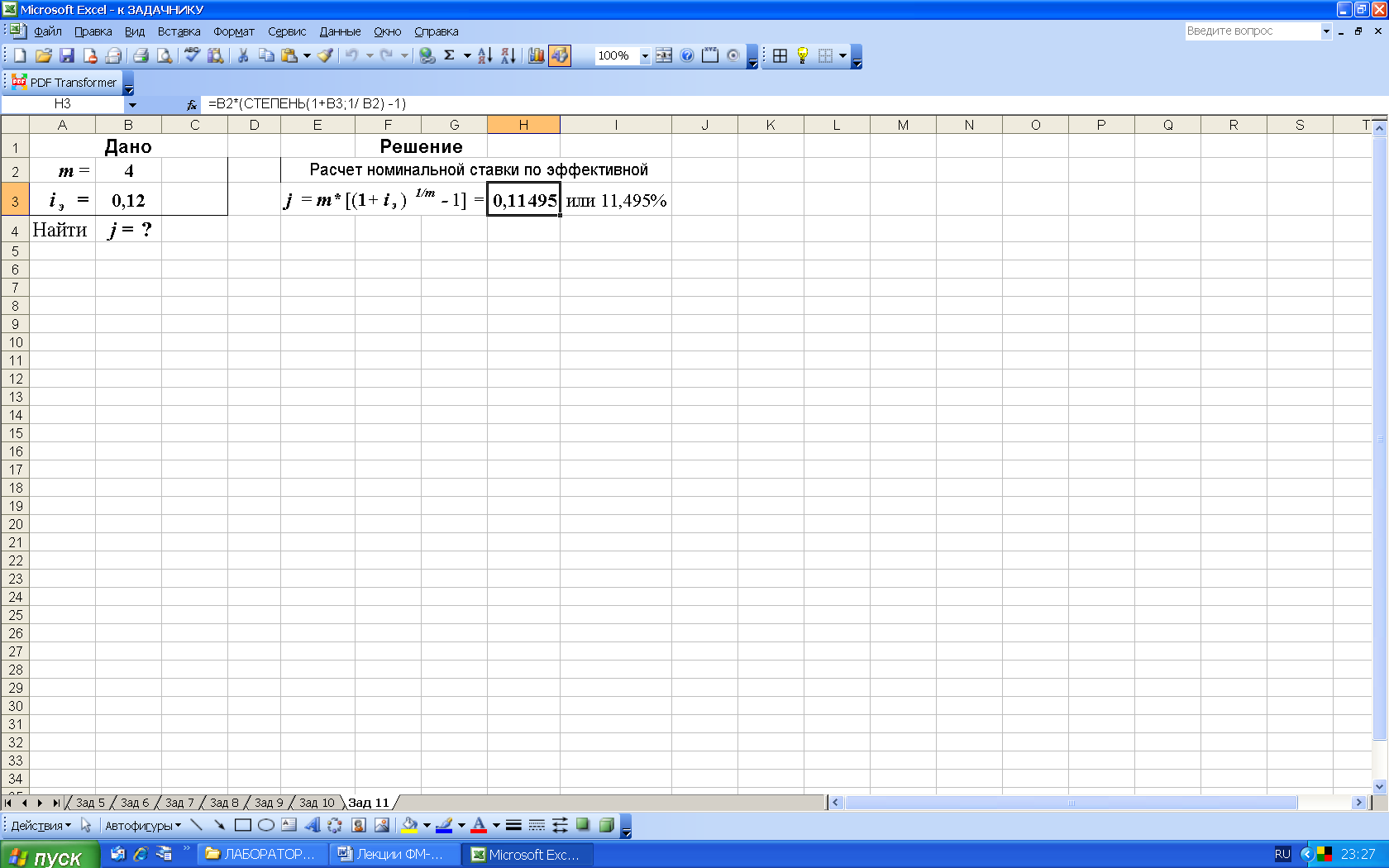
Рис. 17. Результаты расчета эффективной ставки в среде Excel. В ячейку H3 введена формула =B2*(СТЕПЕНЬ(1+B3;1/B2)-1)


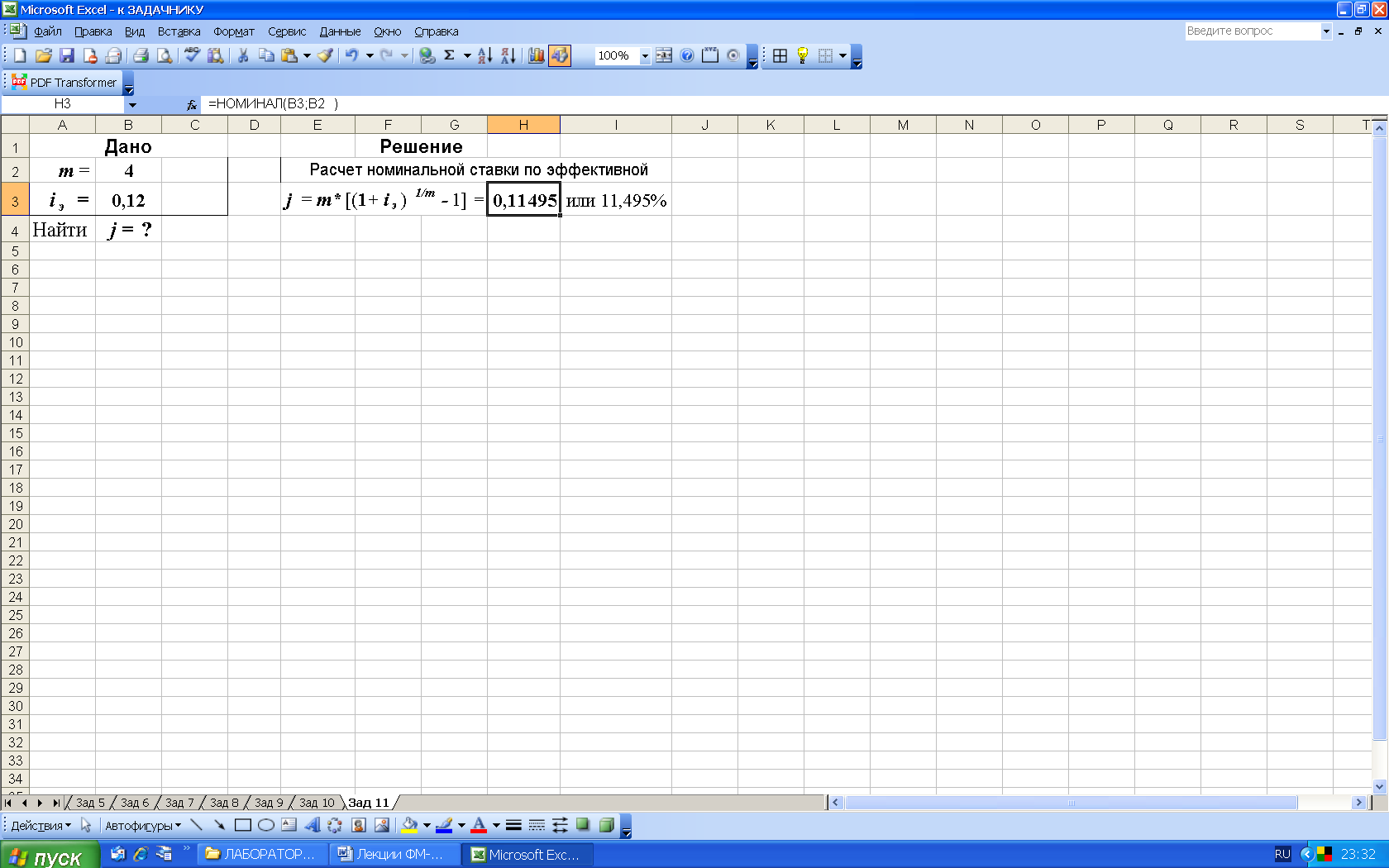
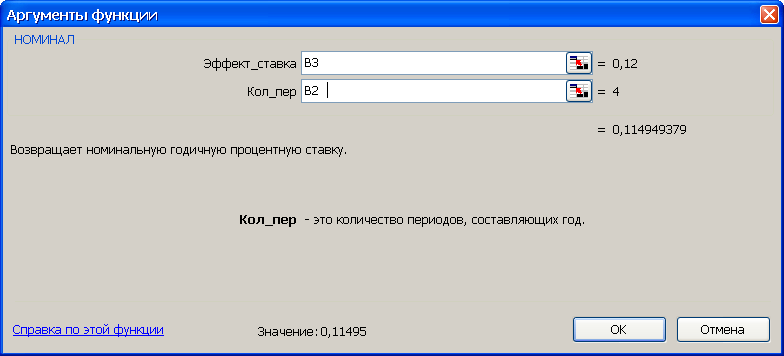
3-й вариант. Для выполнения расчетов номинальной ставки воспользуемся функцией НОМИНАЛ (из категории Финансовые). Данная функция возвращает номинальную годичную ставку при заданной эффективной ставке и числе периодов, за которые начисляются проценты. Результат расчета приведен на 18.



а)



б)

Рис. 18. Результаты расчета номинальной ставки (рис. а) и вид диалогового окна НОМИНАЛ с введенными данными (рис. б). В ячейку H3 введена формула =НОМИНАЛ(B3;B2)

Синтаксис функции НОМИНАЛ (эффект_ставка;кол_пер). Аргументы функции:

эффект_ставка – значение эффективной процентной ставки,

кол_пер – количество периодов начисления.


2.4.Учет (дисконтирование) по сложной ставке процентов

Математический учет. В этом случае решается задача обратная наращению по сложным процентам. Запишем формулу S = P(1 + i )n для наращения по сложной ставке с начислением процентов один раз в год и перепишем ее относительно Р:

P = S/(1 + i ) n = Sν n , (17)

где дробь ν n = 1/(1 + i ) n (18)

является учетным, или дисконтным множителем.


Пример 11. Через 5 лет предприятию будет выплачена сумма 1 000 000 руб. Определить его современную стоимость при условии, что применяется ставка сложных процентов в 14% годовых.

Известно:

n = 5 лет,

S = 1 000 000 руб.,

i = 0,14 или 14% .

Найти P = ?

Решение.

1-й вариант. Вычисления с помощью подручных вычислительных средств выполним по формуле (17):

P = S/(1 + i ) n =1 000 000/(1+0,14) 5 = 519 368,66 руб.

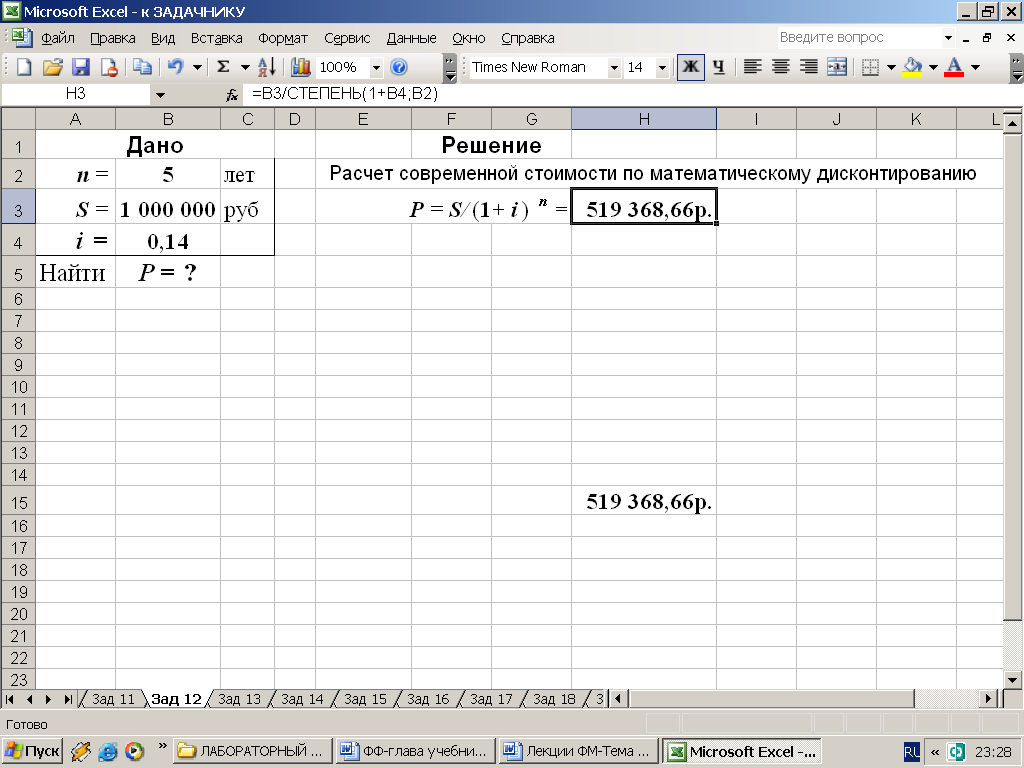
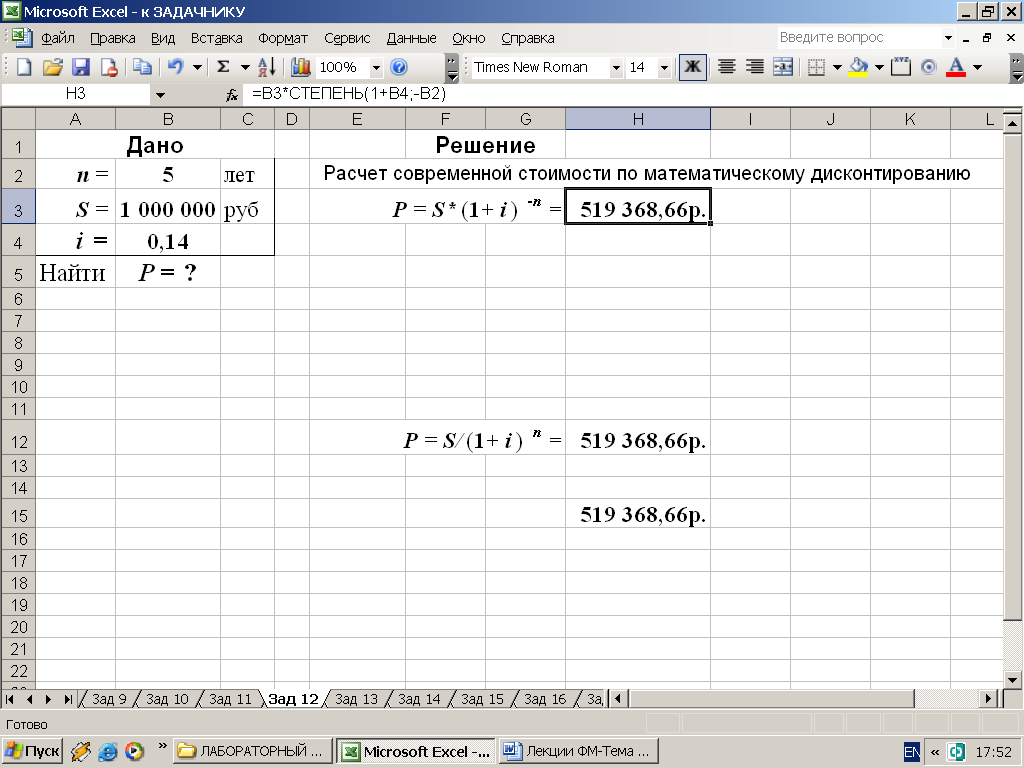
2-й вариант. Для выполнения расчетов в Excel по формулам воспользуемся математической функцией СТЕПЕНЬ. На рис. 19 приведены два варианта использования данной функции.




а)




б)

Рис. 19. Результаты расчета современной стоимости в среде Excel. В ячейку H3 введена формула: вариант а) =B3/СТЕПЕНЬ(1+B4;B2); вариант б) =B3*СТЕПЕНЬ(1+B4;-B2)


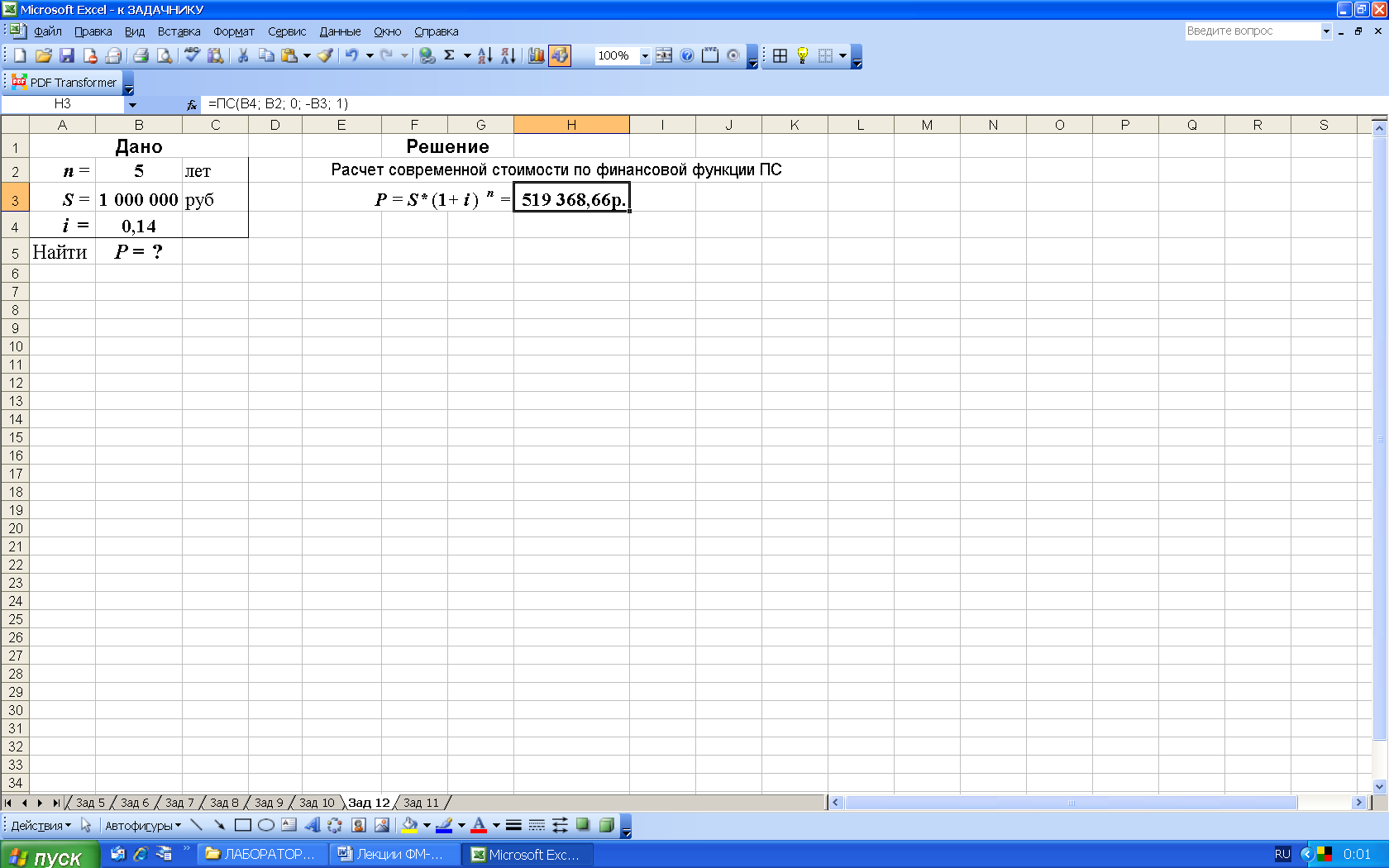
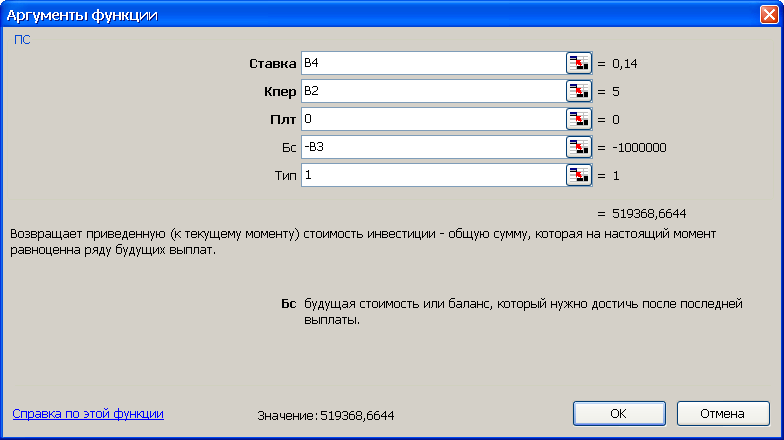
3-й вариант. Для выполнения расчетов по встроенным в Excel функциям воспользуемся финансовой функцией ПС, рис. 20. Данная функция возвращает приведенную стоимость инвестиции при условии периодических равных по величине платежей и постоянной процентной ставки.




а)



б)

Рис. 20. Результаты расчета современной стоимости (рис. а) и вид диалогового окна ПС с введенными данными (рис. б). В ячейку H3 введена формула =ПС(B4; B2; 0; -B3; 1)


Синтаксис функции ПС (ставка;кпер;плт;бс;тип). Аргументы функции:

ставка – значение процентной ставки за один период,

кпер – количество периодов начисления,

плт – величина платежа (можно опускать, когда аргумент принимает нулевое значение),

бс – необязательный аргумент, задает будущую стоимость или остаток средств после последней выплаты;

тип – необязательный аргумент (принимает значения 0, когда выплаты производятся в конце периода, 1- в начале периода).


При начислении процентов т раз в году, используется формула:

P = S / ( 1 + j / m) nm = Sν nm , (19)

где ν nm = 1/(1 + j / m) nm (20)

(дисконтный множитель).

Величину Р, полученную дисконтированием S, называют совре­менной, или текущей стоимостью, или приведенной величиной S.

Суммы Р и S эквивалентны в том смысле, что платеж в сумме S че­рез п лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S - P называется дисконтом.


Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной став­ке осуществляется по формуле:

Р = S(1- dсл )n (21)

где dcл1 - сложная годовая учетная ставка.

Дисконт в этом случае будет равен:

D = S – P = S – S(1- dсл)n = S[1– (1 - dсл)n] (22)

При использовании сложной учетной ставки процесс дисконти­рования происходит с прогрессирующим замедлением, так как учет­ная ставка каждый раз применяется к сумме, уменьшенной за преды­дущий период на величину дисконта.


Пример 12. Через 5 лет по векселю должна быть выплачена сум­ма 1 000 000 руб. Банк учел вексель по сложной учетной ставке в 10% годовых. Определить сумму, которую получит векселедержатель и дисконт, который получит банк по истечении срока векселя.

Известно:

n = 5 лет,

S = 1 000 000 руб.,

i = 0,14 или 14% .

Найти P = ?, D = ?

Решение.

1-й вариант. Вычисления по формулам (21 и 22) с помощью подручных вычислительных средств.

Расчет сумы, которую получит векселедержатель по формуле (21)

Р = S(1- dсл )n = 1 000 000 * (1 - 0,10) 5 = 590 490,00 руб.;

Расчет дисконта, который получит банк, произведем по формуле (22)

D = S - Р = 1 000 000 - 590 490 = 409 510 руб.

2-й вариант. Расчеты в Excel по формулам (21 и 22) с использованием математической функции СТЕПЕНЬ, рис. 21.



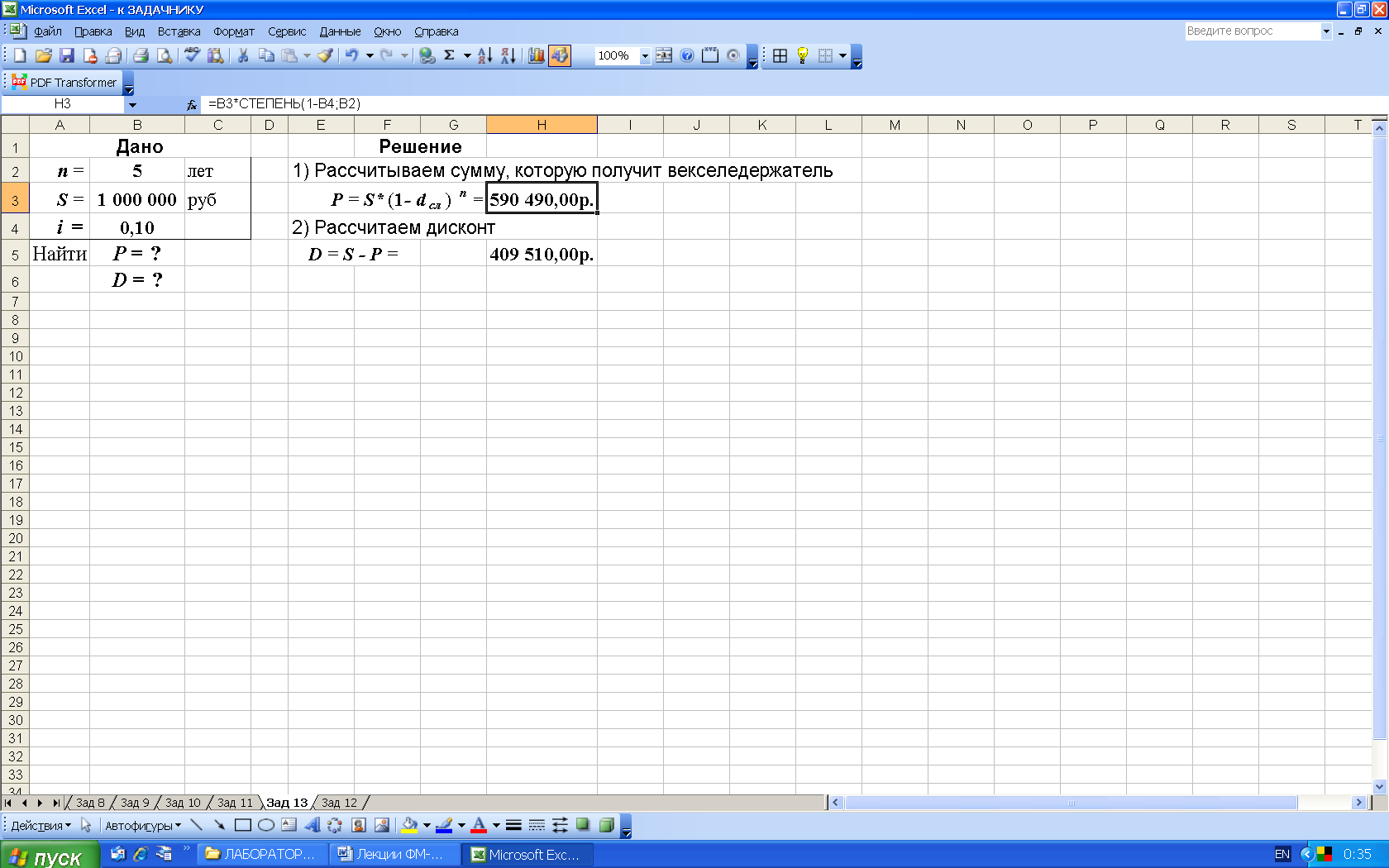
Рис. 21. Результаты расчета значений P и D в среде Excel. В ячейку H3 введена формула =B3*СТЕПЕНЬ(1-B4; B2)