Geum.ru

Финансово-экономические расчеты

Вид материалаЛабораторная работа

Содержание


Краткие теоретические сведения.
Варианты расчета
Подобный материал:
  1   2   3   4   5




Финансово-экономические расчеты.

Лабораторная работа 1.

(4ч)

Простые процентные и учетные ставки.

-расчет простых процентных ставок и суммы процентных денег,

-расчет обыкновенных и точных процентов,

-расчет наращенных сумм по постоянным и переменным простым процентным ставкам,

-математическое дисконтирование,

-определение дисконтной величины по учетной ставке,

-расчет суммы наращивания по простой учетной ставке,

-расчет дисконтной величины по простым процентной и учетной ставкам,

-расчет продолжительности ссуды,

-расчет уровней простых процентной и учетной ставок


Краткие теоретические сведения.

Под процентными деньгами (процентами) в финансовых расчетах понимают абсолютную величину дохода от предоставления денег в долг в любой его форме: выдача денежной ссуды, продажа в кредит, помещение денег на сберегательный счет, учет векселя, покупка сберегательного сертификата или облигаций и т.д.

При заключении финансового или кредитного соглашения стороны (кредитор и заемщик) договариваются о размере процентной ставки - отношения суммы процентных денег, выплачиваемых за фиксированный отрезок времени к величине ссуды.

Интервал, к которому приурочена процентная ставка, называют периодом начисления.

Процесс увеличения суммы денег в связи с присоединением процентов к сумме долга называют наращением, или ростом первоначальной суммы.

Применяют различные виды процентных ставок. Одно из основных отличий связано с выбором исходной базы (суммы) для начисления процентов. Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего срока ссуды (простые процентные ставки) или к сумме с начисленными в предыдущем периоде процентами (сложные процентные ставки).

Начисление процентов, как правило, производится дискретно, причем в качестве периодов начисления принимают год, полугодие, квартал, месяц. Иногда практикуют ежедневное начисление.

Под наращенной суммой ссуды (долга, депозита, других видов инвестированных средств и т.д.) понимается первоначальная ее сумма вместе с начисленными на нее процентами к концу срока.

Наращенная сумма определяется умножением первоначальной суммы ссуды на множитель наращения, который показывает, во сколько раз наращенная сумма больше первоначальной суммы ссуды.

Для записи формулы наращения простых процентов введем обозначения:

P - первоначальная сумма;

S- сумма, образовавшаяся к концу срока ссуды (первоначальная сумма плюс начисленные за весь срок проценты);

i - ставка процентов (в виде десятичной дроби);

I - проценты за весь срок.

Начисленные проценты за один период равны Pi, за n периодов - Pni. Процесс изменения суммы долга с начисленными простыми процентами описывается арифметической прогрессией, члены которой P, P+Pi, P+2Pi, ... ,P+nPi; первый член этой прогрессии равен P, разность Pi, последний член (наращенная сумма) S=P+I=P+nPi=P(1+ni) (формула простых процентов),

(1+ni)-множитель наращения простых процентов.

Пример. Определим проценты и сумму накопленного долга, если ссуда равна 7000 руб., срок долга - 4 года при ставке простого процента, равной 10% годовых.

Находим по формулам: P=7000; n=4; i=0,1; I=nPi=2800; S=9800.

Практика расчета краткосрочных процентов.

В преобладающем числе случаев к наращению по простым процентам прибегают при выдаче краткосрочных ссуд, т.е. ссуд, срок которых равен году или менее его, и в случаях, когда проценты не присоединяются к сумме долга, а периодически выплачиваются. Поскольку ставка процентов обычно устанавливается в расчете за год, то при продолжительности ссуды менее года необходимо выяснить какая часть процента уплачивается кредитору.

Величину n выразим в виде дроби: n=t/K, где t - число дней ссуды, K - число дней в году (временная база). Дата выдачи ссуды и дата погашения считается за один день.

Варианты расчета K:

K=360 (12 месяцев по 30 дней) - обыкновенный процент;

K=365 (366) - точный процент.

Варианты расчета t:

приближенный, если t определяется количеством месяцев и дней ссуды, а месяц принимается равным 30 дням;

точный, если подсчитывается фактическое число дней между двумя датами.

Подсчет точного числа дней между двумя датами существенно упрощается, если воспользоваться специальной таблицей, в которой показаны порядковые номера каждого дня года: из номера, соответствующего дню окончания ссуды, вычитают номер первого ее дня.

Варианты расчета процентов:

а)точные проценты с точным числом дней ссуды (при расчетах за полугодие срок ссуды приравнивается к 182 дням);

б)обыкновенные проценты с точным числом дней ссуды;

в)обыкновенные проценты с приближенным число дней ссуды.

Пример.Ссуда в размере 100 тыс. Рублей выдана 20.01 до 05.10 включительно под 8% годовых, год невисокосный. Необходимо найти размер погасительного платежа.

Точное число дней ссуды 258, приближенное - 255 (8 полных месяцев по 30 дней плюс 11 дней января и 5 дней октября минус 1 день). .

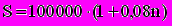Применяя три метода определения продолжительности ссуды, получим:

а) точные проценты с точным числом дней ссуды

n=258/365; S=105654,79 руб.;

б) обыкновенные проценты с точным числом дней ссуды

n=258/360; S=105733,33 руб.;

в) обыкновенные проценты с приближенным числом дней ссуды

n=255/360; S=105666,67 руб.

Переменные ставки.

В кредитных соглашениях иногда предусматриваются дискретно изменяющиеся во времени процентные ставки. В этом случае наращенная сумма определяется по следующей формуле: S=P(1+n1i1+n2i2+...), где it, nt - ставка простых процентов и продолжительность ее начисления в периоде t.

Пример. Контракт предусматривает следующий порядок начисления процентов: первый год - 6%, в каждом следующем полугодии ставка повышается на 0,5%. Необходимо определить множитель наращения за 2,5 года.

Находим .

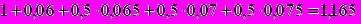Дисконтирование и учет по простым ставкам.

В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. Такая ситуация может возникнуть, например, при разработке условий контракта. Кроме того, задача расчета P по S возникает и тогда, когда проценты с суммы S удерживаются непосредственно при выдаче ссуды. В этом случае говорят, что сумма S дисконтируется, сам процесс начисления и удержания процентов вперед называют учетом, а проценты в виде разности S-P=D - дисконтом. Необходимость дисконтирования возникает, например, при покупке банком или другим финансовым учреждением краткосрочных обязательств (векселей, тратт и т.д.), оплата которых должником производится в будущем. Термин дисконтирование употребляется и в более широком смысле - как средство определения любой стоимостной величины на некоторый момент времени при условии, что в будущем она составит величину S. Такой расчет часто называют приведением стоимостного показателя к заданному моменту времени. Величину P, найденную дисконтированием S, называют часто современной, или приведенной, величиной S.

Исходя из вида процентной ставки применяют два вида дисконтирования - математическое дисконтирование и банковский (коммерческий учет).

Математическое дисконтирование.

Математическое дисконтирование представляет собой решение задачи, обратной наращению первоначальной суммы ссуды, депозита и т.д. Задача в этом случае формулируется так: какую первоначальную сумму надо выдать в долг, чтобы при начислении на нее процентов по ставке i к концу срока получить наращенную сумму, равную S. Выразим P через S: P=S/(1+ni), 1/(1+ni) - дисконтный множитель, n=t/K. Дисконтный множитель показывает какую долю составляет P в величине S. Разность S-P в этом случае можно рассматривать не только как проценты, начисленные на P, но и как дисконт суммы S. Последний обозначим как Di.

Пример. Через 180 дней с момента подписания контракта должник уплатит 31 тыс. руб. Кредит предоставлен под 6% годовых. Определить, какую сумму получит должник и сумму дисконта.

Находим: 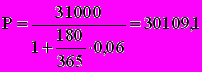руб., Di=S-P=890,9 руб.

Банковский учет (учет векселей).

Суть операции учета заключается в том, что банк или какое-либо иное финансовое учреждение до наступления срока платежа по векселю или другому платежному обязательству покупает его у владельца по цене, меньшей той суммы, которая должна быть выплачена по нему в конце срока, т.е. приобретает (или учитывает) его с дисконтом. Получив при наступлении срока векселя деньги, банк таким образом реализует дисконт. Владелец векселя, с помощью его учета, имеет возможность получить деньги ранее указанного на нем срока. При учете векселей применяется банковский, или коммерческий, учет. Согласно этому методу проценты за пользование ссудой начисляются на сумму, подлежащую уплате в конце срока ссуды. При этом применяется учетная ставка d. По определению простая годовая учетная ставка находится как d=(S-P)/S, в то время как простая ставка процентов равна отношению i=(S-P)/P. Размер дисконта или учета Dd, удерживаемого банком, равен Snd, отсюда P=S-Snd=S(1-nd), где n - продолжительность срока в годах от момента учета до даты уплаты по векселю, (1-nd) - дисконтный множитель.

Дисконтирование по учетной ставке производится чаще всего при условии, что год равен 360 дням, а число дней в периоде обычно берется точным.

Пример. Тратта (переводной вексель) выдана на сумму 100 тыс. рублей с уплатой 17.11. Владелец документа учел его в банке 23.09 по учетной ставке 8%. Так как оставшийся до погашения обязательства период равен 55 дням, то полученная сумма (без уплаты комиссионных) составит 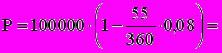98777,78 руб.,

Dd=100000-98777,78=1222,22 руб.

Наращение по учетной ставке.

Простая учетная ставка может быть применена и при расчете наращенной суммы. В этом возникает необходимость, в частности, при определении суммы, которую надо проставить в бланке векселя, если заданы текущая сумма долга, его срок и учетная ставка. Наращенная сумма S=P/(1-nd).

Простая учетная ставка дает более быстрый рост суммы ссуды, чем аналогичная по величине ставка простых процентов.

Пример. Ссуда в размере 100 тыс. рублей выдана 20.01 до 05.10 включительно. Найти наращенную сумму при условии, что проценты начисляются по простой учетной ставке, равной 8%. Находим: 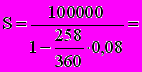106082,04 руб.

Операции начисления процентов и дисконтирования по учетной ставке могут совмещаться, например, при учете платежного обязательства, предусматривающего начисление простых процентов. При учете такого платежного обязательства приходится решать две задачи. Первая заключается в определении наращенной суммы S, вторая - в расчете суммы, полученной при учете.

Пример.

Обязательство уплатить через 180 дней 30 тыс. рублей с процентами (6% годовых) было учтено за 120 дней до наступления срока, учетная ставка 7,5%. Полученная при учете сумма без комиссионных составит 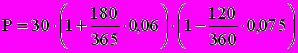=30,115 тыс. рублей.

Определение продолжительности ссуды и уровня процентной ставки.

При разработке условий контрактов или их анализе иногда возникает необходимость в решении обратных задач - определении срока суды или уровня процентной ставки при всех прочих заданных условиях. Формулы для расчета продолжительности ссуды в годах и в днях:

; ; .

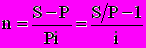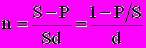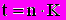Необходимость определения уровня процентной ставки по остальным заданным условиям сделки возникает, в частности, при сравнении контрактов по степени доходности в случаях, когда процентные ставки в явном виде не указаны. Формулы для расчета i и d:

ставка процентов 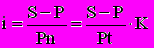; учетная ставка ;

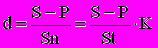где K - временная база начисления процентов, K=365(366) или 360.

Пример. В контракте предусматривается погашение обязательства через 120 дней в сумме 12 тыс. рублей, первоначальная сумма долга - 11,5 тыс. рублей. Необходимо определить доходность операции для кредитора в виде учетной ставки и ставки процентов. В обоих случаях K=360.

Находим 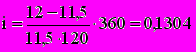, т.е. 13,04%,

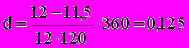, т.е. 12,5%.

Иногда в контрактах размер дисконта фиксируется в виде процента за весь срок ссуды. В этом случае практически важно определить цену кредита в виде процентных ставок i или d. Искомые параметры находятся элементарно:

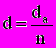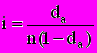, , где da - относительная величина дисконта.

Пример. Стороны договорились о том. что из суммы кредита, выданного на 210 дней, удерживается дисконт в размере 12%. Необходимо определить цену кредита в виде простой учетной ставки d и ставки процентов i.

Находим 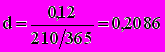, т.е. 20,86%;

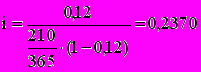, т.е.23,7%/

Выбор конкретного вида ставки существенно влияет на финансовые результаты операции. Возможен такой выбор размеров различных видов процентных ставок, при котором результаты будут равноценными.

Задание 1.

Определить проценты и сумму накопленного долга, если ссуда равна P руб. , срок долга n лет, ставка простого процента i% годовых.

N
P
n
i
N
P
n
i
N
P
n
i

1
7000
3
12
21
7500
4
12
41
3500
3
9

2
6000
5
11
22
6500
3
12
42
3200
4
15

3
5000
4
13
23
9000
4
13
43
3500
5
12

4
4500
3
12
24
8000
5
15
44
6400
5
16

5
5500
5
16
25
7000
4
12
45
3200
4
8

6
6500
6
13
26
4500
6
19
46
4300
6
23

7
8000
3
12
27
3800
5
16
47
8700
3
14

8
9000
4
14
28
4600
4
12
48
5700
4
12

9
3000
5
15
29
7000
5
12
49
5400
4
15

10
5500
3
16
30
8600
5
15
50
4300
6
18

11
3500
4
12
31
9700
4
12
51
5000
4
12

12
6000
4
14
32
6700
3
15
52
5700
5
11

13
8500
3
15
33
4300
5
17
53
6500
4
8

14
9500
5
16
34
5400
3
14
54
8600
3
10

15
6000
6
14
35
7600
4
15
55
9800
6
14

16
5500
5
12
36
8000
5
12
56
6500
4
8

17
4500
4
15
37
9600
4
13
57
8400
5
7

18
3500
5
17
38
4800
6
17
58
7500
3
11

19
6500
4
12
39
6500
4
12
59
2100
4
12

20
7500
4
14
40
6800
3
12
60
6800
5
20