Geum.ru

2. 2 Задания для курсовой работы

Вид материалаКурсовая

Содержание


2.2.2 Расчет вала на статическую прочность и выносливость
При расчетах принять, −
2.2.3 Методические рекомендации по выполнению курсовой работы
Подобный материал:
2.2 Задания для курсовой работы

Курсовая работа содержит выполнение двух заданий, −

− Расчет пространственного стержня в общем случае сложного сопротивления;

− Расчет вала на статическую прочность и выносливость.

Эти задания включают расчеты на прочность и жесткость элементов инженерных конструкций в условиях сложного сопротивления при статическом и циклическом нагружении.

2.2.1 Расчет пространственного стержня в общем случае сложного сопротивления

Стальной пространственный консольный стержень OA−AB−BC с ломаным очертанием осевой линии (рисунок 2.2.1) нагружен в сечении С двумя сосредоточенными силами (в зависимости от схемы − РX, РY; РZ, РX; РY, РZ) и на участке BC равномерно распределенной нагрузкой интенсивностью q.

Участок OA имеет круглое поперечное сечение диаметром d, участок AB − прямоугольное сечение b×h (h = 2b), участок BC − квадратное сечение со стороной a (рисунок 2.2.2).

Требуется:
  1. Определить размеры сечений участков стержня при заданных длинах участков и нагрузках Рi , q.
  2. Определить перемещение сечения С в направлении оси z (рисунок 2.2.2).

Исходные данные взять из таблицы 2.2.1.

2.2.2 Расчет вала на статическую прочность и выносливость

Стальной вал механизма (рисунок 10) передает вращающий момент Мх. На вал насажены два зубчатых колеса с делительными диаметрами d1 и d2. Колеса нагружены окружной Т, радиальной Q и осевой A силами.

Требуется выполнить:
  1. расчет вала на статическую прочность: подобрать диаметр вала в опасном

сечении и определить запас прочности по пределу текучести nT;
  1. расчет вала на выносливость (усталостную прочность): определить запас

прочности по пределу выносливости при изменении нормальных напряжений

от изгиба по симметричному, а касательных напряжений от кручения − по

пульсирующему циклу.

Исходные данные взять из таблицы 2.2.2.





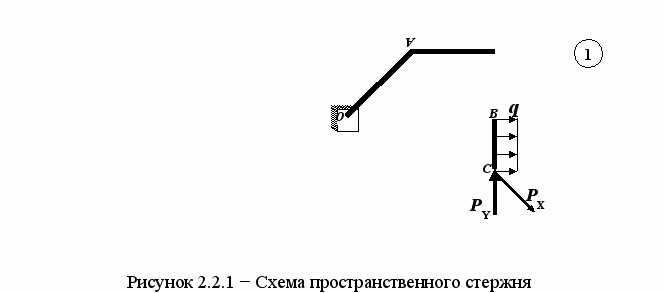
Таблица 2.2.1 − Исходные данные к расчету пространственного стержня

Силы, кН
q,

кН/м
Длины участков, м
σт,

МПа
τт,

МПа
kт

РX
РY
РZ
OA
AB
BC

1,2
0,6
2,8
2
0,8
0,4
0,5
220
160
1,45



kт = σт/[σ]р (τт/[τ]) − коэффициент запаса по пределу текучести









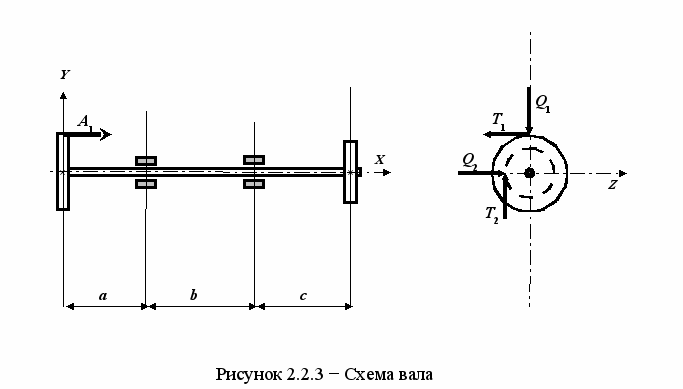
Таблица 2.2.2 − Исходные данные к расчету вала


Параметры элементов передачи
Параметры вала

Мх,

кН.м
Q1/Т1
Q2/Т2
Ai/Тi
d1
d2
a
b
c
kσ
kτ
Вид обработки

мм
мм

5,5
0,14
0,38
0,32
150
320
110
265
210
1,60
1,85
ШТ


Обозначения:

Мх − вращающий момент на валу; Q − радиальное усилие; Т − окружное усилие;

A − осевое усилие.

kσ, kτ − коэффициенты концентрации напряжений, соответствующие конструктивным особенностям сопряжения элементов передачи с валом.

Сокращения:

ШГ – шлифование грубое; ШТ – шлифование тонкое; ОТ – обтачивание тонкое.


Продолжение таблицы 2.2.2

Материал вала

Марка стали
σВ
σТ
τТ
σ−1
τ−1

МПа

45
610
360
220
250
175


При расчетах принять, −

− коэффициент запаса прочности (расчет по допускаемым напряжениям): k = 1,8…2,5;

− наименьшее допускаемое значение запаса прочности по пределу текучести: nTmin = 2,4;

− наименьшее допускаемое значение запаса прочности по пределу выносливости: nmin = 1,4.

2.2.3 Методические рекомендации по выполнению курсовой работы

Задание 1


Последовательность расчета пространственного стержня в общем случае сложного сопротивления:

1). Построить эпюры внутренних силовых факторов (ВСФ): Nx, Mx, My, Mz, Qy, Qz, и определить вид нагружения для каждого участка стержня.

2). Установить на каждом участке опасное сечение − сечение, где одновременно действуют наибольшие по абсолютной величине ВСФ.

3). Установив опасное сечение, определяют нормальные напряжения от совокупности ВСФ Nx, My, Mz и касательные напряжения от крутящего момента Mx (касательными напряжениями от ВСФ Qy и Qz можно пренебречь). Затем исследуют напряженное состояние в точках сечения, чтобы выявить опасные точки. Опасными точками будут:
  1. точки, в которых нормальные напряжения достигают наибольшей величины − точки наиболее удаленные от нейтральной линии сечения (НЛС)

Положение НЛС определяют, приравняв нулю выражение суммарного нормального напряжения в сечении.

Например, при одновременном действии ВСФ Nx, My, Mz нормальные напряжения определяют по формуле:


σ = N/A + MYz/JY + MZy/JZ, (1.1)


где А − площадь поперечного сечения; JY , JZ − главные центральные моменты инерции сечения.

Тогда, уравнение НЛС примет вид:


N/A + MYz0 /JY + MZy0 /JZ = 0, (1.2)


где y0, z0 − координаты точек НЛС.

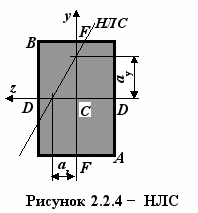
Положение НЛС для прямоугольного сечения изображено на рисунке 2.2.4.

От НЛС наиболее удалена точка А. Нормальное напряжение в точке А:


‌σ(А) = N/A + MYz0А /JY + MZy0А /JZ


В точке А имеет место линейное напряженное состояние, для которого применимо основное условие прочности по допускаемым нормальным напряжениям: ‌׀σ(А)׀ ≤ [σ]

  1. точки, в которых касательные напряжения имеют наибольшее значение.

Продолжая пример с сечением прямоугольной формы, − наибольшие касательные напряжения от кручения действуют в точках D, F, которые определяют по формулам:

τD = τ max= Мх/Wк , (1.3)

где Wк − аналог по­лярного момента сопротив­ления сечения;


τF = η τ max, (1.4)


где η − коэффициент, зависящий от отношения сторон сечения m = h/b (при этом необходимо учесть, что b − малая сторона прямоугольника).

Э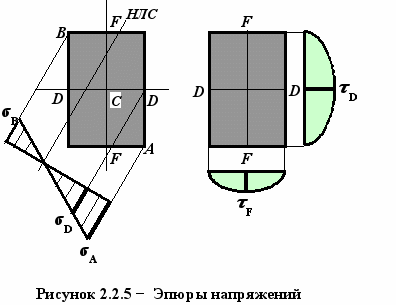пюры напряжений приведены на рисунке 2.2.5.


с) точки, в которых нормальные и касательные напряжения, действуя одновременно, создают плоское напряженное состояние.

Для таких точек применяют условия прочности по эквивалентным напряжениям:


σЭ ≤ [σ] \*, (1.5)


где σЭ = [σ2 + 3τ2]1/2 −

− эквивалентные напряжения по III теории прочности;


σЭ = [σ2 + 4τ2]1/2 − эквивалентные напряжения по IV теории прочности;


σЭ = (1 − m)σ/2 + (1 + m)[σ2 + 4τ2]1/2/2 − эквивалентные напряжения по теории прочности К. Мора (m = σр/σс).


4). Установив на каждом участке опасные сечения и опасные точки в этих сечениях, определяют размеры сечений заданной формы, используя соответствующие условия прочности для опасных точек.


5). Для определения перемещение сечения С в направлении оси z предпочтительнее использовать энергетические методы расчета упругих систем.

Так как заданный стержень состоит из прямолинейных участков, то перемещение можно определить по формуле Максвелла-Мора или по правилу А.Н.Верещагина.


Заключение


Следует оценить рациональность заданной формы сечений участков стержня для работы в условиях сложного сопротивления.




\* − для круглого поперечного сечения условие прочности принимает вид : МЭ/W ≤ [σ],

где МЭ = [MY2 + MZ2 + MX2]1/2 − эквивалентный момент по III теории прочности;


МЭ = [MY2 + MZ2 + 0,75MX2]1/2 − эквивалентный момент по IV теории прочности;


МЭ = (1 − m)[MY2 + MZ2]1/2/2 + (1 + m) [MY2 + MZ2 + MX2]1/2/2 − эквивалентный момент по теории прочности К.Мора.



Задание 2

1. Расчет вала на статическую прочность

Заданный вал нагружен кручением с изгибом \*. Кроме этого, действующие в сечениях вала напряжения переменны во времени.

Предварительно (при проектном расчете) диаметр вала определяют, не учитывая изгиб и цикличность напряжений, из расчета на кручение заданным моментом Мх по пониженным допускаемым напряжениям [τ] = 20…40 МПа:

d = [16Мх/π[τ]]1/3. (2.1)

Затем выполняют проверочный расчет вала:

1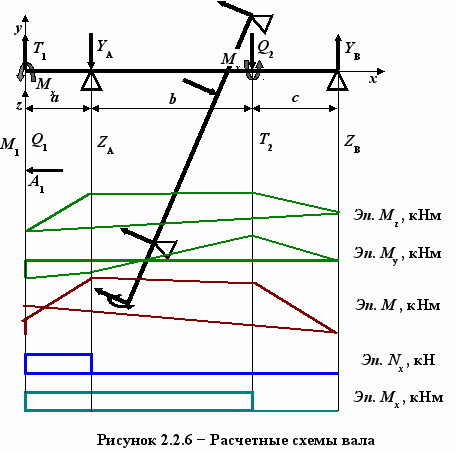) Заданную пространственную схему вала представляют схемами в двух плоскостях: вертикальной − хОу, и горизонтальной − хОz (рисунок 2.2.6), в которых строят эпюры изгибающих моментов Мy и Мz.

Затем вычисляют суммарные изгибающие моменты в сечениях вала: М=[Мy2+ Мz2]1/2, и строят эпюру, ограничивая ее прямыми линиями.

Строят эпюры Nx и Mx.


2) Проверочный расчет вала выполняют при совместном действии кручения с изгибом по эквивалентному моменту, величину которого определяют по III или IV теории прочности (см. формулы в сноске на странице 53), по условию прочности (1.5).

Если в опасном сечении действует и нормальная сила Nx, то нормальные напряжения в опасном сечении определяют по формуле:

σ = Nx/A + MЭ/W (2.2)

\* − при проектном расчете допускается не учитывать действие нормальных сил от осевых нагрузок А.



3) Определяют запас прочности по пределу текучести, −

− по нормальным напряжениям от изгиба: nTσ = σТ/σmax ; (2.3)

− по касательным напряжениям от кручения: nTτ = τТ/τmax; (2.4)

− запас прочности: nT = nTσ nTτ /[ nTσ2 + nTτ2]1/2. (2.5)

Значение запаса прочности по пределу текучести должно удовлетворять условию: nT > nTmin.

4) Определяют прогиб вала в опасном сечении и оценивают его жесткость.

2 Порядок расчета вала на выносливость (усталостную прочность)
  1. Определяют экстремальные напряжения циклов, −


− нормальных напряжений от изгиба: σmax= Мmax/W; σmin= − σmax, (2.6) − для симметричного цикла;


− касательных напряжений от кручения: τmax= Мx/Wρ; τmin= 0, (2.7) − для пульсирующего (отнулевого) цикла.

  1. Определяют характеристики циклов по напряжениям, −


− среднее напряжение цикла:


(σmax + σmin)/2 = σm ((τmax + τmin)/2 = τm); (2.8)


− амплитуда цикла:


(σmax − σmin)/2 = σа ((τmax − τmin)/2 = τа). (2.9)

  1. По справочникам (или эмпирическим соотношениям) находят, −


− коэффициенты, учитывающие факторы, влияющие на предел выносливости:


βмσ(τ)= 1/εмσ(τ) − масштабный коэффициент; (2.10)


βпσ(τ)= 1/εпσ(τ) − коэффициент качества поверхности; (2.11)


ψσ (ψτ) − коэффициент влияния асимметрии цикла. (2.12)


Замечание. Так же находят значения коэффициентов концентрации напряжений kσ и kτ, если они не заданы.
  1. Определяют запас прочности по пределу выносливости, −


− по нормальным напряжениям: nσ = 1/(kσβмσβпσσа/σ−1 + ψσσm/σ−1); (2.13)


− по касательным напряжениям: nτ = 1/(kτβмτβпττа/τ−1 + ψττm/τ−1). (2.14)


Замечание. При отсутствии справочных данных о величине коэффициентов влияния асимметрии цикла ψσ и ψτ их приближенно можно определить из соотношений:

ψσ= σ−1/σВ и ψτ= τ−1/τВ. (2.15)


− общий (по формуле Гафа−Полларда): n = nσ nτ/(nσ2 + nτ2)1/2 . (2.16)


  1. Проверяют условие прочности: n ≥ nmin. (2.17)

Заключение


Следует проанализировать результаты расчета вала на статическую прочность и выносливость, и сделать вывод о прочности вала в опасном сечении.

При этом следует оценить отношения запасов прочности по пределу текучести и пределу выносливости, полученных при расчетах, к их нормированным значениям: nT/nTmin, n/nmin, обратив внимание на то, что для рационально сконструированных валов справедливо соотношение:

nT/n = (0,8…2,7)nTmin/nmin. (2.18)


На основании этого следует, при необходимости, предложить меры по выполнению соотношения (2.18) для рассчитанного вала.