«Активизация познавательного интереса учащихся на уроках математики»

Вид материала

3.2. Устный счет. Как элемент познавательной деятельности школьников
3.3. Приемы активизации познавательной деятельности при проверке домашнего задания.
3.4. Дидактическая игра как средство активизации познавательной деятельности учащихся
Основные структурные элементы дидактической игры
3.5. Решение задач - один из путей активизации познавательной деятельности учащихся.

Подобный материал:

1 2 3 4

3.2. Устный счет. Как элемент познавательной деятельности школьников

Одной из основных и первоначальных задач обучения математики является выработка у ребят навыка хорошего счета. Это лежит в основе успешного обучения в старших классах. Учителю необходимо обратить внимание на устный счет с того момента, когда дети приходят к нему из начальной школы. Потому что именно в 5-6 классах закладываются основы обучения математике. В этих классах необходимо дать детям не только знания, но и не отпугнуть школьников холодной строгостью царицы наук, увлечь их этим предметом.

Итак, первый этап урока математики, в 5-6-х классах – устные упражнения. Цель этого этапа, во-первых, подготовить учащихся к продуктивной работе на всем протяжении урока, значит среди них должны быть задания на восстановление опорных знаний и умений. Во-вторых, необходима постоянная работа по поддержанию и совершенствованию ранее сформированных знаний и умений, в частности вычислительных. И в-третьих, способствовать развитию учащихся, то есть необходимо предлагать задачи, требующие сообразительности, внимания, анализа и обобщения имеющихся знаний и т.п.

Стараюсь сделать так, чтобы устный счет воспринимался учащимся младших классов как игра. Тогда они сами следят за ответом друг друга, придумывают новые задания.

Устный счет я всегда провожу так, чтобы ребята начинали с простых примеров и заданий, а затем брались за более сложные вычисления. Если на детей обрушить сразу сложные задания, они растеряются, обнаружат свое бессилие, потеряют интерес к происходящему.

Существуют 2 вида устного счета. Первый – учитель не только называет числа, но и показывает их учащимся. Подкрепляет тем самым слуховые восприятия, зрительным. Т.е. ребенок может не запоминать данные числа, а сразу вычислять или выполнять то или иное задание. Например: урок можно начать с «Зарядки» (Приложение 1).

В основе второго вида лежит запоминание чисел, над которыми производятся действия. Это наиболее важный момент устного счета. Тот, кто не может удержать в памяти числа, в практической работе оказывается плохим вычислителем. Поэтому очень важно недооценивать этот вид устного счета.

Приведу несколько примеров устного счета, которые я провожу на уроке.

«Ровный счет».

Учитель записывает на доске пример с ответом. Учащиеся должны придумать свои примеры с тем же ответом. Их примеры на доске не записываются. Ребята должны на слух воспринимать названные числа и определить верно ли составлен пример.

«Лесенка».
Счет с дополнением.

Учитель записывает на доске число. Например 1,5. Затем он называет меньшее число, а ребята должны назвать число, которое дополняет его до 1,5. Числа на доске не записываются. Этим обеспечивается тренировка в запоминании чисел.

«Торопись да не ошибись» – это математический диктант. Учитель медленно читает вопросы, дети записывают ответы.

Здесь можно использовать книгу «Математические диктанты в 5-9 классах».

При выборе заданий в математическом диктанте необходимо учитывать следующее:

Задания должны быть различной трудности. Сначала легкие, затем все труднее.
Задание читать различным темпом.
Одновременно с классом работают 2-е у доски. Это дает возможность проверить задания сразу.
Математические карты. (Приложение 2).
Круговые примеры.

Такие примеры позволяют ребятам осуществлять самоконтроль, а так же обличают проверку работ. Их можно найти в учебнике «Математика 5», «Математика 6».

Например

7. Кодированные задания также повышают интерес к предмету. На доске записаны примеры. Ответы закодированы буквами. В конце должно появиться слово (Приложение 3.).

8. Найди ошибку. На доске записаны примеры с ошибками, необходимо найти их и исправить.

9. Восстанови запись. Например:

или дописать предложение. Данный прием можно использовать в средней и старшей звене.

10. Для поддержания и развития навыков устного счета в учебниках «Математики» за 5 и 6 классы даются различные упражнения, так называемые успочки (цепочные вычисления). Они даются в виде схемы, например № 55 «Математика 5»: 73:8

Роль таких упражнений состоит в том, чтобы поддержать умение считать, но так же это инструмент для развития оперативной памяти детей, тренировки внимания.

Эти упражнения не принесут большой пользы, если будут выполняться учащимися по очереди по одному действию. При этом большинство учащихся класса остаются пассивными, постепенно привыкают ничего не делать во время устного счета. Поэтому ребятам необходимо предлагать решить устно столбики, записывая в тетрадь ответы. Затем проверить ответы в классе. Обычно на 1 столбик у учащихся в среднем уходит до 30 секунд. На проверку требуется 2-3 минуты.

10. Задания, связанные с жизненными ситуациями с использованием материала, который они получают на других уроках, так же интересен учащимся, повышает их интерес к предмету.

3.3. Приемы активизации познавательной деятельности при проверке домашнего задания.

Развитию познавательной активности школьников во многом способствует правильно организованная проверка домашнего задания. Одним из важнейших педагогических требований является разнообразие форм ее проведения, которые способствуют повышению интересе учащихся не только к результату, но и самому процессу проверки знаний. Опишу некоторые способы проверки домашнего задания, которые я использую на уроках.

Взаимный опрос вызывает большой интерес у учащихся. Учитель вызывает одного ученика к доске; остальные задают ему вопросы по изученной теме (это могут быть вопросы также и по главе), после ответов которых ученику ставится оценка. В случае, если у ребенка будут трудности с ответом отвечает тот, кто задал его.

Класс во время проведения такого опроса активен, учащиеся с ответственностью относятся к постановке вопроса.

Одним из приемов активизации познавательной деятельности учащихся при опросе является рецензия на ответ. Рецензии могут быть как устными, так и письменными.

Учащиеся смогут познакомить со схемой рецензии, она может быть следующей:

Краткое содержание ответа
Характеристика полноты ответа
Характеристика глубины ответа (достаточно ли обоснования, доказательства и примеры)
Дополнения к ответу

Таким образом, рецензия на ответ будет содержать не только исправление ошибок и дополнения ответу, но и достоинства ответа. Тем самым повышается интерес к ответу, внимание не рассеивается, опрос проходит более плодотворно.

При доказательстве теорем мне нравится проводить опрос следующим образом. На доске строится чертеж к теории. Затем вызываю 1 ученика (наиболее сильного) и предлагаю доказать теорему по чертеже, при этом основные моменты доказательства и формулы можно записать на доске. После этого спрашиваю у ребят: «Какие ошибки были сделаны в доказательстве? Все ли было доказано» или прошу сделать рецензию на ответ. После этого вызываю еще одного ученика к доске, но предупреждая класс, что кто-то продолжит рассказ первого. Этим самым внимание учащихся усиливается, работают все. После ответа предлагаю рассказать шепотом теорему друг другу и поставить оценку. Я при этом хожу по классу и могу услышать и могу услышать ответы некоторых учащихся. Затем спрашиваю учащихся какие оценки они выставили, после чего спрашиваю 1 ученика из класса с доказательством теоремы. Дети очень добросовестно относятся к выставлению оценки, активны, собраны. Опрос при этом проходит примерно 15-20 мин. Такова опроса я считаю состоит в том, что опрошен весь класс.
Для того, чтобы придать домашней работе творческий характер и вызвать интерес к ней я парктикую такие задания как: составление сказок (после изучения темы), кроссвордов на математическую тематику, составление рисунков на координатной плоскости (после изучения темы «Координатная плоскость»), а так же рисунков по теме «Симметрия относительно точки», «Симметрия относительно прямой», а так же занимательные задачи на развитие внимания, памяти, мышления (Приложение)
Так же использую на уроке такие способы проверки домашнего задания:

просмотр тетради в классе, учитель проходит по классу и просматривает тетради, учащиеся в это время выполняют задания;
объяснение на доске хода решения задач;
взаимопроверка;
проверка до урока ассистентами;
выборочная и полная проверка после урока.

Так же для активизации познавательной деятельности использую домашнее задание при изложении нового материала.

При письменном контроле знаний учащихся применяю дифференцированные проверочные работы, математические диктанты.

3.4. Дидактическая игра как средство активизации познавательной деятельности учащихся

Большую роль при активизации познавательной деятельности учащихся можно отвести дидактическим играм на уроке математики.

Современная дидактика, обращаясь к игровым формам обучения на уроках, справедливо усматривает в них возможности эффективной организации взаимодействия педагога и учащихся.

Игра - творчество игра-труд. Итак, игра, учение труд – это три основных вида деятельности человека. Игра готовит ребенка и к учению, и к труду, при этом сама игра всегда – немного учение, немного труд. В процессе игры у детей вырабатывается привычка сосредотачиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлекшись дети не замечают, что учатся, познают, запоминают новое, пополняют запас представлений, понятий.

Во время игры, дети как правило, очень внимательны, сосредоточены, дисциплинированы.

Дидактические игры уживаются хорошо с «серьезным» учением. Включение в урок дидактических игр и игровых моментов делает процесс обучения интересным и занимательным, создает у детей рабочее настроение, облегчает преодоление трудностей в условиях учебного материала.

Дидактическая игра – это не самоцель, а средство обучения и воспитания. Игру нельзя путать с забавой, не следует рассматривать и как деятельность, доставляющее удовольствие ради удовольствия. На дидактическую игру нужно смотреть как на вид преобразующей творческой, познавательной деятельности в тесной связи с другими видами учебной работы.

Игровая познавательная деятельность как конкретный метод активизирует обучение, вовлекая учащихся в процесс приобретения знаний, умений и навыков, развивая мышление, превращая традиционное занятие и учебный материал в творчество.

Рассмотрим в чем состоит специфика дидактической игры, ее существенный признак.

Во-первых, дидактическая игра имеет устойчивую структуру, которая отличает ее от всякой другой деятельности.

ОСНОВНЫЕ СТРУКТУРНЫЕ ЭЛЕМЕНТЫ ДИДАКТИЧЕСКОЙ ИГРЫ

Игровой замысел. Он заложен в той дидактической задаче которую надо решить в учебном процессе, может выступать в виде вопроса или загадки. В любом случае придает игре познавательный характер.
Правила. Они определяют порядок действий и поведение учащихся в процессе игры, способствуют к созданию рабочей обстановки. Правила разрабатываются с учетом целей урока, индивидуальными возможностями учащихся.
Игровые действия. Они регламентируются правилами игры, способствуют познавательной активности учащихся, дает им возможности проявить свои способности, применить знания, умения и навыки для достижения цели игры. Учитель направляет ее в нужное русло при необходимости, подбадривает отстающих.
Познавательное содержание или дидактическая задача. Оно заключается в усвоении тех знаний и умений, которые применяются при решении учебной проблемы поставленной игрой. Оборудование игры в значительной мере включает в себя оборудование урока. Это наличие ТСО.
Результат игры. Это финал игры. Он выступает прежде всего в форме решения поставленной учебной задачи, придает игре законченность. Для учителей результат игры является показателем уровня достижений учащихся и в усвоении знаний и в их применении.

Структурные элементы игры взаимосвязаны между собой и отсутствие одного из них ведет к разрушению игры. Поэтому при подготовке урока содержащего дидактическую игру, необходимо составить сценарий игры, указать временные рамки, при этом учесть возраст детей, уровень их знаний, реализовать межпреодолимые связи.

Реализация игровых приемов и ситуаций при урочной форме занятий происходит по нескольким направлениям.

Дидактическая цель ставится в форме игровой задачи.
Учебная деятельность учащихся подчиняется правилам игры.
Учебный материал используется в качестве средства игры.
В учебную деятельность вводится элемент соревнования.
Успешность выполнения дидактической игры связывается с результатом.

Дидактические игры, применяемые на уроке, должны быть разнообразными, как по содержанию, так и по форме проведения. Их чаще всего проводят при проверке результатов обучения, выработки навыков, формировании умений, при учетом счете.

В зависимости от урока игры могут быть:

обучающими, когда ученики в ходе игры приобретают новые знания;
контролирующие. В ней дидактическая цель состоит из повторения, закрепления и проверки полученных ранее знаний;
обобщающие игры требуют интеграции знаний. Они способствуют установлению межпредметных связей, в умении действовать в различных ситуациях.

Игра по времени может идти весь урок или же, например, 5 минут.

Возникновение интереса к математике во многом зависит от методики ее преподавания. Это особо актуально для учащихся 5-6 классов, когда только определяются постоянные интересы и склонности к тому или иному предмету. Раскрыть притягательные стороны математики помогают различные методы обучения, и методические приемы, в том числе важная роль отводится дидактическим играм.

Использование дидактических игр, игровых ситуация на разных этапах изучения различного по характеру математического материала является средством активизации познавательной и учебной деятельности детей, положительного влияния на повышение качества знаний, умений и навыков школьников. Дидактическая игра дополнит традиционные формы обучения и может быть использована на уроках. Использование на разных этапах урока является эффективным средством активизации познавательной деятельности учащихся.

Приведу несколько дидактических игр, которые я провожу на уроках математики:

Отгадай тему урока.

Цель: Повторить таблицу умножения; активизировать деятельность ребят на уроке.

	6	7	8	9	32, 42, 45, 63, 72, 35, 49, 48, 54, 40, 56, 63, 42, 36, 81, 54 Тема: Сокращение дробей
6	б	о	н	и
7	о	е	д	р
5	с	щ	е	к
9	й	р	а	е

Кто победит.

Цель: повторить понятие разложения числа на 2 множителя из курса начальной школ. Подготовить учащихся к изучению темы «Разложение числа на простые множители»

Ход игры: Класс делится по 2 человека. Даю число. Первый игрок разлагает его на 2 множителя, меньше этого числа. Второй игрок выбирает любое из получившихся чисел и тоже раскладывает его на 2 множителя (меньших). Затем снова первый и т.д. Выигрывает тот, кто уже не сможет увеличить количество множителей. В результате получается следующая запись:

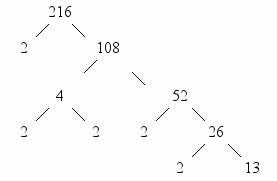
Математическое лото.
Конкурс художников.

Тема: Координатная плоскость (5 (6) кл)

Цель: Отработать новые нахождения точек на координатной плоскости. Активизировать познавательную деятельность учащихся.

Ход игры: На доске записаны координаты точек. Ребятам необходимо выполнить по данным координатам рисунок, соединяя попарно точки.

Например:

(0;0), (-1;1), (-3;1), (-2;3), (-3;3), (-4;6), (-3;1), (0;8), (2;5), (2;11), (6;10), (3;9), (4;5), (3;0), (2;0), (1;-7), (3;-8), (0;-8), (0;0).

Задание может быть следующим: ребята сами делают рисунок, затем меняются с соседом по парте и записывать координаты точек.

В большинстве случаев игровые ситуации применяются как вспомогательное средство для возбуждения познавательного интереса, создания проблемных ситуаций. Это настраивает ребят на изучение определенного материала, они не требуют дополнительного времени на разъяснение правил.

Для создания игровых ситуаций на уроках математики использую исторический материал, жизненные факту, отрывков литературных произведений, в математическом содержании которых содержатся противоречивые данные, факты, а так же она создается во времени проведения практических заданий, использование рисунков.

Тема: «Теорема о сумме углов в треугольнике»

Можно предложить учащимся построить треугольник по заданным углам:

А = 37⁰, B = 28⁰, C = 90⁰,
А = 123⁰, B = 50⁰, C = 23⁰,
А = 60⁰, B = 80⁰, C = 40⁰.

В данном задании а и b не выполняется условие о сумме внутренних углов треугольника. На их основе можно создать проблемную ситуацию. Можно задать при этом такие вопросы: «Зависит ли сумма внутренних углов треугольника от его размеров, положения на плоскости, формы? Затем предложить построить треугольник и измерить углы, найти их сумму. Затем выдвигается гипотеза: «Сумма внутреннего ∆ = 180⁰, после чего доказывается соответствующая теорема.

3.5. Решение задач - один из путей активизации познавательной деятельности учащихся.

В объяснительной записке программы по математике сказано, что изучение математики предполагает, прежде всего, наполнение курса разнообразными, интересными, сложными задачами.

«Задача в обучении – один из важнейших факторов повышения познавательной и практической активности учащихся в труде, важнейшее средство формирования у школьников основных математических знаний, умений, навыков, является ведущей формой учебной деятельности.

Решение математических задач служит многим педагогическим целям:

ученики знакомятся с применением теоретических знаний на практике;
их теоретические знания при этом расширяются, углубляются и закрепляются;
решение задач формирует навыки творческой самостоятельной работы;
решение задач служит надежным средством контроля и учета знаний учащихся.

Задача выполняет такие функции как: воспитывающую, познавательную, развивающую и прикладную. Задача в настоящее время не только цель, но и средство обучения. С позиции ученика задача является целью обучения. Он должен оформить запись, получить ответ, утвердится в правильности решения и ответа. Получив верный ответ ученик испытывает удовлетворение своей деятельностью; решение отдельной задачи для него – реакция на требования учителя решить задачу.

С позиции учителя задача является средством обучения. Он предлагает задачу, чтобы получить выводы, способствующие формированию определенной математической теории, для ее применения.

В учебнике математики даны развивающие, познавательные, прикладные, дидактические задачи.

Школьники должны понимать функции задачи и представлять задачу как цель или как средство обучения.

Познавательный процесс можно охарактеризовать такой последовательностью: заключенная в задаче информация должна быть а) получена, воспринята учеником; б) переработана в его сознании; в) закреплена в памяти. Стимулирующие приемы проявления познавательного процесса в задачи сводится к реализации данной последовательности.

Это может быть:

Словарная работа. Усвоение содержания, задачи можно считать полным, если учащимся понятны все математические термины встречающиеся в тексте. Форматы словарной работы различны. В одних случаях необходимо повторить соответствующие определения, в других – обратить внимание на грамматический состав, на происхождение слов, привести историческую справку. В познавательном отношении учащиеся с интересом воспринимают происхождение терминов.
Сообщение дополнительного познавательного материала. До учащихся не всегда доводится исторический материал, например теорема Пифагора. А следовало бы сообщить и о пифагорейской школе, об истории занимательных соотношений и т.д. Все это повышает познавательный интерес школьников.

Решение задачи различными способами служит одним из способов проверки, а так же развивает у учащихся вариативность мышления. Так же решение задач разными способами является важным средством активизации познавательной деятельности учащихся, средством развития самостоятельности, воли, настойчивости и других качеств личности. Учителю необходимо поощрять учащихся, решивших задачу нестандартным способом.

Например, в 4 (5) классе я предлагаю решить несколькими способами следующую задачу.

С двух станций, расстояние между которыми 720 км, вышли одновременно навстречу 2 поезда. Скорость первого 75 км/ч, а второго на 10 км/ч больше. На каком расстоянии друг от друга будут поезда через 4 ч?

Решение:

I способ	II способ	III способ
75+10=85 км/ч	7524=600 км	75+10=85 км/ч
75*4=300 км	10*4=40 км	85+75=160 км/ч
85*4=340 км	600+40=640 км	160*4=640 км
300+340=640 км	720-640=80 км	720-640=80 км
720-640=80 км

12 альбомов стоят 3600 р. Сколько стоят 10 таких альбомов?

При решении данной задачи учениками было предложено несколько способов решения, я приведу некоторые из них:

I способ

1) 3600:12=300 (р) – стоит один альбом

2) 300*10=3000 (р) – стоят 10 альбомов

II способ

1) 3600:12=300 (р)

2) 12*10=2 (альб)

3) 300*2=600 (р)

4) 3600-600=3000 (р)

III способ

Рассуждение: так как 12 альбомов стоят 3600 рублей, то 2 альбома стоят в 6 раз дешевле, а 10 альбомов в 5 раз дороже 2-х альбомов. 3600:6=600 (р), 600*5=3000 (р)

Использование одной задачи для решения типовых задач помогает учителю организовать самостоятельную работу, используя дифференциальный подход в обучении. Так, если в условие задачи вносить небольшие изменения, можно получить серию задач, решаемых аналогично, но с нарастающей трудностью. Решив первую задачу коллективно, учащиеся получают ориентир для дальнейшей работы, работая по возрастающей сложности. Сильным учащимся учитель может предложить сразу более сложную задачу.

Решение сложных задач комбинированием ранее решенных простых задач.

Решение задач практического характера, задач, показывающих связь между предметами, а так же задачи связанные с любимыми сказочными героями.

Например: Основное свойство дроби.

Задание: Найдите дату исторического события, вычислив натуральное число, которое надо записать вместо буквы, чтобы было верным равенство:

а) 12/21=Х/7, Х – в этом веке началось великое перенаселение народов (Х=IV век)

б) 169/Х=9/81

Х – год гибели Фернандо Магеллана, возглавившего первую в истории кругосветную экспедицию, в результате которой была окончательно доказана шарообразность Земли.

Задание по теме: Умножение и деление десятичных дробей:

Вычислите y и x и определите даты исторического события

а) y=(156,36+258,64)*53,29-20670,35

y – год изобретения книгопечатания И. Гуттенбергом (1445)

б) x=(894,222+3905,5317):14,23+527,81

x – год создания Кириллом и Мефодием славянской азбуки (863)

Задача по теме «Решение задач с помощью уравнения». По «Росписному списку» в 1638 г в Москве работало пирожников на 43 человека больше, чем калачников, а хлебников – на 19 больше, чем пирожников. Сколько мастеров каждой профессии работало в Москве в 1638 г., если известно, что всего их было 167 человек.

Задача по теме: «Действия с дробями: Проценты»

Кролик живет до 12 лет, что составляет: а) 6/7 жизни овцы, б) 2/3 жизни козы, в) 3/5 жизни фазана. Сколько живут овца, коза, фазан?
В Московском Кремле находятся Царь-пушка и Царь-колокол, отлитые русскими мастерам. Масса колокола 200 т, а масса пушки составляет 20% массы колокола. Найдите массу пушки.
Длина попугая 0,24 м, длина удава равна 38 попугаям. Найдите длину удава в метрах.

Использование задач с «изюминкой», над которыми надо сначала подумать, прежде чем найти способы их решения. Такие задачи развивают логическое мышление. Их можно найти как в учебниках в разделе «Задачи повышенной сложности», так и в различных сборниках задач по математике, олимпиадных задач.

Blog

«Активизация познавательного интереса учащихся на уроках математики»