Старинные задачи по математике
| Вид материала | Задача |
- Старинные задачи по математике Учебно-творческий проект моу «сош №118» г. Омска, 52.97kb.
- Программа по математике, 361.56kb.
- Программа пропедевтического курса химии для 7 класса составленная и апробированная, 170.32kb.
- План лекции: Предмет теории и методики обучения математике. Задачи школьного курса, 521.87kb.
- Самостоятельная работа студентов по теории и методике обучения математике, 359.95kb.
- Методические материалы по математике для средних школ. Задачи математических олимпиад, 14.49kb.
- Задачи: Собрать и изучить материал о возникновении системы счета в математике, 331.18kb.
- Задачи практические (старинные) заключение список литературы введение, 165.56kb.
- Задачи практические (старинные) заключение список литературы введение, 388.87kb.
- А. Н. Книга для чтения по охране природы. Охрана окружающей среды: Справочник, 1039.19kb.
Старинные задачи по математике.
1 задание. Определить автора старинной задачи.
Задача №1. Задача Пифагора
В
еликий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности. Воображению юного Пифагора очень скоро стало тесно на маленьком Самосе, и он отправляется в Милет, где встречается с другим ученым — Фалесом. По совету Фалеса Пифагор отправляется в Египет за знаниями.Несмотря на рекомендательное письмо фараона, хитроумные жрецы не спешили раскрывать Пифагору свои тайны, предлагая ему сложные испытания. Но влекомый жаждой к знаниям, Пифагор преодолел их все. Научившись всему, что дали ему жрецы, он двинулся на родину в Элладу. Однако, проделав часть пути, Пифагор решается на сухопутное путешествие, во время которого его захватил в плен Камбиз, царь Вавилона, направлявшийся домой. Не стоит драматизировать жизнь Пифагора в Вавилоне, т.к. великий властитель Кир был, терпим ко всем пленникам. Вавилонская математика была, бесспорно, более развитой (примером этому может служить позиционная система исчисления), чем египетская, и Пифагору было чему поучиться. Но в 530 г. до н.э. Кир двинулся в поход против племен в Средней Азии. И, пользуясь переполохом в городе, Пифагор сбежал на родину. А на Самосе в то время царствовал тиран Поликрат. Конечно же, Пифагора не устраивала жизнь придворного полураба, и он удалился в пещеры в окрестностях Самоса. После нескольких месяцев притязаний со стороны Поликрата, Пифагор переселяется в Кротон, где и задумывает создать собственную философскую школу.
В Кротоне Пифагор учредил нечто вроде религиозно-этического братства или тайного монашеского ордена ("пифагорейцы"), члены которого обязывались вести так называемый пифагорейский образ жизни. Это был одновременно и религиозный союз, и политический клуб, и научное общество. Довольно быстро он завоевывает большую популярность среди жителей Кротона.
Пифагор и его ученики придали геометрии научный характер, внесли ценный вклад в развитие математики и астрономии. Кроме знаменитой теоремы, носящей его имя, Пифагору приписывается доказательство теоремы о сумме внутренних углов треугольника; задача о покрытии, т.е. делении плоскости на правильные многоугольники; геометрические способы решения квадратных уравнений и многое другое....Прошло 20 лет. Слава о братстве разнеслась по всему миру. Однажды к Пифагору приходит Килон, человек богатый, но злой, желая спьяну вступить в братство. Получив отказ, Килон начинает борьбу с Пифагором, воспользовавшись поджогом его дома. При пожаре пифагорейцы спасли жизнь своему учителю ценой своей, после чего Пифагор затосковал и вскоре покончил жизнь самоубийством.
Теорема Пифагора имеет богатую историю. Задолго до Пифагора была известна египтянам, вавилонянам, китайцам и индийцам. По свидетельству Прокла (Византия), доказательство придумано самим Евклидом, оно приведено в предложении 47 первой книги "Начал".
За VIII в. до н.э. теорема была хорошо известна индийцам под названием «правила веревки» и использовалась ими для построения алтарей. Доказательство Пифагора до нас не дошло. В книге Лумиса «Теорема Пифагора», 1968г. Приводится 370 различных доказательств теоремы.
Задача №2. Задача Арибхаты.
А
риабхата (Ариабата)Aryabhata
(476 - ок. 550), по другим источникам (476 г. - год смерти неизвестен)
Индийский астроном и математик. Родился в Кусумапуре (близ Паталипутры, Индия). В Паталипутре (ныне Патна, Бихар) преподавал тригонометрию и алгебру.
Из двух написанных им сочинений сохранилось только одно – Ариабхатия (499), в котором в стихотворной форме изложены математические сведения, необходимые для астрономических вычислений; приведены задачи на составление и решение уравнений, извлечение квадратного и кубического корней и др. Большая часть этой работы посвящена астрономии и сферической тригонометрии. Приведены также 33 правила по арифметике, алгебре и тригонометрии на плоскости. Продемонстрировано исследование неопределенных уравнений с помощью бесконечных дробей.
Ариабхата изобрёл понятие "нуля", нашел весьма точное значение числа «пи» (62832/20000 = 3.1416) и ввел в тригонометрию функцию (1 – cos x). Ученый высказал догадку, что вращение небес – только кажущееся и является следствием вращения Земли вокруг своей оси. Именем Ариабхаты назван первый индийский искусственный спутник Земли, запущенный 19 апреля 1975 с помощью советской ракеты-носителя и предназначенный для изучения Солнца, земной ионосферы и космических рентгеновских источников.
Данная задача взята из трактата «Ариабхатиам» известного индийского математика конца V-начала VI в.в. Ариабхаты. Этот трактат посвящен астрономии и математике. В математической части своего сочинения Ариабхата дает ряд правил по арифметике, алгебре, геометрии и тригонометрии, нужных для астрономии и в первую очередь для составления астрономических таблиц. Ариабхата является автором многих интересных задач по элементарной математике, одна из которых и приводится.
Задача №3. Задача Эйлера.
Леонард Эйлер (1707-1783) – крупнейший математик, друг М.В. Ломоносова.
Родился Эйлер в небольшом городке Базеле. Первоначальное образование получил у своего отца. Свои познания в области математики совершенствовал под руководством крупнейшего швейцарского математика Иоганна Бернулли.
В 19 лет Эйлер написал диссертацию об оснастке кораблей, за что был премирован Парижской академией наук. В 20 лет он по рекомендации братьев Бернулли получил приглашение и стал адъюнктом Петербургской академией наук. В конце 1740 года в России в связи с приходом к власти Анны Леопольдовны сложилась тревожная обстановка, и Эйлер переехал в Берлин. Находясь в Берлине, Эйлер поддерживал тесную связь с русской академией и был ее почетным членом. Через 25 лет он снова вернулся в Россию.
Эйлер отличался исключительной работоспособностью. Последние 27 лет жизни он работал, будучи совершенно слепым, не ослабляя своей огромной продуктивности.
Всего Эйлером написано 865 оригинальных работ, что составляет около 70 томов. Научные интересы Эйлера весьма разнообразны. Он сделал замечательные открытия буквально по всем разделам элементарной и высшей математики, в области механики и астрономии. Эйлер - автор замечательного руководства по алгебре «Полное введение в алгебру» (1770), которое явилось образцом для составления современных учебников по этому предмету.
Эйлер, именем которого названы теоремы, уравнения, формулы и т. д., обрел в России вторую родину и проработал в Петербургской академии наук более 30 лет. Умер он в Петербурге 7 сентября 1783 года. Похоронен в Петербурге в Александро-Невской лавре.
Семь мосто́в Кёнигсберга существовали в Кёнигсберге (нынешнем Калининграде) в XVI—XX веках. Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам, не проходя ни по одному из них дважды? Многие кёнигсбержцы пытались решить эту задачу, как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.
В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, приведшие к возникновению теории графов, пользуясь которым легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них (в случае семи мостов Кёнигсберга это невозможно).
На упрощённой схеме части города (графе) мостам соответствуют линии (рёбра графа), а частям города - точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:
- Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа всегда чётно. Невозможно начертить граф, который имел бы нечётное число нечётных вершин.
- Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
- Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
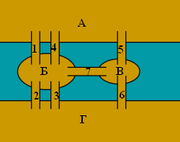
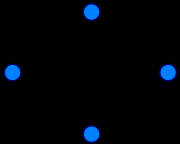
Упрощённая схема мостов Кёнигсберга. Граф кёнигсбергских мостов
Значение букв и цифр - см. комментарий
к старинной карте Кёнигсберга
Созданная Эйлером теория графов нашла очень широкое применение: например, её используют при изучении транспортных и коммуникационных систем, в частности, для маршрутизации данных в Интернете.
Задача №4. Задача из «Азбуки» Л.Н. Толстого.
Лев Николаевич Толстой (28 августа (9 сентября) 1828, усадьба Ясная Поляна Тульской губернии - 7 (20) ноября 1910, станция Астапово (ныне станция Лев Толстой) Рязано-Уральской железной дороги; похоронен в Ясной Поляне), граф, русский писатель.
Толстой был четвертым ребенком в большой дворянской семье. Его мать, урожденная княжна Волконская, умерла, когда Толстому не было еще двух лет, но по рассказам членов семьи он хорошо представлял себе "ее духовный облик": некоторые черты матери (блестящее образование, чуткость к искусству, склонность к рефлексии) и даже портретное сходство Толстой придал княжне Марье Николаевне Болконской ("Война и мир"). Отец Толстого, участник Отечественной войны, запомнившийся писателю добродушно-насмешливым характером, любовью к чтению, к охоте (послужил прототипом Николая Ростова), тоже умер рано (1837). Воспитанием детей занималась дальняя родственница Т. А. Ергольская, имевшая огромное влияние на Толстого: "она научила меня духовному наслаждению любви". Детские воспоминания всегда оставались для Толстого самыми радостными: семейные предания, первые впечатления от жизни дворянской усадьбы служили богатым материалом для его произведений, отразились в автобиографической повести "Детство".
Когда Толстому было 13 лет, семья переехала в Казань, в дом родственницы и опекунши детей П. И. Юшковой. В 1844 году Толстой поступил в Казанский университет на отделение восточных языков философского факультета, затем перевелся на юридический факультет, где проучился неполных два года: занятия не вызывали у него живого интереса и он со страстью предался светским развлечениям. Весной 1847 года , подав прошение об увольнении из университета "по расстроенному здоровью и домашним обстоятельствам", Толстой уехал в Ясную Поляну с твердым намерением изучить весь курс юридических наук (чтобы сдать экзамен экстерном), "практическую медицину", языки, сельское хозяйство, историю, географическую статистику, написать диссертацию и "достигнуть высшей степени совершенства в музыке и живописи".
В 1859 году Толстой открыл в деревне школу для крестьянских детей, помог устроить более 20 школ в окрестностях Ясной Поляны, и это занятие настолько увлекло Толстого, что в 1860 году он вторично отправился за границу, чтобы знакомиться со школами Европы. Толстой много путешествовал, провел полтора месяца в Лондоне (где часто виделся с Герценом), был в Германии, Франции, Швейцарии, Бельгии, изучал популярные педагогические системы, в основном не удовлетворившие писателя. Собственные идеи Толстой изложил в специальных статьях, доказывая, что основой обучения должна быть "свобода учащегося" и отказ от насилия в преподавании. В 1862 году издавал педагогический журнал "Ясная Поляна" с книжками для чтения в качестве приложения, ставшими в России такими же классическими образцами детской и народной литературы, как и составленные им в начале 1870-х годов. "Азбука" и "Новая Азбука". В 1862 году в отсутствие Толстого в Ясной Поляне был проведен обыск (искали тайную типографию).
Годы перелома круто изменили личную биографию писателя, обернувшись разрывом с социальной средой и приведя к семейному разладу (провозглашенный Толстым отказ от владения частной собственностью вызывал резкое недовольство членов семьи, прежде всего жены). Пережитая Толстым личная драма нашла отражение в его дневниковых записях. Поздней осенью 1910 года, ночью, тайно от семьи, 82-летний Толстой, сопровождаемый лишь личным врачом Д. П. Маковицким, покинул Ясную Поляну. Дорога оказалась для него непосильной: в пути Толстой заболел и вынужден был сойти с поезда на маленькой железнодорожной станции Астапово. Здесь, в доме начальника станции он провел последние семь дней своей жизни. За сообщениями о здоровье Толстого, который к этому времени приобрел уже мировую известность не только как писатель, но и как религиозный мыслитель, проповедник новой веры, следила вся Россия. Событием общероссийского масштаба стали похороны Толстого в Ясной Поляне.
Указание Л.Н. Толстого к задаче:
«До тих пор, пока барин выехал из Тулы, сколько мужик ушел? Когда барин выехал и мужик шел, сколько барин в час наверстывал на мужике7 На сколько он приближался к мужику в каждый час? В сколько ж часов барин нагонит мужика? Когда узнаешь , в сколько часов нагонит, тогда сочти, сколько часов ехал барин по 11 верст в час?» (Верста приближенно равна 1, 0668 км).
Задача №5. Задача из рассказа А.П. Чехова «Репетитор»
Чехов Антон Павлович 
(1860 — 1904), прозаик, драматург.
Родился 17 января (29 н.с.) в Таганроге в купеческой семье, со строгими правилами воспитания. С детских лет Чехов помогал отцу в лавке. В 1868 поступил в гимназию. Когда вся семья Чеховых переехала в Москву, будущий писатель остался в Таганроге и зарабатывал на жизнь репетиторством, чтобы окончить учение. Окончив гимназию в 1879, уехал в Москву и поступил на медицинский факультет Московского университета.
В 1884, получив звание уездного врача, Чехов начал заниматься врачебной практикой. Еще будучи гимназистом, он писал юморески, участвуя в гимназическом журнале. В студенческие годы, чтобы зарабатывать себе на жизнь, сотрудничал в журналах "Стрекоза", "Будильник", "Зритель" и др., подписываясь разными псевдонимами, но чаще всего Антоша Чехонте. С 1882 писал для петербургского журнала "Осколки"( №6 «Репетитор» с подзаголовком «Сценка», 1884г.) вел обозрение "Осколки московской жизни". В 1884 вышла первая книга рассказов Чехова — "Сказки Мельпомены", затем следуют "Пестрые рассказы" (1886), "В сумерках" (1887), "Хмурые люди" (1890). В эти годы писатель испытывает сильное влияние Л. Толстого, которое сказывается в рассказах "Именины", "Скучная история". Неудовлетворенность своим творчеством, своими знаниями, особенно знанием жизни, подвигает его на решение, удивившее современников, — ехать на остров Сахалин, остров царской каторги и ссылки. Это путешествие было подвигом писателя. Поездка через всю страну, пребывание на Сахалине, изучение жизни каторжан и ссыльных, проведенная Чеховым перепись населения Сахалина — все это оставило глубокий след в его творческом сознании. После возвращения он написал книгу "Остров Сахалин" (1893 — 94); отразились сахалинские впечатления и в рассказах "В ссылке" (1892), "Палата № б". Поездка значительно ухудшила состояние здоровья Чехова: обострился туберкулезный процесс.
В конце 1880 он много работал для театра: пьесы "Иванов", "Леший", "Свадьба", водевили "Медведь", "Юбилей" и др.
В 1892 Чехов купил имение Мелихово, где помогал местным крестьянам как врач, строил школы для крестьянских детей, выезжал в губернии, охваченные голодом, участвовал во всеобщей переписи населения.
В Мелихово было написано много прекрасных произведений: "Попрыгунья", "Скрипка Ротшильда", "Учитель словесности", "Чайка", "Дядя Ваня" и др. В начале века Чехов создал такие замечательные пьесы, как "Три сестры" и "Вишневый сад". Все пьесы были поставлены на сцене МХАТа.
В 1898 Чехов переехал в Ялту, где построил дом, в котором у него бывали Л. Толстой, М. Горький; Бунин, Куприн, художник И. Левитан. В 1901 Чехов женился на актрисе МХАТа О. Книппер.
В последние годы писатель был занят подготовкой своего собрания сочинений, вышедшего двумя изданиями (1899 — 1902 и 1903) в издательстве А. Маркса.
В 1904 в связи с резким ухудшением здоровья Чехов поехал для лечения в Германию, на курорт Баденвейлер. Здесь 2 июня (15 н.с.) он скончался.
Как известно, Чехов происходил из семьи торговца. Его отец Павел Егорович держал бакалейную лавку с весьма замысловатой вывеской «Чай, сахар, кофе, мыло, колбаса и другие колониальные товары». Дела шли плохо и, окончательно запутавшись в долгах, отец семейства покидает семью и скрывается в Москве. Вот тогда-то сын Антон, будучи гимназистом в Таганроге, был вынужден зарабатывать средства к жизни репетиторством. Отсюда, по всей вероятности, и возникла идея для будущего рассказа. Рассказ "Репетитор" (1884г.) относится к тем произведениям Чехова, в которых он откровенно смеется над людьми. Чехов с тонким юмором описывает, как беспомощно трудились над задачей и семикласник репетитор, и его ученик, 12-летний Петя, пока не выручил их Петин отец, Удодов. Этот рассказ интересен не только с литературной стороны, но и с математической. Эта история с задачей, заставляющая нас смеяться над конфузом злосчастного репетитора, задает сама три задачи: - Как намеревался репетитор решить задачу алгебраически?
- Как должен был решить ее Петя?
- Как решил ее отец Пети на счетах "по-неученому"?
Рассмотрим их по порядку.
1. Семикласник-репетитор готов был решать задачу "с иксом и игреком", будучи уверен, что задача - "собственно говоря, алгебраическая". И он, надо думать, легко справился бы с ней, прибегнув к помощи системы двух уравнений:
X + Y = 138
5X + 3Y = 540
2. Однако, задача легко решается и арифметически. Если бы вам пришлось решать ее, вы начали бы с предположения, что все купленное сукно было синее. Тогда партия в 138 аршин стоила бы 5 * 138 = 690 рублей; это на 690 - 540 = 150 рублей больше того, что было заплачено в действительности. Разница в 150 рублей указывает, что в партии имелось более дешевое сукно по 3 рубля за аршин. Дешевого сукна было столько, что из двух-рублевой разницы на каждом аршине составилось 150 рублей: 150 / 2 = 75 аршин красного сукна и 138 - 75 = 63 - синего сукна.
3. В рассказе говорится очень кратко: "Он щелкает на счетах, и у него получается 75 и 63, что и нужно было". В чем однако состояло это "щелканье на счетах"? Каков способ решения задачи с помощью счетов?
Разгадка такова: злополучная задача решается на счетах тем же приемом, что и на бумаге, - теми же арифметическими действиями. Но выполнение их упрощается, благодаря преимуществам, которые наши русские счеты предоставляют всякому, умеющему с ними обращаться. Очевидно, "отставной губернский секретарь" Удодов хорошо умел считать на счетах, потому-что их косточки быстро, без помощи алгебры, открыли ему то, чего репетитор-семикласник добивался узнать "с иксом и игреком".
Проследим же, какие действия должен был проделать на счетах Петин отец. Прежде всего ему нужно было, как мы знаем, умножить 138 на 5. Для этого он, по правилам действий на счетах, умножил сначала 138 на 10, - т.е. просто перенес 138 одним рядом выше, - а затем разделил это число пополам опять-таки на счетах же. Деление начинают снизу: откидывают половину косточек, отложенных на каждой проволоке; если число косточек на данной проволоке нечетное, то выходят из затруднения, "раздробляя" одну косточку этой проволоки на 10 нижних. В нашем случае делят 1380 пополам так: на нижней проволоке, где отложено 8 косточек, откидывают 4 косточки (4 десятка), на средней проволоке из 3 косточек откидывают 1 , а оставшуюся 1 косточку заменяют мысленно 10-ю нижними и делят пополам, добавляя 5 десятков к косточкам нижней; на верхней проволоке раздробляют одну косточку, прибавляя 5 сотен к косточкам средней проволоки. В результате на верхней проволоке совсем не остается косточек : на средней 1 + 5 = 6 сотен, на нижней 4 + 5 = 9 десятков. Итого 690 единиц. Далее Удодову-старшему нужно было из 690 вычесть 540. Наконец, полученную разность, 150, оставалось разделить пополам: Удодов откинул из 5 косточек (десятков) 2, отдав 5 единиц нижнему ряду косточек; потом из 1 косточки на проволоке сотен отдал 5 десятков нижнему ряду: получилось 7.
Рефлексия:
1. Чем вам понравился данный этап?
Данный этап понравился подбором задач, необходимостью рассказать не только об авторе, но и об истории возникновения задачи. Мы узнали много нового.
2. Какие затруднения были, и в каких заданиях?
Затруднений на данном этапе не возникало.