Электрофизические свойства пленок In
| Вид материала | Документы |
- «Обзор методов получения пленок и их свойств», 131.51kb.
- Свойства млэ пленок нитрида алюминия, 10.62kb.
- Электропроводность тонких пленок ni и сплавов ni-Cu в слабых магнитных полях в интервале, 253.63kb.
- Шматова Юлия Васильевна, 262.24kb.
- Тема: " Арсенид индия. Свойства, применение. Особенности получения эпитаксиальных пленок.", 235.74kb.
- Реферат по научно-исследовательской работе г 08 Нано- и микроструктурная модификация, 64.1kb.
- Иванов В. А.,Викторов И. А.,Гременок В. Ф.,Зарецкая, 17.52kb.
- Гудин Сергей Анатольевич. 15. 15-15. 55 пригл доклад, 457.54kb.
- 1. Определение электронных приборов. Классификация электронных приборов по характеру, 163.96kb.
- Газочувствительные свойства тонких пленок металлокомплексов этиопорфирина-ii, 274.65kb.
Электрофизические свойства пленок In2O3(Sn)
В СЛАБЫХ МАГНИТНЫХ ПОЛЯХ
Ищук Л.В., Жарких Ю.С., Лысоченко С.В.
Киевский национальный университет имени тараса Шевченко, Киев
E-mail : lessya@univ.kiev.ua
Пленки легированного оловом оксида индия (ITO – indium-tin oxide) обладают уникальным сочетаниям свойств, а именно, електропроводностью и прозрачностью в видимой области спектра. Благодаря этим свойствам они могут быть использованы в разнообразных фотоелектрических приборах, полупроводниковых преобразователях солнечной енергии и в других технических применениях [1,....].. Большое значение для применения пленок может иметь наличие в них подсистемы електронов проводимости с малой еффективной массой и сверхбольшими значениями подвижности [2,....]. При низких температурах и наличии размерного квантования 2D газа электронов создаются условия проявления фундаментальных квантовых и спинзависимых эффектов в явлениях переноса.
Исследовались тонкие 2D пленки ITO полученные методом магнетронного распыления. Концентрация олова составляла (9-11)%. В интервале температур Т=(4,2-300)К измерены магнитополевые зависимости кинетических коэфициентов при изменении магнитного поля В от 0 до 2Т.
Относительная величина продольного магнитосопротивления (ρхх(В)-ρхх(0))/ρхх(0) демонстрировала наличие аномального магнитосопротивления (АМС). При увеличении температуры наблюдалась смена знака АМС. Эффект АМС обьяснен на основе терии квантовых поправок к проводимости в которой учитывается спин-зависимая интерференция когерентных електронных волн, распространяющихся по замкнутых траекториях. Проведенное компьютерное моделирование при Т=4,2К позволило определить время релаксации фазы волновой функции електронов
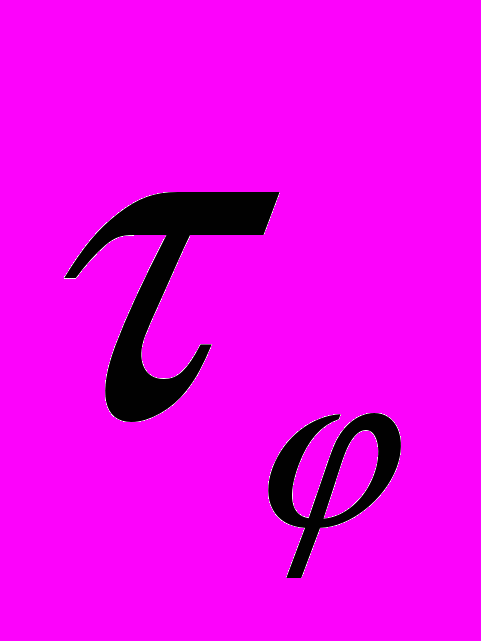 ≈2·10-9с и длину диффузии Lφ=(D
≈2·10-9с и длину диффузии Lφ=(D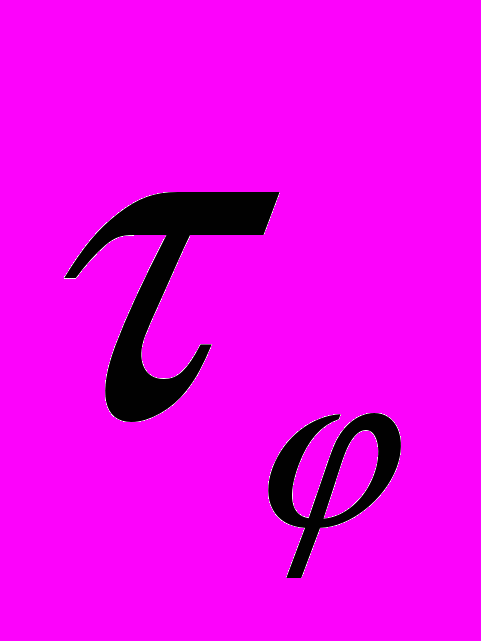 )1/2≈(2-3)·10-6см, величины которых ограничивают сверху вклад неупругих взаимодействий в системе. Согласование экспериментальных и расчетных кривых в интервале температур Т=(4,2-50)К позволило оценить вклад спин-орбитального взаимодействия в случайном поле примесей, которое приводит к хаотическим изменениям ориентации электронных спинов. Оно увеличивает часть интерференционных взаимодействий електронов в синглетном состоянии и уменьшает часть триплетных, которые угнетаются спин-орбитальным взаимодействием.
)1/2≈(2-3)·10-6см, величины которых ограничивают сверху вклад неупругих взаимодействий в системе. Согласование экспериментальных и расчетных кривых в интервале температур Т=(4,2-50)К позволило оценить вклад спин-орбитального взаимодействия в случайном поле примесей, которое приводит к хаотическим изменениям ориентации электронных спинов. Оно увеличивает часть интерференционных взаимодействий електронов в синглетном состоянии и уменьшает часть триплетных, которые угнетаются спин-орбитальным взаимодействием.В интервале магнитных полей (0-0,05)Т наблюдалась аномальная зависимость Холловской подвижности μh от магнитного поля В. Показано, что аномальная часть зависимости μh(В) является следствием индуцированной магнитным полем локализации электронов в высоколегированных пленках с спин-орбитальным взаимодействием. Определена подвижность μ, концентрация Г и величина эффективной массы электронов в исследованых слоях.
2. Дослідні зразки
Плівки ІТО виготовлялись методом магнетронного розпорошення. Концентрація олова в досліджуваних зразках становила 11%. Плівки мали В работе рассмотрено состояние исследований пленок In2O3(Sn), обладающих уникальной комбинацией свойств – высокими электропроводностью, коэффициентом отражения света в ближней ИК и прозрачностью в видимой частях спектра, а также приведены результаты оригинальных исследований таких пленок в слабых магнитных полях в интервале температур 4,2-450К.
Впервые в пленках In2O3(Sn) экспериментально наблюдалась нелинейная зависимость поля Холла от индукции магнитного поля. Эффект объяснен на основе модели, учитывающей наличие в пленке “медленных” и “быстрых” электронов. Из сопоставления результатов эксперимента и теоретических расчетов определены их концентрация и подвижность.
При исследовании пленок In2O3(Sn) в интервале температур 4,2-50К обнаружена аномальная зависимость холловской подвижности от магнитного поля. Показано, что зависимость холловской подвижности от магнитного поля определяется спин-зависимой квантовой интерференцией электронных волн, а ее аномальная часть является следствием индуцированной магнитным полем локализации электронов. Определены границы применения классической теории Холла в условиях локализации и значение эффективной массы электронов в исследуемых пленках.
НАЗВАНИЕ
Фио
Название организации, город
Контактный Емаил
Текст по ширине без переноса слов
І. Вступ
Гальваномагнітні дослідження тонких плівок легованого оловом оксиду індію (ІТО – indium-tin oxide) проведені в [1] виявили ряд особливостей поведінки їх кінетичних коефіцієнтів, пов’язаних із розсіянням двовимірних (2D) електронів на заряджених центрах в умовах розмірного квантування й одночасного прояву ефектів слабкої локалізації. Важливість цих досліджень обумовлена як можливістю експериментальної перевірки існуючих теорій [2, 3] так і практичною необхідністю коректної інтерпретації результатів холівських досліджень в умовах прояву ефектів слабкої локалізації. У роботі подано результати холівських досліджень легованих плівок ІТО в інтервалі температур Т=(4,2-50)К і показано вплив спінзалежної квантової інтерференції на холівську рухливість 2D вільних носіїв заряду.
2. Дослідні зразки
Зразки із плівками ІТО були призначені для вимірювань е.р.с. Хола. Концентрація домішки олова в плівках становила 11%, а їхня товщина d≈2∙10-6см. Довжина зразка a=2 см, ширина b=0,2 см. Планарна конфігурація зразків і особливості технології їхнього виготовлення більш докладно описані в [1]. Для проведення температурних досліджень у надпровідному соленоїді розміщувався теплоізолюючий стакан, усередині якого розміщувалися зразок і нагрівач. Температура контролювалась термозалежним датчиком опору. Магнітне поле можна було орієнтувати нормально або паралельно до площини в якій знаходився зразок.
3. Результати досліджень і їх обговорення
3. 1. Аномальний магнітоопір.
На рис. 1 показані залежності відносної величини повздовжнього магнітоопору (ρхх(В)-ρхх(0))/ρхх(0) від величини магнітного поля В. Величини тензора поверхневого опору ρik, холівських рухливості μh і концентрації електронів Γh тут і надалі розраховувались на одиницю площі плівки.
Для визначення можливого впливу на результати досліджень розігріву зразка під дією струму, вимірювання проводились при п’ятьох значеннях повздовжнього електричного поля Ехх=0,32, 2, 7,6, 17,5 і 35 В/см (рис. 1(а)). Як видно з рисунку, ці залежності демонстрували наявність аномального магнітоопору (АМО), а збільшення поля Ех до величини 17,5 В/см мало впливало на його величину. Спостерігався невеликий зсув залежностей 1-4 у бік зменшення модуля величини магнітоопору |ρхх| в міру зростання Ехх в усьому дослідженому інтервалі зміни індукції В. Виняток становили вимірювання при Ехх=35В/см (крива 5), коли абсолютна величина |ρхх| зменшувалась, розкид експериментальних точок різко збільшувався, а сама величина |ρхх| ставала нестабільною в часі (розкид точок на графіку показано вертикальними рисками). В області полів В<0,5Т ефект АМО зникав, і знак магнітоопору змінювався на позитивний. Така поведінка залежності 5 може бути пояснена нагрівом зразка і є характерною рисою вимірювань у рідкому гелії. При збільшенні температури зразка до деякого критичного рівня, внаслідок утворення бульбашок, умови тепловідводу у зріджений гелій довільним чином змінюються. Виходячи із цього, для проведення вимірювань, у роботі було вибрано значення повздовжнього електричного поля Ехх=15В/см. Така величина поля була компромісною між досяжною точністю електричних вимірювань і неконтрольованими змінами температури зразка під дією протікаючого струму.
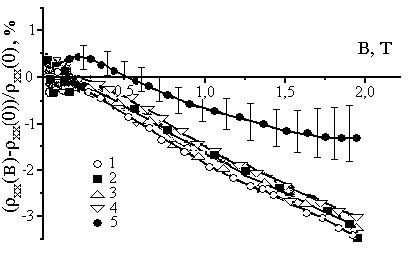
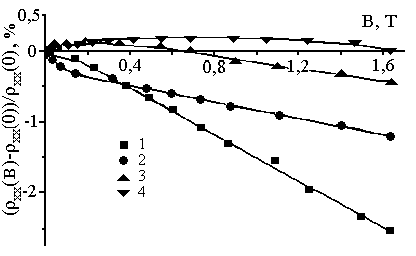
(а) (б)
Рис. 1. Залежності відносної величини повздовжнього магнітоопору (ρхх(В)-ρхх(0))/ρхх(0) від величини магнітного поля В. По рис. (а) електричне поле Ехх, В/см: 1-0,32, 2-2, 3-7,6, 4-17,5 і 5-35. Температура Т=4,2К. По рис. (б) температура вимірювань Т, К: 1-4,2, 2, 2-11, 3-25 і 4-47. Електричне поле Ехх=15В/см.
Зміна напрямку поля В із нормального на паралельний до поверхні зразка призводила до зникнення ефекту АМО, а надійно вимірюваний магнітоопір зразка не спостерігався (не перевищував ±0,5%). Це свідчило про двовимірність газу носіїв по відношенню до ефекту АМО, оскільки магнітоопір тривимірного газу не залежить від напрямку магнітного поля В [2].
На рис. 1(б) показані залежності (ρхх(В)-ρхх(0))/ρхх(0) від поля В в інтервалі температур Т=(4,2-47)К. Як видно з рисунка, збільшення температури спочатку призводило до зменшення абсолютної величини АМО, а з подальшим підвищенням температури магнітоопір змінював свій знак, що видно на кривих 3 і 4, отриманих при Т=25 і 47К. При збільшенні величини поля В ці залежності демонстрували перехід від позитивних до від’ємних значень магнітоопору.
Зміна знаку АМО, що спостерігається по рис. 1(а) і рис. 1(б) на залежностях повздовжньої компоненти тензору ρik від поля В і температури Т, може бути пояснена на основі уявлень теорії квантових поправок (ТКП) до теорії провідності, в якій враховується інтерференція когерентних електронних хвиль, що розповсюджуються по замкнутих траєкторіях. Наслідком такої інтерференції є слабка локалізація електронів при взаємодії в точці самоперетину траєкторій. Зміна знаку магнітоопору пояснюється тим, що внески інтерференційних взаємодій із повними спінами S=0 і S=1 в провідність діють у протилежних напрямках і призводять до позитивного і від’ємного знаків АМО відповідно. Триплетний внесок визначається часом
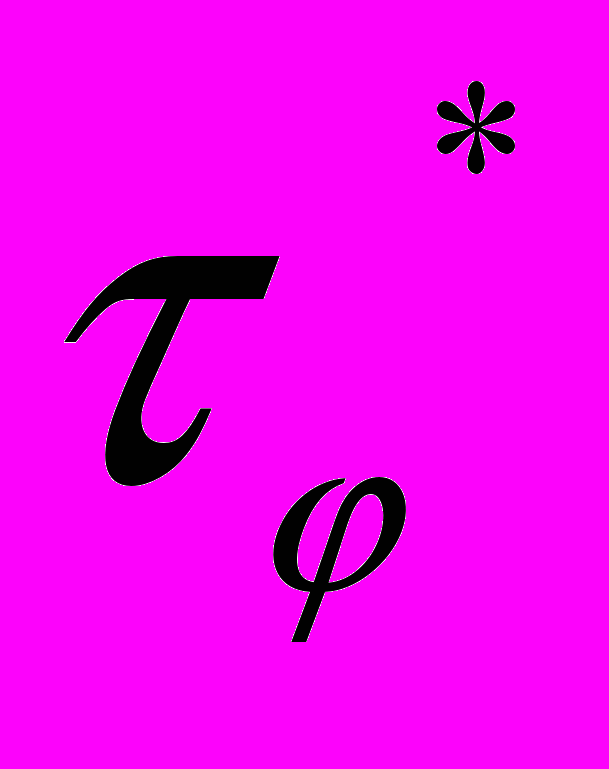 , що дорівнює [2]:
, що дорівнює [2]: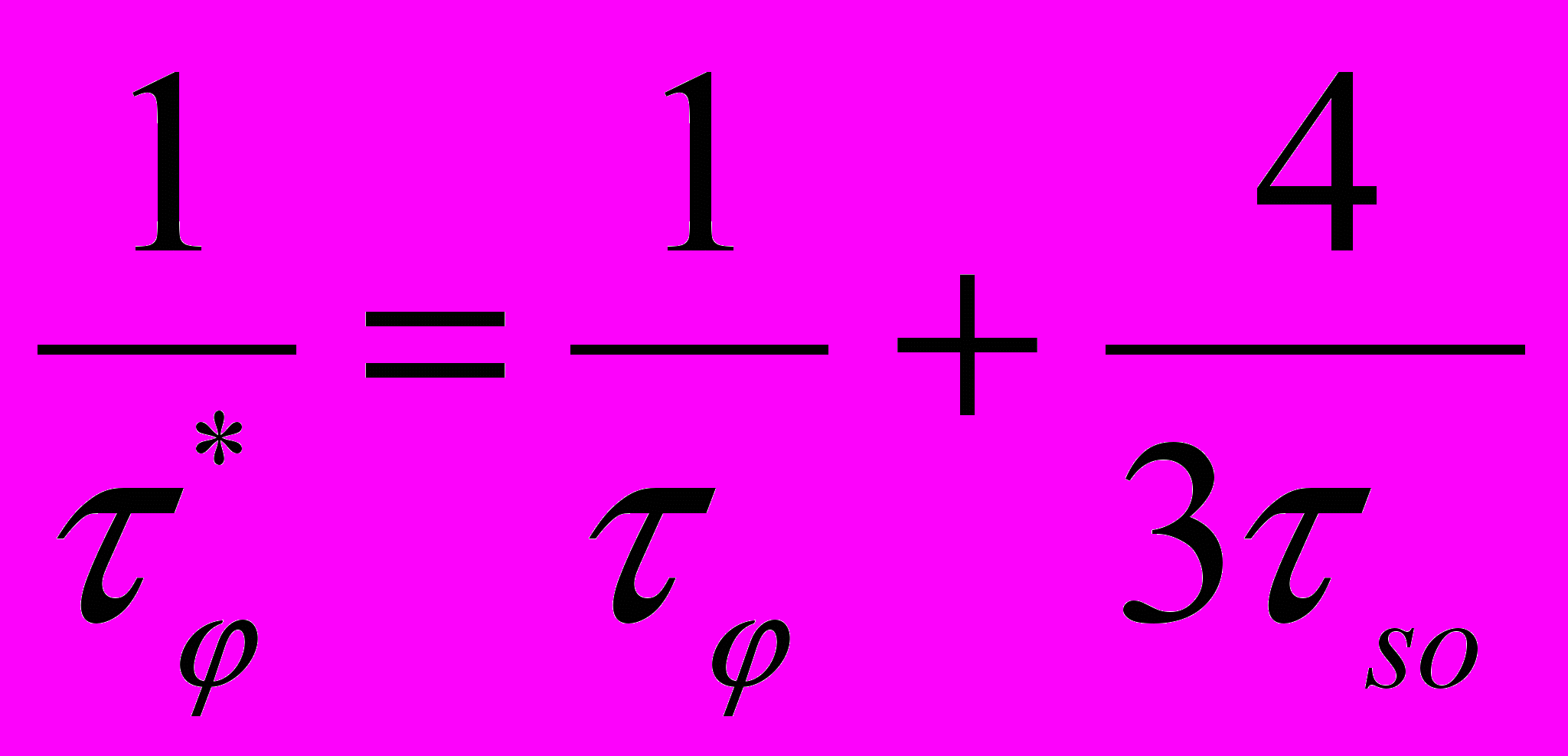 , (1)
, (1)де
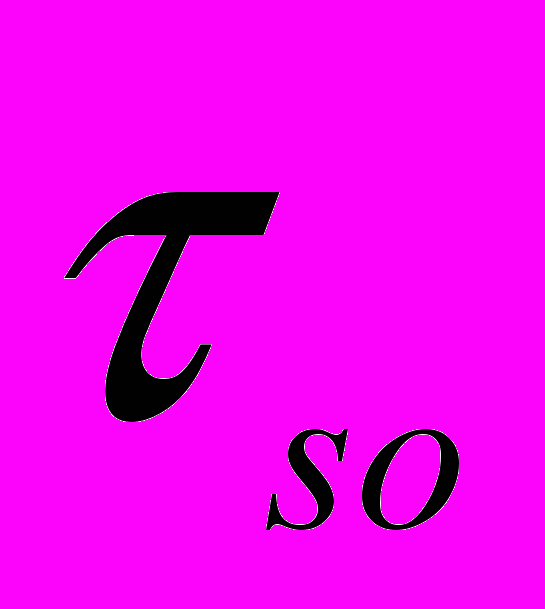 - час релаксації спін-орбітального розсіяння. Час релаксації
- час релаксації спін-орбітального розсіяння. Час релаксації 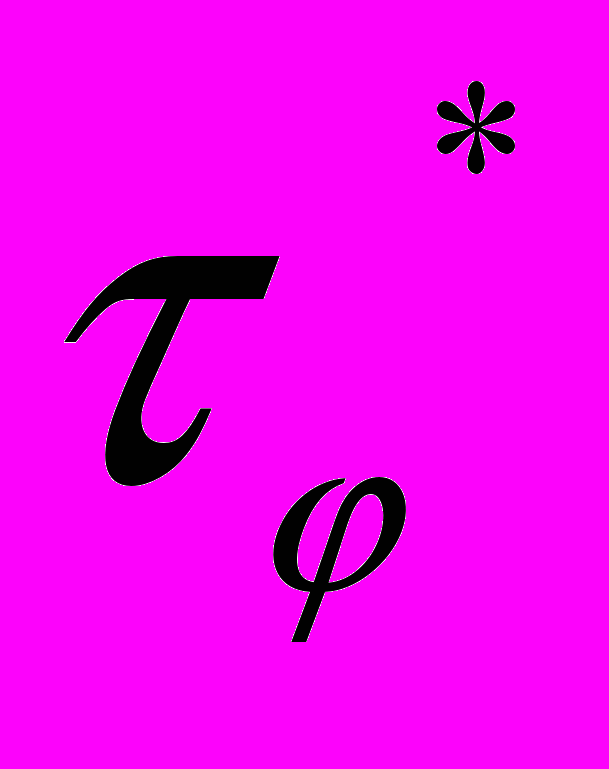 і
і 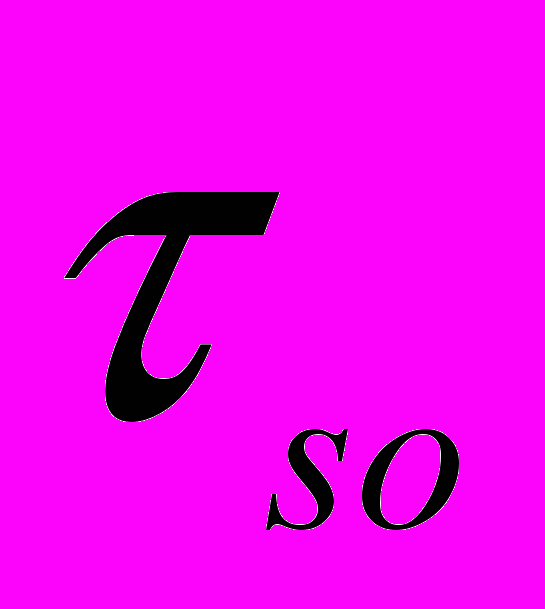 мають різну температурну залежність, що і призводить до зміни знаку АМО в залежності від температури Т і поля В. Сумарний вплив синглетного й триплетного внесків у магнітоопір визначається формулами [2]:
мають різну температурну залежність, що і призводить до зміни знаку АМО в залежності від температури Т і поля В. Сумарний вплив синглетного й триплетного внесків у магнітоопір визначається формулами [2]:σхх(В,Т)-σхх(0)=
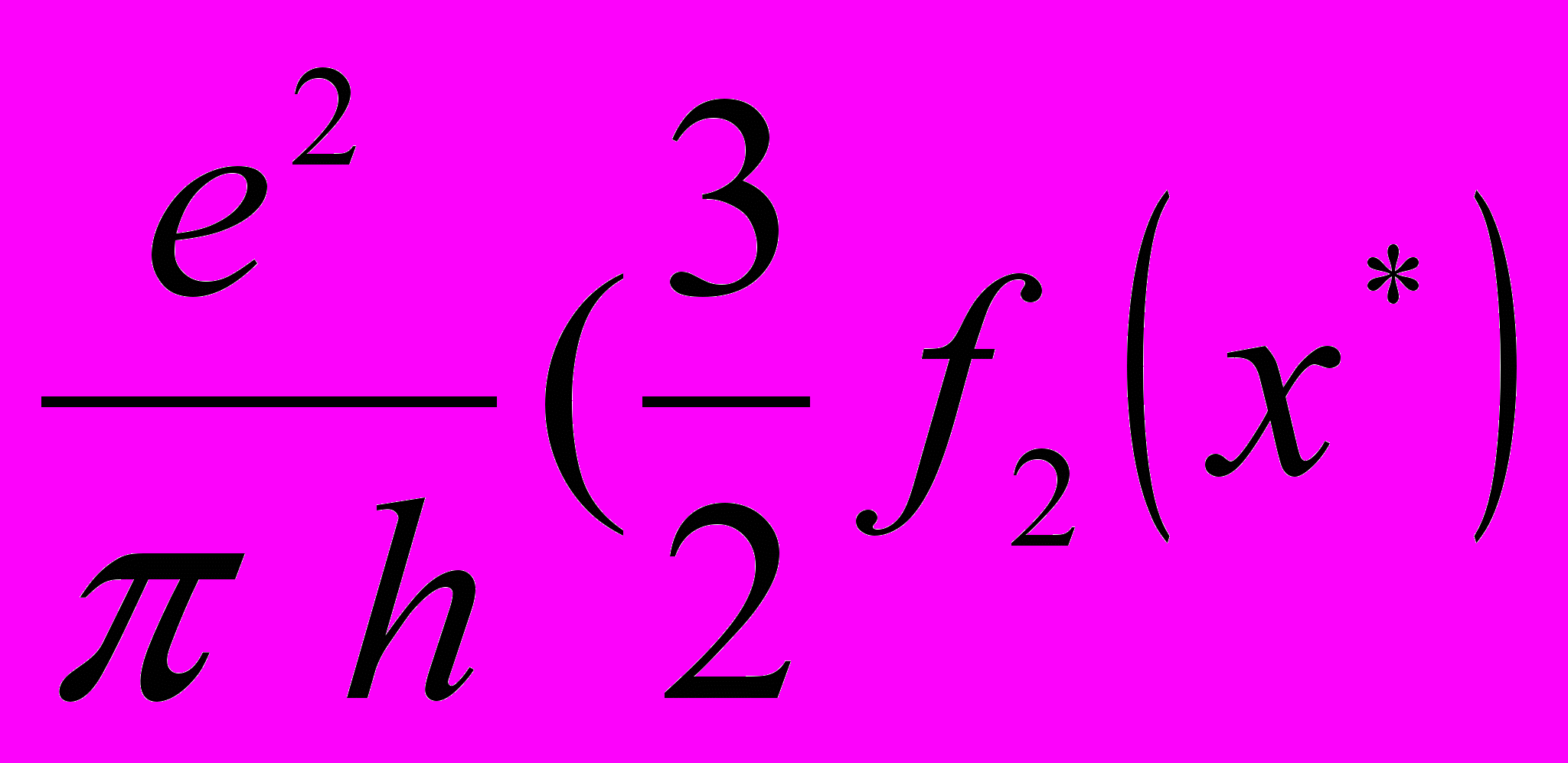 -
-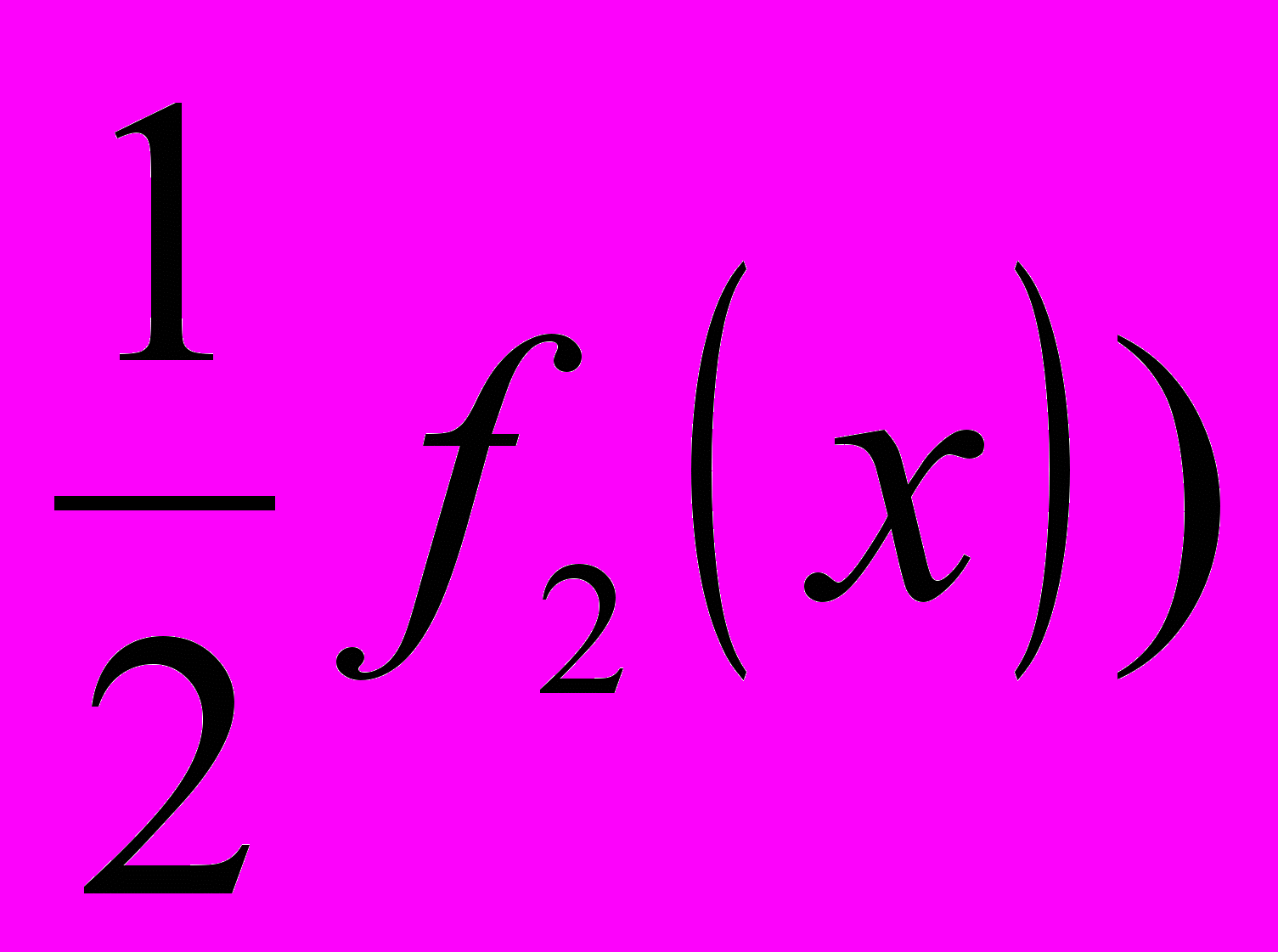 (2)
(2)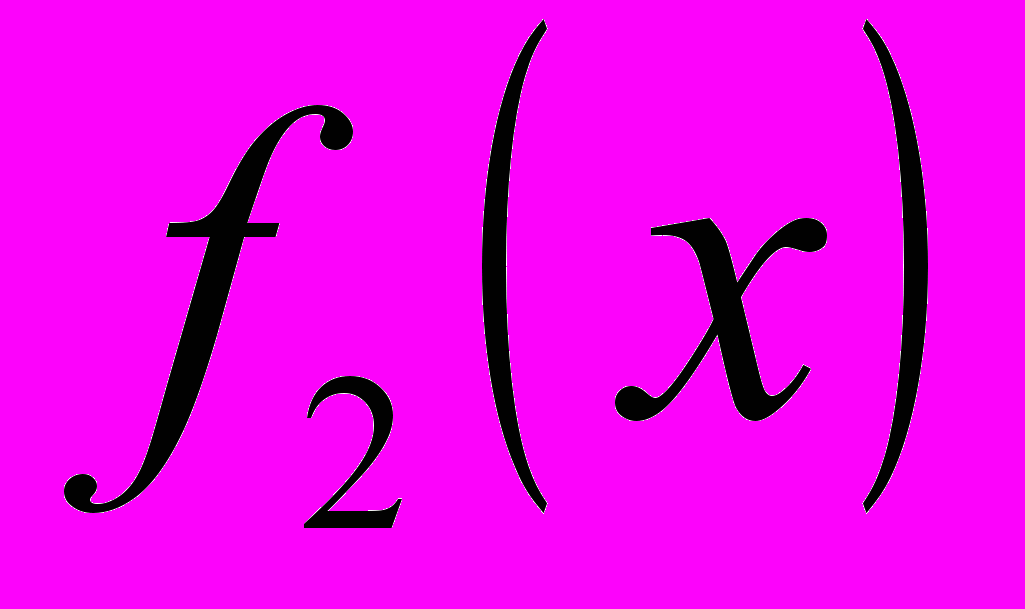 =ln
=ln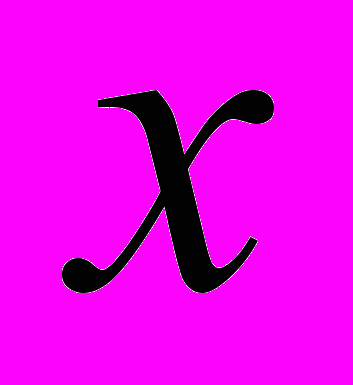 +
+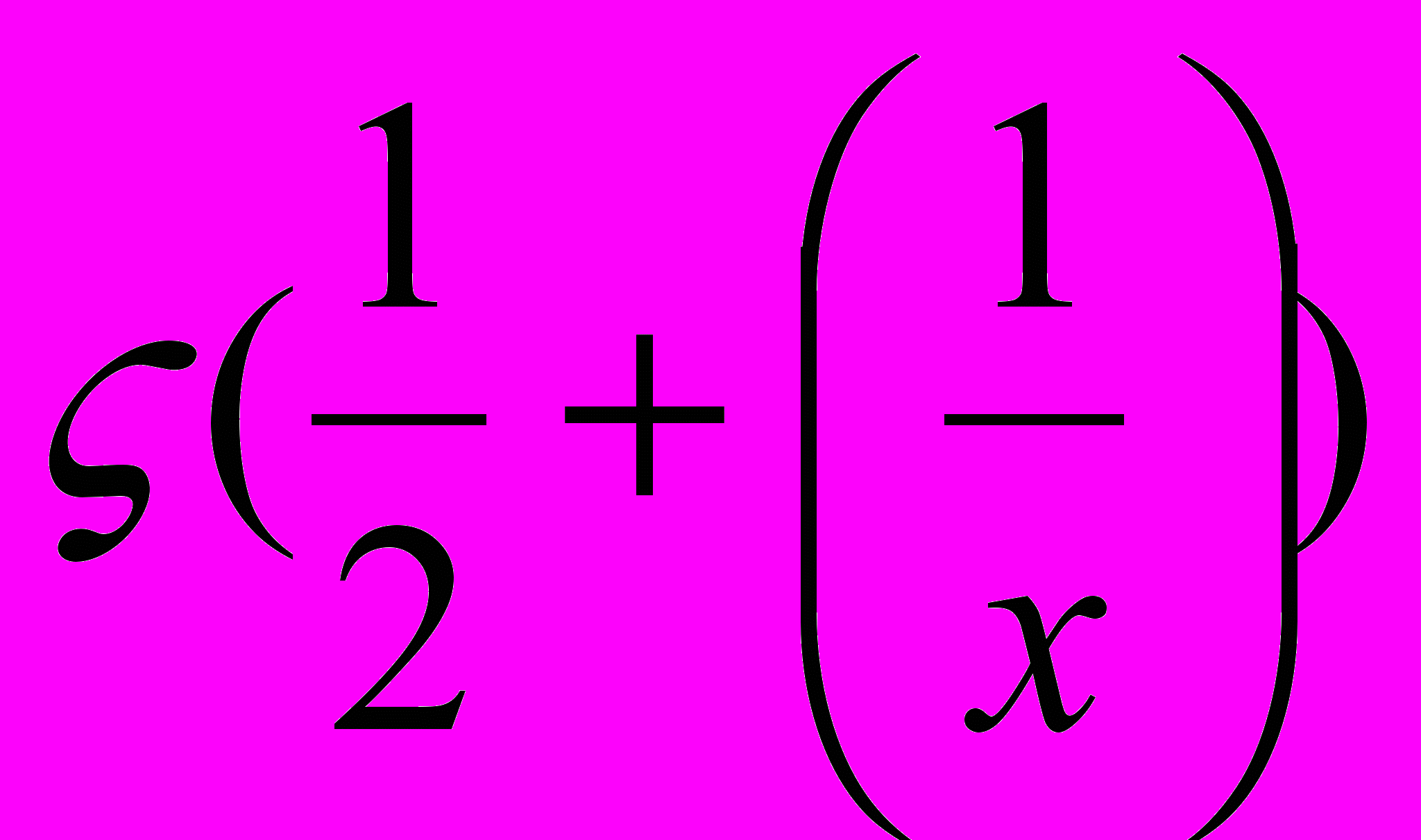 , (3)
, (3)де х*=8πμВkT
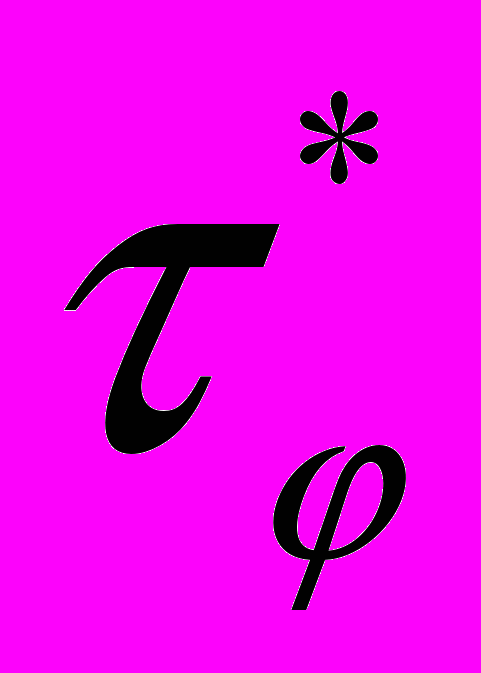 /h, х=8πμВkT
/h, х=8πμВkT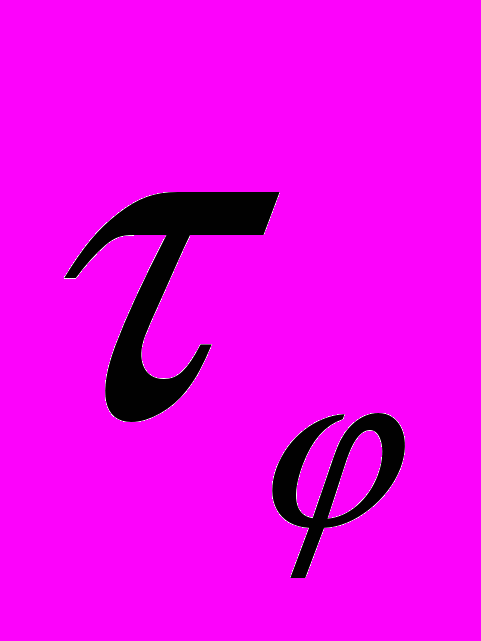 /h, ζ(у) – логарифмічна похідна від Г-функції. Члени правої частини рівняння (2) відповідають за триплетний (від’ємний магнітоопір) і синглетний (позитивний магнітоопір) внески відповідно. У наших дослідах такий перехід від від’ємного до позитивного магнітоопору спостерігається при величині поля В≈0,5Т і температурі 25К (крива 3 рис. 1(б)), а також при неконтрольованому збільшенні температури (крива 5 рис. 1(а)).
/h, ζ(у) – логарифмічна похідна від Г-функції. Члени правої частини рівняння (2) відповідають за триплетний (від’ємний магнітоопір) і синглетний (позитивний магнітоопір) внески відповідно. У наших дослідах такий перехід від від’ємного до позитивного магнітоопору спостерігається при величині поля В≈0,5Т і температурі 25К (крива 3 рис. 1(б)), а також при неконтрольованому збільшенні температури (крива 5 рис. 1(а)). 3. 2. Мінімальна рухливість.
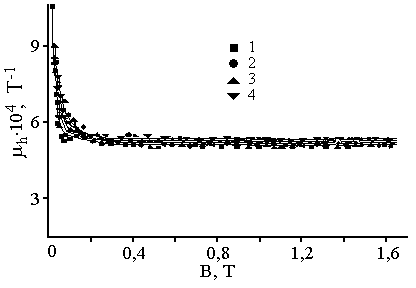
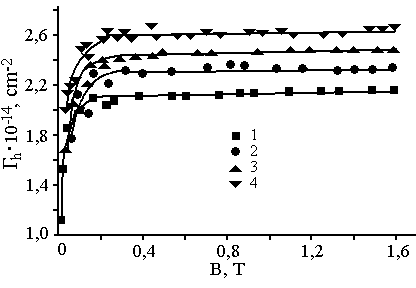
На рис. 2 (а) і (б) представлені залежності холівських рухливості μh(В) і концентрації електронів Γh(В) відповідно, виміряні при температурах Т рівних 4,2, 11, 25 і 47 К. Характерною особливістю залежностей μh(В) є те, що величина μh(В) приймає деяке значення μhmin=const, яке не залежить ні від температури Т, ні від концентрації розсіюючих центрів N=Г. Співставлення рис. 2(а) і рис. 2(б) показує, що при зміні температури Т більш ніж у 10 раз і концентрації Гh на ~30%, розкид експериментальних точок кривих 1-4 по рис. 2(а) не перевищує ±5% від їх середнього значення. Представлені залежності μh(В) підтверджують висновок, зроблений у роботі [1], про превалювання механізму розсіяння 2D електронів на заряджених центрах в умовах сильного виродження. В цих умовах є справедливою формула для мінімальної рухливості вільних носіїв заряду, одержана в борнівському наближенні [4].
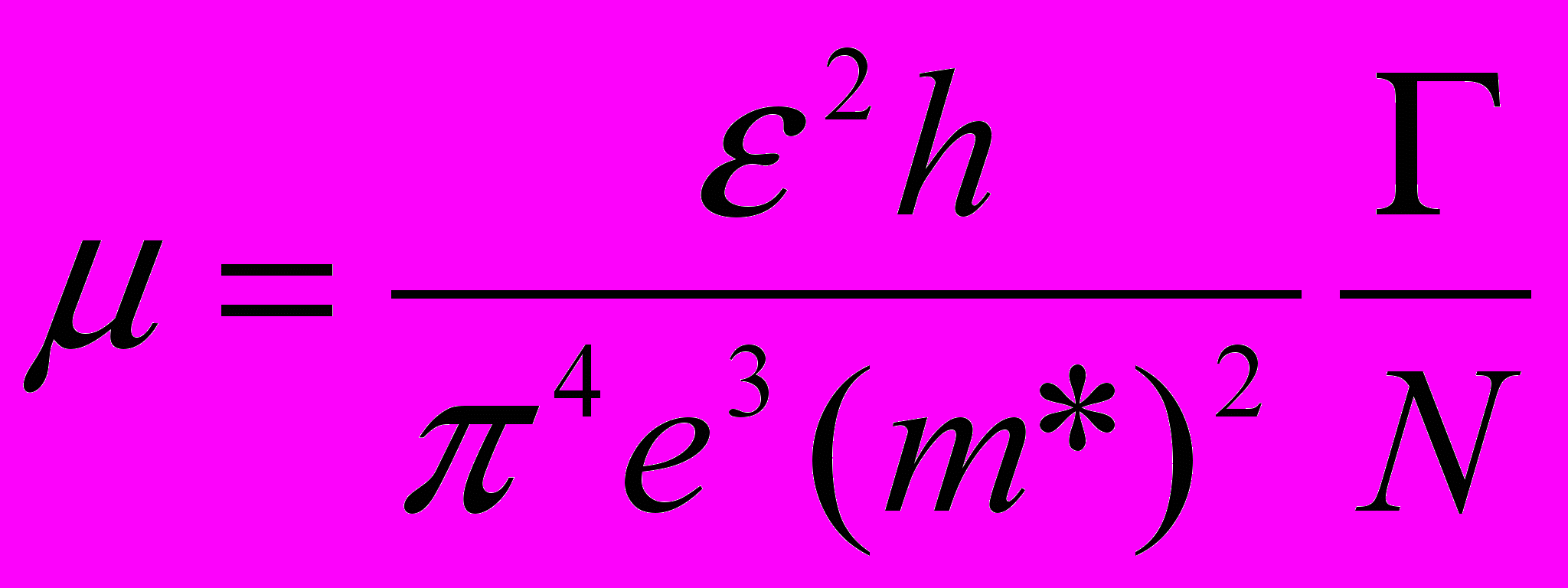 , (4)
, (4)де ε-діелектрична стала, h-стала Планка, m*-ефективна маса електрона.
Як видно з рис. 2(а), відповідно до (4), холівська рухливість μh=μhmin=const і не залежить від температури Т і концентрації електронів Г=N. Наведені експериментальні дані є другим експериментальним спостереженням мінімальної рухливості електронів у широкому інтервалі температури Т=(4,2-50)К. Вперше існування μhmin показано в роботі [4].
(а) (б)
Рис. 2. Залежності холівських рухливості μh (а) і концентрації Γh.(б) від магнітного поля В. Температура вимірювань Т, К: 1-4,2, 2, 2-11, 3-25 і 4-47.
За формулою (4) рухливість μ є сталою величиною і визначається тільки добутком світових сталих (h,e) і параметрів матеріалу (ε, m*). Це дає можливість за даними холівських вимірювань розрахувати величину ефективної маси електрона m* [5]. Розрахунок, за величини діелектричної сталої ε=4 і μ=10-3Т-1, дає m*=0,15m0 (m0 маса вільного електрона), що в два рази менше за величину наведену, в літературі [6]. Ця відмінність може бути віднесена на різницю в технології виготовлення й легування плівок ІТО, а також впливу розмірних ефектів. Перераховані чинники можуть радикально змінювати структуру й енергетичний спектр цієї складної сполуки, тим самим впливаючи на величину m*. Відзначимо, що визначення m* в тонких двовимірних плівках іншими методами зіштовхується зі значними труднощами, а дані таких досліджень мало представлені в літературі.
3. 3. Аномальна залежність рухливості від магнітного поля.
З причини невеликої рухливості, що має місце в плівках ІТО, умова слабкості магнітного поля μВ<<1 виконується дуже добре в усьому дослідженому діапазоні зміни індукції В. Для виродженого газу вільних носіїв заряду хол-фактор γ=μh/μ=<τ2>/<τ>2=1, де τ час релаксації по імпульсу. Відношення <τ2>/<τ>2 для різних механізмів розсіяння лежить у межах від 1 до 2 і не може бути меншим від одиниці. Тому залежність холівської рухливості μh від поля В по рис. 2(а) не може бути пояснена зміною механізмів розсіяння. Разом це означає, що залежність μh від поля В є аномальною і не пояснюється класичною теорією ефекту Хола. Зауважимо, що наведені на рис. 2(б) залежності холівської концентрації Γh(В), є похідними від залежностей μh(В) по рис. 2(а). Вони отримані при перерахунку експериментальних величин повздовжнього опору зразка ρхх(В)=1/eμh(В)Г при підстановці відповідних значень μh і жодним чином не пояснюють хід залежності μh(В).
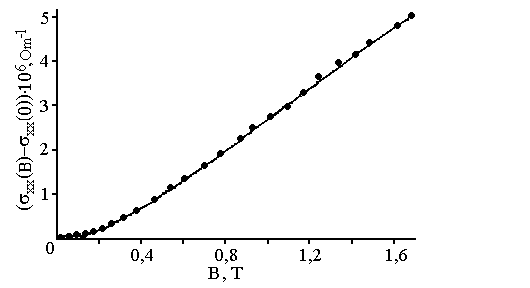
Рис. 3. Експериментальна (точки) і розрахункова (неперервна лінія) криві залежності магнітопровідності σхx(В)-σхх(0) від магнітного поля В. Температура Т=4,2К.
При температурі Т=4,2К вплив синглетної частини (другий член правої частини (2)) на ефект повздовжнього АМО в системі є мінімальним, у порівнянні з більш високими температурами. Виміряна з максимально можливою точністю експериментальна залежність σхx(В)-σхх(0) від поля В для температури Т=4,2К наведена на рис. 3. Узгодження експериментальної й розрахункової кривих було одержано при значенні часу релаксації фази хвильової функції
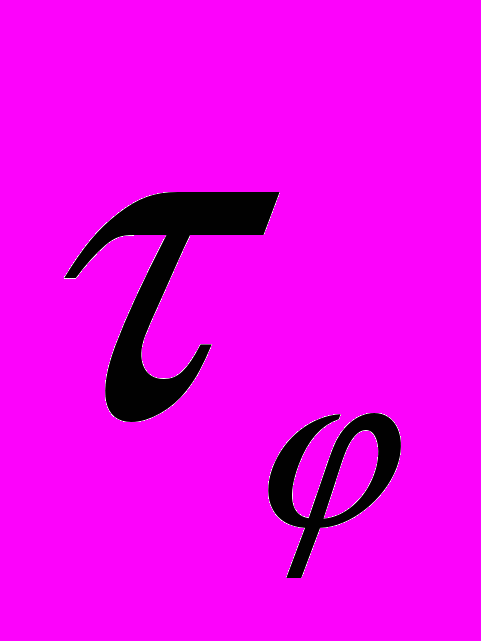 ≈2·10-9с і довжини дифузії Lφ=(D
≈2·10-9с і довжини дифузії Lφ=(D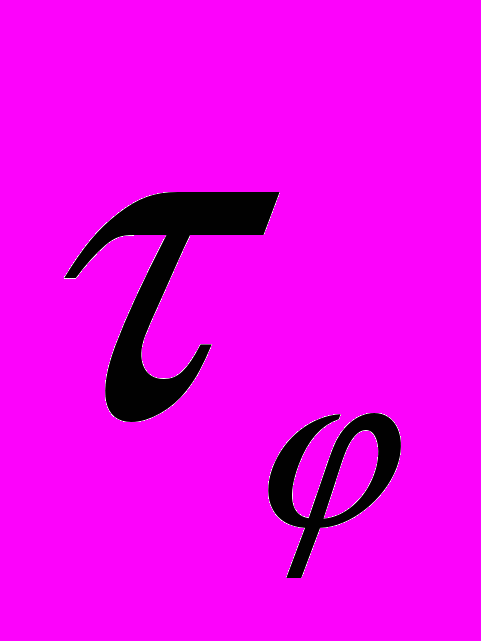 )1/2≈(2-3)·10-6см, величини яких зверху обмежують непружні взаємодії в системі. При розрахунку по (3)-(4) уважалося
)1/2≈(2-3)·10-6см, величини яких зверху обмежують непружні взаємодії в системі. При розрахунку по (3)-(4) уважалося 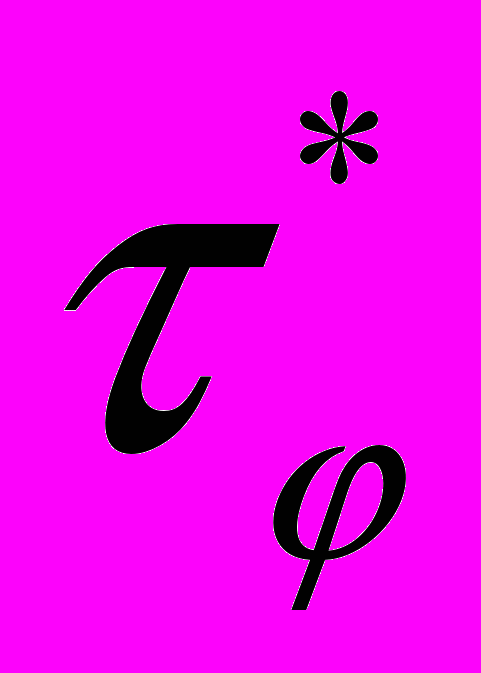 =
=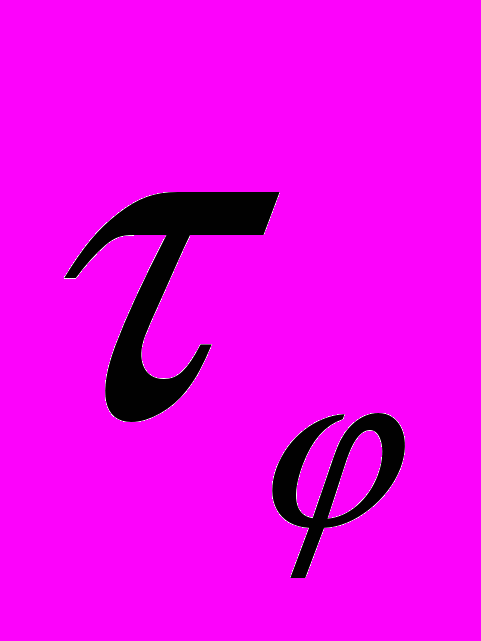 , і внесок інтерференції синглетів не враховувався. Як видно з рисунка, узгодження експерименту й розрахунку було цілком задовільним, і свідчило про те, що розсіянням електронних спінів можна було знехтувати в межах точності даного експерименту.
, і внесок інтерференції синглетів не враховувався. Як видно з рисунка, узгодження експерименту й розрахунку було цілком задовільним, і свідчило про те, що розсіянням електронних спінів можна було знехтувати в межах точності даного експерименту.У той же час, урахування спін-орбітальної взаємодії є необхідним в області слабких полів В≤(0,2)Т, для пояснення аномального ходу залежностей μh(В) по рис. 2(а). При В≈0 в тонких плівках ІТО з високою концентрацією центрів розсіяння N=Г~1014см-2, спін-орбітальна взаємодія в випадковому полі домішок може призводити до хаотичних змін орієнтації електронних спінів. Вона збільшує частку електронних хвиль, інтерференція між якими проходить у синглетному стані з повним спіном S=0 і зменшує частину триплетних взаємодій з S=1, які пригнічуються спін-орбітальною взаємодією. Відповідно ступінь локалізації електронів, що визначається часткою інтерференцій триплетів є найменшим. Збільшення величини магнітного поля В одночасно призводить до збільшення енергії зееманівського розщеплення рівнів ΔЕ~В і збою фази хвильових функцій. Перший чинник змінює співвідношення між внесками когерентних інтерференційних взаємодій з S=0 і S=1 на користь останніх і призводить до збільшення ступня локалізації електронів. Збій фази хвильових функцій зменшує частку когерентних інтерференційних взаємодій у системі. Вплив другого чинника, у порівнянні з першим, в області полів В≤0,2Т, може давати тільки невелику поправку, оскільки повне пригнічення продуктивної частини інтерференції під дією магнітного поля не відбувається навіть в області квантуючих магнітних полів [7]. Тому частка триплетних взаємодій при В≈(0,1-0,2)Т є найбільшою, і в цьому стані плівка ІТО характеризується найбільшим ступнем індукованої магнітним полем локалізації. Надалі, зі збільшенням В, збій фази хвильових функцій порівняно повільно призводить до зменшення ступню локалізації, й у кінцевому підсумку, в області дуже великих полів В, ступінь локалізації електронів у системі повертається до початкового, наближеного до того, що існував при В=0.
Розглянуті зміни внесків когерентних інтерференційних взаємодій синглетних і триплетних станів при В≤(0,2)Т безпосередньо впливають на коефіцієнт дифузії D і, через співвідношення Ейнштейна, на рухливість μ. Тому, хоча зміни механізму розсіяння під дією магнітного поля В не відбувається, на досліді ми спостерігаємо падіння μh по рис. 2(а) в інтервалі полів В≈(0-0,2)Т. Повільним змінам співвідношення між внесками триплетних і синглетних взаємодій відповідає полиця μh(В). Таким чином, μh може розглядатися як параметр, що відображає зміни спін-залежної частини когерентної інтерференції і ступня локалізації електронів у зразку. Відзначимо, що зміни μh, викликані цим фактором, набагато перевищують за величиною відповідні зміни ρхх і відбуваються при невеликих магнітних полях В, що добре видно при порівнянні рис. 2(а) з рис. 3. Використання повздовжнього опору ρхх(В) для дослідження явищ слабкої локалізації, що найчастіше використовується дослідниками (див. наприклад, огляди [8, 9]), утруднено на експерименті, оскільки зміни ρхх в обговорюваному інтервалі полів В є незначними (<1% від величини ρхх) і стають більш помітними тільки при великих магнітних полях. Математично це пояснюється тим, що в рівняннях (2)-(3) при х<<1 асимптотичне наближення функції f(x)=x2/24~В2, у той час, як холівська рухливість μh~1/В.
Додаткового обговорення потребує інтерпретація холівських даних при визначенні рухливості μ і концентрації електронів Г. При В→0 і мінімального ступня локалізації, величина μh→μ. Відповідно розрахована через провідність величина Гh→Г. При значеннях В>0 на отримані μh і Гh впливають зміни ступня локалізації електронів в зразку. Але оскільки μh=μhmin=const, то коректними є розраховані зміни концентрації ∆Гh=∆Г при зміні температури на полицях залежностей Гh(В) по рис. 2(а). Вони прямо пропорційні й точно віддзеркалюють зміни ρхх(Т), що відбуваються при зміні температури. Визначивши концентрацію Г за нахилом ρху(В) при В→0 і вважаючи Г(В)=const при зміні ступня локалізації, можна для кожної температури Т, при перерахунку через опір ρхх(В), отримати залежність рухливості по провідності μ(В). Така залежність буде віддзеркалювати вплив слабкої локалізації тільки на опір ρхх(В) і не буде залежати від цього впливу на холівський опір ρху(В). Відзначимо, що при холівських дослідженнях зразків із проявами ефектів слабкої локалізації, окреме визначення μ(В) і Г(В) можливе тільки з точністю до величини локалізаційних поправок. Останнє не заперечує обґрунтовану вище пропорційну залежність величини μh(В)~ρху(В) від результатів спін-залежної інтерференції, оскільки μh~D і, на відміну від Гh, безпосередньо вимірюється на досліді незалежно від ρхх.
Висновки
У тонких високолегованих плівках ІТО із сильною домішковою спін-орбітальною взаємодією спостерігається аномальна залежність холівської рухливості μh від магнітного поля В, а відносні зміни μh в області В→0 набагато перевищують відповідні зміни повздовжнього АМО. Причиною цього є те, що магнітне поле впливає на перерозподіл внесків інтерференційних взаємодій електронних хвиль із синглетними й триплетними станами при самоперетині траєкторій і має подвійну дію. Зееманівське розщеплення рівнів в області малих полів В зменшує ймовірність домішкового розсіяння спінів при спін-орбітальній взаємодії й призводить до збільшення триплетного інтерференційного внеску й, відповідно, збільшення ступня індукованої магнітним полем локалізації. Цей процес призводить до зменшення вимірюваного значення рухливості μh і насичується при В=(0,1-0,2)Т. Подальше збільшення поля В призводить до збою фази хвильових функцій електрона й поступовому зменшенню ступеню локалізації й відповідного збільшення рухливості. Співставлення холівських даних із розрахунками мінімальної рухливості μmin дозволяє дати коректну інтерпретацію даним холівських вимірювань і визначити величину ефективної маси електронів m*.
Література
- Лисоченко С.В., Іщук Л.В., Жарких Ю.С., Третяк О.В. Гальваномагнітні дослідження плівок Іn2O3 при температурі рідкого гелію. // Вісник Київського університету", сер.:Фіз.-мат.науки. - 2005, №3. - C.407-416.
- Альтшулер Б.Л., Аронов А.Г., Ларкин А.И., Хмельницкий Д.Е. Об аномальном магнитосопротивлении в полупроводниках //ЖЭТФ. - 1981. - Т. 81. - Вып. 2(8). - С. 768-783.
- Kivelson S., Lee D-H., Zhang S-C. Global phase diagram in the quantum Hall effect // Physical Review B. - 1992. - v.46. - №4. - p.2223-2238.
- Жарких Ю.С., Лысоченко С.В. Минимальная подвижность носителей заряда, образующих двумерный газ.//Письма в ЖЭТФ. - 1982. - Т. 35. - Вып. 5. - С. 204-206.
- Жарких Ю.С., Лисоченко С.В., Третяк О.В. Спосіб визначення ефективних мас в тонких струмопровідних каналах транзисторних напівпровідникових структур. - Висновок про видачу декларативного патенту на винахід № 200117300 від 18.06.2002.
- Ridge M., Howson R. P. Composition control in conducting oxide thin films//Thin solid films. - 1982. - V. 96. - №2. - P. 121-127.
- Грошев А.Г., Новокшонов С.Г. Отрицательное магнитосопротивление и коефициент Холла двумерной неупорядоченной системі // Физика твердого тела. - 2000. - Т.42. - Вып.7. - с.1322-1330.
- Полянская Т.А., Шмарцев Ю.В. Квантовые поправки к проводимости в полупроводниках с двумерным и трехмерным электронным газом// Физика и техника полупроводников // - 1989. - Т.23. - №1. - с.3-32.
- Садовский М.В. Диаграмматика. Лекции по избранным задачам теории конденсированого состояния. – М.-Ижевск: Институт компьютерных исследований, 2004. –336с.
УДК 621.315.592
Сергій В. Лисоченко, Лариса В. Іщук, Юрій С. Жарких, Олег В. Третяк
Гальваномагнітні дослідження плівок Іn2O3 при температурі рідкого гелію
Представлені результати електрофізичних досліджень процесів переносу двовимірних (2D) вільних електронів в плівках легованого оловом оксиду індія при температурі рідкого гелію. Досліджені залежності компонент тензору поверхневого опору ρik, холлівської рухливості μh і концентрації Γ 2D електронів від індукції магнітного поля В в полях до 1,6 Т. Вперше в таких плівках знайдено аномальну залежність обох компонент магнітоопору від величини В. Отримані результати пояснені на основі теорії квантових поправок до величини провідності. Визначено час релаксації фази хвильової функції
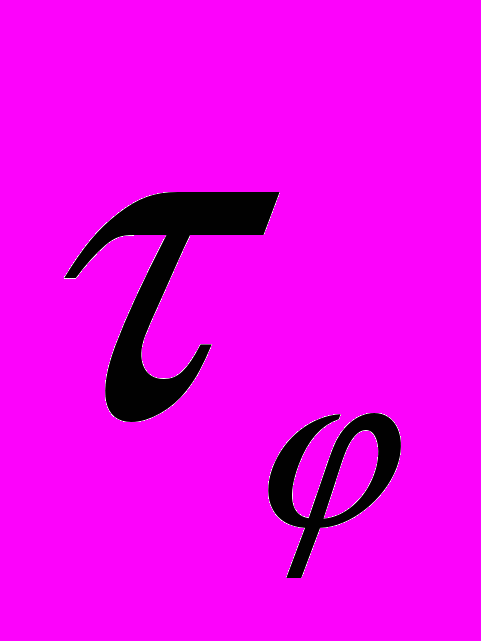 .
.Ключові слова: оксид індію, двовимірний електронний газ, аномальний магнітоопір, час релаксації фази хвильової функції .
Sergiy V. Lysochenko, Larisa V. Ishchuk, Yuriy S. Zharkikh, Oleg V. Тretyak
The halvanomagnetic studies of the Іn2O3 films at the liquid helium temperature
The electrophysical investigations results of transport processes of two dimensional (2D) free electrons in indium-tin oxide films at the liquid helium temperatures are present. The dependences of surface resistivity tensor components ρik, Hall mobility μh and concentration Γ of 2D electrons upon the magnetic field B were investigated up to the B value of 1,6T. In the first time the anomalous dependence of both magnetoresistivity components upon the B is found in such films. The results are explained on the base of the theory of the quantum correction factors to the conductivity value. The phase relaxation time
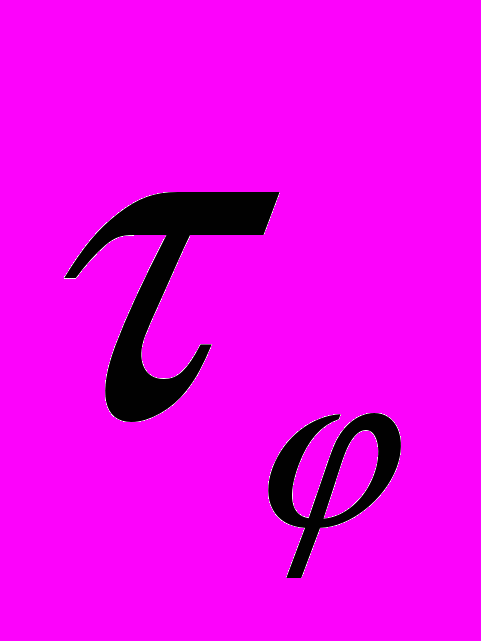 of the wave function was determined.
of the wave function was determined.Key Words: indium-tin oxide, two dimensional electron gas, anomalous magnetoresistivity, wave function phase relaxation time.
E-mail:lys@univ.kiev.ua
І. Вступ
Плівки легованого оловом оксиду індія (ІТО – indium-tin oxide) широко використовуються завдяки унікальній комбінації їх властивостей, а саме: великій електропровідності, високому коефіцієнту відбиття світла в близькій інфрачервоній і великому коефіцієнту інтегральної прозорості у видимій ділянці спектру. Завдяки цим властивостям вони використовуються в сучасних напівпровідникових перетворювачах сонячної енергії, фотоелектричних приладах і в інших технічних застосуваннях [1-3]. Велике значення для їх застосування, може мати наявність в таких плівках підсистеми електронів провідності з малою ефективною масою і надвисокими значеннями рухливості, повідомлення про можливість чого з’явилось нещодавно [4]. Поряд з цим, в тонких плівках ІТО з розмірноквантованим 2D газом електронів, можливий прояв нових фундаментальних квантових і спінзалежних ефектів в явищах переносу, на основі яких в майбутньому можуть бути створені нові напівпровідникові прилади [5,6]. В поданій роботі показано вплив квантової інтерференції на магнітоопір плівок ІТО в слабких магнітних полях (μВ<<1) при температурі рідкого гелію Т=4,2К.
2. Дослідні зразки
Плівки ІТО виготовлялись методом магнетронного розпорошення. Концентрація олова в досліджуваних зразках становила 11%. Плівки мали високий коефіцієнт якості
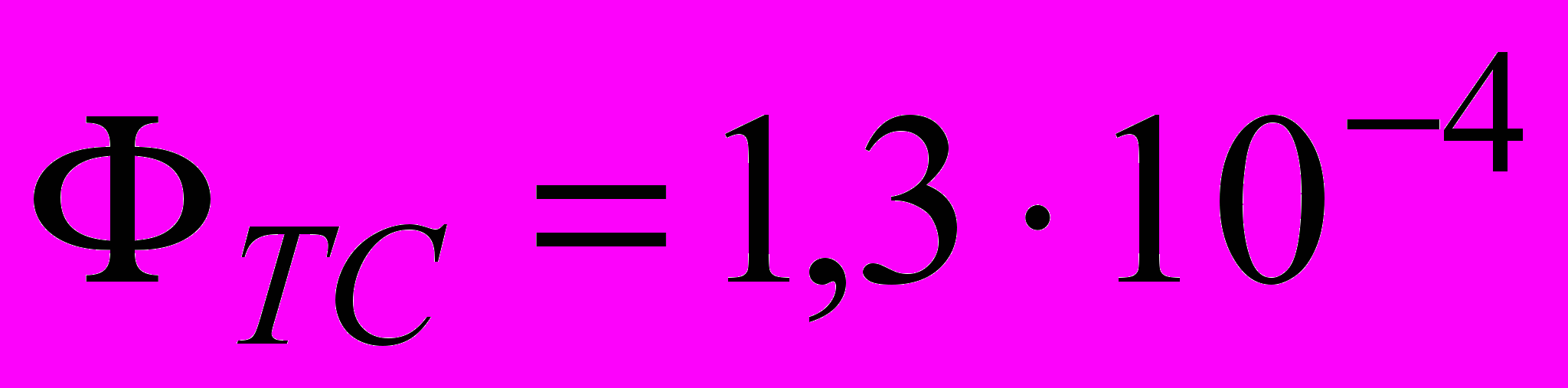 Ом-1, що є добутком інтегральної прозорості плівки в видимій частині спектру на її провідність. Товщина плівки d≈2∙10-6см. Особливості кристалічної структури плівок і технологія їх виготовлення більш докладно описані в [7].
Ом-1, що є добутком інтегральної прозорості плівки в видимій частині спектру на її провідність. Товщина плівки d≈2∙10-6см. Особливості кристалічної структури плівок і технологія їх виготовлення більш докладно описані в [7].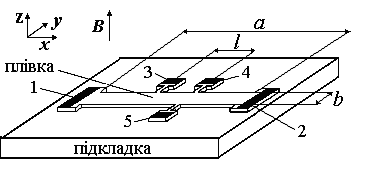
Рис.1. Планарна конфігурація дослідних зразків.
Планарна конфігурація дослідних зразків, призначених для вимірювань е.р.с. Холла, представлена на рис.1. Плівка знаходилась в площині координат ху. Магнітне поле В нормальне до поверхні плівки. Довжина зразка a=2 см, ширина b=0,2 см, відстань між поздовжніми контактами l=0,4 см. Контакти до зразка, омічність яких контролювалась, створювались напаюванням індію.
3. Результати досліджень
Дослідні зразки розміщувалися в кріостаті в середовищі зрідженого гелію при температурі Т=4,2К. Для зміни температури зразок піднімався над поверхнею гелію, що давало можливість виміряти температурну залежність повздовжньої провідності σхх зразка в діапазоні температур Т=(4,2-300)К. Експериментальна залежність σхх в плівках ІТО від температури Т показана на рис.2.
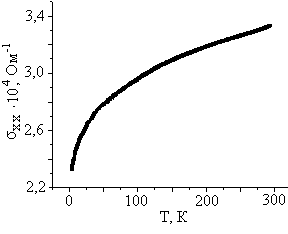
Рис. 2. Залежність провідності σхх від температури Т.
Для створення магнітного поля при холлівських вимірюваннях при температурі Т=4,2К застосовувався надпровідний соленоїд. Ці вимірювання проводились за величини індукції магнітного поля В(0.02-1,6)Т. Напруга на зразок подавалась між контактами 1-2 (рис. 1). На дослідах вимірювався струм провідності Іх, падіння напруги U
 між контактами 3-4 і холлівська напруга Uy між контактами 4-5 в залежності від величини магнітного поля В. Значення струму провідності Іх вибиралась такими, що виключали нагрівання зразка.
між контактами 3-4 і холлівська напруга Uy між контактами 4-5 в залежності від величини магнітного поля В. Значення струму провідності Іх вибиралась такими, що виключали нагрівання зразка.Обчислення величин компонент тензорів поверхневого опору ρik, концентрації електронів Γ(В) і холлівської рухливості μх(В) проводились з розрахунку на одиницю площі плівки по формулам (1-4).
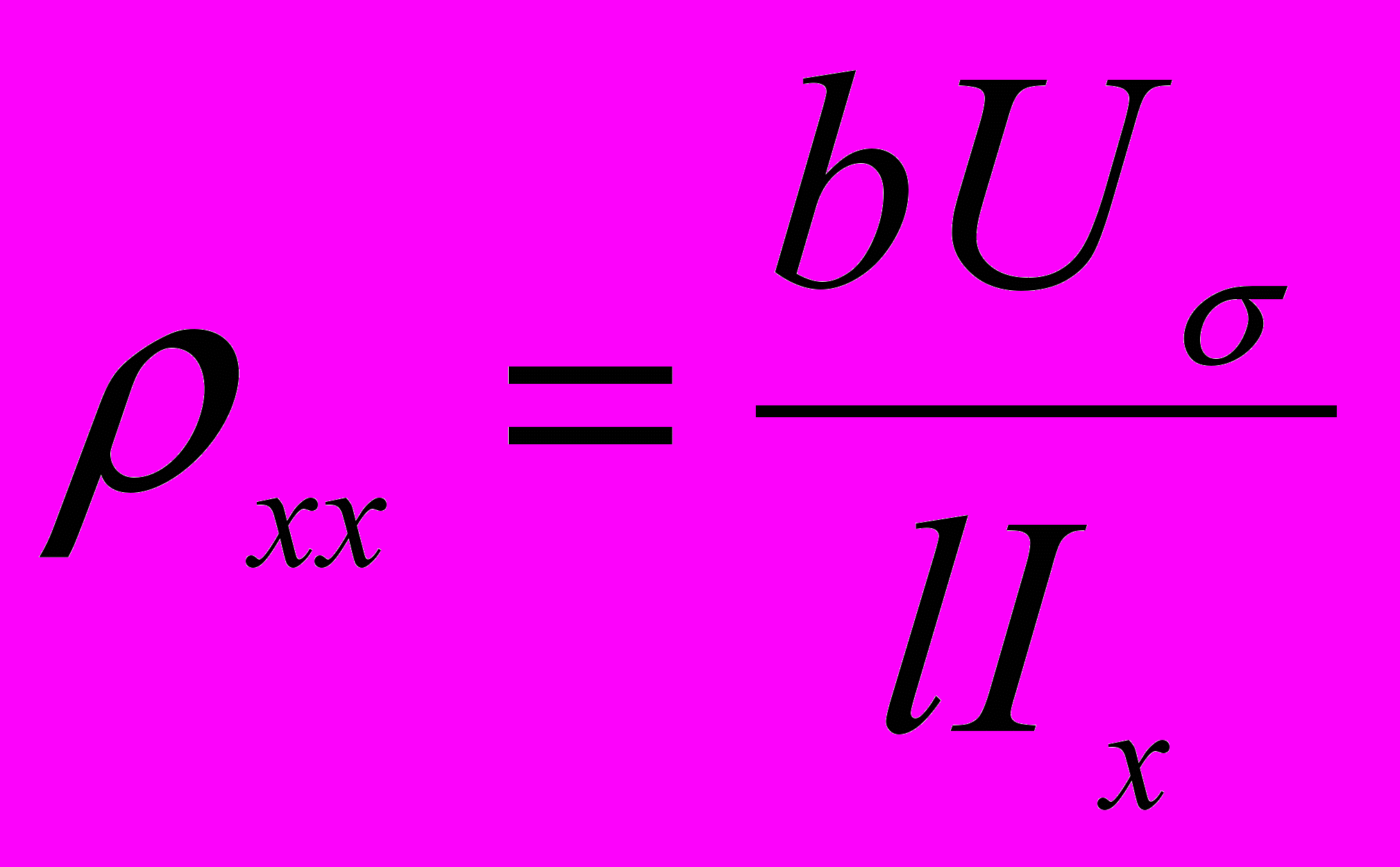 (1)
(1)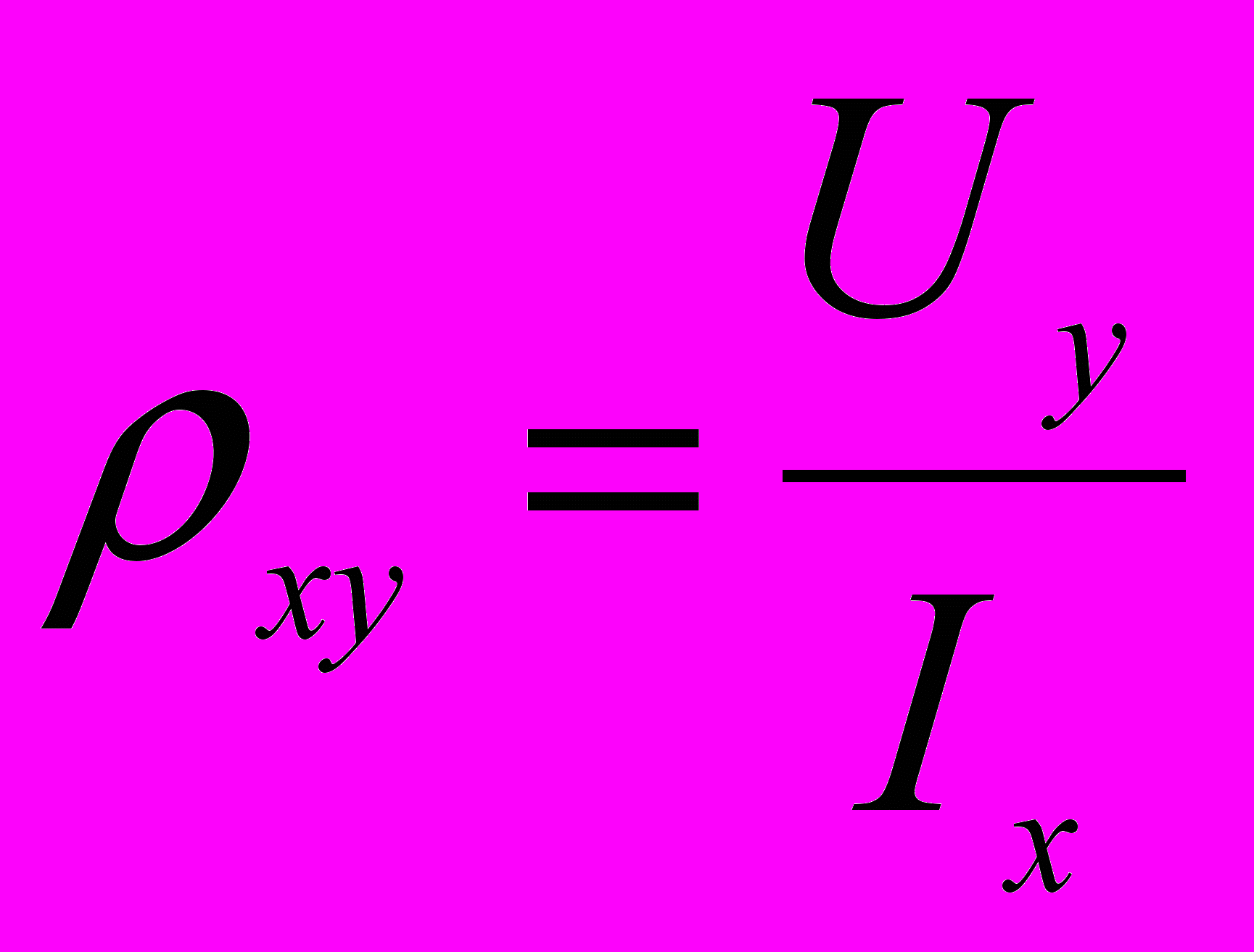 (2)
(2)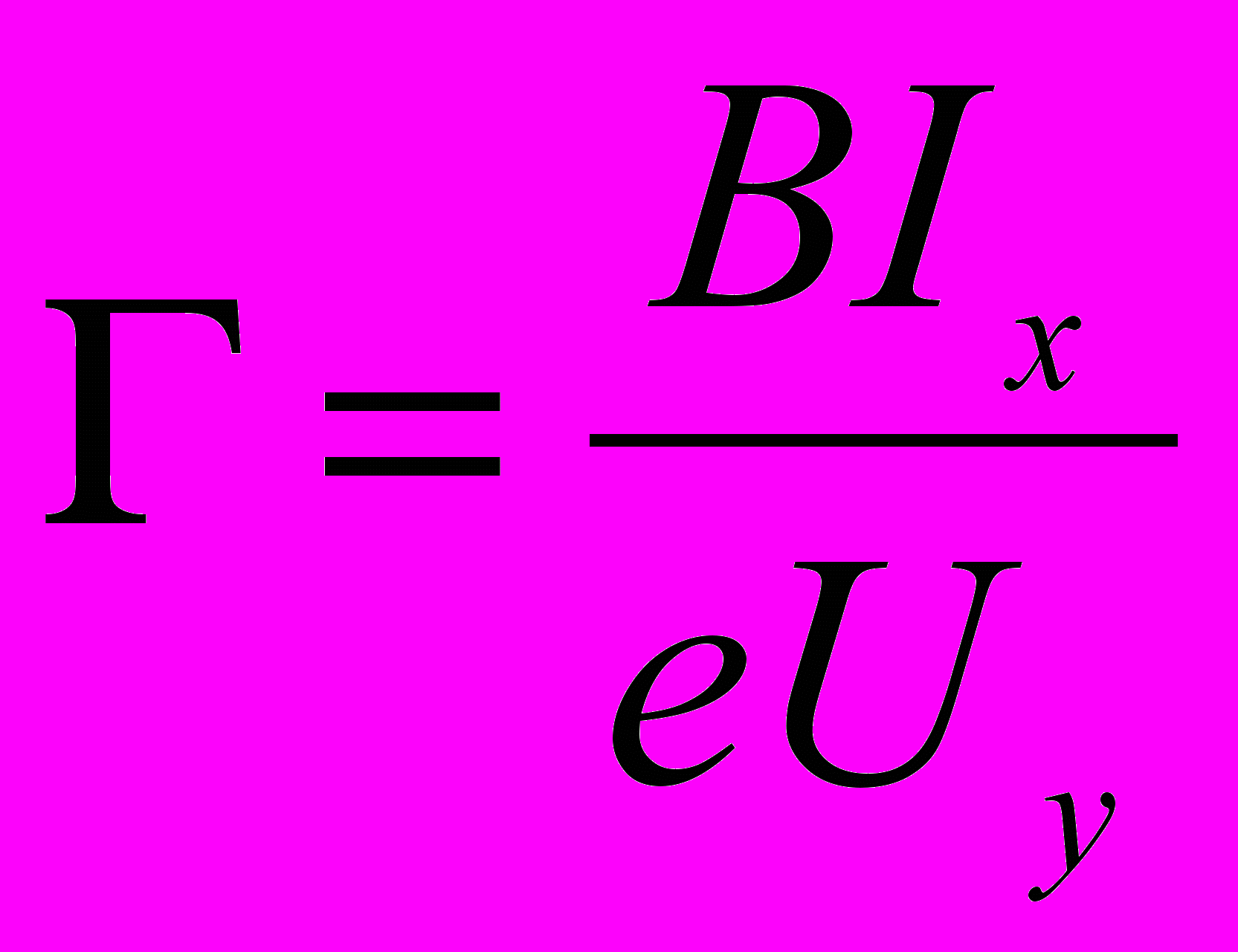 (3)
(3)
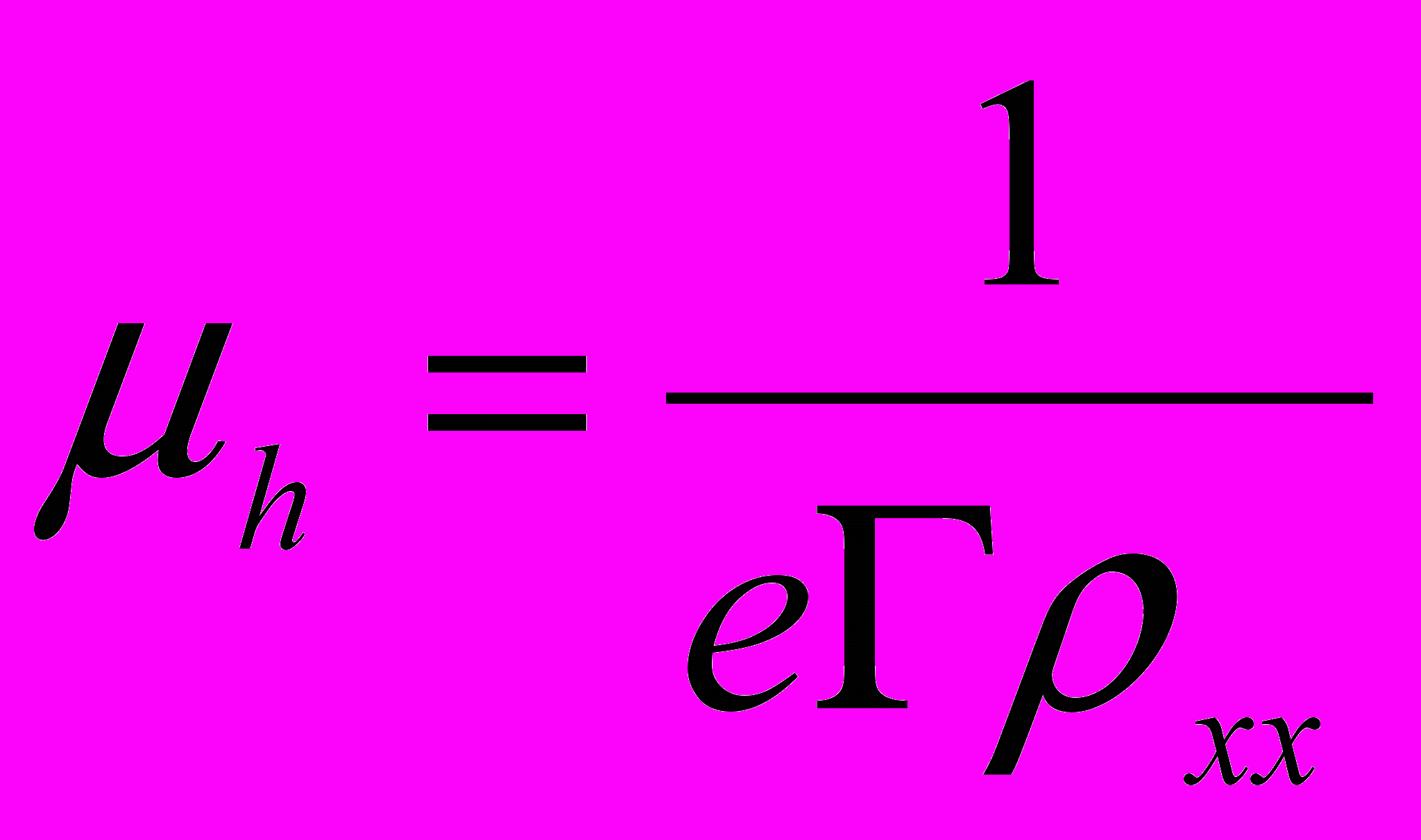 (4)
(4)де е-заряд електрона.
На рис. 3 представлені залежності холлівської рухливості μh(В) (а), концентрації Γ(В) (б), провідності σхх(В) (в), і магнітопровідності σхх(В)-σхх(0) (г) від магнітного поля В (σхх(0)- провідність плівки при В=0). Величина σхх розраховувалась як величина, обернена до ρхх, оскільки ρxx>>ρxy.
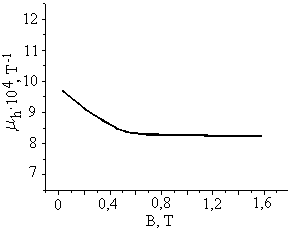
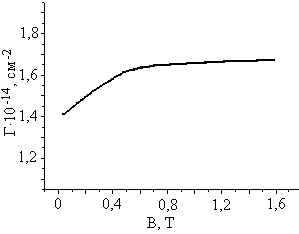
(а) (б)
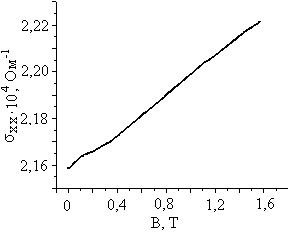
(в) (г)
Рис. 3. Залежності рухливості μh(В) (а), концентрації Γ(В) (б), провідності σхх(В) (в), і магнітопровідності σхх(В)-σхх(0) (г) від магнітного поля В.
4. Обговорення результатів досліджень
4.1.Рухливість 2D електронів
Аналіз залежності σхх(Т) по рис.2 показує порівняно незначні зміни величини σхх (менш ніж в 1,5 рази) при зміні температури Т майже на два порядки (σхх≈2,3∙10-4Ом-1 при Т=4,2К і σхх≈3,3∙10-4Ом-1 при Т=300К). Величина концентрації електронів Г≈1014см-2 при Т=4,2К (рис. 3б) порівняно з Г виміряною при Т=300К [4] також змінюється мало. Причиною цього є перетворення домішкових рівнів на домішкову зону і наближення, чи перекриття її з зоною провідності, внаслідок високої концентрації легуючої домішки (глибина залягання домішкових рівнів ~0,02еВ). Така температурна залежність σхх і високі значення концентрації електронів Г≈1014 см-2 є характерними для виродженого газу вільних носіїв заряду в сильно легованому напівпровіднику. Розрахунок положення рівня Фермі також показує значне виродження електронного газу при температурах від 4,2К-300К. Положення рівня Фермі в зоні провідності ІТО складало величину ~0,18еВ при Т=4,2К.
Товщина плівки ІТО d~2·10-6см близька до довжини хвилі де-Бройля електронів з енергією Фермі λД-Б~10-6см і тому в таких плівках спостерігається розмірне квантування руху електронів. За умови температури рідкого гелію, коли внесок розсіяння на коливаннях кристалічної ґратки є мінімальним, найбільш вірогідним домінуючим механізмом розсіяння можна вважати механізм розсіяння на заряджених центрах. Тому, для порівняння отриманої величини μh з теоретичним, було проведено розрахунок рухливості 2D електронів в борнівському наближенні за формулою, справедливою в умовах сильно виродженого газу вільних носіїв заряду [8].
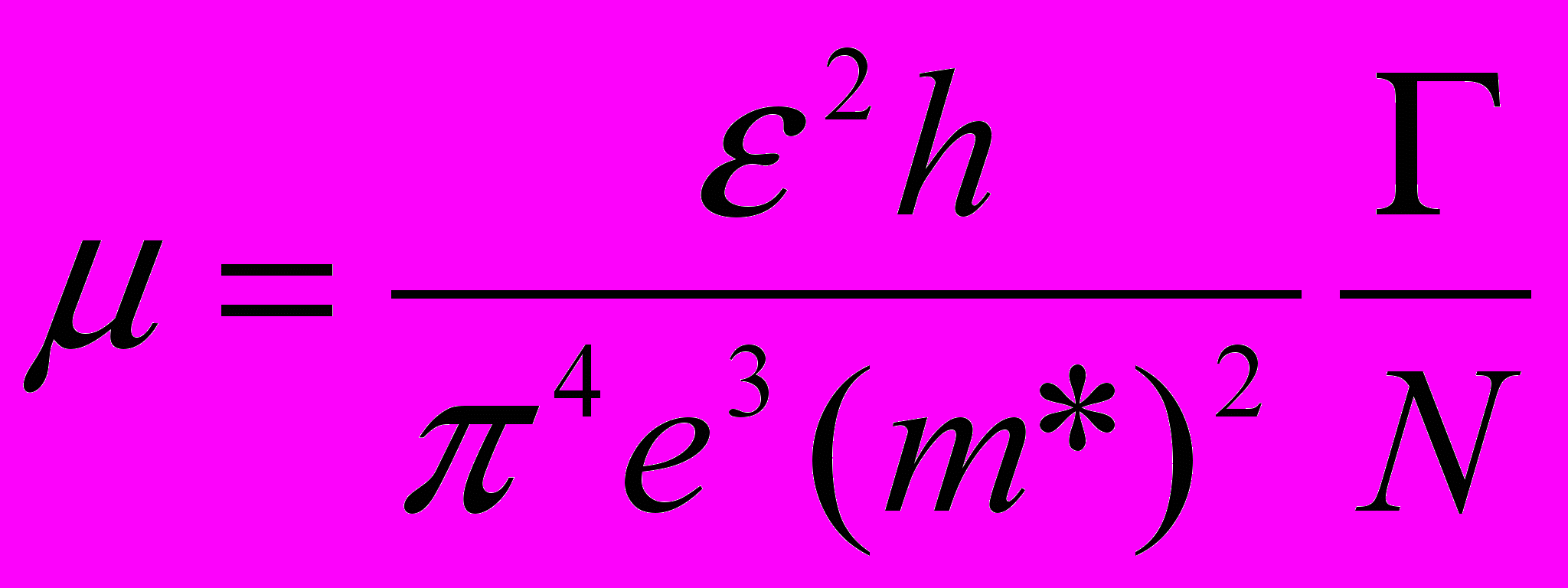 (4)
(4)де ε-діелектрична стала, h-стала Планка, m*-ефективна маса електрона, N концентрація розсіюючих центрів.
За формулою (4) рухливість μ 2D газу носіїв залежить від концентрації вільних електронів Г, концентрації розсіюючих центрів N і не залежить від температури. За умови електронейтральності зразка і відсутності зарядів на поверхні плівки і межі поділу плівка-підкладка Г=N і відповідно відношення Г/N=1. Тому рухливість μ є сталою величиною і визначається тільки добутком світових сталих (h,e) і параметрів матеріалу (ε, m*).
Для кількісних розрахунків візьмемо діелектричну сталу ε=4, ефективну масу m*=0,3m0 (m0 маса вільного електрона) [9]. Розрахунок по формулі (4) для вказаних значень ε і m* дає величину розрахункової рухливості μр≈3∙10-4Т-1, що приблизно в 3 рази менше виміряного експериментального значення. Якісно співвідношення μh>μр свідчить про наявність превалювання розсіяння 2D електронів на заряджених центрах, оскільки в протилежному разі, тобто при μh<μр, для узгодження розрахунку і експерименту необхідно було б врахування додаткових механізмів розсіяння. Кількісну розбіжність між значеннями μh і μр можна пояснити екрануванням потенціалу кулонівських центрів [4,5], що не враховується формулою (4). Тому, можна вважати, що основним механізмом розсіяння в досліджених плівках ІТО є механізм розсіяння на кулонівських центрах, а газ електронів є двовимірним, оскільки співвідношення (4) справедливо саме для 2D газу носіїв заряду.
4.2. Аномальний повздовжній магнітоопір
В досліджуваних плівках ІТО було вперше виявлено наявність від’ємного магнітоопору 2D газу електронів. На рис 3в видно, що при зростанні магнітної індукції В спостерігається монотонне зростання провідності σхх зразка. Величиною класичного магнітоопору в наших плівках можна було знехтувати.
Існує теорія аномального магнітоопору (АМО) [10,11], що враховує квантові поправки до теорії провідності. Відповідно до [10], причиною появи від’ємного магнітоопору є слабка локалізація. В теорії враховується інтерференція когерентних електронних хвиль в особливому випадку, а саме електронних хвиль, що розповсюджуються по замкнутих траєкторіях. Наслідком такої інтерференції є збільшення розсіяння в малому конусі кутів в околі напряму точно назад. В точці інтерференційної взаємодії ймовірність знаходження електрона буде більшою, ніж при класичному розгляді, що має наслідком зменшення коефіцієнта дифузії. Магнітне поле призводить до додаткової різниці фаз і збою когерентності електронних хвиль, внаслідок чого зменшується ймовірність локалізації і збільшується провідність зразка під дією магнітного поля.
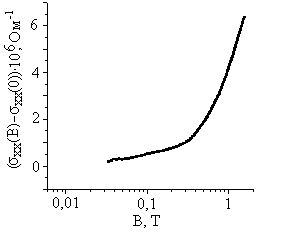
На рис. 3г наведена залежність абсолютної величини магнітопровідності σхх(В)-σхх(0) від поля В, на якому величина В відкладена в логарифмічному масштабі. Графік залежності магнітопровідності σхх(В)-σхх(0) в таких координатах виявляє асимптотичні залежності з універсальними нахилами, характерними для прояву АМО в електронному газі. На рис. 3г такий нахил спостерігається при В>1Т. Тому ефект АМО в досліджуваній системі порівнювався з розрахунками одержаними в [10].
Відповідно до теорії, аналізуючи залежність АМО від магнітного поля, можна визначити час релаксації фази хвильової функції
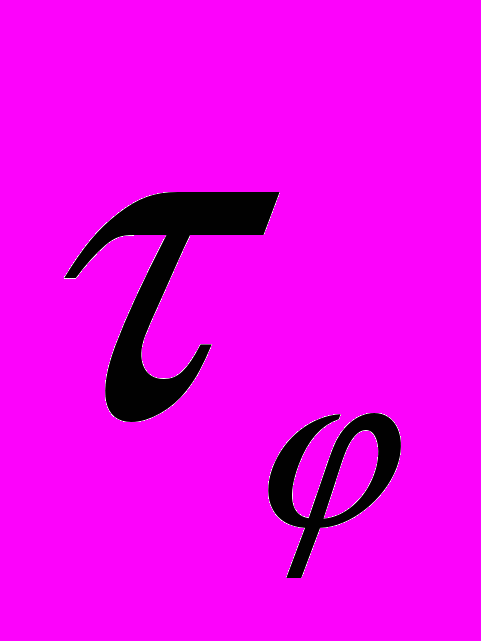 і довжину дифузії Lφ=(D
і довжину дифузії Lφ=(D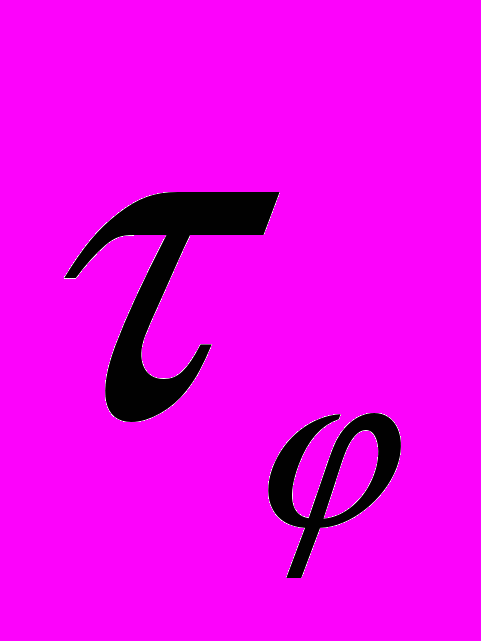 )1/2, де D – коефіцієнт дифузії. Величина часу
)1/2, де D – коефіцієнт дифузії. Величина часу 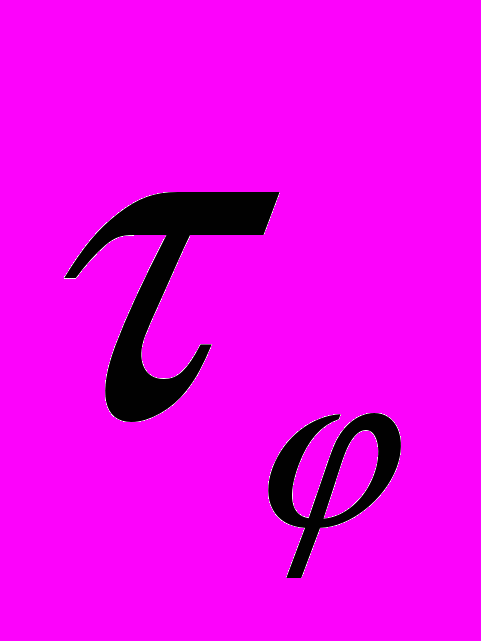 визначається часом непружних взаємодій в системі, основними з яких є електрон-електронні або електрон-фононні взаємодії.
визначається часом непружних взаємодій в системі, основними з яких є електрон-електронні або електрон-фононні взаємодії.Порівняння експериментальних даних з теорією проводилось за формулами (5-6) для невзаємодіючих електронів [10]
σхх(В)-σхх(0)=
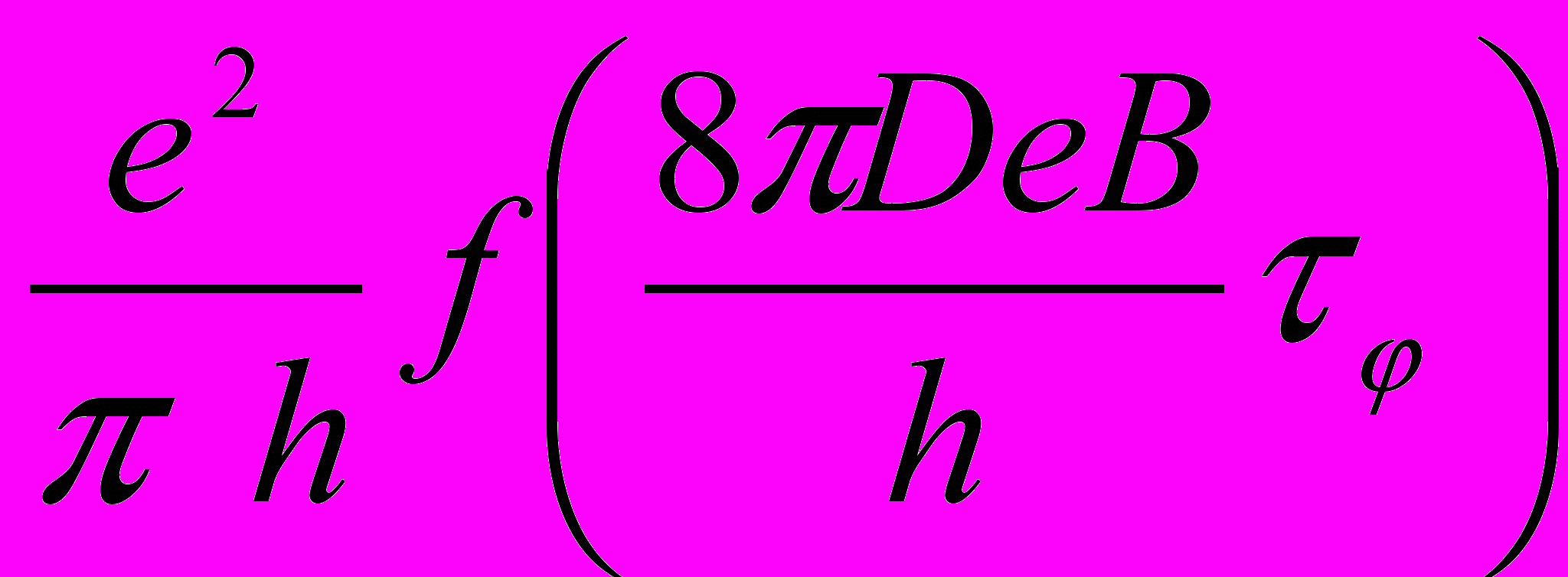 (5)
(5)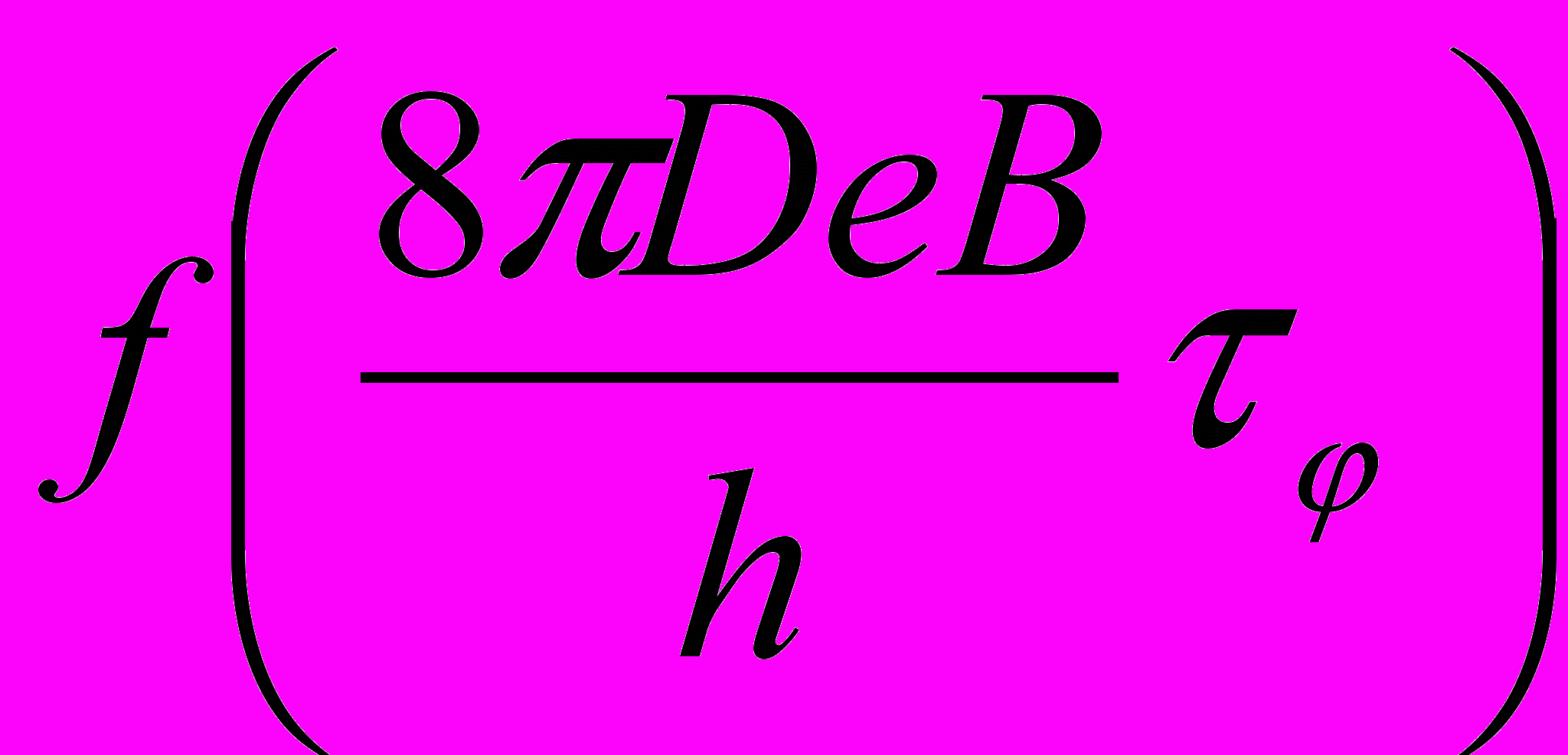 =ln
=ln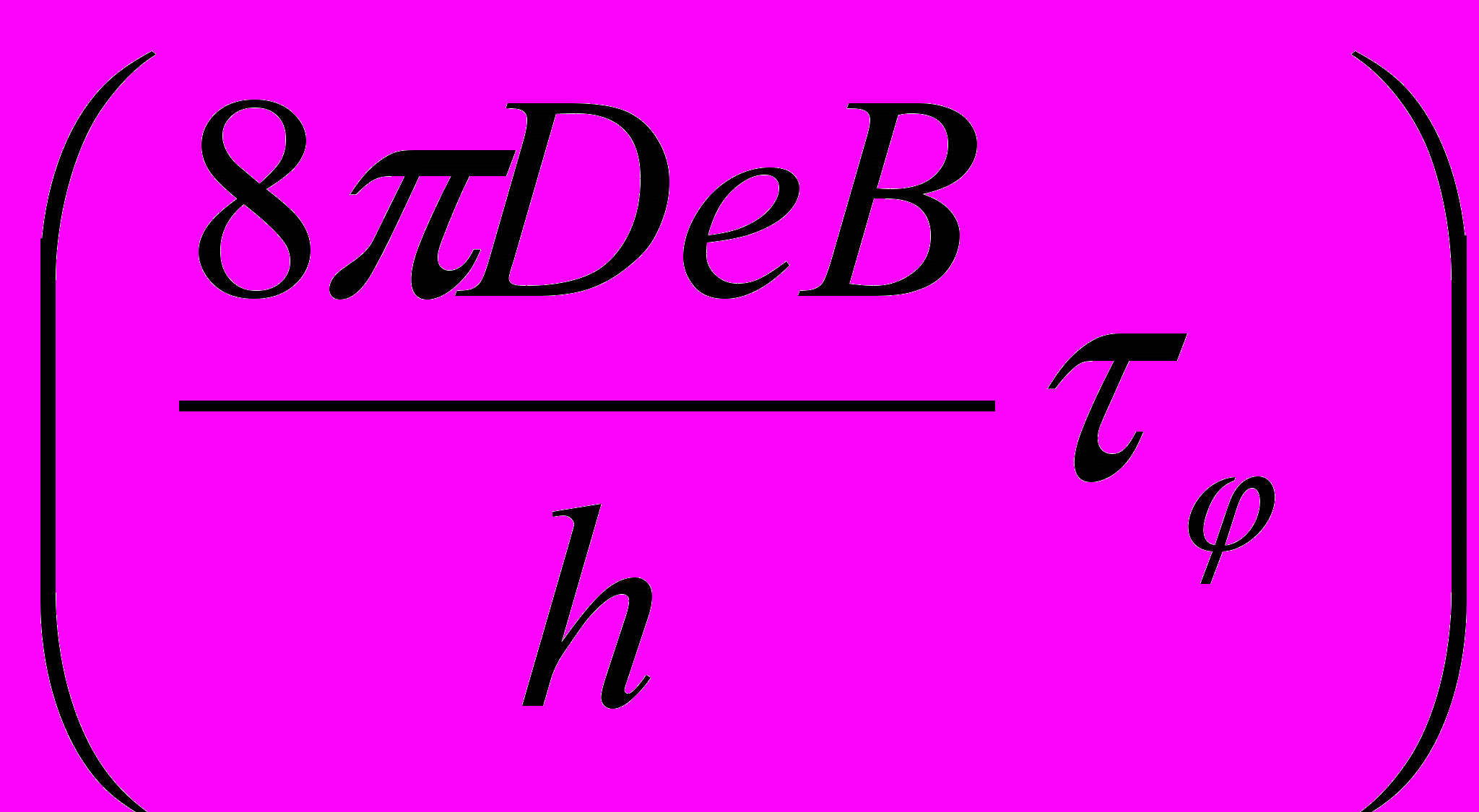 +
+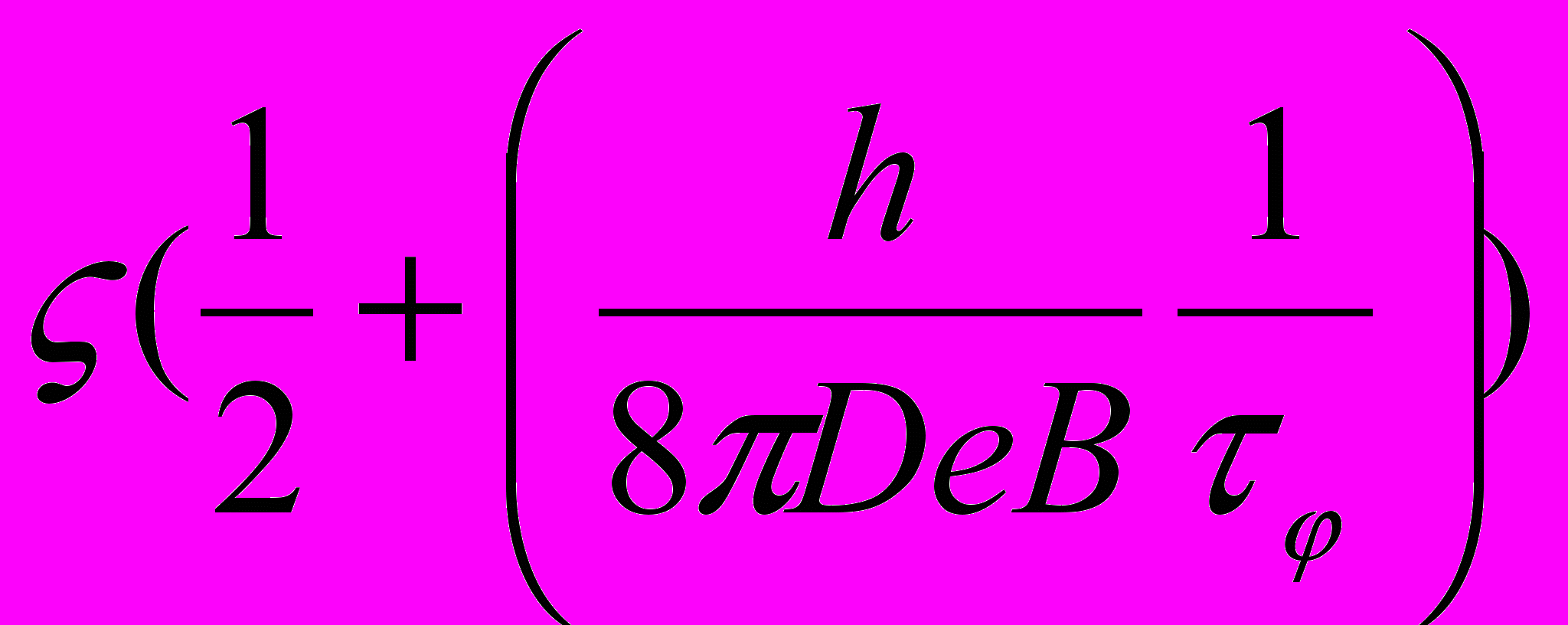 , (6)
, (6)де ζ(у) – логарифмічна похідна від Г-функції.
На рис. 4 представлені експериментальна і розрахункова залежності магнітопровідності σхх(В)-σхх(0) від магнітного поля В. Підгоночним параметром в розрахунку був час релаксації фази хвильової функції
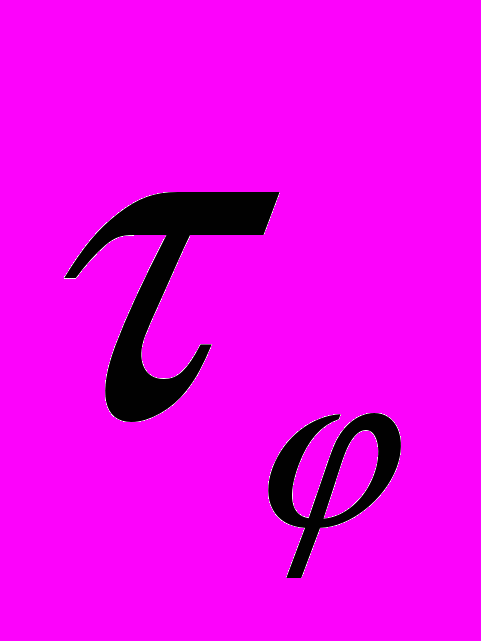 . Найкраще узгодження експериментальної і розрахункової кривих було одержано при величині
. Найкраще узгодження експериментальної і розрахункової кривих було одержано при величині 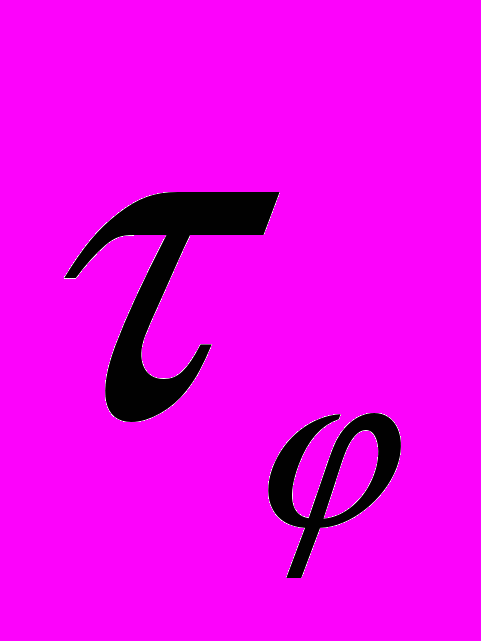 ≈2·10-9с. Як видно з рисунка узгодження експерименту і розрахунку є цілком задовільним в більшій частині дослідженого діапазону змін магнітного поля В. Незначне неспівпадання кривих при малих значеннях магнітного поля В може бути викликане додатковими ефектами, що не враховувалися в даному розрахунку.
≈2·10-9с. Як видно з рисунка узгодження експерименту і розрахунку є цілком задовільним в більшій частині дослідженого діапазону змін магнітного поля В. Незначне неспівпадання кривих при малих значеннях магнітного поля В може бути викликане додатковими ефектами, що не враховувалися в даному розрахунку.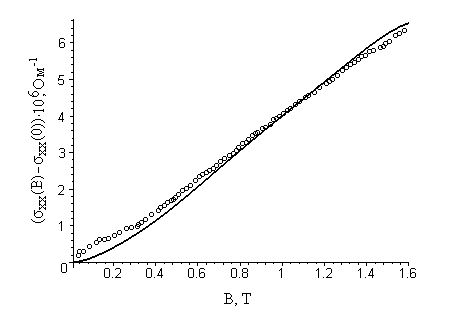
Рис. 4. Експериментальна (точки) і розрахункова (неперервна лінія) криві залежності магнітопровідності σхx(В)- σхх(0) від магнітного поля В
Підставивши знайдене значення
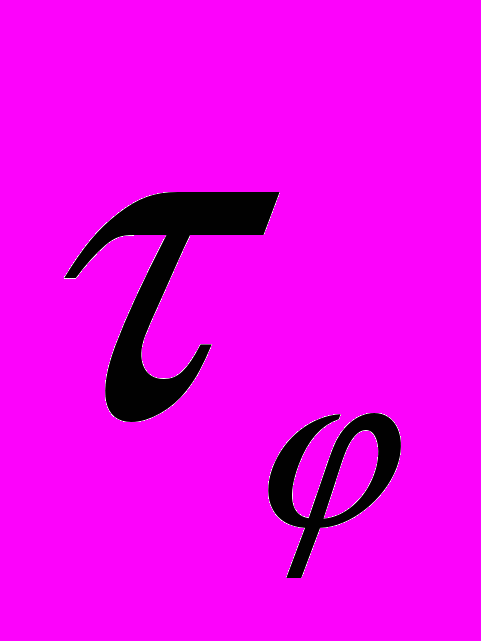 в формулу для величини довжини дифузії Lφ=(D
в формулу для величини довжини дифузії Lφ=(D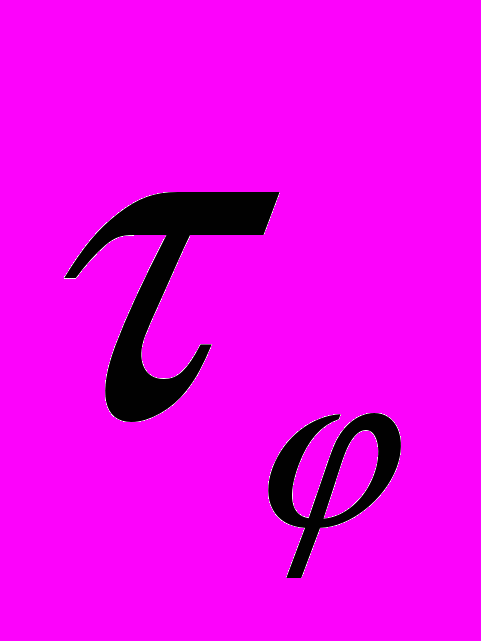 )1/2, отримаємо величину Lφ≈(2-3)·10-6см, що є близькою до товщини зразка. Оцінивши час релаксації по імпульсу
)1/2, отримаємо величину Lφ≈(2-3)·10-6см, що є близькою до товщини зразка. Оцінивши час релаксації по імпульсу 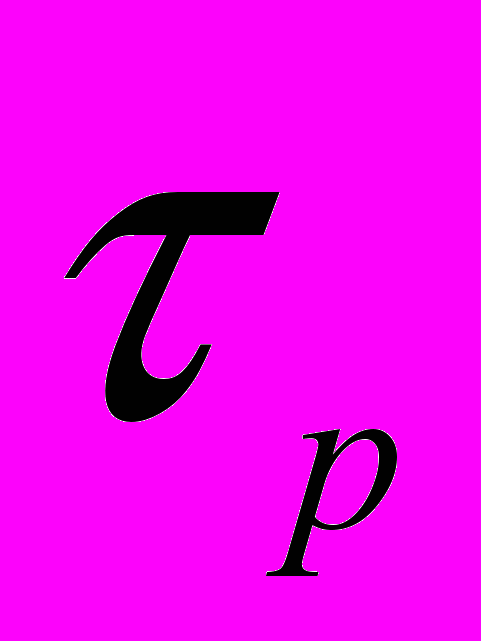 ≈μhm*/e≈2·10-15с, можна визначити відношення
≈μhm*/e≈2·10-15с, можна визначити відношення 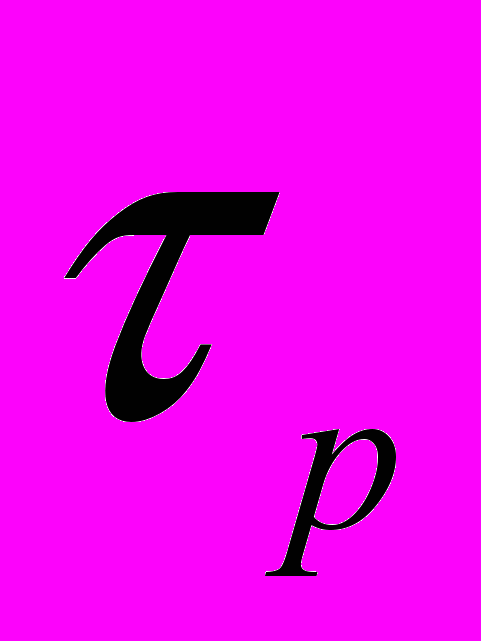 /
/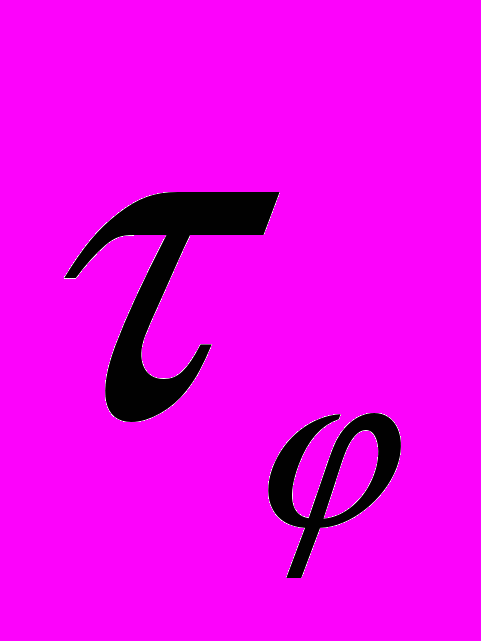 ≈10-6. Для порівняння, відношення
≈10-6. Для порівняння, відношення 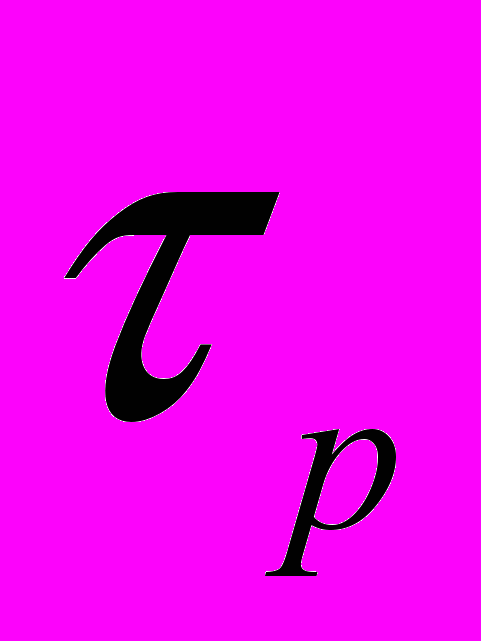 /
/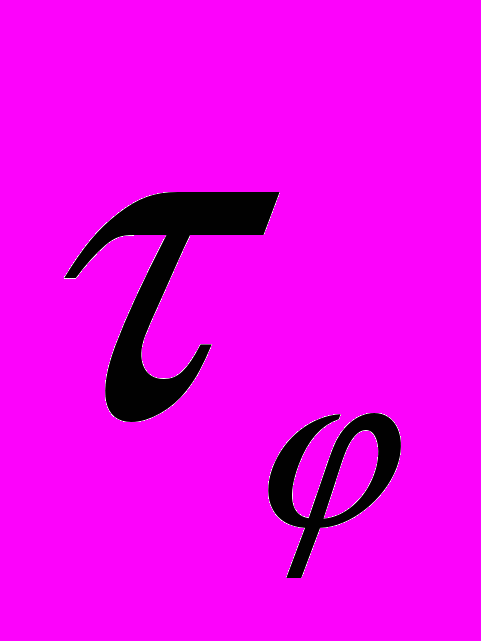 в струмопровідних каналах на кремнії складає ~(10-2 -10-3). Таке співвідношення між часом
в струмопровідних каналах на кремнії складає ~(10-2 -10-3). Таке співвідношення між часом 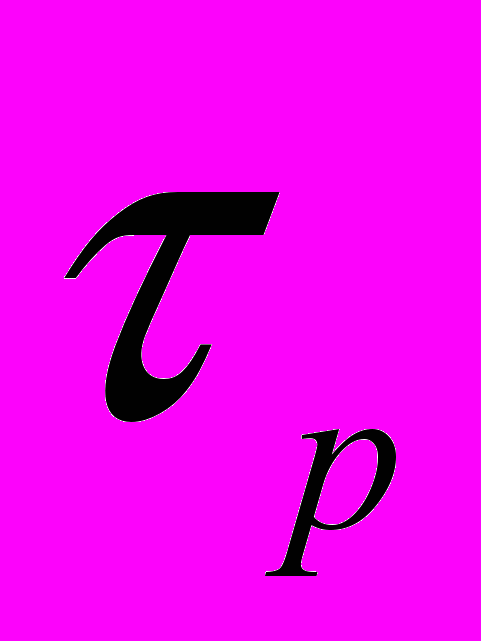 і
і 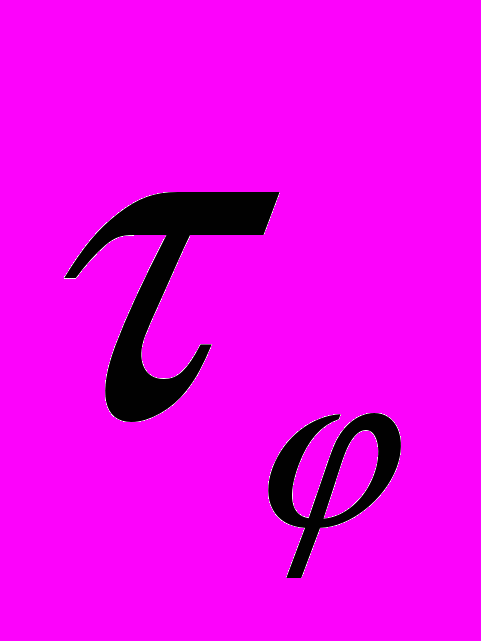 свідчить про надзвичайно сильне домінування пружних взаємодій (розсіяння на кулонівських центрах) над непружними і є особливістю досліджуваних плівок ІТО, що визначає ефект АМО в системі.
свідчить про надзвичайно сильне домінування пружних взаємодій (розсіяння на кулонівських центрах) над непружними і є особливістю досліджуваних плівок ІТО, що визначає ефект АМО в системі.Додатковими ефектами, що можуть впливати на ефект АМО, є ефекти електрон-електронної і спін-орбітальної взаємодії. Характерним масштабом теорії для поправок при електрон-електронній взаємодії є довжина LT=(Dћ/kT)1/2– довжина, на якій зберігається когерентність хвильових функцій двох електронів з різницею енергій порядку kT. В нашому випадку LT≈10-7см. і є близькою до міжатомних відстаней. Тому в випадку наявності електрон-електронної взаємодії, пов’язаний з нею окіл когерентної інтерференції хвильових функцій є незначним, в порівнянні з довжиною Lφ. Тому внесок в АМО інтерференції, пов’язаної з електрон-електронною взаємодією, можна вважати малим. Ефект спін-орбітальної взаємодії найчастіше відбувається на дефектах, або на поверхні зразка. Він призводить до позитивного знаку магнітоопору в області слабких магнітних полів і не домінує в АМО.
4.3. Аномальний холлівський магнітоопір
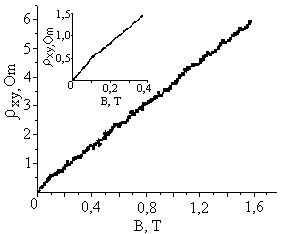
При дослідженні холлівського магнітоопору ρху(В) в роботі була отримана аномальна залежність цієї величини від магнітного поля поля В. Ця залежність показана на рис. 5(а), і на вставці до нього в збільшеному вигляді. Як видно з рис. 5(а), графік ρху(В) змінює свій початковий нахил і не є прямою лінією, що мало б бути в досліджуваній області змін В (μВ<<1). За величини В~0,1Т нахил залежності ρху(В) має точку перегину, а пряма ρху(В) в області полів В≈(0,1-1,6)Т не має продовження в точку з координатами х=0, у=0. Тому хід залежності ρху(В) можна вважати аномальним в порівнянні з класичним випадком і таким, що включає в себе аномальну компоненту магнітоопору.
(а) (б)
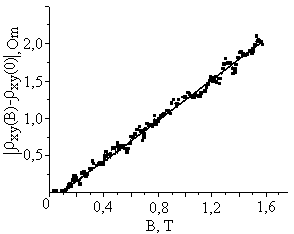
Рис. 5. Залежності холлівського магнітоопору ρху від магнітного поля В (а), і абсолютної величини її аномальної частини |ρху(В)-ρху(0)| від магнітного поля В (б).
Нахил залежності ρху(В) в класичному випадку визначається концентрацією електронів Г при μВ<<1. За величини магнітного поля В→0 залежність ρху(В) близька до прямої лінії (рис. 5а). Тому концентрацію Г0 при В=0 можна визначити за нахилом початкової ділянки залежності ρху(В). В цьому випадку, так само, як і при розгляді АМО повздовжнього опору ρхх, можна розрахувати холлівський аномальний магнітоопір, що визначається різницею ρху(В)-ρху(0), де ρху(0)=В/еГ0 і призводить до зменшення величини холлівського опору. Залежність абсолютної величини холлівського АМО від магнітного поля В представлена на рис. 5(б).
Аналізуючи залежність |ρху(В)-ρху(0)| від поля В перш за все зазначимо, що теорія розвинута в [10], а також іншими дослідниками (див., наприклад, огляд [11]) не передбачає АМО холлівської компоненти опору ρху. В теоретичній роботі [12] розглянута задача локалізаційних поправок як до повздовжнього ρxх, так і до холлівського ρху опорів 2D системи. Згідно цієї роботи локалізаційні поправки до холлівського опору ρху відмінні від нуля і мають знак, протилежний знаку заряду носіїв, що призводить до зменшення абсолютної величини ρху. В частині розрахунків АМО по відношенню до повздовжнього опору ρxх висновки [12] співпадають [10]. За оцінкою відносних локалізаційних внесків в АМО ρxх і ρху зроблених в [12], ці величини є одного порядку для обох аномальних компонент тензора поверхневого опору.
В досліджуваних нами плівках ІТО, в діапазоні змін магнітного поля В≈(0,2-1,6)Т, відносна величина аномального холлівського магнітоопору |ρху(В)-ρху(0)|/ρху(0) в декілька раз перевищує відповідне значення аномальної компоненти ρхх. Тому одержані результати тільки якісно можуть бути пояснені на основі [12]. На наш погляд, кількісні розбіжності теорії і експерименту є наслідком особливо великої ролі, яку можуть відігравати поправки обумовлені квантовою інтерференцією в досліджуваних плівках ІТО. Велике значення відношення
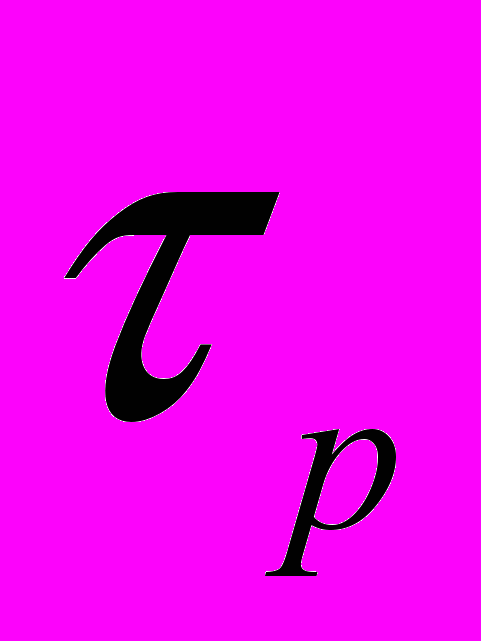 /
/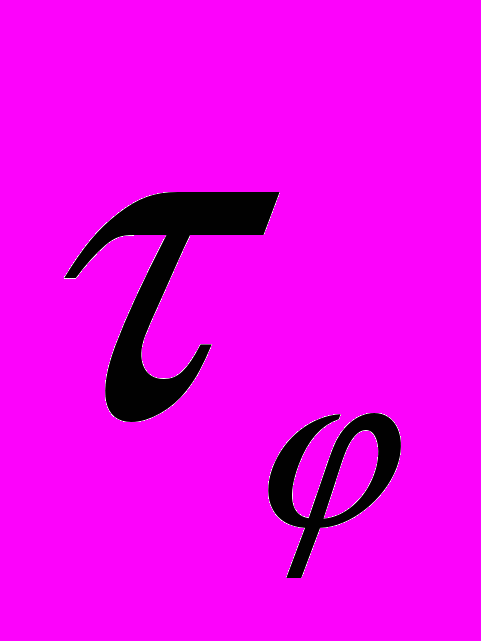 ≈10-6 вказує на можливість когерентної інтерференції з участю декількох центрів розсіяння. Відповідно, це призводить і до збільшення впливу локалізаційних поправок. В цьому випадку поправки вже не можна вважати малими. На це безпосередньо вказують залежності холлівської рухливості μh(В) і концентрації Г(В) по рис. 3а,б, що віддзеркалюють зміни вимірюваних μh і Г при зміні ступеню локалізації, що відбувається під дією магнітного поля. В цих умовах визначені μh і Г можуть відрізнятися від існуючих в зразку при В=0 навіть при малих магнітних полях. Подібні труднощі інтерпретації даних холлівських вимірювань були розглянуті при вивченні контрольованого впливу сильної локалізації на провідність каналу МДП транзистора [13].
≈10-6 вказує на можливість когерентної інтерференції з участю декількох центрів розсіяння. Відповідно, це призводить і до збільшення впливу локалізаційних поправок. В цьому випадку поправки вже не можна вважати малими. На це безпосередньо вказують залежності холлівської рухливості μh(В) і концентрації Г(В) по рис. 3а,б, що віддзеркалюють зміни вимірюваних μh і Г при зміні ступеню локалізації, що відбувається під дією магнітного поля. В цих умовах визначені μh і Г можуть відрізнятися від існуючих в зразку при В=0 навіть при малих магнітних полях. Подібні труднощі інтерпретації даних холлівських вимірювань були розглянуті при вивченні контрольованого впливу сильної локалізації на провідність каналу МДП транзистора [13].Висновки
В тонких плівках ІТО, легованого оловом, досліджені залежності компонент тензора поверхневого опору ρik, холлівської рухливості μh і концентрації Γ 2D електронів від величини магнітного поля В в полях до 1,6Т, при температурі Т=4,2К.
Вперше в плівках ІТО знайдена аномальна залежність компонент тензору поверхневого магнітоопору ρik від величини В. Відносне значення величини аномального холлівського магнітоопору перевищує відповідне значення повздовжнього в декілька раз. Отримані результати якісно пояснені на основі теорії квантових поправок до провідності. Показано, що квантові інтерференційні поправки не можна вважати малими. Визначено час релаксації фази хвильової функції
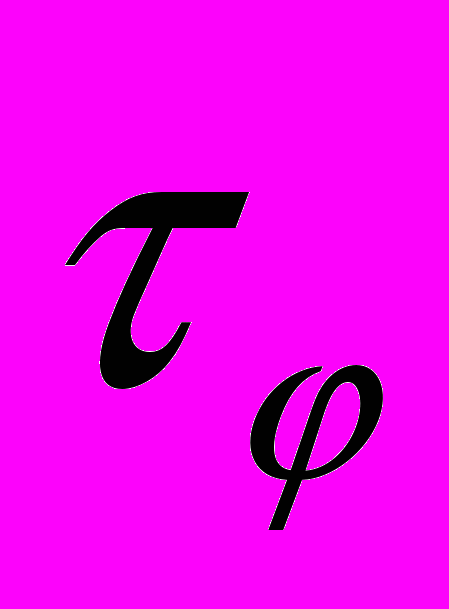 і довжину дифузії Lφ=(D
і довжину дифузії Lφ=(D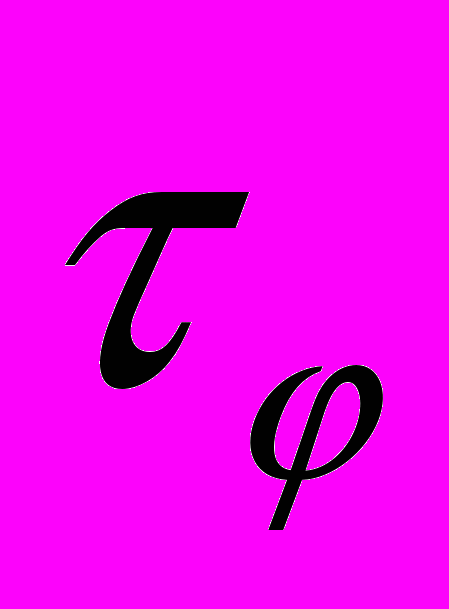 )1/2.
)1/2.Література
- Dawar A.L., Joshi J.C. Review. Semiconducting transparent films: Their properties and applications // J.Mater.Sci. - 1984. - V.19, № 1. - P.1-23.
- Deforest S.E. Spacecraft Charging at Synchronous Orbit // J.Geophys.Res. – 1972. – V.77,№4. – P.651-659.
- Vaufrey D., Ben Khalifa M., Tardy J. et al. ITO-on-top organic light-emitting devices: a correlated study of opto-electronic and structural characteristics // Semicond. Sci. Technol. – 2003. – V.18, N4. – P.253-260.
- Добровольський В.М., Іщук Л.В., Нінідзе Г.К., Гуденко Ю.М., Лозова О.Ю. Нелінійність ефекту Холла у слабких магнітних полях у плівках легованого оловом оксиду індію // Вісник Київського університету", сер.:Фіз.-мат.науки. - 2004, №2. - C.395-401.
- Электронные свойства двумерных систем. Пер. с англ./ Т. Андо, а. Фаулер, Ф. Стерн. М.: Мир, 1985.-416с.
- Третяк О.В., Львов В.А., Барабанов О.В. Фізичні основи спінової електроніки. - Київ: Київський університет, 2002. –314с.
- Добровольський В.Н., Ищук Л.В., Нинидзе Г.К. Рассеяние электронов в легированных оловом пленках индия и оксида индия // Неорганические материалы. - 1989. - № 8. - С.1321-1324.
- Жарких Ю.С., Лысоченко С.В. Минимальная подвижность носителей заряда, образующих двумерный газ.//Письма в ЖЭТФ. - 1982. - Т. 35. - Вып. 5. - С. 204-206.
- Ridge M., Howson R. P. Composition control in conducting oxide thin films//Thin solid films. - 1982. - V. 96. - №2. - P. 121-127.
- Альтшулер Б.Л., Аронов А.Г., Ларкин А.И., Хмельницкий Д.Е.. Об аномальном магнитосопротивлении в полупроводниках //ЖЭТФ. - 1981. - Т. 81. - Вып. 2(8). - С. 768-783.
- Полянская Т.А., Шмарцев Ю.В. Квантовые поправки к проводимости в полупроводниках с двумерным и трехмерным электронным газом// Физика и техника полупроводников // - 1989. - Т.23. - №1. - с.3-32.
- Грошев А.Г., Новокшонов С.Г. Отрицательное магнитосопротивление и коефициент Холла двумерной неупорядоченной системі // Физика твердого тела. - 2000. - Т.42. - Вып.7. - с.1322-1330.
- Абесонова Л.Н., Добровольський В.М., Жарких Ю.С., Фролов О.С., Шик А.Я. Об интерпретации результатов холловских измерений в неоднородных полупроводниках // Физика и техника полупроводников. - 1976, - №2. - C.395-401.
Надійшла до редакції 31.05.05
© С.В. Лисоченко, Л.В. Іщук,
Ю.С. Жарких, О. В. Третяк, 2005
