Вступительная статья

Вид материала

Статья

Содержание Модель зрительной области мозга Простота, а не правдоподобие Незавершенность трехмерного пространства

Подобный материал:

• В. В. Забродина Вступительная статья Ц. И. Кин Художник А. Е. Ганнушкин © Составление,, 3300.88kb.
• Мацуо Басё Путевые дневники Перевод с японского, вступительная статья, 1145.66kb.
• Содержание, 1765.31kb.
• М. Л. Спивак\ А. Белый На склоне Серебряного века Последняя осень Андрея Белого: Дневник, 736.18kb.
• Евангелие от Фомы, 571.12kb.
• Введение в методику демоскопии, 5847.27kb.
• Стихотворения, 1401.51kb.
• К. К. Станиславский Работа актера над ролью, 8199.71kb.
• Леви-Стросс К. Первобытное мышление, 5695.75kb.
• К. К. Станиславский Работа актера над ролью, 15947.17kb.

Модель зрительной области мозга


До сих пор я пользовался понятием фронтальной (двухмерной) модели как основным. Я пытался ответить на вопрос, какими свой­ствами должна обладать такая модель для того, чтобы воспринима­лась тенденция в трехмерном пространстве к наклонному положе­нию. Данный метод служит для определения того, какие разновид­ности изобразительных фигур на рисунке или картине создают этот эффект. Однако было бы ошибочным предполагать, что в психофи­зиологических процессах восприятия двухмерная модель имеет подобный же приоритет. И все-таки это делается очень часто по следующей причине. Независимо от того, является ли предмет фи­зически плоским или объемным, расположенным перпендикулярно или наклонно, когда мы смотрим на него, восприятие всегда бази­руется на зрительных образах этого объекта, спроецированных с помощью глазного хрусталика на сетчатку глаза. Сетчатка глаза представляет собой двухмерную поверхность, но не горизонтальную плоскость, потому что она является частью внутренней поверхности глазного яблока и, следовательно, ее поверхность носит шарообраз­ный характер, а не плоскостный. Но тем не менее это все-таки по­верхность, и все зрительные образы, отражаемые на сетчатке глаза, являются двухмерными, подобно картине, нарисованной на дне ча­ши. Поэтому можно часто услышать высказывание, что любое зрительное восприятие начинается с двухмерных проекций. Подоб­ное представление является неверным. На форму образа, запечат­ленного на сетчатке глаза, оказывается влияние только в том случае, если процессы возбуждения, которые протекают внутри поверхно­сти, находятся во взаимодействии друг с другом. Эту мысль можно проиллюстрировать следующей аналогией. Представьте себе целый ряд телефонных будок, в каждой из которых разговаривает человек. Если пространственная близость будок будет способствовать взаим­ному наложению разговоров, так что каждый абонент на противо­положном конце провода услышит беспорядочную смесь всех шести сообщений, то в этом случае действительно следует серьезно пораз­мыслить над изменением пространственного расположения телефон­ных будок. Но так как подобного наложения разговоров не проис­ходит, то разница между тем, располагаются ли телефонные будки близко друг к другу по прямой линии или по кривой или они на­ходятся друг от друга на расстоянии целой мили, является несу­щественной. Это, насколько нам известно, является компетенцией ретинальных рецепторов — палочек и колбочек. Каждый из этих не­больших одиночных рецепторов или группы рецепторов независимо, возбуждается одной точкой зрительного образа. Предприняв дробле­ние этой визуальной информации, ретинальный рецептор становится не чем иным, как транзитной станцией, на которой свет превращается в нервные импульсы. Однако то, что все эти станции-преобразова­тели располагаются на общей поверхности, и то, какую форму имеет эта поверхность, не оказывает какого-либо воздействия на простран­ственные размеры получившегося в итоге восприятия.

Можно допустить, что взаимодействие в этом пространстве как целом происходит в той части головного мозга, на которую опти­ческим нервом проецируются ретинальные возбуждения. Это есть часть коры головного мозга, которая хорошо известна под названи­ем визуальной области коры головного мозга. Каждая характерная особенность того, что мы воспринимаем, имеет соответствующее отражение в этом органе. Так как восприятие охватывает три из­мерения, то соответственно три измерения должны фигурировать и в коре головного мозга. Эти измерения необязательно должны быть пространственными по самой своей природе. А также все простран­ственные отношения при восприятии не должны обязательно иметь точную копию в мозгу. Однако в наших целях удобнее допустить, что происходит именно так. Согласно Кёлеру и Д. А. Эмери, «лишь немногие поддержали бы идею, что объекты, которые появляются на различных расстояниях от [воспринимающего их субъекта], представлены процессами, протекающими в коре головного мозга на различных уровнях; некоторые из этих процессов протекают ближе к поверхности коры, а другие в более глубоких ее слоях. Однако с прагматической точки зрения, по-видимому, не существует какого-либо серьезного вреда в оперировании с мысленной картиной, кото­рая в точности предполагает эту топологическую схему третьего измерения в зрительной области головного мозга» [3].

Мы обрисовали визуальную область коры головного мозга как область трехмерного пространства, в котором возбуждения, как только они возникают, становятся изолированными и в принципе свободны принимать любую пространственную конфигурацию — пло­скую или имеющую объем, фронтальную или расположенную наклон­но. Какой-либо приоритет здесь отсутствует. Однако возбуждения будут ограничены в своей свободе одним важным обстоятельством: они не могут отклоняться от проективной модели, образованной на сетчатке глаза. Чтобы проиллюстрировать это положение, я при­бегну к искусному инструменту, при помощи которого китайцы производят арифметические действия и который представляет собой каркас из параллельно натянутых проволок с¹ нанизанными на них бусами, то есть счеты. Рискуя быть занесенным в черные списки любым почтенным психологом, я буду воображать теперь визуаль­ную области коры головного мозга как трехмерные счеты, на кото­рых возбуждения представлены в виде бусинок. На рис. 159 пока­зана стимулирующая модель четырьмя точками. Посредством про­ективной модели, образованной на сетчатке глаза, точки в нашем расположены таким образом, что образуют во фронтальной плоскости квадрат. Но в принципе это необязательно должно быть квадратом. Четыре бусинки могут беспрепятственно скользить вдоль своих проволочек, образуя в любой из бесчисленного числа плоско­стей какую-нибудь четырехстороннюю фигуру. Или же вообще они могут не находиться в общей плоскости.

Все, что было здесь сказано о плоскостных фигурах, справедливо также и в отношении объемных тел. Фигура, изображенная на рис. 160,а. состоит из трех параллелограммов. Если каждый из этих параллелограммов примет наклонное положение, которое превратит его форму в квадрат, то модель в целом будет восприниматься как куб со свойственными ему тремя измерениями, а не как плоский и неправильный шестиугольник, расположенный во фронтальной плоскости и обладающий более простой визуальной структурой. Рис. 160, а воспринимается как проекция куба. Однако не каждая такая проекция заставляет нас видеть фигуру куба. На рис. 160, 6








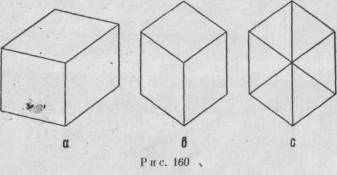
этот эффект значительно слабее, потому что симметрия фронталь­ной фигуры несколько способствует восприятию данного изображе­ния как двухмерного. И для большинства зрителей довольно трудно увидеть в изображении на рис. 160, с просвечивающийся рис. 160, b. Эти примеры иллюстрируют закономерность, которую сформулиро­вал в своем раннем исследовании по данному вопросу Коффка. «Когда простая симметрия достигается в двух измерениях, то мы будем видеть плоскую фигуру. Если достижение симметрии влечет за собой третье измерение, тогда мы будем видеть уже объемное тело» [4]. Слегка перефразировав эти слова, можно сказать, что дан­ное правило утверждает следующее: восприятие модели как двух­мерной или как объемной зависит от того варианта, с помощью ко­торого образуется более простая модель.

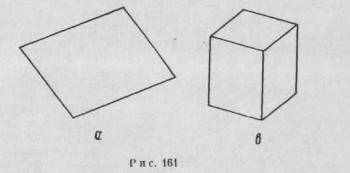
В этом месте нашего изложения необходимо внести две неболь­шие поправки. Как фигура, изображенная на рис. 156, так и фигура на рис. 160, а не выглядят совершенно законченными. С точки зрения третьего измерения фигура, изображенная на рис. 156, слишком высока. Если слегка сократить ее размеры по высоте (рис. 161, а), то результат окажется вдвойне удовлетворительным. Эффект объемности является здесь более неотразимым, а получив­шаяся в результате наклонная модель выглядит гораздо убедитель­нее как фигура квадрата. Аналогичным образом, если ту же самую операцию проделать с рис. 160, а, то эффект объемности станет сильнее, а получившаяся в результате сокращения модель воспри­нимается скорее как куб. Взглянув на наши счеты, мы поймем, что этого и следовало ожидать. Если модель изгоняется из фронтальной плоскости, то ее края, принявшие наклонное положение, будут вы­тягиваться. Степень этого удлинения будет зависеть от угла накло­на. Следовательно, если во фронтальном варианте все грани являют­ся одинаковыми (как это имеет место в нашем примере), то в плоскости, расположенной наклонно, они будут неравными. Равно­сторонние ромбы образуют фигуры прямоугольников, а не фигуры квадрата. Чтобы получить квадрат, мы должны исправить длины граней в соответствии с их наклоном. Становится понятным, почему это усиливает эффект объемности. Если мы получим вместо квадра­та фигуру прямоугольника, то в результате образуется менее про­стая фигура. Это означает в свою очередь, что выгода, которую не­сет с собой простота, достигаемая посредством устранения искаже­ния в ромбе, оказывается меньшей. Следовательно, будет меньшей и напряженность в ромбе, а также и побуждение избавиться от него благодаря трехмерности.

Вторая коррекция привносится другим недостатком наших ри­сунков. Хотя на бумаге каждый ромб состоит из двух пар парал­лельных сторон, и объемном варианте они выглядят слегка непра­вильными. Кажется, что они расходятся назад, так что получающие­ся в результате квадраты приобретают неправильную форму. Эта ситуации остается загадкой. Наше основное предположение, что каждая характерная особенность визуального опыта имеет в корко­вой модели своего двойника, обязывает нас прийти к выводу, что счеты, изображенные на рис. 159, нарисованы неправильно. Прово­лочки должны располагаться не параллельно, а расходиться назад гак. чтобы расстояния между бусинками увеличивались по мере их скольжения. В таком случае в любой наклонно расположенной пло­скости параллельные фронтальные линии будут расходиться. Сте­пень этого расхождения будет зависеть от угла наклона. А чтобы стать параллельными в наклонной плоскости, фронтальные линии должны сойтись. На рис. 162 показано, например, как фронтально расположенная трапеция может быть преобразована в прямоуголь­ную фигуру посредством наклонного размещения плоскости.

В чем же заключается причина этой любопытной асимметрии в корковой модели? Возможно, сторонник эволюционной теории поже­лал бы объяснить это явление как такое средство, которое застав-




ляет организм лучше приспособиться к выживанию, потому что это искажение в коре головного мозга стремится скомпенсировать иска­жения формы и размера в проективных образах, отражаемых глаз­ными хрусталиками на сетчатке глаза. В проекциях размер любого объекта уменьшается в зависимости от расстояния до воспринимаю­щего субъекта. Мозг, создавая противоположный эффект, стремится восстановить полезное соответствие между физической формой и размером и их психологическим двойником.

Каким бы ни было объяснение этого феномена, рис. 163 показы­вает, что, если парные грани ромба заставить в некоторой степени сходиться, пространственный эффект усиливается и мы будем вос­принимать фигуры квадратов или кубов.


Простота, а не правдоподобие


Модели в виде тех, которые представлены на рис. 163, могут быть получены путем фотографирования квадратов и кубов под наклонным углом. В объемном варианте эти модели очень часто при­обретают форму физических объектов, проекцией которых они яв­ляются. Это явление побудило психологов сформулировать следую­щую психологическую закономерность. Несмотря на наличие иска­жений, возникающих на сетчатке глаза, объекты воспринимаются почти в соответствии с их физической формой и размером (принцип постоянства). Хотя для практических целей эта формулировка яв­ляется, в общем, правильной, тем не менее она вводит нас в заблуж-




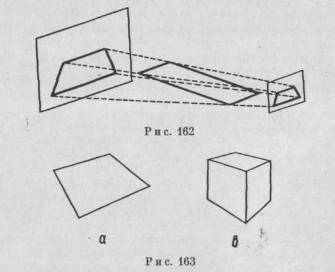
дение. Данный вывод базируется на случайном критерии и, следо­вательно, не дает возможность понять, как происходит это явление.

Предположим, что трапеция, выполненная из светящихся ли­ний, установлена на полу темной комнаты на некотором расстоянии от воспринимающего субъекта. Расположение этой трапеции та­ково, что она видится воспринимающему как проекция квадрата (рис. 164). Если воспринимающий будет рассматривать эту фигуру





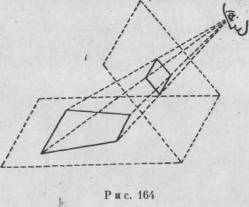
через смотровое окошечко, он увидит фронтально расположенный квадрат, потому что квадрат является наипростейшей фигурой, доступной для проективной подели. С точки зрения идентичности С физическим объектом он видит искаженный предмет, то есть прин­цип постоянства а этом случае отсутствует. Мы можем прийти к выводу, что соответствие между тем, что существует в физическом пространстве, и том, что нами воспринимается, имеет место только тогда, когда форма сокращенного в ракурсе физического объекта окалывается той самой наипростейшей фигурой, проективная модель которой может восприниматься как искажение. К счастью, это про­исходит довольно часто. В мире искусственно созданных вещей прямоугольники, квадраты, кубы, параллельные линии и окружности встречаются очень часто, а в природе, кроме того, существует еще тенденция к простой форме. Но когда форма объектов является не­правильной (как, например, форма горного хребта), их проекции могут не казаться искажениями более простых фигур. Следователь­но, постоянство формы нарушается, и объемное восприятие должно полагаться на другие факторы.

Закономерность, которая иллюстрируется на рис. 164, служит практическим целям в театральной декорации и в архитектуре. Часто желательно создать впечатление большей глубины, чем это доступно физически. Если художник-декоратор построит на сцене комнату правильной формы с простым горизонтальным полом и перпендикулярно возвышающимися стенами (рис. 165, а, вид свер­ху), зритель будет воспринимать проективную модель, указанную на рис. 165, b, и, следовательно, увидит комнату приблизительно в таком виде, в каком она изображена на рис. 165, с. Если, однако, пол будет иметь наклон кверху, потолок — вниз, а трапециевидные стены будут сходиться где-то в глубине перспективы (рис. 165, d), физический уклон будет накладываться на уклон проективный, и в результате образуется проекция, имеющая вид рис. 165, е. Из-за того, что отверстие, расположенное во фронтальной плоскости, имеет большие размеры, а задняя стена меньше его, комната в форме куба будет восприниматься значительно более глубокой (рис. 165, f). Все это противоречит принципу постоянства, но в точности со­гласуется с принципом простоты. В качестве яркого примера можно привести палаццо Спада в Риме. Когда около 1635 года Борромини заново перестроил это палаццо, он построил сводчатую колоннаду, суживающуюся к концу, чтобы получить впечатление глубокой ар­хитектурной перспективы. Если зритель стоит во дворе палаццо и смотрит внутрь колоннады, он видит длинный туннель с располо­женными на его флангах колоннами, которые уводят его взгляд во­внутрь к открытому пространству, где он замечает огромную статую воина. Но, вступая внутрь этой колоннады, он испытывает сильное ощущение морской болезни, вызванное потерей пространственной ориентации. Борромини имел в своем распоряжении лишь ограни­ченный участок, и колоннада оказалась действительно короткой. Она насчитывает около восьми с половиной метров длины от фрон­тальной арки до арки, расположенной в ее конце. Высота фронталь





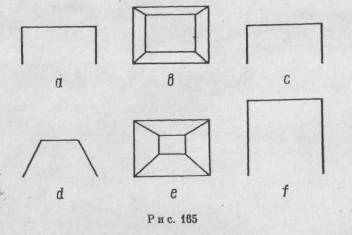
ной арки равняется пяти метрам восьмидесяти сантиметрам, а ее ширина составляет немногим более трех метров. Задняя арка имеет высоту два с половиной метра, а ширину около девяноста сантимет­ров. Потолок имеет легкий уклон вниз, пол несколько возвышается, боковые стены сходятся, а промежутки между колоннами постепен­но уменьшаются. Достигнув статуи воина, зритель с удивлением об­наруживает, что она совсем не велика по своим размерам.

Средневековые архитекторы добивались эффекта усиления глу­бины тем, что заставляли боковые стороны церковных сооружений сходиться к месту, где обычно располагается хор, и постепенно со­кращая пространство, занимаемое колоннами.

Существуют проекты, основанные на противоположном приеме. Их авторы стремятся сохранить правильную форму от искажающе­го влияния перспективы и сократить видимое расстояние. Эта тен­денция проявляется в равноугольнике, который образует колоннады, построенные Бернини на площади Св. Петра в Риме, и площади перед Капитолием, спроектированной Микеланджело. В обоих при­мерах происходит схождение перспективы навстречу приближающе­муся зрителю. Согласно Витрувию, толщина верхней части колонн в древнегреческих храмах по сравнению с ее нижней частью уве­личивалась по мере увеличения их высоты. Джорджо Вазари во времена Ренессанса утверждал: «...когда статуи предназначены для высокого места, а внизу нельзя отойти достаточно далеко, дабы судить о них издали, и приходится стоять под ними, подобные фигуры следует делать выше на одну голову или на две». Если это сделано, тогда «фигуры, поставленные высоко, теряют от сокраще­ния, если смотреть на них, стоя внизу, снизу вверх. Поэтому прида­ваемое им увеличение поглощается сокращением, и тогда соразмер­но этому они уже кажутся правильными и не приземистыми, но обладающими должным изяществом» [5].

Не так давно Адальберт Джерри Эймс продемонстрировал факт расхождении между физическим пространством и его психологиче­ским восприятием. В этих хорошо известных экспериментах (рис. 166) испытуемый глядел через узкое смотровое отверстие (о) в комнату, которая казалась ему нормальной, прямоугольной формы (efсd). Фактический план этой комнаты — abсd. Комната спроекти­рована таким путем, чтобы вызвать у воспринимающего субъекта образ на сетчатке глаза, тождественный с образом от комнаты, имеющей прямоугольную форму. С этой целью стены, потолок и иол были соответственно деформированы и имели некоторый уклон. В такой комнате происходят таинственные вещи. Человек, стоящий в точке р, воспринимается так, словно он стоит в точке q, и, следо­вательно, выглядит совсем карликом по сравнению с другим чело-





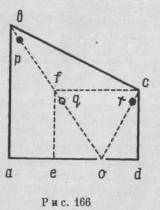
веком, находящимся в точке r. Человек ростом в 180 сантиметров, находящийся в точке р, выглядит меньшим, чем его сын, стоящий в точке г. В задней стене имеются два окна. Лицо человека, смотря­щего через окно, расположенное слева, выглядит значительно мень­ше, чем лицо человека в правом окне.

Данное явление остается загадочным до тех пор, пока мы не вспомним, что восприятие человека, который смотрит через узкое отверстие одним глазом, за­висит главным образом от проективной модели, отраженной на сетчатке его гла­за. Независимо от того, получена ли эта модель от деформированной или от пря­моугольной комнаты или даже с их фото­графий, никакой, даже самой небольшой, разницы не наблюдается. Если деформи­рованная комната воспринимается как прямоугольная, то для объяснения этого потребуется не больше аргументов, чем для объяснения факта, при котором пря­моугольная в действительности комната и воспринимается прямоугольной. Это объ­яснение, как я думаю, будет в обоих случаях одним и тем же. Про­ективная модель представляет собой искажение полого куба, и, следовательно, самая простая доступная форма достигается в объ­емном восприятии.


Незавершенность трехмерного пространства


Ранее были рассмотрены только две разновидности пространст­венной ситуации: двухмерная проекция во фронтальной плоскости и трехмерная ориентация, в которой зрительно воспринимаемый объект приобретает наипростейшую форму. Однако на практике вряд ли можно добиться полного упразднения искажений. Компенсация размеров в колоннах и статуях не потребовалась бы, если глаз воспринимающего их субъекта целиком и полностью умел бы кор­ректировать перспективные искажения. Психологи обнаружили, что, когда мы смотрим на объект, расположенный наклонно, мы видим форму, которая является компромиссом между двумя крайностями: "действительной формой", с одной стороны, и ее фронтальной про­екцией — с другой. Когда мы находимся в церкви или когда глядим вдоль полотна железнодорожных путей, мы видим, что ряды колонн сходятся в сторону алтаря, а железнодорожные рельсы не парал­лельны. Схождение в этом случае является не таким сильным, ка­ким оно было бы во фронтальной проекции. На фотографическом снимке углы наклонены уже гораздо сильнее. Соответственно и различия по глубине воспринимаются значительно меньшими, чем они являются на самом деле.

Происходящая при этом компенсация зависит от нескольких факторов. В первую очередь восприятие глубины усиливается сте­реоскопическим видением, основанным на совместном зрении обоих глаз, а также на других условиях, которые я рассмотрю позднее. Чем более точно воспринимается глубина, тем в большей мере ком­пенсируется искажение формы. Если мы смотрим на реальное фи­зическое пространство обоими глазами или через стереоскоп, эффект глубины ощущается в сильной степени. На картине, нари­сованной по законам перспективы, тот же эффект будет слабее. Различие зависит также и от отношения самого воспринимающего субъекта. В то время как «человеку с улицы» трудно убедить себя, что он видит ряды зданий и сооружений, наклоненных друг к другу, то учащийся, который обучен законам проективного ри­сунка, это сделает гораздо быстрее. Существуют также и некоторые доказательства того, что тип пространственного изображения, при­сущий данной культуре, оказывает влияние на восприятие людей. Роберт Ч. Таулесс выяснил, что индийские студенты, которые были слабо знакомы с законами перспективного изображения, восприни­мали наклонно расположенные объекты в более «реальной» форме, чем английские учащиеся.

Другой и наиболее важный фактор непосредственно связан с самой проективной моделью. Мы выяснили, что пространственное представление зависит от относительной простоты двух- и трех­мерных ' моделей. Одним из условий, которое всегда способствует восприятию объекта как плоского предмета, является фронтальность ориентации. Объемные твердые тела всегда должны выступать в на­клонной отношению воспринимающему субъекту ориентации, а наклонное расположение является менее простым, чем фронталь­ное. Кроме того это условие всегда противодействует уничтожению перспективного искажения. Более того, фронтальная проекция пред­ставляет собой часто такую простую форму, которая оказывает свое влияние в сильной степени. Когда мы стоим в дверях церкви и смотрим в сторону алтаря, проективная модель, которая образуется в данном случае, симметрична. Эта симметрия будет уменьшать вос­приятие глубины, подобно тому как симметричная модель па рис. 160, b воспринимается нами как куб в значительно меньшей степе­ни, нежели фигура на рис. 160, а. Если мы будем рассматривать внутреннее помещение церкви с наклонной позиции, объемность возрастает. Конструкция сцены, выступающей для зрителя в каче­стве симметричной модели (рис. 167, а), будет производить впечат­ление меньшей глубины, чем в том случае, когда она асимметрична (рис. 167,6). В картинах и рисунках компенсация искажений всегда является неполной, потому что глаза замечают «плоскостность» изобразительной плоскости, которая нейтрализует стремление изображения к объемности. Художник избегает или усиливает симмет­ричность фронтальной модели в зависимости от того, благоприят­ствует или нет изображению глубины его художественный стиль. Наконец следует отметить, что в скульптуре объективная форма статуи всегда является довольно сложной, так что побудительный мотив уничтожить перспективное искажение не может быть таким же сильным, каким он является, например, при восприятии наклон­но расположенного правильного куба.