Тема. Функції та їх графіки
| Вид материала | Урок |
- Диференціальне числення функції однієї змінної, 18.73kb.
- Розділ: Різне Класифікація графіки, 96.86kb.
- Тема. Білки, їхня будова, класифікація та функції. Мета, 74.26kb.
- Голосківська зош І – ІІІ ступенів Фортеця чотирьох королев: Фонетики, Орфоепії, Графіки, 113.98kb.
- На обласний конкурс на кращу методичну розробку з науково технічної творчості, 78.25kb.
- Урок №1 тема: Засоби виразності графіки, 597.79kb.
- Назва модуля: Алгоритмічні мови та програмування Код модуля: кса 6022 С01, 22.16kb.
- 10. Функції рівнів моделі osi тема 10. Функції рівнів моделі osi, 125.17kb.
- Тема: Дослідження спектрів відбивання та пропускання речовин за допомогою спектрофотометру, 189.21kb.
- Характеристика навчальних дисциплін кафедри (складова Інформаційного пакету), 587.13kb.
Урок № 1
Тема. Функції та їх графіки
Мета. Узагальнення і систематизація знань учнів про функції та
їх графіки.
Формування готовності пам’яті відтворення того, що потрібно по темі.
Обладнання. Кодоскоп, таблиця.
І. Мотивація навчання
У математиці поняття функції виникло разом з поняттям змінної величини, введеної Р. Декартом (1596-1650) і П. Ферма (1601-1665). Означення функції вперше сформулював у 1718 р. швейцарський математик Й. Бернулі (1667-1748). Нові відкриття розширювали поняття функції.
Більшість природничих і суспільних явищ, процесів можна описати за допомогою функції. Досліджуючи властивості функції, маємо можливості грунтовніше пізнавати реальний світ.
Повідомляємо тему і мету уроку.
ІІ. Систематизація й узагальнення основних відомостей про функцію.
Повторюємо означення, поняття області визначення й області значень. Повторюємо області визначення й області значень відомих простих елементарних функцій
y=kx+b, у=к/х, у=х2 ,
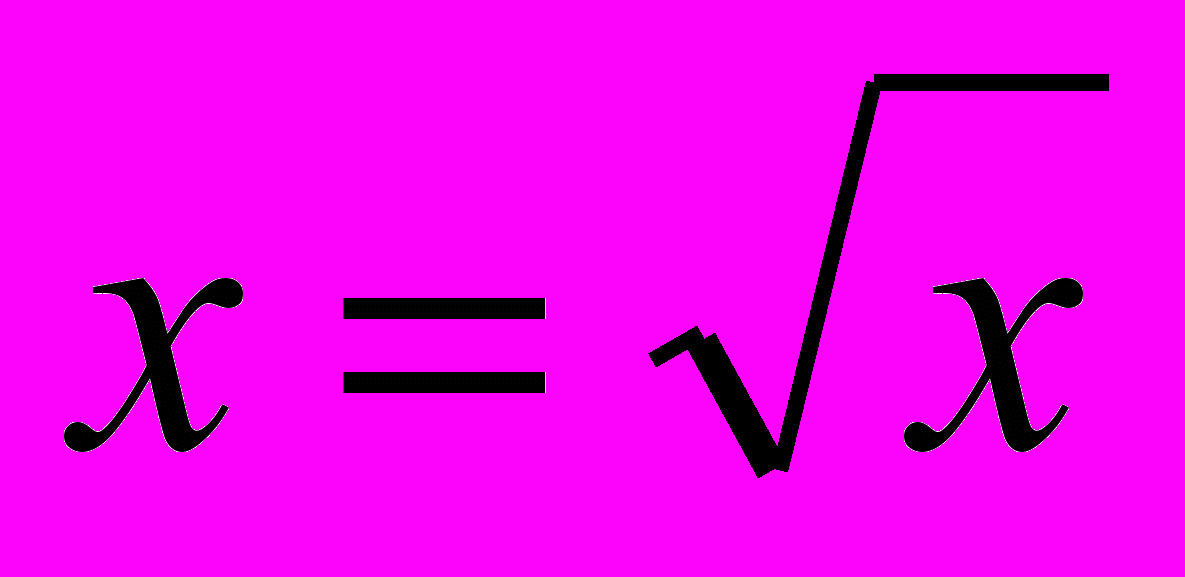 , у=х3
, у=х3Повторюємо знаходження області визначення складових функцій на прикладах функцій:
а)
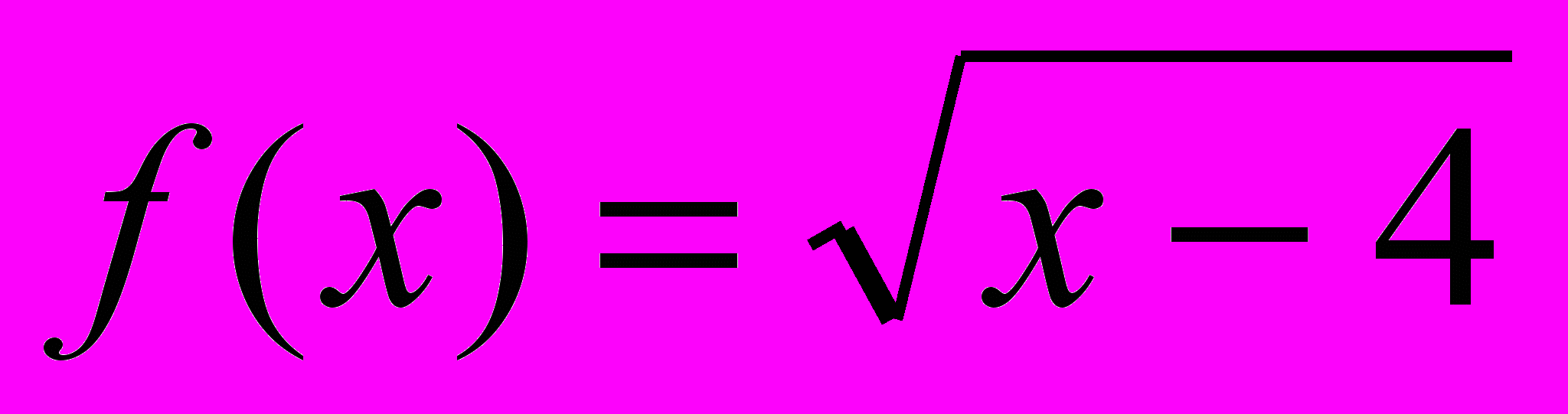 ; б)
; б) 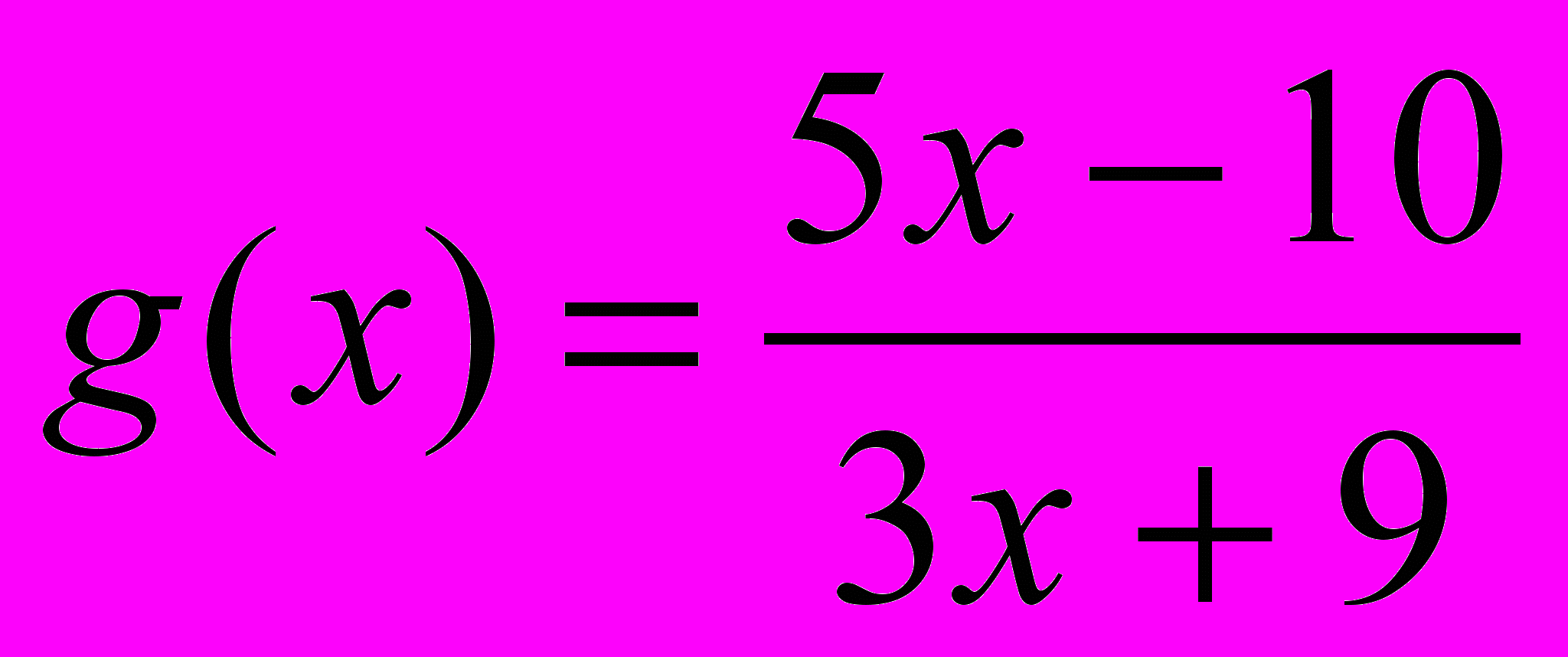 ; в)
; в) 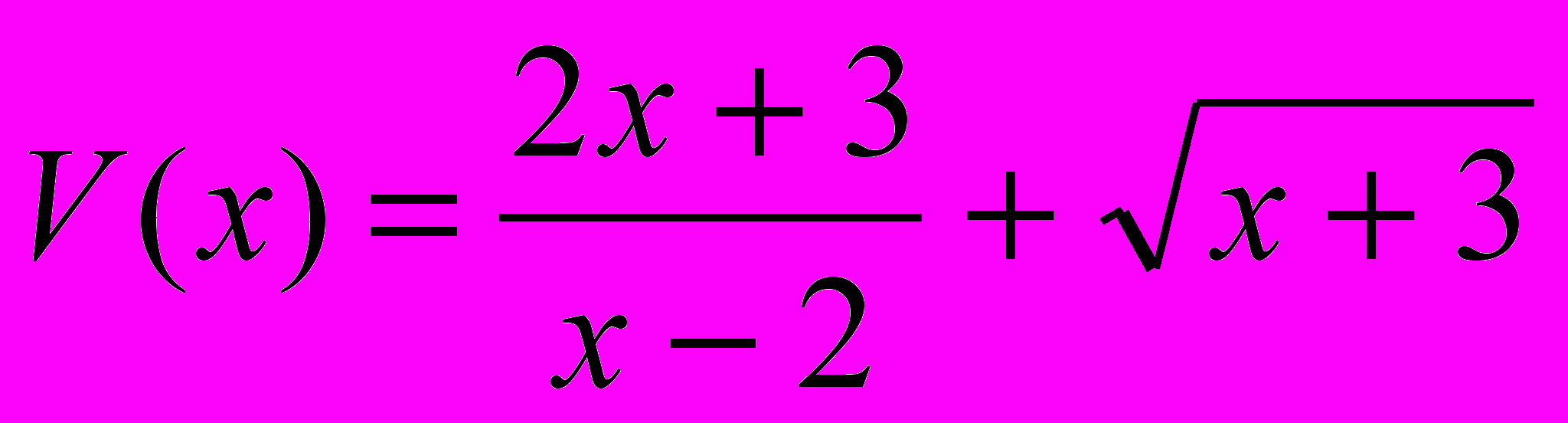
ІІІ. Систематизація й узагальнення знань учнів про графіки функцій, способи задання функцій.
Повторюємо відомості про способи задання функцій (за допомогою формули словесного опису, табличний, графічний).
Даємо означення графіка функції.
Проектуємо на екран таблицю і пропонуємо учням описати кожну із заданих функцій:
а) у= 4х+3; б) у=1/х; в) g(х)=х2; г) U(х)= х3; д) φ(х)=
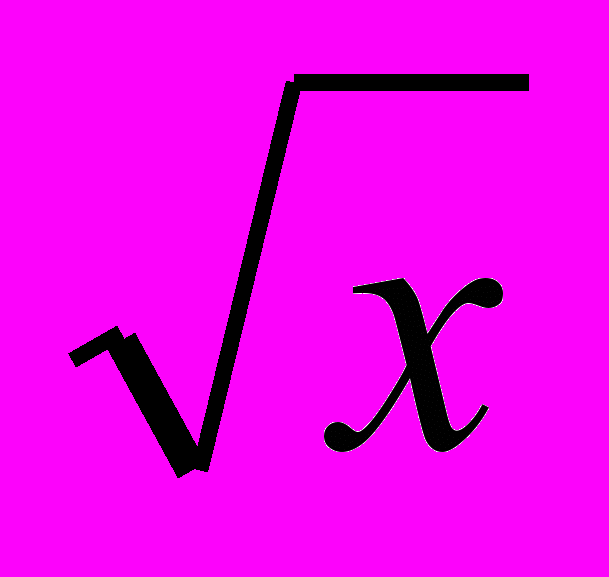 ;
; е)
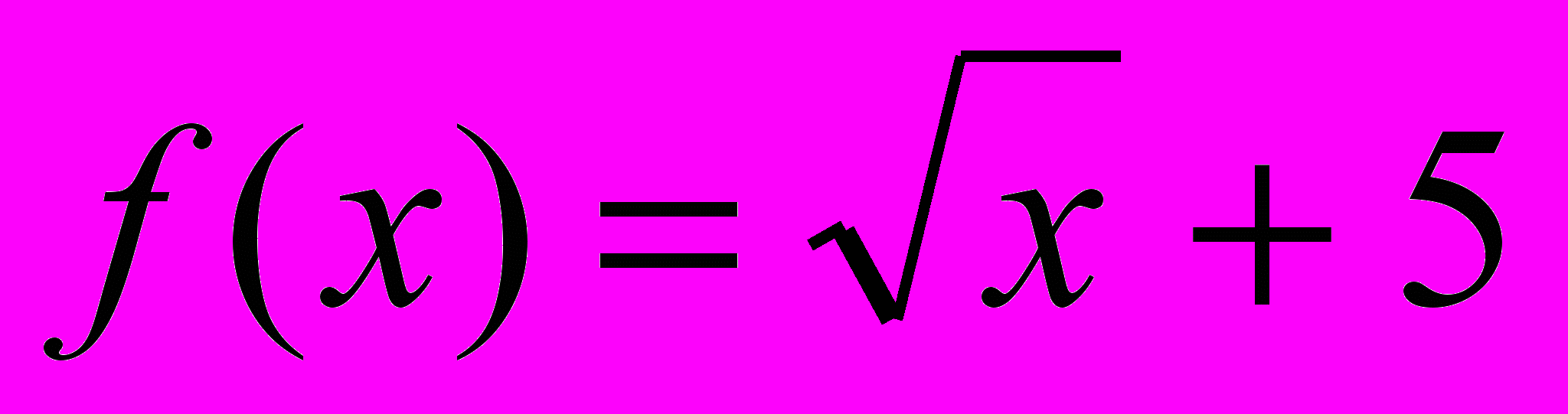 .
.Колективно будуємо графік функції
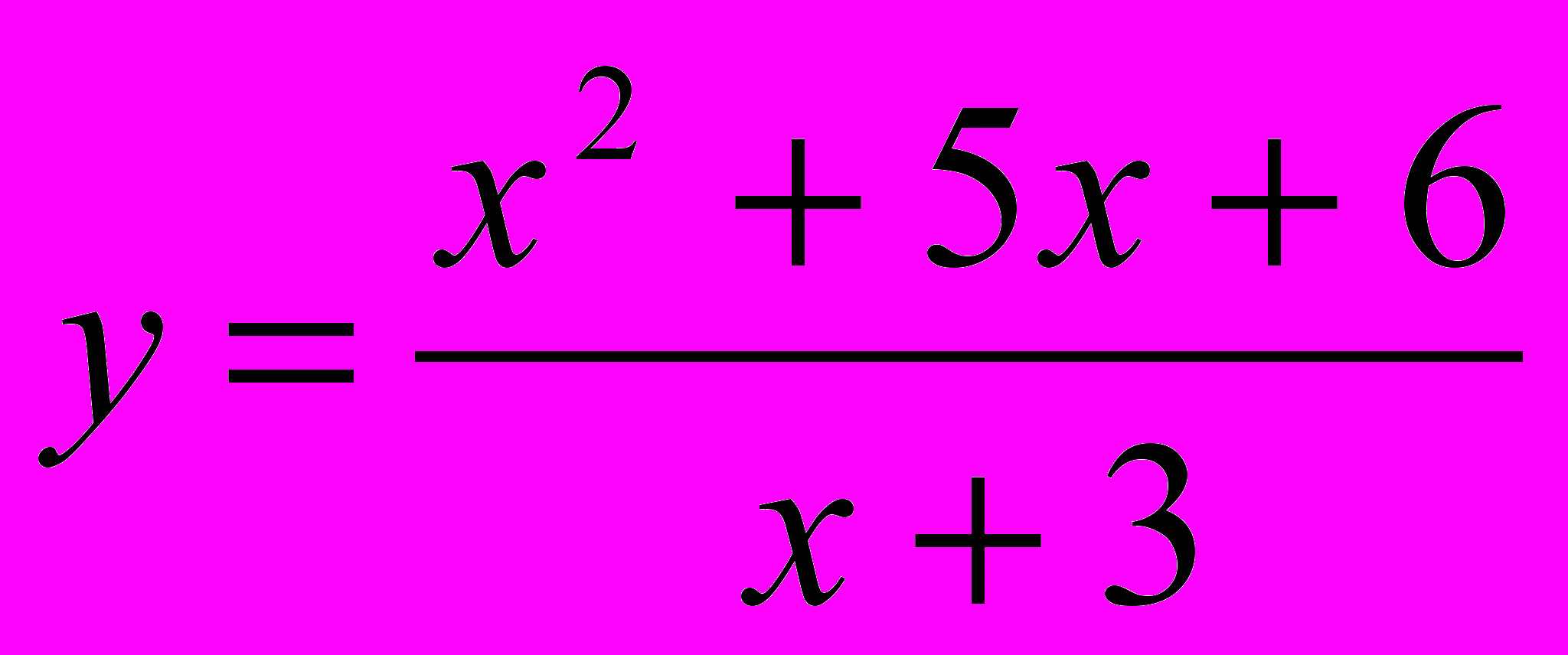
Учні міркують так: дріб
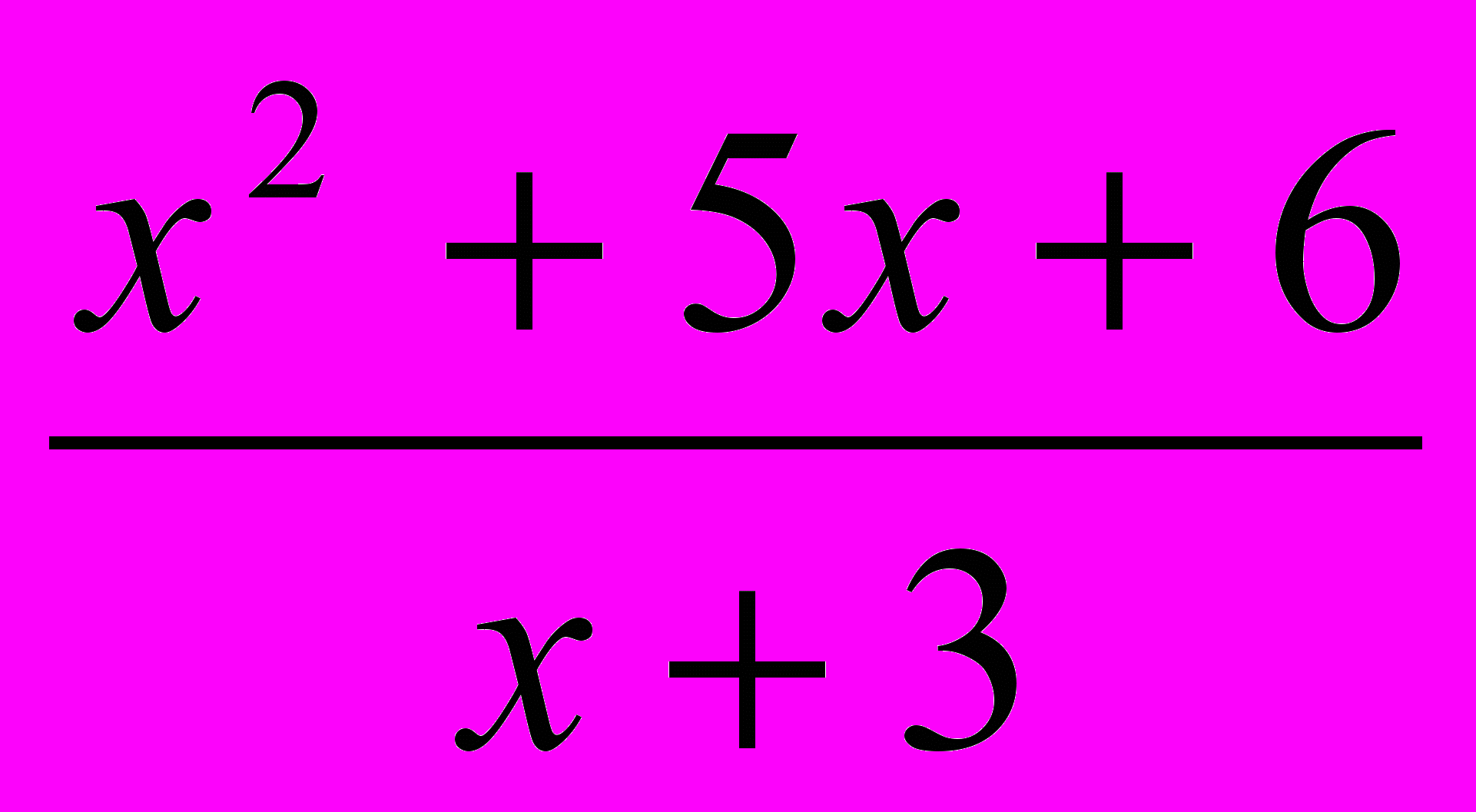 має зміст, якщо
має зміст, якщо 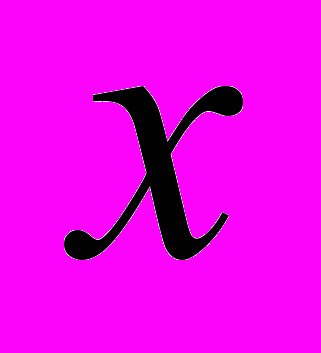 ≠ -3 і D(у)=(-∞;-3)U(-3;∞).
≠ -3 і D(у)=(-∞;-3)U(-3;∞).Отже,
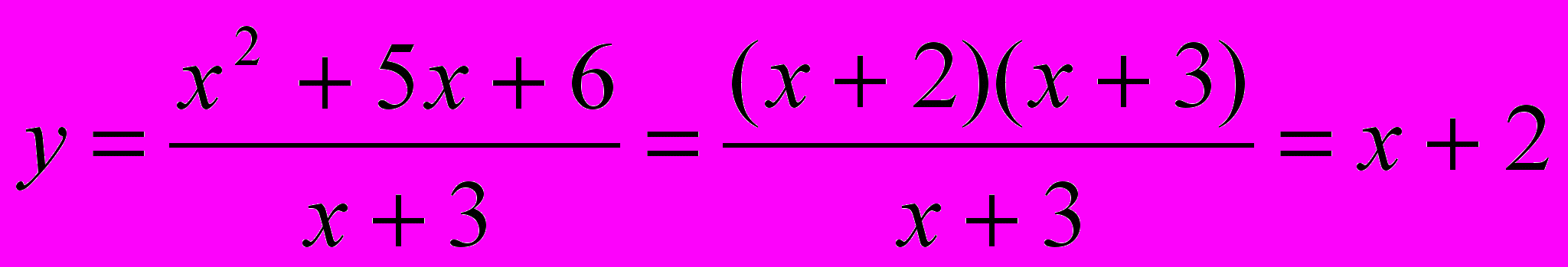 , якщо
, якщо 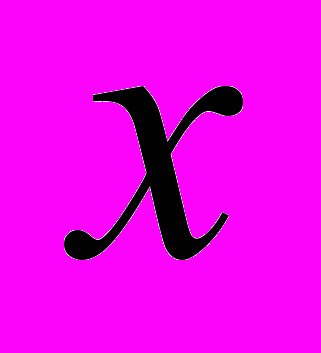 ≠ -3
≠ -3 Щоб дістати графік функції Y, будуємо графік функції Y1=х +2
і на цьому графіку виключаємо точку з абсцисою х =-3. Кажуть, що графіком функції Y є пряма з виключеною точкою при х =-3.
Пояснення вчителя.
Розглянута функція Y не визначена при х =-3. Кожна функція описує певний процес або явище. Може бути так, що при всіх х -3 виконується відповідність , а при х =-3 функція набуває конкретного значення, наприклад –1.
Тоді функцію Y2 задають так:
-
Y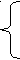 2 (х)=
2 (х)=
х+2, якщо х0,
-1, якщо х= -3,
Область визначення функції D(Y2)=(-; ), графік її функції зображено на мал. 1.






Деякі процеси відбуваються так, що їх можна описати функцією, заданою різними формулами на різних проміжках.
Наприклад,
-
f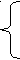 (х)=
(х)=
х2, якщо х≤0,
х+2, якщо х≥0,
Графік функції зображено на мал. 2.
Колективно обчислюємо (-2), (4).
Підсумок уроку
Повторили поняття числової функції області визначення й значень функції та їх знаходження для деяких складених функцій, графіки раніше вивчених функцій. Ознайомилися із способом задання функції різними формулами на різних проміжках.
Домашне завдання: § 53, повт. § 43 (Г.П. Бевз); № 432; 435; 437; 443 (а;в).
Урок № 2
Тема. Властивості функцій
Мета. Узагальнення і систематизація знань учнів про властивості
функцій.
Обладнання. Кодоскоп.
І. Перевірка домашнього завдання
Проектуємо на екран мал. 1 і мал. 2.
Фронтальне опитування учнів:
- Дайте означення числової функції.
- Коли вперше виникло поняття функції?
- Хто вперше сформулював поняття функції?
- Що таке область визначення і область значень функції?
- Якими способами можна задати функцію?
- Що таке графік функції?
- На мал. 1 вкажіть графіки функцій.
- Чому на мал. 1 у випадку а) і в) зображені множини не є графіками функцій?
- Встановіть відповідність між графіками функцій, зображених на мал.2 і формулами:
у= -2/х; у=х2; у= -х3; у=х3; у=
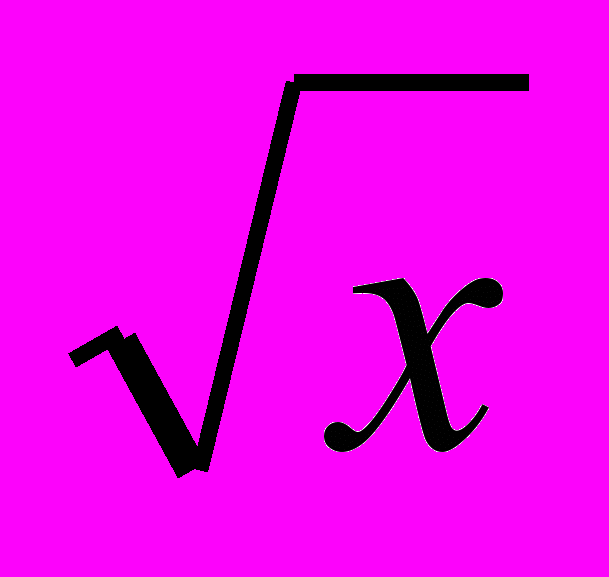
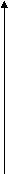
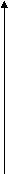


















ІІ. Мотивація навчання.
Функції відрізняються одна від одної не тільки областями визначення і значень, а й іншими властивостями. Деякі властивості ми вже вивчали.
Повідомляю тему і мету уроку.
ІІІ. Систематизація знань учнів про властивості функції.
1. Графік функції Y=(х) може перетинати координати осі. Обчисливши (0), знайдемо ординату точки перетину графіка функції з віссю ординат. Абсциси точок перетину графіка функції з віссю абсцис знаходимо, розв’язавши рівняння (х)=0. Абсциси точок перетину графіка функції з віссю абсцис називаються нулями функції, або коренями.
На графіках мал. 2 вкажіть нулі функції. Вкажіть на цих малюнках проміжки, на яких функція набуває додатних значень, від’ємних значень. Проміжки, на яких функція має однакові знаки, називають проміжками знакосталості. Для визначення проміжків знакосталості треба розв’язати нерівності (х)>0, (х)<0.
2. Охарактеризуйте зміну значення функції із зростанням аргументу на мал. 2. Вкажіть проміжки зростання й спадання функції на мал. 2 (табл.), а також на мал. 71-78 (§ 53). Дайте означення зростаючої і спадаючої функції на проміжку.
Графічне задання функції наочно ілюструє проміжки її зростання і спадання.
3. Даємо означення парної і непарної функцій. Поняття парної і непарної функції поширюємо на всі функції з областю визначення, симетричною відносно початку координат. Наводимо приклади дослідження функцій на парність.
ІV. Закріплення навичок та вмінь застосовувати означення парної (непарної) функції.
- (х)=х3+х;
Д()=(-∞;∞) – симетр. Відносно початку координат;
(-х)=(-х)3-х= -х3-х= -( х3+х)= -(х). Функція непарна і її графік симетричний відносно початку координат.
- g(х)= - х4+4х2;
D(g)= (-∞;∞) – симетрична відносно початку кооординат;
g(-х)= - (-х)4+4(-х)2= -х4+4х2= g(х). Функція g парна і її графік симетричний відносно осі у.
3) Ψ(х)= х3+3х2
D(Ψ)= (-∞;∞)- симетрична відносно початку координат;
Ψ(-х)= (-х)3+3(-х)2= -х3+3х2 ≠ ± Ψ (х)
Функція Ψ ні парна, ні непарна, і її графік не симетричний ні відносно осі ординат, ні відносно початку координат.
Підсумок уроку
Узагальнення і систематизація знання учнів про нулі проміжки знакосталості, зростання й спадання функцій. Засвоїли поняття парності і непарності функцій та властивості графіків цих функцій.
Домашнє завдання: Г.П. Бевз, § 58, повт. § 53; №193 (б;в;е); 196; 198.
Уроки № 3-4 (лекція)
Тема. Квадратична функція. Функція у=ах2, її графік і
властивості
Мета. Засвоєння учнями поняття квадратичної функції; засвоєння
властивостей функції у=ах2 і побудова її графіка.
Виховання у учнів наукового світогляду і розвиток стійких
Пізнавальних інтересів.
Обладнання. Кодоскоп, таблиця, дидактичний матеріал.
І. Перевірка домашнього завдання
Двоє учнів біля дошки працюють за картками, виконують завдання, подібні № 443 (ст. 169), № 198 (ст. 232)
З класом - фронтальне опитування.
- Дайте означення функції, області її визначення та області значень.
- Назвіть властивості функції, що характеризують її поведінку.
- Як визначають нулі та проміжки знакосталості функції?
- Як визначити парність (непарність) функції, яка властивість парної (непарної) функції?
- Дати означення зростаючої й спадної функції та проміжку.
ІІ. Актуалізація опорних знань учнів.
Повторюємо, що є графіком функції у=х2 і її властивості. Вивішуємо таблицю і працюємо за таблицею: у=х2; у= -х2.
ІІІ. Сприйняття і усвідомлення нового матеріалу.
- Означення квадратичної функції.
Функція, яку можна задати формулою у=ах2+вх+с, де а≠0, в,с - довільні числа, а х – аргумент, називаються квадратичною функцією.
Прикладом квадратичної функції є залежність шляху від часу при рівноприскореному русі
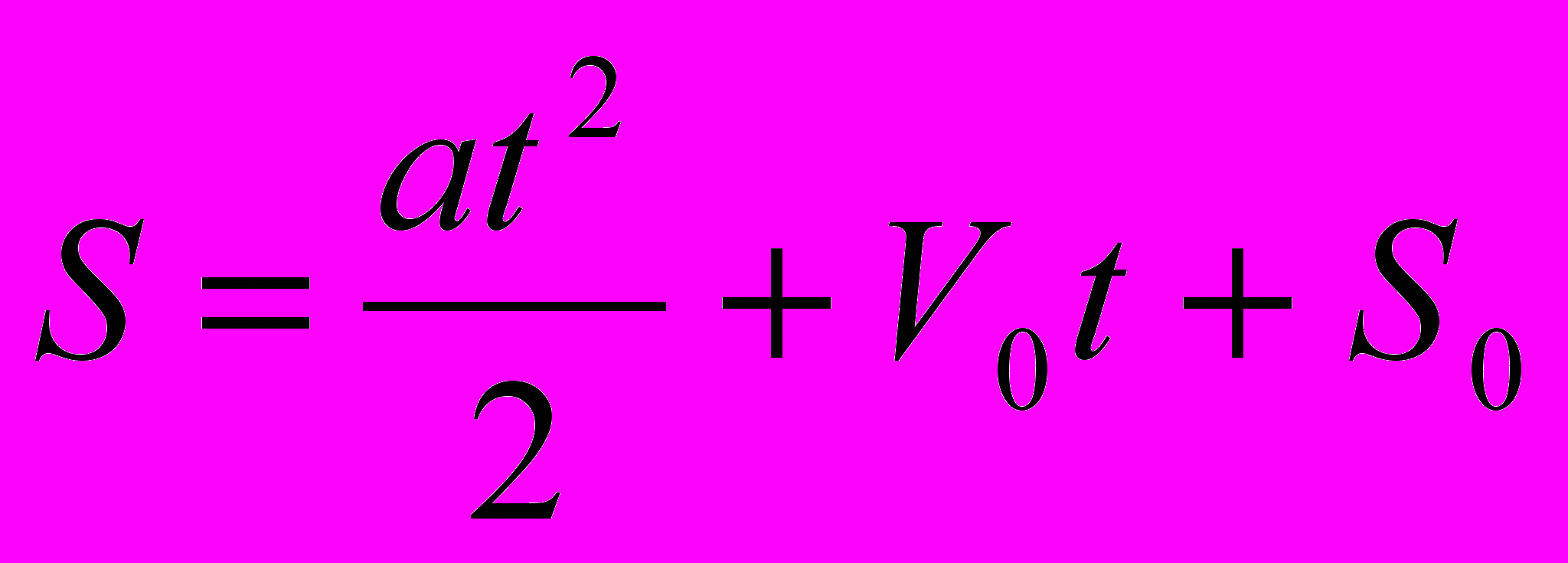 , де а – прискорення, t – час, S0 – початковий шлях, V0 – початкова швидкість.
, де а – прискорення, t – час, S0 – початковий шлях, V0 – початкова швидкість.2. В одній системі координат побудуємо графіки функцій у=х2; у=2х2; у=1/2х2 (відомим табличним способом). Мал. 1.
Бачимо, що щоб одержати із параболи у=х2 графік функції у=2х2 , треба її розтягнути від осі х в два рази, а графік функції у=1/2х2 можна одержати із параболи у=х2 зжиманням до осі х в два рази.
Взагалі графік функції у=ах2 можна отримати із параболи у=х2 розтягуванням від осі х в а раз, якщо а > 1, і зжиманням до осі х в 1/а раз, якщо 0<а<1.
3. Розглянемо функцію у=ах2 при а<0.
Побудуємо в одній системі координат графіки функцій у=1/2х2 і у= -1/2х2. При любому х значення цих функцій є протилежними числами. Значить, відповідні точки графіків симетричні відносно осі х. Другими словами, графік функції у= -1/2х2 можна одержати із графіка функції у=1/2х2 за допомогою симетрії відносно осі х.
Взагалі графіки функції у= ах2 та у= -ах2 (при а≠0) симетричні відносно осі х.
4. Сформулюємо властивості функції
а) у= ах2 при а>0
- Якщо х=0, то у=0. Графік функції проходить через початок координат.
- Якщо х≠0, то у>0. Графік розташований в верхній півплощині.
- Протилежним значенням аргументу відповідають рівні значення функції. Графік функції симетричний відносно осі у.
- Функція спадає на проміжку (-∞;0] і зростає на проміжку [0; ∞). Доводимо цю властивість.
- Найменше значення, яке дорівнює 0, функція приймає при х=0, найбільшого значення функція не має! Областю значень функції є проміжок [0; ∞).











б) у= ах2 при а<0
- Якщо х=0, то у=0. Графік функції проходить через початок координат.
- Якщо х≠0, то у<0. Графік розташований в нижній площині.
- Протилежним значенням аргументу відповідають рівні значення функції. Графік функції симетричний відносно осі у.
- Функція зростає на проміжку (-∞;0] і спадає на проміжку [0; ∞).
- Найбільше значення, яке дорівнює 0, функція приймає при х=0, найменшого значення немає. Областю значень функції є проміжок (-∞;0].
Із наведених властивостей маємо, що при а>0 вітки параболи у= ах2 направлені вверх, а при а<0 – вниз. Вісь у є віссю симетрії параболи. Точку перетину параболи з її віссю симетрії називають вершиною параболи. Вершиною параболи у= ах2 є початок координат.
Побудова графіка симетричного даному відносно осі х, розтягування графіка від осі х або зжимання до осі х – різні види перетворень графіків функцій. Перетворення графіків, розглянуті нами для функції у= ах2 можна використовувати для любої функції.
ІV. Формування навичок та вмінь будувати графіки функцій у= ах2 і відповідати на запитання, поставлених у вправах.
Розглянемо: №№ 73; 75; 79; 80 (С.О. Теляковський, ст. 28, 29).
Підсумок уроку
Засвоїли поняття квадратичної функції і властивості функції у= ах2 при а>0 і при а<0. Формували навички та вміння будувати графіки функції у= ах2.
Домашнє завдання:
Теоретичний матеріал по конспекту , повт. § 53; 58 – Г.П. Гевз.
№№ 76; 78; 81 (С.О. Теляковський);
та повт. № 85 (а).
Урок № 5
Тема. Графіки функцій у=ах2+n і у=а(х-m)2
Мета. Формування навичок та вмінь побудови графіків у=ах2+n і
у=а(х-m)2 (винятків квадратичної функції).
Формування у школярів конкретних уявлень формування
Здібностей швидкої орієнтації у несподіваних ситуаціях.
Обладнання. Кодоскоп, таблиця.
І. Перевірка домашнього завдання
- Перевірка теоретичного матеріалу:
- означення квадратичної функції;
- властивості функції у=ах2 при а>0;
- властивості функції у=ах2 при а<0.
- Побудувати в одній системі координат графіки функцій
а) у=х2 ; б) у=3х2 ; в) у=1/3х2
- Побудувати в одній системі координат графіки функцій у=2х2 і у=-2х2.
ІІ. Актуалізація опорних знань.
Знову повторюємо, як будуються графіки функцій у=ах2 .
Як побудувати графіки функцій у=1/2х2 +3, у=1/2(х-5)2 ?
Будуємо – за допомогою таблиць до кожної із функції.
ІІІ. Приклад 1. у=1/2х2 +3 (ст. 29 Теляковський).
В одній системі координат будуємо графіки функцій у=1/2х2 і у=1/2х2 +3. Таблиці в підручнику готові. Виясняємо, що щоб одержати таблицю значень функції у=1/2х2 +3 для тих же значень аргументу, досить до знайдених значень функції у=1/2х2 додати 3.
Графік функції у=1/2х2 +3 – парабола, яку одержали в результаті переміщення вверх графіка функції у=1/2х2 на 3 одиниці .










Аналогічно можна одержати графік функції у=1/2х2+2 перенесенням параболи у=1/2х2 на дві одиниці вверх.
Приклад 2. у=1/2(х-5)2
Побудуємо в одній системі координат графіки функцій у=1/2х2 і у=1/2(х-5)2 .
Замічаємо, що кожній точці (х0; у0) графіка функції у=1/2х2 відповідає єдина точка (х0+5; у0) графіка функції у=1/2(х-5)2 і навпаки.





Висновки.
1. Графік функції у=ах2+n є парабола, яку можна одержати із графіка функції у=ах2 за допомогою паралельного перенесенням вздовж осі у на n одиниць вверх, якщо n>0, або на – n одиниць вниз, якщо n<0.
2. Графік функції у=а(х-m)2 є парабола, яку можна одержати із графіка функції у=ах2 за допомогою паралельного перенесення вздовж осі х на m одиниць вправо, якщо m>0, або на – m одиниць вліво, якщо m<0.
3. Взагалі графік функції у=а(х-m)2+n є парабола, яку можна одержати із графіка функції у=ах2 за допомогою двох паралельних перенесень: зміщення вздовж осі х на m одиниць вправо, якщо m>0, або на – m одиниць вліво, якщо m<0, і зміщенням вздовж осі у на n одиниць вверх, якщо n>0, або на – m одиниць вниз, якщо n<0.
ІV. Формування навичок та вмінь побудови графіків у=ах2+n, у=а(х-m)2, у=а(х-m)2+n схематично, враховуючи висновки 1-3.
- Схематично будуємо графіки функцій № 87 (а;в;г).
- В яких координатних чвертях розташований графік? № 90 – усно.
- № 91 (а;б) – схематично.
Підсумок уроку.
Засвоїли висновки 1-3. Формували навички та вміння будувати схематично (за висновками 1-3) графіки функцій у=ах2+n, у=а(х-m)2 та у=а(х-m)2+n.
Домашнє завдання.
Конспект в зошиті; п.6 (С.О. Теляковський)
№№ 89; 92. Виготовити шаблон графіка функції у=х2.
Урок № 6
Тема. Графіки функцій у=ах2+n і у=а(х-m)2.
Найпростіші перетворення графіків функцій.
Мета. Засвоєння учнями навичок та вмінь побудови графіків у=ах2+n
у=а(х-m)2 і у=а(х-m)2+n; виконувати найпростіші перетворення
графіків.
Обладнання. Таблиця, дидактичний матеріал.
І. Перевірка домашнього завдання
Проглядаю виконання домашнього завдання в робочих зошитах.
ІІ. Актуалізація опорних знань.
Повторюємо правила, за якими будуються графіки функцій у=ах2+n, у=а(х-m)2 і у=а(х-m)2+n.
Чи справедливі ці правила тільки для квадратичної функції?
ІІІ. Перетворення графіків любих функцій.
Самостійно опрацьовуємо § 54 (Г.П. Бевз). Робимо висновки.
ІV. Закріплення навичок та вмінь будувати графіки.
- № 88 (С.О. Теляковський) – за допомогою виготовленого шаблону. № 93 (шаблон).
- № 95 (С.О. Теляковський) – скласти формулу для кожного графіка по малюнку.
- № 122 ( ст. 217 – Г.П. Бевз).
V. Самостійна робота (4 варіанти) – дидактика.
Підсумок уроку
Повторили, закріпили навички та вміння побудови графіків квадратичної функції, засвоїли методи перетворення любих графіків.
Домашнє завдання
П. 6 (С.О. Теляковський); § 54 (Г.П. Бевз); №№ 124; 127; 128(ж;з); 129 (а-в).
Уроки № 7-8 (лекція)
Тема. Функція у=ах2+вх+с, її властивості і графік.
Мета. Засвоєння вмінь та навичок дослідження функції у=ах2+вх+с
Обладнання. Кодоскоп.
І. Перевірка домашнього завдання.
ІІ. Аналіз самостійної роботи.
ІІ. Актуалізація опорних знань.
- Наведіть властивості функції.
- Дайте означення області визначення й області значень функції.
- Що таке нулі функції й проміжки знакосталості?
- Дайте значення зростаючої й спадної функції.
- Які функції називають парними й непарними та яка властивість їх графіків?
- Дайте означення квадратичної функції.
- Як побудувати графіки функцій у=ах2+n, у=а(х-m)2
і у=а(х-m)2+n ?
ІV. Мотивація навчання.
Якщо функція задана формулою у=ƒ(х), то її графік можна побудувати за точками, склавши для цього таблицю. Але такий спосіб не достатньо точний, оскільки можна не виявити поведінку функції між зображеними точками графіка. Тому треба вміти досліджувати функції.
Повідомляємо тему і мету уроку.
V. Формування навичок та вмінь дослідження квадратичної функції (елементи дослідження) і побудови графіка.
Розглянемо квадратичну функцію у=ах2+вх+с. Виділимо із виразу у=ах2+вх+с квадрат двочлена:
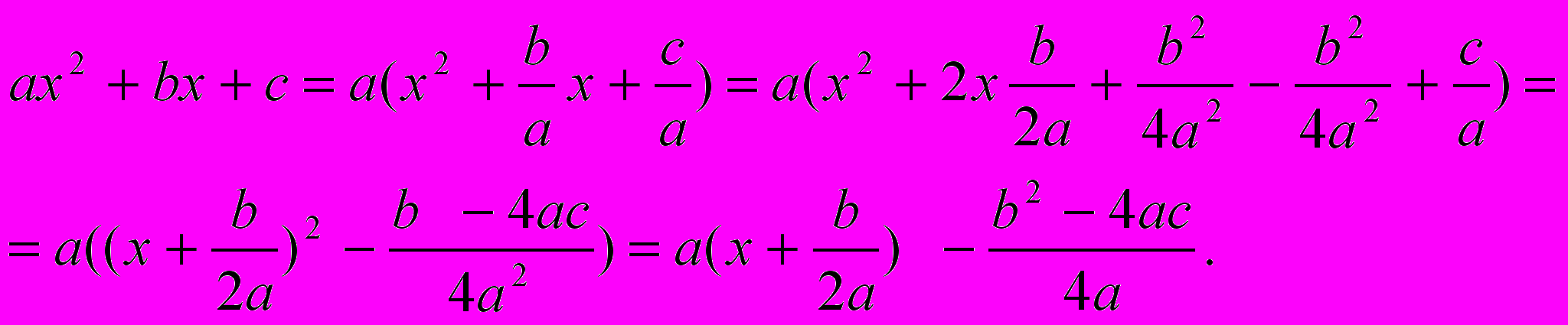
Звідки
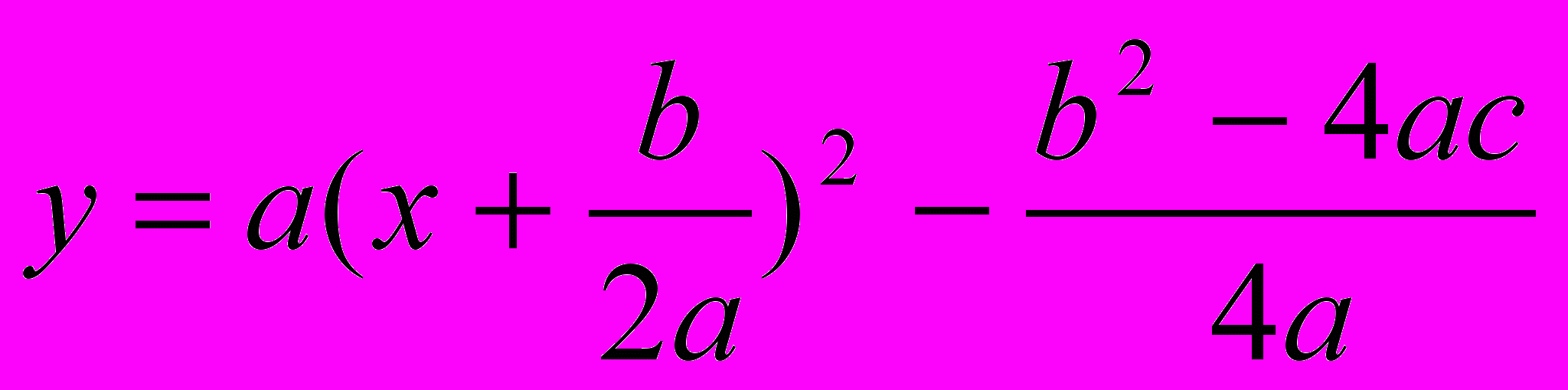
Отже, графік функції у=ах2+вх+с є парабола, яку можна одержати із графіка функції у=ах2 за допомогою двох паралельних переносів – зміщення в напрямі осі х і зміщення в напрямі осі у. Звідси маємо, що графік функції у=ах2+вх+с є парабола, вершиною якої є точка (m;n), де m= -в/2а; n= (-в2+4ас)/4а.
Віссю симетрії параболи є пряма х=m, паралельна осі у. При а>0 вітки параболи напрямлені вверх, при а<0 – вниз.
Щоб побудувати графік квадратичної функції потрібно:
1) Знайти координати вершини параболи і відмінність їх в координатній площині. Абсцису m знаходимо за формулою m= -в/2а; підставивши її знайдене значення у формулу у=ах2+вх+с, знайдемо ординату n.
2) Розв’язавши рівняння ах2+вх+с=0, знайдемо нулі функції – абсциси точок перетину графіка з віссю абсцис.
3) Знайдемо точку перетину графіка з віссю у, взявши х=0.
(0;с) –точка перетину графіка з віссю у.
- З’єднуємо відмічені точки.
ІV. Закріплення навичок та вмінь досліджувати квадратичну функцію і будувати її графік.
- Розв’язуємо № 140 (б) – Г.П. Гевз.
Побудувати графік функції у=ах2+вх+с.
Розв’язання. ОДЗ: R
1. m= -в/2а; m= -(-2/-2)= -1; n= -(-1)2-2(-1)+3=4.
(-1;4) – вершина параболи.
2. Розв’яжемо рівняння: -х2-2х+3=0; х2+2х-3=0.
х1=-3 ; х2=1 – корені рівняння ( нулі функції).
(-3;0), (1;0) – точки перетину параболи з віссю х.
3. х=0, тогда у=3. (0;3) – очка перетину з віссю у.
Так як у функції у= -х2-2х+3 а= -1, то вітки параболи напрямлені вниз.
Вісь симетрії параболи – пряма х= -1.
Побудуємо графік даної функції.

Відповідаємо на запитання:
- х= -3; 1 – нулі функції
- max у=4 при х= -1.
- у>0 при х (-3;1).
- у
 <0 при х (-∞;-3) U (1; ∞).
<0 при х (-∞;-3) U (1; ∞).
- у зростає при х(-∞;-1],
у спадає при х[-1; ∞).
- Розв’язуємо: № 136 (б), 137 (б).
Підсумок уроку.
Засвоїли елементи дослідження квадратичної функції, формували навички та вміння будувати графік функції у= х2+вх+с та знаходили проміжки знакосталості й проміжки зростання (спадання) функції.
Домашнє завдання.
Конспект; п. 7 ( С.О. Теляковський); § 54; 55 ( Г.П. Бевз).
№№ 135 ( на повт.); 136 (а), 137 (а), 140 (а).
Урок № 9
Тема. Побудова графіків квадратичних функцій, що
містять знак модуля
Мета. Засвоєння учнями вмінь та навичок побудови графіків
квадратичних функцій, що містять знак модуля.
Обладнання. Кодоскоп.
І. Перевірка домашнього завдання.
Один учень відображає на дошці № 140 (а) з домашнього завдання. В цей час з класом виконуємо № 138 (б).
ІІ. Актуалізація опорних знань.
Повторюємо алгоритм побудови графіка квадратичної функції, знову повертаємося до розв’язаного на дошці № 138 (б).
ІІІ. Сприймання й усвідомлення нового матеріалу.
Пояснення матеріалу лекційним методом.
- Графік функції у =ƒ(│х│).
Згідно з означенням модуля маємо:
-
ƒ(│х│)=
ƒ(х), якщо х≥0,
ƒ(-х), якщо х<0,
Отже, щоб дістати графік функції у =ƒ(│х│), треба побудувати графіки функції ƒ(х) і ƒ(-х) відповідно на проміжках [0;∞) і (-∞;0]. Але графік цієї функції можна дістати з графіка функції у= ƒ(х), якщо врахувати, що функція у =ƒ(│х│) – парна (ƒ(│-х│)=ƒ(│х│)). Тому досить побудувати графік функції у= ƒ(х) для х≥0, симетрично відобразити його відносно осі ординат.
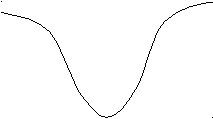
Д
 істанемо криву АВ’С’.
істанемо криву АВ’С’.Крива С’В’АВС і буде шуканим графіком.
П
 ри х≥0 графіки функцій у= ƒ(х) і у =ƒ(│х│) збігаються.
ри х≥0 графіки функцій у= ƒ(х) і у =ƒ(│х│) збігаються.Приклад 1. Побудувати графік функції у =х2-4│х│+3
Оскільки функція парна, то побудуємо спочатку її графік для х≥0, тобто у =х2-4х+3, оскільки для х≥0 х2-4│х│+3=х2-4х+3, а потім симетрично відобразимо його відносно осі ординат.





- Графік функцій у =│ƒ(х)│
Область визначення функції у=│ƒ(х)│збігається з областю визначення функції у=ƒ(х).
Ця функція може набувати лише невід’ємних значень, тому в нижній півплощині графіка не буде.
За означенням модуля
-
│ƒ(х)│=
ƒ(х), якщо ƒ (х)≥0,
-ƒ(х), якщо ƒ (х)<0
Графіки функцій у=ƒ(х) і у= -ƒ(х) симетричні відносно осі абсцис.
П


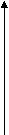

 лан побудови графіка функції у=│ƒ(х)│:
лан побудови графіка функції у=│ƒ(х)│:а


 ) будуємо графік функції у=│ƒ(х)│(мал.);
) будуємо графік функції у=│ƒ(х)│(мал.);б

 ) ту частину графіка, яка міститься у верхній півплощині, в тому числі точки перетину
) ту частину графіка, яка міститься у верхній півплощині, в тому числі точки перетину графіка з віссю 0х, залишаємо без змін, а частину графіка, розміщену в нижній півплощині, симетрично відображаємо відносно осі абсцис.
Крива МNАВС і є графіком функції у=│ƒ(х)│.
Приклад 2. Побудувати графік функції у=│х2-4х+3│
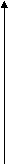
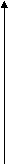








Робимо висновки, як побудувати графік функції у=│ƒ(│х│)│. І приклад графіка функції у=│х2-4│х│+3│ праворуч.
ІV. Закріплення навичок та вмінь будувати графіки квадратичної функції, що містять знак модуля.
Побудувати графіки таких функцій:
а) у=х2-4│х│+7; б) у=│-2х2-5х-2│; в) у=│-х2+2│х│+8│.
Підсумок уроку.
- Закріпили план побудови графіка квадратичної функції за схемою.
- Формували вміння та навички побудови графіків квадратичної функції, що містять знак модуля.
Домашнє завдання.
Конспект в зошиті, повт. п.7 (С.О. Теляковський), повт. § 54; 55 (Г.П. Бевз); №№ АР-3, В-2, № 8 │у│;
АР-20, В-2, № 11;
АР-53, В-2, № 10 – збірник завдань для підсумкової
атестації за 2002 р. (З.І. Сліпкань).
Урок № 10
Тема. Побудова графіків квадратичних функцій, що
містять знак модуля
Мета. Закріпити учнями знання та вміння будувати графіки
квадратичних функцій, графіки квадратичних функцій, що
містять знак модуля. Повторити властивості квадратичних
функцій, підготуватися до уроку – семінару.
Обладнання. Кодоскоп, таблиці.
І. Перевірка домашнього завдання.
- Як побудувати графік функції у =ƒ(│х│) ?
- Як побудувати графік функції у=│ƒ(х)│?
- Як побудувати графік функції у=│ƒ(│х│)│?
Перевіряємо в зошитах побудову графіків домашнього завдання.
ІІ. Актуалізація опорних знань.
Повторюємо, що називається функцією, областю визначення та областю значення функції; якими властивостями характеризують функцію; що називається квадратичною функцією, її властивості і основні етапи побудови графіка.
ІІІ. Закріплення навичок та вмінь будувати графіки квадратичних функцій та застосування їх властивостей при розв’язуванні вправ.
1

 ) АР-3, В-2, № 8;
) АР-3, В-2, № 8;2

 ) АР-64, В-2, № 11;
) АР-64, В-2, № 11;3
 ) АР-63, В-2, № 11;
) АР-63, В-2, № 11;4
 ) АР-56, В-2, № 12.
) АР-56, В-2, № 12.По збірнику завдань
державної підсумкової
атестації за 2002 р.
(З.І. Сліпкань)
Запитання до уроку – семінару
- Дайте означення числової функції.
- Коли вперше виникло поняття функції ?
- Що таке область значень і область визначення функцій?
- Якими способами можна задати функцію?
- Що таке графік функції?
- Що називається квадратичною функцією?
- Функція у=ах2 її дослідження і графік.
- Графік функції у=ах2+вх+с, дослідження цієї функції.
- Графіки квадратичних функцій, що містять знак модуля.
- Розв’язати:
1

 ) АР-13, В-2, № 11;
) АР-13, В-2, № 11;2

 ) АР-3, В-1, № 8;
) АР-3, В-1, № 8;3
 ) АР-56, В-1, № 12;
) АР-56, В-1, № 12;4
 ) АР-64, В-1, № 11.
) АР-64, В-1, № 11.По збірнику завдань
державної підсумкової
атестації за 2002 р.
(З.І. Сліпкань)
Підготувати реферати
Тема № 1: “Функція. Квадратична функція, цікаві властивості
параболи.”
Тема № 2: “Квадратична функція в задачах сільськогосподарського
змісту”.
ЛІТЕРАТУРА
- В.А. Куженко. Математичні задачі сільськогосподарського змісту, 1983, ст. 38-44;
- Н.М. Шунда. Функції і графіки. 1971, ст.32;
- У.М. Гельфанд. Функції і графіки. ст. 61;
- З.І. Сліпкань. Збірник завдань державної підсумкової атестації. 2002р.
Урок № 11-12
(урок – семінар)
Тема. Функція у=ах2+bх+с, її властивості і графік
Мета. Узагальнення і систематизація знань учнів про квадратичну
функцію.
Формування інтересів до методів одержання знань і
необхідності використання джерел додаткової літератури.
Обладнання. Кодоскоп, таблиці, шаблон параболи, додаткова
література, додаткові картки.
І. Вступне слово вчителя.
Оголошую тему і мету уроку.
ІІ. Реферат на тему:
“Функція. Квадратична функція, цікаві властивості параболи”.
ІІІ. Повторення, систематизація й узагальнення основних теоретичних знань про функції, про квадратичну функцію.
- Повторюємо відомості про функції. Згадуємо про відношення між елементами двох множин, нагадуємо означення функції, відпрацьовуємо поняття області визначення, множини значень та способи задання функції.
Повторюємо відомості про квадратичну функцію:
а) означення квадратичної функції;
б) властивості функції у=ах2 і її графік;
в) Функція у=ах2+bх+с.
- За допомогою кодоскопу проектуємо на екран графіки різних функцій.
Учням пропонуємо визначити: D(ƒ), Е(ƒ) ; множину на якій функція набуває додатних (від’ємних) значень, проміжки зростання (спадання) функції і чи можна лінію назвати графіком функції.
На малюнках з графіками квадратичних функцій відслідковуємо рух графіків в напрямі координатних осей в залежності від формули, якою задається функція.
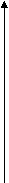






Що об’єднує функції, графіки яких зображено на малюнку ?

а
 ) б) в)
) б) в)




г) д)





Мал..2
у=ах2+bх+с
у=ах2
у=ах2+bх
у=ах2+с
у=а(х-m)2+n
Визначити вершини парабол:
а) у=ах2+4; г) у=4(х+2)2- 4;
б) у= -2х2- 4; д) у=1/4х2;
в) у=1/2(-3)х2; е) у=3(х-4)2+2.




Мал..3
у=ах2







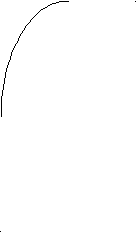

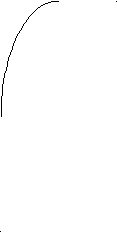



Мал..4
Який із графіків є графіком функції у=х2-4|х|+4 ?









Мал..5
ІV. Реферат на тему:
“Квадратична функція в задачах сільськогосподарського змісту”.
V. Закріплення навичок та вмінь побудови графіків квадратичної функції і використання її властивостей при розв’язуані вправ.
Двоє учнів працюють біля дошки за картками.
Картка № 1
В одній системі координат графіки функцій:
а) у=1/2х2 ; б) у=-1/2(х-3)2 ; у=1/2(х+3)2-2.
Для кожного випадку записати область значень і проміжки зростання (спадання).
Картка № 2
Побудувати графік функції у=х2+2х+3.
Відповісти на запитання:
а) D (у) ; г) у ↑; у ↓ ;
б) Е (у) ; д) записати нулі функції;
в) у>0; у<0; е) знайти min i max функцій,
точки min і точки max.
З класом за допомогою шаблона функції у=2х2 в одній системі координат схематично будуємо графіки функцій:
а) у=2х2+4; г) у= -2(х-8)2 +4;
б) у= -2х2-4; д) у= 2(х-4)2 –3.
в) у=2(х+6)2;
Визначаємо проміжки зростання і спадання кожної функції; визначаємо область значень функцій.








VІ. Робота з підручником
№№ 131 і 132 – усно.
VІІ. Побудувати самостійно графіки функцій (по рядам):
а)
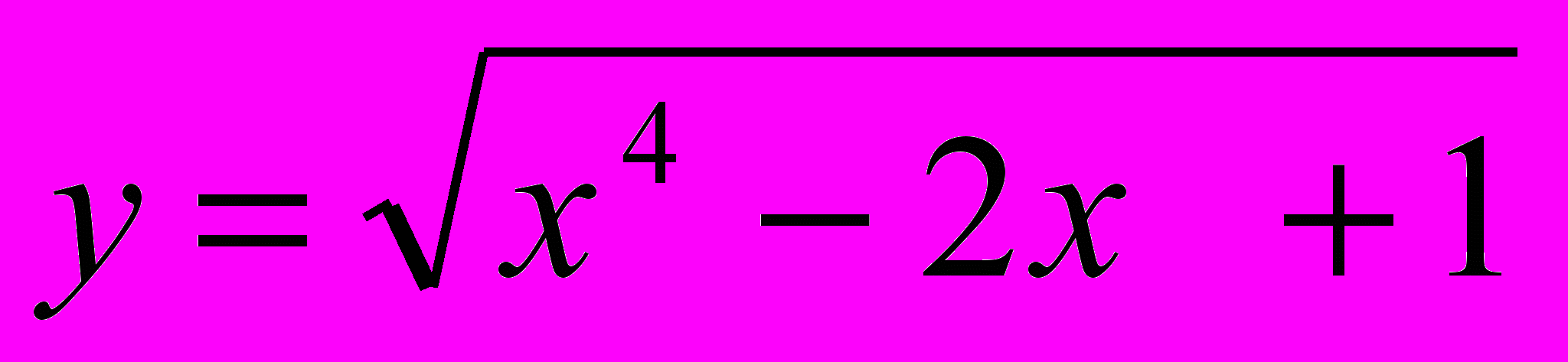 ; б) у=2х2+4|х|+3 ; в) у=|х2-4|х|+3|.
; б) у=2х2+4|х|+3 ; в) у=|х2-4|х|+3|. Результати проектуємо на екран.
















Мал..7
VІІІ. Самостійна робота
В зошитах для самостійних робіт кожному учневі окремо підготовлено диференційоване завдання на побудову графіків квадратичної функції ( схематично) і відповісти на запитання (робота на 10 хвилин).
ІХ. Цікава хвилинка (розгадати математичний термін).
- На чому будується система координат ?
- Що одержуємо при побудові графіків ?
- Як ще називають вісь у ?
- Якою крейдою працюємо на дошці ?
- Як називається перша координата точки ?
| п | лощина |
| а | бсциса |
| р | |
| а | бсциса |
| б | ілою |
| о | рдината |
| л | інія |
| а | бсциса |
Да, путь познания не гладок,
Но знаем мы со школьных лет:
Загадок больше, чем разгадок,
И поискам предела нет!
Підсумок уроку
Систематизували навички та вміння будувати графіки квадратичної функції, закріпили знання застосовувати властивості квадратичної функції при розв’язуванні вправ; ознайомилися з цікавими властивостями параболи та із задачами сільськогосподарського змісту, де використовується дана тема.
Домашнє завдання
Повторити § 53; 54; 58 (Г.П. Гевз); конспекти в зошиті; № 193 (б,в,с) ; № 198. Побудувати графік функції у=|х2+6|х|+5|.
Урок № 13-14
(контрольно-заліковий)
Тема. Квадратична функція
Мета. Перевірити знання та вміння учнів.
Обладнання. Збірник завдань державної підсумкової атестації під
Редакцією З.І. Сліпкань, 2002 р.
І варіант
- Графік і властивості функції у=ах2 при а <0.
- АР-14, В-1, № 8;
- АР-17, В-1, № 10;
- АР-20, В-1, № 11;
- АР-27, В-1, № 11;
- АР-46, В-1, № 13*;
- Побудувати графік функції у=|х2+6|х||.
ІІ варіант
- Графік і властивості функції у=ах2 при а >0.
2. АР-14, В-2, № 8;
3. АР-17, В-2, № 10;
4. АР-20, В-2, № 11;
5. АР-27, В-2, № 11;
6. АР-46, В-2, № 13*;
7. Побудувати графік функції у=|х2+4|х||.
Учні обов’язково розв’язують 5 завдань, а шосте і сьоме на вибір.
Кожне правильно розв’язане завдання оцінюється двома балами.
