§iv інтерполювання функцій
| Вид материала | Документы |
СодержаниеОбчислити значення в точці x=0,5 Побудувати на проміжку [0,1] многочлен Чебишева четвертого степеня з коефіцієнтом 1 при старшому степені. Обчислити її відхиленн |
- «Дослідження функцій за допомогою похідної та побудова графіків функцій», 30.16kb.
- Для заказа доставки работы воспользуйтесь поиском на сайте, 787.35kb.
- Інститут комп’ютерних технологій, автоматики І метрології, 31.24kb.
- Урок з алгебри у 10 класі на тему: «Обернені тригонометричні функції», 34.75kb.
- Програма кандидатських та вступних іспитів за спеціальністю 01. 01. 07 обчислювальна, 90.49kb.
- 2 Підстави класифікації та види функцій сучасної держави розділ формування та реалізація, 902.01kb.
- Реферат 2011, 129.92kb.
- Центр професійно-технічної освіти у вінницькій області вище професійне училище №11, 1018.49kb.
- Зміст навчальної програми з вищої математики для студентів 1 курсу фармацевтичного, 32.69kb.
- Методика визначення інвестиційного прибутку професійним торговцем цінними паперами, 507.12kb.
§IV Інтерполювання функцій
Приклад 1. За допомогою формули Лагранжа побудувати інтерполяційний многочлен для функції, що задана наступною таблицею
Таб.
-
xi
–2
–1
0
1
2
fi
3
–1
–1
3
–13
Обчислити значення в точці x=0,5.
Розв’язання. За формулою Лагранжа
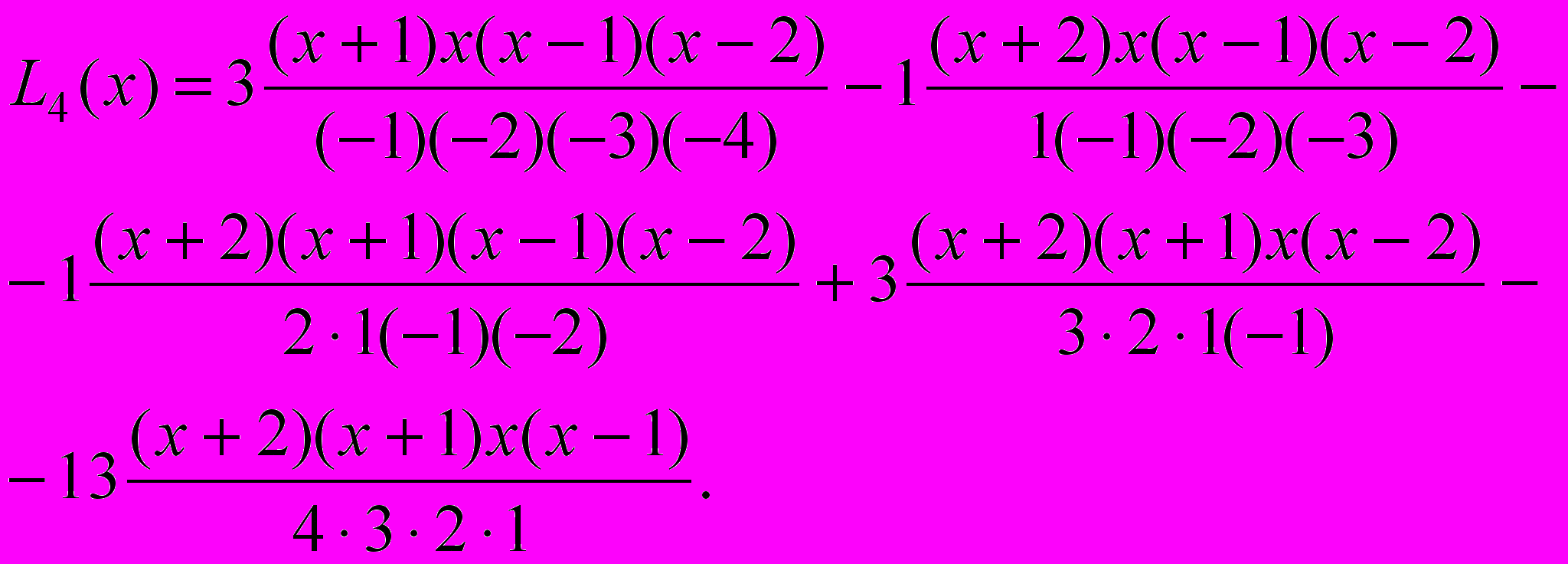
Далі
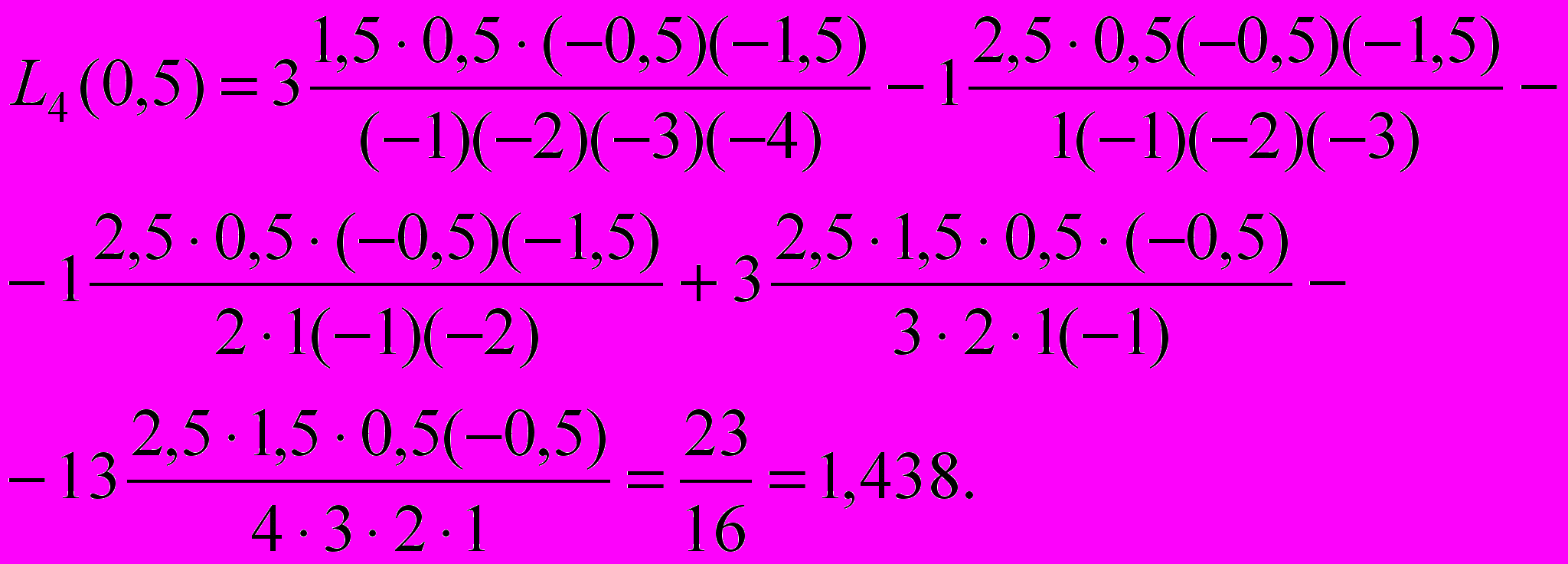
Приклад 2. Побудувати інтерполяційний многочлен за формулою Ньютона для функції, що задана таблицею (х), та обчислити значення в точці x=0,5.
Розв’язання. Таблиця розділених різниць для цих даних має вигляд
-
xi
fi
–2
3
–4
–1
–1
2
0
0
0
–1
2
–1
4
–4
1
3
–10
–16
2
–13
Тоді за формулою Ньютона
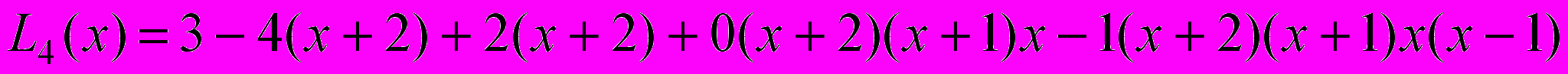.Далі
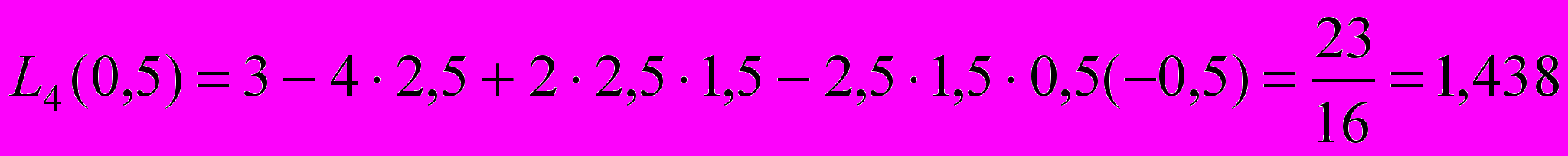.Приклад 3. За допомогою інтерполяції обчислити e0,15, якщо
-
xi
0.
0.1
0.2
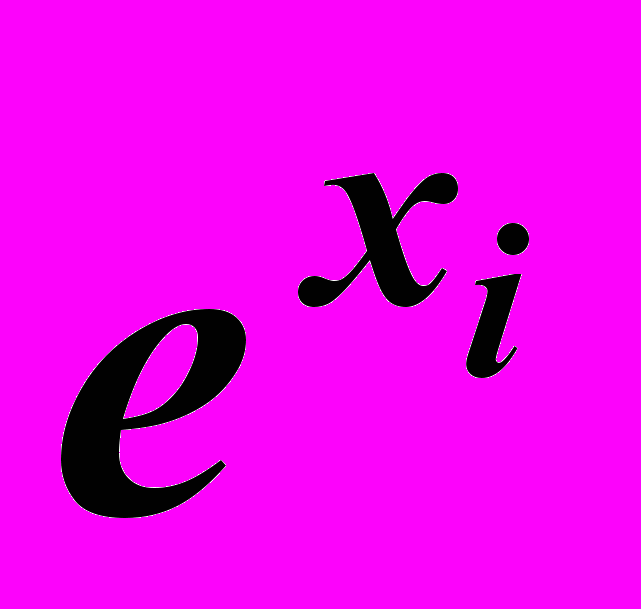
1
1,10517
1,22140
Оцінити похибку.
Розв’язання. Позначимо
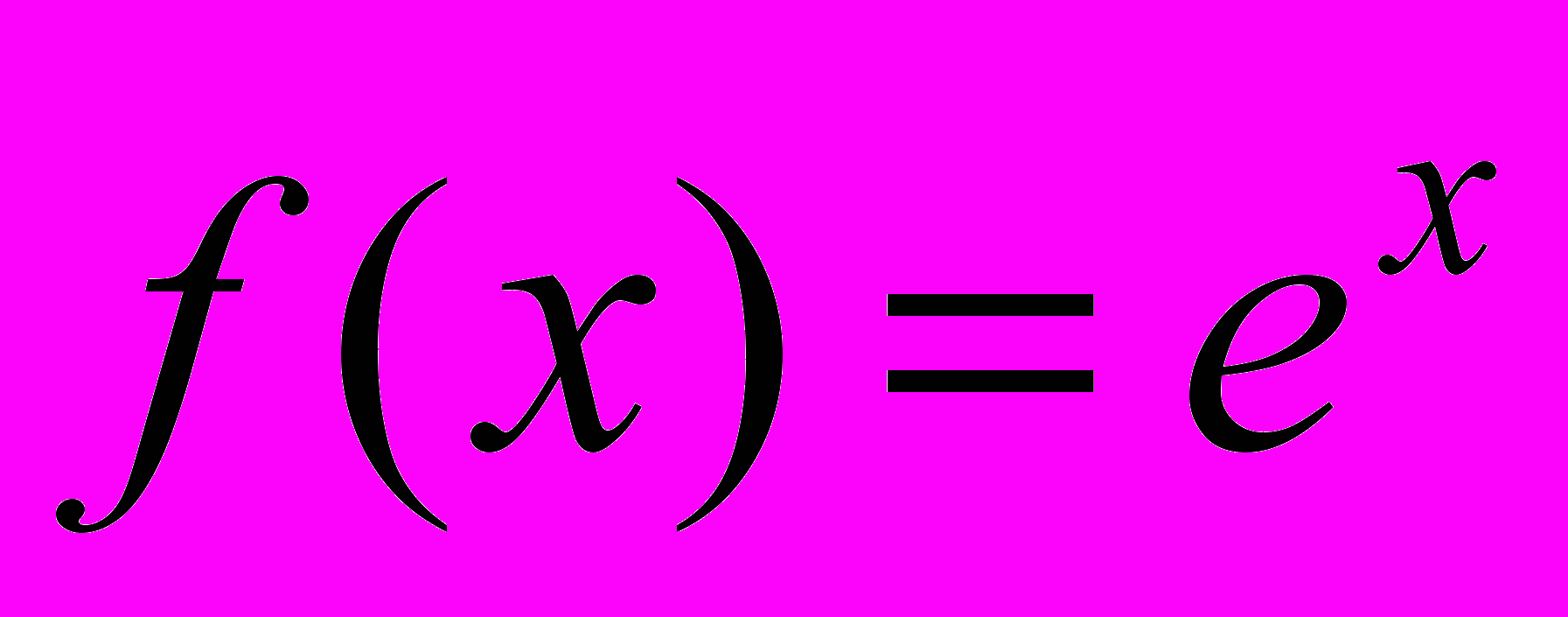. Тоді таблиця розділених різниць для даних в таблиці має вигляд-
xi
fi
0
1,0
1,0517
0,1
1,105187
0,553
1,1623
0,2
1,22140
Тому
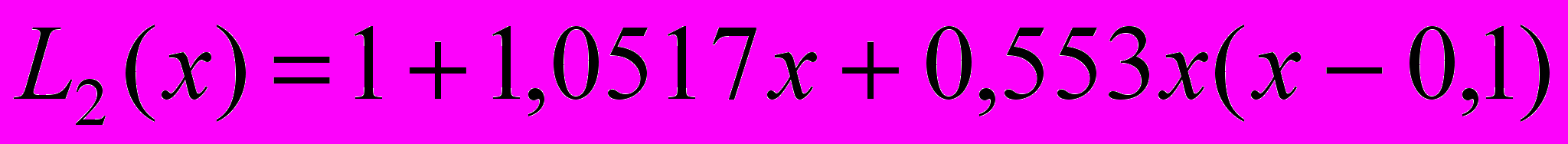
та
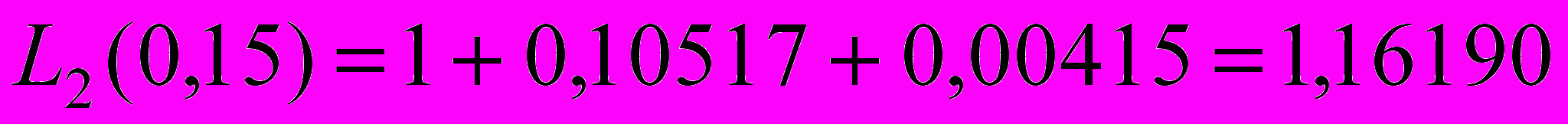.Оцінка для похибки буде мати вигляд
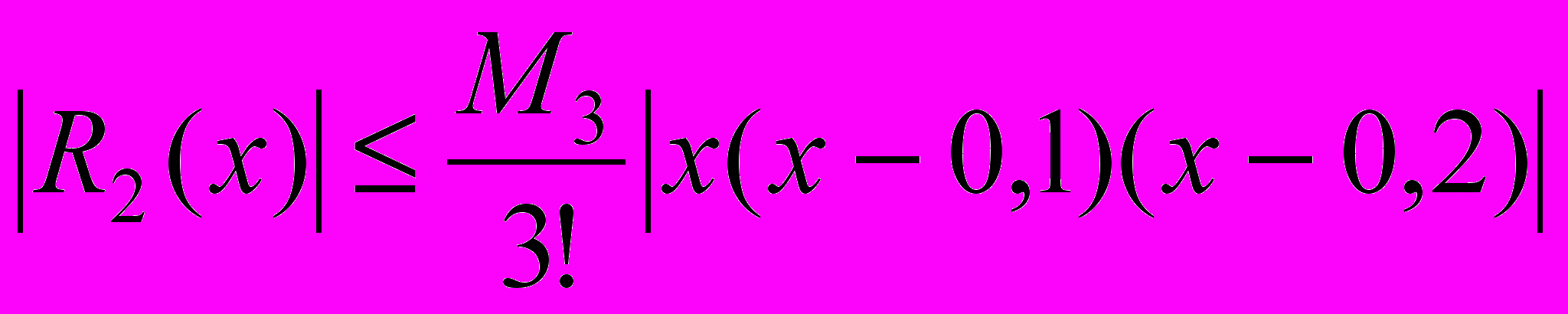,де
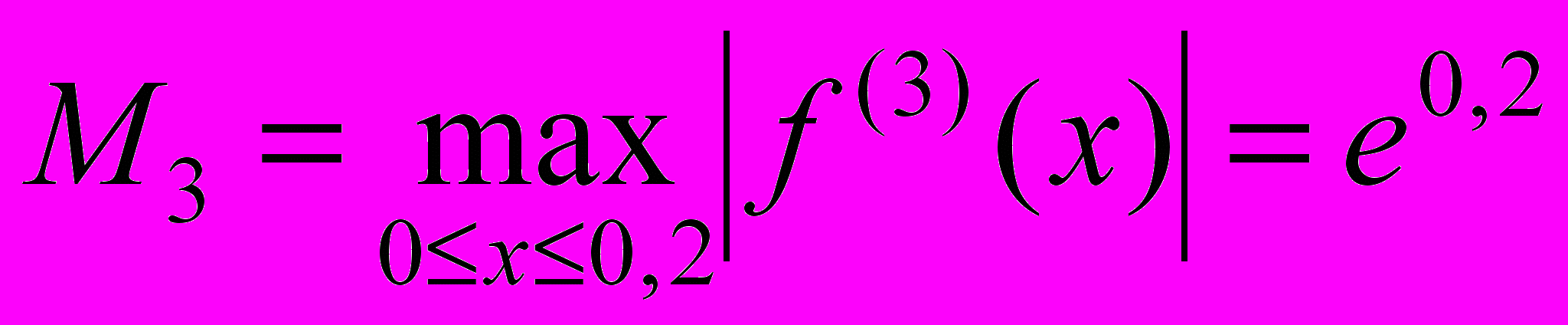. Тому
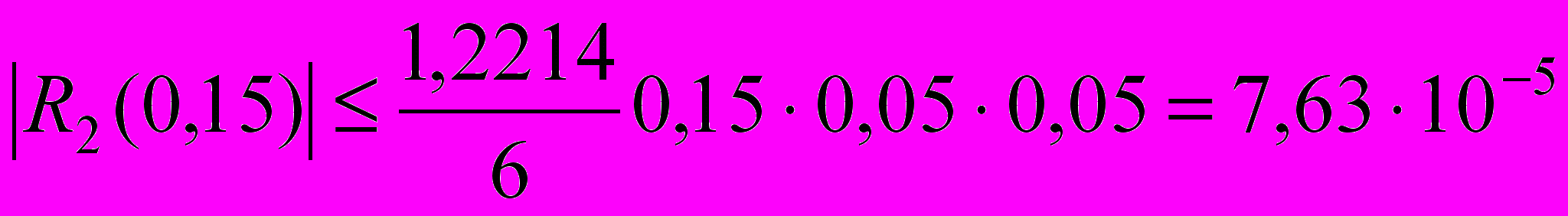.Приклад 4. За значеннями
в точках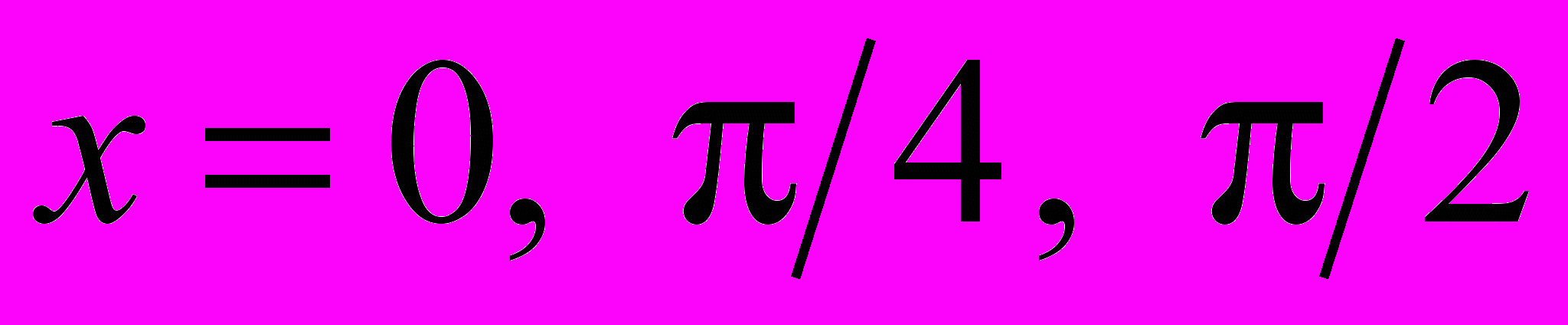 
знайти 
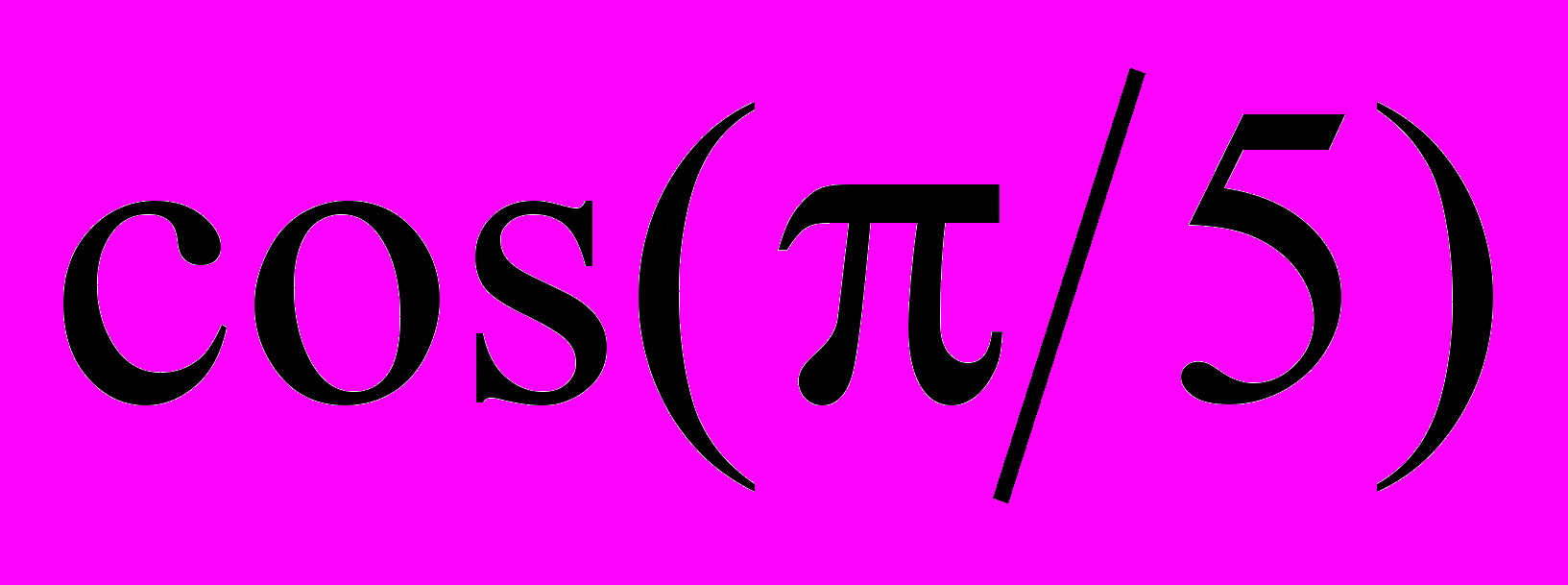. Оцінити похибку.Розв’язання. Таблиця розділених рівнянь має вигляд
-
xi
fi
0
1,0
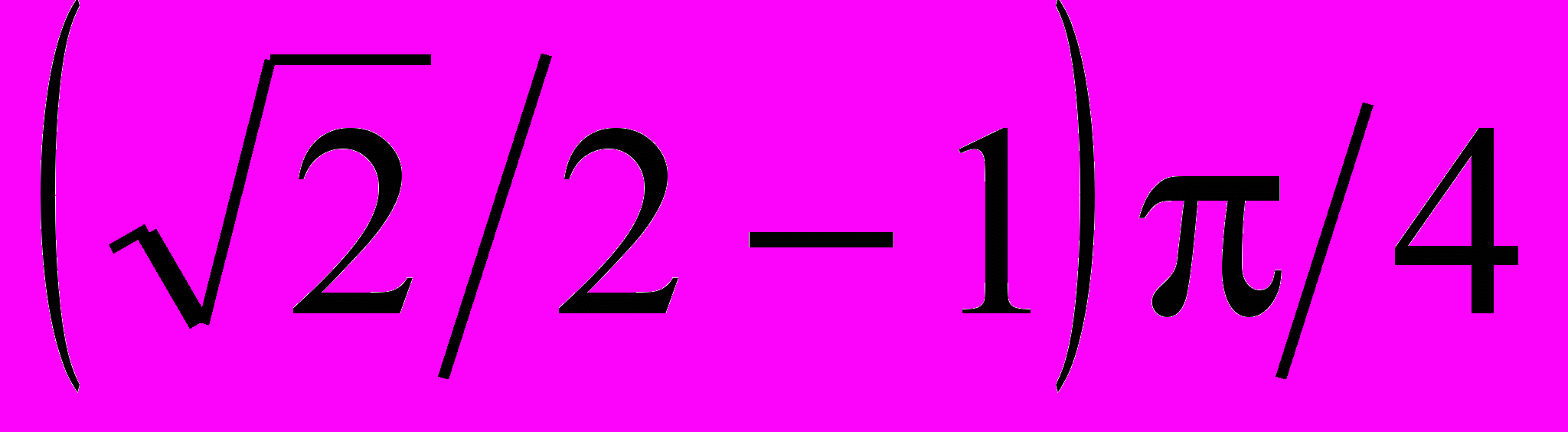
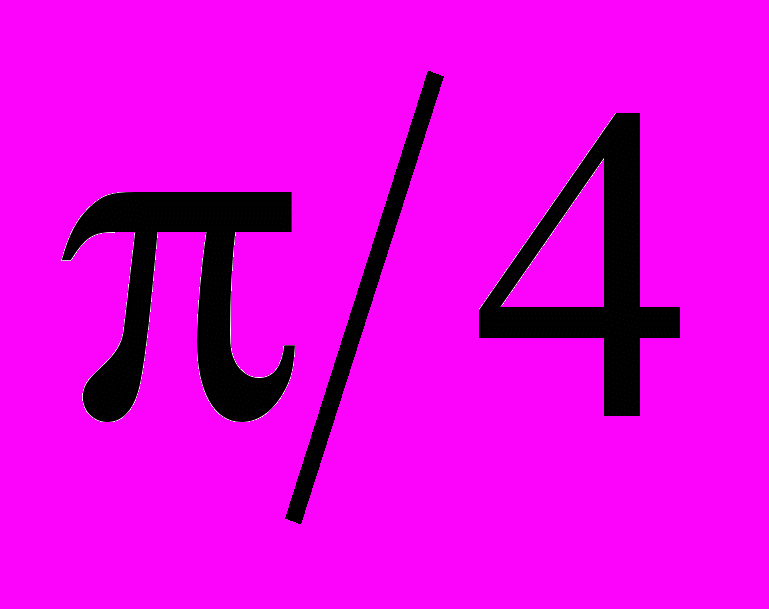
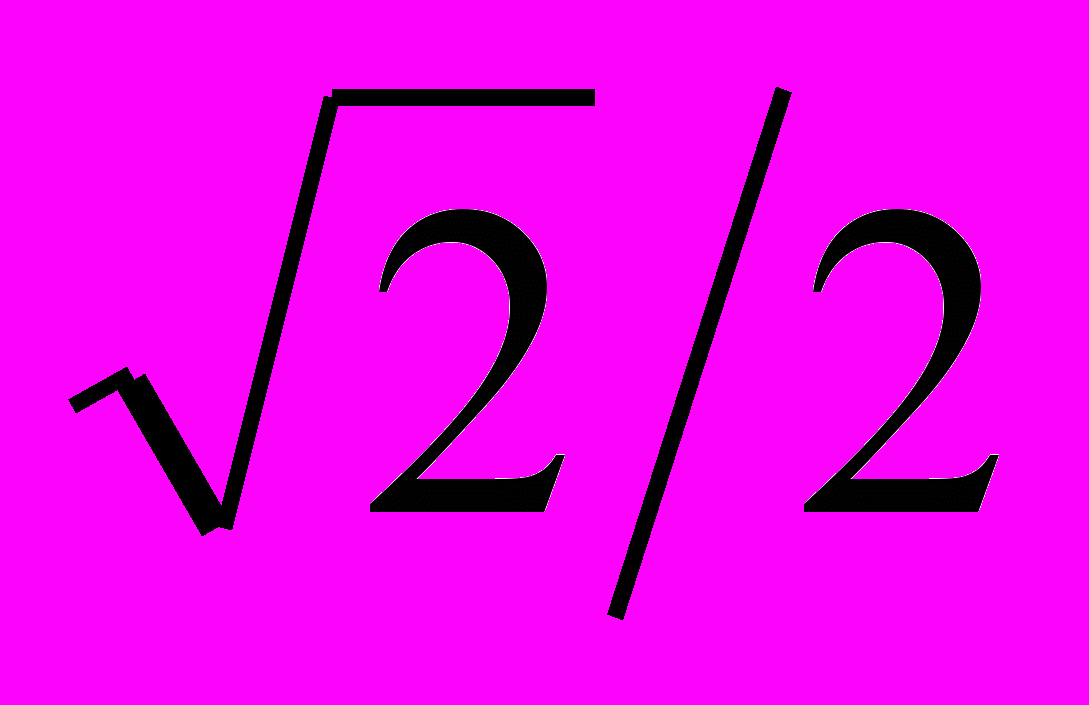
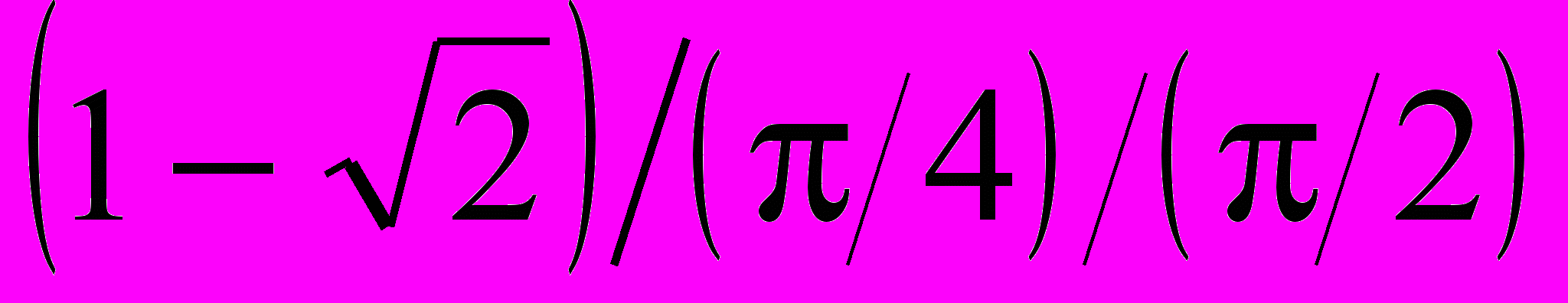
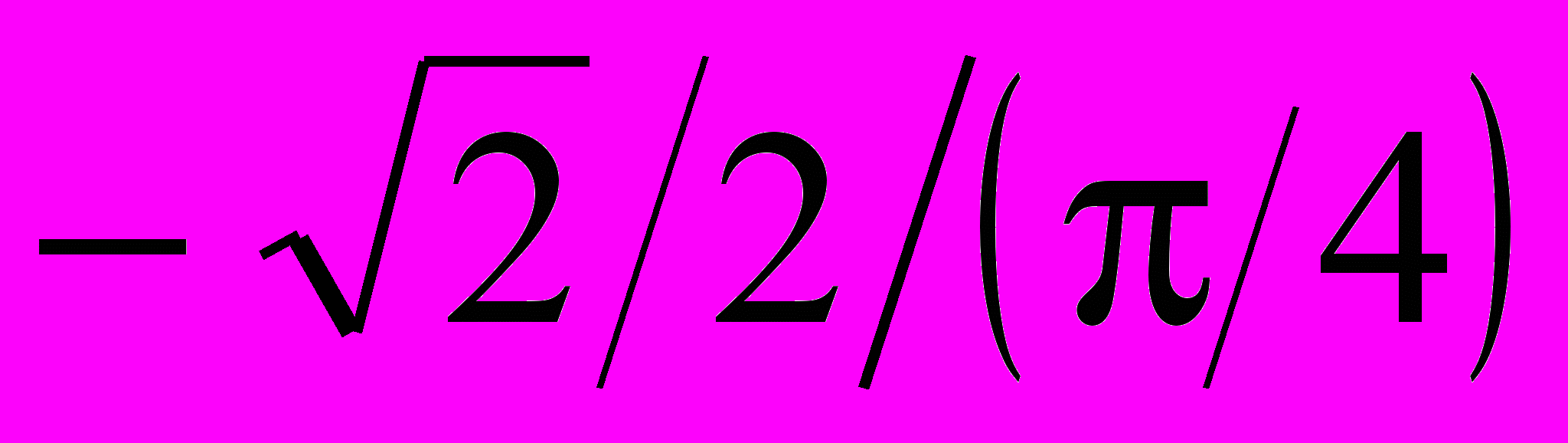
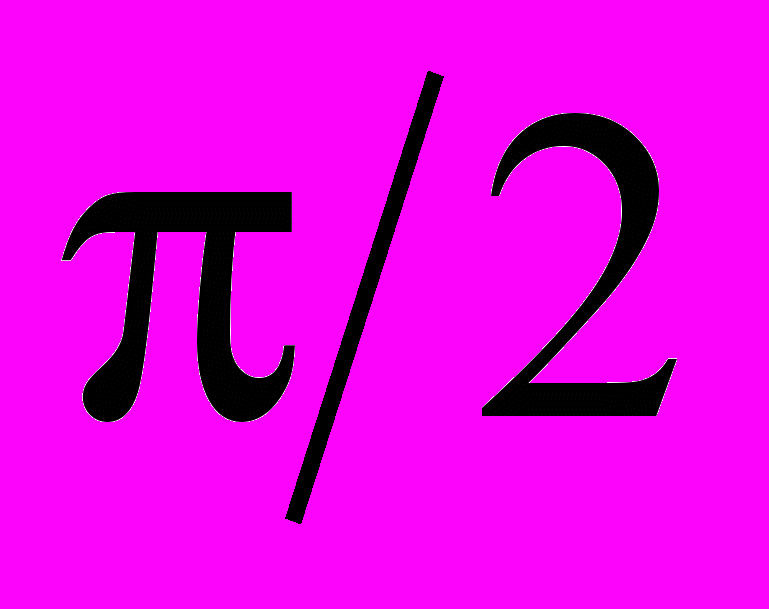
0
Приклад 5. а) Побудувати на проміжку [–1,1] многочлени Чебишева четвертого та п’ятого степеня з коефіцієнтом 1 при старшому степені. Обчислити їх відхилення від 0. Побудувати графіки.
Розв’язання. За рекурентною формулою
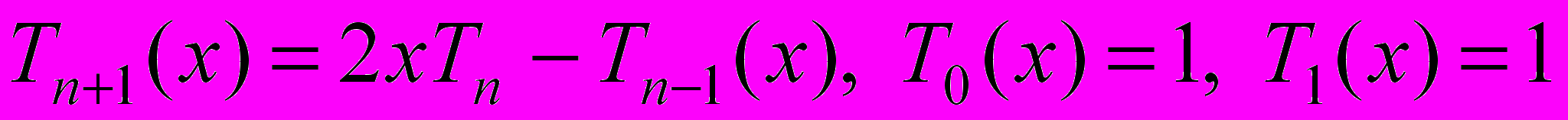
знаходимо
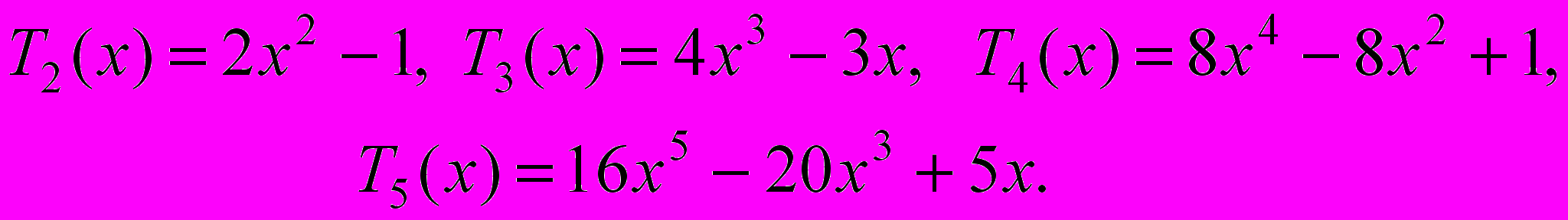
Шукані многочлени Чебишева мають вигляд
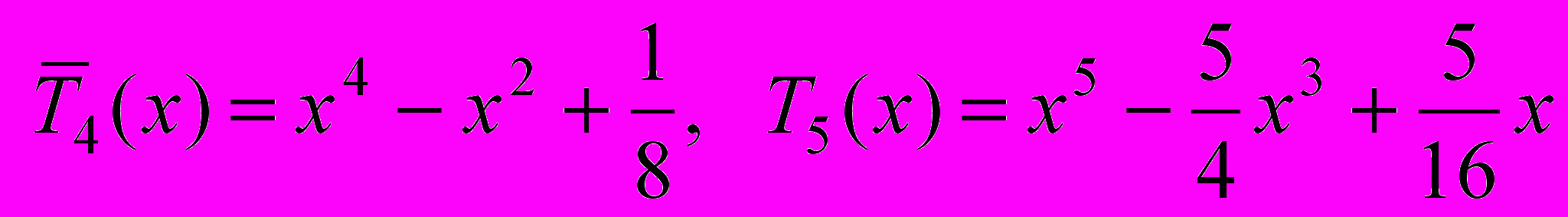.За формулою відхилення від нуля такі
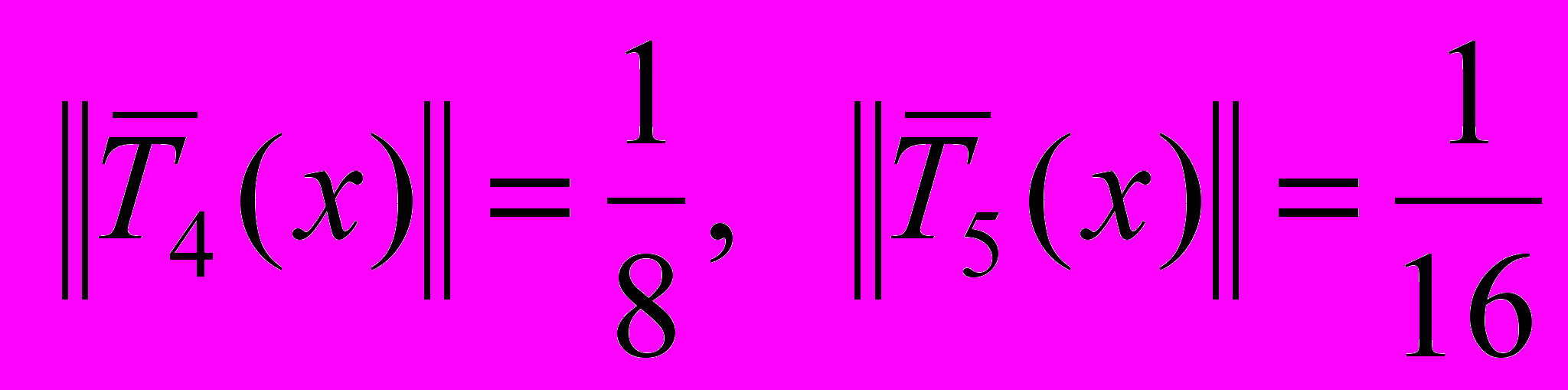.б) Побудувати на проміжку [0,1] многочлен Чебишева четвертого степеня з коефіцієнтом 1 при старшому степені. Обчислити її відхилення від 0.
Розв’язання. У многочлені Чебишева
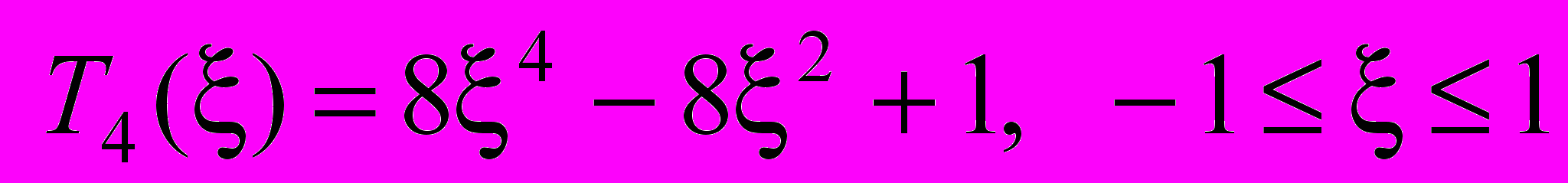
(див. попередню задачу) зробимо заміну змінної
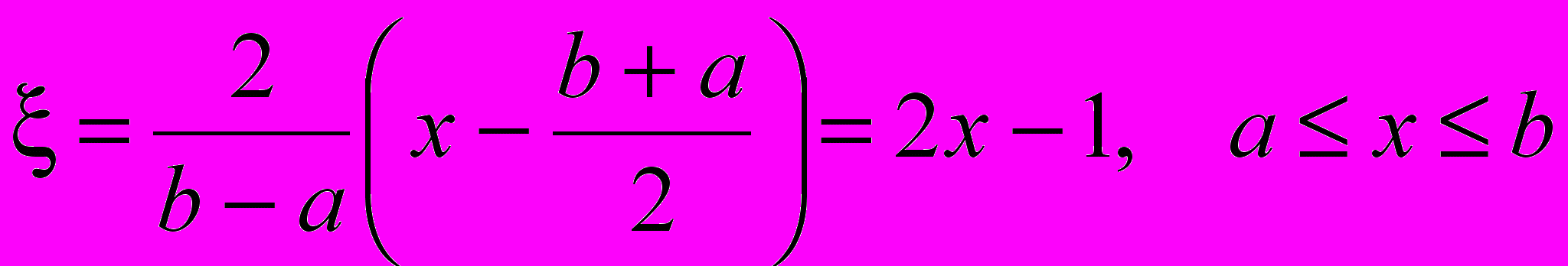.При a=0, b=1 маємо -2x-1. Тоді многочлен Чебишева для проміжку [0,1] має вигляд
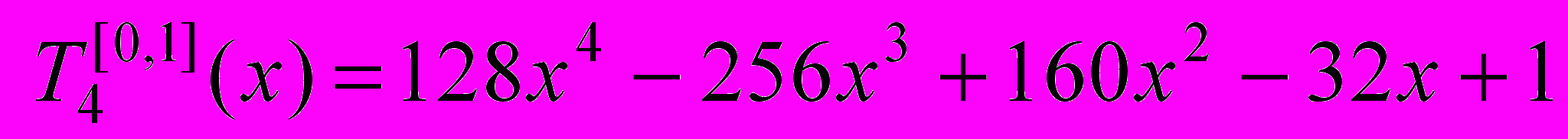.Шуканий многочлен такий
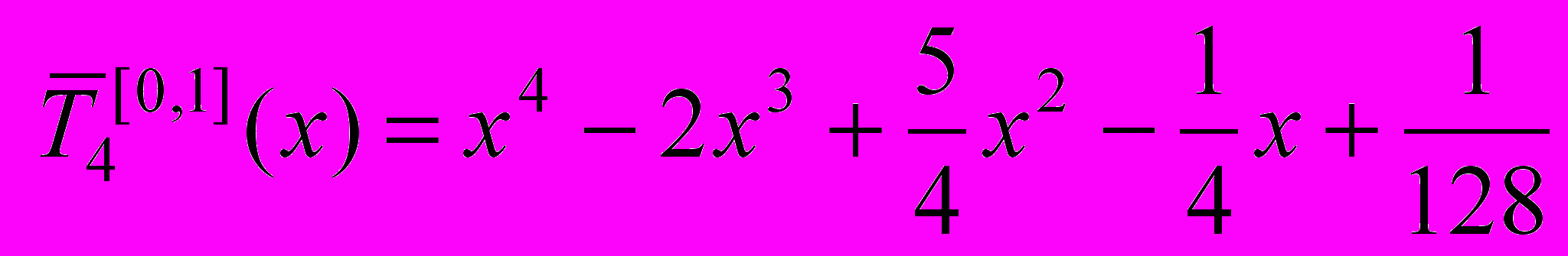.Його відхилення від 0 дорівнює
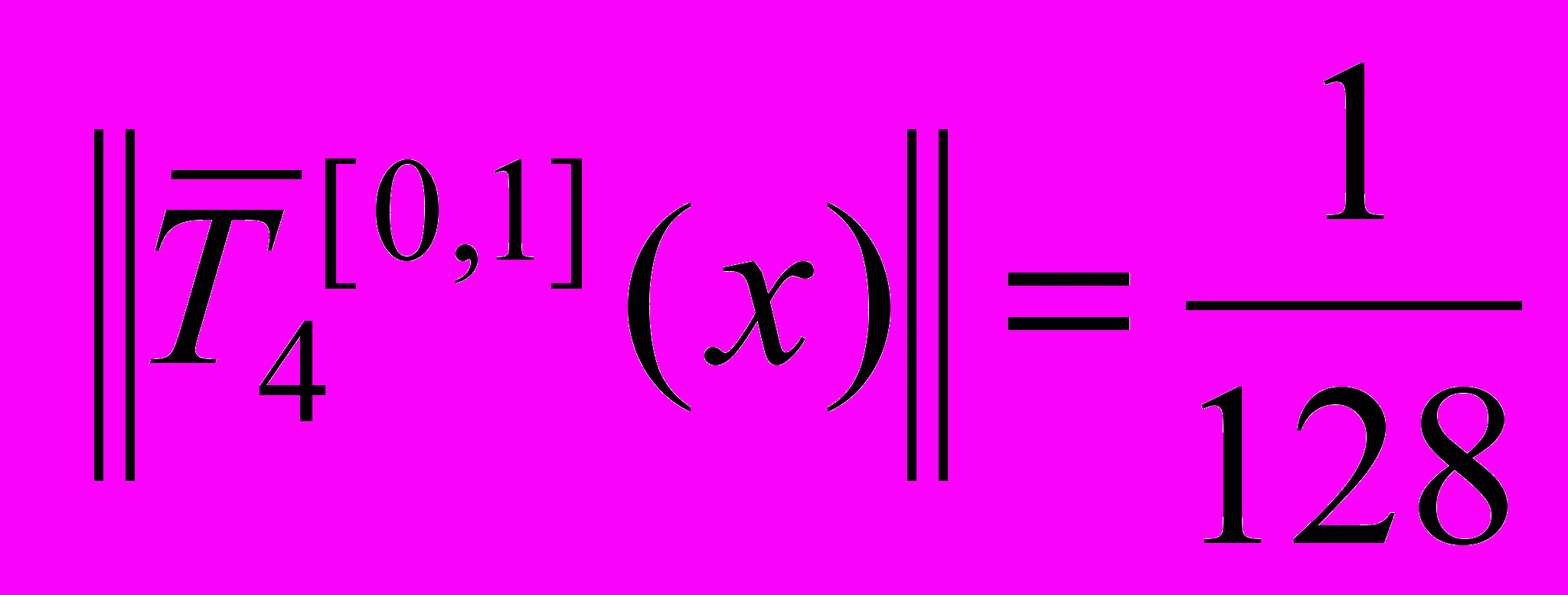.Приклад 6. Оцінити похибку інтерполяції функції ex на[0,1] многочленом четвертого степеня побудованим за вузлами.
Розв’язання. З оцінки залишкового члена інтерполяційної формули маємо
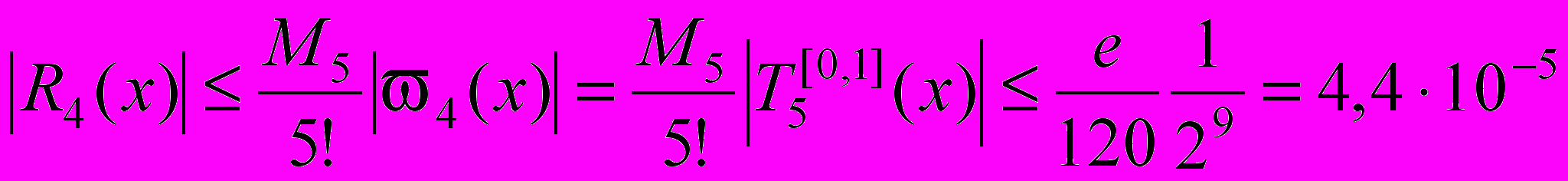.Приклад 7. Скільки чебишевських вузлів інтерполяції необхідно вибрати, щоб похибка інтерполяції для функції
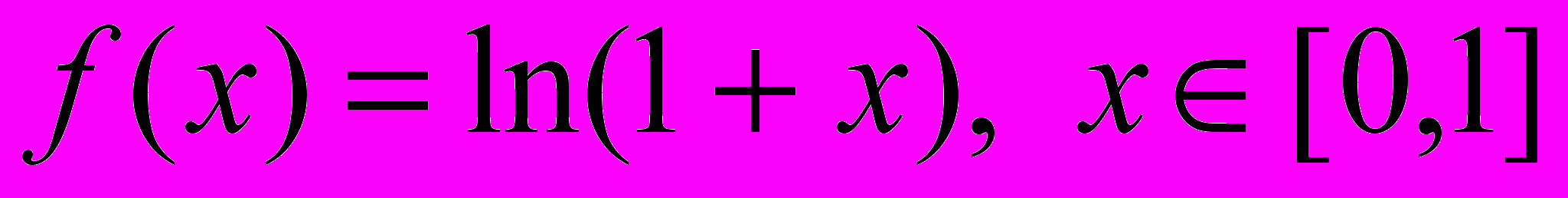не перевищувала =10–4.Розв’язування. З оцінки залишкового члена інтерполяційної формули маємо
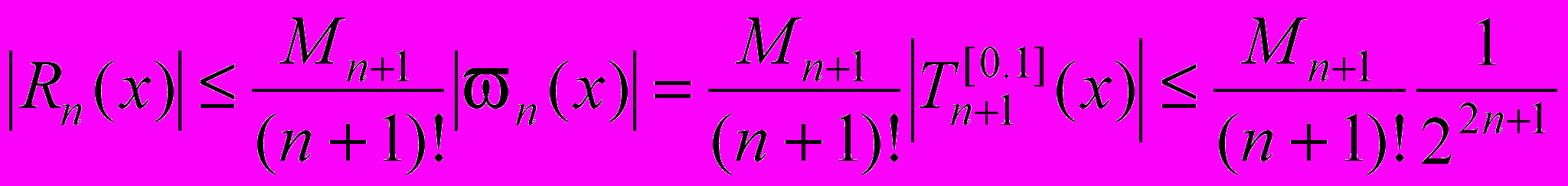.Далі
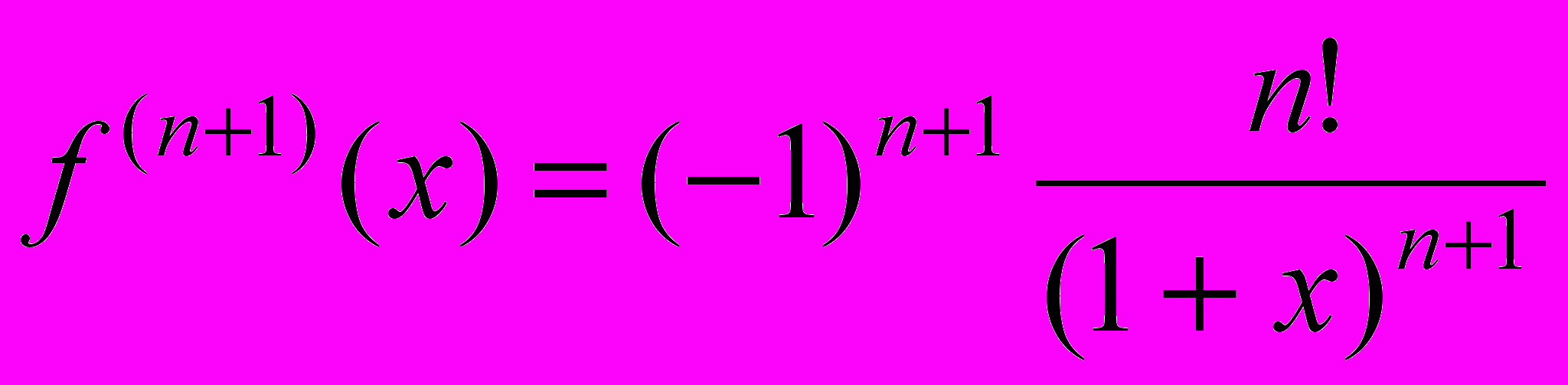.Тому n шукаємо з умови
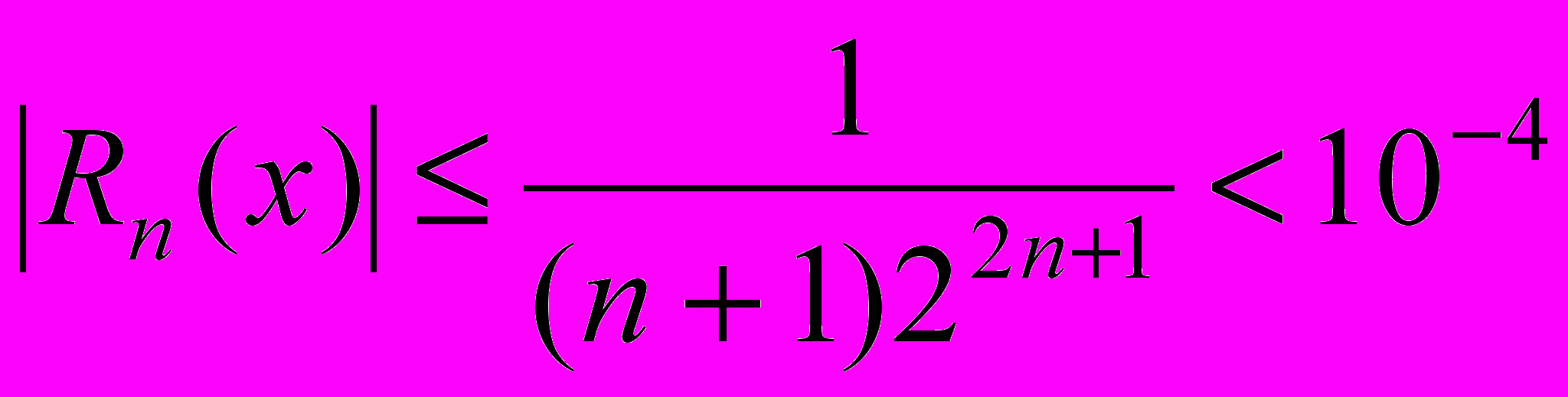.Підстановкою знаходимо, що
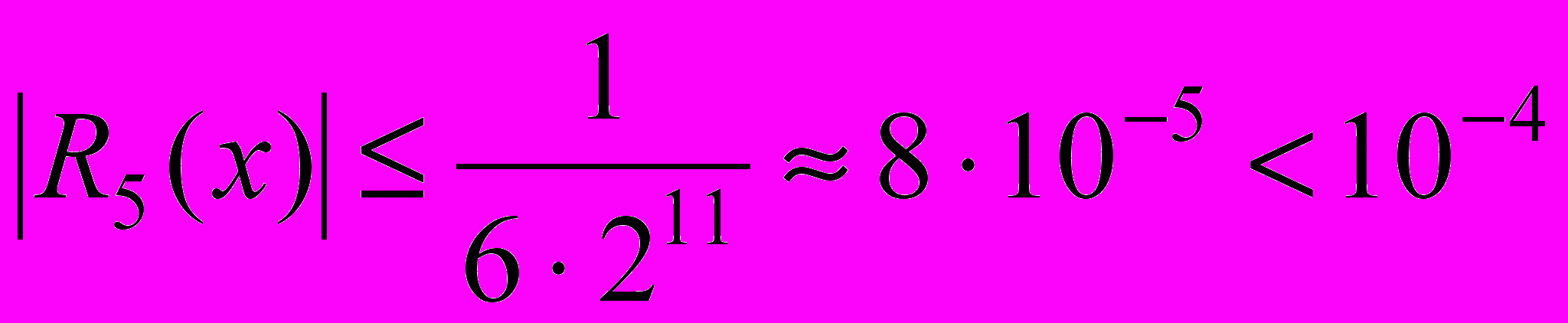.Таким чином треба вибрати 6 чебишевських вузлів.