Програма поглибленого вивчення математики в X
| Вид материала | Документы |
- Навчальна програма для поглибленого вивчення історії для у 9-12 класах загальноосвітніх, 360.72kb.
- Програма вступних випробувань з математики р екомендовано розглянуто та схвалено вченою, 131.9kb.
- Програма поглибленого вивчення інформатики (8-12 класи), 270.18kb.
- Методичні рекомендації щодо вивчення математики, 673.36kb.
- Програми Тихоша В.І. Програми для вивчення української мови в профільних філологічних, 228.4kb.
- Методика формування творчої особистості при вивченні математики Роль гри та нестандартних, 268.12kb.
- Навчальна програма поглибленого вивчення інформатики для учнів 8-12 класів загальноосвітніх, 206.93kb.
- Навчальна програма поглибленого вивчення інформатики для учнів 10-11 класів загальноосвітніх, 818.66kb.
- Програма вивчення студентської групи Програма вивчення особистості студента І складання, 187.57kb.
- Програма державного екзамену з теорії та практики навчання І виховання та методики, 181.72kb.
ПРОГРАМА
поглибленого вивчення
математики в X – XI профільних класах
Пояснювальна записка
Основним завданням навчання математики в середньому закладі освіти є забезпечення рівня математичної культури, необхідного для повноцінної участі в повсякденному житті, продовження освіти та трудової діяльності. Математика є унікальним засобом формування не лише освітнього, але і розвиваючого та інтелектуального потенціалу особистості.
У процесі поглибленого навчання математики в профільних класах основні завдання суттєво доповнюються. Це обумовлено необхідністю виявлення та розвитку в учнів математичних здібностей, формування в них стійких інтересів до математики та професійної діяльності, суттєво пов’язаної з математикою і, нарешті, підготовки учнів до навчання у вищому закладі освіти.
Поглиблене вивчення математики в старшій школі (X – XI профільні класи) має відповідати віковим можливостям і потребам школярів.
Навчання в старшій школі в профільному класі з поглибленим вивченням математики передбачає наявність стійкого усвідомленого інтересу до математики та схильності до вибору в майбутньому пов’язаної з нею професії.
Результати навчання на цьому етапі мають забезпечувати підготовку старшокласника до продовження освіти у вищому навчальному закладі.
Програма призначена для профільних класів з поглибленим вивченням математики на двох рівнях складності відповідно до математичної підготовки учнів із розрахунку 6 або 8 год. математики на тиждень.
Рівнева структура змісту забезпечується за допомогою квадратних дужок.
Текст програми структурований за темами курсу математики. Для кожного розділу визначено орієнтовну кількість навчальних годин, мету, основні вимоги до результатів навчання та перелік підтем.
Якщо навчальним планом школи передбачена інша кількість годин для поглибленого вивчення математики, то вчитель самостійно здійснює та обгрунтовує модифікацію даної програми та тематичне планування відповідно до вибраного підручника, з урахуванням підготовленості класу, інтересів учнів тощо. Підручник вибирається з діючих у загальноосвітніх класах, пробних та спеціально призначених для поглибленого навчання математики. Відповідно вчитель може варіювати кількість годин, що відводяться на вивчення певної теми, обґрунтовано змінювати послідовність вивчення тем, доповнювати її зміст деякими додатковими теоретичними та практичними питаннями або обмежуватись програмою для загальноосвітніх класів. У будь-якому разі виконання програми для загальноосвітніх шкіл є обов’язковим.
Порівняно із загальноосвітніми класами суттєво підвищується теоретичний рівень вивчення навчального матеріалу, зокрема, при вивченні всіх видів рівнянь, нерівностей та їх систем послідовно акцентується увага на основних поняттях: корінь, розв’язок, рівносильність, наслідок, можливість втрати та появи сторонніх коренів, перевірка як важлива складова процесу розв’язування. Вводяться елементи теорії множин та математичної логіки. Зазначимо, проте, що ці теорії не є предметом вивчення в загальноосвітній школі. Їх елементи використовується для збагачення та осучаснення математичної мови учнів, розширення їх математичної ерудиції та розвитку мислення.
Зважаючи на це, вимоги до математичної підготовки учнів, що навчаються в класах із поглибленим навчанням математики, сформульовані в дещо загальному вигляді. Проте мається на увазі, що учні повинні оволодіти програмним матеріалом на рівні не нижче достатнього за критеріями оцінювання навчальних досягнень із математики в системі загальної середньої освіти, а вимоги вчителя мають відповідати тим, що висуваються перед абітурієнтами на вступних іспитах у вищих навчальних закладах.
Методичні підходи та організаційні форми навчання добираються вчителем у відповідності з віковими особливостями учнів та змістом навчального матеріалу.
Багаторічний досвід функціонування в Україні класів із поглибленим навчанням математики переконує в тому, що недоцільно надмірно заповнювати програми додатковими питаннями. Це спричинює перевантаження і, як наслідок, відсів учнів. Розвитку стійких пізнавальних математичних інтересів сприяють дібрані в системі різноманітні складні задачі з достатнім евристичним навантаженням, пов’язаний з темою історичний матеріал.
Варіативність обсягу теоретичного навчального матеріалу закладена і в самій програмі. Додаткові питання та теми програми, які можна не вивчати або вивчати в порядку ознайомлення, взято в квадратні дужки. Залежно від конкретних умов учитель може використати цей матеріал для роботи з усім класом, групою учнів або для індивідуальної роботи.
Критерії оцінювання навчальних досягнень учнів єдині для загальноосвітніх класів та класів із поглибленим навчанням математики. Небажано завищувати вимоги під час контролю результатів навчання, оскільки це може негативно вплинути на розвиток творчих здібностей учнів.
Дедалі більше комп’ютер стає універсальним помічником людини в цивілізованому світі. Використання його в навчальному процесі поряд із допомогою у вирішенні дидактичних завдань активізує дію мотиваційних чинників у створенні позитивного ставлення до навчання.
Ефективність засвоєння знань учнями за умов широкого впровадження засобів нових інформаційних технологій навчання (НІТН) у значній мірі залежить від педагогічних програмних засобів (ППЗ), що дозволяють поєднати високі моделюючі та обчислювальні можливості при дослідженні різноманітних математичних об’єктів з унаочненням результатів на всіх етапах процесу навчання.
На сьогодні розроблено значну кількість програмних засобів, орієнтованих на використання при вивченні математики. Це такі програми як DERIVE, EUREKA, GRAN1, Maple, MathCAD, Mathematika, MathLab, Maxima, Numeri, Reduce та інші.
При вивченні в школі курсу алгебри та початків аналізу, а також деяких розділів геометрії для аналізу функціональних залежностей та статистичних закономірностей доцільно використовувати ППЗ GRAN1 та DERIVE, можливості використання яких розглянуто в посібнику для вчителів: Жалдак М. І. Комп’ютер на уроках математики. - К.: Техніка, 1997.– 304 с.
Указані програмні засоби призначені перш за все для розв’язування широкого класу задач шляхом моделювання об’єктів, що фігурують в умові задачі.
В рамках змісту шкільної математичної освіти та найбільш поширених методичних систем навчання математики реалізація ідей комп’ютерної підтримки процесу навчання відбувається звичайно шляхом здійснення міжпредметних зв’язків курсів математики та інформатики у формі інтегрованих уроків при вивченні таких, наприклад, тем: графічне розв’язування нерівностей і систем нерівностей; розв’язування лінійних і квадратних рівнянь, нерівностей та їх систем з однією та двома змінними, зокрема, графічним методом; дослідження властивостей функцій та побудова і читання їх графіків і побудова графіка функції
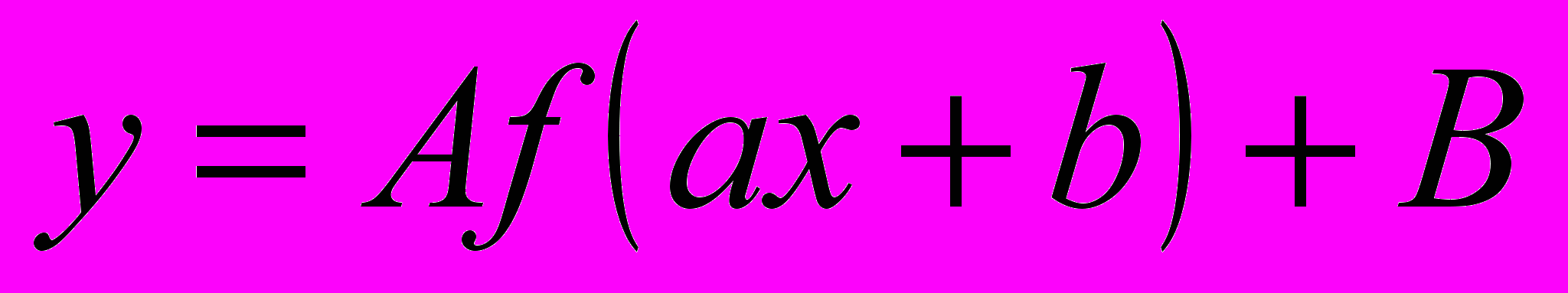за графіком функції 
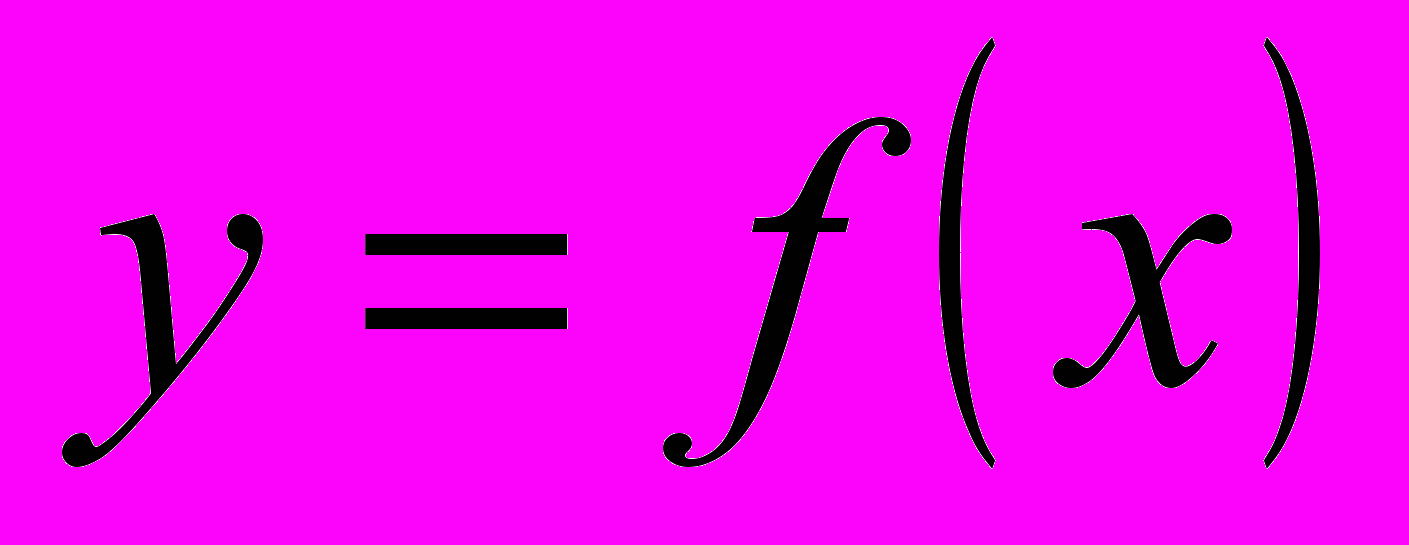; дослідження статистичних вибірок; відсоткові розрахунки; наближене визначення коренів многочленів і розв’язування рівнянь та нерівностей вищих степенів; границя числових послідовностей та функцій; дослідження функцій на неперервність; дослідження тригонометричних та обернених тригонометричних функцій; графічне розв’язування тригонометричних рівнянь і нерівностей; наближене обчислення значень функції; опрацювання статистичних даних: побудова полігону частот, гістограм, обчислення відносних частот різних подій; визначення центра розсіювання відносних частот та величини розсіювання (дисперсії); обчислення визначених інтегралів; визначення площ криволінійних трапецій та об’ємів тіл обертання тощо.Тематичне планування навчального матеріалу.
X клас
(6 - 8 год. на тиждень, всього 204 - 272 год.)
Алгебра і початки аналізу1
(4 - 5 год. на тиждень, всього 136 - 170 год.)
1. Вступ (12 – 20 год.).
Множина. Елементи множини. Порожня множина. Підмножина. Переріз, об’єднання та різниця множин.
Висловлення. Висловлювальні форми. Логічні операції: заперечення, кон’юнкція, диз’юнкція, логічне слідування, рівносильність.
Аксіоматична побудова математики. Алгебраїчна операція. Алгебраїчні структури. Групи, кільця, поля. Поле дійсних чисел.
Поняття комплексного числа. Поле комплексних чисел. [Геометрична інтерпретація комплексного числа]. [Тригонометрична форма комплексного числа].
Числові функції. Властивості функцій. Перетворення графіків функцій.
Основна мета:
подальше збагачення математичної мови школярів, формування культури їхнього логічного мислення; ознайомлення з новими поняттями в контексті систематизації та повторення набутих раніше знань;
систематизувати, узагальнити та підвищити теоретичний рівень набутих раніше знань і зокрема тих, що створюють грунт для курсу математичного аналізу; завершити змістовну числову лінію курсу алгебри розширенням множини дійсних чисел до множини комплексних чисел та введенням поняття алгебраїчної операції.
У процесі повторення з’ясувати готовність учнів до поглибленого вивчення математики.
Основні вимоги:
точно та грамотно формулювати вивчені теоретичні положення та викладати власні міркування при розв’язуванні рівнянь, нерівностей, їх систем та задач;
правильно користуватись математичною термінологією та символікою;
правильно проводити логічні міркування, наводити приклади та контр
приклади;
мати уявлення про алгебраїчні структури як предмет вивчення сучасної алгебри;
знати необхідні умови розширення числової множини; означення та властивості алгебраїчних операцій; означення комплексного числа; означення та основні властивості числових функцій;
уміти знаходити суму, різницю, добуток та частку комплексних чисел; досліджувати властивості відомих видів числових функцій та будувати їх графіки; будувати графік функції
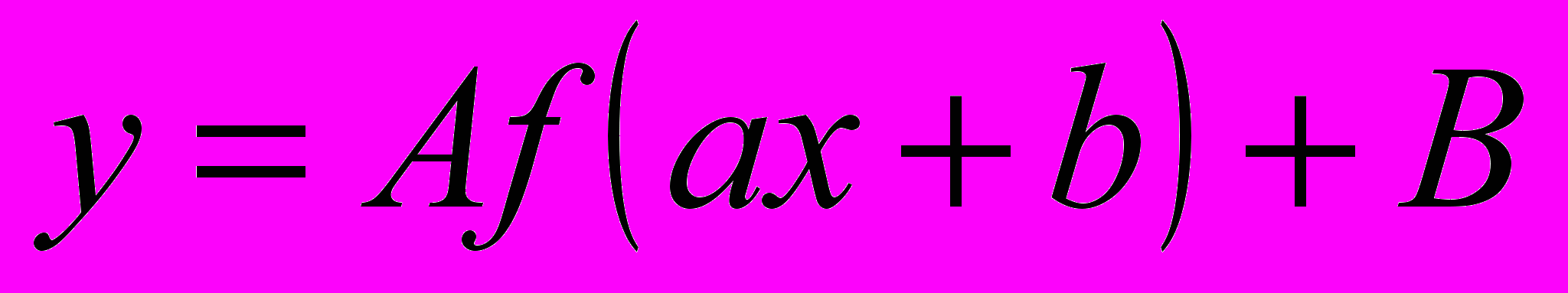за відомим графіком функції 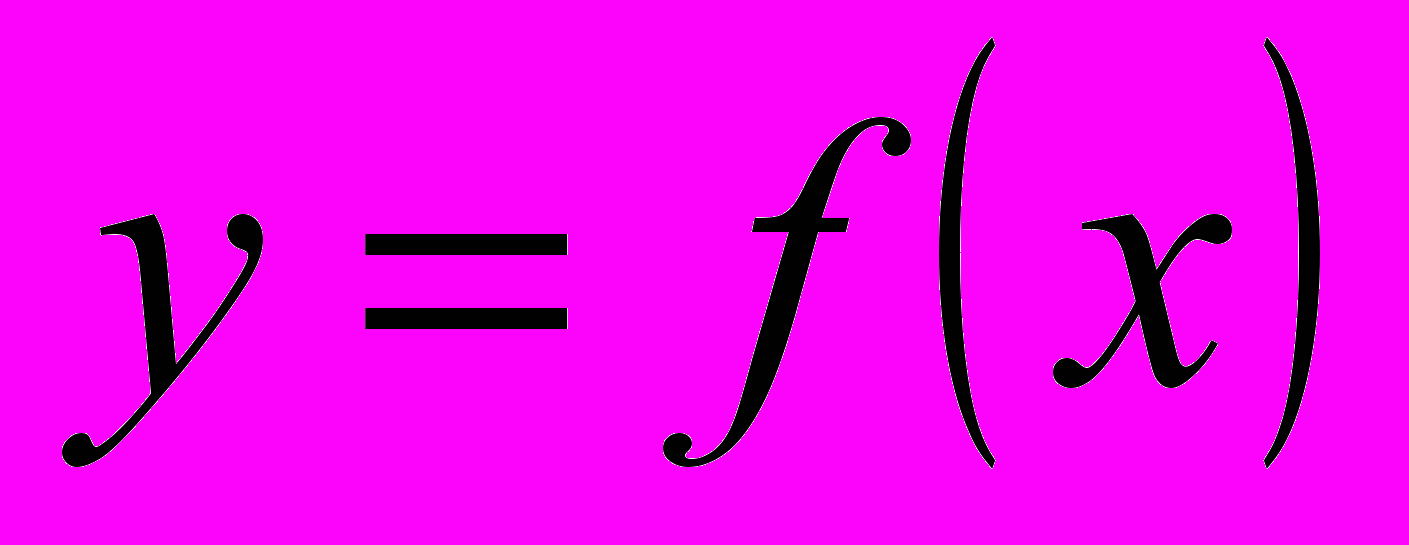.2. Алгебраїчні рівняння та нерівності вищих степенів (25 – 30 год.).
Раціональні вирази з однією змінною.
Многочлени від однієї змінної. Ділення многочленів. Корені многочлена. [Узагальнена теорема Вієта].
Методи розв’язування алгебраїчних рівнянь та нерівностей вищих степенів. [Рівняння та нерівності з параметрами].
Основна мета:
систематизувати відомості про раціональні вирази з однією змінною; з’ясувати, що теорія подільності многочленів будується за аналогією до теорії подільності цілих чисел; виробити вміння знаходити корені многочленів та розкладати їх на множники; ознайомити з основними методами розв’язування рівнянь та нерівностей вищих степенів та виробити вміння їх застосовувати.
Основні вимоги:
знати означення многочлена; алгоритми ділення многочленів “кутом”, із застосуванням методу невизначених коефіцієнтів і за схемою Горнера; означення кореня многочлена та алгоритм знаходження раціональних коренів многочлена; основні методи розв’язування алгебраїчних рівнянь та нерівностей вищих степенів;
уміти реалізовувати алгоритми ділення многочленів та знаходження раціональних коренів многочленів та застосовувати їх до розв’язування рівнянь і нерівностей вищих степенів.
3. Границя та неперервність (10 – 20 год.).
Числова послідовність та її границя. [Властивості збіжних числових послідовностей]. Обмежені послідовності. Обмеженість збіжної послідовності. Монотонні послідовності. [Збіжність монотонної та обмеженої послідовності]. Теореми про границі послідовностей.
Границя функції в точці. [Властивості функцій, що мають границю в точці]. Властивості границь функцій. [Границя функції на нескінченності. Похилі та горизонтальні асимптоти кривої].
Неперервність функції в точці. Операції над неперервними функціями. [Властивості функцій, неперервних на відрізку].[Вертикальні асимптоти кривої].
Основна мета:
ввести поняття границі числової послідовності, границі функції в точці; навчити учнів використовувати ці поняття та їх властивості при виконанні вправ і розв’язуванні задач.
Основні вимоги:
знати означення границі числової послідовності, границі функції в точці і неперервності функції в точці та основні властивості границь і неперервних функцій;
уміти знаходити границі числових послідовностей, границі функцій; досліджувати функції на неперервність.
4. Тригонометричні та обернені тригонометричні функції (35 – 40 год.).
Вимірювання кутів. Радіан. Радіанна міра кута.
Синус, косинус, тангенс і котангенс довільного кута. Співвідношення між тригонометричними функціями одного аргументу. Формули зведення. Формули додавання. Формули подвійного та половинного аргументу. Перетворення суми і різниці тригонометричних функцій у добуток і добутку у суму та різницю.
Тотожні перетворення тригонометричних виразів.[Перетворення виразів з модулями і параметрами].
Функції y = sinx, y = cosx, y = tgx, y = ctgx їх властивості і графіки. Перша важлива границя:
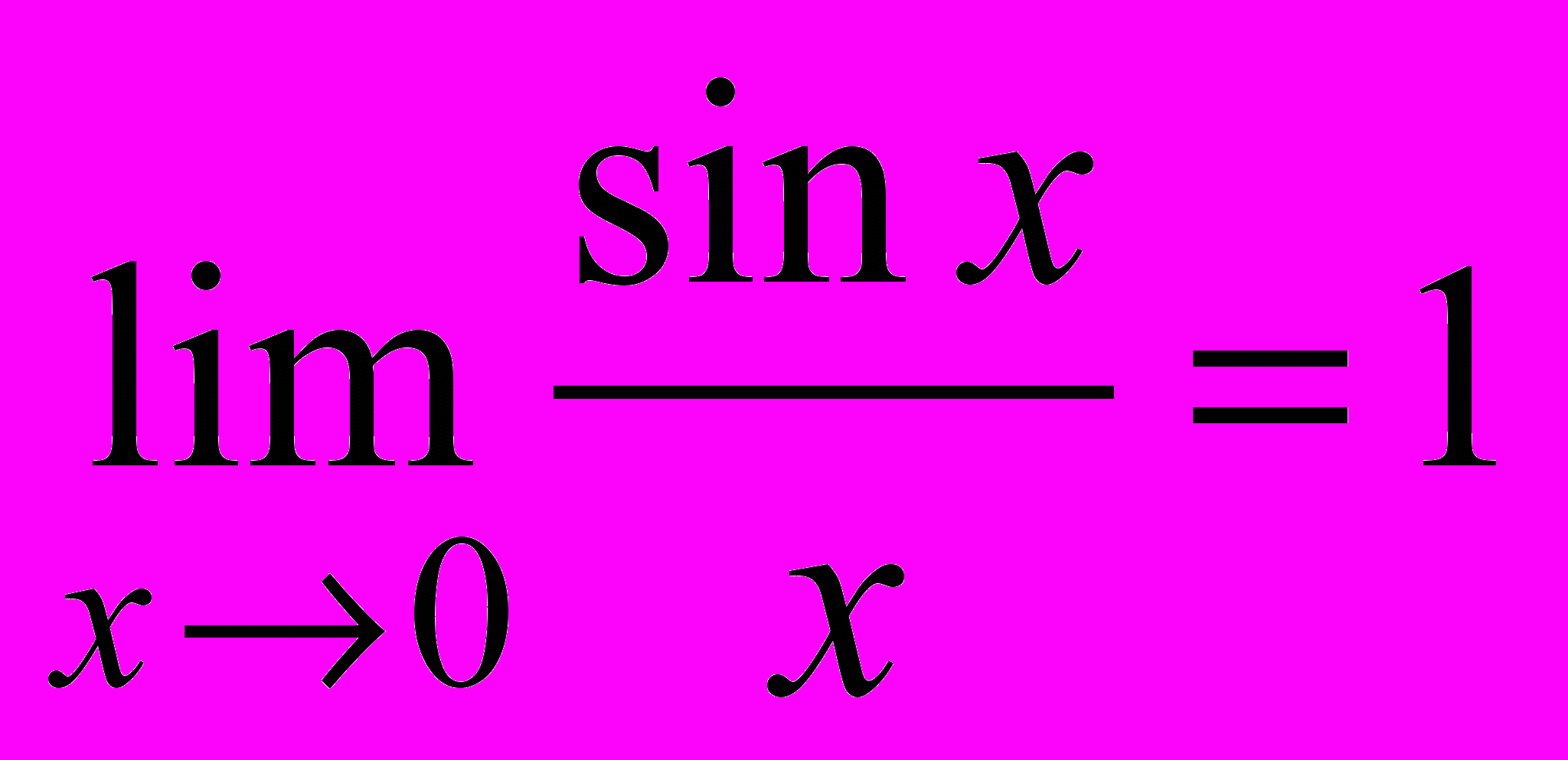. Гармонічні коливання.Існування та неперервність оберненої функції.
Функції y = arcsinx, y = arccosx, y = arctgx, y = arcctgx, їх властивості і графіки.
Найпростіші тригонометричні рівняння. Основні методи їх розв’язування.
Найпростіші тригонометричні нерівності. Основні методи їх розв’язування.
[Рівняння та нерівності з параметрами].
Основна мета:
ввести поняття синуса, косинуса, тангенса і котангенса довільного кута; сформувати вміння обчислювати значення тригонометричних функцій за відомим значенням однієї з них; виконувати перетворення тригонометричних виразів;
вивчити властивості тригонометричних та обернених тригонометричних функцій; закріпити і поглибити знання і вміння, пов’язані із застосуванням вивчених раніше формул тригонометрії до перетворень тригонометричних виразів; сформувати вміння розв’язувати тригонометричні рівняння і нерівності.
Основні вимоги:
знати означення синуса, косинуса, тангенса і котангенса довільного кута; співвідношення між тригонометричними функціями одного аргументу; формули зведення; формули додавання; формули подвійного та половинного аргументу; формули перетворення суми і різниці тригонометричних функцій у добуток і добутку в суму та різницю; означення, властивості і графіки основних тригонометричних функцій та обернених тригонометричних функцій; найпростіші тригонометричні рівняння і нерівності та їх розв’язки; основні методи розв’язування тригонометричних рівнянь і нерівностей;
уміти здійснювати перехід від радіанної міри кута до градусної і навпаки; використовувати відповідні формули для знаходження значень тригонометричних функцій за даним значенням однієї з них, для спрощення і тотожних перетворень тригонометричних виразів та доведення тотожностей; будувати графіки тригонометричних функцій за допомогою перетворень графіків основних тригонометричних функцій та читати їх властивості; розв’язувати тригонометричні рівняння і нерівності.
5. Похідна та її застосування (30 – 46 год.).
Задачі, що приводять до поняття похідної.
Приріст функції і приріст аргументу. Похідна. Геометричний та механічний зміст похідної. [Диференціал функції]. Диференційовність функції.
Похідна суми, різниці, добутку та частки. Похідна складеної та оберненої функцій. Похідні елементарних функцій. [Поняття про похідні вищих порядків].
Застосування похідної до дослідження функцій. Теореми Ферма і Лагранжа. Дослідження функції на монотонність. Екстремуми функції. Найбільше та найменше значення функції на відрізку. [Дослідження функції на опуклість. Точки перегину]. Побудова графіків функцій.
Основна мета:
сформувати поняття похідної, з’ясувати її геометричний і механічний зміст; навчити учнів знаходити похідні функцій; розглянути застосування похідної до дослідження функцій і побудови їх графіків.
Основні вимоги:
знати означення похідної, її геометричний і механічний зміст; правила знаходження похідної суми, різниці, добутку, частки функцій, похідної складеної функції; похідні деяких елементарних функцій; умови монотонності функції; необхідну і достатню умови екстремуму функції;
уміти знаходити похідні функцій, використовуючи правила диференціювання і таблицю похідних; розв’язувати задачі, пов’язані з геометричним і механічним змістом похідної та найбільшим і найменшим значенням функції; досліджувати функції і будувати їх графіки.
6. Елементи прикладної математики (12 – 12 год.).
Застосування похідної до наближених обчислень значень елементарних функцій.
Елементи статистики. Предмет і метод статистики. Генеральна сукупність та вибірка. Частота появи елемента у вибірці. Властивості частот. Точковий та інтервальний розподіли частот. Гістограма. Відносна частота як наближене значення ймовірності випадкової події. Дискретна випадкова величина, закон її розподілу. Числові характеристики дискретної випадкової величини та їх властивості. Середнє арифметичне спостережених значень як наближене значення математичного сподівання.
Основна мета:
ознайомити з формулами наближеного обчислення значень елементарних функцій; з відомостями про статистику як науку, її основні поняття і способи подання та дослідження певних характеристик статистичних даних.
Основні вимоги:
знати відомості про статистику як науку; про статистичну вибірку, зміст понять абсолютна та відносна частота появи елемента вибірки та частота попадання в заданий інтервал; властивості частот; зміст понять наближене значення ймовірності випадкової події як відносна частота; зв’язок середнього арифметичного даних спостережень із наближеною оцінкою математичного сподівання;
уміти застосовувати формули наближених обчислень; наводити приклади генеральних сукупностей та вибірок даних спостережень з навколишньої дійсності; обчислювати частоти для невеликих вибірок (до 30 значень); подавати статистичні дані у вигляді таблиць, відповідних точковим та інтервальним розподілам частот, будувати гістограму розподілу частот, обчислювати частоту попадання значень спостережуваної величини в довільну підмножину можливих значень; визначати центр розсіювання частот (наближене значення математичного сподівання) за точковим та інтервальним розподілом частот.
7. Повторення. Розв’язування задач (12 год.).
Х клас
Геометрія
(2 - 3 год на тиждень, всього 68 - 102 год)
1. Вступ до стереометрії (6 - 9 год.)
Виникнення і розвиток стереометрії. Основні поняття стереометрії. Аксіоми стереометрії та наслідки з них. Просторові геометричні фігури. Простіші задачі на побудову перерізів. [Аксіоматична побудова геометрії].
Основна мета:
розширити і систематизувати відомості про властивості основних геометричних фігур на площині і в просторі.
Основні вимоги:
мати уявлення про аксіоматичну побудову геометрії;
знати аксіоми стереометрії та наслідки з них;
уміти застосовувати аксіоми та наслідки з них до розв’язування геометричних і практичних задач.
- Паралельність прямих і площин (16 - 24 год.)
Розміщення двох прямих у просторі (перетинаються, паралельні, мимобіжні). Ознака паралельності прямих.
Розміщення прямої і площини у просторі (перетинаються, паралельні). Ознака паралельності прямої і площини.
Розміщення двох площин у просторі (перетинаються, паралельні). Ознака паралельності площин. Існування площини, паралельної даній площині. Властивості паралельних площин.
Паралельне проектування та його властивості. Зображення просторових фігур на площині.
Основна мета:
дати систематизовані знання про паралельність прямих і площин у просторі; сформувати вміння застосовувати відповідні властивості і ознаки до розв’язування задач.
Основні вимоги:
знати означення паралельних і мимобіжних прямих, паралельних прямої і площини, паралельних площин; властивості і ознаки паралельності прямих і площин;
уміти доводити властивості і ознаки паралельності прямих і площин та застосовувати їх до розв’язування задач.
- Перпендикулярність прямих і площин (16 - 24 год.)
Перпендикулярність прямих у просторі. Перпендикулярність прямої і площини. Ознака перпендикулярності прямої і площини. Побудова перпендикулярних прямої і площини.
Перпендикуляр і похила. Теорема про три перпендикуляри.
Перпендикулярність площин. Ознака перпендикулярності площин. Теореми про залежності між паралельністю і перпендикулярністю прямих і площин. Практичне значення паралельності і перпендикулярності прямих і площин.
Кути в просторі (між прямими, прямою і площиною, площинами). Відстані в просторі ([від точки до фігури], від точки до площини, від прямої до площини, [між фігурами], між паралельними площинами, між мимобіжними прямими).
[Ортогональне проектування, його застосування в технічному кресленні]. Площа ортогональної проекції многокутника.
Основна мета:
дати систематизовані знання про перпендикулярність прямих і площин у просторі; сформувати вміння застосовувати відповідні властивості і ознаки до розв’язування задач.
Основні вимоги:
знати означення перпендикулярних прямих у просторі; прямої, перпендикулярної до площини; перпендикуляра і похилої; перпендикулярних площин; кутів і відстаней у просторі;
уміти доводити властивості і ознаки перпендикулярності прямих і площин та застосовувати їх до розв’язування задач.
- Координати і вектори у просторі (18 - 30 год.)
Прямокутна система координат у просторі. Відстань між точками. Координати середини відрізка. [Поділ відрізка в даному відношенні]. Застосування координат до розв’язування стереометричних задач.
Переміщення фігур у просторі та його властивості. Симетрія, паралельне перенесення, поворот у просторі. Перетворення подібності та його властивості. Подібність просторових фігур. Застосування властивостей переміщень і перетворень подібності до розв’язування задач.
Вектори у просторі. Додавання, віднімання векторів, множення вектора на число та їх властивості. Розкладання вектора за трьома некомпланарними векторами. Розв'язування афінних задач за допомогою векторів. Скалярний добуток векторів. Розв’язування метричних задач за допомогою векторів. [Рівняння прямої, площини і сфери].
Основна мета:
узагальнити та систематизувати відомості про координати і вектори, переміщення і перетворення подібності у просторі; завершити вивчення системи загальних метричних понять стереометрії.
Основні вимоги:
знати означення понять вивченого матеріалу; формули відстані між точками, координат середини відрізка і елементів векторної алгебри; властивості переміщень і перетворення подібності;
уміти доводити властивості і виводити формули, передбачені програмою; застосовувати їх до розв’язування задач.
5. Повторення. Розв’язування задач (10 - 15 год.)
XІ клас
(6 - 8 год. на тиждень, всього 204 - 272 год.)
Алгебра і початки аналізу1
(4 - 5 год. на тиждень, всього 170 год.)
1. Первісна та інтеграл (20 – 30 год.).
Первісна та її властивості. Невизначений інтеграл. [Основні методи інтегрування: метод розкладання, метод підстановки, інтегрування частинами].
Площа криволінійної трапеції. Визначений інтеграл. Формула Ньютона – Лебніца.
Застосування визначеного інтегралу до розв’язування геометричних задач: обчислення площ, об’ємів. [Використання комп’ютера до розв’язування геометричних задач].
Застосування визначеного інтегралу до розв’язування задач фізики: обчислення шляху, роботи змінної сили.
[Наближене обчислення визначених інтегралів: метод прямокутників, трапецій та парабол]. [Використання комп’ютера до наближеного обчислення визначених інтегралів].
Основна мета:
ознайомити учнів з інтегруванням як операцією, оберненою диференціюванню; показати застосування визначеного інтегралу до розв’язування задач геометрії та фізики.
Основні вимоги:
знати означення первісної і невизначеного інтеграла та їх основні властивості; формулу Ньютона – Лейбніца; формули обчислення площі фігури, об’єму тіла обертання; обчислення шляху та роботи змінної сили;
уміти знаходити первісні та нескладні невизначені інтеграли; обчислювати площі фігур, об’єми тіл обертання, шлях і роботу змінної сили.
2. Показникова, логарифмічна та степенева функції (35 – 45 год.).
[Степінь з дійсним показником].
Показникова функція, її властивості і графік.
Логарифмічна функція, її властивості і графік.
Означення і властивості логарифмів. Основна логарифмічна тотожність. Формула переходу від однієї основи логарифма до іншої. Тотожні перетворення показникових та логарифмічних виразів.
Показникові і логарифмічні рівняння, нерівності та їх системи, методи їх розв’язування.
[Число е. Натуральні логарифми. Друга важлива границя:
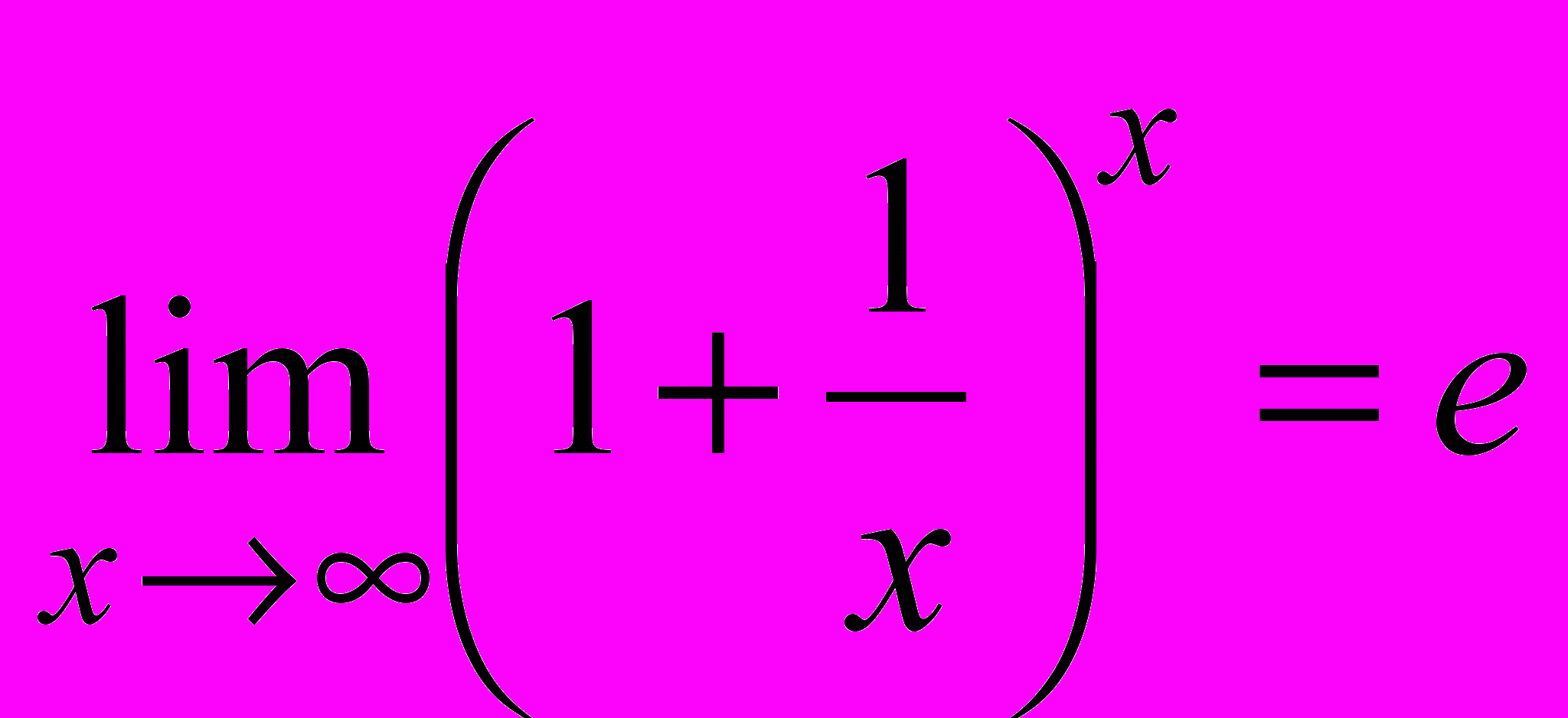].Похідна і первісна показникової функції. Похідна логарифмічної функції.
Степенева функція, її похідна і первісна. Властивості і графіки функції
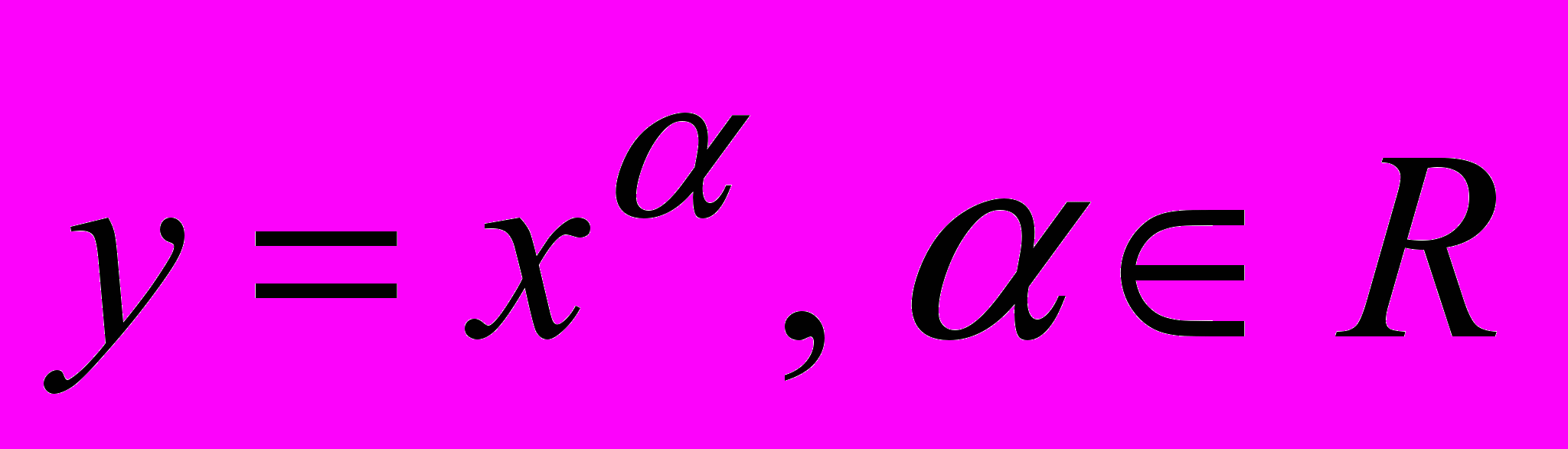. [Порівняння зростання показникової, логарифмічної та степеневої функцій].Ірраціональні рівняння та нерівності.
Диференціальні рівняння. Основні поняття. Диференціальні рівняння 1-го порядку (з відокремлюваними змінними, лінійні).
[Диференціальні рівняння 2-го порядку і коливання].
Основна мета:
систематизація та узагальнення відомостей про степінь на основі введення поняття степеня з дійсним показником; ввести поняття, вивчити властивості і графіки показникової, логарифмічної і степеневої функцій; виробити вміння тотожних перетворень показникових і логарифмічних виразів; навчити учнів розв’язувати показникові, логарифмічні рівняння і нерівності та їх системи; ознайомити з диференціальними рівняннями та їх застосуваннями.
Основні вимоги:
знати означення, властивості і графіки показникової, логарифмічної і степеневої функцій; означення логарифма числа та його властивості; найпростіші показникові, логарифмічні рівняння і нерівності та їх розв’язки; основні відомості про диференціальні рівняння;
уміти будувати графіки показникових, логарифмічних та степеневих функцій за допомогою перетворень графіків функцій
(
), 
(), 
(
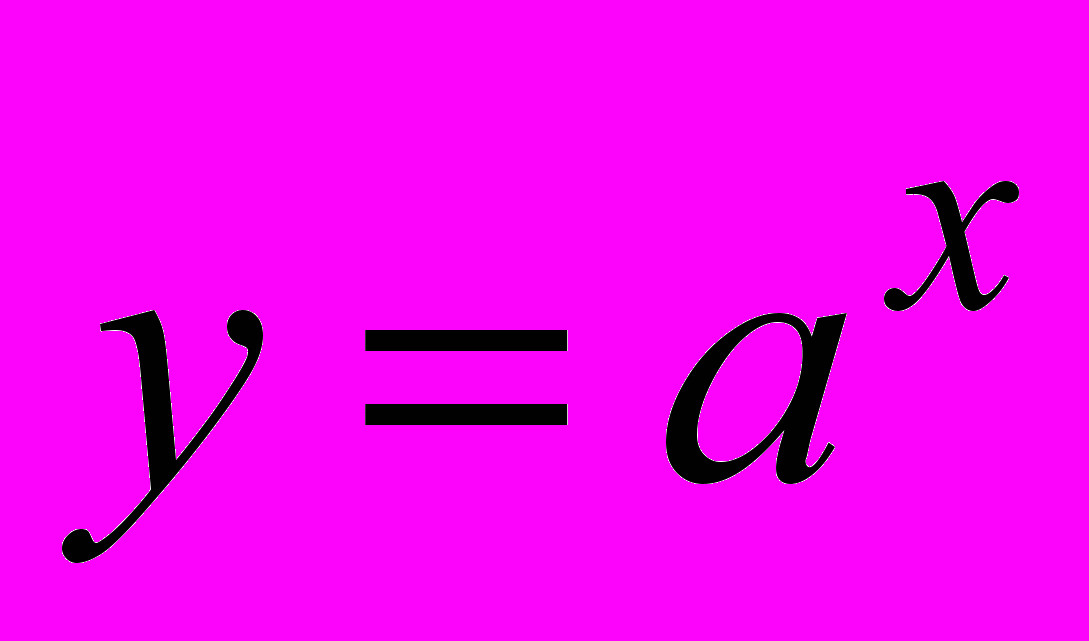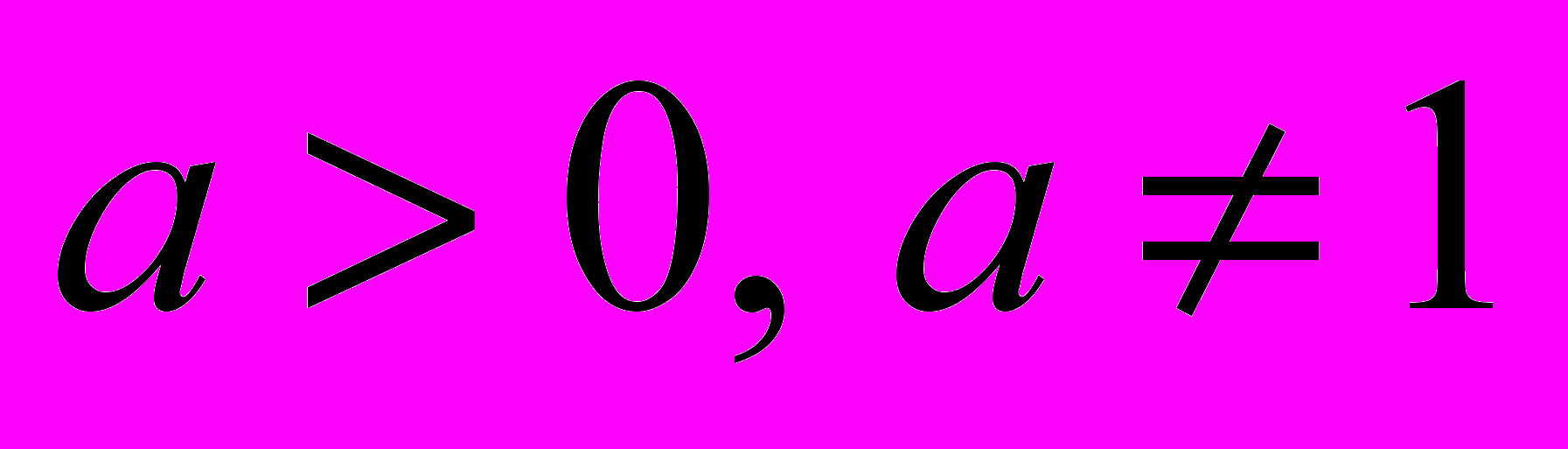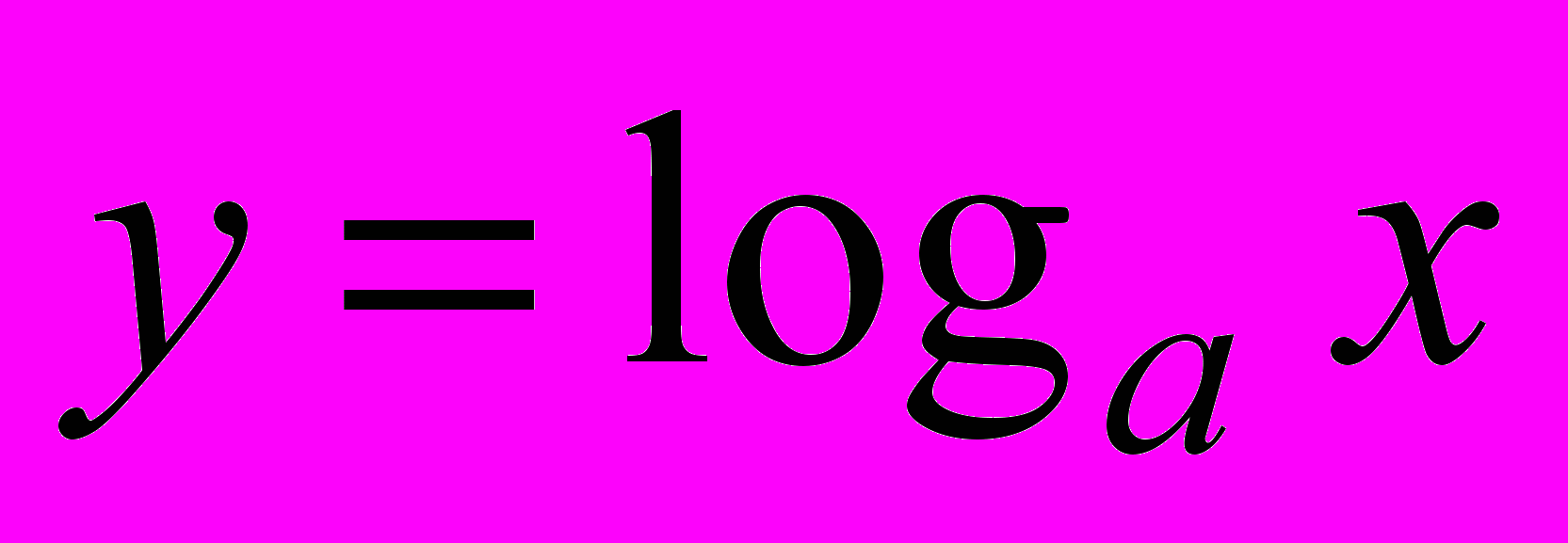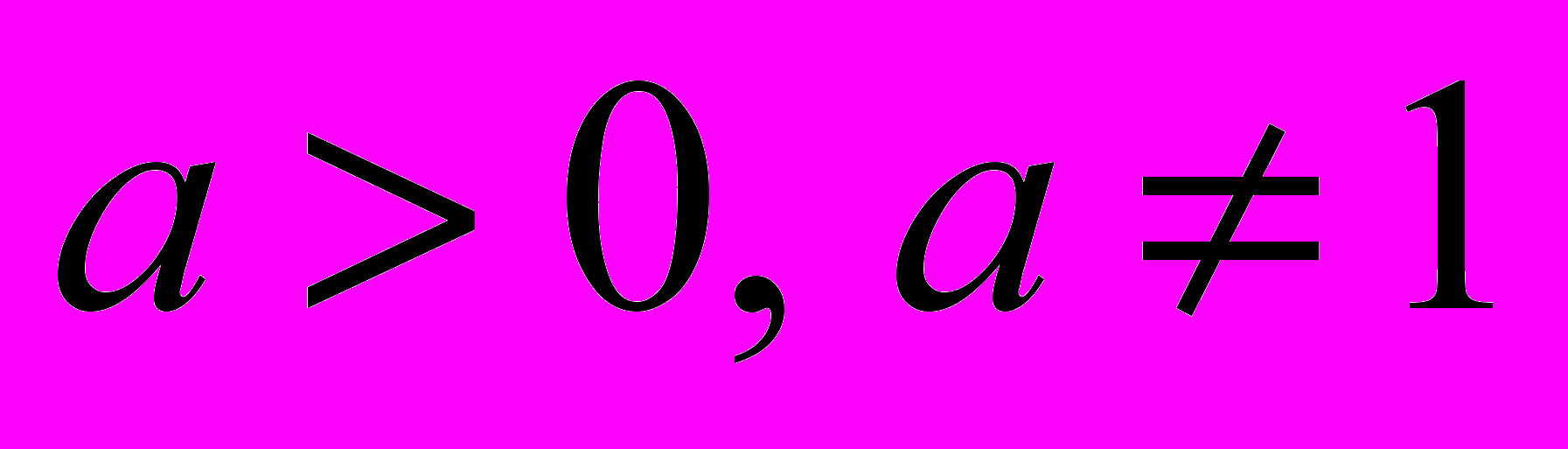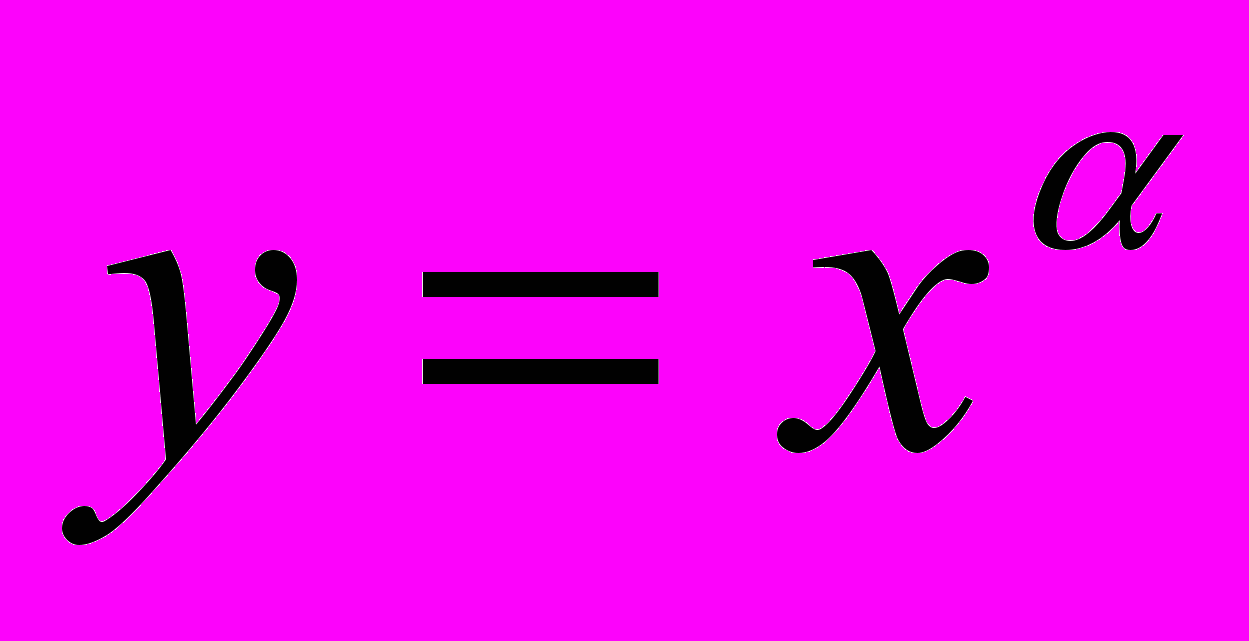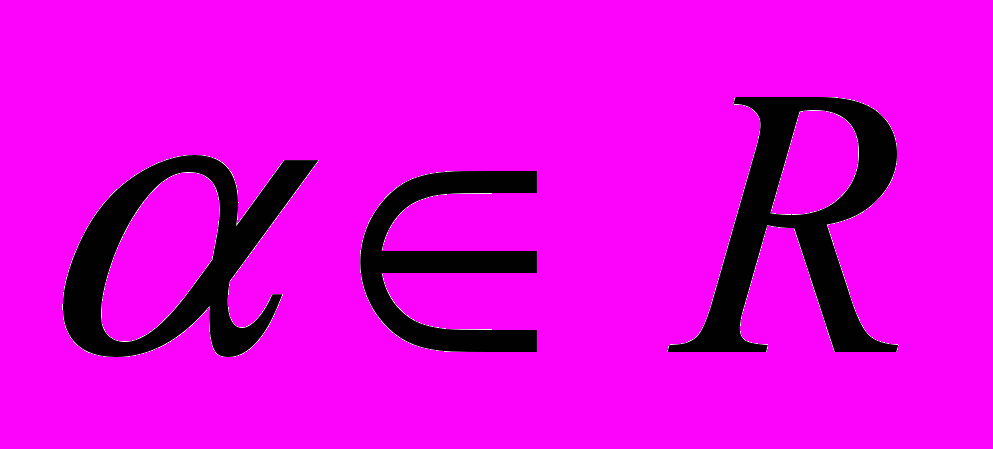) та читати їх властивості; перетворювати показникові та логарифмічні вирази, розв’язувати показникові, логарифмічні, ірраціональні рівняння і нерівності та їх системи; розв’язувати найпростіші диференціальні рівняння і задачі, пов’язані з ними.3. Рівняння, нерівності, системи (34 – 40 год.).
Огляд основних відомостей: область визначення, розв’язок, рівносильність, втрата коренів та поява сторонніх коренів, перевірка розв’язків.
Методи розв’язування рівнянь та нерівностей: розклад на множники, заміна змінної, піднесення до степеня, графічний та інші. Узагальнений метод інтервалів розв’язування нерівностей.
Системи рівнянь та нерівностей. Методи розв’язування систем рівнянь: підстановка, алгебраїчне додавання, введення нових змінних, графічний та інші.
Системи лінійних рівнянь: формули Крамера, метод Гаусса.
[Рівняння, нерівності і системи з параметрами. Методи їх розв’язування]. Поняття про задачі лінійного програмування. [Застосування комп’ютера для розв’язування відповідних задач].
Основна мета:
систематизація основних відомостей про рівняння, нерівності, їх системи та основні методи їх розв’язування.
Основні вимоги:
знати основні поняття стосовно рівнянь, нерівностей та їх систем: область визначення, розв’язок, рівносильність, втрата та поява сторонніх коренів, перевірка розв’язків, методи їх розв’язування; методи розв’язування систем лінійних рівнянь (формули Крамера і метод Гаусса);
уміти розв’язувати рівняння, нерівності та їх системи з аналізом та обгрунтуванням рівносильності здійснюваних перетворень; розв’язувати системи лінійних рівнянь за формулами Крамера та методом Гаусса.
4. Комбінаторика (12 – 17 год.).
Комбінаторне правило множення та додавання. Впорядковані множини.
Перестановки, розміщення, сполуки без повторень. Біном Ньютона.
Кортеж, перестановки, розміщення та сполуки з повторенням елементів.
Основна мета:
сформувати поняття перестановки з т елементів, розміщення та сполук з п по т елементів без повторення та з повторенням елементів і виробити вміння застосовувати ці знання до розв’язування комбінаторних задач.
Основні вимоги:
знати означення понять перестановки з т, розміщення та сполук з п по т елементів без повторення та з повторенням елементів; формули для обчислення кількості зазначених видів перелічувань;
уміти використовувати формули для знаходження кількості перестановок, розміщень та сполук без повторення та з повторенням елементів до розв’язування комбінаторних задач.
5. Початки теорії ймовірностей (20 – 25 год.).
Елементарна подія. Множина елементарних подій. Операції над подіями. Геометрична інтерпретація операцій над подіями. Поняття ймовірності випадкової події. Обчислення ймовірностей випадкових подій. Поняття про математичне сподівання. Умовні ймовірності. Формула повної ймовірності. Залежні і незалежні події. Ймовірність добутку і суми подій. Повторні незалежні випробування. Формула Бернуллі. Уявлення про закон великих чисел. Статистичні оцінки розсіювання ймовірностей.
Основна мета:
сформувати уявлення про основні поняття теорії ймовірностей та виробити вміння їх застосовувати до розв’язування задач.
Основні вимоги:
мати уявлення про стохастичний експеримент, елементарну подію та множину елементарних подій, про випадкову подію як деяку підмножину множини елементарних подій та розуміти зміст висловлень з виразом “подія відбулась”; про еквівалентність подій, неможливу подію, несумісні події; про ймовірність події та різні підходи до означення ймовірності (статистичний, класичний, аксіоматичний); про розподіл ймовірностей на множині елементарних подій; про центр розподілу ймовірностей; про умовні ймовірності, залежні та незалежні події; про схему Бернуллі повторних незалежних випробувань; про можливість передбачення усередненого результату великої серії випробувань; дискретну та неперервну випадкову величину, середнє випадкової величини, математичне сподівання та дисперсію;
знати означення суми, добутку, різниці двох подій, протилежної події, основні властивості ймовірностей, правила обчислення ймовірності добутку і суми кількох подій; знати формулу Бернуллі (повної ймовірності);
уміти геометрично інтерпретувати операції над подіями (за аналогією з операціями над множинами); обчислювати в найпростіших випадках імовірності випадкових подій; застосовувати правила обчислення добутку і суми кількох подій та формулу Бернуллі до розв’язування задач.
6. Повторення. Розв’язування задач (15 год.).
XІ клас
Геометрія
(2 - 3 год. на тиждень, всього 68 - 102 год.)
1. Многогранники (28 год)
Многогранні кути. [Найпростіші випадки рівності тригранних кутів]. Двогранні кути. Лінійний кут двогранного кута.
Многогранник та його елементи. Опуклі многогранники. [Теорема Ейлера (без доведення)]. Призма, паралелепіпед, піраміда, зрізана піраміда. Перерізи многогранників. Задачі на побудову перерізів. [Проекції призми і піраміди].
Площі бічної і повної поверхонь призми, піраміди, зрізаної піраміди.
Правильні многогранники. Види правильних многогранників.
Основна мета:
дати систематизовані відомості про основні види многогранників та площі їх поверхонь.
Основні вимоги:
знати означення многогранного кута; многогранників, вказаних у змісті програми, та їх властивості; формули площ бічної і повної поверхонь призми, правильної піраміди, зрізаної піраміди;
вміти зображати на площині многогранники та їх елементи, користуючись властивостями паралельного проектування; будувати перерізи многогранників; доводити властивості, виводити формули площ поверхонь многогранників та застосовувати їх до розв’язування геометричних і практичних задач.
- Тіла обертання (16 - 20 год)
Поняття про тіло і поверхню обертання. Циліндр, конус, зрізаний конус. Перерізи циліндра і конуса.
Площі бічної і повної поверхні циліндра, конуса, зрізаного конуса. Відношення площ поверхонь подібних фігур.
Куля і сфера. Переріз кулі площиною. Площина, дотична до сфери. Перетин двох сфер. [Комбінації многогранників і тіл обертання].
Основна мета:
ознайомити учнів з тілами обертання та їх властивостями.
Основні вимоги:
знати означення тіл обертання та їх властивості; формули площ бічної і повної поверхонь циліндра, конуса, зрізаного конуса;
вміти зображати на площині тіла обертання та їх елементи; будувати перерізи; доводити властивості, виводити формули площ поверхонь тіл обертання та застосовувати їх до розв’язування геометричних і практичних задач.
3. Об’єми тіл. Площа сфери (18 - 24 год)
Поняття про об’єм тіла. Основні властивості об’ємів. Об’єми многогранників: паралелепіпеда, призми, зрізаної піраміди. Відношення об’ємів подібних тіл.
Об’єми тіл обертання: циліндра, конуса, зрізаного конуса, кулі та її частин.
Площа сфери.
Основна мета:
дати систематизовані відомості про об’єми многогранників і тіл обертання; ознайомити з площею сфери.
Основні вимоги:
мати поняття про об’єм тіла;
знати властивості об’ємів; формули об’ємів многогранників, тіл обертання та площі сфери;
вміти розв’язувати геометричні і практичні задачі на знаходження об’ємів, вказаних у змісті програми тіл.
4. Повторення і систематизація знань. Розв’язування задач (14 - 30 год)
Укладачі програми : Бурда М.І., Жалдак М.І.,
Колесник Т.В., Хмара Т.М.,
Шкіль М.І., Ядренко М.Й.
1 Планування орієнтоване на використання підручника:Шкіль М. І., Колесник Т. В., Хмара Т. М. Алгебра і початки аналізу. Підручник для учнів 10 класу з поглибленим вивченням математики в середніх закладах освіти.– К.: Освіта, 2000.
1 Планування орієнтоване на використання підручника:Шкіль М. І., Колесник Т. В., Хмара Т. М. Алгебра і початки аналізу. Підручник для учнів 11 класу з поглибленим вивченням математики в середніх закладах освіти.– К.: Освіта, 2001.