Програма державного екзамену з теорії та практики навчання І виховання та методики викладання математики
| Вид материала | Документы |
- Питання до державного іспиту з теорії І методики фізичного виховання для студентів, 43.84kb.
- Програма вступного іспиту, 453.67kb.
- Секції математики І теорії та методики навчання математики керівник секції, 14.62kb.
- Програма співбесіди з теорії та методики фізичного виховання для вступників на здобуття, 167.35kb.
- Львівський державний університет фізичної культури кафедра теорії І методики фізичного, 75.57kb.
- Програма з «Методики викладання іноземних мов у середніх навчальних закладах» до державного, 238.02kb.
- Програма з математики для 10 11 класів загальноосвітніх навчальних закладів (для класів, 519.89kb.
- Програма з математики для 10 11 класів загальноосвітніх навчальних закладів (для класів, 522.34kb.
- Програма з математики для 10 12 класів загальноосвітніх навчальних закладів (для класів, 524.18kb.
- Програма комплексного фахового екзамену з інформатики для вступу на навчання для здобуття, 117.08kb.
Міністерство освіти і науки України
Ніжинський державний університет імені Миколи Гоголя
Кафедра вищої математики
“Затверджую”
Ректор НДУ імені Миколи Гоголя
______________ проф. Бойко О.Д.
“___” __________ 2009 року
П Р О Г Р А М А
державного екзамену з теорії
та практики навчання і виховання та методики викладання математики
Напрям підготовки 0101 Педагогічна освіта
Спеціальність: Педагогіка і методика середньої освіти. Математика.
Кваліфікація: Вчитель математики і фізики; математики та основ економіки; математики та основ інформатики.
(Денна та заочна форми навчання)
Освітньо-кваліфікаційний рівень: 7.010103 – спеціаліст
| | |
| Рекомендовано кафедрою вищої математики, протокол № 7 від 22.12.2009 р. р.___ | Схвалено на засіданні вченої ради фізико- математичного факультету протокол № 5 від 23.12.2009 р. Голова вченої ради: ____________ доц. Аніщенко В.О. |
Ніжин – 2009
Ч А С Т И Н А ІІ
Пояснювальна записка
Програма державного екзамену складається з двох частин “Теорія і практика навчання й виховання” (частина І), “Методика викладання математики” (частина ІІ).
Головним завданням державного екзамену з методики викладання математики є виявлення у випускників університету ступеня підготовки до практичної діяльності в якості вчителя математики.
Екзамен має на меті перевірити рівень засвоєння програмового матеріалу з курсів елементарної математики та методики математики, рівень методичної підготовки, готовність до подальшої професійної діяльності на посаді вчителя математики.
Основою програми екзамену є нині діючі програми з елементарної математики та з методики навчання математики.
Рівень сформованості знань, умінь та навичок студентів відповідно до освітньо-кваліфікаційної характеристики повинен задовольняти наступні вимоги:
- вміти виконувати логіко-дидактичний аналіз шкільних підручників, конкретних тем;
- проводити методичний аналіз педагогічної і математичної літератури, програм, навчально-методичних комплексів;
- планувати і конструювати систему різних форм організації навчального процесу;
- здійснювати оптимальний відбір змісту, методів, прийомів навчання, засобів навчання та СКТ;
- організовувати і управляти діяльністю учнів на різних етапах засвоєння знань;
- мати уміння і навички в організації і проведенні факультативних курсів з математики;
- здійснювати контроль за роботою учнів.
Результати складання державного екзамену оцінюються у формі рейтингового балу за національною шкалою та в системі ЕСТS.
Узгодження національної системи оцінювання зі шкалою ЕСТS
| Національна шкала оцінювання (4-бальна) | Оцінка за шкалою ЕСТS (7-бальна) | Критерії оцінювання навчальних досягнень студентів з курсу “Методика навчання математики” |
| Відмінно (5) | А | Студент володіє: понятійним і фактичним апаратом шкільного курсу математики (ШКМ) на поглибленому рівні; комплексом методичних знань та вмінь, який характеризується системністю та концептуальністю. Застосування знань здійснюється на основі самостійного цілеутворення, побудови власних програм діяльності. Студент проявляє нешаблонність мислення у виборі і використанні елементів комплексу методичних знань, здатний самостійно і творчо використовувати методичні уміння відповідно до варіативних ситуацій навчання математики. Студент спроможний самостійно формулювати нові методичні задачі, розв'язувати нестандартні методичні задачі. Навчально-пізнавальна активність обумовлена пізнавальними Інтересами, мотивами саморозвитку і професійного становлення. Студент проявляє інтерес до актуальних проблем МНМ, може під керівництвом викладача вибрати предмет дослідження, проводити самостійну науково-дослідну роботу. |
| Добре (4) | В | Студент володіє понятійним і фактичним апаратом ШКМ на поглибленому рівні. Студент володіє комплексом методичних знань та вмінь, який є частково-впорядкованим. У процесі застосування знань студент спроможний самостійно вибрати необхідний елемент комплексу знань та вмінь. Застосування знань та вмінь здійснюється як у стандартних ситуаціях, так і при незначних варіаціях умов на основі використання загальних рекомендацій. Відбувається перенесення сформованих методичних умінь або їх комплексів на розв'язування незнайомих методичних задач. Навчально-пізнавальна активність стимулюється пізнавальними інтересами, продукт діяльності оцінюється як професійно значущий. |
| Добре (4) | С | Студент володіє понятійним і фактичним апаратом ШКМ на поглибленому рівні, усвідомлює взаємозв'язок між компонентами методичної системи як предмета дослідження МНМ, може усвідомлено застосовувати знання про цілі, зміст, методи та прийоми, організаційні форми і засоби навчання математики при реалізації функцій планування, керування діяльністю учнів, у ході власної аналітико-синтетичної діяльності. Комплекс знань з МНМ частково-структурований. Знання застосовуються переважно у знайомих ситуаціях. Студент усвідомлює особливості навчальних, математичних та методичних задач. Пошук способів їх розв'язання здійснюється за зразком. Студент спроможний аргументувати застосування певної методичної дії у ході розв'язування задач. Навчально-пізнавальна активність стимулюється мотивами професійного становлення і пізнавальними інтересами. |
| Задовільно (3) | D | Студент володіє понятійним і фактичним апаратом ШКМ на підвищеному рівні, може проілюструвати власними прикладами особливості реалізації змістових ліній ШКМ, цілі, зміст, методи і прийоми, організаційні форми та засоби навчання математики, частково усвідомлює специфіку навчальних, математичних та методичних задач, має знання про дії та відповідні їм операції щодо розв'язування типових задач. Однак процес самостійного розв'язування методичних задач потребує опори на зразок. Навчально-пізнавальна активність студентів є ситуативно-евристичною. Домінують мотиви обов'язку та особистого успіху. Використання засобів саморозвитку та самопізнання відбувається не усвідомлено. |
| Задовільно (3) | E | Студент володіє понятійним і фактичним апаратом ШКМ на підвищеному рівні, може відтворити особливості реалізації основних змістових ліній ШКМ, частково усвідомлює зміст прийомів, які застосовує вчитель з метою прийняття учнями цілей навчання математики, може відтворити перелік методів, засобів та організаційних форм навчання математики і методів математики, які вивчаються в ШКМ. Має уявлення про специфіку навчальних, математичних та методичних задач. Виконання методичних дій при розв'язуванні методичних задач частково усвідомлюється, здійснюється частково правильно. |
| Незадовільно (2) | Fx | Студент володіє понятійним і фактичним апаратом ШКМ на елементарному рівні, має уявлення про логічну будову ШКМ, його змістові лінії, про цілі, методи і прийоми, організаційні форми і засоби навчання математики в ЗОШ, має інтуїтивні уявлення про прийоми прийняття учнями цілей навчання математики, специфіку методів математики і методів навчання математики, може їх розрізняти. Виконання окремих методичних дій відбувається не усвідомлено, однак переважно правильно, навчально-пізнавальна активність мотивується ситуативно-прагматичним інтересом. |
| Незадовільно (2) | F | Студент володіє понятійним і фактичним апаратом ШКМ на елементарному рівні, має уявлення про логічну будову ШКМ, його змістові лінії, про цілі, методи і прийоми, організаційні форми і засоби навчання математики в ЗОШ. Виконання окремих методичних дій відбувається неусвідомлено, у більшості випадків неправильно, навчально-пізнавальна активність проявляється лише у ситуаціях зовнішнього примусу. |
Екзамен проводиться в усній формі. На екзамені студентам пропонується 2 комплекти білетів, структура білету з методики математики така: білет складається з одного теоретичного питання, методичної задачі та задачі із шкільного курсу математики. Ознайомившись із змістом білета, студент готує відповідь, у якій показує рівень своєї загальної підготовки.
Під час підготовки до відповіді на питання екзаменаційного білета студент може користуватися програмою з математики для середніх загальноосвітніх навчальних закладів, підручниками, моделями, наочністю, ТЗН, використання яких передбачаються при відповіді на питання з методики викладання математики.
Розділ І.
ШКІЛЬНИЙ КУРС МАТЕМАТИКИ
З МЕТОДИКОЮ ВИКЛАДАННЯ
ТЕМА 1. Комплексні числа
Принципи розширення числової множини. Методика вивчення поняття комплексного числа та дії над комплексними числами. Геометрична інтерпиритація комплексних чисел. Тригонометрична форма комплексного числа. Методика вивчення формули Мавра. Формування умінь і навичок розв’язування задач на використання комплексних чисел.
ТЕМА 2. Тригонометричні вирази
Пропедевтика вивчення тригонометричних виразів у курсі планіметрії основної школи. Методика вивчення тригонометричних тотожностей додавання, суми й різниці однойменних тригонометричних функцій, перетворенню добутку тригонометричних функцій на суму, формул пониження степеня, універсальних підстановок. Методика формування умінь та навичок виконувати тотожні перетворення тригонометричних виразів.
ТЕМА 3. Степеневі та показникові вирази
Методика формування поняття кореня
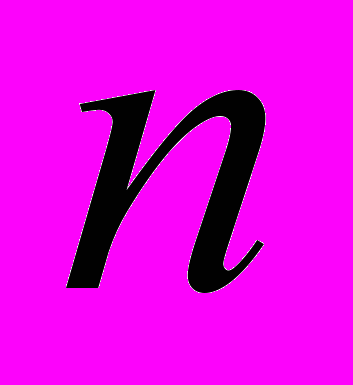-го степеня з числа 
, поняття степеня з дійсним показником. Методика вивчення властивостей степенів. Методика використання тотожних перетворень виразів, що містять радикали та степені з дійсним показником.ТЕМА 4. Логарифмічні вирази
Методика формування поняття логарифма невід’ємного числа. Методика вивчення властивостей логарифмів (теореми про логарифм частки, добутку, степеня та наслідки з них). Методика формування умінь та навичок виконувати тотожні перетворення логарифмічних виразів.
ТЕМА 5. Тригонометричні функції
Методика формування поняття тригонометричної функції дійсного аргументу. Особливості застосування методичної схеми до вивчення властивостей тригонометричних функцій. Застосування похідної до вивчення властивостей тригонометричних функцій та побудови їх графіків. Методика застосування властивостей функцій до розв’язування задач.
ТЕМА 6. Логарифмічні функції
Методика формування поняття логарифмічної функції. Методика вивчення властивостей логарифмічних функцій та побудова графіків з використанням похідної. Методична схема та її застосування на прикладі вивчення логарифмічної функції. Методика розв’язування вправ на застосування властивостей логарифмічної функції.
ТЕМА 7. Показникова функція
Методика узагальнення поняття степеня, формування поняття показникової функції. Особливості застосування методичної схеми до вивчення властивостей показникової функції. Застосування похідної до вивчення властивостей показникової функції та побудови її графіка. Методика розв’язування вправ на застосування властивостей показникової функції.
ТЕМА 8. Обернені тригонометричні функції
Методика формування поняття обернених тригонометричних функцій
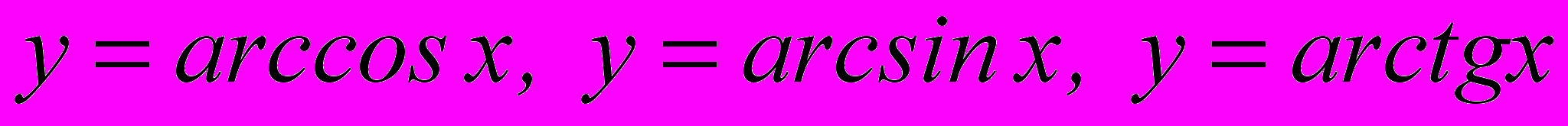. Застосування теореми про обернену функцію та її властивості до вивчення властивостей обернених тригонометричних функцій та побудови їх графіків. Методика розв’язування вправ на застосування властивостей обернених тригонометричних функцій.ТЕМА 9. Тригонометричні рівняння й нерівності
Методика формування поняття тригонометричного рівняння, найпростіших тригонометричних рівнянь та їх розв’язків. Основні види тригонометричних рівнянь та способи їх розв’язування.
ТЕМА 10. Показникові рівняння й нерівності
Методика формування поняття показникового рівняння. Методика навчання розв’язуванню основним методам розв’язування показникових рівнянь та нерівностей.
ТЕМА 11. Ірраціональні рівняння й нерівності
Методика формування поняття ірраціонального рівняння. Основні види ірраціональних рівнянь та методика навчання розв’язуванню ірраціональних рівнянь.
ТЕМА 12. Логарифмічні рівняння й нерівності
Методика формування поняття логарифмічного рівняння. Методика навчання розв’язуванню основних видів логарифмічних рівнянь та нерівностей.
ТЕМА 13. Похідна
Методика формування поняття похідної. Застосування означення похідної до знаходження похідних елементарних функцій. Методика розв’язування задач на геометричний та механічний зміст похідної. Методика вивчення теорем про похідну суми, добутку, частки функцій.
ТЕМА 14. Застосування похідної
Методика формування поняття функції монотонної в точці, точки екстремуму та екстремумів функції, стаціонарної та критичної точки. Методика вивчення тверджень, що виражають достатню умову монотонності функцій, достатні умови існування екстремумів. застосування похідної до дослідження властивостей функцій та побудови графіків. Методика розв’язування текстових задач на найбільше і найменше значення функцій.
ТЕМА 15. Границя послідовності. Границя функції
Методика формування поняття послідовності, нескінченно малої (великої, обмеженої, збіжної послідовностей; поняття границі послідовності, границі функції в точці та на нескінченності. Методика вивчення правил знаходження границі послідовності та границі функції. Поняття асимптоти та неперервності функції.
ТЕМА 16. Первісна. Визначений інтеграл
Методика формування поняття первісної, визначеного інтеграла. Геометричний зміст визначеного інтеграла. Методика вивчення правил знаходження первісних, формул Ньютона-Лейбніца. Методика розв’язування задач на застосування визначеного інтеграла до обчислення площ плоских фігур, об’ємів тіл обертання, многогранників та розв’язування інших задач з прикладним змістом.
ТЕМА 17. Диференціальні рівняння
Методика формування поняття диференціального рівняння, загального і частинного розв’язку рівняння. Методика розв’язування диференціального рівняння радіоактивного розпаду та показникового зростання і спадання. Методика застосування диференціальних рівнянь до задач з прикладним змістом.
ТЕМА 18. Елементи комбінаторики. Біном Ньютона
Методика формування комбінаторних понять (перестановки, комбінації, розміщення). Методика виведення формул для обчислення кількості комбінаторних сполук, формули бінома Ньютона. Властивості біноміальних коефіцієнтів та їх застосування до розв’язування задач. Методика застосування правил комбінаторики до розв’язування задач.
ТЕМА 19. Елементи статистики та теорії ймовірностей
Методика вивчення основних понять статистики та теорії ймовірностей: генеральна сукупність, вибірка, мода, медіана, середнє значення, події та їх видів, класичного означення імовірності. Методика вивчення теорем множення ймовірностей незалежних подій. Методичні особливості розв’язування задач статистики та теорії ймовірностей.
ТЕМА 20. Аксіоми стереометрії
Аксіоматичний метод побудови геометрії. Методика вивчення аксіом. Особливості проведення перших уроків стереометрії. Методика доведення теорем, які стверджують існування та єдність площини. Методика розв’язування задач на застосування аксіом стереометрії в задачах на побудову перерізів многогранників.
ТЕМА 21. Паралельність прямих у просторі
Методика формування поняття паралельності прямих у просторі. Методика вивчення тверджень, які виражають існування і єдність прямої, що проходить через точку паралельно до даної прямої; ознаку паралельності прямих. Методика формування умінь та навичок розв’язування задач.
ТЕМА 22. Паралельність прямої і площини
Методика формування поняття прямої паралельної до площини. Методика вивчення ознаки паралельності прямої і площини. Методика розв’язування задач по темі.
ТЕМА 23. Паралельність площин
Методика формування поняття паралельних площин. Методика вивчення теорем: ознаки паралельності двох площин, теореми про існування площини паралельної даній площині. Методика формування умінь та навичок розв’язування задач на паралельність у просторі.
ТЕМА 24. Паралельність у просторі
Методика вивчення правил паралельного проектування; теорем, що виражають властивості паралельних площин. Методичні особливості розв’язування задач на застосування правил паралельного проектування.
ТЕМА 25. Перпендикулярність прямої і площини
Методика формування поняття прямої перпендикулярної площині та перпендикулярних прямих у просторі.
Методика вивчення ознаки перпендикулярності прямих у просторі та прямої перпендикулярної до площини.
Методика розв’язування задач на уявні побудови у просторі (прямої перпендикулярної площині, площини перпендикулярної прямій).
ТЕМА 26. Перпендикулярність площин у просторі
Методика вивчення означення перпендикулярності площин. Методика вивчення ознаки перпендикулярності двох площин. Методичні особливості розв’язування задач на перпендикулярність у просторі.
ТЕМА 27. Декартові координати і вектори у просторі
Методичні особливості введеняд екартових координат у просторі. Методика вивчення теорем про відстань між точками та координати середини відрізка. Методика розв’язування стереометричних задач координатним та векторним методом..
ТЕМА 28. Геометричні перетворення у просторі
Методика введення понять симетрії у просторі, паралельного перенесення, руху, подібності просторових фігур.
Методика вивчення властивостей руху та властивостей гомотетії. Методика розв’язування задач на перетворення у просторі.
ТЕМА 29. Многогранники та тіла обертання
Методика вивчення понять двогранних та многогранних кутів і многогранників та їх видів, циліндра, конуса, кулі, поняття дотичної площини до тіл обертання, вписаних та описаних многогранників.
Методика вивчення властивостей многогранників та способів їх доведень, теорем про переріз тіл обертання площиною. Методика розв’язування задач на тіла обертання.
Методика розв’язування задач на застосування властивостей многогранників та тіл обертання.
ТЕМА 30. Геометричні величини в стереометрії.
Об’єми та площі поверхонь просторових тіл
Методика формування поняття об’єму та площі поверхні просторових тіл.
Методика вивчення теорем про об’єми многогранників та тіл обертання та їх площ поверхонь. Методика розв’язування задач на обчислення об’ємів та площ поверхонь просторових тіл.
ЛІТЕРАТУРА:
Вища освіта України і Болонський процес: Навч. посіб. / За ред. В. Г. Кременя. Авт. колект.: М. Ф. Степко, Я. Я. Болюбаш, В. Д. Шинкарук, В. В. Грубіо, І. І. Бабин. — Тернопіль: Навч. книга - Богдан, 2004.
Глейзер Г.И. История математики в средней школе. - М., 1971.
Груденов Я.И. Совершенствование методики работы учителя
математики: Кн. для учителя. – М., 1990.
Державний загальноосвітній стандарт з математики (проект) // Математика в школі. – 2003, – № 1, С. 2-6.
Дубинчук О.С. та ін. Методичні особливості навчання геометрії в
середньому ПТУ: Посібник. - К., 1992.
Журавський В. С., Згуровський М. 3. Болонський процес: головні принципи входження в європейський простір вищої освіти. — К.: Політехніка, 2003.
Иржавцева В.П., Федченко Л.Я. Систематизация и обобщение знаний учащихся в процессе изучения математики. - К., 1988.
Концепція 12-річної середньої загальноосвітньої школи: Проект // http: // www.ime.edu-ua.net/kons.htm.
Лабораторные и практические работиы по методике преподавания математики. / Под ред. Е.Д. Лященко. - М., 1988.
Методика преподавания математики в средней школе. Частная методика / Сост. В.И. Мишин.- М., 1987.
Методика преподавания математики. Общая методика / Сост.: Р.С.
Черкасов, А.А. Столяр. - М., 1985.
Нелін Є.П., Дольова О.Є.. Алгебра і початки аналізу. Підручник. 11 клас.
Нелін Є.П.. Алгебра в таблицях. 7-11 кл., 2005.
Нелін Є.П.. Алгебра і початки аналізу. Підручник. 10 клас., 2004.
Нелін Є.П.. Геометрія в таблицях. 7-11 кл., 2005.
Осинская В.Н. Формирование умственной культуры учащихся в
процессе обучения математике. - К., 1989.
Погорєлов О.В. Геометрія: Стереометрія: Підруч. для 10-11 кл. серед. шк. – 4-те вид. – К.: Освіта, 1998. – 128 с.
Програми з математики для 5-12 класів середньої загальноосвітньої
школи. - К., 2006.
Рогановський Н.М. Методика преподавания математики в средней школе: Учеб. пособие. - Мн., 1990.
Слєпкань З.И. Психолого-педагогические основы обучения математике. - К., 1983.
Слєпкань З.І. Методика вивчення алгебри і початків аналізу. К. Р.Ш. 1978.
Слєпкань З.І. Методика навчання математики 2-ге видання доповнене і перероблене К., 2006.
Слєпкань З.І. Методика навчання математики К., 2002.
Тарасенкова Н.А., Акуленко І. Оцінювання навчальних досягнень студентів при вивченні дисципліни “Методика навчання математики”. – 2005, № 2, С. 5-11.
Тесленко И.Ф. и др. Методика преподавания планиметрии. - К.,
1986.
Шкіль М.І. та ін. Алгебра і початки аналізу: Підруч. для 10 кл. загальноосвіт. навч. закладів / М.І. Шкіль, З.І. Слєпкань, О.С. Дубінчук. – К.: Зодіак-ЕКО, 2003. – 272 с.
Шкіль М.І. та ін. Алгебра і початки аналізу: Підруч. для 11 кл. загальноосвіт. навч. закладів / М.І. Шкіль, З.І. Слєпкань, О.С. Дубінчук. – К.: Зодіак-ЕКО, 2003. – 384 с.
Шкіль М.І., Колесник Т.В., Хмара Т.М. Алгебра і початки аналізу: Експерим. навч. посібник для 10 кл. шк. з поглибл. вивченням математики і спеціалізов. шк. фізико-мат. профілю. – К.: Освіта, 1993. – 336 с.
Шкіль М.І., Колесник Т.В., Хмара Т.М. Алгебра і початки аналізу: Проб. підруч. для 11 кл. шк. та кл. з поглибл. вивченням математики. – К.: Освіта, 1994. – 304 с.
В. о. зав. кафедрою вищої математики,
доцент Астаф’єва М.М.