Задача монжа-канторовича и ее приложения в математической экономике

Вид материала

Задача

Содержание Cписок литературы

Подобный материал:

• Программа заседаний Секции Математической экономики Международной школы семинара «Методы, 32.87kb.
• Методические указания по производственной практике для студентов 5 курса специальности, 218.41kb.
• Методические указания к дипломному проектированию для студентов специальности 080801, 369.09kb.
• Методические указания к курсовому проектированию для студентов специальности 080801, 311.04kb.
• Задача и экономическая задача, 1378.27kb.
• Современные Аспекты математики гармонии и её приложения в экономике, естествознании,, 35.55kb.
• «Интеграция как условие повышения качества методико-математической подготовки студентов, 2052.62kb.
• Уравнения математической физики Лектор 2010/11 уч года д ф. м наук, и о. проф. Косимов, 67.08kb.
• Элементы математической логики, 189.46kb.
• Конспект лекций для 16-и часового курса начертальная геометрия издание 2-ое, 578.52kb.

ЗАДАЧА МОНЖА-КАНТОРОВИЧА И ЕЕ ПРИЛОЖЕНИЯ

В МАТЕМАТИЧЕСКОЙ ЭКОНОМИКЕ

КОНДРАКОВ Иван Александрович

E-mail: ivankondrakov@mail.ru

Научный руководитель: ШАНАНИН Александр Алексеевич

Кафедра Системного Анализа

Задача перемещения масс Монжа-Канторовича (ЗМК) – это обобщение задачи о "выемках и насыпях", поставленной Гаспаром Монжем еще в 1781 году. В работах В.Л. Левина по теории двойственности ЗМК (см., например, [1]) получены эффективные средства исследования систем неравенств, которые, как показано в [2], возникают и в математической экономике. Целью дипломной работы является исследование приложений теории двойственности ЗМК в двух областях математической экономики: теории спроса и моделях неманипулируемых налоговых систем.

В дипломной работе:

• Подробно рассмотрено приложение теории двойственности ЗМК в теории спроса. Результаты, полученные с помощью ЗМК, оказываются обобщением теоремы Африата-Вериана о рационализируемости торговой статистики. Исследовано, какое место эти результаты занимают среди условий рационализируемости, рассмотренных, в [3]-[4]. Такое исследование проводилось впервые.
  
• Рассмотрены две модели неманипулируемых налоговых систем. В [2] описан общий подход к таким моделям, в дипломной работе подробно исследованы две модели, поставлена и решена задача максимизации собираемых налоговых поступлений.
  
• В первой модели агенты, характеризующиеся своих доходом, предоставляют информацию о нем в налоговые органы и на основе этих сведений платят налог. В случае указания ложных сведений и обнаружения несоответствия агенты будут обязаны заплатить штраф. Хотелось бы так взимать налоги, чтобы система была неманипулируемой, т.е. агенты не выигрывали, предоставляя ложные сведения. В гладком (вырожденном) и негладком (невырожденном) случаях исследованы условия неманипулируемости в терминах функций вероятности обнаружения 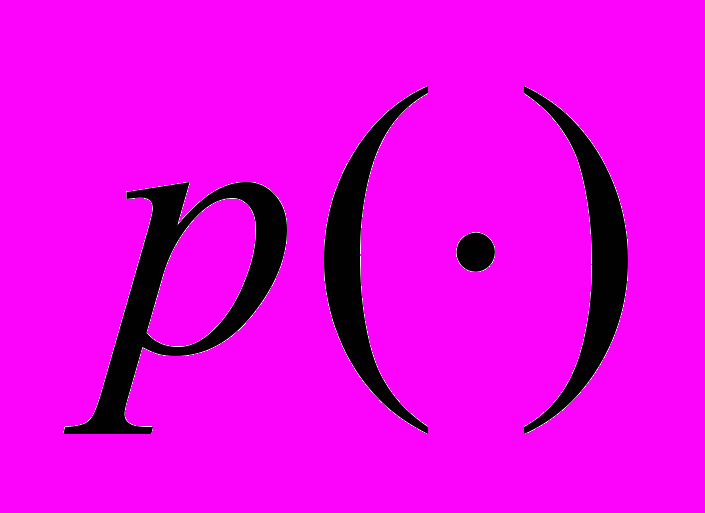и штрафа 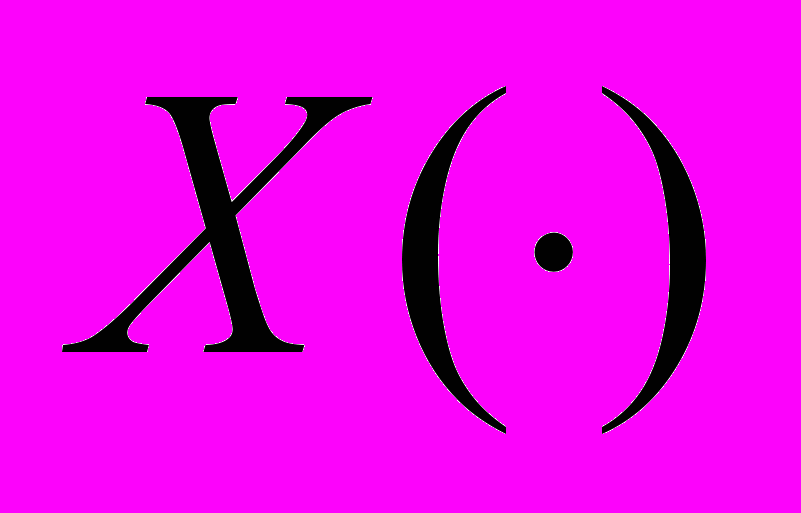. Поставлена и решена задача о максимизации взимаемых налогов.
  
• Во второй модели - модели Роше([7]) - государство распределяет некоторый ресурс, взимая за это налог. Можно, например, считать, что оно распределяет лицензии на добычу полезных ископаемых. С помощью теории двойственности ЗМК получено описание вида функций налоговых выплат при условии неманипулируемости.
  
• Поставлена и в одном случае решена задача максимизации налоговых поступлений при ограничении на количество ресурса у государства. При исследовании зависимости общего сбора налогов от величины доступного ресурса выявлен эффект насыщения, характеризующий эффективность всей системы. Начиная с некоторого момента государству не выгодно распределять весь ресурс, что связано с падением доходов агентов из-за быстро растущих издержек на добычу.
  

Работа имеет форму законченного исследования. Исследования в теории спроса планируется применить при разработке программного комплекса анализа торговой статистики на основе обобщенного непараметрического метода.

CПИСОК ЛИТЕРАТУРЫ

1. Levin V.L. A method in demand analysis connected with the Monge-Kantorovich problem. // Advances in mathematical economics. Springer-Verlag, 2005, p.47-93
   
2. Carlier, G., Ekeland, I., Levin, V.L., Shananin, A.A.: A system of inequalities arising in mathematical economics and connected with the Monge-Kantorovich problem. Ceremade-UMR 7534-Universite Paris Dauphine, No 0213, 3 Mai 2002
   
3. Корнюшина Д.С., Шананин А.А. О рационализируемости функций спроса в классе гладких положительно однородных функций полезности.
   
4. Поспелова Л.Я., Шананин А.А. Показатели нерациональности потребительского поведения и обобщенный непараметрический метод // Математическое моделирование, 1998, Т.10, №4, с.105-116.
   
5. Lawrence C. Evans. Partial Differential Equations and Monge-Kantorovich Mass Transfer // Current Developments in Mathematics, 1997.
   
6. Rochet J.-C. A necessary and sufficient condition for rationalizability in a quasi-linear context. // Journal of Mathematical Economics, v. 16, 1987, 191-200
   
7. Rochet J.-C. The taxation principle and multi-time Hamilton-Jacobi equations. // Journal of Mathematical Economics, v. 14, 1985, 113-128
   
8. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. Москва, "Наука", 1983.
   
9. Monge G. Memoire sur la Theorie des Deblais et des Remblais, Histoire de l’Academie Des Sciences de Paris, 1781.