Міністерство освіти І науки України Чернівецький національний університет імені Юрія Федьковича Факультет прикладної математики Підготовка фахівців освітньо-кваліфікаційного рівня
| Вид материала | Документы |
- Міністерство освіти І науки, молоді та спорту України Чернівецький національний університет, 455.37kb.
- Міністерство освіти І науки, молоді та спорту України Чернівецький національний університет, 479.77kb.
- Міністерство освіти І науки україни чернівецький національний університет імені юрія, 5658.45kb.
- Міністерство освіти І науки україни чернівецький національний університет імені юрія, 3398.91kb.
- Міністерство освіти І науки україни чернівецький національний університет імені юрія, 5355.91kb.
- Міністерство освіти І науки україни чернівецький національний університет імені юрія, 4781.7kb.
- Міністерство освіти І науки україни чернівецький національний університет імені юрія, 8176.59kb.
- Міністерство освіти І науки україни чернівецький національний університет імені юрія, 3361.25kb.
- Міністерство освіти І науки україни чернівецький національний університет імені юрія, 3131.05kb.
- Міністерство освіти І науки україни чернівецький національний університет імені юрія, 2382.22kb.
НЕ 4.2. Простори основних та узагальнених елементів
Простори
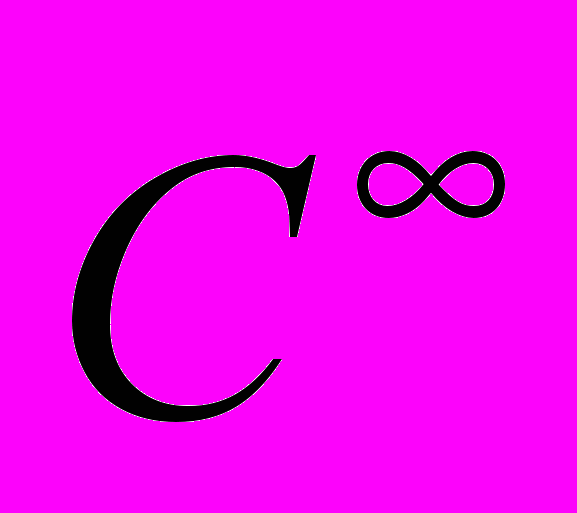-векторів самоспряженого оператора та спряжені до них. Індуктивні та проективні границі гільбертових просторів, пов’язаних ланцюжком. Означення та властивості аналітичних векторів самоспряженого оператора. Топологічна структура простору аналітичних векторів. Класи Жере самоспряженого оператора. Приклади.Основна література до дисципліни:
- Горбачук В.И., Горбачук М.В. Граничные задачи для дифференциально-операторных управлений. – К.: Наукова думка, 1984. – 284с.
- Березанский Ю.М., Ус Г.Ф., Шефтель З.Г. Функциональный анализ. Курс лекций. – К.: Вища школа, 1990. – 600с.
- Городецький В.В., Нагнибіда М.І., Настасієв П.П. Методи розв’язування задач з функціонального аналізу. Частина перша. – Київ: Ін-т математики НАН України, 1997. – 295с.
- Городецький В.В., Нагнибіда М.І., Настасієв П.П. Методи розв’язування задач з функціонального аналізу. Частина друга. – Київ: Ін-т математики НАН України, 1997. – 316с.
«Еволюційні рівняння та їх застосування»
135 год. (4 кредити)
Еволюційні рівняння як скінченного, так і нескінченного порядків широко використовуються при математичному моделюванні різних реальних процесів, при розв’язуванні задач математичної фізики, при вивченні багатьох процесів у хімії, біології тощо. За допомогою таких рівнянь описуються різні складні явища в сучасному природознавстві, економіці, техніці.
Метою викладання дисципліни є ґрунтовне засвоєння студентами теоретичного матеріалу, формування навичок застосування набутих знань при дослідженні теоретичних питань і прикладних задач.
У результаті вивчення дисципліни студенти повинні набути таких компетенцій:
знання:
основних класів розв’язності еволюційних рівнянь скінченного та нескінченного порядків, методів дослідження задачі Коші для таких рівнянь, структури та властивостей фундаментальних розв’язків;
уміння:
застосовувати набуті знання при розв’язуванні задач, які можуть зустрітися у практичній діяльності за обраною спеціальністю.
Вивчення дисципліни здійснюється за двома змістовими модулями:
Змістовий модуль 1
«Простори основних та узагальнених функцій»
НЕ 1.1. Простір
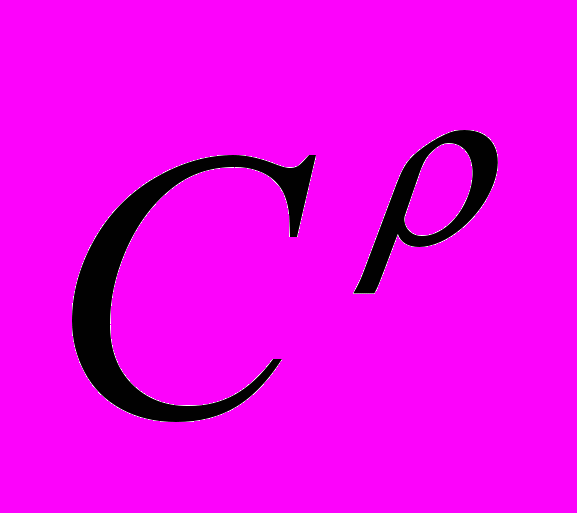. Простори 
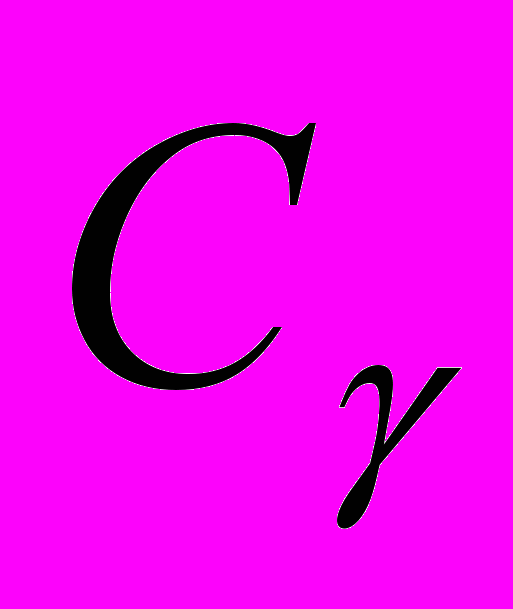та 
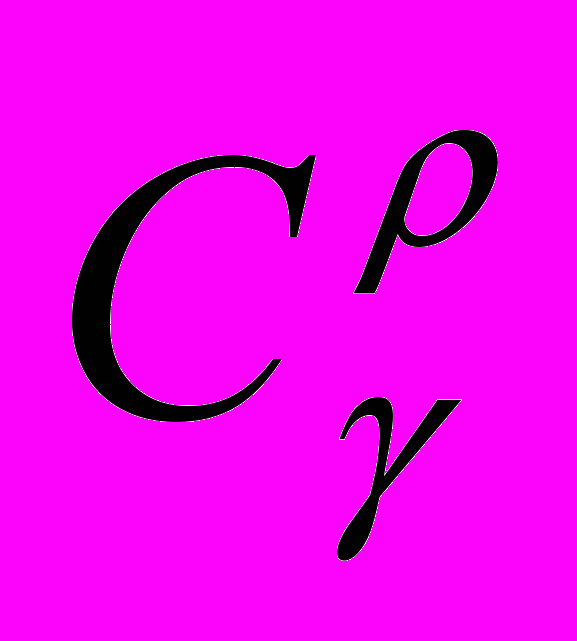
Означення простору
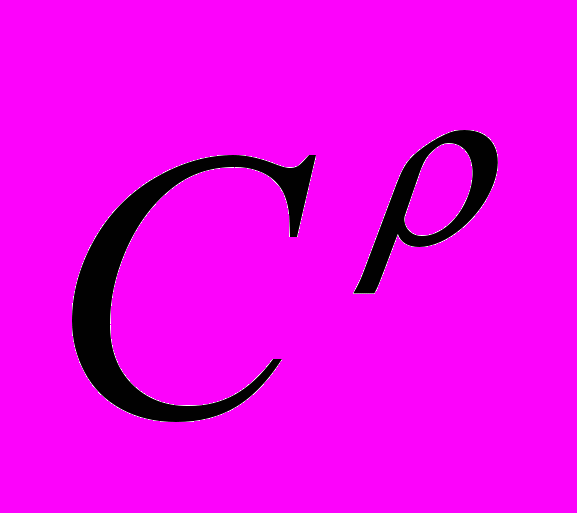. Приклади просторів 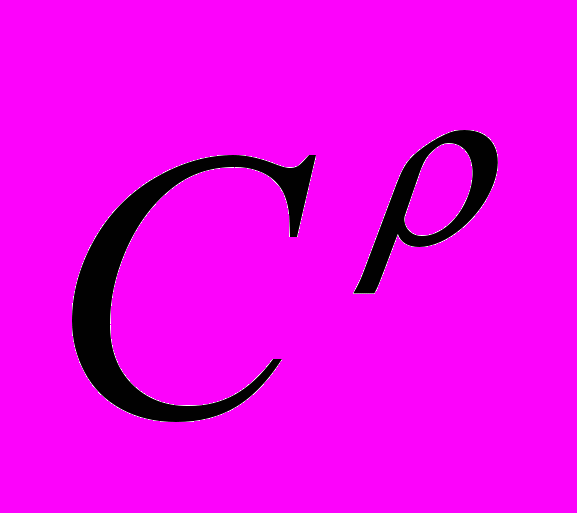. Основні операції в просторі 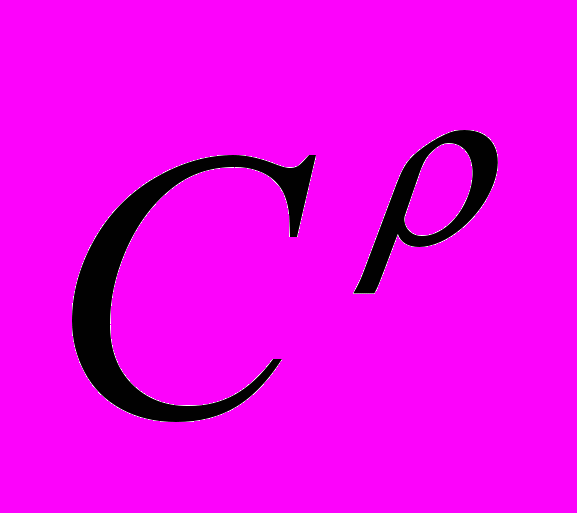(диференціювання, множення на незалежну змінну, зсуву аргументу). Означення просторів 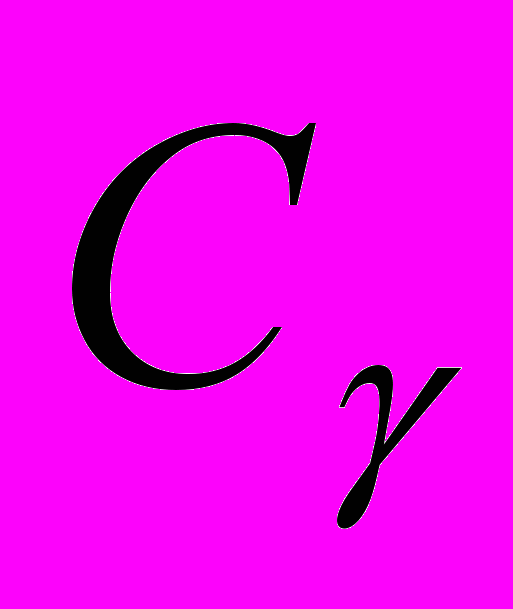та 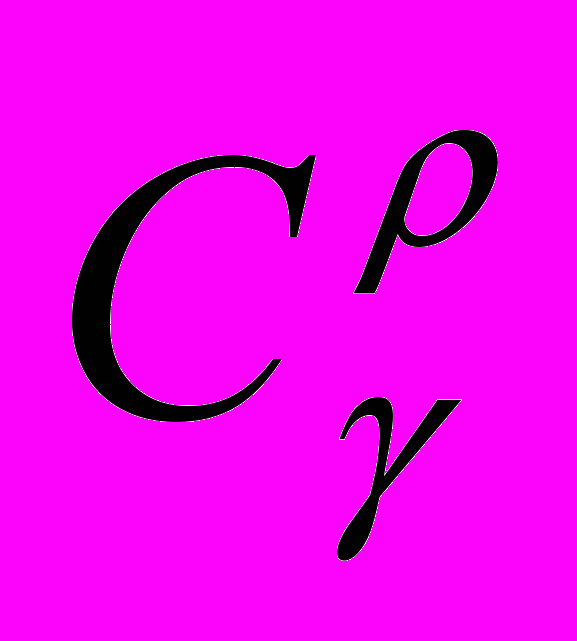, основні операції у цих просторах. Характеристика просторів 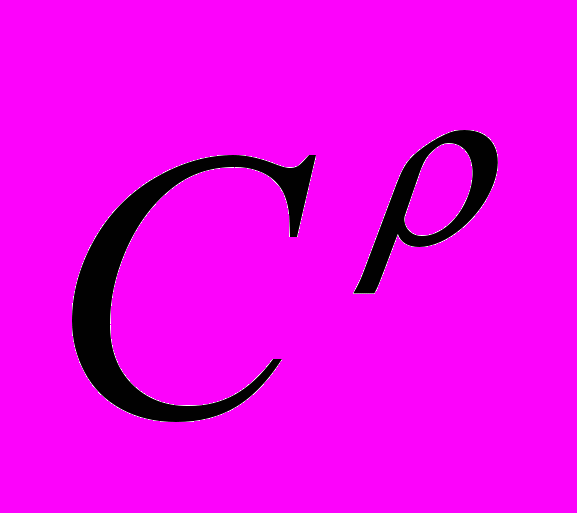,,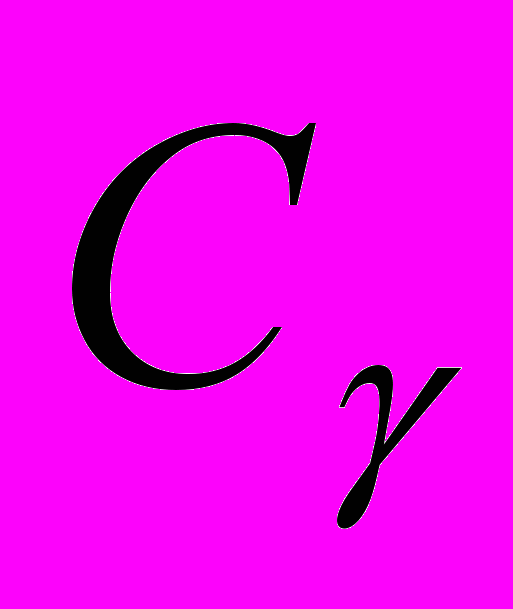 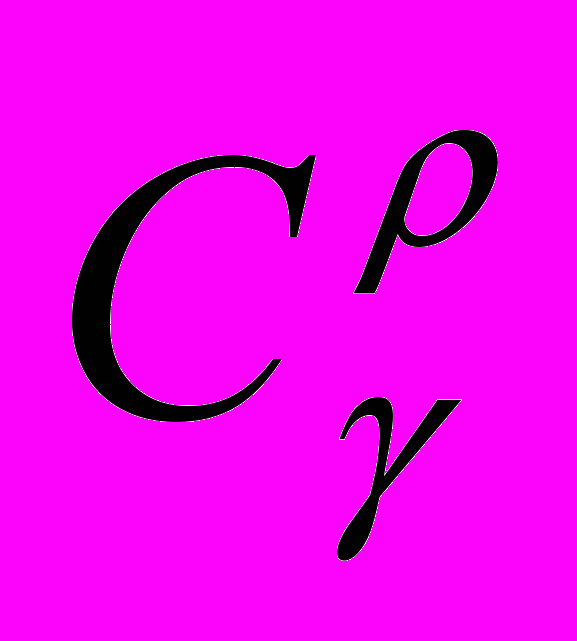у термінах поведінки похідних функцій з цих просторів на дійсній осі.НЕ 1.2. Перетворення Фур’є функцій з просторів типу С
Властивості перетворення Фур’є. Характеристика просторів Фур’є – образів у термінах двоїстих за Юнгом функцій. Перетворення Фур’є функцій з просторів типу S як функцій з просторів типу С.
НЕ 1.3. Оператори диференціювання нескінченного порядку в просторах типу С
Означення оператора диференціювання нескінченного порядку в просторах типу С. Критерій існування та неперервності такого оператора в просторах типу С. Побудова операторів диференціювання нескінченного порядку в просторах типу С за конкретними аналітичними функціями, які є мультиплікаторами в просторах типу С.
НЕ 1.4. Простори узагальнених функцій типу
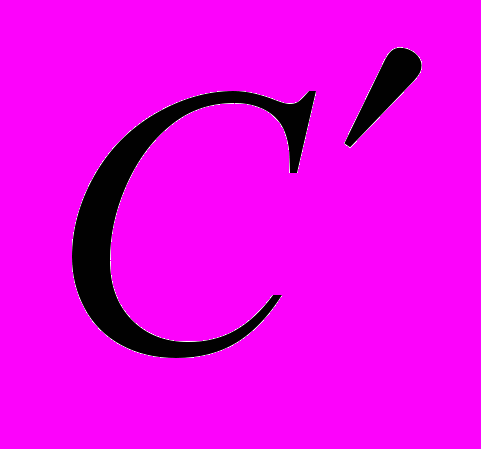
Згортка узагальнених функцій у просторах типу
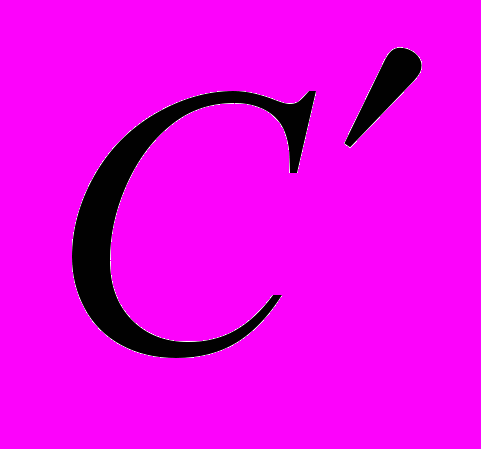. Перетворення Фур’є згортки. Згортувачі та мультиплікатори у просторах типу 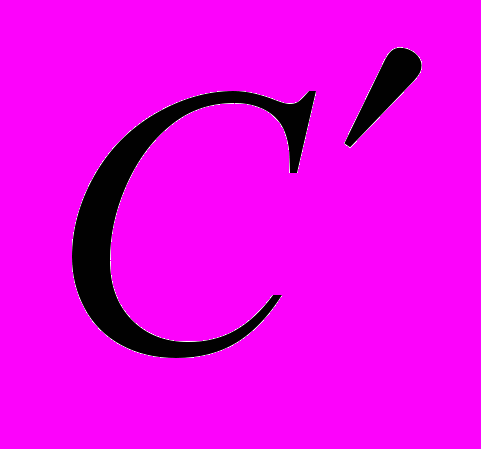. Приклади згортувачів та мультиплікаторів.Змістовий модуль 2
«Еволюційні рівняння з оператором диференціювання нескінченного порядку»
НЕ 2.1. Властивості фундаментального розв’язку задачі Коші
Оцінки похідних фундаментального розв’язку задачі Коші (ФРЗК). Диференційовність ФРЗК по часовій змінній як абстрактної функції параметра t. Оператор, спряжений до оператора диференціювання нескінченного порядку як псевдодиференціальний оператор, побудований за аналітичним символом.
НЕ 2.2. Коректна розв’язність задачі Коші
Встановлення коректної розв’язності задачі Коші у класі початкових умов, які є аналітичними функціоналами. Зображення розв’язку задачі Коші у вигляді згортки ФРЗК з початковою умовою. n-вимірний випадок.
Основна література до дисципліни:
- Городецький В.В. Задача Коші для еволюційних рівнянь нескінченного порядку. – Чернівці: Рута, 2005. – 291с.
- Городецький В.В. Еволюційні рівняння в зліченно-нормованих просторах нескінченно диференційовних функцій. – Чернівці: Рута, 2008. – 400с.
«Інваріантні многовиди динамічних систем»
135 год. (4 кредити)
Метою викладання дисципліни є засвоєння студентами теоретичного матеріалу, оволодіння методами розв’язування задач практики.
У результаті вивчення дисципліни студенти повинні набути таких компетенцій: знання фазових просторів та фазових кривих автономних систем, векторних полів на диференційованих многовидах, диффеоморфізмів та локальних координат в околі тороїдального многовиду, функції Гріна динамічної системи, уміння застосовувати набуті знання при розв’язуванні конкретних задач.
Вивчення дисципліни здійснюється за трьома змістовими модулями:
Змістовий модуль 1
«Векторні поля на прямій і на площині»
НЕ 1.1. Векторні поля на прямій
Фазові простори і фазові потоки. Приклади. Диффеоморфізми. Векторні поля. Інтегральні криві. Векторні поля на прямій. Основні теореми.
НЕ 1.2. Векторні поля на площині
Векторні поля на площині. Приклади векторних полів і фазових потоків на площині. Дотичний простір. Основні теореми.
Змістовий модуль 2
«Лінійні системи»
НЕ 2.1. Лінійні системи. Експонента
Лінійні системи. Експонента. Визначник експоненти, його властивості. Комплексифікація. Приклад лінійного рівняння, фазовий простір якого – комплексна пряма. Класифікація особливих точок на площині. Приклад маятника з тертям.
НЕ 2.2. Стійкість положення
Стійкість положення рівноваги. Асимптотична стійкість. Випадок чисто уявних власних чисел. Приклад однієї системи в
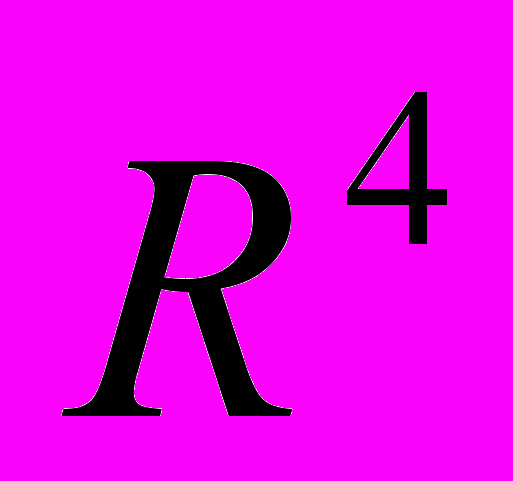(задача про тор). Локальні координати в околі тороїдального многовиду. Лінійні неавтономні рівняння з періодичними коефіцієнтами. Варіація сталих (неоднорідні рівняння).Змістовий модуль 3
«Інваріантні многовиди»
НЕ 3.1. Функція Гріна
Задача про обмежений інваріантний многовид динамічної системи. Функція Гріна. Основні властивості.
Основна література до дисципліни:
- Митропольский Ю.А., Лыкова О.Б. Интегральные многообразия в нелинейной механике. – М.: Наука, 1973. – 512с.
- Самойленко А.М. Элементы математической теории многочастотных колебаний. – М.: Наука, 1987. – 302с.
- Филлипов А.Ф. Сборник задач по дифференциальным уравнениям. – М.: Наука, 1992. – 128с.
Кафедра математичного аналізу
Спеціалізація: математичний аналіз
«Додатні оператори»
162 год. (5 кредитів)
Мета викладання дисципліни: вивчити поняття векторної ґратки і познайомитися з деякими розділами сучасної теорії такими як «Додатні оператори»; «Порядкова структура векторної ґратки»;розглянути різні теореми про продовження додатних операторів і зв’язок між порядково обмеженими та регулярними операторами;познайомитися з різними еквівалентними умовами порядкової збіжності напрямленостей у порядково повних векторних ґратках; вивчити умови порядкової збіжності послідовностей у деяких класичних векторних ґратках.
У результаті вивчення курсу студент має набути таких компетенцій: знати поняття векторної ґратки, додатного оператора, порядкової повноти векторної ґратки, порядкової збіжності напрямленості, банахової ґратки, тілесної множини, ідеалу і бенду у векторній ґратці; різні теореми про додатні і регулярні оператори; різні еквівалентні умови порядкової збіжності напрямленості у довільній порядково повній векторній ґратці, а також спеціальні умови порядкової збіжності послідовності у класичних ґратках
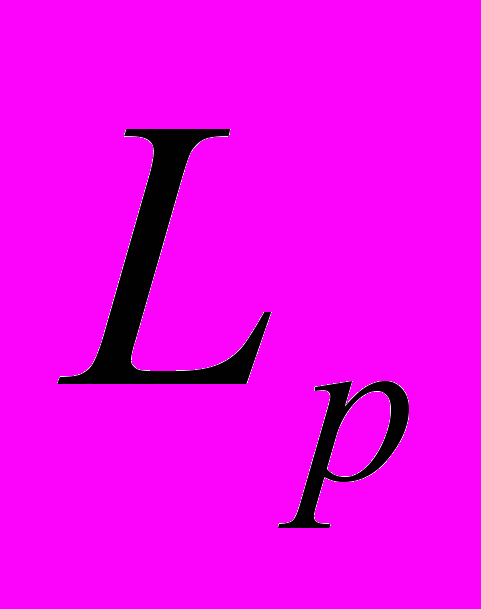при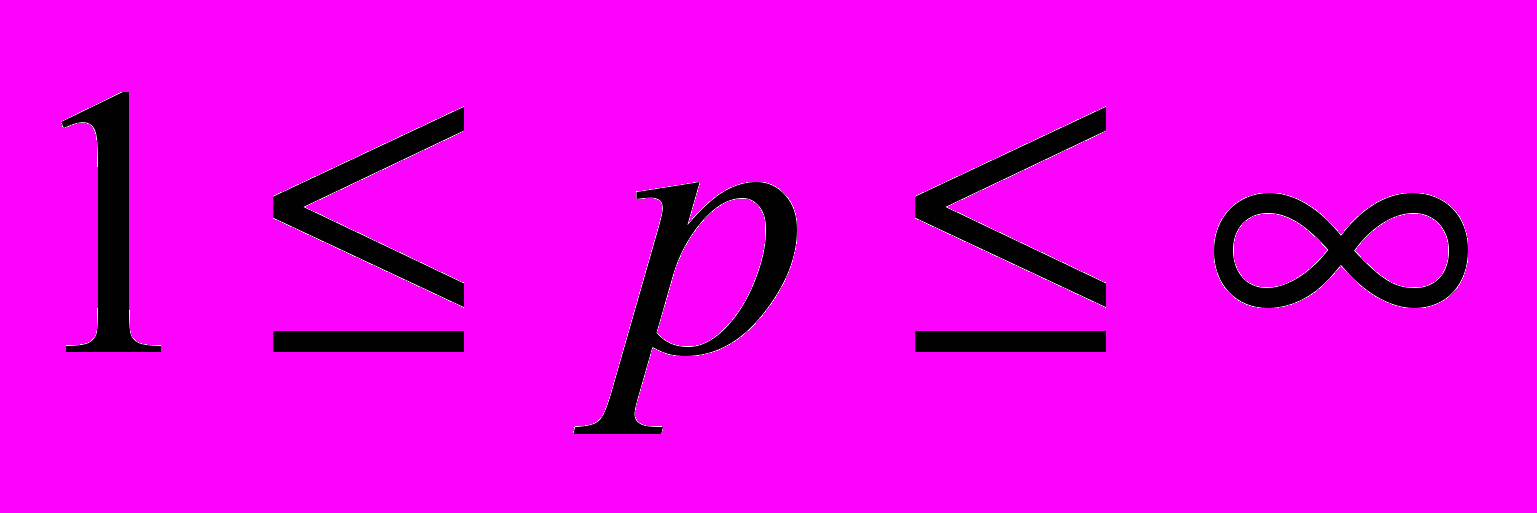 
; задачі про порядкову збіжність конкретних послідовностей у конкретних ґратках; уміти застосовувати поняття порядкової збіжності та прості факти про порядкову збіжність до дослідження порядкової сепарабельності і питань існування порядкових базисів у деяких класичних ґратках.Вивчення курсу здійснюється за двома змістовими модулями:
Змістовий модуль 1
«Лінійні оператори на векторних ґратках»
НЕ 1.1. Додатна, від’ємна частини і модуль елементів векторних ґраток. Означення векторної ґратки, приклади і елементарні властивості елементів. Різні тотожності і нерівності між додатною, від’ємною частиною і модулем елементів. Гра Шоке та ігрова характеризація беровості. Топологічні ігри. Повнота та зліченна повнота за Чехом. Компактифікація Стоуна Чеха. Паракомпактні простори і теорема Стоуна.
НЕ 1.2. Додатні і регулярні оператори. Теорема Канторовича про продовження. Архімедові векторні ґратки. Модуль оператора. Розкладна властивість векторних ґраток. Порядково повні векторні ґратки. Формули для модуля оператора. Приклади порядково повних і не порядково повних векторних ґраток. Порядково обмежені, додатні і регулярні оператори.
Змістовий модуль 2
«Порядкова структура векторних ґраток»
НЕ 2.1. Порядкова збіжність напрямленостей. Поняття порядкової збіжності; приклади. Порядкова обмеженість порядково збіжних послідовностей. Властивості збіжних напрямленостей та їх границь. Порядково неперервні відображення. Нижня і верхня границі порядково обмежених напрямленостей. Фундаментальні напрямленості. Критерій Коші порядкової збіжності напрямленостей.
НЕ 2.2. Банахові ґратки. Поняття банахової ґратки; приклади. Відносна порядкова збіжність послідовностей та її властивості. Зв’язок між відносно порядковою, порядковою і нормованою збіжністю у банахових ґратках. Граничний перехід у нерівностях. Додатні оператори в банахових ґратках.
НЕ 2.3. Порядкова структура ґраток
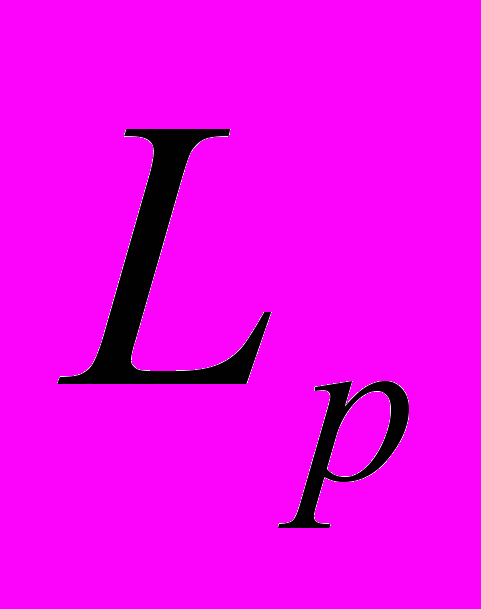при 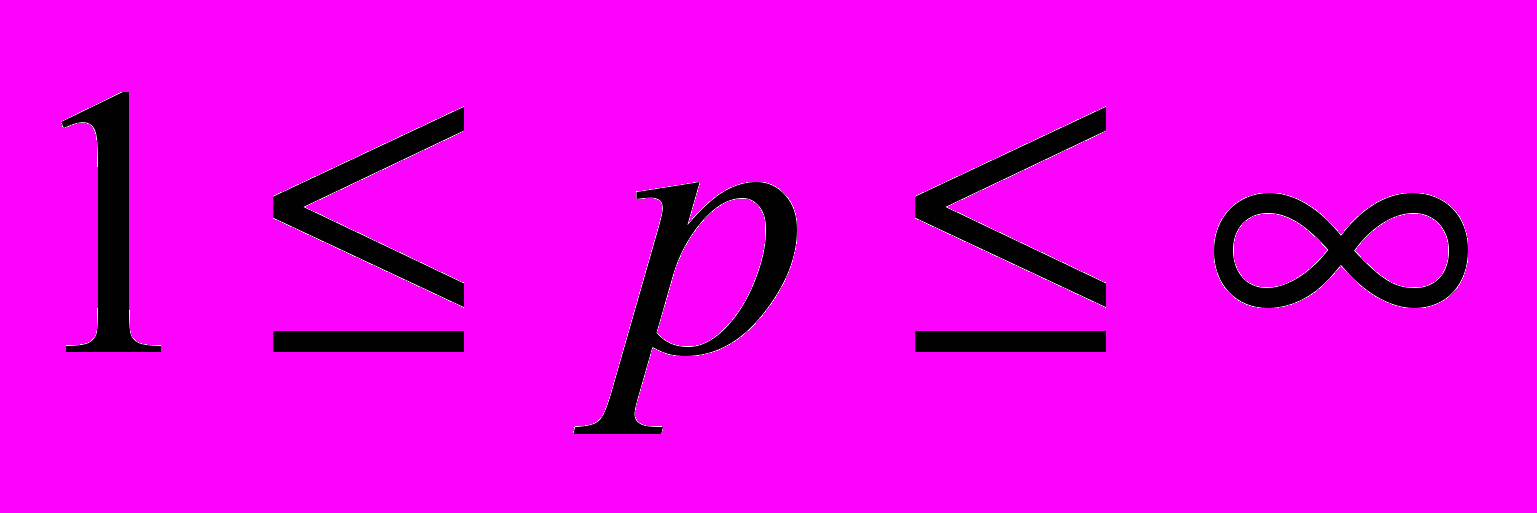. Характеризація порядкової збіжності в 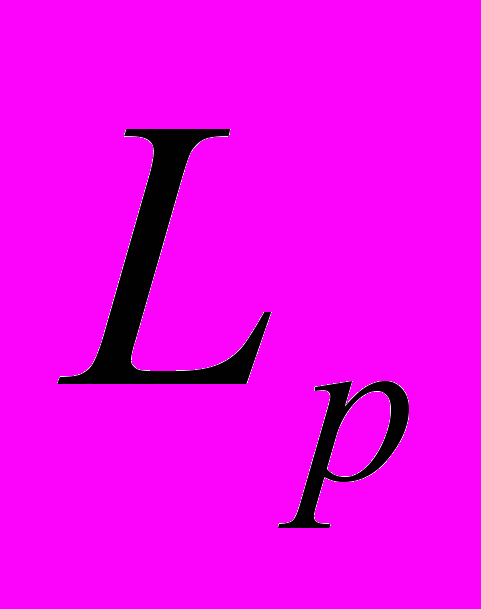. Зв’язок між відносно порядковою і нормованою збіжністю в 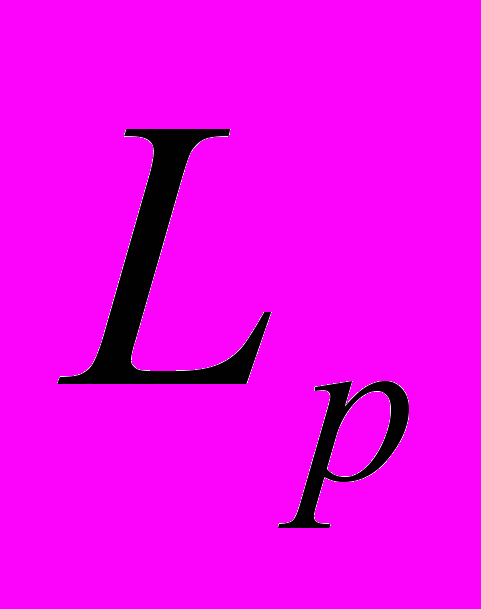. Порядкова сепарабельність ґраток 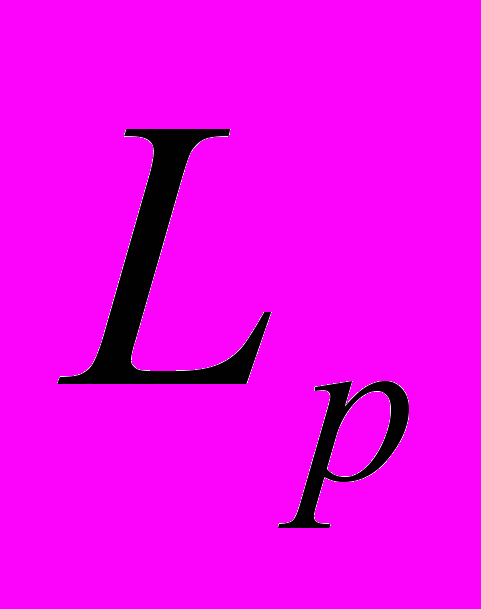при 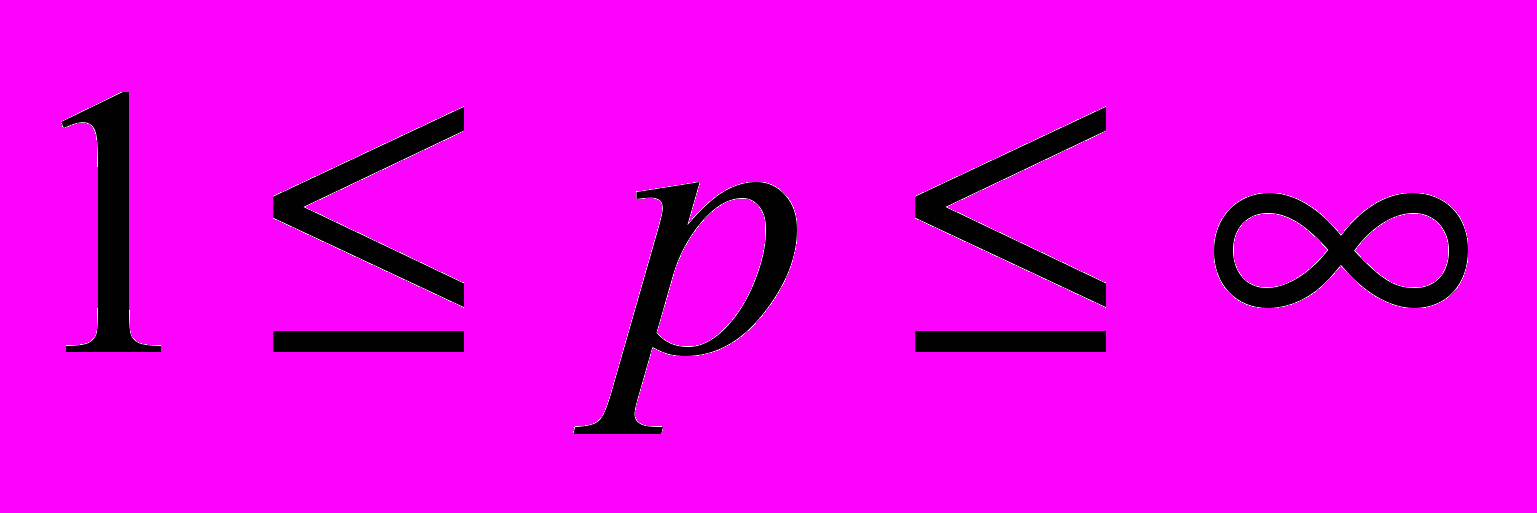. Порядкові базиси в ґратках 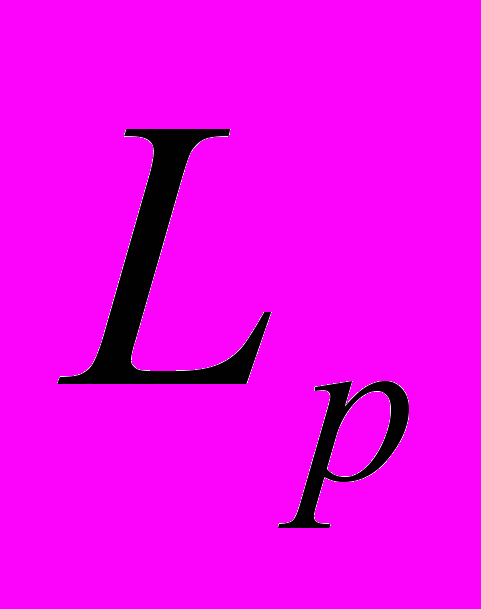при 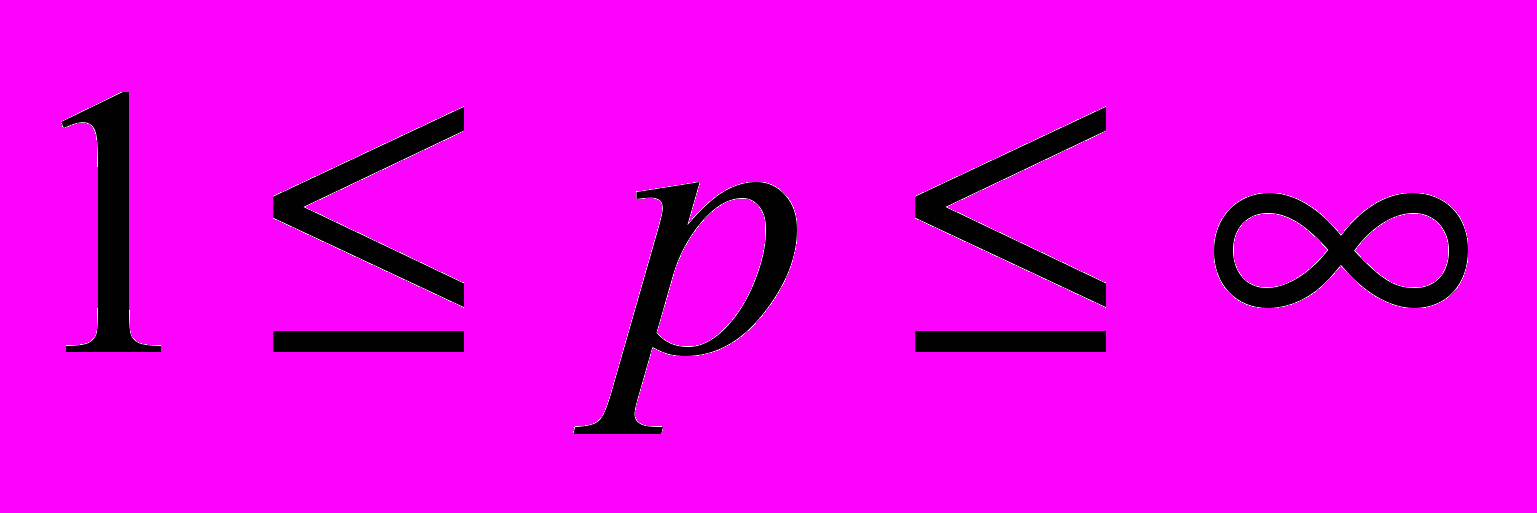.Основна література до курсу:
1. Aliprantis C.D., Burkinshaw O. Positive operators. – 1985. – Academic Press, Inc. – Orlando. – 367 p.
2. Біркгоф Г. Теория решеток. – 1948. – Радянська школа. – Киев 216с.
3. Канторович Л.В., Вулих В.З., Пинскер А.Г. Функциональный анализ в частично упорядоченных пространствах. – 1950. – Гос. изд-во техн.-теор. лит-ры. – Москва -Ленинград. – 550 с.
4. Schaefer H.H. Banach Lattices and Positive Operators. – 1974. – Springer. – Berlin etc. 376 p.
«Вибрані питання теорії операторів у просторах аналітичних функцій»
162 год. (5 кредитів)
Мета викладання дисципліни: ознайомити студентів з основними поняттями та базовими результатами теорії лінійних операторів у просторах аналітичних функцій; ознайомити студентів з різними методами розв’язування задач цієї теорії.
У результаті вивчення курсу студент має набути таких компетенцій: знати основні поняття та базові результати теорії лінійних операторів у просторах аналітичних функцій; уміти використовувати типові методи розв’язування задач теорії лінійних операторів у просторах аналітичних функцій.
Вивчення курсу здійснюється за двома змістовими модулями:
Змістовий модуль 1
« Простір
»НЕ 1.1. Топологічні поняття в просторі
. Простір . Збіжні послідовності в та їхня характеристика. Метризовність і повнота простору .НЕ 1.2. Повні системи в
. Умова неперервності та опис лінійних неперервних функціоналів на просторі . Спряжений простір до . Повні системи в . Критерій повноти С. Банаха. Умови повноти в деяких класичних систем аналітичних функцій. Змістовий модуль 2
«Лінійні неперервні оператори в просторі
»НЕ 2.1. Умова неперервності операторів в
. Умова неперервності та опис лінійних неперервних операторів, що діють з 
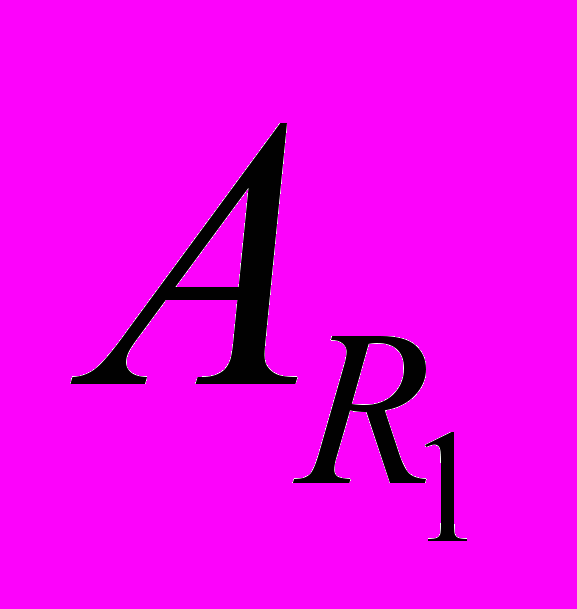в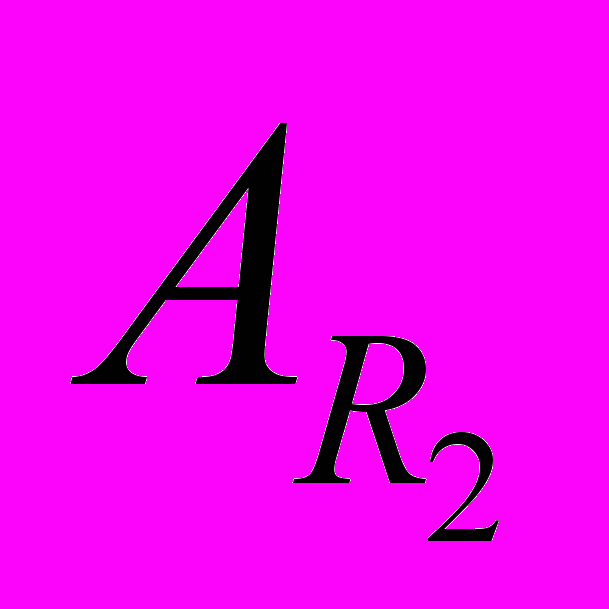 
. Оператори узагальненого диференціювання та узагальненого інтегрування і умови їхньої неперервності.НЕ 2.2. Комутанти деяких класичних операторів в
. Комутант операторів множення на незалежну змінну та інтегрування. Комутант степеня оператора інтегрування. Комутант оператора Помм’є.НЕ 2.3. Матричний опис лінійних неперервних операторів в
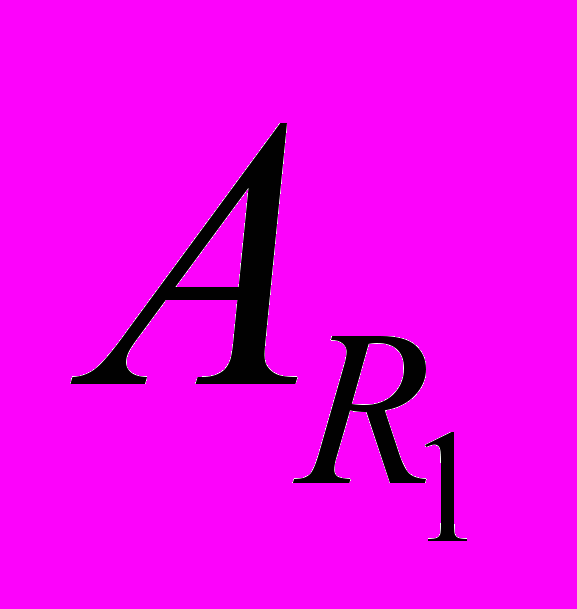. Матричний опис лінійних неперервних операторів, що діють з в 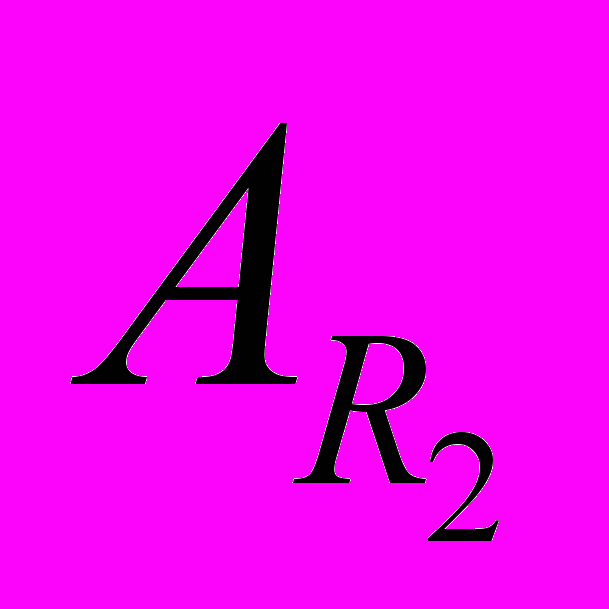. Застосування матричного опису операторів до знаходження комутантів операторів множення на незалежну змінну та диференціювання.НЕ 2.4. Квазістепеневі базиси в
. Базиси в . Ізоморфізми та квазістепеневі базиси в . Теорема Банаха про обернений оператор. Критерій квазістепеневої базисності систем. Умови квазістепеневої базисності деяких класичних систем аналітичних функцій. Теорема Пінкерле та її застосування.НЕ 2.5. Еквівалентні оператори в
. Еквівалентні оператори в . Необхідні умови еквівалентності операторів. Умови еквівалентності операторів узагальненого диференціювання.Основна література до курсу:
- Хавин В.П. Пространства аналитических функций. – В кн.: Итоги науки, математический анализ. – М.: Наука, 1966.– 237 с.
- Маркушевич А.И. Теория аналитических функций. Т.1. – М.: Наука, 1967.– 488 с.
- Маркушевич А.И. Теория аналитических функций. Т.2. – М.: Наука, 1968.– 624 с.
- Нагнибіда М.І. Класичні оператори в просторах аналітичних функцій. – К.: Ін-т математики НАН України, 1995.– 297с.
- Леонтьев А.Ф. Целые функции. Ряды экспонент. – М.: Наука, 1983.– 176 с.
- Эдвардс Р. Функциональный анализ. – М.: Мир, 1969.– 1071 с.
- Методичні вказівки та завдання для самостійної роботи з теорії лінійних операторів в аналітичних просторах. – Чернівці, ЧДУ, 1986. – 48 с.
- Драгилев М.М. Базисы в пространствах Кете. – Ростов н/Д: Изд-во Рост. ун-та, 1983.– 144 с.
- Ибрагимов И.И., Нагнибида Н.И. Матричный метод и квазистепенные базисы в пространстве аналитических в круге функций // Успехи мат. наук. – 1975.– 30, №6.– С. 101-146.
- Коробейник Ю.Ф. Операторы сдвига на числовых семействах.– Ростов н/Д: Изд-во Рост. ун-та, 1983.– 160 с.
- Леонтьев А.Ф. Обобщения рядов экспонент. – М.: Наука, 1981.– 320 с.
- Нагнибіда М.І. Інтегральні оператори в просторі аналітичних функцій. –Чернівці: Рута, 1996.– 69 с.
- Нагнибіда М.І. Оператори Помм'є в просторі аналітичних у крузі функцій. – К.: Ін-т математики НАН України, 1997.– 125 с.
«Нарізні і сукупні властивості функцій багатьох змінних»
189 год. (5 кредитів)
Мета викладання дисципліни: вивчити поняття берівського простору і познайомитися з різними топологічними іграми;
розглянути різні теореми про сукупну неперервність нарізно неперервних функцій двох змінних;
познайомитися з різними типами квазінеперервності та їх застосуваннями до дослідження нарізно неперервних функцій багатьох змінних на сукупну неперервність;
вивчити обернені задачі для нарізно неперервних відображень;
познайомитись з теоремами про берівську та лебеґівську класифікацію нарізно неперервних відображень.
У результаті вивчення курсу студент має набути таких компетенцій: знати поняття берівського простору і різні топологічні ігри; різні теореми про сукупну неперервність нарізно неперервних функцій двох змінних; різні типи квазінеперервності та їх застосуваннями до дослідження нарізно неперервних функцій багатьох змінних на сукупну неперервність; обернені задачі для нарізно неперервних відображень; теореми про берівську та лебеґівську класифікацію нарізно неперервних відображень; уміти застосовувати поняття берівського простору і топологічних ігор в теорії нарізно неперервних відображень; використовувати різні теореми про сукупну неперервність нарізно неперервних функцій двох змінних; застосовувати квазінеперервність до дослідження нарізно неперервних функцій багатьох змінних на сукупну неперервність; розв’язувати обернені задачі для нарізно неперервних відображень; доводити теореми про берівську та лебеґівську класифікацію нарізно неперервних відображень.
Вивчення курсу здійснюється за двома змістовими модулями: