Програма вступних іспитів до Інституту інформатики І штучного інтелекту за спеціальністю 04030301(спеціаліст), 04030301(магістр)
| Вид материала | Документы |
Содержание2. Критерії оцінювання 3. Перелік рекомендованої літератури |
- Програма вступних іспитів зі спеціальності «Психологія» на кваліфікаційний рівень «Магістр», 323.92kb.
- Програма фахового вступного випробування на навчання за освітньо-професійною програмою, 279.92kb.
- Програма фахового вступного випробування для навчання за освітньо-кваліфікаційним рівнем, 274.89kb.
- Програма вступних випробувань за спеціальністю «Облік І аудит» «спеціаліст» І «магістр», 898.78kb.
- Програма фахових вступних випробувань для проведення вступних випробувань при вступі, 339.95kb.
- Програма фахового вступного випробування для вступу на навчання за освітньо-кваліфікаційними, 120.12kb.
- Програма фахового вступного випробування для навчання за освітньо-кваліфікаційним рівнем, 329.95kb.
- Програма фахового вступного випробування для участі в конкурсі щодо зарахування, 455.41kb.
- Програма фахових вступних випробувань для зарахування на навчання за освітньо-кваліфікаційним, 368.34kb.
- Програма вступних іспитів на окп «спеціаліст» за фахом «Економіка підприємства», 233.08kb.
Затверджено:
Ректор ДонНТУ,
проф. О.А.Мінаєв
__________________
«___»____________ 201__ р.
Програма вступних іспитів до
Інституту інформатики і штучного інтелекту
за спеціальністю 7.04030301(спеціаліст), 8.04030301(магістр)
«Системний аналіз і управління»
Затверджено на засіданні кафедри САМ
Протокол № ___ від «___»___________201__р.
Зав.каф.САМ _____________
Програма складена для студентів, що отримали освітньо-кваліфікаційний рівень «бакалавр» за напрямом підготовки 0403 «Системні науки та кібернетика» і мають бажання продовжити навчання за спеціальністю «Системний аналіз і управління» з метою отримання освітньо-кваліфікаційного рівня «спеціаліст», «магістр».
До програми внесені основні розділи дисциплін, що визначають зміст даної спеціальності і вивчались студентами під час отримання освітньо-кваліфікаційного рівня «бакалавр» за напрямом підготовки 0403 «Системні науки та кібернетика»:
- математичний аналіз;
- функціональний аналіз;
- дискретна математика;
- теорія ймовірностей та математична статистика;
- диференціальні рівняння;
- програмування та алгоритмічні мови;
- організація баз даних та знань;
- чисельні методи;
- методи оптимізації та дослідження операцій;
- моделювання складних систем;
- основи системного аналізу;
- теорія керування.
У програмі також наведені критерії оцінювання результатів вступних випробувань та перелік рекомендованої літератури.
1. Програма вступних іспитів
Дисципліна «Математичний аналіз»
- Обчислення границі функції у точці.
- Границя відношення двох раціональних функцій.
- Таблиця еквівалентних функцій. Використання для знаходження границь.
- Класифікація точок розриву функції.
- Поняття диференційованості функції, зв’язок його с неперервністю.
- Диференціал функції. Визначення й обчислювальна формула.
- Правила обчислення похідної.
- Диференціювання елементарних функцій. Таблиця похідних.
- Похідні вищих порядків.
- Монотонність.
- Екстремум. Найбільше та найменше значення функції на відрізку.
- Основна таблиця інтегралів.
- Властивості невизначеного інтегралу.
- Метод заміни змінних для невизначеного інтегралу.
- Метод інтегрування частинами для невизначеного інтегралу.
- Інтегрування простих дробів.
- Формула Ньютона-Лейбніца.
- Площа фігури в декартових координатах.
- Диференційованість функції кількох змінних. Частинні похідні.
- Похідна за напрямком. Градієнт.
- Числові ряди. Збіжність, сума, необхідна умова збіжності.
- Ознаки порівняння збіжності рядів з додатними членами.
- Степеневі ряди. Ряди Тейлора й Маклорена.
- Стандартні розкладання деяких функцій у степеневі ряди.
- Подвійні інтеграли. Зміна послідовності інтегрування.
- Обчислення подвійних інтегралів двома послідовними інтегруваннями.
- Визначення комплексних чисел, властивості.
- Добуток й частка комплексних чисел в алгебраїчній формі.
- Тригонометрична форма комплексних чисел, зв’язок с алгебраїчною формою.
- Добуток й частка комплексних чисел у тригонометричній формі.
- Формула Муавра.
Дисципліна «Функціональний аналіз»
1. Метрика. Метричні простори. Збіжність. Фундаментальні послідовності.
2. Відкрита й замкнута куля, околиця, гранична точка, ізольована точка, замикання.
3 Відкриті й замкнуті множини. Повні та неповні простори.
4. Визначення стискаючого відображення у метричному просторі.
5 Принцип стискаючих відображень.
6. Лінійні простори. Норма. Нормовані простори, порівняння їх з метричними.
7. Скалярний добуток (над полем R). Евклідові простори.
8. Нерівність Коши-Буняковского. Кут між векторами. Ортогональні вектори.
9. Лінійні функціонали. Обмеженість й неперервність.
10. Лінійні оператори. Власні вектори й власні значення лінійного оператора.
Дисципліна «Дискретна математика»
- Множини. Операції над множинами.
- Властивості відношень. Рефлексивність, симетричність, транзитивність. Відношення еквівалентності.
- Розбиття на класи. Класи еквівалентності.
- Відношення порядку.
- Основний принцип комбінаторики.
- Скінчені множини. Правила додавання та добутку. З’єднання з повторами та без повторів.
- Перестановки. Принцип включення та виключення. Формула включень та виключень. Окремі випадки.
- Функції алгебри логіки. Формули. Реалізація функцій формулами.
- Принцип двоїстості.
- Розкладання булевих функцій за змінними. Досконала диз’юнктивна нормальна форма.
- Приведення до досконалої диз’юнктивної нормальної форми.
- Повнота та замкненість. Найважливіші замкнені класи.
Дисципліна «Теорія ймовірностей та математична статистика»
- Випадкові події. Класи Подій.
- Операції над подіями.
- Класичне визначення ймовірності.
- Теореми додавання, множення та повної ймовірності.
- Повторення випробувань. Формула Бернуллі.
- Граничні формули Пуассона, Лапласа, Муавра-Лапласа.
- Способи завдання дискретної випадкової величини. Властивості закону розподілу. Числові характеристики.
- Завдання неперервної випадкової величини. Властивості функції розподілу F(x) і щільності розподілу f(x). Числові характеристики.
- Числові характеристики і властивості найважливіших дискретних розподілів (біноміального, Пуассону, геометричного та гіпергеометричного).
- Числові характеристики і властивості найважливіших неперервних розподілів (рівномірного, показникового, нормального).
Дисципліна «Диференціальні рівняння»
- Поняття звичайного диференціального рівняння.
- Загальний та частковий розв’язок диференціального рівняння.
- Рівняння з відокремлюваними змінними.
- Однорідне диференціальне рівняння.
- Лінійні рівняння першого порядку.
- Рівняння Бернуллі.
- Рівняння Ріккаті.
- Рівняння Лагранжа і Клеро.
- Рівняння у повних диференціалах.
- Найпростіші типи рівнянь, які є нерозв’язними відносно похідної
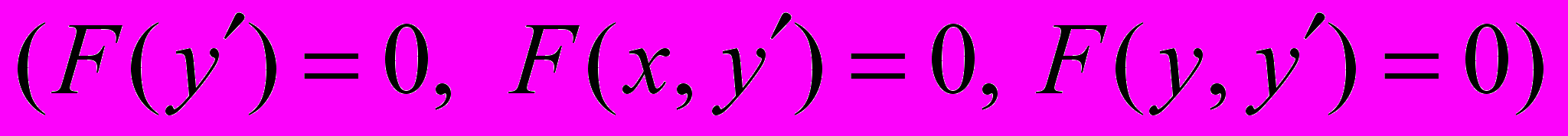 .
.
- Найпростіші випадки зниження порядку диференціальних рівнянь (4 випадки).
- Лінійні однорідні рівняння вищих порядків зі сталими коефіцієнтами.
- Рівняння Ейлера.
- Поняття характеристичного рівняння лінійного рівняння n–го порядку. Випадки:
а) різних дійсних коренів характеристичного рівняння;
б) дійсних кратних коренів характеристичного рівняння;
в) комплексно-спряжених коренів характеристичного рівняння.
- Знаходження часткового розв’язку неоднорідного лінійного рівняння вищого порядку методом невизначених коефіцієнтів:
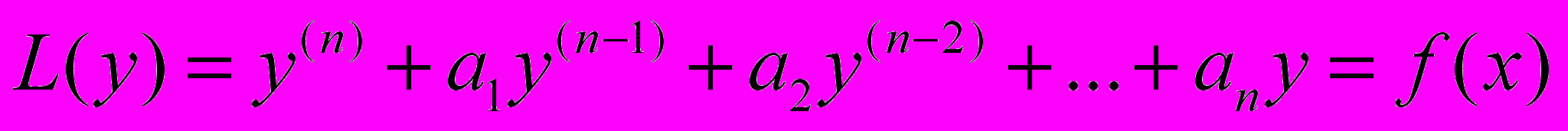
Випадки:
а)
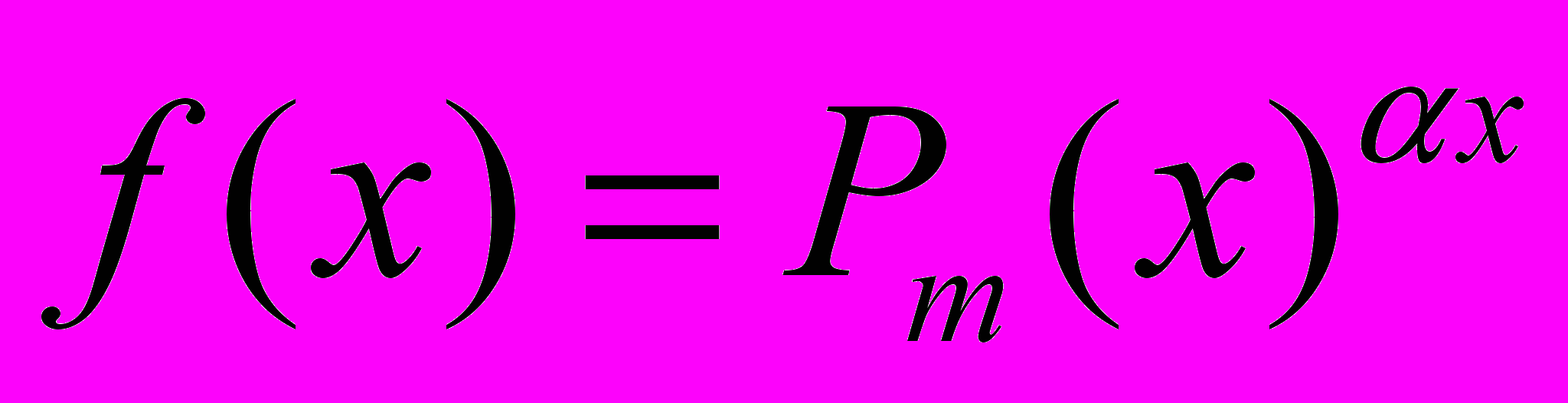 , де
, де 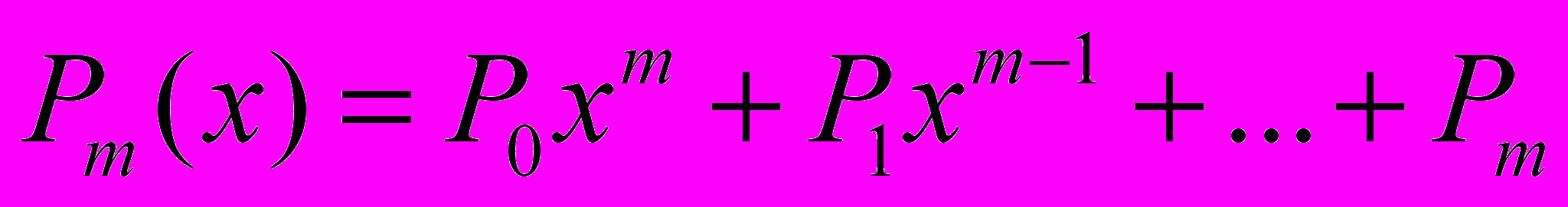 .
.б)
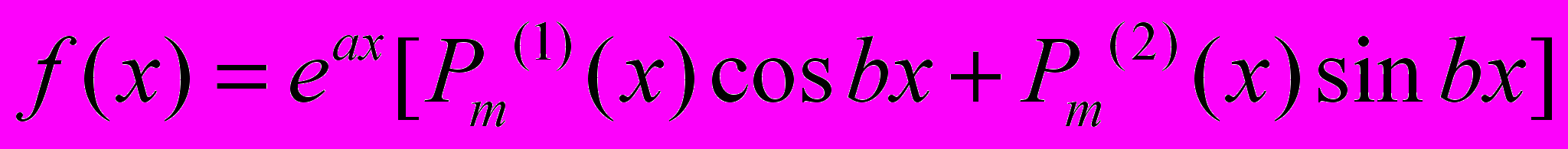 , де
, де 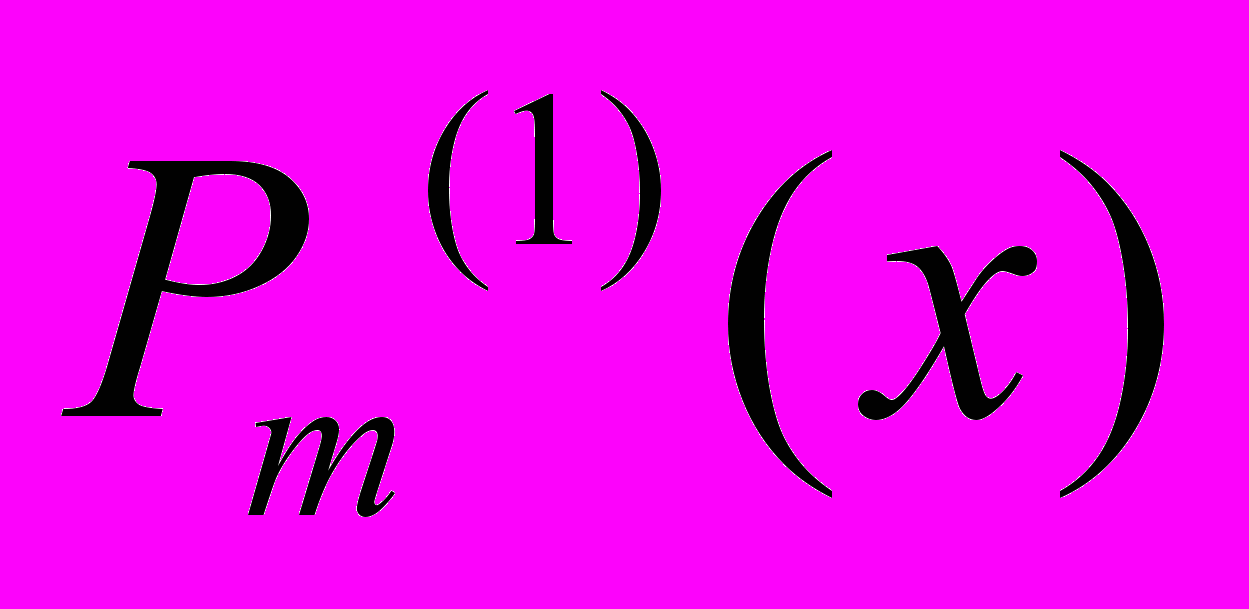 і
і 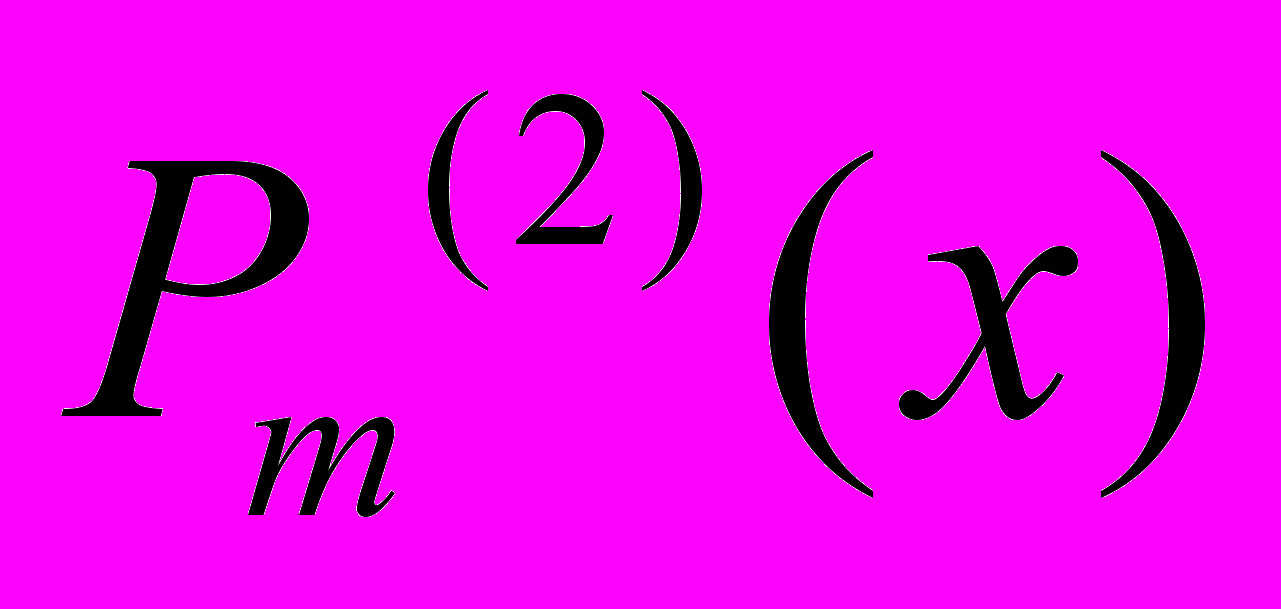 – задані поліноми від х степеню рівного або меншого за m.
– задані поліноми від х степеню рівного або меншого за m.Дисципліна «Програмування та алгоритмічні мови»
- Основні типи даних у С++.
- Змінні та операції в мові програмування С++.
- Побудова функцій в С++. Рекурсія. Перевантаження функцій і шаблони.
- Вказівники в С++.
- Масиви в С++.
- Препроцесор. Компіляція та виконання програм.
- Основи об’єктно-орієнтованого програмування.
- Складні структури даних (стек, дерево, черга)
Дисципліна «Організація баз даних та знань»
- Система баз даних. Призначення. Основні характеристики.
- Типи СУБД.
- Поняття СУБД.
- Реляційна система управління базами даних.
- Моделі даних
- Мова SQL (основні поняття)
- Потенційні ключі. Визначення. Призначення.
- Зовнішні ключі. Правила зовнішніх ключів.
- Null-значення. Особливості використання.
- Реляційна алгебра. Призначення і вживання.
- Реляційні операції.
- Нормальні форми. Основні поняття і призначення.
- Предмет вивчення і задачі науки СШІ.
- Визначення експертної системи. Основні елементи. Класифікація.
- Напрями СШІ
- Моделі представлення знань
- Інженерія знань
- Знання. властивості знань. Джерела знань. Стратеги здобуття знань.
Дисципліна «Чисельні методи»
- Апроксимація функцій.
- Побудова інтерполяційних поліномів.
- Методи розв’язання систем лінійних рівнянь алгебри.
- Чисельні методи розв’язання алгебраїчних і трансцендентних рівнянь.
- Методи чисельного інтегрування.
- Методи чисельного диференціювання.
- Методи розв’язання диференціальних рівнянь.
- Методи чисельного розв’язання задачі Коші.
Дисципліна «Методи оптимізації та дослідження операцій»
- Загальна постановка задачі оптимізації. Основні поняття та визначення: екстремум, градієнт, лінії рівня, матриця Гессе, унімодальна функція тощо.
- Необхідні та достатні умови існування безумовного екстремуму. Критерій Сильвестра.
- Класифікація задач математичного програмування.
- Задачі лінійного програмування (ЛП). Геометричне представлення і розв’язання задач ЛП. Симплекс-метод Данцига.
- Транспортна задача, стратегія її розв’язання. Методи північно-західного кута та мінімального елементу. Метод потенціалів.
- Методи одномірної мінімізації: метод дихотомії, золотого зрізу, Фібоначчі.
- Методи першого порядку: градієнтного спуску з постійним кроком, най скорішого градієнтного спуску.
- Методи другого порядку: метод Ньютона, метод Ньютона-Рафсона.
- Чисельні методи пошуку умовного екстремуму: метод штрафів, метод бар’єрних функцій.
Дисципліна «Моделювання складних систем»
- Основні поняття моделювання. Визначення і класифікація моделей.
- Методика математичного моделювання.
- Статичне статистичне моделювання (регресійний аналіз).
- Динамічне детерміноване моделювання.
- Імітаційне моделювання.
- Система імітаційного моделювання GPSS: основні об’єкти, оператори.
Дисципліна «Основи системного аналізу»
- Основні поняття та визначення системного аналізу.
- Властивості системи.
- Морфологічна модель системи: модель типу «чорний ящик», модель состава системи, модель структури системи.
- Функціональна модель системи: основні поняття, принципи розробки моделі з використанням IDEF-методології.
- Інформаційна модель системи: состав і структура моделі.
- Кваліметрична модель системи: основні поняття та визначення, шкали для вимірювання показників властивостей якості, модель оцінки якості системи.
- Порівнювальний аналіз формальних статичних моделей складної системи.
Дисципліна «Теорія керування»
- Визначення об’єкту управління.
- Математичні моделі лінійних неперервних елементів.
- Типові динамічні елементи.
- Типові закони управління.
- Аналіз лінійних неперервних систем управління.
- Аналіз нелінійних неперервних систем управління.
- Аналіз дискретних систем управління.
- Синтез систем управління.
- Адаптивні и робастні системи управління.
- Статистична динаміка систем управління.
2. Критерії оцінювання
Кожна тестова задача має 4 варіанти відповіді, із яких тільки один може бути вірним. За вірну відповідь на питання нараховується 1 бал, за невірну – 0 балів. Всього тест містить 80 задач. Сума балів S за вступний іспит визначається за формулою:
S=120+n,
де n – кількість вірних відповідей.
Максимальна кількість балів, яку можна отримати за вступне випробування дорівнює 200. Іспит вважається зданим на невід’ємну оцінку, якщо S ≥ 124.
3. Перелік рекомендованої літератури
- Шкіль М.І. Математичний аналіз: Підручник: У 2ч. Ч. 1. – К.: Вища шк., 2005. – 447с. Ч. 2. – К.: Вища шк., 2005. – 510с.
- Петренко И.В., Гладун А.В., Кравец Т.Н. Лекции и практикум по введению в математический анализ: Учебно-метод. пособие. – Донецьк: ІПШІ «Наука і освіта», 2010. – 84с.
- Гладун А.В., Кравец Т.Н., Беда Е.Н. Функции нескольких переменных: Учебное пособие. – Донецк: ИПИИ «Наука і освіта», 2008. – 74с.
- Колмогоров А.Н. Фомин С.В. Элементы теории функций и функционального анализа. М.: ФИЗМАТЛИТ, 2006. 572с.
- Яблонский С.В. Введение в дискретную математику.-М.:Высш.школа.; 2003.-384 с.
- Новиков Ф.А. Дискретная математика для программистов. С-т Петербург, 2000, -304 с.
- Теория вероятностей. Методическое пособие в двух частях. ( сост. Бархатова И.В., Кравец Т.Н., Грамотина О.В., Габриель Л.А.). – Донецк: ІПШІ «Наука і освіта», 2010, - Ч.1. – 112 с., Ч.2. – 128 с.
- В. И. Арнольд. Обыкновенные дифференциальные уравнения. М.: Наука, 1966.
- Л. Э. Эльсгольц. Дифференциальные уравнения и вариационное исчисление. М.: Наука, 1969.
- А. Ф. Филиппов Введение в теорию дифференциальных уравнений. - Изд. 2-е. - 2007. - 240 с.
- Гради Буч. Объектно-ориентированный анализ и проектирование с примерами приложений на С++, второе издание, Rational Санта-Клара, Калифорния.
- Иан Грэхем Объектно-ориентированные методы. Принципы и практика - Object-Oriented Methods: Principles & Practice. - 3-е изд. - М.: «Вильямс», 2004. - c. 880.
- Липпман, Стєнли, Б. Основы программирования на С++. –М.: Издательский дом „Вильямс”, 2002.
- Либерти, Джесс, Хорват, Дэвид. Освой самостоятельно С++ за 24 часа. –М.: Издательский дом „Вильямс”, 2007
- Д.Вейскас. Эффективная работа в Microsoft Access. Перевод с англ. -СпБ:Питер, 1995, -864с.
- Дейт., К.Дж. Введение в системы баз данных. Пер с англ. - 6-е изд.-К.: Диалектика, 1998, -784с.: ил.
- Системы управления базами данных и знаний. Справ. Изд./И.Н.Наумов, А.М.Вендров, В.Иванов/ Под ред. А.Н.Наумова.-М.:Финансы и статистика, 1998, -352с. :ил.
- Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. – М.: Высшая школа, 2005 г.
- Катренко А.В. Дослідження операцій: Підручник / За наук.ред. В.В.Пасічника. – Львів: «Магнолія 2006», 2007
- Таха, Хэмди А. Введение в исследование операций. М.: Изд. дом «Вильямс», 2001. – 912с.
- Банди Б. Методы оптимизации. Вводный курс. – М.: Радио и связь, 1988 г
- Советов Б.Я., Яковлев С.А. Моделирование систем: Учеб. для вузов. – М.: Высш.шк., 2001.– 343 с.
- Советов Б.Я., Яковлев С.А. Моделирование систем. Практикум: Учеб. пособие для вузов. – М.: Высш.шк., 2005.– 295 с.
- Томашевский В., Жданова Е. Имитационное моделирование в среде GPSS. − М.:Бестселлер, 2003. − 416 с
- Томашевский В.М. Моделирование систем. К.: BHV, 2005, -352с
- Тарасевич Ю.Ю. Математическое и компьютерное моделирование: Вводный курс. М.: УРСС, 2004.
- Згуровский М.З., Панкратова Н.Д. Основи системного аналізу. – К.: Видавнича група BHV, 2007. – 544 с.
- Лямец В.И., Тевяшев А.Д. Системный анализ. Вводный курс. – Харьков: ХНУРЭ, 2004. – 448 с.
- Бесекерский В.А. Теория систем автоматического управления. – СПб.: Профессия, 2003. – 752 с.
- Дорф Р., Бишоп Р. Современные системы управления. – М.: Лаборатория базовых знаний, 2002. – 832 с.
- Ким Д.П. Теория автоматического управления. Т.1: Линейные системы: Учебное пособие. – М.: Физматлит, 2003. – 288 с.
- Ким Д.П. Теория автоматического управления. Т.2: Многомерные, нелинейные, оптимальные и адаптивные системы: Учебное пособие. – М.: Физматлит, 2003. – 464 с.
- Резников В.А., Пряничникова Е.А. Теория автоматического управления: Методическое пособие к лабораторным и практическим занятиям для студентов специальности «Системы управления и автоматики». – Донецк: IПШI «Наука i освiта», 2008 – 84 с.
