Вестник Брянского государственного технического университета. 2011. №1(29)

Вид материала

Документы

Подобный материал:

• Вестник Брянского государственного технического университета. 2011. №4(32), 114.16kb.
• Вестник Брянского государственного технического университета. 2011. №3(31), 389.65kb.
• Вестник Брянского государственного технического университета. 2011. №3(31), 141.24kb.
• Вестник Брянского государственного технического университета. 2011. №2(30), 81.9kb.
• Вестник Брянского государственного технического университета. 2010. №2(26), 83.85kb.
• Вестник Брянского государственного технического университета. 2008. №1(17), 121.05kb.
• Вестник Брянского государственного технического университета. 2008. №3(19), 168.61kb.
• Вестник Брянского государственного технического университета. 2008. №3(19), 138.83kb.
• Вестник Брянского государственного технического университета. 2008. №3(19), 114.86kb.
• Вестник Брянского государственного технического университета. 2011. №2(30), 213.37kb.

УДК 621.865.8

О.Н.Крахмалев, А.П.Болдырев


МОДЕЛИРОВАНИЕ ОБОБЩЁННЫХ СИЛ,

ДЕЙСТВУЮЩИХ НА ЗВЕНЬЯ МАНИПУЛЯЦИОННЫХ СИСТЕМ


Получены в матричной форме аналитические выражения для определения обобщённых сил от основных силовых факторов, действующих на звенья манипуляционных систем. Сформирована правая часть уравнения движения манипуляционных систем.


Ключевые слова: манипуляционные системы, уравнение движения, обобщённые силы.


При моделировании динамики манипуляционных систем (МС) промышленных роботов (ПР) методом, основывающимся на уравнении Лагранжа 2-го рода, возникает необходимость в определении обобщённых сил, действующих на звенья МС. Математическая модель, в которой МС представлена системой твёрдых тел (СТТ), соединённых между собой кинематическими парами 5-го класса и образующих разомкнутую кинематическую цепь, имеет вид [1]


.. . . .

[M]{q} + [S]{q²} + 2[K]{q_iq_j} = {Q} , (1)




где [M], [S] и [K] – матричные коэффициенты, соответствующие инерционным свойствам моделируемой системы; {Q} - вектор обобщённых сил, действующих на звенья МС, элементами которого Q_i являются суммы всех обобщённых сил, действующих на систему, по соответствующей обобщённой координате q_i; i=(1,…,n), n – количество звеньев системы.

Каждый элемент вектора {Q} можно разложить на составляющие, определяемые основными силовыми факторами, действующими на систему и определяющими её динамику. Например,

Q_i= Q_Fi+ Q_Gi+ Q_Pi, i=(1,…,n),


где Q_Fi - обобщённая сила от внешних нагрузок (F); Q_Gi – обобщённая сила от сил тяжести звеньев (G); Q_Pi – усилие, развиваемое приводом i-го звена (Q_Pi=P_i), или векторно:


{Q} = {Q_F} + {Q_G} + {Q_P} .


Обобщённая сила Q_i, соответствующая координате q_i, определяется как коэффициент (скалярная величина) при вариации δq_i в выражении для элементарной работы δW всех приложенных к МС сил: δW=∑Q_iδq_i.

Определим обобщённую силу Q_i от действия внешних нагрузок (F). Заменим систему сил F_k, действующих на k-е звено, главным вектором R_k (R_k = ∑ F_k) и главным моментом M_k (M_k = ∑ r_kxF_k) [2]. За центр приведения удобнее всего принимать центр тяжести звена С, который будем определять расширенным радиусом-вектором r_ck^(k) в системе S_k. Главный вектор R_k и главный момент M_k в инерциальной системе координат S₀ будем представлять четырёхмерными векторами:


R_k = [R_kx R_ky R_kz 0 ]^T ,

M_k = [M_kx M_ky M_kz 0]^T .


Запишем выражения для элементарных работ, совершаемых главным вектором и главным моментом на возможном перемещении k-го звена:

δW_Rk = R_k δr_сk⁽⁰⁾,

δW_Mk = M_k δφ_k⁽⁰⁾,

где δr_сk⁽⁰⁾ – возможное перемещение центра тяжести k-го звена (точка приведения сил) в инерциальной системе координат S_0; δφ_k⁽⁰⁾ – возможный поворот k-го звена в инерциальной системе координат S₀ (вектор δφ_k коллинеарен вектору возможной угловой скорости δω_k k-го звена).

Выражение для возможных перемещений точек приложения сил получим из функции положения [3]. Для выбранной точки С, жёстко связанной с k-м звеном, функция положения имеет вид


_(o) _ _(k)

r_сk = A_оk(q) r_сk , (2)



где r_ck^(k)- расширенный (4х1) радиус-вектор точки C в системе координат S_k, связанной с k-м звеном (подвижная, неинерциальная система отсчёта); r_ck⁽⁰⁾- расширенный (4х1) радиус-вектор точки C в системе координат S₀, связанной с основанием (инерциальная система отсчёта); A_0k(q) – матрица (4х4) преобразования однородных координат, является функцией обобщённых координат q_i (i=1,…,k)) [4].

Из выражения (2) для функции положения точки С множество возможных перемещений δr_ck⁽⁰⁾ этой точки будет иметь вид




_(0) k ∂A_0k _(k)

δr_ck = ∑ −−− r_ck δq_i .

i = 1 ∂q_i





В развёрнутом виде векторы δr_сk^(о)и δφ_k^(о) могут быть представлены выражениями [5]



∂A_0k ∂A_0k ∂A_0k

δr_сk^(о) = ¯¯¯¯ r_сk^(k) δq₁ + ¯¯¯¯ r_сk^(k) δq₂ + … + ¯¯¯¯ r_сk^(k) δq_k ,

∂q₁ ∂q₂ ∂q_k




δφ_k^(o) = A₀₁Ө₁δq₁ + A₀₂Ө₂δq₂ + … + A_0kӨ_kδq_k .



Ө_i (i= (1,…,k)) представляет собой единичный вектор относительного поворота i-го звена и для принятого расширенного способа задания координат имеет вид


Ө_i = [0 0 δ_i 0]^T ,


г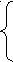де 1 – для вращательной кинематической пары;

δ_i =

0 – для поступательной кинематической пары.

С учётом изложенного, сгруппировав члены при δq_i (i=(1,…,k)), запишем выражение для элементарной работы δW_k внешних сил F_k, действующих на k-е звено, представленных главным вектором R_k и главным моментом M_k: δW_k= δW_Rk + δW_Mk , или

∂A_0k

δW_k = (R_k ¯¯¯¯ r_сk^(k) + M_k A₀₁Ө₁) δq₁ +

∂q₁


∂A_0k

+ (R_k ¯¯¯¯ r_сk^(k) + M_k A₀₂Ө₂) δq₂ + … + (3)

∂q₂


∂A_0k

+ (R_k ¯¯¯¯ r_сk^(k) + M_k A_0kӨ_k) δq_k ,

∂q_k


или в матричной записи с учётом свойства скалярного произведения двух векторов (V₁○V₂= tr[V₁V₂^T]=tr[V₂ V₁^T], tr - след матрицы):


∂A_0k

δW_k = tr [R_k r_сk^(k)T ¯¯¯¯ + M_k Ө₁^TA₀₁^T]δq₁ +

∂q₁


∂A_0k^T

+ tr [R_k r_сk^(k)T ¯¯¯¯ + M_k Ө₂^TA₀₂^T]δq₂ + … +

∂q₂


∂A_0k^T

+ tr [R_k r_сk^(k)T ¯¯¯¯ + M_k Ө_k^TA_0k^T]δq_k .

∂q_k


В окончательном виде элементарную работу внешних сил представим выражением


∂A_0k^T

δW_k = tr [F_Rk ¯¯¯¯ + F_1Mk A₀₁^T]δq₁ +

∂q₁

∂A_0k^T

+ tr [F_Rk ¯¯¯¯ + F_2Mk A₀₂^T]δq₂ + … + (4)

∂q₂

∂A_0k^T

+ tr [F_Rk ¯¯¯¯ + F_kMk A_0k^T]δq_{k ,}

∂q_k


где F_Rk и F_iMk - соответственно матрицы сил и моментов, определяемые выражениями

	Rkxxckk	Rkxyckk	Rkxzckk	Rkx
FRk = Rk rсk(k)T =	Rkyxckk	Rkyyckk	Rkyzckk	Rky	,
	Rkzxckk	Rkzyckk	Rkzzckk	Rkz
	0	0	0	0

	0	0	δi Mkx	0
FiMk = MkӨiT=	0	0	δi Mky	0	.
	0	0	δiMkz	0
	0	0	0	0

Обобщённая сила Q_i, отнесенная к соответствующей координате, равна коэффициенту перед вариацией δq_i (i=(1,…,n)) этой координаты. Следовательно, составляющие обобщённой силы Q_Fi (i=(1,…,n)) от действия внешних сил (F_k), представленных главным вектором R_k и главным моментом M_k (k=(1,…,n)), можно выделить из уравнения (3) в форме выражений, стоящих перед соответствующими вариациями обобщённых координат δq_i. Полная обобщённая сила Q_Fi от действия всей внешней нагрузки (F=∑F_k, k=(1,…,n)) вычисляется суммированием по всем звеньям МС соответствующих составляющих полной элементарной работы. Полная элементарная работа


δW = ∑δW_k= ∑Q_Fi δq_i , (k,i=(1,…,n)). (5)


Учитывая, что ∂A_0i/∂q_i+1= 0, выражение для Q_Fi можно представить в следующем виде:

n ∂A_0k^T

Q_Fi = ∑ tr [ F_Rk ¯¯¯¯ + F_iMk A_0i^T] . (6)

k = i ∂q_i

Выражение для вектора обобщённых сил от внешней нагрузки Q_F будет иметь вид

	n ∂A0iT ∑ tr [ FRi ¯¯¯¯ + F1Mi A01T] i =1 ∂q1
QF =	n ∂A0iT ∑ tr [ FRi ¯¯¯¯ + F2Mi A02T] i =2 ∂q2	. (7)
	. . . . . . . . . . .
	n ∂A0iT ∑ tr [ FRi ¯¯¯¯ + FnMi A0nT] i = n ∂qn

Если скалярное произведение векторов в выражении (3) для элементарной работы внешних сил, действующих на k-е звено, заменить на матричное произведение по правилу V₁○V₂= V₁^T V₂, то после суммирования по формуле (5) получим выражение для обобщённой силы от действия всей внешней нагрузки в виде


n ∂A_0k

Q_Fi = ∑ (R_k^T ¯¯¯¯ r_сk^(k) + M_k^TA₀₁Ө₁) . (8)

k = i ∂q₁


Выражение (8) имеет некоторые вычислительные преимущества перед выражением (6).

Обобщённые силы от действия консервативных (потенциальных) сил, к которым относятся силы тяжести звеньев и перемещаемого груза (инструмента), а также силы упругости, возникающие в элементах конструкции манипулятора, могут быть определены дифференцированием выражения для потенциальной энергии W МС по соответствующей обобщённой координате:

∂ W

Q_Wi = ¯¯¯ , i = (1, …,n) . (9)

∂q_i

Потенциальная энергия МС в гравитационном поле может быть представлена следующим выражением:


n n _ _

W = ∑ W_k = ∑ f_gk^(о) (A_0k r_сk ^(k)) , (10)

k=1 k=1



_ _

где r_сk ^(k) = [x_ck y_ck z_ck 1]^T – радиус- вектор центра тяжести k-го звена в системе S_k; f_gk^(о) = [f_gkx f_gky f_gkz 0]^T – вектор силы тяжести k-го звена в системе S_0.

З
n _ __{T T} n _T

W = ∑ tr [f_gk^(о) r_сk ^(k)A_0k] = ∑ tr [F_Gk A_0k] , (11)

k=1 k=1
аменим в выражении (10) скалярное произведение векторов его матричным представлением


где через F_Gk обозначена матрица силы тяжести k-го звена, определяемая следующим образом:

	fgkxxck	fgkxyck	fgkxzck	fgkx
FGk =	fgkyxck	fgkyyck	fgkyzck	fgky	. (12)
	fgkzxck	fgkzyck	fgkzzck	fgkz
	0	0	0	0

Для определения обобщённых сил от сил тяжести звеньев Q_Gi в уравнение (9) необходимо подставить выражение (11). С учётом выражения (12) получим


n ∂A_0k^T

Q_Gi = ∑ tr [F_Gk ¯¯¯¯ ] . (13)

k = i ∂q_i


Вектор обобщённых сил от сил тяжести Q_G с учётом полученного выражения (13) может быть представлен в матричном виде [см. выражение (7)]. Стоит отметить, что выражение (13) соответствует выражению (6) в части задания обобщённой силы от главных векторов внешней нагрузки. Поэтому, рассматривая силу тяжести как составляющую внешней нагрузки, для вычисления обобщённых сил можно использовать только общее выражение (6) или (8).

Обобщённые силы Q_P, соответствующие силам P_i (i=(1,…,n)), развиваемым приводами, равны самим этим силам, так как

δW_P = P₁δq₁ + P₂δq₂ + … + P_nδq_{n .}


Полную обобщённую силу, действующую на МС, будем обозначать вектором Q размерности nx1, элементами которого Q_i (i=(1,…,n)) являются суммы всех обобщённых сил, действующих на МС, по соответствующей обобщённой координате (q_i):

{Q} = {Q_F} + {Q_G} + {Q_P} .


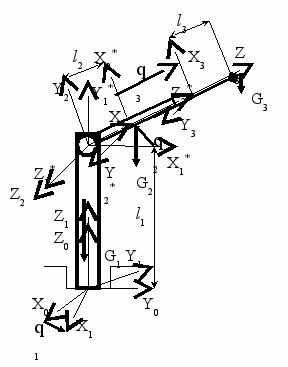
Рассмотрим использование полученных аналитических выражений для определения обобщённых сил от сил тяжести и внешней нагрузки на примере манипулятора с 3 звеньями. Кинематическая схема такого манипулятора (рис.1) была реализована в ПР «Универсал -15».

Рассмотрим движение манипулятора по прямолинейной траектории, часто используемой при программировании промышленных роботов. Закон движения, определяемый изменением обобщённых координат во времени (q_i= q_i(t), i=1…3), представлен на рис.2. Такая форма закона движения типична для промышленных роботов (равноускоренный разгон с последующим торможением).

Исходные данные для расчёта: l₁=0,6м; l₂=0,28м; l₃=0,28м; m₁=20кг; m₂=10кг; m₃=5кг; r_с1⁽¹⁾ = [0 0 l₁/2 1]^T; r_с2⁽²⁾ = [l₂ 0 0 1]^T; r_с3⁽³⁾ = [0 0 l₃ 1]^T; R₁⁽⁰⁾=R₂⁽⁰⁾=R₂⁽⁰⁾=[10 10 10 0]^T Н; М₁⁽⁰⁾=М₂⁽⁰⁾=М₂⁽⁰⁾=[1 1 1 0]^T Нм,

г
Рис.1. Кинематическая схема манипулятора
де l₁, l₂, l₃ и m₁, m₂, m₃ – длины и массы соответствующих звеньев; r_сi ⁽ⁱ⁾ - радиус- вектор центра тяжести соответствующего звена в локальной системе координат, связанной с этим звеном; R_i⁽⁰⁾, М_i⁽⁰⁾ – соответственно главный вектор и главный момент внешней нагрузки, заданные в неподвижной (инерциальной) системе координат.




Рис. 2. Закон движения МС


Для расчётной схемы, представленной на рис.1, методами кинетостатики получены аналитические выражения для обобщённых сил от сил тяжести Q_Gi (i=1,2,3), действующих на звенья. Вектор Q_G обобщённых сил от сил тяжести будет иметь вид

	0
{QG} =	- (m2l2 + m3(l2+ l3+ q3))gCosq2	.
	- m3gSinq2

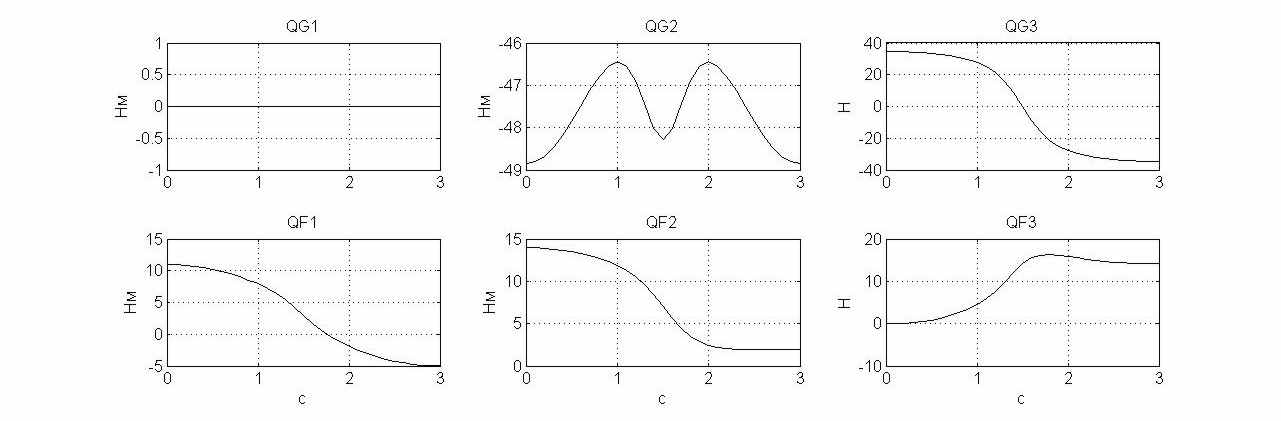
Результаты расчёта обобщённых сил от сил тяжести (Q_Gi) и внешней нагрузки (Q_Fi) представлены на рис.3.



c

c

c


Рис. 3. Обобщённые силы от сил тяжести и внешней нагрузки


Представленные в статье аналитические выражения для обобщённых сил от основных силовых факторов позволяют сформировать правую часть уравнения (1), описывающего движение манипуляционной системы.


СПИСОК ЛИТЕРАТУРЫ

1. Крахмалев, О.Н. Моделирование движения манипуляционных систем с упругими звеньями / О.Н.Крахмалев, А.П.Болдырев, Л.И.Блейшмидт // Вестн. БГТУ.-2010.-№3. -С.31-38.
   
2. Айзерман, М.А. Классическая механика : учеб. пособие / М.А. Айзерман.– 2-е изд., перераб. – М.: Наука, 1980. – 368 с.
   
3. Блейшмидт, Л.И. Вычисление кинематических параметров манипуляционных систем промышленных роботов / Л.И. Блейшмидт, О.Н.Крахмалев. – Брянск : БИТМ, 1991. – Деп. в ВИНИТИ, №1617 –В91.
   
4. Блейшмидт, Л.И. Геометрия манипуляционных систем промышленных роботов / Л.И. Блейшмидт, О.Н.Крахмалев. – Брянск : БИТМ, 1991. – Деп. в ВИНИТИ, №1618 –В91.
   
5. Блейшмидт, Л.И. Основы механики манипуляционных систем промышленных роботов : метод. указ. по лекц. курсу / Л.И. Блейшмидт. - Брянск : БИТМ, 1990. -64с.
   

Материал поступил в редколлегию 19.01.11.