А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор пгу им. С. Торайгырова. Н. Е. Тарасовская доктор биологических наук, профессор. Химич Г. З., Хлущевская О. А. Введение в биометрию. Учебное пособие
| Вид материала | Учебное пособие |
- Секция интенсивных методов обучения, 2428.86kb.
- Альманах издан при поддержке народного депутата Украины, 3190.69kb.
- Ветеринария. – 2011. №1(17). – С. 20-21 Нужен ли нам сегодня новый аграрно-технический, 46.59kb.
- Общеобразовательная программа дошкольного образования Авторский коллектив, 5619.19kb.
- Образовательная программа дошкольного образования Москва «Просвещение», 5670.3kb.
- Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби,, 5487.66kb.
- Пояснительная записка, 12621.4kb.
- В. О. Бернацкий доктор философских наук, профессор; > А. А. Головин доктор медицинских, 5903.36kb.
- Д. В. Петров Диапозитивы текста изготовлены в тц сфера, 1451.22kb.
- «Слова о Полку Игореве», 3567.27kb.
ПОКАЗАТЕЛИ РАЗНООБРАЗИЯ ПРИЗНАКОВ
В каждой частной совокупности, взятой для исследования, отдельные экземпляры в различной степени отклоняются от средней величины, поэтому для характеристики изучаемой выборки одного среднего недостаточно; необходимо привести показатели, характеризующие степень этого разнообразия (в ряде учебников вместо выражения «разнообразие признаков» используются термины «разброс», «варьирование»).
Показателями разнообразия признаков служат лимиты, амплитуды изменчивости, среднее квадратическое отклонение σ (сигма), варианса σ2 и коэффициент вариации Сv. Общим свойством показателей разнообразия является их способность отмечать различные степень и особенности разнообразия.
Американский генетик Дж. Л. Брюйбекер в книге «Сельскохозяйственная генетика» приводит в качестве примера рост игроков двух баскетбольных команд в футах и дюймах (фут =0,3 м, дюйм =2,54 см).
Команда А. Рост игроков: 6 ф. 1 д.; 6 ф. 2 д; 6 ф. 3 д; 6 ф. 4 д; 6 ф. 5 д. Средняя арифметическая 6 ф. 3 д.
Команда Б. Рост игроков: 5 ф. 5д.; 5 ф. 6 д.; 6 ф. 3 д; 7 ф. О д.; 7 ф. 1 д. Средняя арифметическая 6 ф. 3 д.
Средний рост игроков в обеих командах одинаков, но болельщики баскетбола, несомненно, видят, что шансов на победу у команды Б с ее высокими семифутовыми игроками больше, чем у команды А.
Характеристика команд будет полнее, если мы приведем лимиты, т. е. показатели разнообразия, указывающие максимальное и минимальное значения изучаемого признака. Лимиты команды А — lim1 — 6 ф. 1 д.— 6 ф. 5 д. (4 д.).
 Лимиты команды Б — lim2 — 5 ф. 5 д.— 7 ф. 1 д. (1 ф. 6 д.);
Лимиты команды Б — lim2 — 5 ф. 5 д.— 7 ф. 1 д. (1 ф. 6 д.);(в скобках указана амплитуда изменчивости).
Н. А. Плохинский приводит следующий пример. При изучении массы быков в двух совхозах получены следующие данные (табл. 12).
Средняя живая масса быков в обоих совхозах одинакова — 650 кг, но разнообразие быков по массе во втором совхозе в пять раз больше, чем в первом. Наиболее просто это можно показать при помощи лимитов и амплитуды изменчивости :
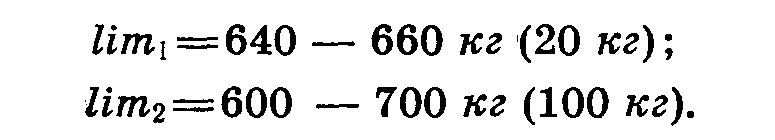
Таблица 12 Таблица 13
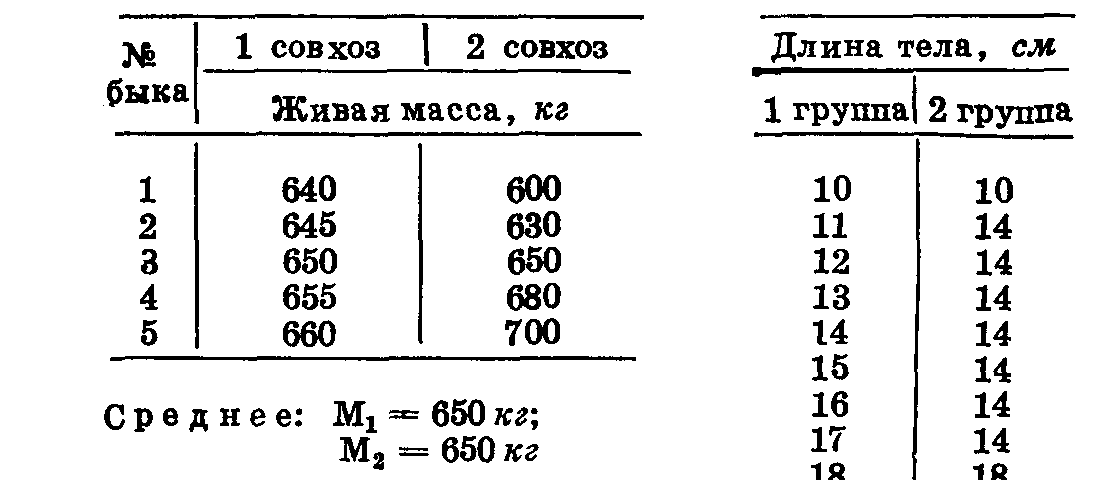
оплаты продукта. Например, если средняя масса тушек бекона в одной партии М1=90 кг,lim1 88—92 (4 кг), а в другой М2=90 кг и
lim2 80—100 (20 кг), то ясно, что первая партия как стандартная получает более высокую оценку по сравнению со второй.
В некоторых случаях лимиты могут служить единственной характеристикой признака. Например, при описании простейших приводятся только лимиты их размеров:
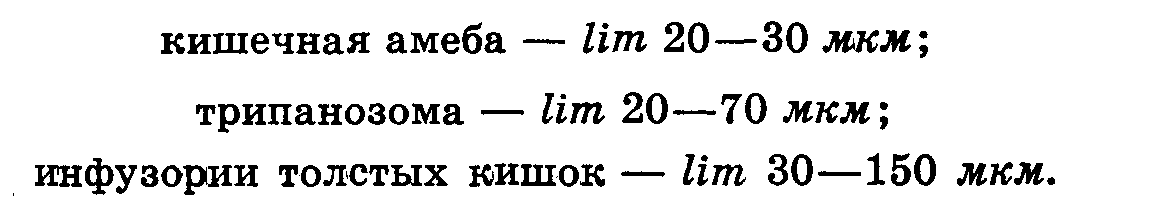
Эти данные вполне достаточны для первого ознакомления с указанными объектами. Поэтому лимиты представляют большой интерес даже при наличии более точных показателей разнообразия.
Но тем не менее надо отметить, что лимиты не отражают очень важных особенностей. Предположим, что сравниваются две группы особей по длине тела (табл. 13).
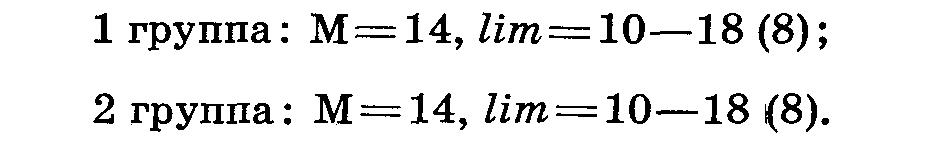
Средние и лимиты в обеих группах одинаковы, в то же время степень разнообразия этих групп явно различна. В первой группе все особи имеют разную длину тела, во второй группе семь особей из девяти одного и того же размера. Изменчивость первой группы явно больше, чем второй, но отметить это при помощи лимитов в данном случае невозможно. Наиболее точно охарактеризовать степень разнообразия можно при помощи особого показателя — среднего квадратического отклонения (Плохинский, 1961, с. 36—37).
СРЕДНЕЕ КВАДРАТИЧЕСКОЕ ОТКЛОНЕНИЕ а (СИГМА)
Известный математик Гаусс в качестве показателя степени разнообразия предложил использовать основное отклонение, т. е. корень квадратный из суммы произведений квадратов отклонений от среднего на частоты, деленные на число наблюдений:
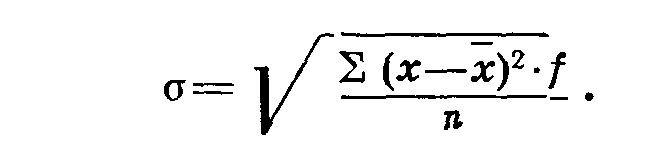
Известно, что сумма отрицательных и положительных отклонений от среднего равна нулю. При возведении отклонений в квадрат все знаки становятся положительными. Чтобы устранить влияние величины отдельных выборок, сумму произведений квадратов отклонений на частоты делят на число наблюдений.
Позднее формула Гаусса была немного изменена: за знаменатель в приведенной выше формуле стали принимать не число наблюдений (га), а га—1, т. е. число степеней свободы, равное числу независимых величин. Если сумма двух чисел равна 10, а одно из них равно 3, то второе число может быть только 7. При трех числах два являются независимыми, а третье определяется суммой двух первых. Поэтому число степеней свободы равно п—1. Формула Гаусса принимает значение:
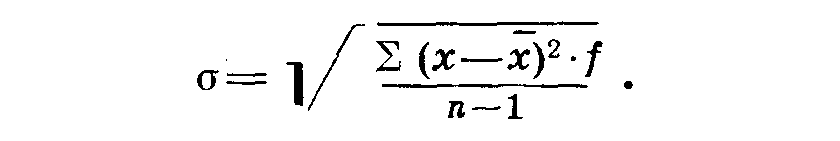
Число степеней свободы обозначается греческой буквой v или двумя буквами латинского алфавита — df (degree of fredom — степень свободы). Для вычисления квадратического или основного отклонения {σ) строят вариационный ряд. Расположенную в средине вариационного ряда варианту принимают за условное среднее, находят отклонения от условного среднего, умножают отклонения на частоты. Затем находят алгебраическую сумму произведений отклонений на частоты, делят полученную сумму на число наблюдений (т. е. поступают так же, как при вычислении арифметического среднего). Потом находят произведение квадрата отклонений на частоты, суммируют их и вычисляют корень квадратный из суммы произведений квадратов отклонений на частоты, деленной на число степеней свободы, минус квадрат поправки (табл. 14).
Рассмотрим эти действия на другом примере: после разноски вариант мы получили вариационный ряд с амплитудой изменчивости, равной 6 (лимиты 5—11), число наблюдений —45. Принимаем варианту 8 за условно взятое среднее, записываем отклонение от среднего (х—
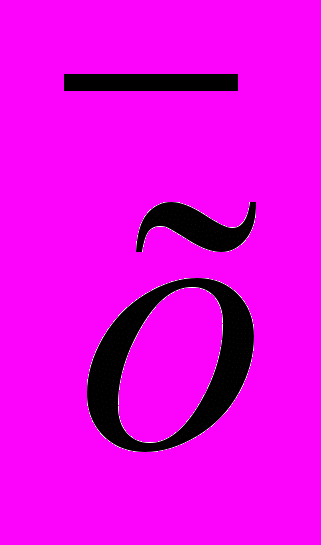 ), умножаем отклонения на частоты (х—
), умножаем отклонения на частоты (х—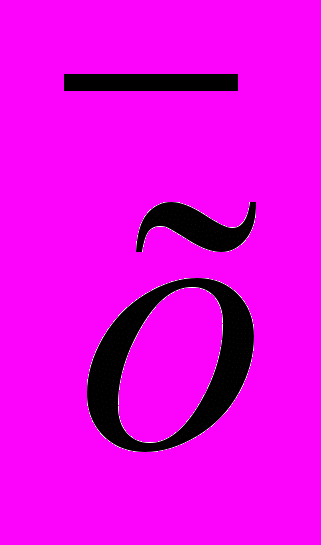 ),• f. Находим алгебраическую сумму этих произведений, делим ее на число наблюдений и таким образом получаем поправку b. Находим среднее, т. е. проделываем все расчеты, указанные в предыдущей главе. Для определения квадратичеокого отклонения возводим все отклонения в квадрат, умножаем квадраты отклонений на соответствующие частоты, находим сумму этих произведений (табл.15).
),• f. Находим алгебраическую сумму этих произведений, делим ее на число наблюдений и таким образом получаем поправку b. Находим среднее, т. е. проделываем все расчеты, указанные в предыдущей главе. Для определения квадратичеокого отклонения возводим все отклонения в квадрат, умножаем квадраты отклонений на соответствующие частоты, находим сумму этих произведений (табл.15).Таблица 14
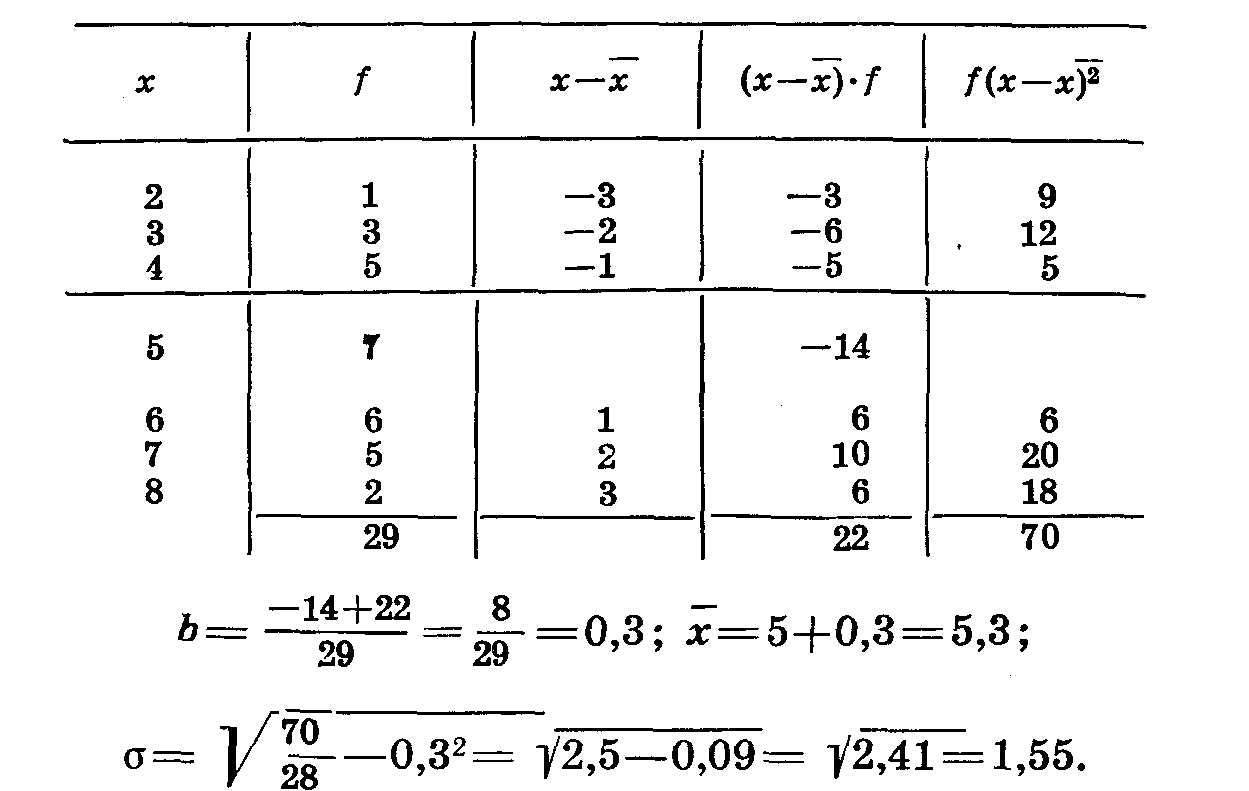
Таблица 15

При вычислении среднего квадратического отклонения по вариантам, разбитым на классы, число, полученное после извлечения корня, умножается на размер класса (l) (табл.16)
Таблица 16
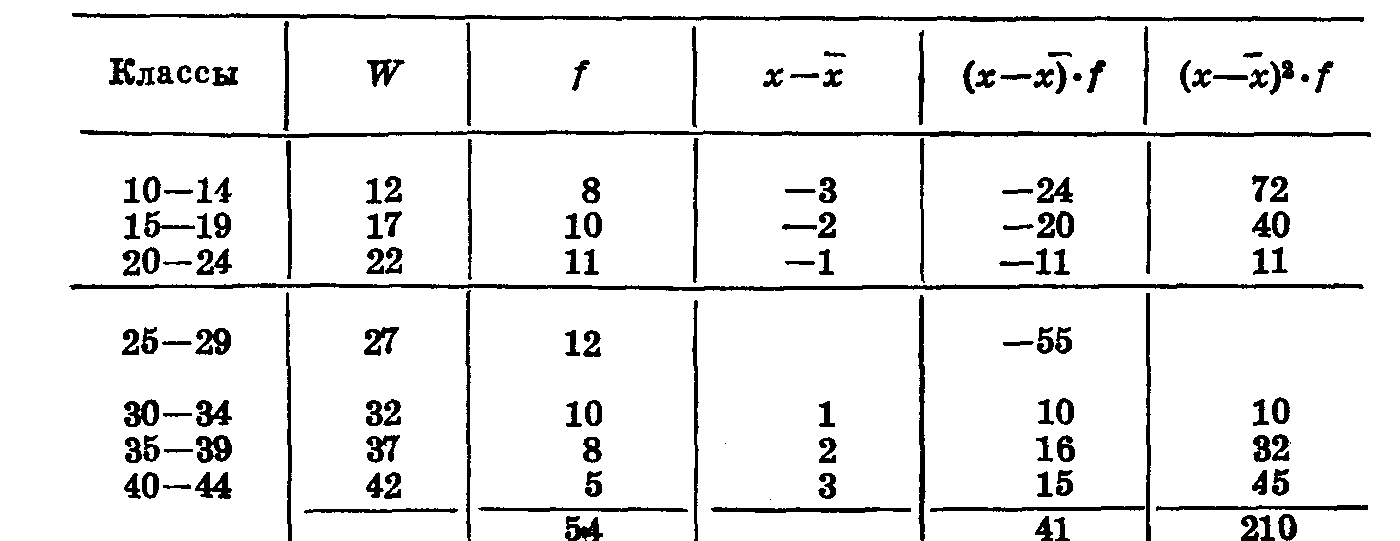
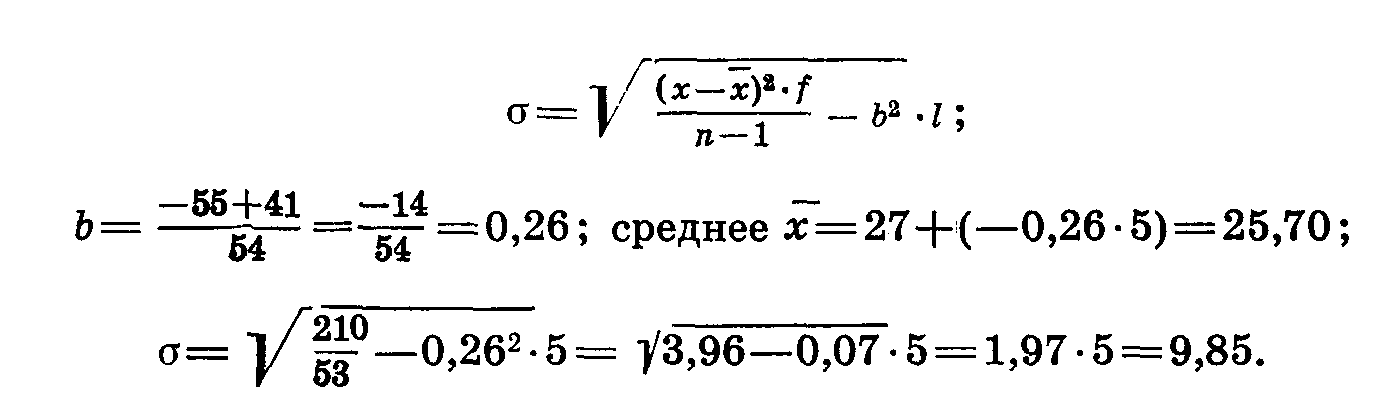
Вычислим среднее квадратическое отклонение для данных, приведенных в таблице 10, характеризующих длину тела животных двух групп, (средние и лимиты у обеих группклонение позволило выявить различие в изменчивости указанных групп животных. одинаковы). По первой группе
отклонения от средней приведены
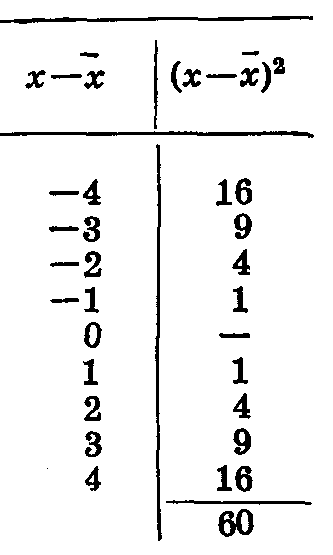
 в таблице 17. Таблица 17.
в таблице 17. Таблица 17. клонение позволило выявить различие в изменчивости указанных групп животныx.
Основное или квадратическое отклонение а выражается в тех же единицах, что и среднее. Следовательно, оно всегда является числом именованным. Чем меньше амплитуда изменчивости, тем меньше сигма. При отсутствии изменчивости (гипотетический случай) сигма равна 0. Изменчивость живых организмов по росту, весу и другим показателям очень значительна, и абсолютное значение сигмы может варьировать в широких пределах.
Представим себе гипотетический случай, когда 100 семян одного сорта, абсолютно одинаковых по весу, химическому составу и другим показателям, высеваются в идеально выровненных условиях и подвергаются совершенно одинаковым воздействиям внешней среды. В таком случае мы вправе ожидать, что вырастут 100 растений совершенно одинаковых. Графически ряд будет представлен одной вертикальной линией. Однако абсолютно одинаковых семян не бывает. Изменчивость только одного показателя (качества семян) даст уже варьирующий сжатый ряд. Не существует в приводе и совершенно одинаковых условий почвенного плолородия, освещения и пр. Изменчивость возрастает, ряд становится более широким.
Однако математиками установлено, что при нормальном распределении, свойственном большинству биологических объектов, изменчивость 95% вариант укладывается в пределах минус 2σ—плюс 2σ, 98% —в пределах минус Зσ, — плюс Зσ, 99 % — в пределах минус 3,5σ — плюс 3,5σ.
Коэффициент вариации. Для сравнения степени изменчивости по различным признакам, а также степени изменчивости отдельных объектов используется коэффициент вариации, который представляет собой квадратическое отклонение, выраженное в процентах, от средней величины. Обозначается коэффициент вариации С или су .
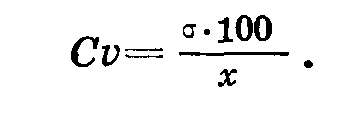
С его помощью мы можем сравнивать изменчивость различных объектов по самым различным показателям. Установление коэффициента изменчивости имеет большое значение при многих биологических исследованиях. Например, селекционер, работающий над созданием новых сортов, изучает коэффициент изменчивости различных признаков у исходного материала. Ясно, что отбор даст лучшие результаты, если будет проводиться по признакам, имеющим большую изменчивость. У готового сорта, наоборот, большой коэффициент (изменчивости по основным признакам недопустим — сорт должен иметь устойчивые показатели. Большое значение изучению коэффициента вариации придают исследователи, работающие по акклиматизации животных и растений, морфологии, систематике и т. д.
ОШИБКА СРЕДНЕГО АРИФМЕТИЧЕСКОГО
Квадратическое (основное) отклонение (сигма) используется для вычисления очень важного статистического показателя — ошибки среднего арифметического. Точное среднее арифметическое может быть определено, если мы исследуем всю генеральную совокупность. Практически же мы имеем дело с более или менее большими по объему выборками. В таких случаях среднее всегда бывает не вполне точным.
Возьмем 100 растений, измерим их высоту, вычислим среднюю арифметическую. Допустим, что средний рост растений данной выборки 50,5 см. Разобьем эти растения на группы по 20 экз. в каждой. Вновь проведем измерения и вычислим средние. Эти новые средние точно не совпадут с уже установленным средним 50,5, а будут в каждом отдельном случае отклоняться от него в ту или другую сторону: 49,8; 50,9; 50,1; 51,3; 50,4 в зависимости от того, попадут ли во взятую для измерения группу более высокие или более низкие растения. Поэтому, называя среднее арифметическое, необходимо указать и возможные колебания этой средней величины. Это достигается путем вычисления ошибки среднего арифметического, которая обозначается т или Sх и определяется по формуле
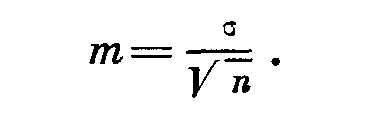
Приводя среднее арифметическое, указывают и его ошибку:
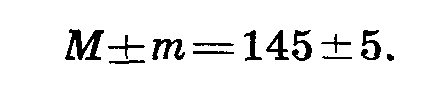
Это показывает, что среднее в исследованной выборке колеблется от 140 до 150.
Ошибка средней арифметической зависит от двух величин: от степени разнообразия признака в генеральной совокупности и от размера выборки: чем больше выборка, тем меньше ошибка. Поэтому при вычислении ошибки квадратическое отклонение делится на корень квадратный из числа наблюдений.
Часть никогда не может полностью характеризовать целое, поэтому характеристика генеральной совокупности на основе выборочных данных всегда будет иметь некоторую большую или меньшую ошибку. Такие ошибки являются ошибками обобщения, связанными с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность, и называются ошибками репрезентативности. (Репрезентативность происходит от французского слова representatiue — представительный).
Помимо ошибок репрезентативности при исследовании могут встретиться ошибки самого разнообразного характера. К ним относятся:
1. Методические ошибки (нарушение правильной методики проведения фиксации материала для цитологических и биохимических исследований, невыравненность условий в опытных вариантах и контроле).
2. Ошибки точности (использование непроверенных измерительных приборов, расчеты с недостаточной точностью и т. д.).
3. Случайные ошибки (ошибки, просчеты, путаница в материале и т. д.).
4. Ошибки, связанные с неправильным отбором проб для изучения.
Все эти причины повлекут за собой очень сильное увеличение ошибки среднего. (Иногда у начинающих работников ошибка бывает почти равна среднему. Ясно, что такие данные должны выбраковываться).
УПРОЩЕННОЕ ВЫЧИСЛЕНИЕ ОШИБКИ СРЕДНЕГО АРИФМЕТИЧЕСКОГО
При обработке данных по многочисленным вариантам опыта и небольшом количестве повторностей можно применить упрощенный способ вычисления ошибки среднего арифметического по Петерсу с использованием фактора Молденгауэра (константы К) по формуле
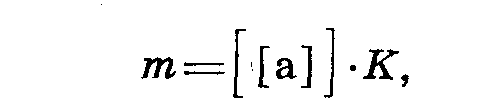
где [ [а] ]— сумма отклонений независимо от знака, а К —
— константа, изменяющаяся в зависимости от количества повторностей, вычисленная по формуле:
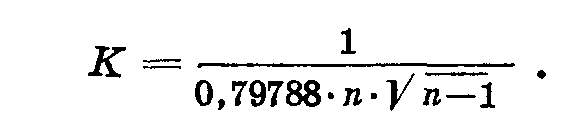
В книге П. Н. Константинова «Методика полевых опытов (с элементами теории ошибок)», 1939, дана таблица констант К для ошибок среднего. Приводим выписку из нее (табл. 18).
Таблица 18

(При большем количестве повторностей использование упрощенного способа вычисления ошибки экономит немного времени). Допустим, мы изучали действие различных микроэлементов в разных дозах на урожайность пшеницы. У нас было 40 вариантов опытов. Каждый вариант испытывался в четырех повторностях.
В первом варианте (контроль) был получен следующий урожай (табл. 19).
Для проверки правильности вычисления среднего в отклонений мы сначала суммируем положительные и отрицательные отклонения:
—0,6+(—0,8) = —1,4;
+0,8+0,6 = +1,4.
Эти вычисления нужны только для проверки и в дальнейших расчетах не участвуют.
Суммы положительных и отрицательных отклонений равны, значит, вычисления сделаны правильно. (В случае. когда среднее и отклонение вычисляются с округлением, между суммой положительных и отрицательных отклонений может быть небольшая разница, выражающаяся в десятых долях. Этой разниией можно пренебречь).
Находим сумму отклонений независимо от знака (в нашем примере она равна 3,0) и умножаем ее на константу К для четырех повторностей, равную 0,1809.
3,0 ∙ 0,1809 = 0,5427
Таблица 19 Таблица 20
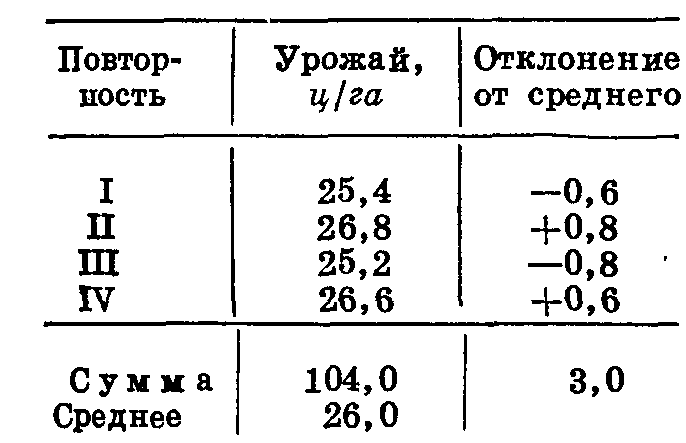

Среднее равно 26 ± 0,54 ц. Рассмотрим еще один пример (табл. 20).
24 • 0,0934 = 2,24
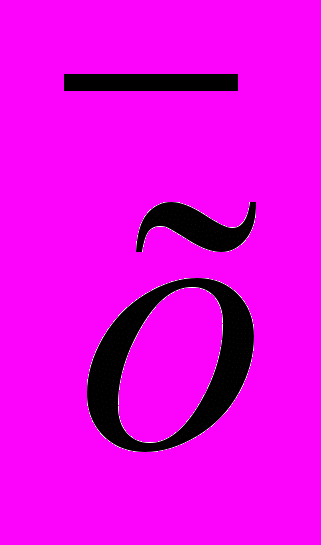 =15 ± 2,24
=15 ± 2,24Вычислим ошибку обычным способом (табл. 21):
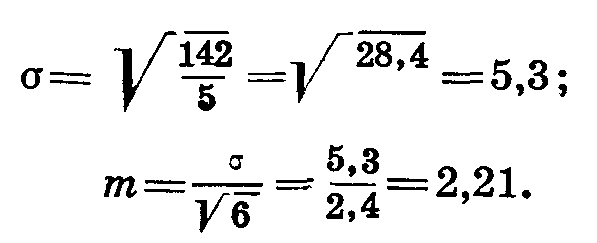
Разница в определении ошибки среднего составляет 0,03, что не имеет существенного значения.
Точность опыта имеет большое значение, так как она определяет степень надежности полученных данных.
Точность опыта обозначается Р или m% и вычисляется по формуле
P = m• 100 /
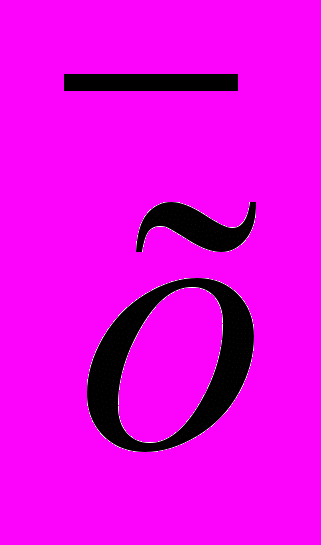
т. е. путем вычисления процентного отношения ошибки к средней величине.
В только что разобранном примере
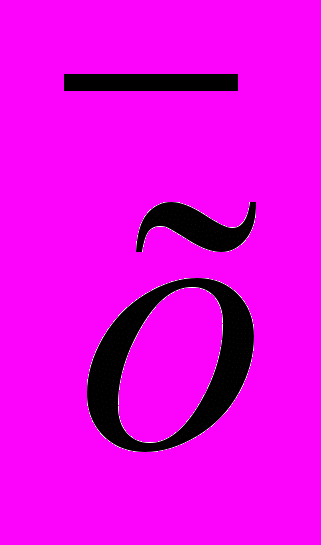 =15; т=2,2, Р или
=15; т=2,2, Р или m% = 2,2 • 100 / 15 = 14,6% - опыт недостоверен.
Опыт считают достаточно точным, если Р меньше 3 %, и удовлетворительным при Р, равной 5%. При Р, равной б—7% и более, к полученным выводам следует отнестись очень осторожно. Опыт следует повторить с соблюдением всех требований методики.
Таблица 21
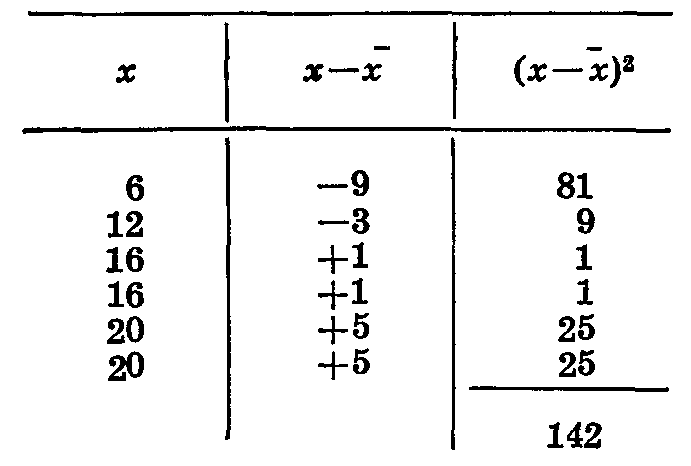
ОПРЕДЕЛЕНИЕ ДОСТОВЕРНОСТИ РАЗЛИЧИЙ МЕЖДУ СРЕДНИМИ
Конечной целью каждого опыта является установление достоверности различий между изучаемыми вариантами опыта (различие в урожайности сортов, возделывавшихся в производстве, и новыми, выведенными селекционерами;
различие в урожайности культур под влиянием внесения удобрений; различие по количественным показателям между разными видами животных и растений и т. д.).
Мы уже говорили, что средние арифметические для выборок всегда несколько колеблются и при указании среднего следует приводить ошибку среднего, показывающую возможные колебания: '.
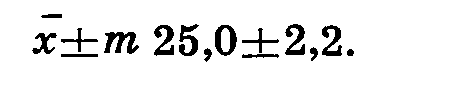
Видно, что среднее колеблется от 22,8 до 27,2. Но поскольку ошибка {т) вычисляется на основе квадратического отклонения (σ), то все возможные значения средней величины лежат в пределах
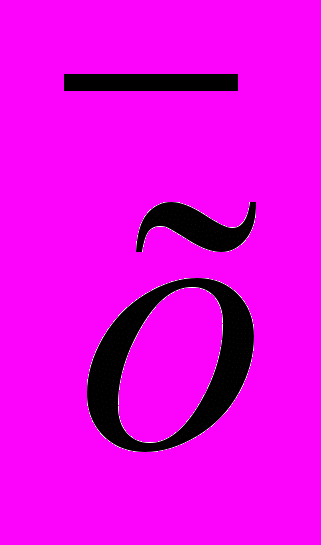 ± 3 т или, точнее,
± 3 т или, точнее, 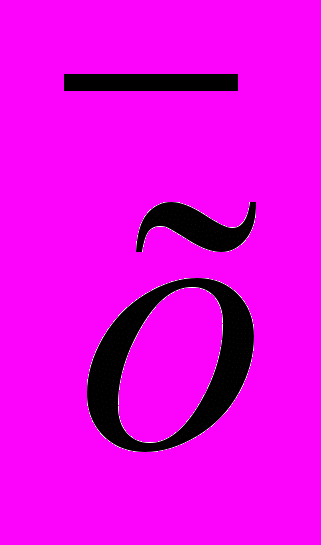 ± 3,5 т, так же как все варианты ряда, лежат в пределах
± 3,5 т, так же как все варианты ряда, лежат в пределах 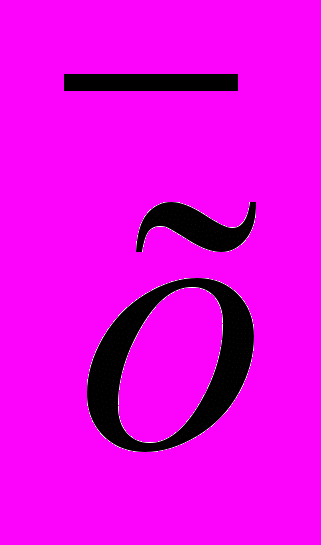 - 3σ или х +З,5 σ. Отсюда значение 3 т или 3,5 т называется предельной ошибкой среднего арифметического.
- 3σ или х +З,5 σ. Отсюда значение 3 т или 3,5 т называется предельной ошибкой среднего арифметического.Достоверность разности между двумя средними величинами определяют по отношению этой разности к ее ошибке. Ошибка разности равна корню квадратному из суммы квадратов ошибок:
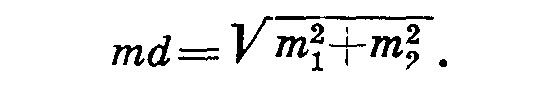
Например, в опыте по изучению влияния фосфорного удобрения на урожай яровой пшеницы в условиях недостатка влаги получены следующие данные (опыт проведен в четырехкратной повторности):
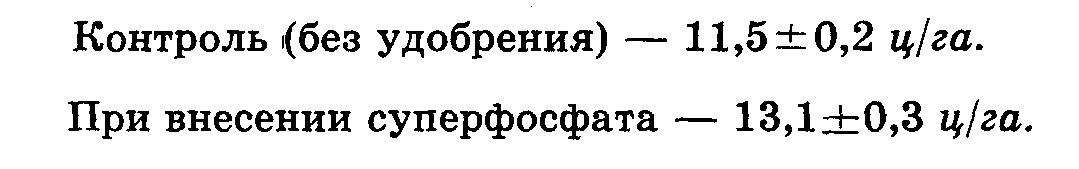
Достоверно ли полученное превышение? Определяем раз-гость между средними:
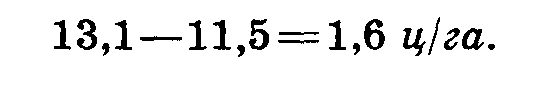
Вычисляем ошибку разности:
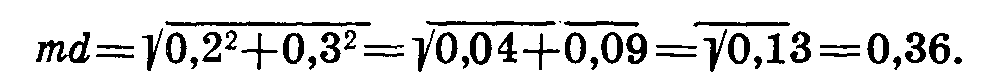
Находим отношение разности к ее ошибке:
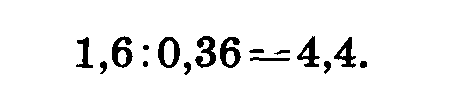
В старых руководствах по биометрии указано, что разность достоверна в тех случаях, когда это отношение равно или более трех. Точнее, достоверность разности определяется по критерию Стьюдента t. (Значение критерия Стьюдента приведено в таблице 45, с. 62). t равно отношению разности к ее ошибке.
Рассматриваемый опыт приведен в четырех повторностях. Следовательно, число степеней свободы равно 4+4— —2 = 6. При 6 степенях свободы разность при вероятности 0,95 (на уровне 5%) достоверна при t, равном 2,45, при вероятности 0,99 (на уровне 1%) при t равном 3,71. Следовательно, разность между урожаем контрольного и опытного вариантов достоверна при уровне вероятности, несколько превышающем 0,99.
УЧЕНИЕ О КОРРЕЛЯЦИЯХ
Слово корреляция происходит от латинского correlation, что означает связь, соотношение, сопряженность. В практике биологических исследований часто возникает необходимость изучить связь между признаками одного организма или зависимость между признаками организма и условиями внешней среды.
В курсе высшей математики излагаются основные положения функциональной зависимости между двумя переменными, при которой каждому значению одной переменной — аргументу — соответствует тоже одно вполне определенное значение другой переменной — функции.
В качестве примера функциональной зависимости можно привести площадь треугольника, которая всегда определяется его высотой и основанием, площадь круга, определяющуюся его радиусом, и т. д.
При изучении живых объектов — растений, животных, микроорганизмов — связь между признаками проявляется в виде так называемой корреляционной связи, или корреляции, при которой каждому значению одного признака соответствует не одно, а несколько значений другого признака, т. е. его распределение.
Например, хорошо известна связь между ростом человека и его весом, но при одинаковом росте (например, в 160 см) вес тела может колебаться в известных пределах и составлять, допустим, 55, 60, 65 кг. Задача исследования корреляционной связи заключается в том, чтобы определить характер и измерить тесноту связи между отдельными признаками или развитием признаков и условиями среды.
При изучении корреляции решающее значение имеет всесторонний качественный анализ материала. Например, изучая зависимость между содержанием белка в зерне и условиями возделывания культуры, необходимо сопоставить эти показатели в образцах одного сорта, выращенного при различных, но вполне определенных в каждом отдельном случае условиях. Так, если мы хотим установить зависимость содержания белка в зерне озимой пшеницы Безостая 1 от применения азотных удобрений, необходимо, чтобы остальные условия (тип почвы, предшественники, приемы обработки почвы, сроки посева и т. д.) были одинаковыми, а изменялась только доза внесения азотных удобрений.
Прежде чем приступить к вычислению корреляционной зависимости, необходимо проанализировать возможность связи между изучаемыми явлениями, иначе можно получить совершенно ложные результаты. Так, в работе Устинова была установлена корреляция между урожайностью и числом пожаров.
Известно, что засуха всегда снижает урожай, что опасность пожаров увеличивается в сухие годы. Таким образом, два совершенно независимых явления (пожары и урожай) определяются третьей величиной — количеством осадков, но сопоставлять эти два явления нет никаких оснований.
Зависимость урожая от количества осадков может быть различной в разных географических пунктах. В районах недостаточного увлажнения, при отсутствии орошения, уменьшение количества осадков всегда снижает урожай, хотя степень этого снижения может быть различной в зависимости от уровня агротехники; в районах избыточного увлажнения, наоборот, увеличение количества атмосферных осадков может быть неблагоприятным для урожая, особенно при недостатке тепла. Следовательно, установление корреляции между этими величинами представляет интерес в определенных географических условиях.
Для разработки рациональной системы орошения большое значение имеет установление связи между обеспеченностью растений влагой в определенные периоды развития и урожайностью и т. д.
Корреляция может быть прямой или положительной, если с возрастанием одного показателя увеличивается второй или, наоборот, с уменьшением одного показателя уменьшается второй.
Такая корреляция выражается словами «чем больше, тем больше» или «чем меньше, тем меньше». Например, чем больше вес клубней картофеля в одном гнезде, тем выше урожай; чем меньше длина туловища животного определенного вида, тем меньше его вес.
Корреляция является обратной или отрицательной, если с увеличением одного показателя уменьшается второй или с уменьшением первого показателя увеличивается второй. Такая зависимость выражается словами: «чем меньше, тем больше» или «чем больше, тем меньше». Например, чем больше растений кукурузы в гнезде, тем меньше початков на растении.
Как прямая, так и обратная корреляция может быть линейной, если с увеличением одного показателя планомерно увеличивается или уменьшается второй показатель, или криволинейной, если с увеличением одного показателя до известных пределов второй показатель также повышается, а затем начинает снижаться. Например, при увеличении нормы высева до определенного для конкретных условий уровня урожай повышается, но дальнейшее увеличение нормы высева вызывает излишнее загущение посева, и урожай снижается. Степень сопряженности выражается в виде отвлеченного числа, которое при корреляции называется коэффициентом корреляции, при криволинейной зависимости — корреляционным отношением.
Корреляция может быть выражена графически. Рассмотрим примеры вычисления коэффициента корреляции и графического ее выражения на гипотетическом примере, приведенном в книге П. Н. Константинова «Методика полевых опытов (с элементами теории ошибок)».
Взято два показателя: вес многолетних растений и их кустистость (число стеблей на одно растение). Обозначим эти показатели как х и у.
Первый пример.
Кустистость растений (х): 4; 6; 10; 12, в среднем 8.
Вес растений в г (у): 30; 34; 42; 46, в среднем 38.
Таблица 22
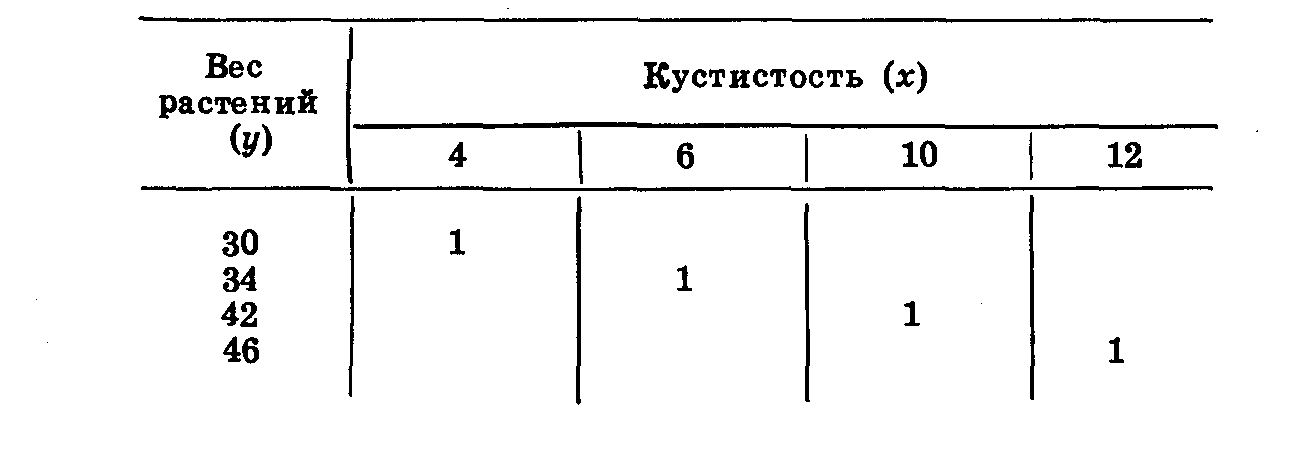
Мы видим, что с увеличением кустистости планомерно увеличивается и вес, т. е. существует прямая зависимость. Изобразим ее графически (табл. 22): расположим по горизонтали показатели кустистости (х), по вертикали — вес растений (у).
Поместим растения в клетки, соответствующие обоим показателям. Первое растение имело кустистость 4, вес 30 г помещаем его в первую клетку и т. д.
Такое сопряженное изображение обоих вариационных рядов называется корреляционной решеткой. Мы видим что при полной прямой положительной корреляции варианты располагаются по диагонали, идущей из верхнего левогo угла решетки в правый нижний угол.
Второй пример.
Кустистость растений (х): 4; 6; 10; 12, в среднем 8. Вес растений в г (у): 46; 42; 34; 30, в среднем 38. В этом случае наблюдалась бы совершенно невероятная обратная зависимость между кустистостью и весом растений. Построим корреляционную решетку (табл. 23).
Таблица 23
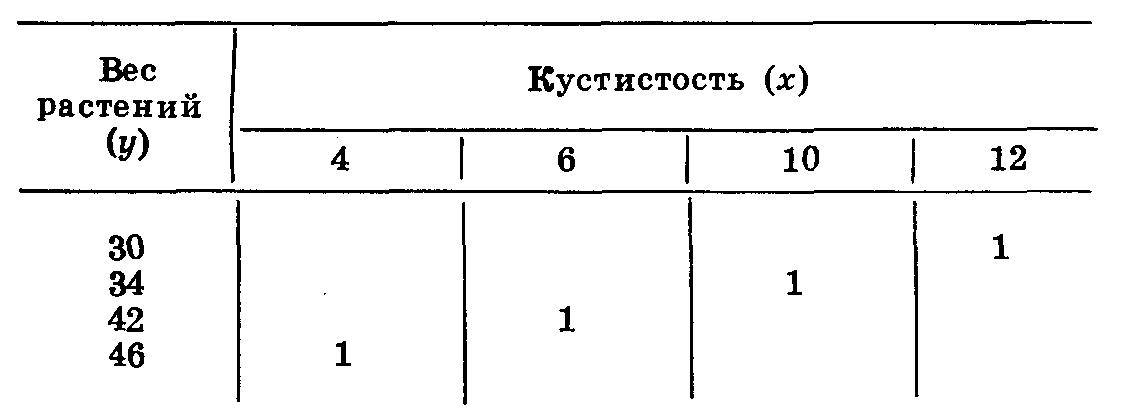
При обратной (отрицательной) корреляции варианты располагаются в корреляционной решетке по диагонали, идущей из верхнего правого угла в левый нижний угол.
Третий пример.
Кустистость растений (х): 4; 6; 10; 12, в среднем 8. Вес растений в г (у): 42; 30; 46; 34, в среднем 38. Нетрудно заметить, что в этом случае отсутствует определенная связь между кустистостью и весом растений: минимальной кустистости соответствует максимальный вес, затем кустистость возрастает, а вес резко падает, далее кустистость продолжает увеличиваться, возрастает и вес. При дальнейшем увеличении 'кустистости вес снова уменьшается.
Таблица 24
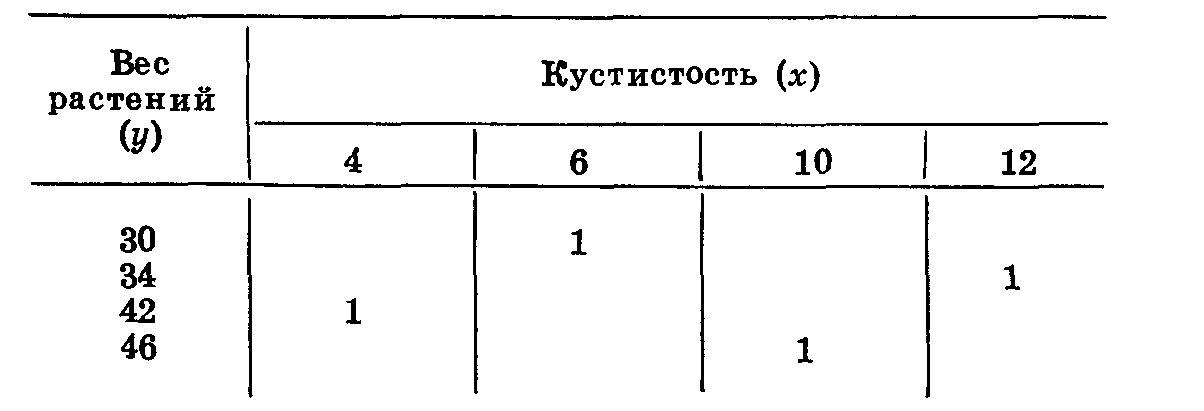
Графическое изображение представлено в таблице 24.
При отсутствии корреляции варианты располагаются беспорядочно по всей решетке.
Полная прямая или обратная корреляция встречается редко. Рассмотрим пример неполной прямой корреляции. Кустистость растений (х): 4; 6; 10; 12. Вес растений в г (у}: 30; 42; 34; 46.
За исключением одного случая, вес растений увеличивается по
Таблица 25
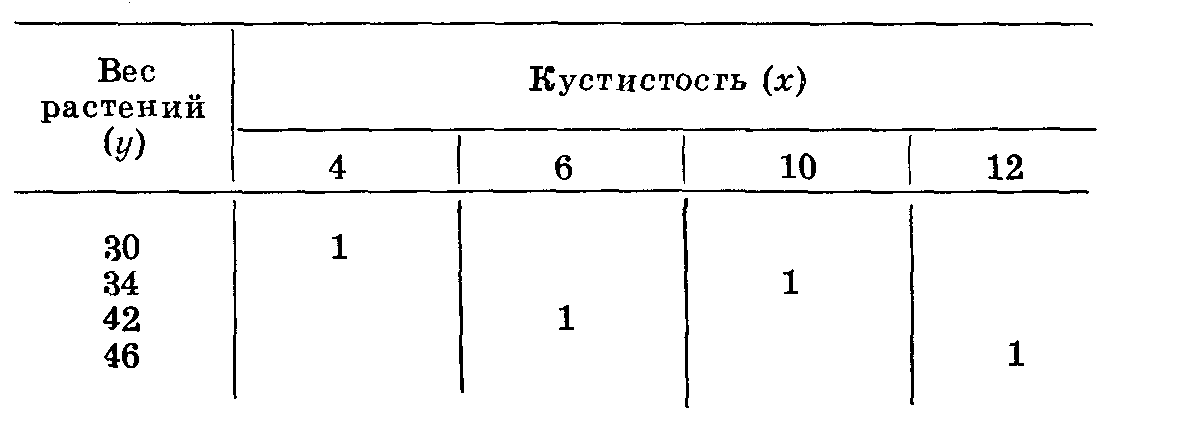
мере повышения кустистости. Графическое изображение дает такие результаты (табл. 25).
При неполной прямой корреляции варианты группируются вокруг диагонали, идущей из левого верхнего угла в правый нижний. При неполной отрицательной корреляции варианты
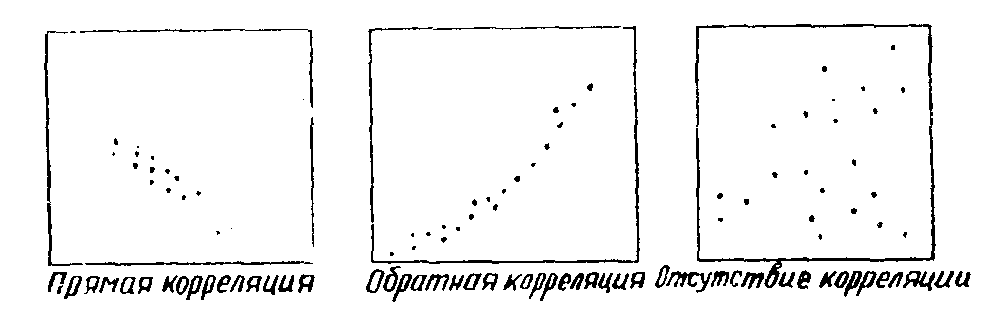
Рис. 6. Графическое изображение расположения вариант в корреляционной решетке.
располагаются вокруг диагонали, идущей из правого верхнего угла корреляционной решетки в левый нижний.
Иногда в печатных работах, не приводя коэффициента корреляции, ограничиваются графическим изображением расположения вариант (рис. 6).
Однако такой способ слишком громоздок и неприменим в случаях, когда надо показать корреляцию по ряду признаков. Кроме того, он дает лишь ориентировочное представление о тесноте связи между изучаемыми признаками, поэтому прибегают к вычислению коэффициента корреляции.
Коэффициент корреляции обозначается r. Он является отвлеченным числом и имеет значение от 1 (полная положительная корреляция) до —1 (полная отрицательная корреляция) с переходом через 0 (отсутствие корреляции). Так же, как и для других биометрических показателей, вычисляется ошибка коэффициента корреляции — тr. или Sr .
ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
Рассмотрим приведенные выше упрощенные примеры зависимости между кустистостью и весом растений. Вычислим по обоим рядам отклонение от среднего. Отклонение обозначается как ax и ay или (х—
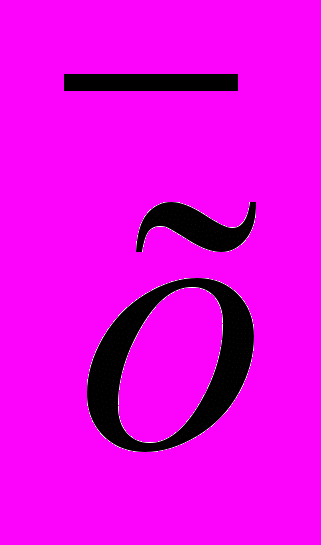 )а и (х—
)а и (х—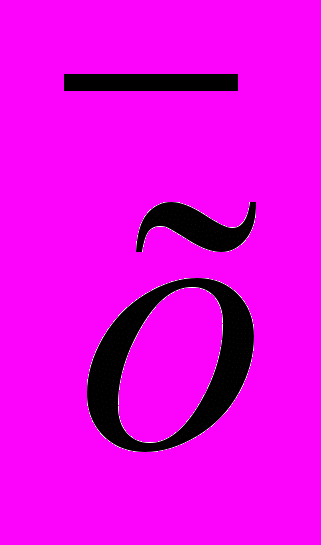 )y
)y Первый пример.
Кустистость растений (х): 4; 6; 10; 12, в среднем 8. Вес растений в г (у): 30; 34; 42; 46, в среднем 38. Отклонение от среднего: по ряду х: аx — 4; —2; +2; +4;
по ряду у: aу—8; —4; +4; +8.
Произведение отклонений 32; 8; 8; 32. Сумма произведений
равна 80.
Второй пример.
Кустистость растений (х): 4; 6; 10; 12, в среднем 8. Вес растений в г (у): 46; 42; 34, в среднем 38. Отклонение от среднего: по ряду х: аx — 4; —2; +2; +4; по ряду у: aу +8; +4; —4; —8. Произведение отклонений —32; —8; —8; —32. Сумма произведений равна —80.
Третий пример.
Кустистость растений (х): 4; 6; 10; 12, в среднем 8. Вес растений в г (у): 42; 30; 46; 34, в среднем 38. Отклонение от среднего: по ряду х: а.х —4; —2; +2; +4;
по ряду у: а.у +4; —8; +8; —4.
Произведение отклонений —16; +16; +16; —16. Сумма
произведений равна 0.
Четвертый пример.
Кустистость растений (х): 4; 6; 10; 12, в среднем 8. Вес растений в г (у): 30; 42; 34; 46, в среднем 38. Отклонение от среднего: по ряду х: а,х —4; —2; +2; +4;
по ряду у: а,у —8; +4; —4; +8.
Произведение отклонений 32; —8; —8; + 32. Сумма произведений равна 48.
Мы видим, что сумма попарных произведений отклонений характеризует степень связи в изменчивости двух рядов:
при полной положительной корреляции Σ ax ay = 80,
при полной отрицательной корреляции Σ ax ay = - 80,
при частичной положительной корреляции Σ ax ay = 48,
при отсутствии корреляции Σ ax ay = О.
При сравнении различных рядов числовое выражение суммы попарных произведений отклонений от среднего будет меняться. Необходимо выразить эту зависимость в относительных числах, для этого надо разделить полученные суммы на постоянное и наибольшее число. Таким числом является среднее геометрическое (G), т. е. корень n-ой степени из произведения n-то количества дат:
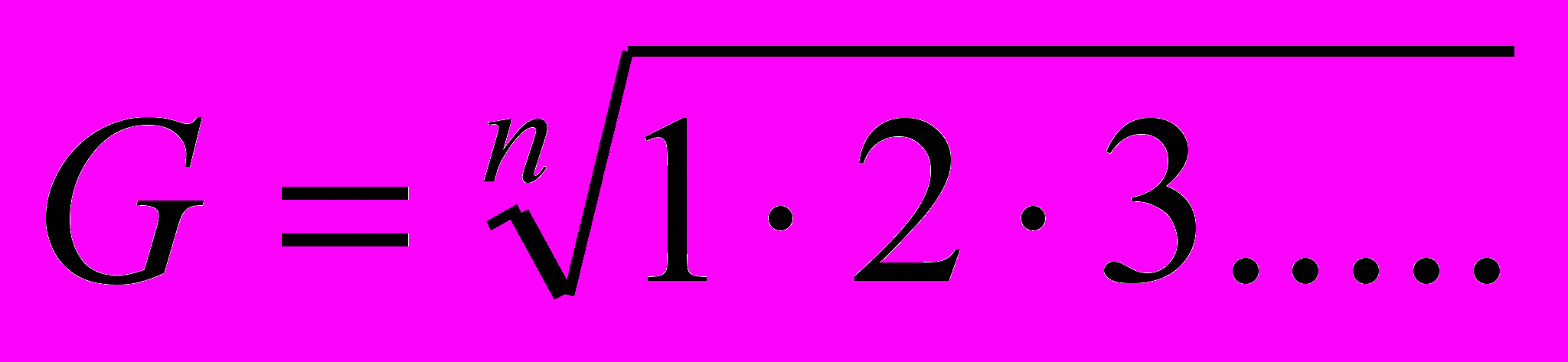
В нашем случае среднее геометрическое равно корню квадратному из произведения сумм квадратов отклонений от среднего по обоим рядам.
Вернемся к нашим примерам.
Первый пример. Возведем в квадрат отклонения от средних по обоим рядам и суммируем их,

Для небольших рядов вычисление коэффициента корреляции производится по этой формуле. Для вычисления в больших рядах эта формула преобразуется.
Мы знаем, что квадратическое отклонение σ равно корню квадратному из суммы квадратов отклонений, деленной на число наблюдений:
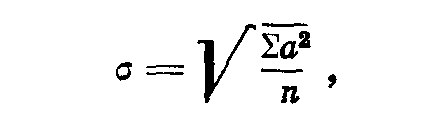

При наличии большого числа наблюдений непосредственное вычисление коэффициента корреляции по данной формуле слишком громоздко. Обычно прибегают к составлению
Таблица 26
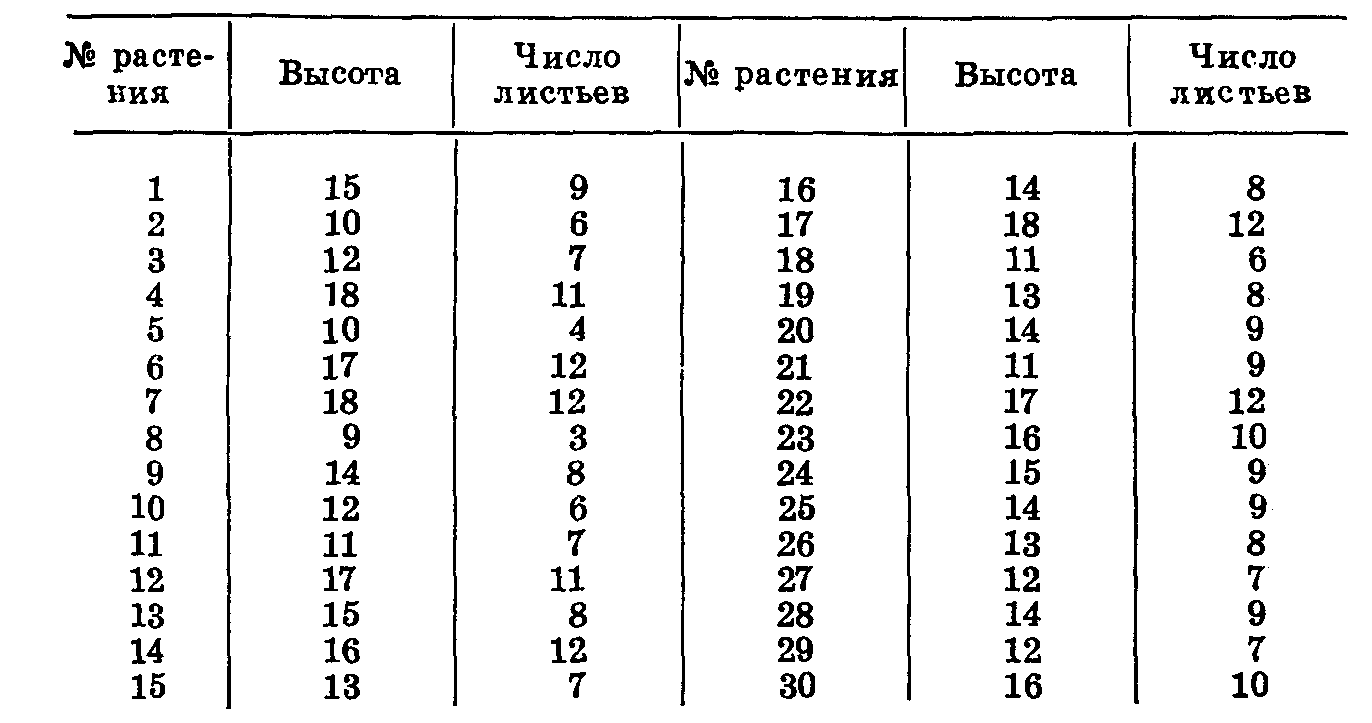
корреляционной решетки. Делается это следующим образом. При сборе данных изучаемые показатели записываются по каждому объекту. Например, изучая связь между высотой растения и числом листьев, записываем (табл. 26).
Мы получили данные по двум показателям: х — высота растений и y — число листьев. Построим вариационные ряды и расположим их: один — в горизонтальном и второй — в вертикальном направлении. Наименьший показатель высоты растений (ряд х) 9, наибольший — 18. Наименьший показатель числа листьев (ряд у) 3, наибольший — 12. В обоих случаях амплитуда изменчивости равна 9.
Разбивать варианты на классы нет необходимости. Построим корреляционную решетку (табл. 27).
Таблица 27
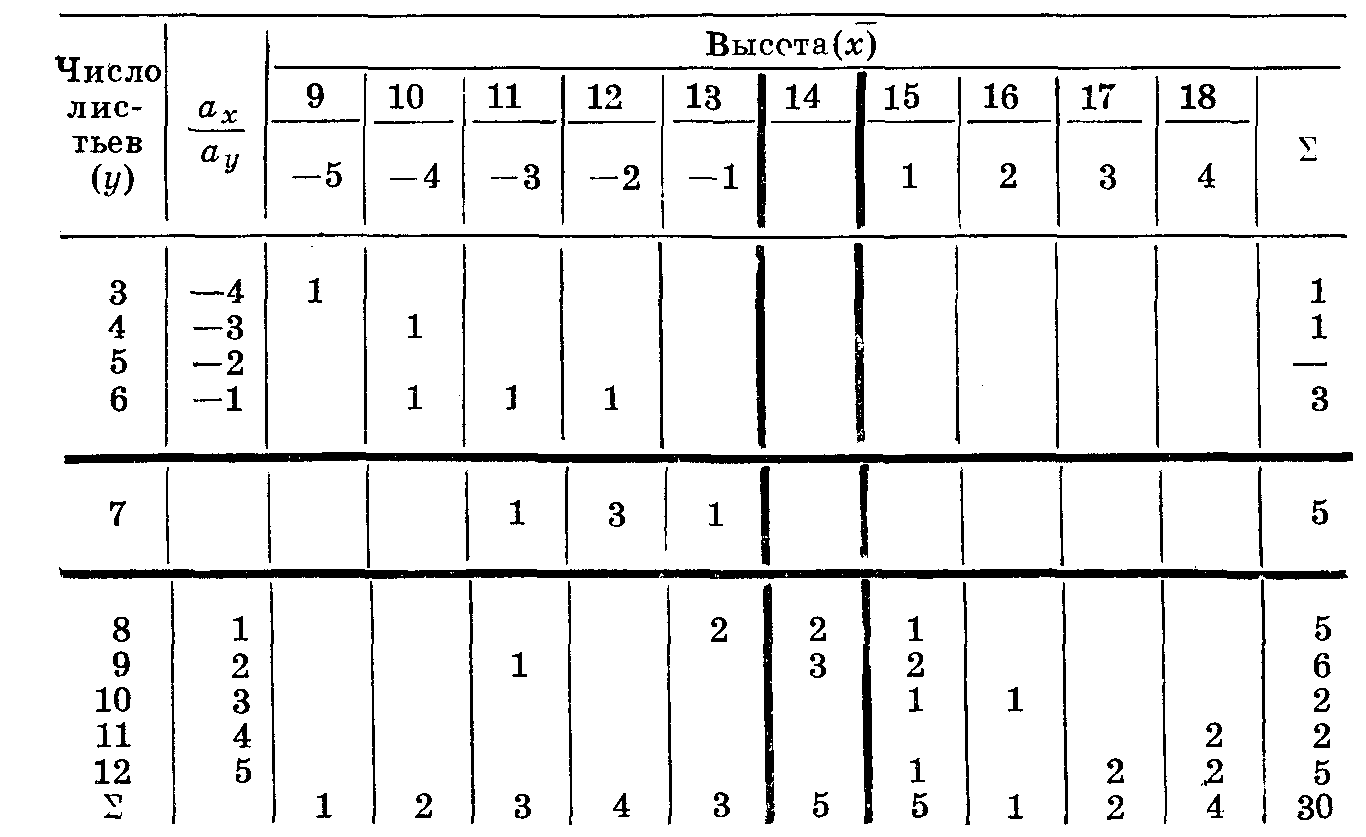
Сделаем разноску. Для этого, пользуясь принятым в статистике приемом, обозначим частоты точками. Первое растение имело высоту 15 см и число листьев 9. Ставим точку на пересечении графы 15 и строчки 9. У второго растения высота 10 см и число листьев 6. Ставим точку на пересечении графы 10 и строчки 6 и т. д. После разноски заменяем условные знаки цифрами.
Подсчитываем сумму дат по вертикали и горизонтали. Находим общую сумму (она должна быть одинаковой при подсчете по вертикали и горизонтали и равна числу наблюдений). У нас эта сумма равна 30, что соответствует числу взятых для опыта растений. Следовательно, разноска произведена правильно.
В качестве условных средних возьмем 14 по ряду x и 17 по ряду y. (Можно взять и другие даты). Отграничим условные средние волнистыми чертами или красным карандашом. Вычислим отклонения от условного среднего и запишем их в рубрики аx и аy Корреляционная решетка подготовлена для дальнейших вычислений. Даже не производя вычислений, по расположению вариант мы видим, что между двумя изучавшимися величинами существует хорошо выраженная положительная корреляция (даты расположены вокруг диагонали, идущей из левого верхнего угла в правый нижний).
Линиями, отграничивающими средние, решетка разбита на четыре квадрата. Обозначим их I, II, III, IV.
Для вычисления коэффициента корреляции нам необходимо найти сумму произведений отклонений на частоты (Σахан). Удобнее находить эту сумму по квадратам.

Нам надо найти bx, by,, σx , σy. Вычислим эти показатели для рядов x и у. (Табл. 28 и 29). Таблица 28
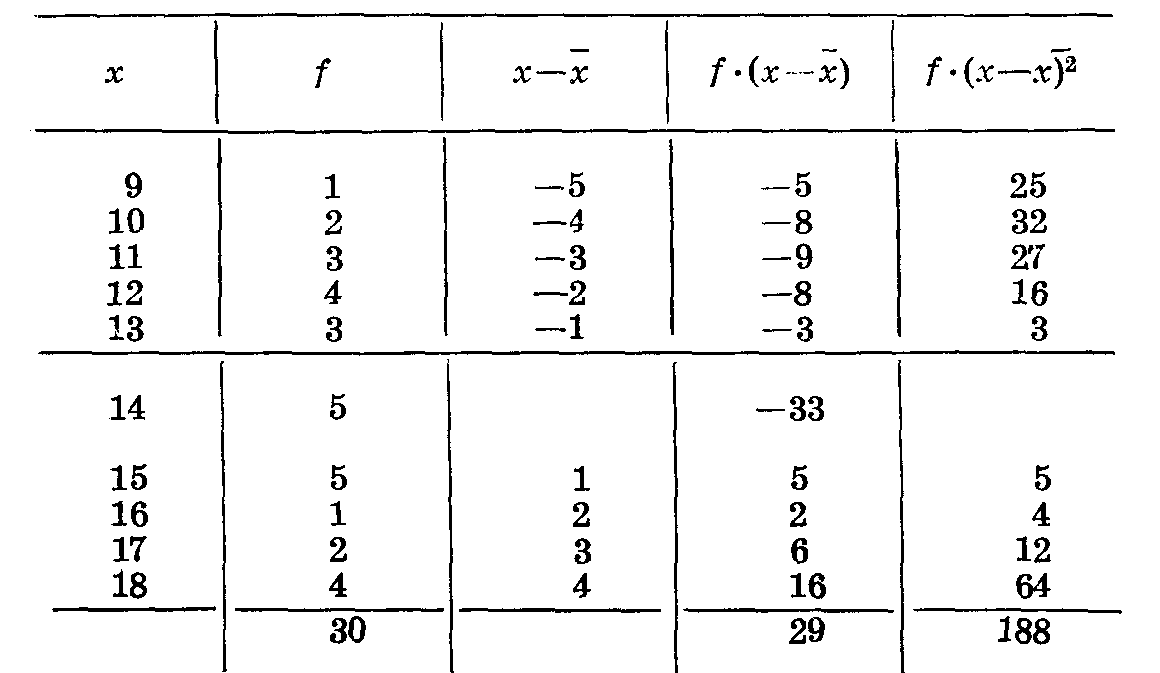
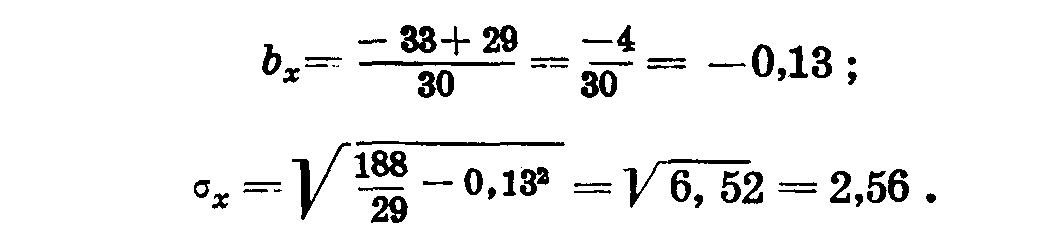
Таблица 29

Определим ошибку коэффициента корреляции по формуле:
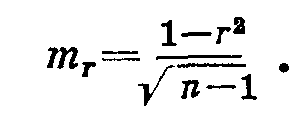
В нашем примере
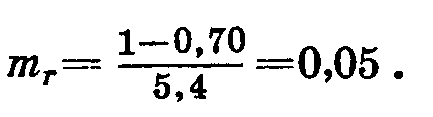
Следовательно, мы записываем результаты наших расчетов в виде
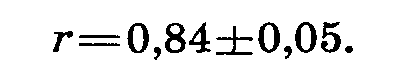
Мы убедились, что между высотой растений и числом листьев существует ясно выраженная положительная корреляция.
Разберем другой пример. Определим коэффициент корреляции между количеством колосков и количеством зерен в колосе пшеницы (табл. 30).
Таблица 30
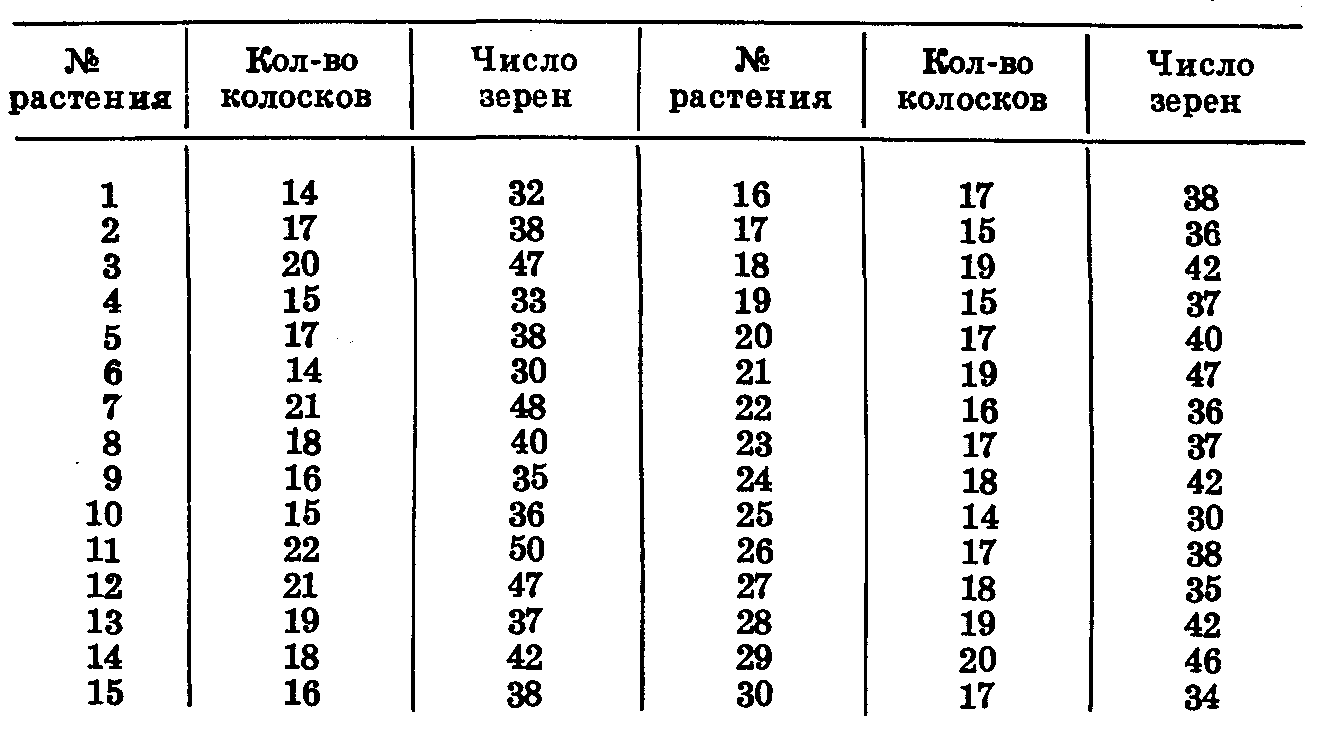
Число колосков в колосе колеблется от 14 до 22, амплитуда изменчивости равна 8. Разбивать варианты на классы не надо.
Количество зерен в колосе колеблется от 30 до 50, амплитуда изменчивости составляет 20. Этот ряд необходимо разбить на классы таким образом, чтобы число классов было близко к числу вариант первого ряда. Примем размер класса равным 3. Построим корреляционную решетку (табл. 31). Число колосков — х, число зерен в колосе у.
Таблица 31
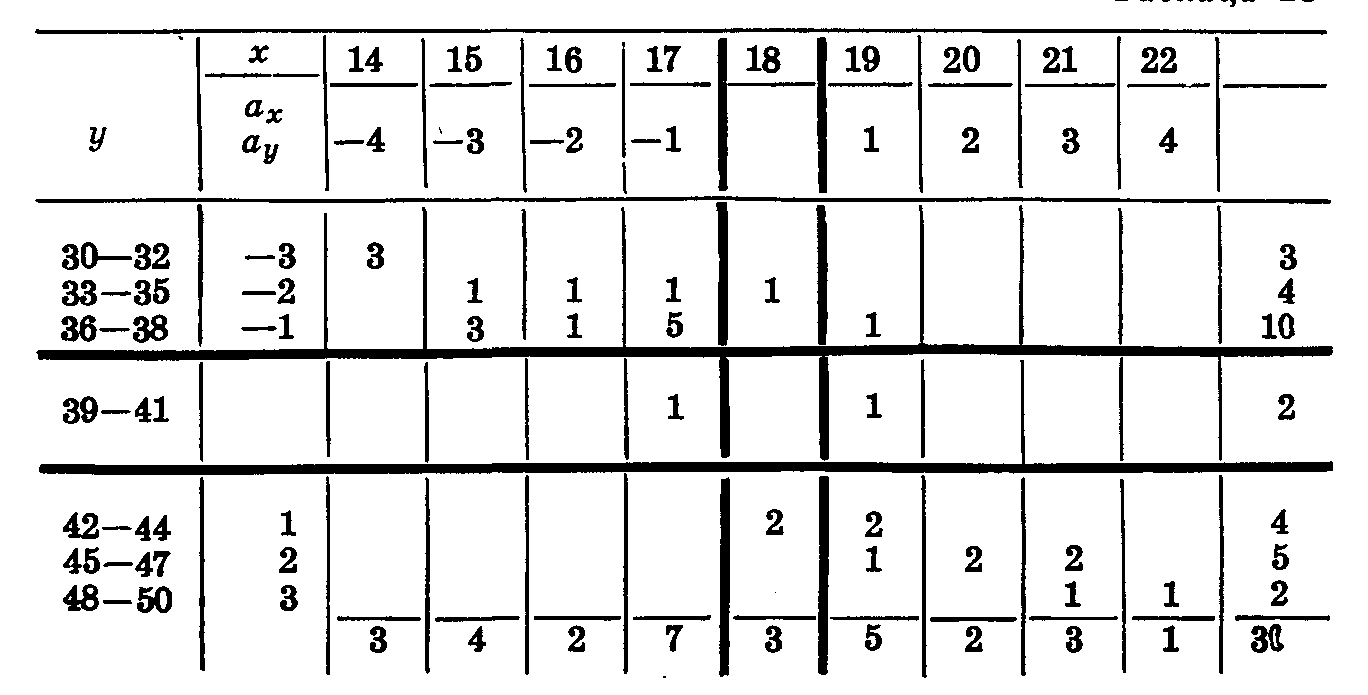
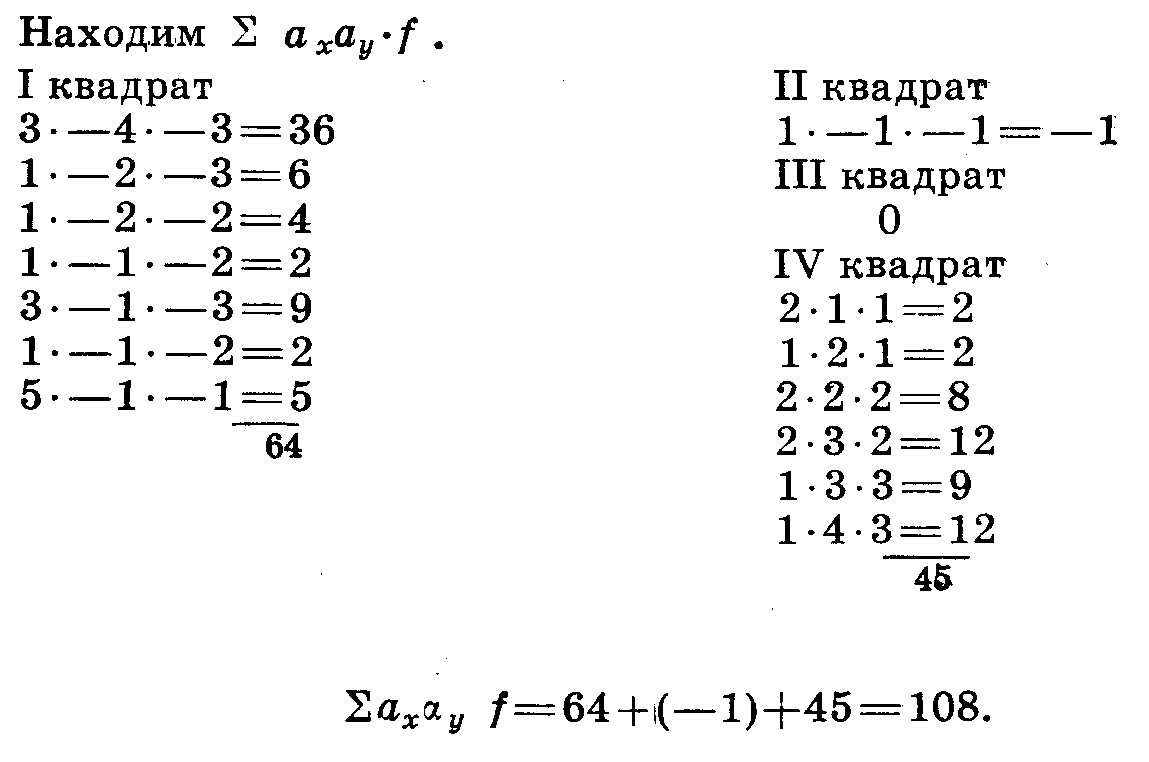
Сумма произведений частот на отклонения Σ ax ay f = 108. Находим b и σ по рядам х и у (табл. 32, 33).
Таблица 32
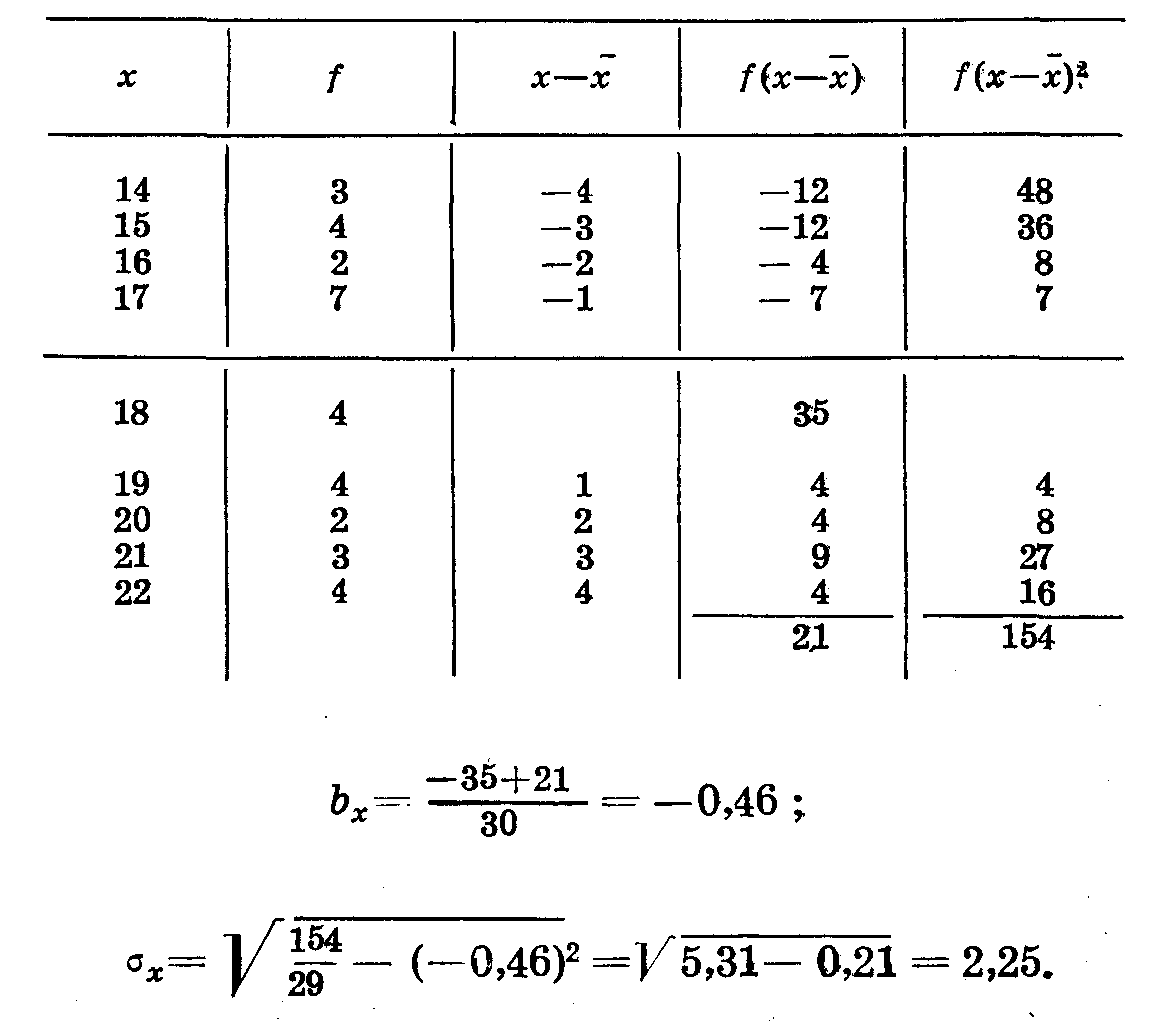
Таблица 33
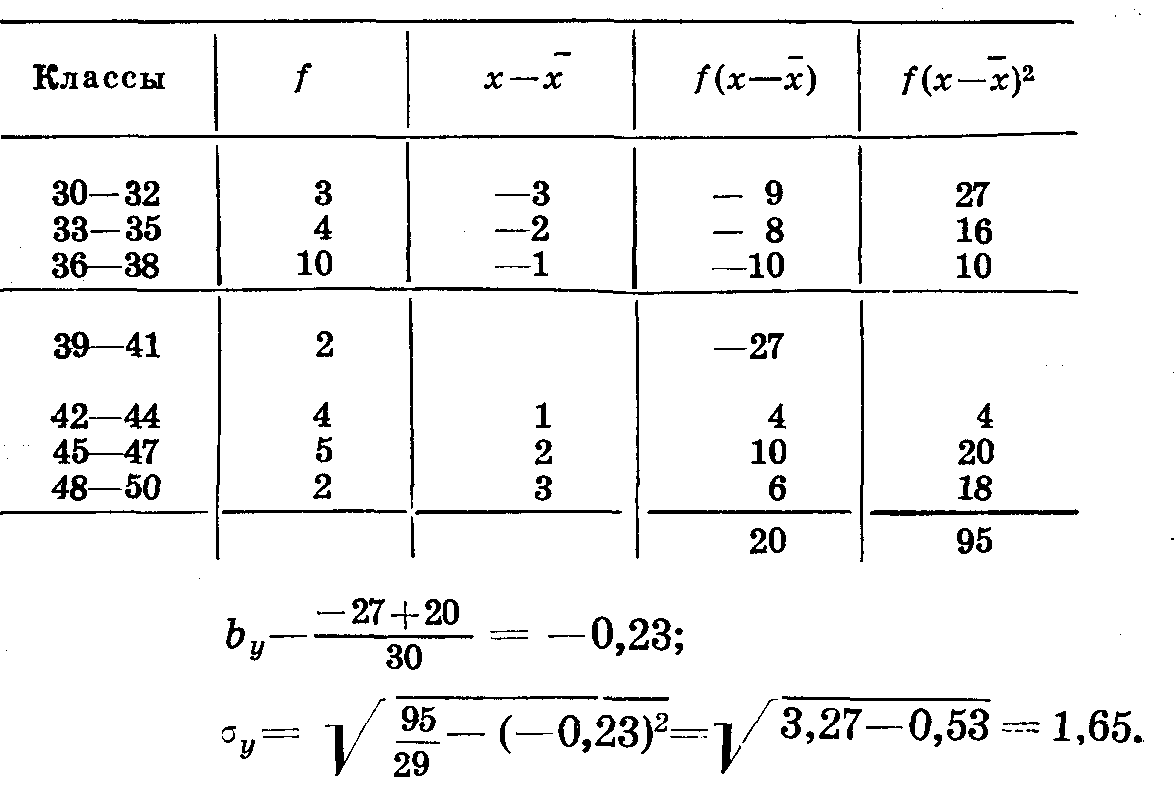
Примечание. При вычислении коэффициента корреляции r умножение на размер класса не производится.
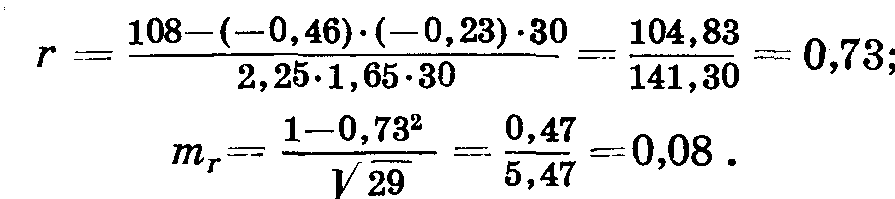
Таким образом,
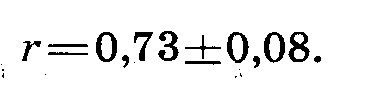
Между числом колосков и числом зерен в колосе имеется хорошо выраженная положительная корреляция.
КОРРЕЛЯЦИЯ КАЧЕСТВЕННЫХ ПРИЗНАКОВ
Между качественными признаками часто наблюдается корреляция. Из повседневных наблюдений мы знаем, что большинство людей, у которых темные волосы, имеют и темные глаза и, наоборот, у большинства блондинов светлые глаза. Исключения встречаются, но сравнительно редко.
Часто установление корреляции между качественными признаками представляет интерес для исследователя. Назовем в качестве примера корреляцию между формой куста злаков и характером расположения корневой системы, окраской и качеством шерсти у пушных животных, типом телосложения и молочностью у коров и т. д.
 Математик Юл разработал способ определения корреляции между качественными показателями.
Математик Юл разработал способ определения корреляции между качественными показателями.При сборе данных показатели, степень взаимосвязи между которыми мы хотим определить, записываются параллельно по каждому объекту (табл. 34).
Составляют корреляционную решетку, имеющую 4 поля. Затем делают разноску, пользуясь обычными, принятыми в статистике знаками После окончания разноски знаки заменяют цифрами. Допустим, мы получили следующие данные (табл. 35):
Таблица 34 Таблица 35

Формулу Юла можно применять и для упрощенного вычисления корреляции между количественными признаками после того, как составлены обычные корреляционные решетки. Возьмем в качестве примера вычисление коэффициента корреляции между весом семян и общим весом растений житняка, приведенное в книге П. Н. Константинова. Вес семян —у, общий вес —х (табл. 36. 37, 38).
Таблица 36
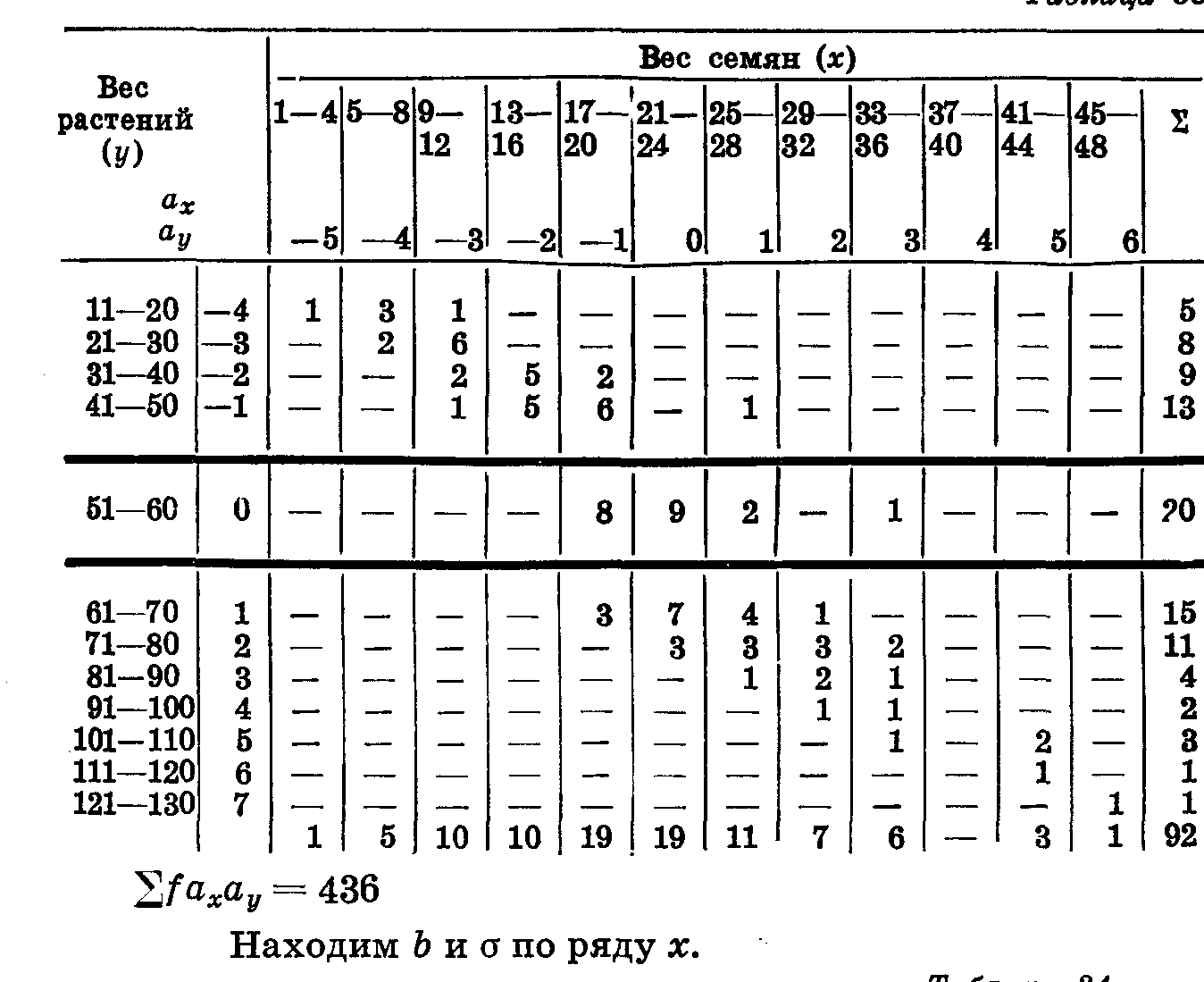
Таблица 37
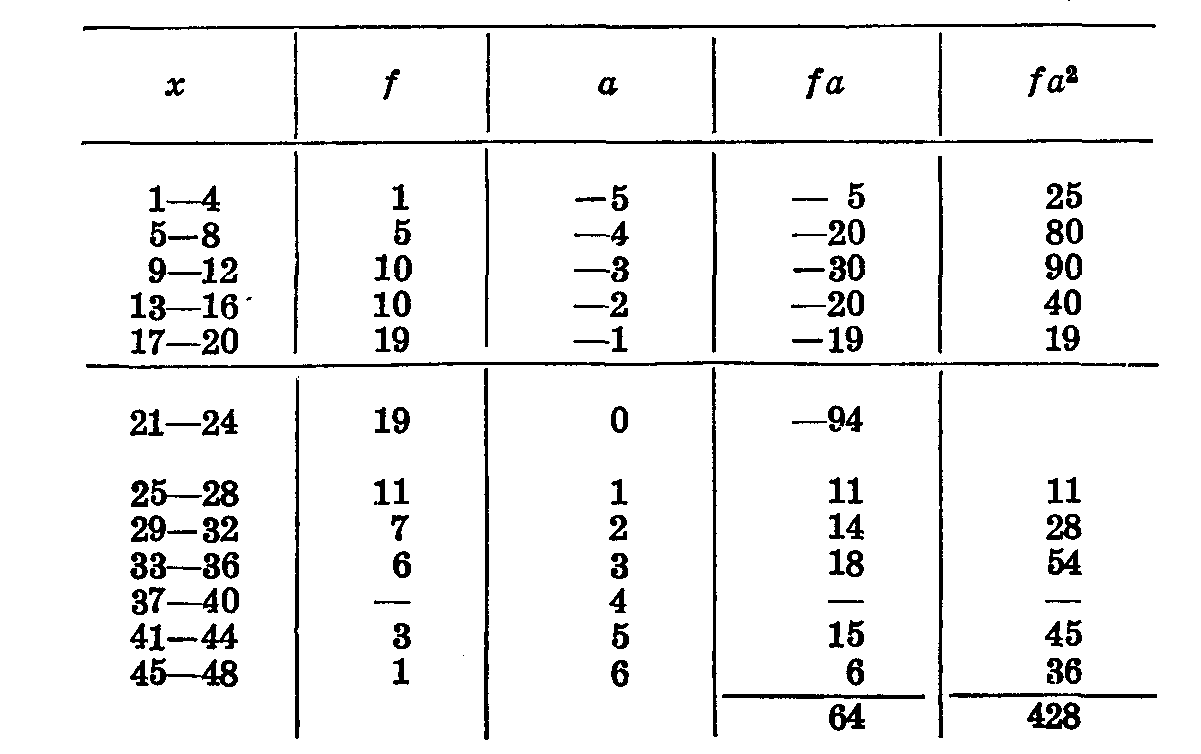
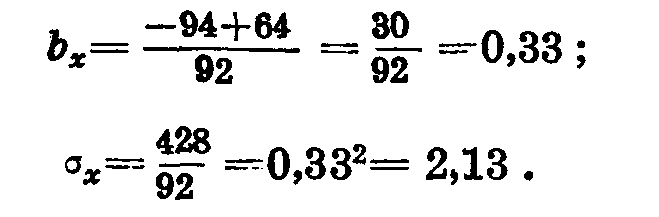
Находим b и σ по ряду у.
Таблица 38
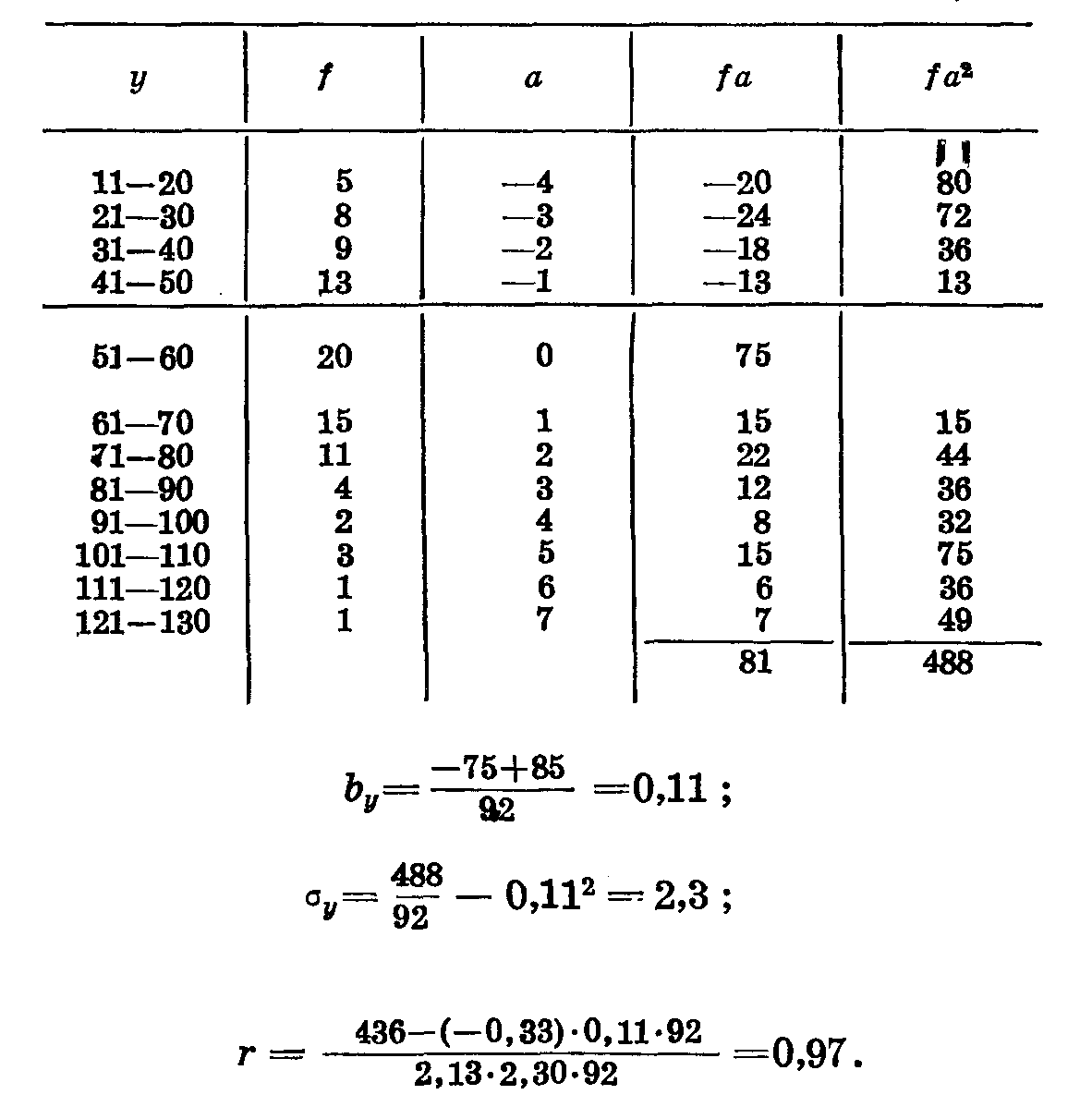
Применим к вычислению коэффициента корреляции формулу Юла. Для этого разобьем корреляционную решетку на 4 поля, приняв за границы полей линии, отграничивающие условные средние.
В первом квадрате нашей корреляционной решетки (табл. 39) 34 варианты. Записываем их в левую верхнюю клетку. Во втором квадрате 1 варианта, записываем ее в правую верхнюю клетку (ниже среднего по ряду х и выше среднего по ряду у). В третьем квадрате 3, в четвертом — 24 варианты. Записываем их в соответствующие клетки. Находим суммы по вертикали и горизонтали. Заносим все эти данные в решетку. Число наблюдений уменьшилось потому, что мы отбросили варианты, расположенные на средних линиях. Находим коэффициент корреляции по формуле Юла:
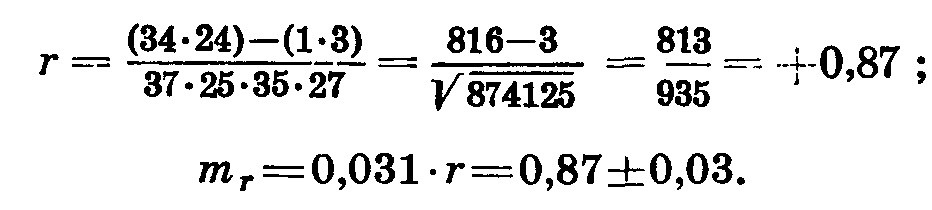
Таблица 39
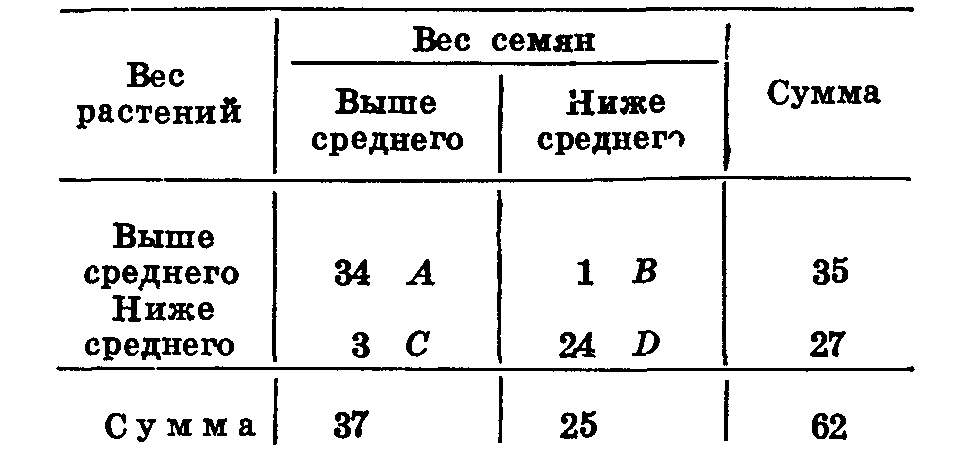
Результат указывает на наличие очень высокой степени корреляции и близок к определенному нами при детальных расчетах. Такой способ вычисления применяют в тех случаях, когда требуется дать приблизительную характеристику взаимной связи большого количества пар признаков.
КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ
Поставленный опыт по изучению влияния нормы высева семян на урожай ярового ячменя дал такие результаты (табл. 40)
. Таблица 40

Попробуем изобразить (табл. 41) намечающиеся закономерности на корреляционной решетке (х — урожай, у — норма высева).
Таблица 41

Корреляция отсутствует. Между тем, анализируя данные таблицы, видим, что между нормой высева и урожайностью имеется вполне определенная связь: с увеличением нормы высева от 100 до 150 кг]га урожайность растет. Дальнейшее увеличение нормы высева влечет за собой ее снижение.
Связь между изменением двух признаков, при которой равномерному изменению признака соответствуют неравномерные изменения второго признака, причем эта неравномерность имеет определенный и закономерный характер, называется криволинейной. Степень взаимной зависимости двух переменных величин при криволинейной связи показывает корреляционное отношение.
На существование прямолинейной (корреляционной) или криволинейной связи между двумя переменными указывает расположение вариант в корреляционной решетке: при наличии прямолинейной корреляции варианты группируются вокруг той или иной диагонали, образуя в общем очертании эллипс, размеры меньшего диаметра которого зависят от тесноты связи между признаками. При криволинейной связи общее очертание расположения вариант в корреляционной решетке имеет вид неправильно изогнутой фигуры.
Корреляционное отношение обозначается греческой буквой η (эта). Оно имеет значение от 0 до 1.
Рассмотрим определение корреляционного отношения сначала на упрощенном примере, взятом из книги «Биометрия» Н. А. Плохинского.
Имеется группа из 6 особей, у каждой особи измерено два признака — V1 и V2. В результате получены следующие данные:
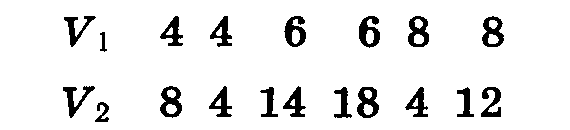
Особи по первому признаку могут быть разбиты на группы с одинаковым значением этого признака (4, 6, 8). К каждой такой группе по второму признаку относится по 2 особи. Найдем среднее значение второго признака для каждой группы. Теперь к имеющимся двум рядам мы можем приписать третий, состоящий из частных средних по второму признаку.
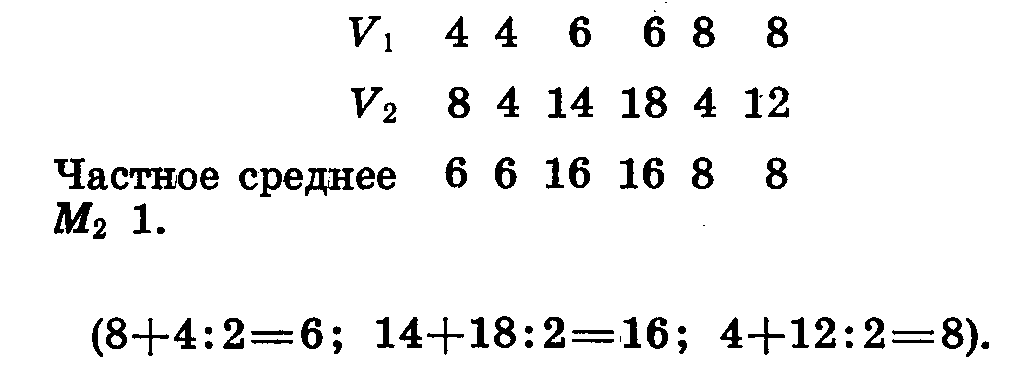
Сопоставляя частные средние по второму признаку с рядом значений первого признака, видим, что при увеличении первого признака на одну и ту же величину (2) второй признак сначала резко увеличивается (с 6 до 16), а затем так же резко уменьшается (с 16 до 8).
Степень разнообразия частных средних можно выразить суммой квадратов отклонений частных средних от общей средней по второму признаку.
Определим это общее среднее:
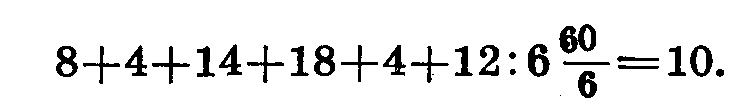
Отклонения частных средних от общего среднего равно —4, —4, +6, +6, —2, —2. Возведя эти данные в квадрат, получаем 16, +16, +36, +36, +4, +4. Сумма квадратов отклонений равна 112.
Найдем отклонения от общей средней по каждой дате второго признака:
—2, —6, +4, +8. Возведем эти данные в квадрат:
+4, +36, +16, +64== 160. Запишем все ати показатели в общую таблицу (табл. 42).
Таблица 42
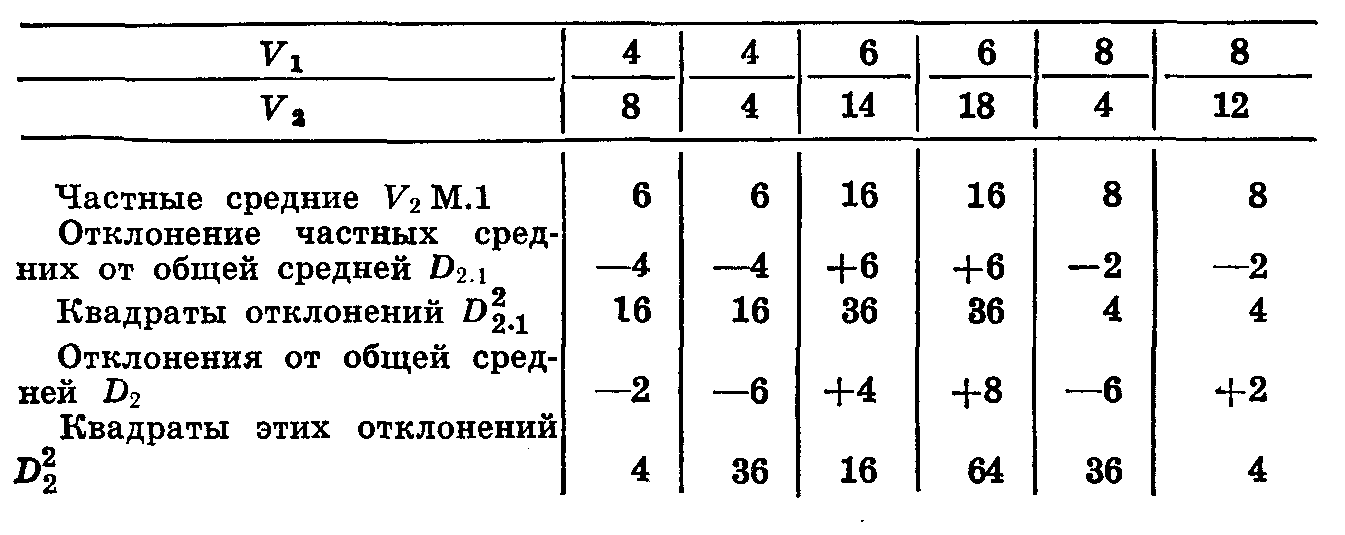
Общее среднее равно 10.
Сумма квадратов отклонений частных средних от общего среднего по второму признаку (V2) равна 16+16+36+36+ +4+4 ==112 (частное разнообразие). Сумма квадратов отклонений каждого признака второго ряда от общего среднего равна 4+36+16+64+36+4 ===160 (общее разнообразие).
Отношение частного разнообразия к общему равно квадрату корреляционного отношения второго признака по первому:
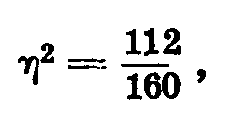
отсюда корреляционное отношение второго признака по первому в рассматриваемом примере равно
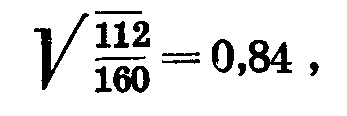
что указывает на сильную связь второго призняка с первым. Рассмотрим теперь приведенный в таблице 40 пример влияния норм высева на урожайность ячменя. Для сокращения расчетов возьмем пять вариантов опыта. Нормы высева: 100, 125, 150, 175 и 200 кг/га. —V1 нормы высева, V2— урожайность. Нормы высева предусмотрены схемой опыта и безусловно одинаковы для всех трех повторностей. Урожаи по повторностям варьируют. Каждому значению V1 соответствуют три значения V2. Составим таблицу 43.
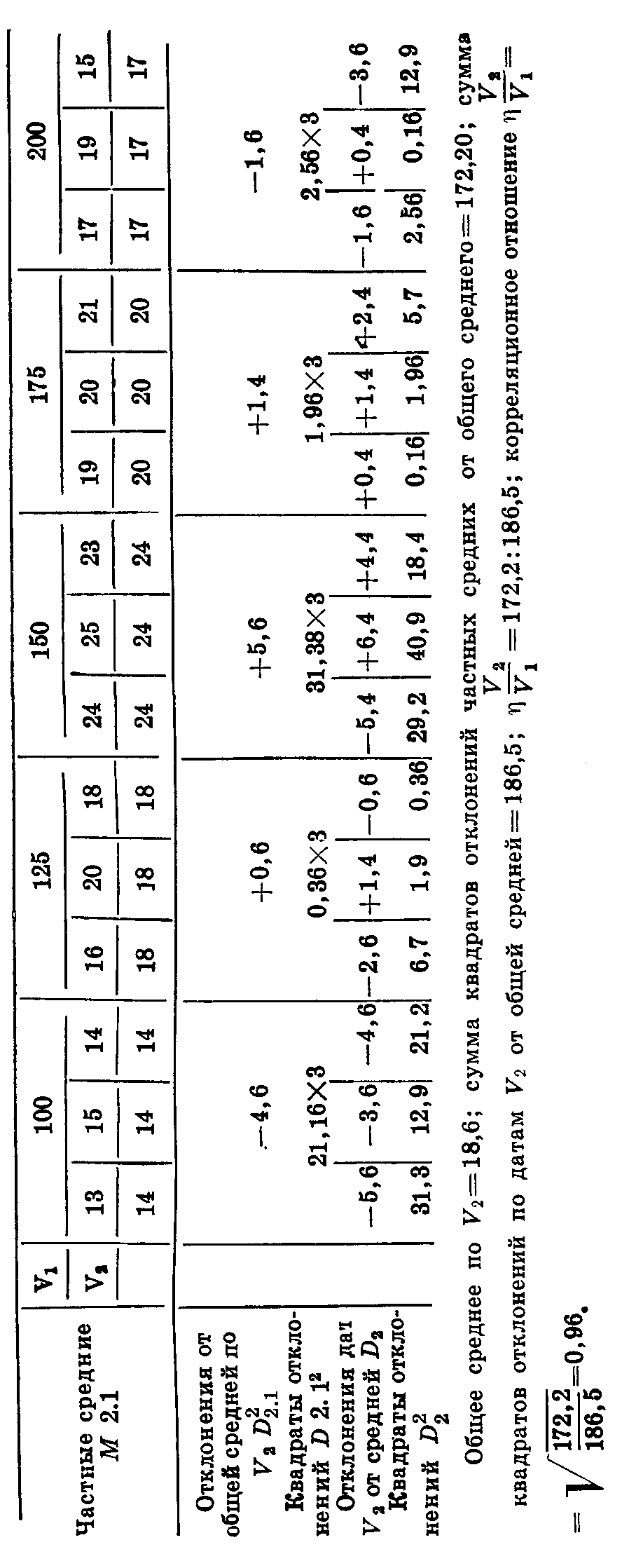
Поскольку частное среднее первого признака (урожайности) для всех трех повторностей одинаково при одном и ром же значении второго признака (нормы высева), то и отклонение от среднего для каждой группы общее. При вычищении суммы квадратов отклонений мы производим умножение полученных по группам квадратов отклонений на частоты (в данном случае на три, так как опыт проведен в трехкратной повторности).
Отношение V2/V1 указывает на зависимость изменения дорого признака (урожайности) от первого (нормы высева). 3 данном случае возможна только зависимость V2/V1 , потопу что норма высева не может изменяться в зависимости от урожайности, но в ряде случаев вычисляют как V2/V1 так и V1/V2. Тогда вычисление проводят так же, как и в разобранных примерах, но группировку данных проводят по V2.
В результате вычисления (табл. 43) получено корреляционное отношение V2/V1 равное 0,96. Это показывает, что норма высева оказывает большое влияние на урожай. Ошибка корреляционного отношения вычисляется по формуле:
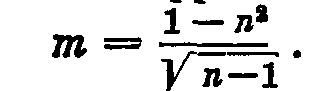
Корреляционное отношение считается существенным в тех случаях, если оно превосходит свою ошибку в три раза и более.
ДИСПЕРСИОННЫЙ АНАЛИЗ
При постановке полевых, вегетационных и лабораторных опытов, так же как и при изучении живых объектов в естественной обстановке, мы всегда наблюдаем некоторое разнообразие изучаемых показателей. Как уже было отмечено, показателем степени разнообразия служит основное отклонение — σ (сигма). Еще более чувствительным показателем степени разнообразия (варьирования, дисперсии, разброса данных) служит σ2 (варианса, девиата, дисперсия) — сумма квадратов отклонений, деленная на число степеней свободы:
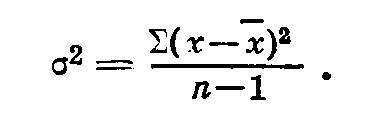
Использование этого показателя для обработки экспериментальных данных, получившее название «дисперсионный анализ», было впервые разработано и применено английским ученым Р. А. Фишером. В настоящее время дисперсионный анализ широко применяется для обработки данных в биологии, промышленности и сельском хозяйстве.
Рассмотрим суть дисперсионного анализа. При постановке опытов мы всегда преследуем цель выявить действие определенного фактора (или факторов) на результативный признак — влияние различных форм и доз удобрений на урожайность, химический состав и другие хозяйственно-ценные свойства культур; сравниваем урожайность и качество различных сортов, изучаем влияние факторов внешней среды на физиологические свойства организмов и т. д. Планируя опыт, мы предусматриваем проведение его в определенном количестве повторностей.
На результативный признак оказывают влияние:
1. Факторы, взятые для изучения.
2. Выровненность условий в отдельных повторностях опыта.
3. Случайные, не предусмотренные в процессе проведения опыта явления.
Основная задача дисперсионного анализа — выявить степень влияния перечисленных факторов на результаты опыта.
Рассмотрим применение дисперсионного анализа на модельном примере: мы берем модельные данные для того, чтобы не отвлекать внимания на сложные расчеты, неминуемо возникающие при обработке фактически полученных данных, где всегда встречаются дробные и смешанные числа.
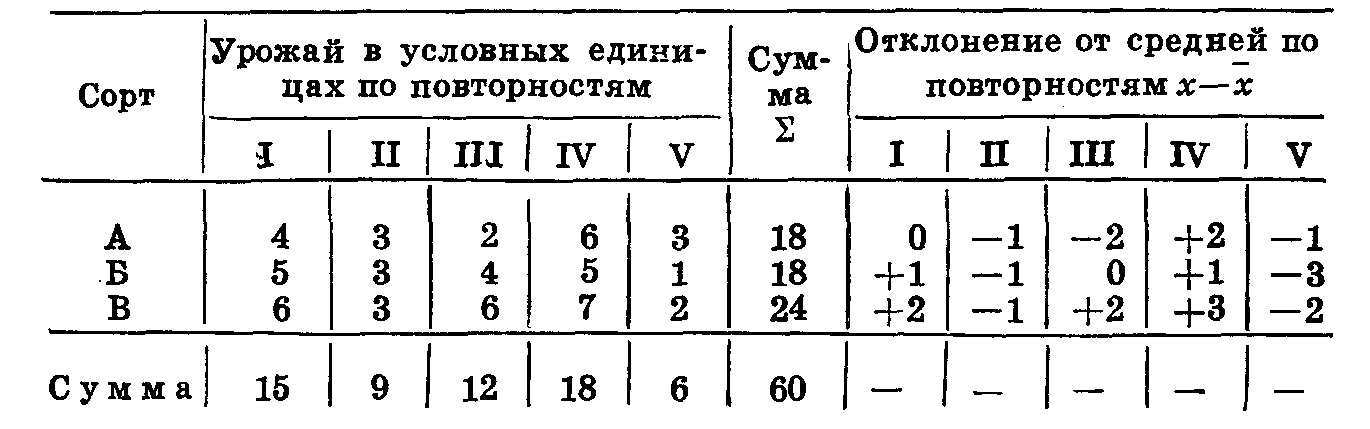
Допустим, мы хотим сравнить в полевых условиях урожайность пяти сортов: А, Б, В, Г, Д. Д — стандарт, лучший районированный в данной области сорт. Остальные сорта выведены селекционером. Нам необходимо установить, какие из новых сортов достоверно превышают по урожайности стандарт. Обычно такой опыт проводят в шести повторностях, мы сокращаем число повторностей до трех, чтобы упростить расчеты (табл. 44).
Таблица 44
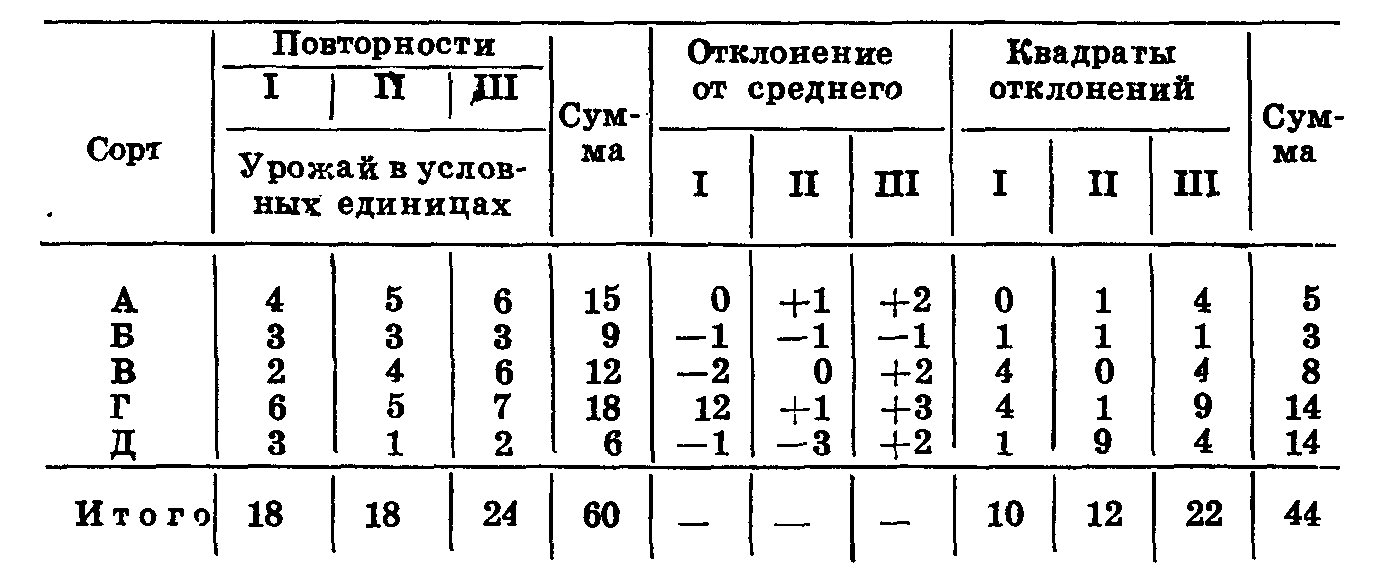
При подсчете суммы урожая по сортам и повторностям итог должен быть одинаковым. В нашем примере он равен 60. У нас было 15 вариантов (5 сортовЗ повторности). Следовательно, средний урожай равен 4. Вычисляем отклонения от среднего по каждой делянке, записываем их в трех столбцах, идущих за суммой урожая по сортам. Возводим эти отклонения в квадрат и суммируем их по столбцам и строкам. Итог должен сойтись. Мы получили 44 — это сумма квадратов отклонений по опыту в целом.
При наличии счетной техники это же вычисление можно
сделать по формуле
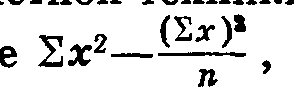
т. е. сумма квадратов отклонений в целом по опыту равна сумме квадратов всех данных опыта минус квадрат суммы данных, деленное на число вариантов (сорта повторности). Нетрудно убедиться, что мы получим такие же данные:
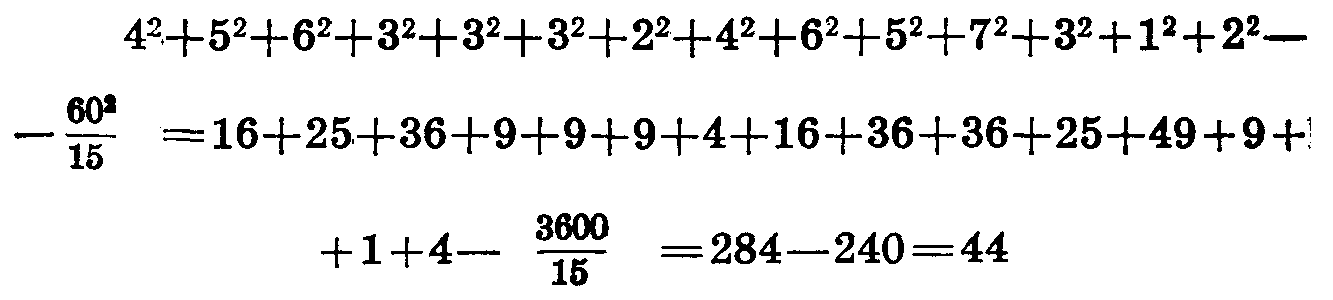
Вычислим сумму квадратов отклонений (табл. 45) по сортам (по вариантам опыта).
Таблица 45
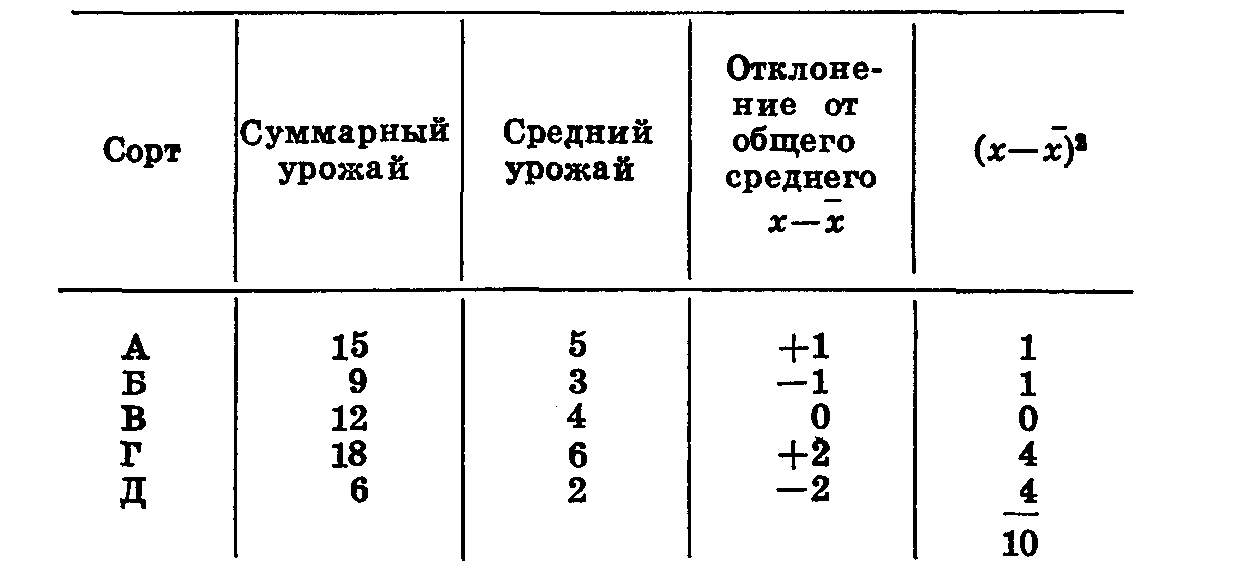
Умножаем полученную сумму на количество повторностей
103=30.
Сумма квадратов отклонений по вариантам опыта (сортам) равна 30. При использовании счетных машин этот показатель вычисляется по формуле:
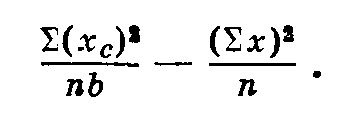
На нашем примере:
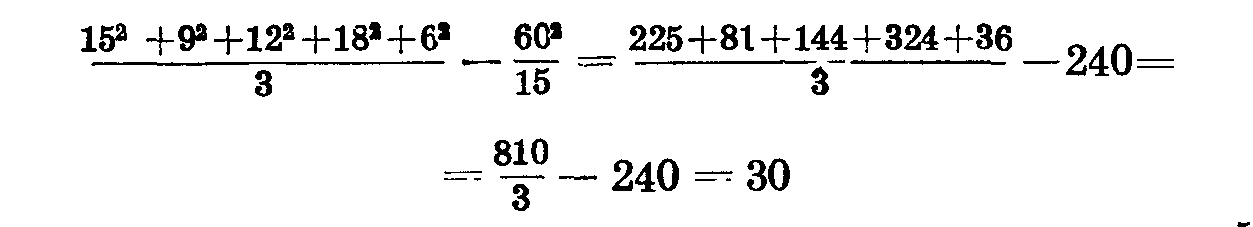
(пb — число повторностей, n — число вариантов опыта).
Сумма квадратов отклонений по сортам равна 30.
Вычислим сумму квадратов отклонений по повторностям
(табл.46).
Таблица 46

Полученную сумму квадратов отклонений умножаем на количество сортов:
0,96 5 = 4,8.
Сумма квадратов отклонений по повторностям равна 4,8. При использовании счетных машин этот показатель вычисляется по формуле:
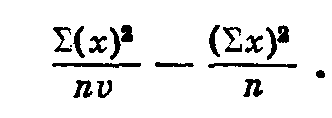
В нашем примере
 (nv — число сортов).
(nv — число сортов). Сумма квадратов отклонений, обусловленных случайными причинами, вычисляется по разности; общая сумма квадратов отклонений по опыту минус сумма квадратов отклонений по сортам (вариантам), минус сумма квадратов отклонений по повторностям.
44—30—4,8 = 9,2.
Составим таблицу дисперсионного анализа (табл. 47). Число степеней свободы для случайного варьирования равно произведению чисел степеней свободы по сортам и повторностям :
4 Х 2 = 8.
F равно частному от деления вариансы по вариантам опыта на вариансу случайную:
7,5 : 1,15 = 6,52.
Табличное F при двух уровнях вероятности находят по таблице, имеющейся во всех руководствах по биометрии.
Таблица 47

Если фактическое F больше табличного, то различия между вариантами опыта реальны. Мы видим, что по сортам F больше табличного при вероятности 0,95, по повторностям F меньше табличного. Следовательно, между урожайностью сортов есть различия, повторности же выровнены, разница между ними лежит в пределах ошибки опыта.
Для сравнения урожайности сортов необходимо вычислить наименьшую существенную разность — НСР. Для этого определяем σ (основное отклонение), равное корню квадратному из вариансы случайной:
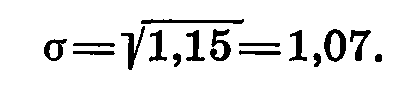
Ошибка среднего вычисляется по формуле
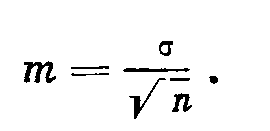
При дисперсионном анализе она равна σ, деленной на корень квадратный из числа повторностей.
Определим обобщенную ошибку среднего. Для этого разделим σ на корень квадратный из числа повторностей:
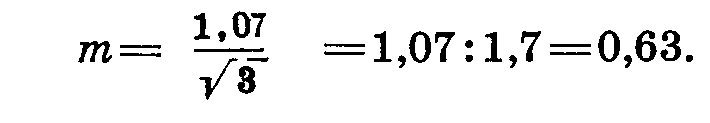
Поскольку ошибка для всех сравниваемых вариантов одна, формула ошибки разности
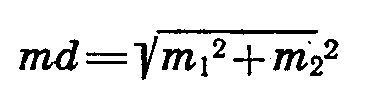
превращается в формулу
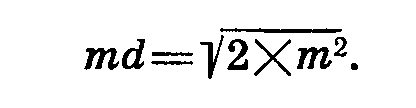
В нашем примере
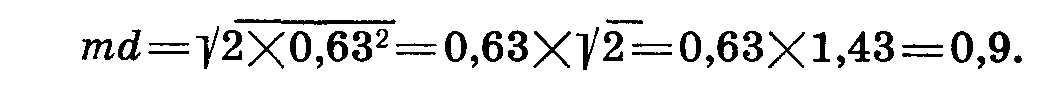
Достоверность разности определяется с помощью критерия t Стьюдента, который представляет собой отношение разности к ее ошибке при различном числе степеней свободы и различном уровне вероятности. Приводим таблицу 48.
Таблица 48
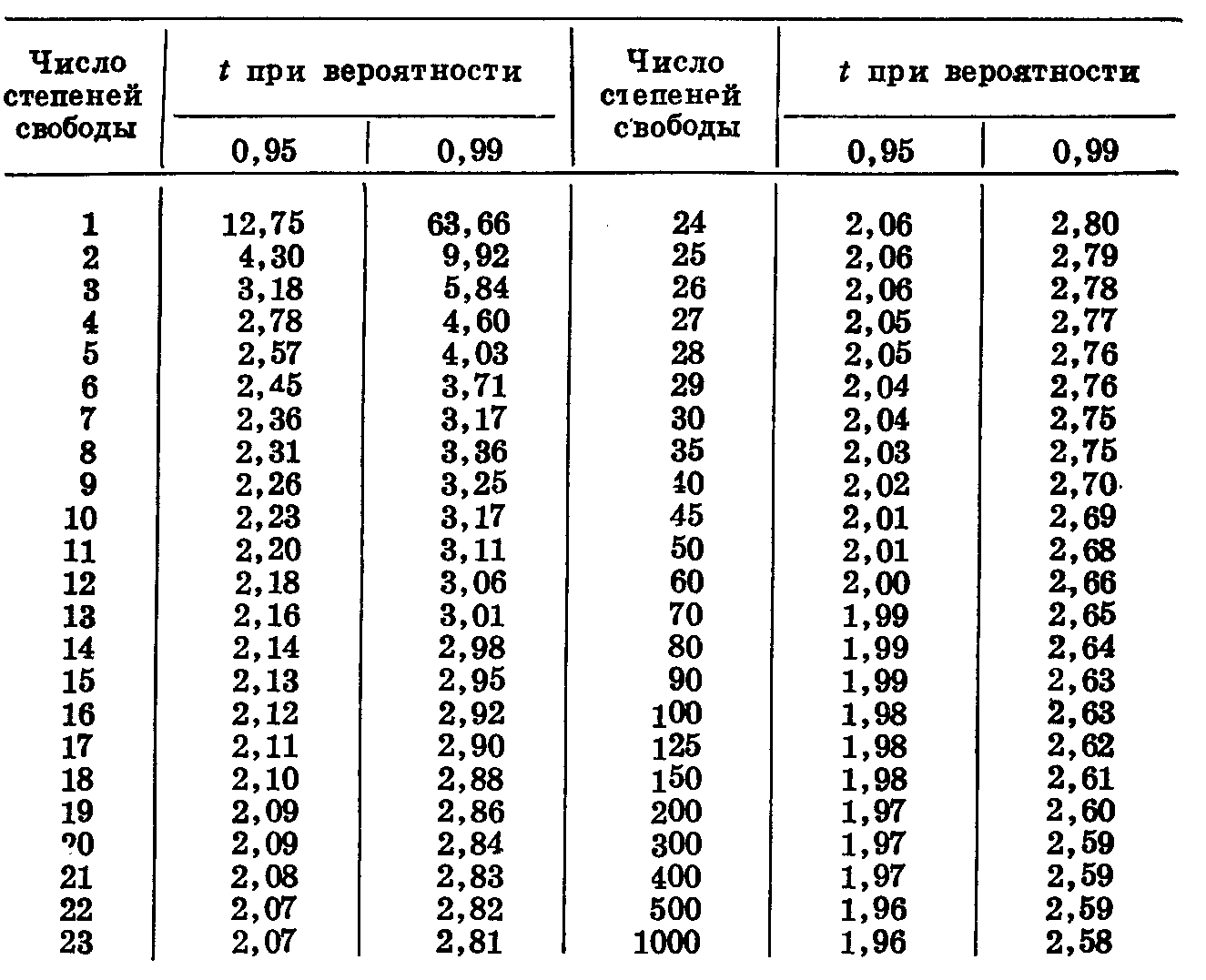
Наименьшая существенная разница (НСР) между изучаемыми вариантами опыта определяется путем умножения ошибки разности на t при принятой вероятности и числе свободы по случайной вариансе. В нашем опыте при вероятности Р = 0,95
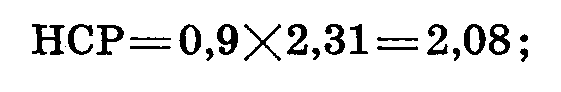
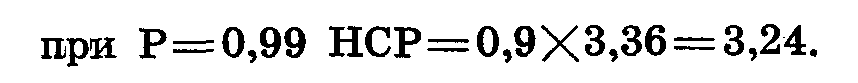
Вернемся к результатам опыта (табл. 49).
Сорта А и Г дали достоверное Таблица 49
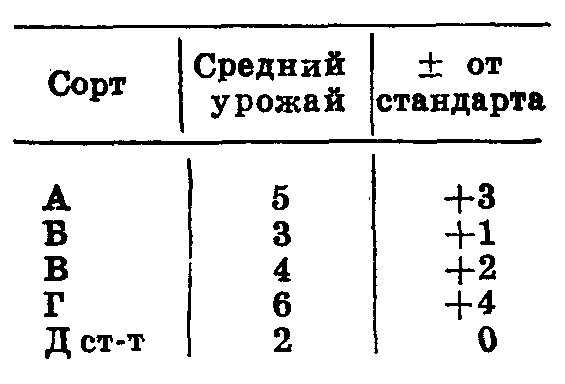
превышение над стандартом
А — при вероятности 0,95, Г — при вероятности 0,99. Урожайность сортов В и Б достоверно не отличается от стандарта (разница меньше НСР).
Возьмем другой пример. Испытывалось три сорта в пятикратной повторности. Получены следующие данные (табл. 50). Средний урожай по опыту
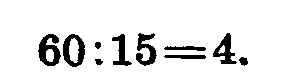
Возводим отклонения в квадрат и суммируем. Сумма квадратов отклонений — 44. Сумма квадратов отклонений по сортам — 4,8, по повторвостям — 30.
Составим таблицу дисперсионного анализа (табл. 51).
Таблица 50
F по сортам значительно меньше табличного. Следовательно, опыт не позволил выявить особенности сортов. По повторностям F больше табличного: в пределах одного сорта
Таблица 51

получены достоверные различия по повторностям. Отсюда вывод: опыт не удался потому, что условия по повторностям были не идентичны. При повторении опыта следует выбрать более выровненный участок.
Таким образом, дисперсионный анализ позволяет не только убедиться в существовании достоверных различий по изучаемым вариантам, но и понять причину неудачи (если F по повторностям было бы меньше табличного, то отсутствие разницы между сортами по урожайности можно было объяснить фактическим отсутствием такой разницы. Это говорило бы о том, что включенные в опыт сорта не отличались по урожайности).
Таблица 52
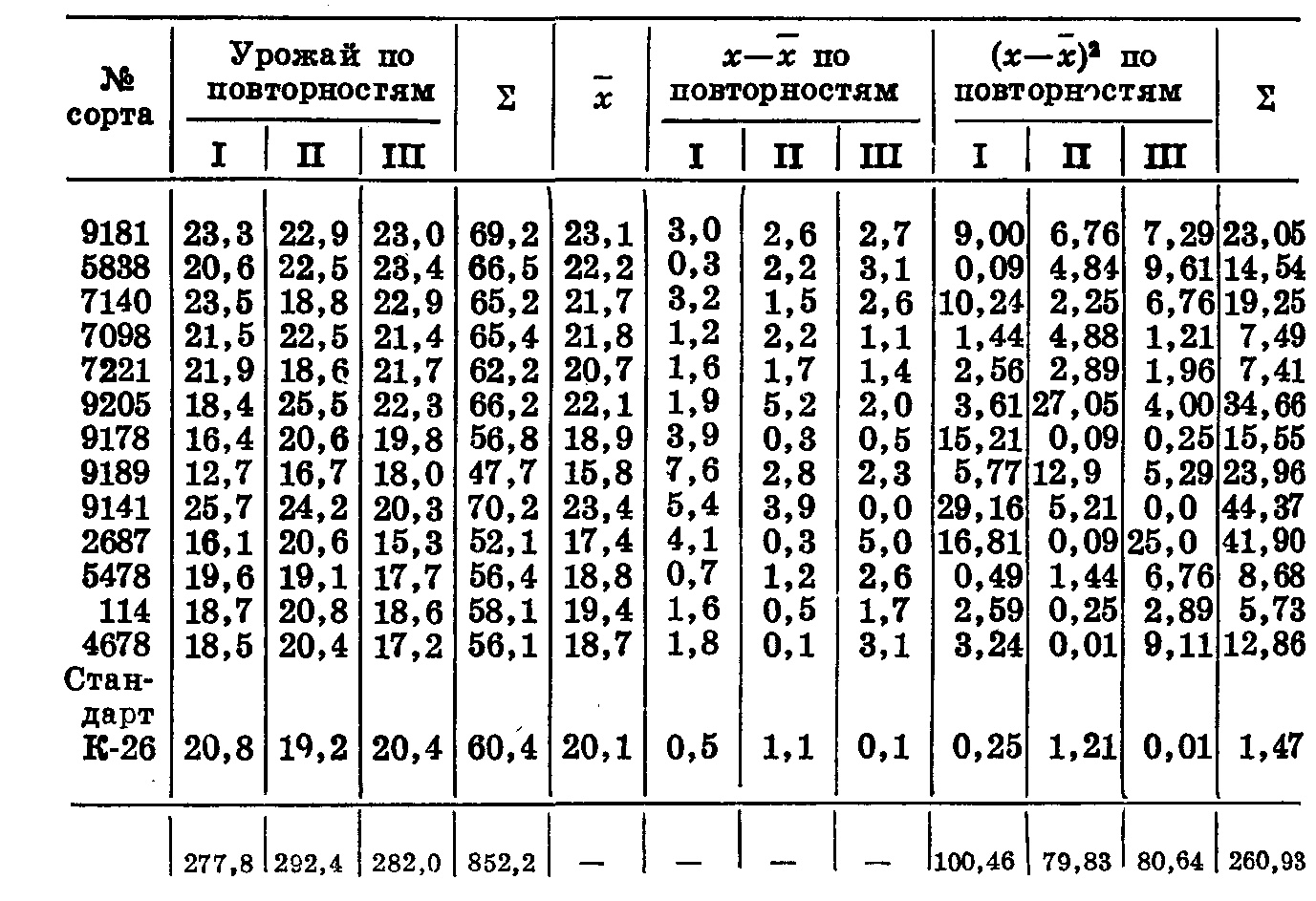
Рассмотрим применение дисперсионного анализа на фактическом материале (табл. 52). В таблице 52 показаны урожайность сортов яровой пшеницы, испытывавшихся в конкурсном сортоиспытании, и расчеты, позволившие определить сумму квадратов отклонений по опыту в целом.
Определим сумму квадратов отклонений по сортам (табл. 53).
Определим сумму квадратов по повторностям (табл. 54). Составим таблицу дисперсионного анализа (табл. 55).
Наличие сортовых различий доказано (F больше F табличного).
Таблица 53
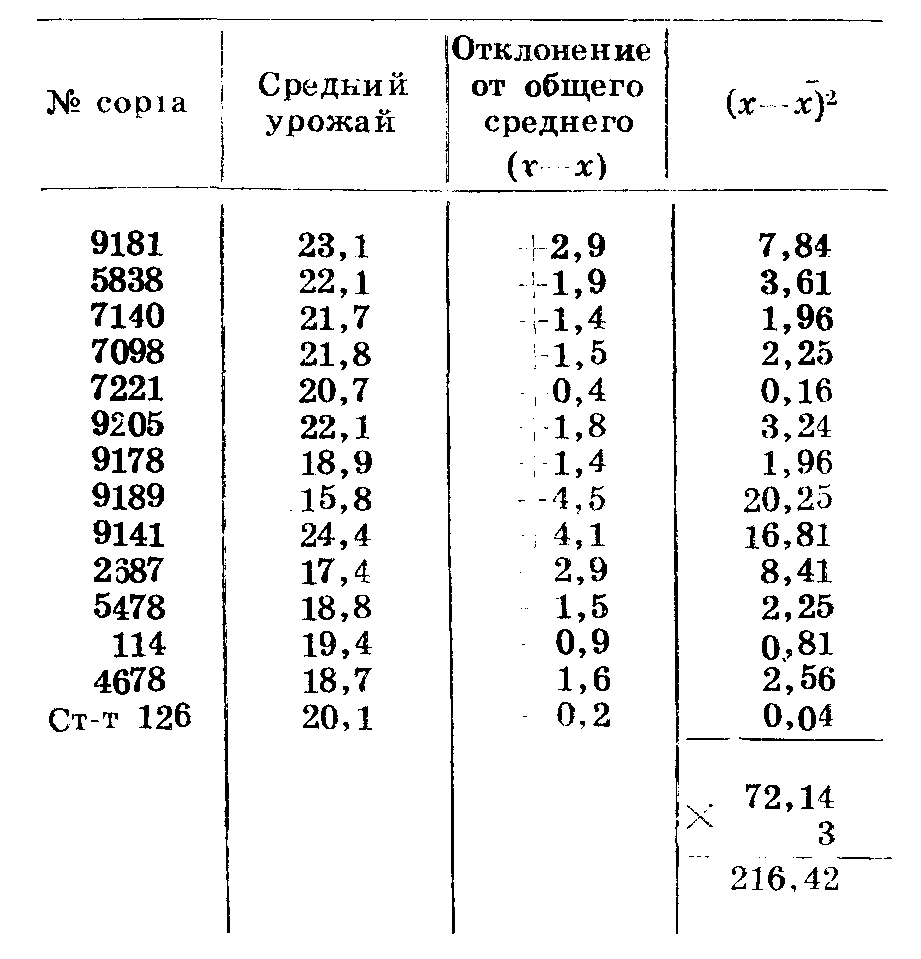
Таблица 54

Таблица 55

Различия по повторностям незначительны (F меньше F табличного):
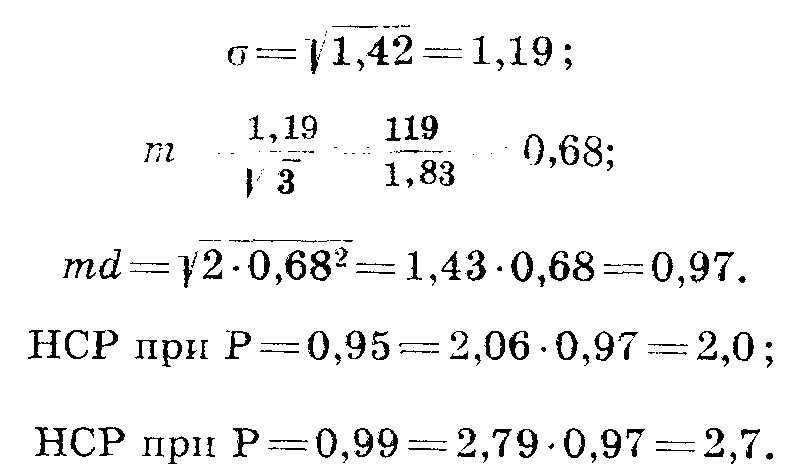
Сопоставим урожайность испытывавшихся сортов с урожайностью стандарта (табл.56).
Таблица 56
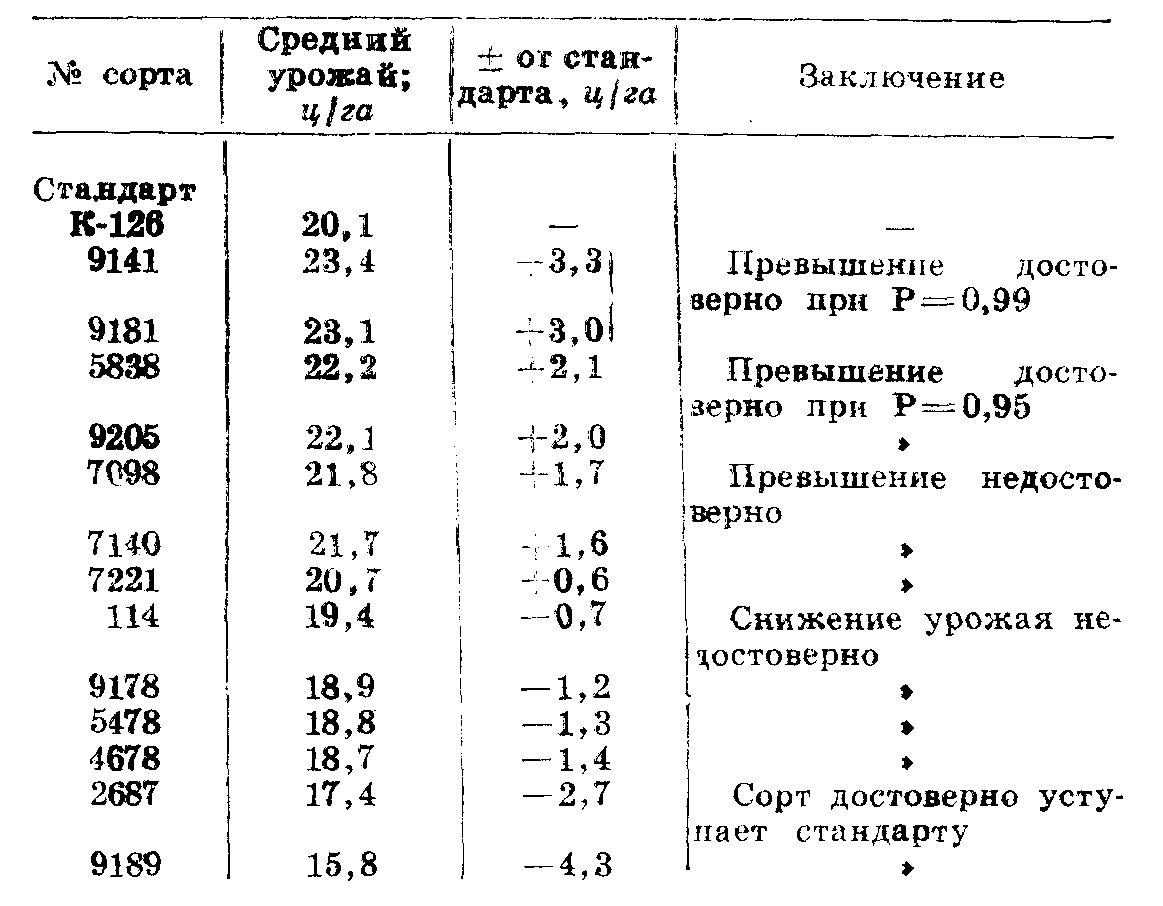
Задачи
1. В опытах по изучению влияния облучения привоев яблони гамма лучами подсчитано число листьев на 1 м однолетнего прироста. Получены следующие данные.
Число листьев на 1 м однолетнего побега:
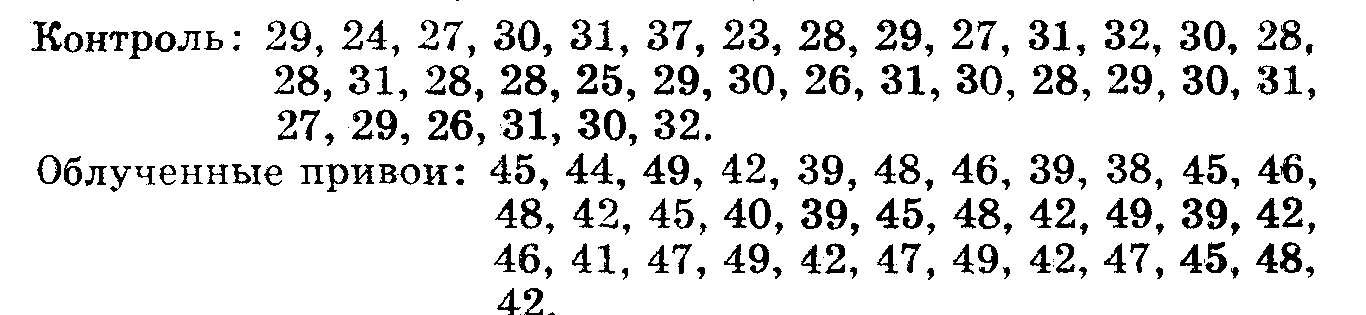
Проведите необходимые вычисления, чтобы доказать:
а) Повлияло ли облучение на облиственность побегов?
б) Усилило ли облучение степень изменчивости по этому признаку?
2. Поражение пыльной головней исходного сорта яровой пшеницы и заложенных из него линий характеризовалось следующими показателями (табл. 57).
Таблица 57
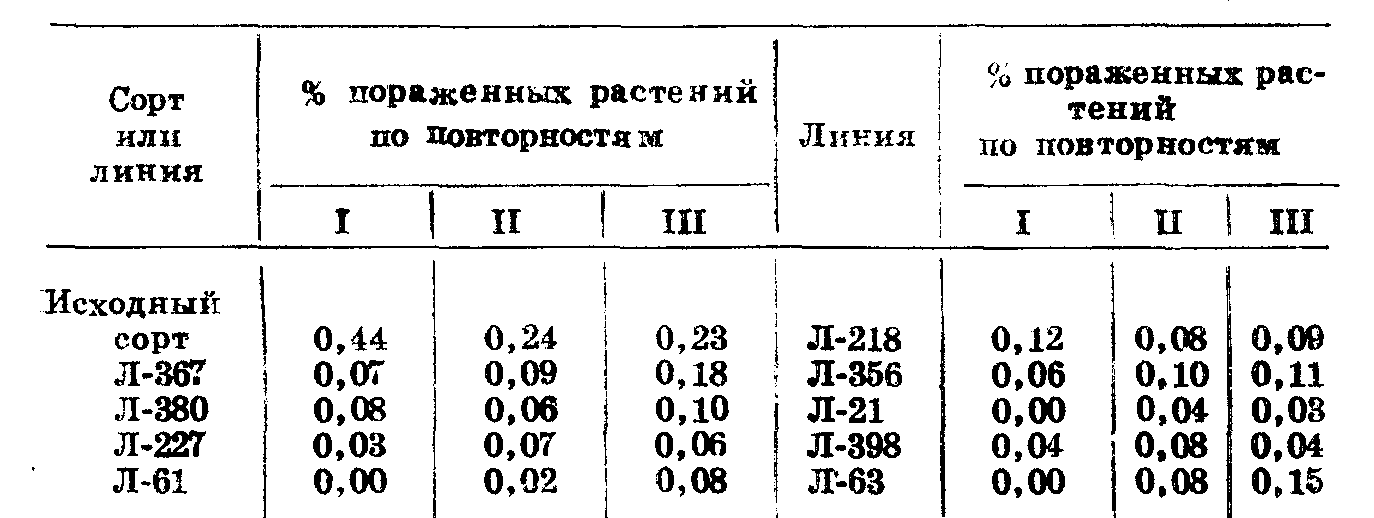
Примечание. Данные взяты из работы О. С. Хохрикова (1971.).
