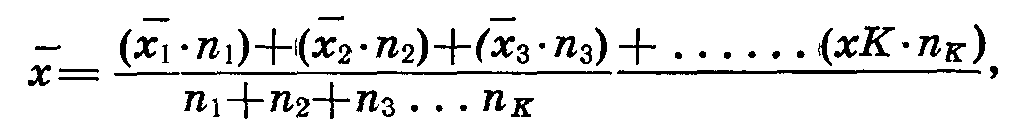А. М. Мубараков доктор пед наук, профессор. Н. Э. Пфейфер доктор пед наук, профессор пгу им. С. Торайгырова. Н. Е. Тарасовская доктор биологических наук, профессор. Химич Г. З., Хлущевская О. А. Введение в биометрию. Учебное пособие
| Вид материала | Учебное пособие |
| Вариационным рядом Разбивка вариант на классы. составление гистограмм, замена гистограмм кривыми. двухвершинные и многовершинные кривые, протуберан Вычисление арифметического среднего Взвешенное среднее |
- Секция интенсивных методов обучения, 2428.86kb.
- Альманах издан при поддержке народного депутата Украины, 3190.69kb.
- Ветеринария. – 2011. №1(17). – С. 20-21 Нужен ли нам сегодня новый аграрно-технический, 46.59kb.
- Общеобразовательная программа дошкольного образования Авторский коллектив, 5619.19kb.
- Образовательная программа дошкольного образования Москва «Просвещение», 5670.3kb.
- Т. С. Рамазанов доктор физико-математических наук, профессор, Казну им. Аль-Фараби,, 5487.66kb.
- Пояснительная записка, 12621.4kb.
- В. О. Бернацкий доктор философских наук, профессор; > А. А. Головин доктор медицинских, 5903.36kb.
- Д. В. Петров Диапозитивы текста изготовлены в тц сфера, 1451.22kb.
- «Слова о Полку Игореве», 3567.27kb.
Таблица 1
| Школьные классы | Обнаружено детей | Всего | |
| здоровых | больных | ||
| Третьи и четвертые Пятые и шестые | 63 71 | 92 39 | 155 110 |
| Всего | 134 | 131 | 265 |
Из таблицы 1 видно, что заболевание нёбных миндалин, по-видимому, чаще встречается среди учащихся третьих и четвертых классов.
К сложным относятся многопольные таблицы, применяемые при изучении корреляционной зависимости и при выяснении причинно-следственных отношений между варьирующими признаками. Примером корреляционной таблицы служат классические данные Гальтона, показывающие наличие положительной зависимости между ростом родителей и ростом их детей (табл. 2).
В качестве примера группировки, применяемой при выяснении причинно-следственных отношений между признаками, приведены данные, полученные в Научно-исследовательском институте имени В. В. Докучаева при испытании гречихи сорта «Богатырь» на урожайность в зависимости от предшественников (табл.3).
Таблица 2
| | Рост детей, дюймы | | |||||||
| Рост | | | | | | | | | |
| родителей, | | | | | | | | | Всего |
| дюймы | 60,7 | 62,7 | 64,7 | 66,7 | 68,7 | 70,7 | 72,7 | 74,7 | |
| 74 | | | | | | | 4 | | 4 |
| 72 | | | 1 | 4 | 11 | 17 | 20 | 6 | 62 |
| 70 | 1 | 2 | 21 | 48 | 83 | 66 | 22 | 8 | 251 |
| 68 | 1 | 15 | 56 | 130 | 148 | 69 | 11 | | 430 |
| 66 | 1 | 15 | 19 | 56 | 41 | 11 | 1 | | 144 |
| 64 | 2 | 7 | 10 | 14 | 4 | | | | 37 |
| Всего | 5 | 39 | 107 | 255 | 387 | 163 | 58 | 14 | 928 |
Из табл. З ясно, что в данных условиях лучшим предшественником для гречихи является, по-видимому, ячмень.
Таблица 3
| | Урожай гречихи по поаторностям, | | ||
| Предшественники | Ц/га | Средний урожай | ||
| | | | ||
| | 1 | 2 | 3 | |
| Горох раннезеленый | 23,7 | 20,1 | 20,5 | 21,4 |
| Чечевица | 23,6 | 25,1 | 21,1 | 23,2 |
| Чина степная № 21 | 26,7 | 23,2 | 23,8 | 24,6 |
| Ячмень | 26,0 | 24,9 | 25,3 | 25,4 |
Приведенными таблицами не исчерпывается их многообразие. Здесь рассмотрены лишь типичные для курса биометрии примеры. Из этих примеров видно, что статистические таблицы имеют не только иллюстративное, но и аналитическое значение, позволяя обнаруживать связи .между варьирующими признаками.
Особую форму группировки представляют так называемые статистические ряды Статистическим называется ряд числовых значений признака, расположенных в определенном порядке. В.зависимости от того, какие признаки изучаются, статистические ряды делят на атрибутивные, вариационные, ряды динамики и регрессии, а также ряды ранжированных значений признаков и ряды накопленных частот, являющихся производными вариационных рядов. Примером атрибутивного ряда могут служить данные, показывающие зависимость между содержанием гемоглобина НЬ в крови и высотой организации позвоночных животных:
Класс животных ….. Рыбы Амфибии Рептилии Птицы Млекопитающие
Количество НЬ, г/кг
массы тела . ....... …….1,6 2,9 3,8 11,2 11,7
Среди группировок видное место занимают вариационные ряды. На их описании следует остановиться более подробно. Ряды регрессии, динамики и другие будут рассмотрены в последующих главах.
Вариационным рядом или рядом распределения называют двойной ряд чисел, показывающий, каким образом числовые значения признака связаны с их повторяемостью в данной статистической совокупности.
Рассмотрим конкретный пример. Нам надо определить число колосков в колосьях пшеницы данного сорта. Размер выборки — 50 колосьев. Отобрав рендомизированно необходимое количество (50) колосьев, мы приступаем к подсчетам (табл. 4). Сначала пишем: «Число колосков в колосе (Казахстанской 126 или другого изучаемого сорта)». Чертим таблицу: № пп, число колосков и т. д.
Таблица 4
| № пп | Число колосков | № пп | Число колосков | № пп | Число колосков |
| 1 | 18 | 18 | 15 | 35 | 19 |
| 2 | 13 | 19 | 14 | 46 | 16 |
| 3 | 20 | 20 | 14 | 37 | 17 |
| 4 | 13 | 21 | 12 | 38 | 16 |
| 5 | 19 | 22 | 18 | 39 | 14 |
| 6 | 15 | 23 | 14 | 40 | 15 |
| 7 | 16 | 24 | 15 | 41 | 13 |
| 8 | 15 | 25 | 15 | 42 | 17 |
| 9 | 17 | 26 | 16 | 43 | 13 |
| 10 | 14 | 27 | 15 | 44 | 12 |
| 11 | 15 | 28 | 14 | 45 | 17 |
| 12 | 13 | 29 | 17 | 46 | 15 |
| 13 | 15 | 30 | 13 | 47 | 16 |
| 14 | 18 | 31 | 14 | 48 | 14 |
| 15 | 15 | 32 | 16 | 49 | 16 |
| 16 | 15 | 33 | 17 | 50 | 17 |
| 17 | 16 | 34 | 15 | | |
Поскольку мы растения брали без выбора, то в таблице 4 цифры расположены без каких-либо закономерностей и из нее нельзя сделать никаких выводов.
Количественное выражение признака называется вариантой или (у некоторых авторов) датой и изображается буквами V или Х {приложение 1). Варианты, расположенные в восходящем или нисходящем порядке, образуют вариационный ряд. Чтобы составить вариационный ряд, найдем и отметим максимальную и минимальную варианты. В нашем примере минимальная варианта — 12, максимальная — 20. Разность между минимальной и максимальной вариантами называется размахом варьирования или амплитудой изменчивости.
Для составления вариационного ряда расположим варианты в восходящем порядке и определим, сколько раз каждая варианта встречается в нашей выборке.
Число, показывающее, сколько раз встречается в данной выборке каждая варианта, называется частотой и изображается буквами f или p. Для определения частот произведем разноску: зачеркиваем первую цифру таблицы 4. и против варианты 18
Таблица 5
с
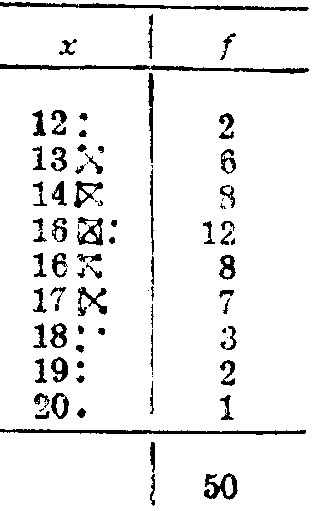 тавим точку, затем зачеркиваем вторую цифру — 13 и ставим точку против варианты 13, зачеркиваем третью цифру и ставим точку против варианты 20 и т. д. Числа 1, 2, 3, 4 изображаются точками; 5 и 6 — диагоналями, 7, 8, 9, 10 — сторонами квадрата. Закончив разноску наших данных, заменим точки и черточки цифрами — узнаем частоты. Сумма частот должна быть равна количеству взятых для исследования объектов. В нашем примере 2+6+8+12+8 + . . . +1=50, следовательно, разноска произведена правильно. Правильность разноски обязательно надо проверять, иначе допущенная и незамеченная своевременно ошибка при разноске сделает неверной всю дальнейшую работу. Сумма в вариационной статистике изображается заглавной буквой «сигма» греческого алфавита — Σ, количество объектов исследования — латинской буквой п. Запишем первую формулу:
тавим точку, затем зачеркиваем вторую цифру — 13 и ставим точку против варианты 13, зачеркиваем третью цифру и ставим точку против варианты 20 и т. д. Числа 1, 2, 3, 4 изображаются точками; 5 и 6 — диагоналями, 7, 8, 9, 10 — сторонами квадрата. Закончив разноску наших данных, заменим точки и черточки цифрами — узнаем частоты. Сумма частот должна быть равна количеству взятых для исследования объектов. В нашем примере 2+6+8+12+8 + . . . +1=50, следовательно, разноска произведена правильно. Правильность разноски обязательно надо проверять, иначе допущенная и незамеченная своевременно ошибка при разноске сделает неверной всю дальнейшую работу. Сумма в вариационной статистике изображается заглавной буквой «сигма» греческого алфавита — Σ, количество объектов исследования — латинской буквой п. Запишем первую формулу:Σ f = n
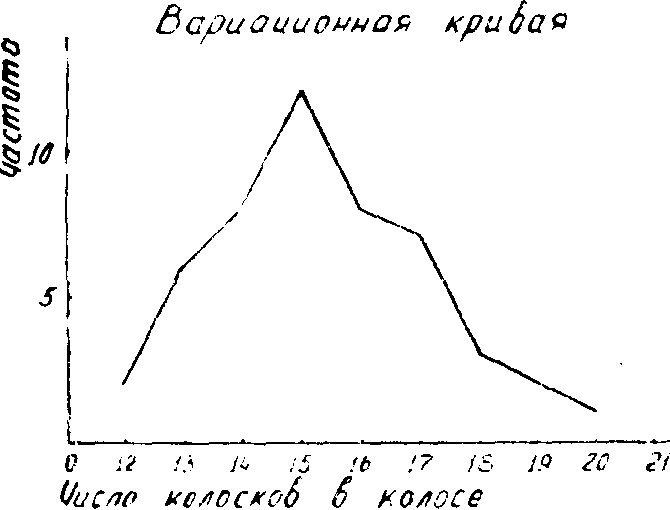
Изобразим наш вариационный ряд графически (рис. 1); на горизонтальной оси отложим варианты, на вертикальной — частоты.
Графическое изображение вариационного ряда называется вариационной кривой, наиболее часто
Рис. 1. Число колосков в
колосе пшеницы
встречающаяся в вариационном ряду варианта — модой. В нашем
.примере мода равна 15 Варианта, расположенная в середине вариационного ряда, называется медианой. Мода изображается Мо, медиана —. Ме. В биологических исследованиях мода имеет большое значение.
Например, среди клеверов есть одноукосные и многоукосные формы. Они различаются по количеству междоузлий. При проведении апробации клевера нак надо знать не среднее количество междоузлий, а число растений, обладающих определенным количеством междоузлий, т. е. относящихся к одноукосным или многоукосным формам. Мода дает нам необходимые показатели.
РАЗБИВКА ВАРИАНТ НА КЛАССЫ. СОСТАВЛЕНИЕ ГИСТОГРАММ, ЗАМЕНА ГИСТОГРАММ КРИВЫМИ. ДВУХВЕРШИННЫЕ И МНОГОВЕРШИННЫЕ КРИВЫЕ, ПРОТУБЕРАНЦЫ ОШИБОК
Исследуя непрерывную изменчивость, а также анализируя данные, полученные при изучении прерывной изменчивости при большом размахе варьирования, необходимо разбивать варианты на классы. Например, число икринок у рыб одного вида и возраста нередко изменяется более чем на 500. Совершенно ясно, что выписывать столбиком все варианты невозможно.
При непрерывной изменчивости варианты чаще всего представлены смешанными числами: высота растений — 1,25; 2,15; 3,45 м и т. д. Содержание белка в зерне пшеницы — 15,2; 16,1; 16,5% и т. д. Между двумя целыми числами может располагаться 100 вариант, различающихся на 0,01 м или 0,р1%.
В этих случаях варианты разбиваются на классы. При этом следует соблюдать следующие правила:
1. Границы классов должны быть такими, чтобы каждая варианта могла быть отнесена только к одному классу:
5—9, 10—14, 15—19 и т. д., но не 5—10, 10—15, 15—20 и т. д.
2. Размеры всех классов должны быть равными.
3. Первый и последний классы могут быть неполными. Например, при размере класса 10 и амплитуде изменчивости 76 размер последнего класса 70—79, хотя варианты 77—79 в нашем примере отсутствуют.
4. Количество классов должно быть не более 10—15 и не менее 6—7.
5. Для определения размера классов находят минимальную и максимальную варианты, определяют амплитуду изменчивости и делят ее на установленное количество классов, округляя полученное число до целого. Например: измерения высоты стеблей кукурузы 25/VIII 1972 г. дало результаты, приведенные в таблице 6.
Таблица 6
| № пп | Высота | № пп | Высота | № пп | Высота | № пп | Высота |
| 1 | 132 | 17 | 125 | 33 | 147 | 49 | 142 |
| 2 | 160 | 18 | 144 | 34 | 238 | 50 | 141 |
| 3 | 100 | 19 | 116 | 35 | 131 | 51 | 115 |
| 4 | 155 | 20 | 138 | 36 | 166 | 52 | 144 |
| 5 | 126 | 21 | 123 | 37 | 132 | 53 | 128 |
| 6 | 129 | 22 | 134 | 38 | 114 | 54 | 124 |
| 7 | 125 | 23 | 118 | 39 | 133 | 55 | 108 |
| 8 | 106 | 24 | 179 | 40 | 103 | 56 | 132 |
| 9 | 164 | 25 | 153 | 41 | 126 | 57 | 143 |
| 10 | 114 | 26 | 116 | 42 | 143 | 58 | 147 |
| 11 | 127 | 27 | 131 | 43 | 141 | 59 | 131 |
| 12 | 163 | 28 | 173 | 44 | 125 | 60 | 154 |
| 13 | 111 | 29 | 133 | 45 | 154 | 61 | 102 |
| 14 | 131 | 30 | 110 | 46 | 116 | 62 | 157 |
| 15 | 128 | 31 | 152 | 47 | 105 | 63 | 118 |
| 16 | 136 | 32 | 144 | 48 | 133 | 64 | 123 |
Амплитуда варьирования 100—179=79 см. Если примем размер класса за 10, то 79:10 ==7,9 ==8 классов. Наметим границы классов и составим таблицу 4.
При разноске мы зачеркиваем в нашей таблице очередную цифру и ставим точку или черточку против соответствующего класса. Так, в класс 100—109 мы отнесем варианты 100, 102, 103, 105, 106, 108. Мы получили вариационный ряд. Мода его — класс 130—139.
Графическое изображение вариационного ряда, разбитого на классы, называется гистрограммой. При составлении гистрограммы на горизонтальной оси наносятся размеры классов, на вертикальной - частоты. Гистрограмму можно превратить в вариационную кривую. Для этого надо соединить прямыми линиями середины классов. Изобразим при помощи гистрограммы полученные нами данные по высоте растений кукурузы (рис. 2).
При анализе количественных данных исследователь обычно получает много чисел. Построение гистограмм и вариационных кривых помогает осмыслить эти числа, наметить определенные закономерности. Графики часто помещают в печатных изданиях и в отчетах о научно-исследовательской работе. Для удобства сравнения на одном чертеже помещают несколько кривых. На рабочих чертежах удобно эти кривые чертить цветной тушью или карандашами. Для печати кривые обычно чертят черной тушью, но разными шрифтами. Каждый чертеж сопровождается экспликацией, показывающей, как изображен тот или другой вариант опыта. Например, мы провели измерение высоты пяти гибридов кукурузы. Экспликация будет выглядеть следующим образом:
_________________________ Гибрид ВИР 156 (контроль)
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ Юбилейный
……………………………….. Днепровский 56
-х-х-х-х-х-х-х-х-х-х-х-х-х-х-х Краснодарский 4
-0-0-0-0-0-0-0-0-0-0-0-0-0-0-0 Южный 3
Таблица 7

Рис.2 Высота растений кукурузы в см.
На одном чертеже неудобно располагать больше 5—6 вариантов опыта, поэтому если сравнивается большее количество вариантов опыта, то составляется несколько графиков, причем вариант, служащий контролем, помещается на каждом чертеже. Чтобы на одном чертеже можно было поместить несколько кривых, при разбивке вариант на классы надо границы классов устанавливать не по минимальной варианте каждого варианта опыта, а брать границы классов, общие для всех вариантов. Например, если минимальная высота растений в одном варианте опыта 100, в другом — 113, в третьем —98 см, а размер класса принят за 10 см, то границы классов должны быть 90—99, 100—109, 110—119 и т. д. То, что первые классы могут отсутствовать или быть неполными, не имеет значения.
Для большинства признаков сельскохозяйственных и биологических объектов характерно нормальное распределение. Его отличительной чертой является то, что, чем больше отклоняется значение отдельной варианты от средней, тем реже она наблюдается. Например, большинство людей имеет средний рост. Великаны (более 200 см) и карлики (менее 100 ел») встречаются крайне редко.
Наиболее часто отклоняются от нормального скошенное (асимметрия), крутовершинное (эксцесс), двух- и многовершинное распределения (рис. 3).
Основной причиной возникновения двух- и многовершинных кривых является неоднородность взятого для исследования материала. Еще в начале возникновения науки биометрии известный голландский ученый Гуго де Фриз провел биометрическое изучение длины лепестков и чашелистиков у растения семейства онагриковых — Энотера Ламаркиана.
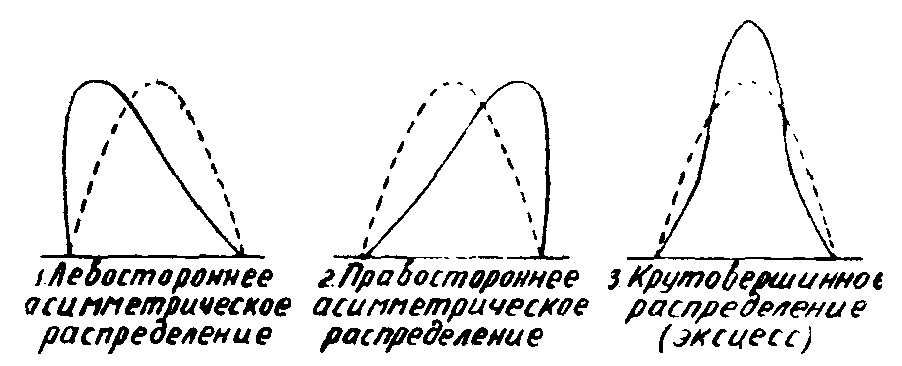
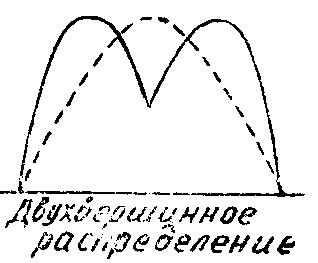
Рис. 3 Типы распределений. Пунктиром показано нормальное распределение.
Вместо ожидаемых (на основании работ Ф. Гальтона) одновершинных нормальных кривых он в обоих случаях получил двухвершинные (или, как их еще называют, бимодальные) кривые. Подробно изучив взятые для опыта растения, он установил, что вид Энотера Ламаркиана состоит из двух хорошо отличимых видов: обычной Энотеры Ламаркиана и Энотеры гирас, отличающейся большими размерами всех органов
Для двух- и многовершинных кривых характерно постепенное нарастание частот, затем также постепенное их снижение и вновь наступающее нарастание.
В практической работе иногда наблюдается резкое снижение или возрастание частоты отдельных вариант (рис. 4).
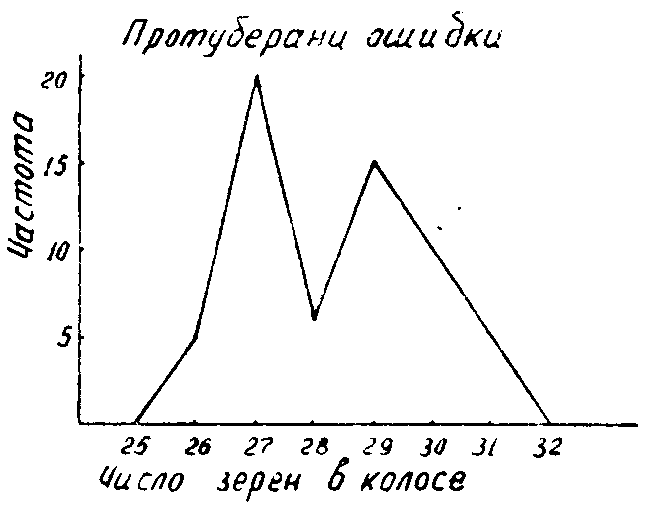
Рис. 4 Протуберанц ошибки.
Такие выступы на кривых называются протуберанцами ошибок. Причины их возникновения:
1. Недостаточное количество объектов исследования.
2. Слишком мелкие градации изучаемых признаков.
3. Допущенные ошибки в измерениях или подсчетах. Например, изучая количество зерен в колосьях пшеницы определенного сорта, мы получили данные, представленные в таблице 8.
Если мы объединим количество зерен в классы по два, то кривая примет нормальный вид (рис. 5). Это естественно, так как разница в одно зерно может быть случайной.
| Кол-во зерен | Частота |
| 25 | 4 |
| 26 | 8 |
| 27 | 2 |
| 28 | 16 |
| 29 | 11 |
| 30 | 13 |
| 31 | 14 |
| 32 | 8 |
Таблица 8
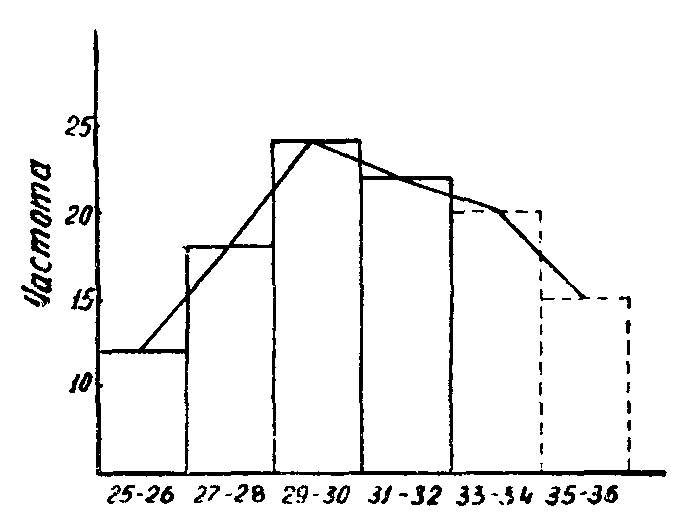
Рис.5 Устранение протуберанца ошибки
ВЫЧИСЛЕНИЕ АРИФМЕТИЧЕСКОГО СРЕДНЕГО,
ОШИБКИ СРЕДНЕГО, ОСНОВНОГО (КВАДРАТИЧЕСКОГО) ОТКЛОНЕНИЯ, КОЭФФИЦИЕНТА ВАРИАЦИИ
Одна из основных задач статистической обработки материала— найти показатели, характеризующие особенности эмпирических совокупностей, дающие возможность сравнивать их друг с другом.
Статистические совокупности с достаточной полнотой характеризуют два показателя:
1. Средняя величина признака;
2. Степень варьирования, или рассеяния.
Рассмотрим понятие «средняя величина признака». В статистике используются средняя арифметическая, средняя взвешенная, средняя гармоническая, средняя геометрическая. Наибольшее значение в биологических и сельскохозяйственных исследованиях имеет средняя арифметическая.
Средней арифметической называется такая величина, сумма отрицательных и положительных отклонений от которой равна нулю. Например, количество плодов на растениях составляет 4; 5; 9. Среднее количество плодов — 6; 4 отклоняется от 6 на минус 2; 5— на минус 1; 9— на плюс 3:
—2—1+3=0
Чтобы найти арифметическое среднее, надо сложить все I варианты и разделить их на число наблюдений. Средняя арифметическая в вариационной статистике обозначается как М или
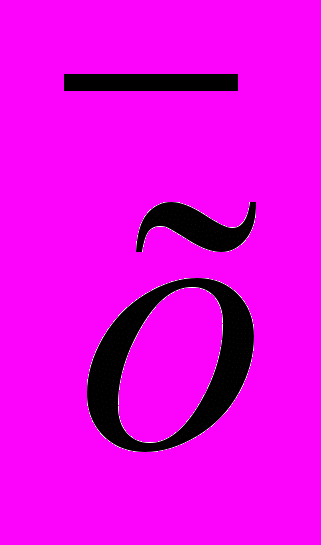 (читается как икс покрытое). Формула определения среднего арифметического
(читается как икс покрытое). Формула определения среднего арифметического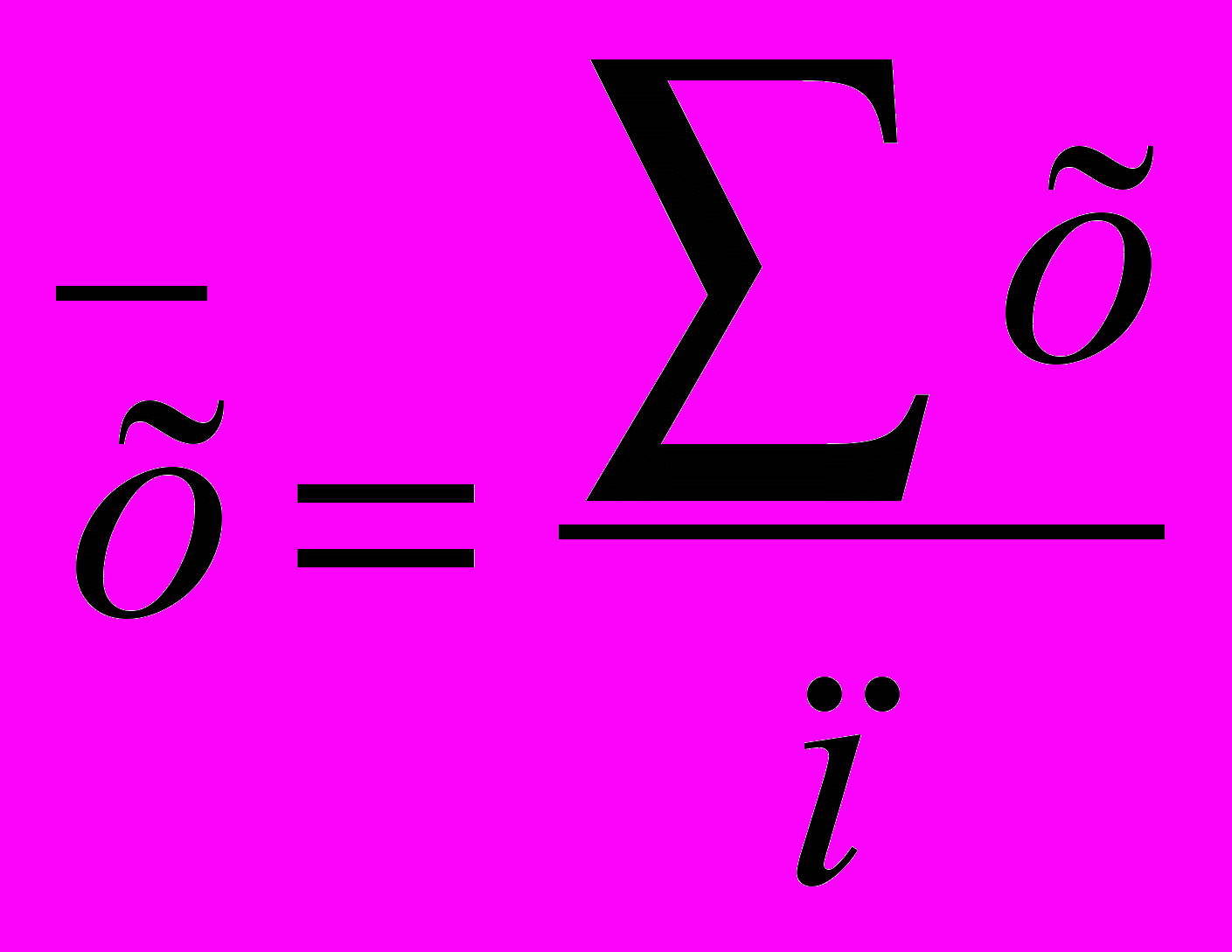 ,
, 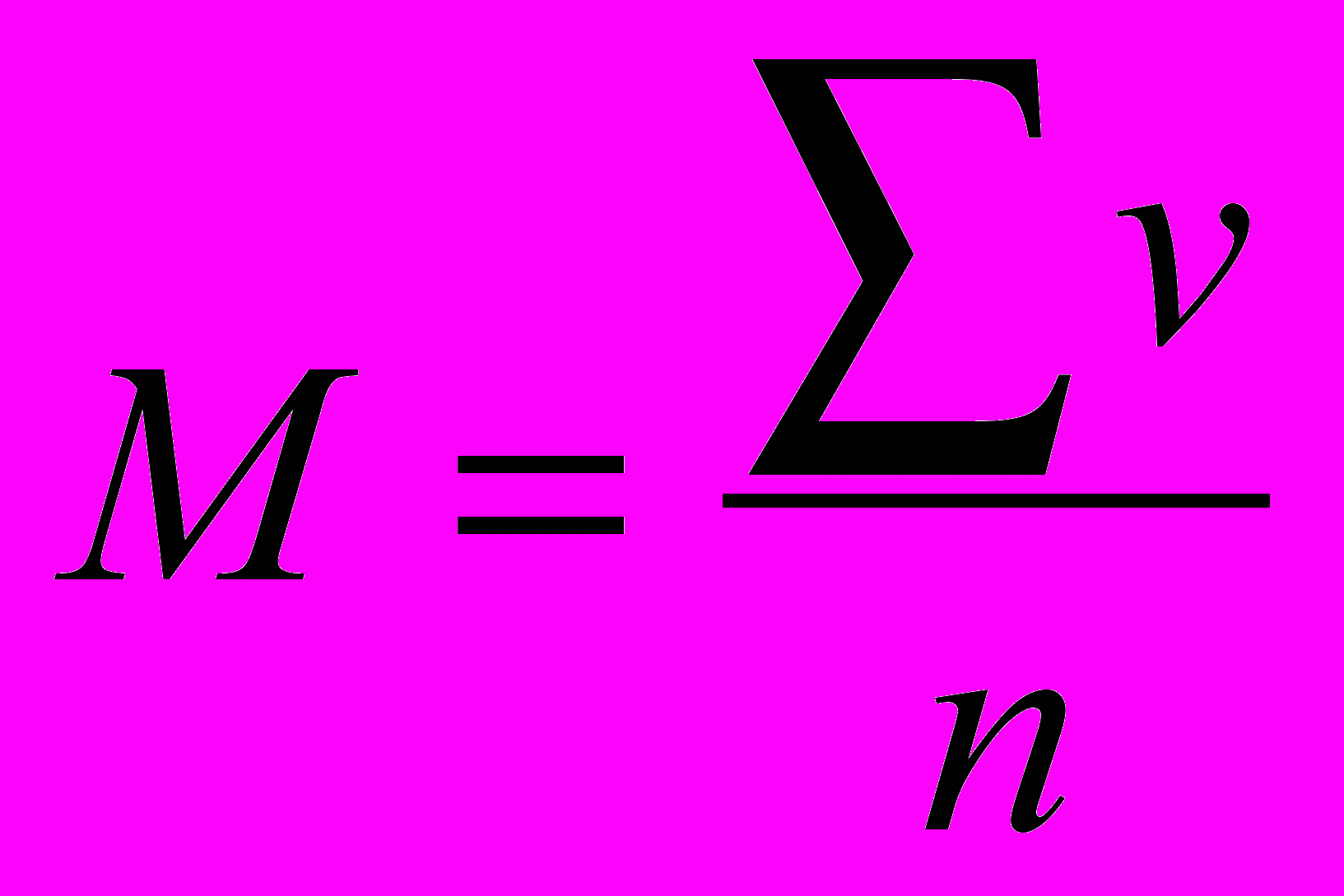 (что одно и то же).
(что одно и то же).При небольшом количестве наблюдений или при использовании электронных счетных машин вычисление среднего арифметического производится таким образом.
При обработке сложных вариационных рядов при большом количестве вариант такой способ вычисления слишком трудоемок. Применяется способ вычисления среднего «по способу моментов», или «от произвольного начала». Рассмотрим этот способ вычисления на примере простого вариационного ряда (табл. 9). (Вариационный ряд, в котором каждая варианта встречается один раз, называется простым, несколько раз — сложным).
 Отклонения от произвольно взятого среднего обозначаются а
Отклонения от произвольно взятого среднего обозначаются а или
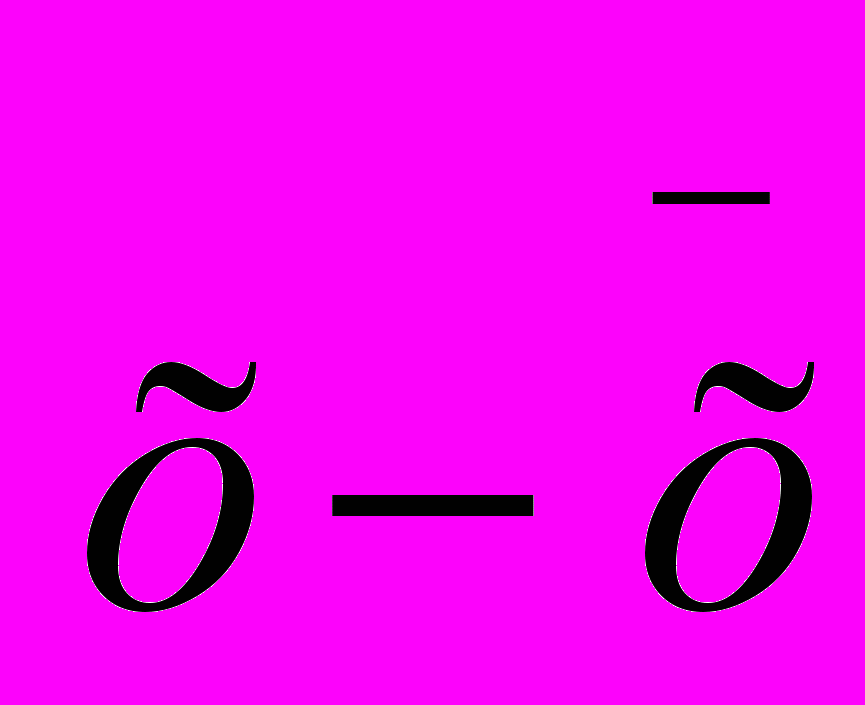 . В качестве произвольно взятого среднего (или условного среднего) берем любую варианту, лежащую в средине или близко к средине вариационного ряда. Отграничиваем ее прямыми линиями. Мы взяли в нашем примере в качестве произвольного среднего варианту 13. Вычислим отклонения от произвольной средней каждой варианты. Поскольку наш ряд построен в восходящем порядке, варианты, лежащие выше произвольного среднего, имеют знак —, ниже его +.
. В качестве произвольно взятого среднего (или условного среднего) берем любую варианту, лежащую в средине или близко к средине вариационного ряда. Отграничиваем ее прямыми линиями. Мы взяли в нашем примере в качестве произвольного среднего варианту 13. Вычислим отклонения от произвольной средней каждой варианты. Поскольку наш ряд построен в восходящем порядке, варианты, лежащие выше произвольного среднего, имеют знак —, ниже его +.Найдем, алгебраическую сумму отклонений:
—6+10==+4.
Мы знаем, что сумма отрицательных и положительных отклонений от среднего равна 0. Разделив полученную нами сумму отклонений на число наблюдений (8), получаем поправку b.
b = 4 : 8 = 0,5
Формула поправки
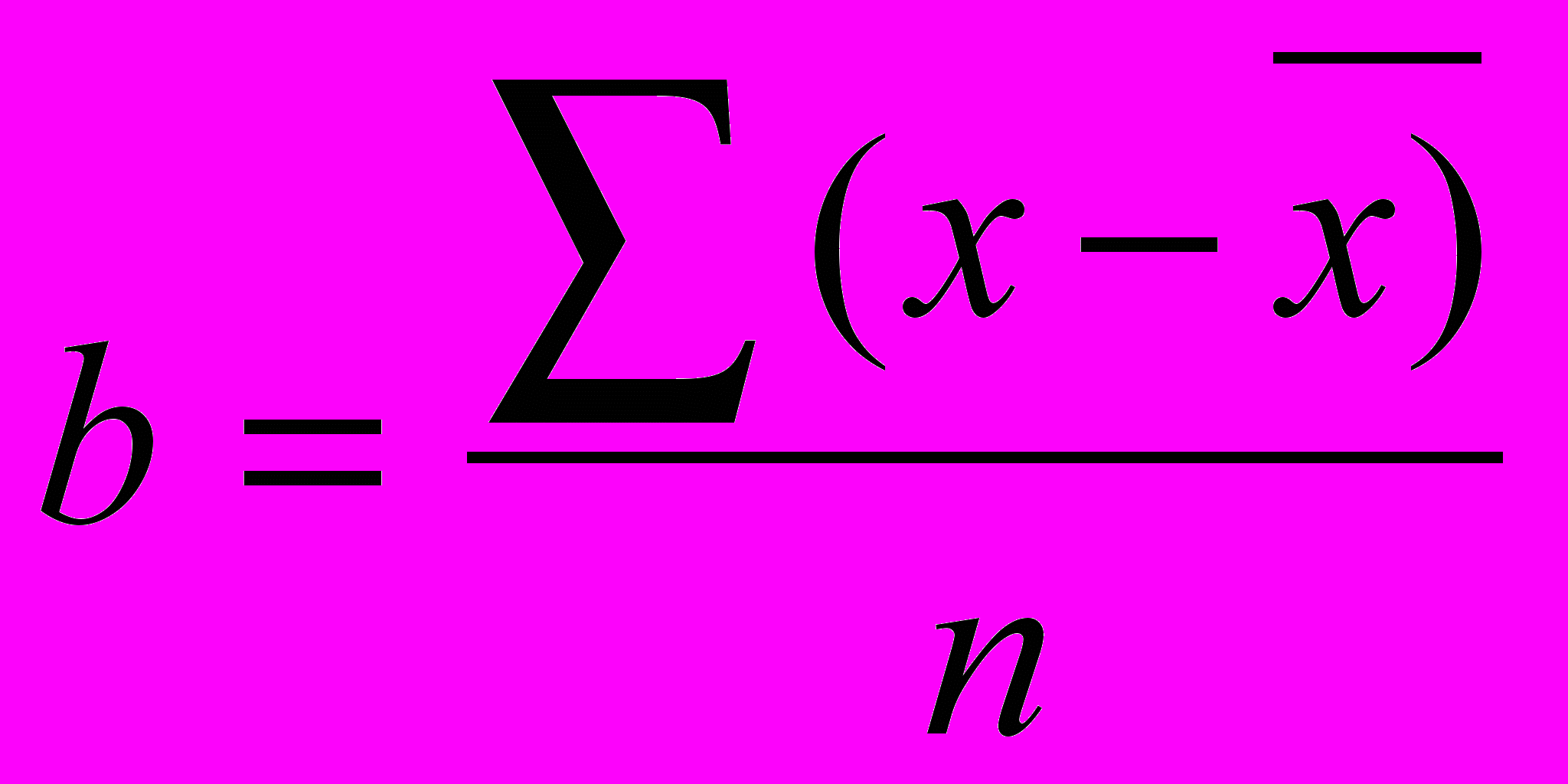 , а истинное среднее равно произвольно взятому среднему Мо + поправка.
, а истинное среднее равно произвольно взятому среднему Мо + поправка. М = Мо + b.
Таблица 9.
| | Отклоне |
| | ния от |
| Варианта х | произвольно взятого среднего |
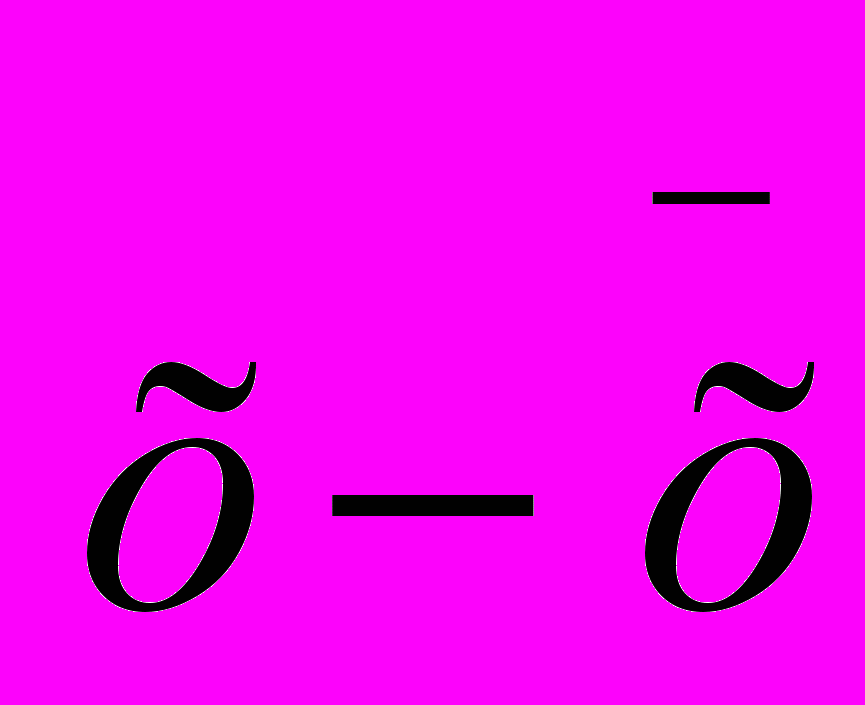 | |
| 10 11 12 13 | -3 -2 —1 —6 |
| 14 15 16 17 | 1 2 3 4 |
| | 10 |
| х | f | 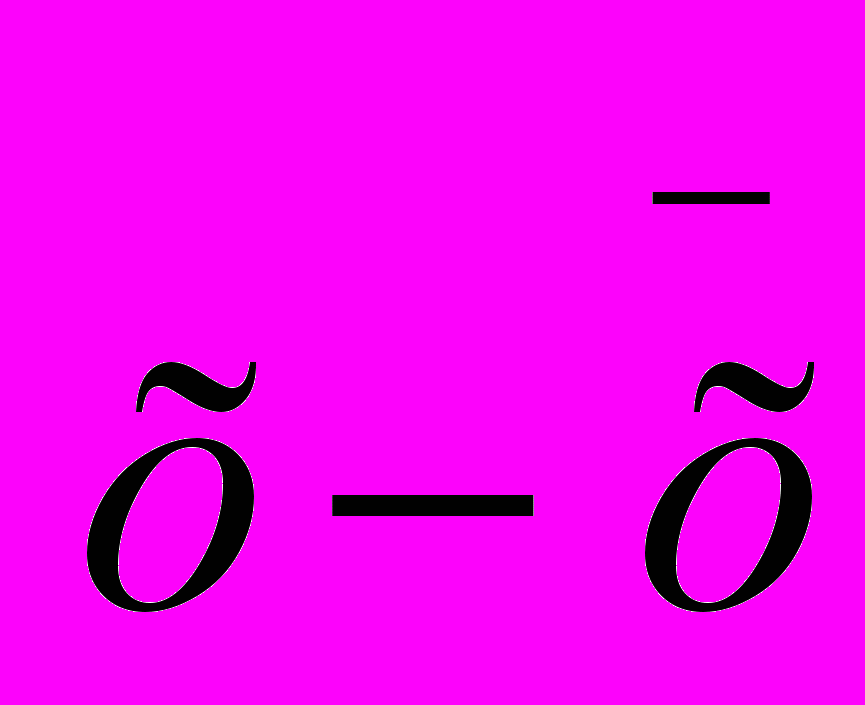 | f ( 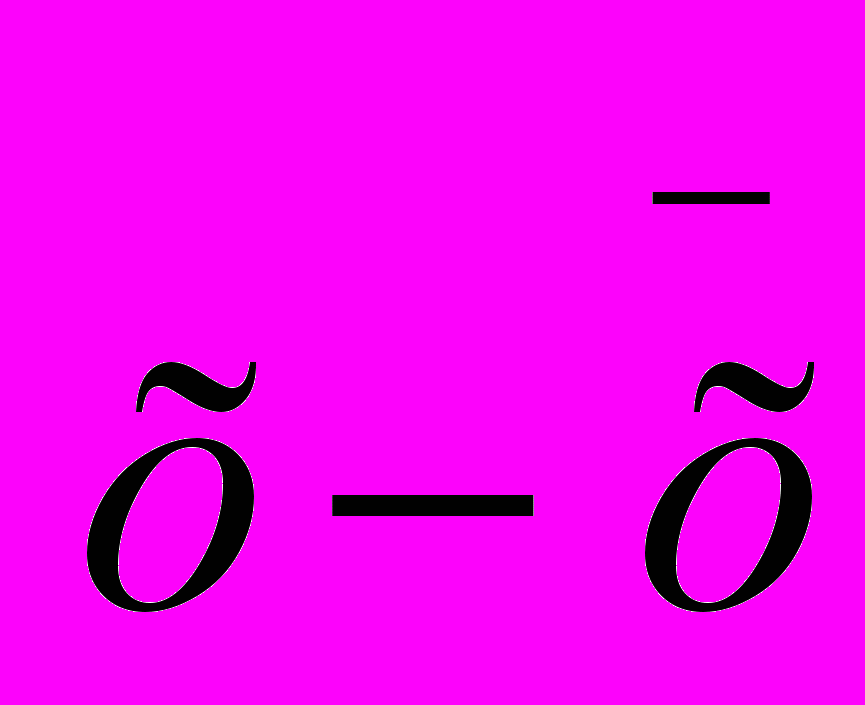 ) ) |
| 10 | 2 | -3 | - 6 |
| 11 | 4 | -2 | - 8 |
| 12 | 5 | -1 | - 5 |
| 13 | 8 | | -.19 |
| 14 | 6 | 1 | 6 |
| 15 | 4 | 2 | 8 |
| 16 | 3 | 3 | 9 |
| 17 | 2 | 4 | 8 |
| | 34 | | 31 |
Нельзя забывать, что речь идет об алгебраической сумме: если мы получили поправку b с отрицательным знаком, то М=Мо+ ( - b), т. е. Мо - b.
В нашем примере М или x = 13+0,5=13,5. Проверим наше вычисление:
10+11+12+13+14+15+16+17=108; M= 108: 8 = 13,5 (n = 8).
Мы получили одинаковые результаты, что и при вычислении с помощью произвольно взятой средней.
Если в качестве произвольного среднего мы возьмем варианту 14, то сумма отрицательных отклонений будет равна —10; сумма положительных +6, поправка b = (- 10 +6) : 8 = - 0,5.
Среднее =14+(—0,5) =13,5.
Для проверки правильности вычисления среднего рекомендуется повторить вычисление, взяв за произвольное среднее другую варианту.
В сложных вариационных рядах, где варианты встречаются по несколько раз, также берут одну из вариант, лежащих в средине ряда, за произвольную среднюю, вычисляют отклонение от среднего (х -
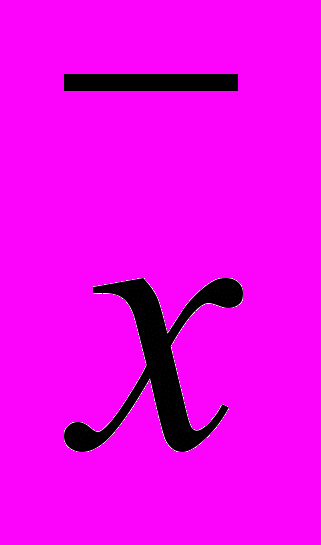 или а), умножают отклонения на соответствующие частоты, находят суммы положительных и отрицательных отклонений (а-f), делят на количество наблюдений и найденную таким образом поправку добавляют или вычитают из произвольно взятого среднего (в зависимости от знака). Рассмотрим пример (табл. 10).
или а), умножают отклонения на соответствующие частоты, находят суммы положительных и отрицательных отклонений (а-f), делят на количество наблюдений и найденную таким образом поправку добавляют или вычитают из произвольно взятого среднего (в зависимости от знака). Рассмотрим пример (табл. 10). Поправка b = (-19 + 31) : 34= 0,35, n=34. Вычисления производятся с точностью до 0,01. Средняя равна 13+0,35== =13,35.
При вычислении среднего в рядах, разбитых на классы, во избежание получения слишком больших чисел при расчетах, отклонения от произвольно взятого среднего каждого класса принимают за единицу, а затем полученную поправку умножают на размер классового промежутка, обозначаемого К или l, и добавляют или вычитают (в зависимости от знака) к центральному значению класса, взятого в качестве произвольного среднего. Центральное значение класса обозначается W, X или х.. В качестве примера вычислим среднее по данным таблицы 11.
Сумма произведений частот на отклонение с отрицательным знаком равна —20, с положительным знаком 34. Алгебраическая сумма составляет 14.
Найдем b, для этого 14 разделим на 41 (41=Σf = n), получим 0,34. W— центральное значение класса, принятого за среднее, равно 37. Отсюда М=37+0,34 •5 = 38,70.
Формула вычисления среднего вариационного ряда, разбитого на классы:
М = W + b •l.
При вычислении следует следить за правильностью знаков плюс или минус у b
Таблица 11
| Классы | Центр.значение клас | Частота f | Очклонение от среднего, | f (х - 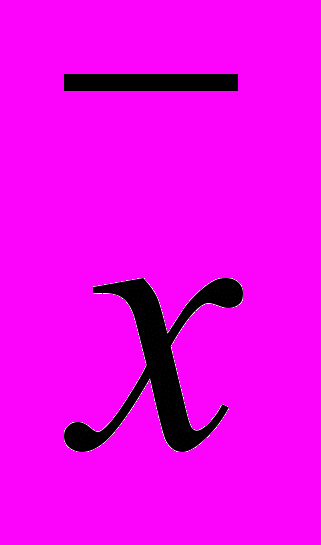 ) ) |
| | са w | | х - 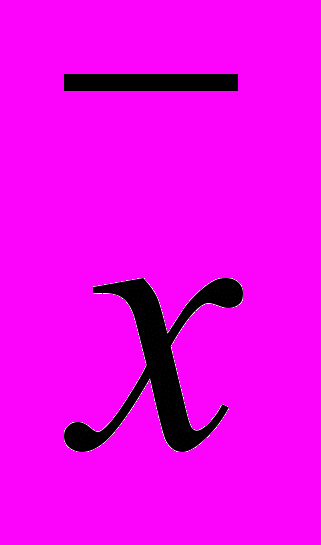 | |
| 20-24 | 22 | 2 | —3 | —в |
| 25-29 | 27 | 4 | -2 | -8 |
| 30—34 | 32 | 6 | -1 | —6 |
| 36-39 | 37 | 10 | | 20 |
| 44-44 | 42 | 8 | 1 | 8 |
| 45-49 | 47 | 7 | 2 | 14 |
| 50-54 | 52 | 4 | 3 | 12 |
| | | 41 | | 34 |
ВЗВЕШЕННОЕ СРЕДНЕЕ
Часто для практических и научных целей необходимо объединить полученные для однородного материала средние и на этой основе найти одно общее среднее, характеризующее весь изученный материал. Число наблюдений, послужившее для вывода каждого отдельного среднего, называется его весом.
Рассмотрим самый обычный пример.
Передовая бригада совхоза на площади 200 га получила урожай озимой пшеницы 60 ц/га. На остальной площади — 10 000 га — средний урожай составил 30 ц/га. Каков средний урожай озимой пшеницы в совхозе?
200 га дали в среднем урожай по 60 ц/га
10 000 га » » по 30 ц/га
Средний урожай ?
Если для определения среднего урожая мы воспользуемся арифметическим средним —(60+30) : 2 = 45, то получим явно завышенный урожай — 459 000 ц. Фактически же совхоз собрал: (60Х200)+(ЗОХ10000) = 312000 ц.
Выражения 60; 30 ц/га и т. п. означают, что в среднем с каждого гектара из 200 га, закрепленных за передовой бригадой, получено по 60 ц, со всей остальной площади — 10 000 га — по 30 ц. Следовательно, 200 является весом среднего 60 ц, а 10 000 — весом среднего 30 ц. Для получения правильного представления о полученном среднем урожае мы должны вычислить взвешенное среднее, т. е. помножить каждое среднее на его вес, найти сумму произведений и разделить ату сумму на сумму весов:
(60 • 200) + (30 • 10000) ׃ 200 +10000 = 30,5 ц/га
Рассмотрим еще один пример. На овцеводческой ферме 10 баранов-производителей дали в среднем по 11 кг шерсти, 400 молодых маток — по 5 кг, 600 старых маток — по 7 кг. Каков средний настриг шерсти на ферме?
(11 •10) + (5 •400) + (7 • 600) ׃ (10 + 400 +600 = 6,24 кг.
Формула для вычисления взвешенного среднего: