Geum.ru

Разработка теории и основных принципов принятия решений в сапр на основе методов, инспирированных природными системами

Вид материалаАвтореферат диссертации
В четвертом разделе.
Подобный материал:
1   2   3
В третьем разделе. Фундаментальным методом повышения производительности при проектировании систем на кристалле (СнК) является повторное использование IP-блоков (начиная с маленьких и переходя к большим). Это соответствует созданию стандартных блоков в генетических алгоритмах. В этой связи необходимы разработка и построение новых и модернизация существующих моделей эволюции. В работе проведен анализ и обзор состояния основных моделей эволюции.

Модель эволюции Ч. Дарвина – это условная структура, реализующая процесс, посредством которого особи некоторой популяции, имеющие более высокое функциональное значение, получают большую возможность для воспроизведения потомков, чем «слабые» особи. Такой механизм часто называют методом «выживания сильнейших». Модель эволюции Ж. Ламарка основана на предположении, что характеристики, приобретенные особью (организмом) в течение жизни, наследуются его потомками. Эти изменения, как утверждал Ж. Ламарк, вызываются прямым влиянием внешней среды, упражнением органов и наследованием приобретенных при жизни признаков. В основе модели эволюции Г. де Фриза лежит моделирование социальных и географических катастроф, приводящих к резкому изменению видов и популяций.

Модель прерывистого равновесия Гулда-Элдриджа является развитием и модификацией модели Г. де Фриза. Метод прерывистого равновесия использует палеонтологическую теорию, которая строит модели эволюции на основе описаний вулканических и других изменений земной коры. Модель К. Поппера – это условная структура, реализующая иерархическую систему гибких механизмов управления, в которых мутация интерпретируется как метод случайных проб и ошибок, а отбор – как один из способов управления при взаимодействии с внешней средой. Отметим, что модель эволюции Поппера естественно вкладывается в человеко-машинную систему принятия решений. Человек-оператор практически всегда работает методом «проб и ошибок». М. Кимура предложил модель нейтральной эволюции с нейтральным отбором. Теория нейтральности предполагает, что большая часть молекулярных вариантов имеет равную приспособленность друг относительно друга. Изменчивость здесь поддерживается балансирующим отбором. Рассматриваемый процесс всегда сходится к одному из поглощающих состояний.

Основная задача синтетической теории эволюции – определение природы противоречий или постепенной эволюции, то есть разных форм противоречий между наследственностью и постоянно меняющимися потребностями в приспособлениях, а также взаимодействие между микро-, макро- и метаэволюцией на разных иерархических уровнях.

Автор считает важным объединение всех видов и моделей эволюций в интегрированную многоуровневую модель. На рис.6 приведена условная интегрированная схема эволюции. Отметим, что блоки 1-n соответствуют рассмотренным схемам моделей эволюции. Основным этапом в каждой модели эволюции является анализ популяции, ее преобразование тем или иным способом и эволюционная смена форм.



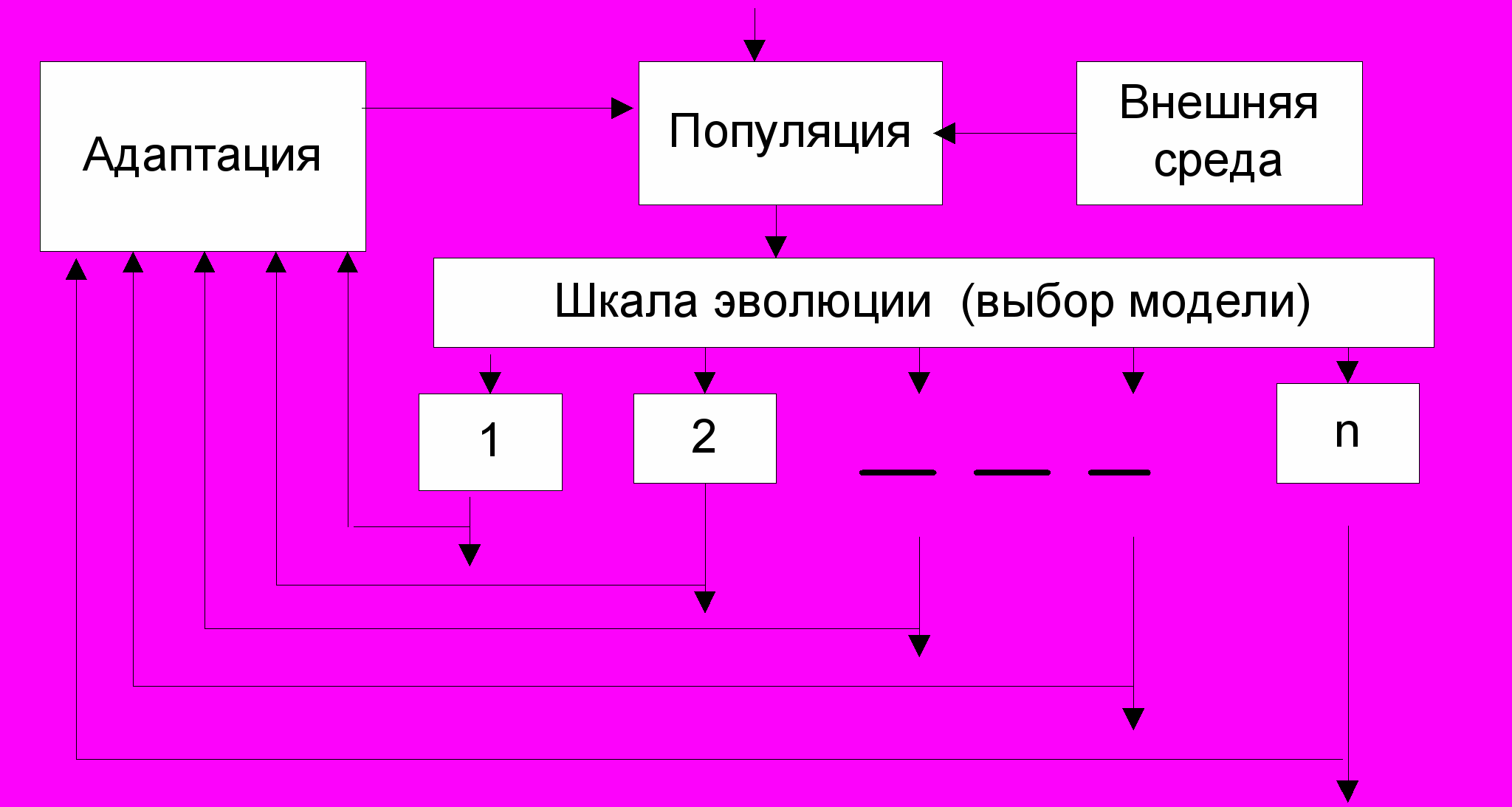
Рис.6. Условная интегрированная схема эволюции

Приведем условную архитектуру поиска для принятия решений в САПР (рис.7). Она состоит из четырех основных блоков. В блоке инициализации производится выбор и построение моделей эволюции. В блоке обработки на основе выбранных моделей строится алгоритм поиска решений. Далее в блоке вычислений производится генерация альтернативных решений, построение целевой функции и выбор квазиоптимальных решений при проектировании. В случае получения неудовлетворительных решений, в блоке распределения, производится распараллеливание процесса решения и реализация алгоритмов с помощью многопроцессорных систем.

В работе описана модифицированная модель эволюции Шмальгаузена, основанная на преобразовании специальных кубов. Автор использовал четыре типа скрещиваний и четыре основные формы отбора в СППР при принятии решений по выбору эффективных алгоритмов проектирования. Эксперименты показали, что при компоновке целесообразным является инбридинг, а для остальных задач проектирования ассортативное и селективное скрещивание. Эволюция здесь - это авторегулируемый процесс, основанный на обратной связи. На ее основе происходит анализ микроэволюции. Она рассматривает процессы, протекающие на уровне популяций, начиная с механизмов изменчивости.



Рис.7. Условная архитектура поиска

На рис.8 приведена схема алгоритма на основе модифицированной модели ЭШ. Эволюционирующую популяцию и внутривидовую дифференциацию популяций представим как трехмерную решетку. В ней каждая плоскость – это эволюция особи, прошедшей естественный отбор, а вершины (узлы) ячейки – результат их скрещивания. Модель демонстрирует процесс перехода от микроэволюции популяций к макроэволюции (эволюции надвидов). Будем считать, что узлы решетки это особи (хромосомы), т.е. альтернативные сценарии анализируемой задачи принятия решений. Они образуют начальную популяцию альтернативных решений P = {X1, X2,…, X8}, |P| = 8. Согласно произвольному генетическому алгоритму для каждого элемента XjP определяется целевая функция (функция приспособленности). Далее согласно целевой функции (ЦФ) производится отбор элементов для реализации генетического поиска.



Рис.8. Схема алгоритма на основе модифицированной модели ЭШ.

Он состоит из последовательной, параллельной или комбинированной реализации генетических операторов (ГО). На основе решетки Шмальгаузена построен новый оператор кроссинговера (ОК).

Начальную популяцию особей (хромосом, альтернативных решений), предлагается создавать таким образом, чтобы ее размер был кратным 8. Далее исходная популяция разбивается на ряд подпопуляций P = {P1, P2,…, Pn}, при этом строится две решетки (рис.9).



Рис.9. Пример работы ЭШ на двух решетках

Причем |Pi|=8, i  1,2,…,n. n (mod 2) т.е. четное и обязательно делится на 8. Это сделано для того, чтобы каждый раз иметь возможность строить трехмерные решетки Шмальгаузена.

Произведем ранжирование исходной популяции по значению целевой функции. Далее начинаем реализовать параллельную микроэволюцию внутри каждого куба. Процесс реализации ОК продолжается, пока не будет достигнут критерий остановки. Основными критериями останова алгоритма являются следующие: время (ЦФ1), выполнение всех итераций ГА (ЦФ2), попадание в локальный оптимум (ЦФ3), получение заданного результата, если он известен (ЦФ4). Построим аддитивный обобщенный критерий:

K = ЦФ11+ ЦФ22+ ЦФ33+ ЦФ44, причем 1+2+3+4=1.

Отметим, что обычно один критерий задается как основной, а остальные учитываются как ограничения. Приведем описание генетического алгоритма на основе модифицированной ЭШ.
  1. Во взаимодействии с внешней средой строится одна из возможных популяций P1, P2 и P3 или P4 на основе прямого, случайного, направленного или комбинированного взаимодействий.
  2. Производится построение целевой функции для определения степени приспособленности каждой хромосомы. Производится ранжирование каждой хромосомы (альтернативного решения) по максимальному значению ЦФ.
  3. Выполняется удаление “плохих” хромосом таким образом, чтобы мощность популяции была кратной восьми.
  4. Популяция разбивается на подпопуляции P1, P2,…Pn, P1 U P2 U… U Pn = P, P1 ∩ P2 ∩ … ∩ Pn ≠ 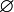, где n- кратно восьми.
  5. Для каждой подпопуляции строится решетка (куб) Шмальгаузена.
  6. В каждом кубе, используя механизмы “дробовика”, “одеяла”, ”фокусировки”, “колеса рулетки” и др., выбираются вершины кубов. Они определяют, какие хромосомы будут в дальнейшем скрещиваться, мутировать и т.п., т.е. каким образом будут реализовываться генетические операторы.
  7. На основе ЭШ производится реализация ГО. Если критерии останова достигнуты, то переход к 8, если нет, то t=t+1 и переход к 4 с разбитием популяции на другие подпопуляции.
  8. Выполнение операции объединения кубов и повторения операций 1-7.
  9. Построение подмножества оптимальных или квазиоптимальных альтернативных решений.
  10. Конец работы алгоритма.

В процессе макроэволюции преобразование будет происходить на уровне популяции и ее подпопуляций. На этапе метаэволюции процесс преобразования происходит между большим числом частей популяций и даже целых популяций. Понятие надуровень предполагает взаимодействие целых популяций, видов и частей видов, согласно идеям, предположенным Вернадским. В работе отмечено, что все преобразования выполняются под управлением внешней среды (стандарты, ГОСТы, технологии, опыт конструктора и технолога), внутри которой происходят эти преобразования.

В работе приведены основные элементы теории биоинспирированных алгоритмов (БА). Она основана на основных положениях теории множеств, теории алгоритмов, теории графов, алгебры логики, оптимизации и др. На ее основе построены модифицированные схемы научных теорий индуктивного метода и К. Поппера (рис.10).



Рис. 10. Модифицированная структура построения теории К. Поппера

В рассматриваемой теории объектами являются хромосомы (альтернативные решения задач проектирования и конструирования), а универсумом - вся их совокупность. Введем следующие понятия: Объекты – хромосомы. Универсум – популяция хромосом. Константы – простейшие из выражений, обозначающих предметы, т.е. их имена.

Приведем основные аксиомы этой теории:

1. Высказывания принимают логические значения.

2. Единственными общепринятыми логическими значениями являются истина и ложь.

3. Каждая теория имеет свой универсум, т.е. множество рассматриваемых предметов. Если универсумов несколько, они называются сортами или типами.

4. Высказывания о предметах образуются при помощи отношений или предикатов.

5. Выражения, обозначающие предметы, называются термами.

6. Термы строятся из переменных и констант при помощи операций или функциональных символов, которые применяются к предметам и в результате дают предмет.

7. Отношения (предикаты) применяются к термам и в результате дают высказывания (элементарную формулу).

Пусть каждому исходному понятию и отношению аксиоматической теории БА поставлен в соответствие некоторый конкретный математический объект. Совокупность таких объектов называется полем интерпретации. Всякому утверждению U теории БА ставится в соответствие некоторое высказывание U* об элементах поля интерпретации, которое может быть истинным или ложным. Тогда можно сказать, что утверждение U теории БА соответственно истинно или ложно в данной интерпретации. Поле интерпретации и его свойства сами обычно являются объектом рассмотрения другой теории простых генетических алгоритмов (ПГА), которая, в частности, может быть аксиоматической. Этот метод позволяет доказывать суждения типа: если теория БА непротиворечива, то непротиворечива и теория ПГА. Пусть теория БА проинтерпретирована в теории ПГА таким образом, что все аксиомы Ai теории БА интерпретируются истинными суждениями Ai* теории ПГА. Тогда всякая теорема теории БА, то есть всякое утверждение А, логически выведенное из аксиом Ai в БА, интерпретируется в ПГА некоторым утверждением A*, выводимым в ПГА из интерпретаций Ai* аксиом Ai и, следовательно, истинным. Уточнением понятия аксиоматической теории является понятие формальной системы. Это позволяет представлять математические теории как точные математические объекты и строить общую теорию или метатеорию таких теорий. Общая схема построения произвольной формальной системы БА такова:
  1. Язык системы БА: аппарат алгебры логики; теория четких и нечетких множеств; теория графов и гиперграфов, теория четких и нечетких алгоритмов, основные положения биоинформатики, теории систем, синергетики и теория принятия решений.
    1. Алфавит – перечень элементарных символов системы: двоичный, десятичный, буквенный, Фибоначчи и др.
    2. Правила образования (синтаксис), по которым из элементарных символов строятся формулы теории БА: построение моделей эволюций; конструирования популяций; построения ЦФ; разработки новых и модифицированных генетических операторов; репродукции популяций; рекомбинации популяций; редукции; адаптации; выбор структуры генетических алгоритмов; построение комбинированных генетических, биоинспированных и квантовых алгоритмов проектирования.

Последовательность элементарных символов считается формулой тогда и только тогда, когда она может быть построена с помощью правил образования.
  1. Аксиомы системы БА. Выделяется некоторое множество конечных формул, которые называются аксиомами системы. В БА существует большое число наборов аксиом. Например, следующий базовый набор аксиом:
  • Выбор модифицированной модели эволюции Дарвина.
  • Популяция конструкторских и технологических решений строится случайным образом.
  • Размер хромосомы (альтернативных решений) остается постоянным.
  • Выполнение оператора репродукции производится на основе «колеса рулетки».
  • Обязательное использование операторов кроссинговера, мутации и инверсии.
  • Размер популяции после каждой генерации остается постоянным.
  • Редукция выполняется на основе элитной схемы.
  • Размер популяции задается экспертной системой, внешней средой или лицом, принимающим решения.
  • Число копий (решений), переходящих в следующую генерацию, определяется согласно теореме генетических алгоритмов.
  • Целевая функция определяется на основе принципа «Выживание сильнейших».

3. Правила вывода БА. Фиксируется конечная совокупность предикатов П1, П2,…, Пk на множестве всех формул системы.

Заданием 1,2,3 исчерпывается задание формальной системы БА как математического объекта.

Итак, можно выстроить следующую цепочку построения и реализации теории генетических алгоритмов. Стратегия – теория – концепция – принципы – аксиомы – гипотезы – практическая реализация.

Предлагается ряд основных стратегий взаимодействия методов эволюционного и локального поиска в задачах САПР: «поиск – эволюция»; «эволюция – поиск »; «поиск – эволюция – поиск»; «эволюция – поиск – эволюция»; «эволюция – поиск – эволюция – поиск – эволюция – поиск»; «поиск – эволюция - адаптация»; «эволюция – поиск - адаптация»; «поиск – эволюция – поиск – миграция - адаптация»; «эволюция – поиск – эволюция – миграция - адаптация». Заметим, что иерархически можно строить стратегии такого типа любого уровня сложности. Например, «эволюция – поиск – эволюция – поиск – эволюция – поиск», используя последовательную, параллельную или любые другие стратегии поиска. Отметим, что такое построение зависит от наличия вычислительных ресурсов и времени, заданного на получение окончательного решения.

В последнее время появились новые подходы решения NP–полных проблем и неструктурированных проблем поиска. При поиске и обнаружении данных предлагается новая технология на основе квантового поиска. Для реализации поиска квантовое пространство преобразуется в общую суперпозицию, которая концентрируется в 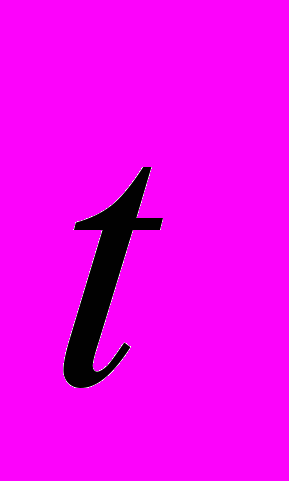векторе, определяющем путь до цели поиска. Для решения NP–полных проблем принятия решений при поиске неструктурированных знаний предлагается анализировать базу знаний (БЗ), чтобы «выращивать» полные решения, рекурсивно расширяя последовательные частичные решения. Приведем модифицированный алгоритм квантового поиска.
  1. Начало.
  2. Ввод исходных данных.
  3. Проверка условий существования инвариантных частей в БЗ.
  4. Анализ математической модели БЗ, и на ее основе построение подмножества деревьев частичных решений.
  5. Суперпозиция частичных решений на основе «жадной» стратегии, квантового, генетического или бионического поиска.
  6. В случае наличия тупиковых решений возврат к шагу 4 и проведение параллельного поиска.
  7. Последовательный поиск в ветвях дерева решений с пошаговым возвращением.
  8. Если набор полных решений построен, то переход к 9, если нет, то к 4.
  9. Лексикографический перебор полных решений и выбор из него оптимального или квазиоптимального решения.
  10. Конец работы алгоритма.

Следует отметить, что, изменяя параметры, алгоритмы и схему квантового поиска, в некоторых случаях можно выходить из локальных оптимумов. На рис.11 приведена схема распараллеливания квантового поиска на основе октаэдра. Введение экспертной подсистемы позволит определить назначение каждого блока квантового алгоритма. Например, КА1 – определяет целевую функцию, КА2 – операцию суперпозиции и т.п.



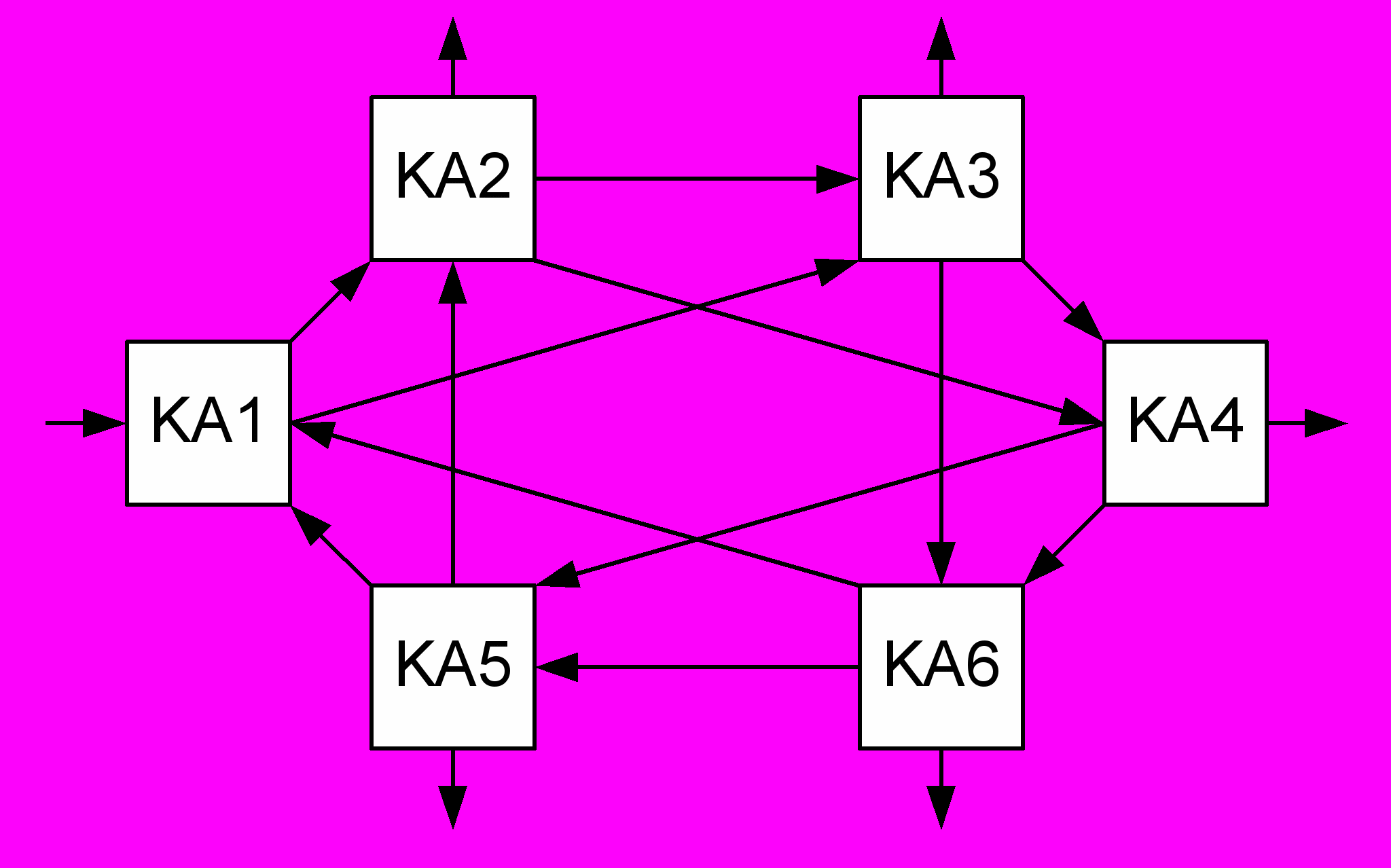
Рис. 11. Схема распараллеливания квантового поиска на основе октаэдра

Для повышения скорости нахождения оптимальных решений предлагаются комплексные алгоритмы, основанные на взаимодействии жадных, генетических, квантовых и бионических алгоритмов (рис.12). Очевидно, что данные схемы можно взять как строительные блоки (IP-блоки при проектировании систем на кристалле) и наращивать иерархически. При этом возможно построить схему последовательного или параллельного совместного поиска любой сложности.



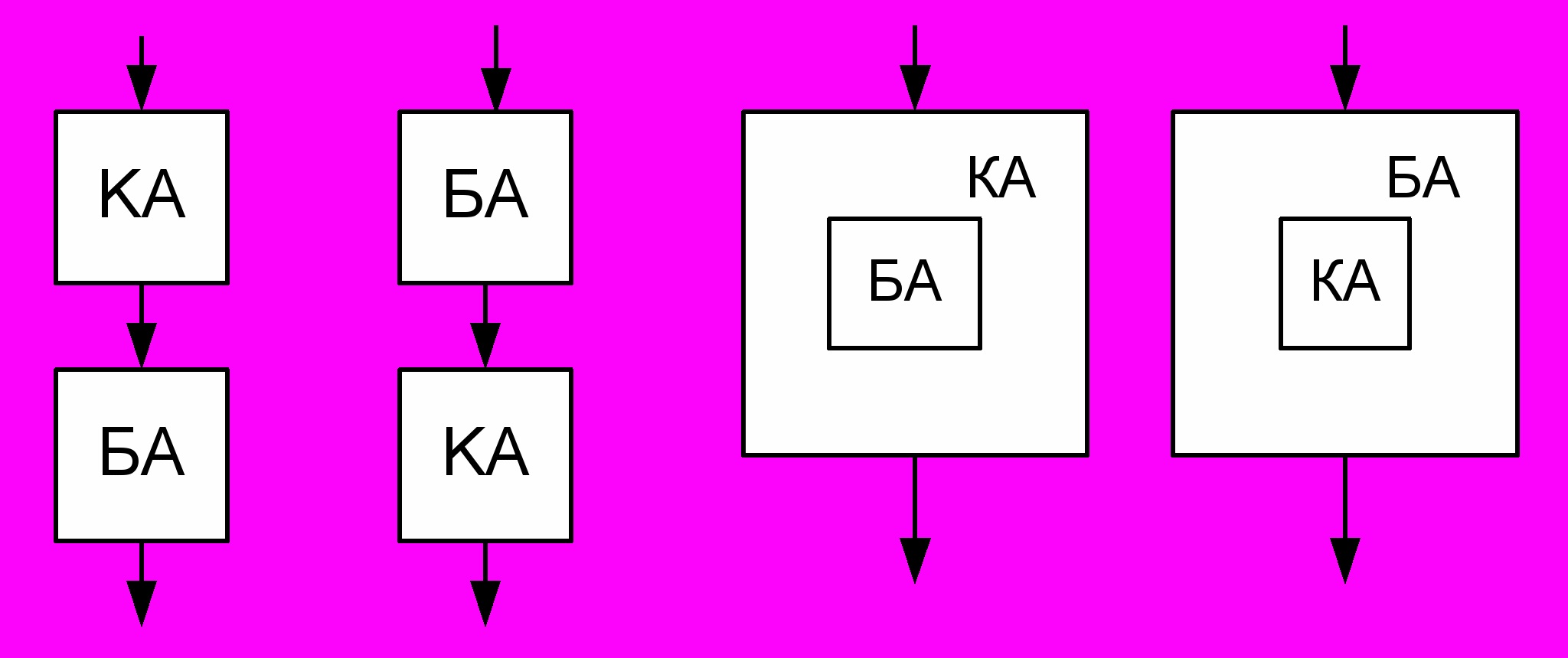
Рис.12. Схемы взаимодействия алгоритмов


На рис.13 приведена схема каскадной реализации бионического поиска. Идея подхода заключается в каскадном построении схемы бионического поиска. Здесь ГА - генетический, МА – муравьиный, КА - квантовый, ЭА – эволюционный, МО - моделирования отжига алгоритмы. Они реализуются каждый на своем процессоре. Коммутаторы Ki (i I = 1,2,…,n) обеспечивают полнодоступную коммутацию между процессорами i-го и (i +1) – го каскадов. Имеется также возможность прямой передачи результатов поиска с коммутатора Ki на входы коммутатора Ki + 1 следующего каскада. Отметим, что такой поиск обеспечивает более гибкую коммутацию между процессорными элементами. В этой связи затраты на реализацию поиска будут уменьшаться. Заметим, что такой макроконвейер можно строить не только на уровне алгоритмов, но и на уровне крупных операций, использую принцип «матрешки».



Рис.13. Схема каскадной реализации бионического поиска

Для управления и реализации процессом совместного поиска автор предлагает ввести следующие модифицированные принципы:
  • Принцип целостности. В квантовых, жадных, генетических и бионических алгоритмах значение целевой функции альтернативного решения не сводится к сумме целевых функций частичных решений. Такие алгоритмы будем называть инспирированными природными системами (ИПА).
  • Принцип чувствительности к начальным условиям. Результат работы ИПА существенно зависит от представления входных данных исследуемой модели.
  • Принцип дополнительности. При принятии решений в неопределенных и нечетких условиях возникает необходимость использования различных несовместимых и взаимодополняющих моделей эволюций и операторов, инспирированных природными системами.
  • Принцип неточности. При росте сложности анализируемой задачи уменьшается возможность построения точной модели.
  • Принцип управления неопределенностью. При принятии решений в неопределенных и нечетких условиях необходимо вводить различные виды неопределенности в ИПА.
  • Принцип соответствия. Язык описания исходной задачи должен соответствовать наличию имеющейся о ней информации.
  • Принцип «007». Используй только те входные данные, которые необходимы для решения задачи принятия решений.
  • Принцип спонтанного возникновения Пригожина. Инспирированные природными системами алгоритмы позволяют спонтанно генерировать наборы альтернативных решений, среди которых с большой вероятностью может возникнуть оптимальное.
  • Принцип разнообразия путей развития. Реализация ИПА многовариантна и альтернативна. Основная задача выбрать путь, приводящий к получению оптимального или квазиоптимального решения.
  • Принцип единства и противоположности порядка и хаоса. «Хаос не только разрушителен, но и конструктивен», т.е. в хаосе области допустимых решений обязательно содержится порядок, определяющий искомое решение.
  • Принцип совместимости и разделительности. Процессы поиска решений носят поступательный, пульсирующий или комбинированный характер.
  • Принцип иерархичности. Инспирированные природными системами алгоритмы могут надстраиваться по горизонтали и вертикали (например, сверху вниз и снизу вверх).
  • Принцип «Бритвы Оккама». Нежелательно увеличивать сложность архитектуры поиска и ИПА без необходимости.
  • Принцип гомеостаза. Инспирированные природными системами алгоритмы конструируются таким образом, чтобы любое полученное альтернативное решение не выходило из области допустимых решений.

Использование данных принципов позволяет строить алгоритмы принятия решений в САПР с локальными оптимумами за полиномиальное время. Сложность алгоритмов имеет в среднем квадратичный порядок.

В четвертом разделе. Проведен синтез алгоритмов принятия решений при разбиении графовых моделей в САПР. При проектировании систем на кристалле важным является дублирование и троирование графовых моделей для учета современных критериев энергосбережения и задержек сигналов при проектировании объектов в наносекундном диапазоне. Основой алгоритмов дублирования и троирования является метод определения точек сочленения в графовых моделях. Приведем алгоритм определения точек сочленения и блоков.
  1. Анализируем поочередно все вершины графа 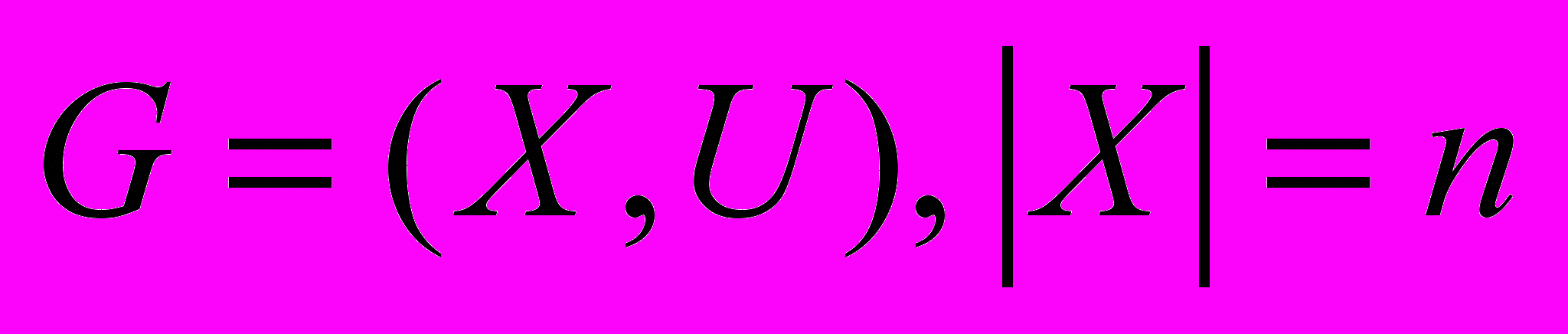xiX, i=1,2,…,n, удаляя одну за другой вершины с инцидентными ребрами.
  2. Просматриваем поочередно полученные подграфы и проверяем получение компонент связности. В результате получаем все точки сочленения G.
  3. Образуем систему строк. Каждая строка соответствует точке сочленения. Причем в эти строки добавлены индексы соответствующих точек сочленения.
  4. Выполняем операцию пересечения строк первой со второй, третьей с суммарным результатом пересечения первой и второй строк и т. д. В результате получим все блоки графа и точки сочленения.
  5. Конец работы алгоритма.

В работе рассмотрены новые комбинированные подходы для размещения вершин графовых моделей систем на кристалле. Задача размещения сводится к отображению заданного графа-модели 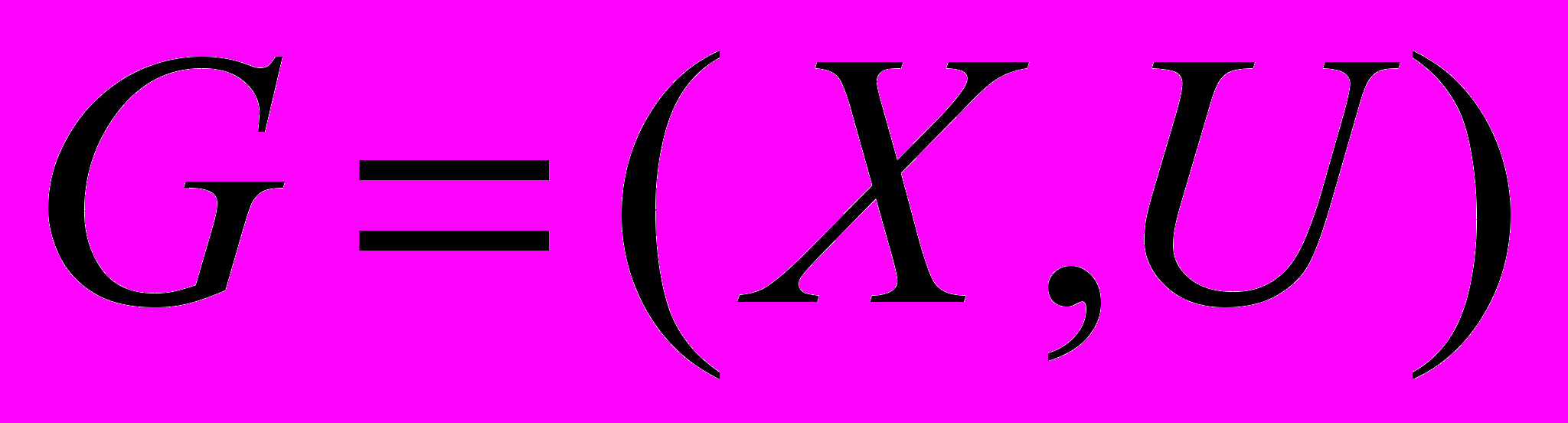схемы в решетку 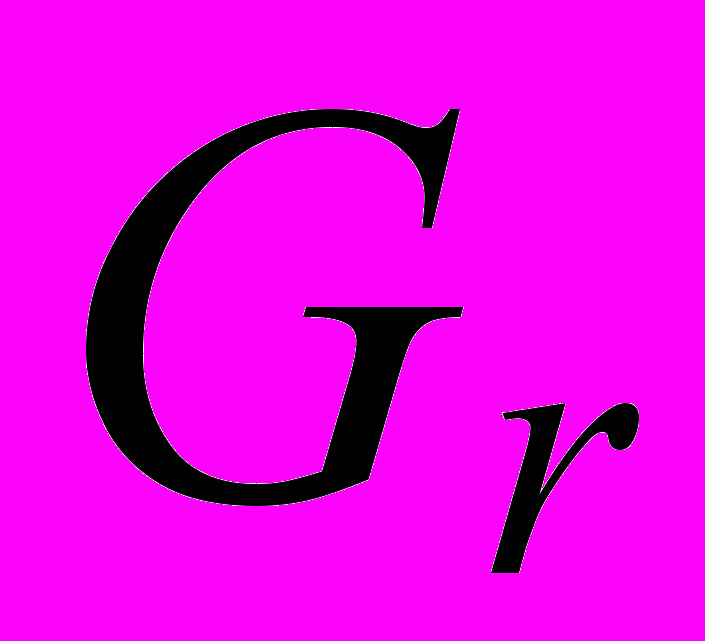таким образом, чтобы множество вершин 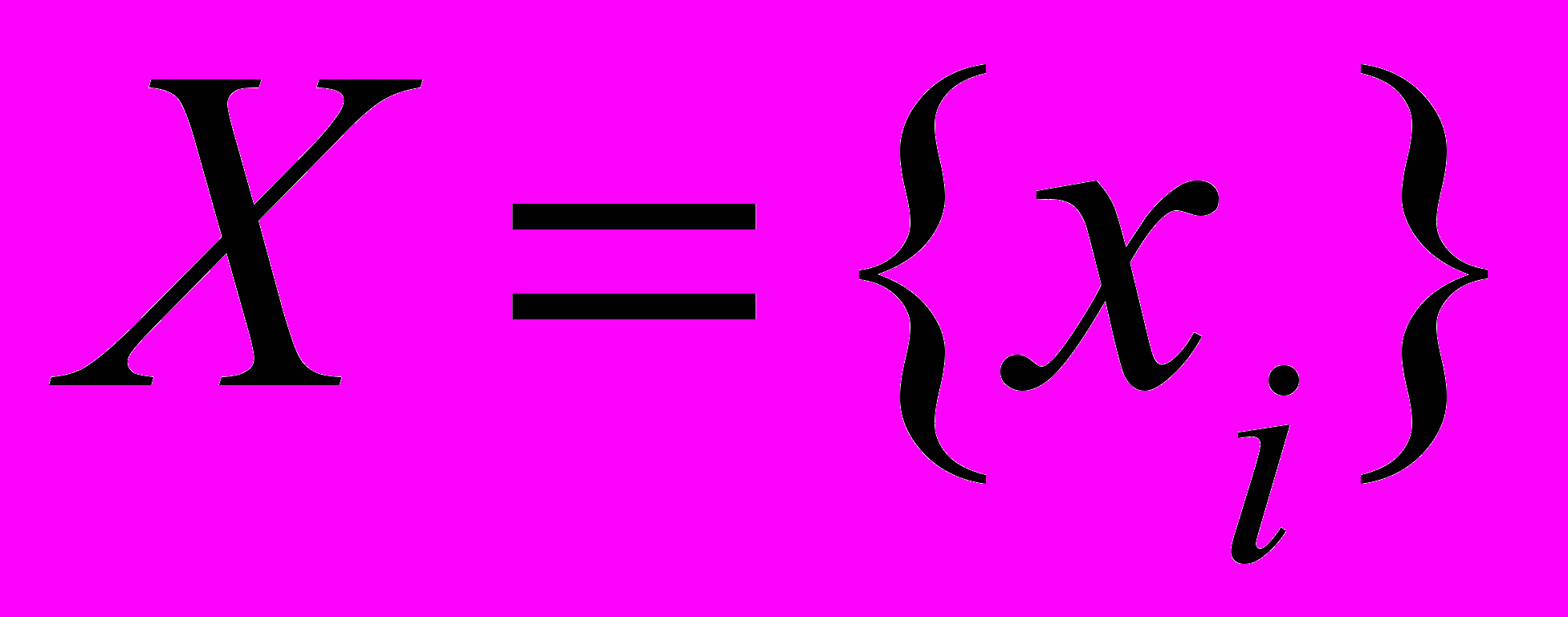, , 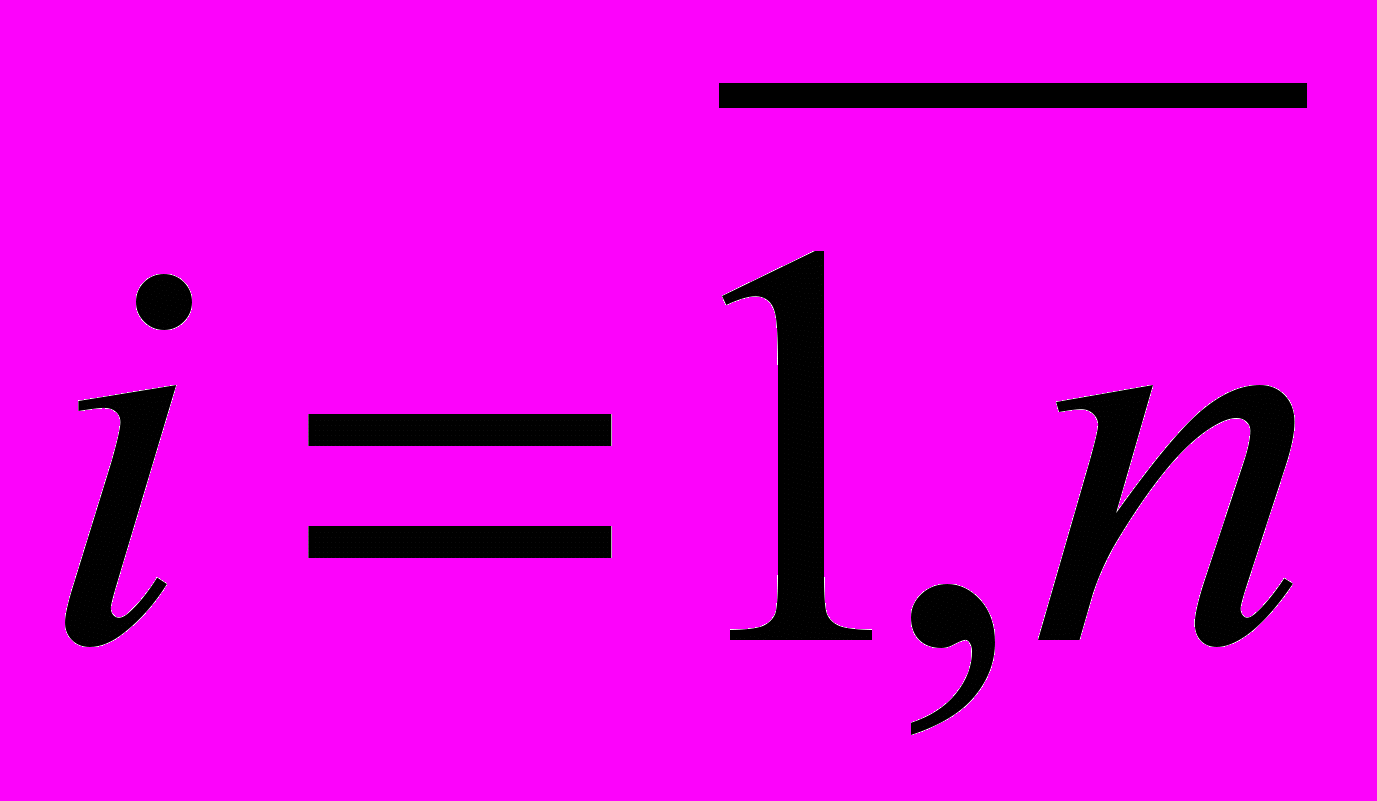графа 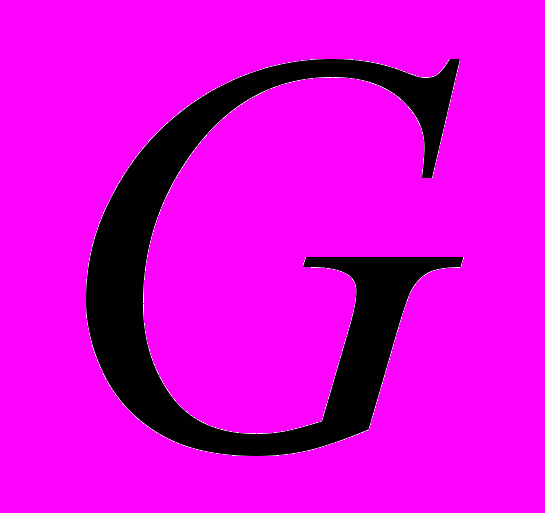размещалось в узлах решетки, число которых конечно, а также соблюдался интегрированный критерий, представляющий собой интегрированную целевую функцию (ЦФ). Требование оптимизации: весовая функция должна быть наименьшей для всевозможных способов отождествления вершин графа и узлов решетки. Здесь предлагается каждое альтернативное решение (хромосому) представлять в виде строки переменной длины. Вместо того, чтобы определять хромосому как последовательность битов, ее, подобно естественной копии, будем определять как последовательность генов.

На рис.14 приведена упрощенная схема комбинированного поиска при решении задачи размещения. Здесь ИПА – алгоритмы, инспирированные природными системами, AC – модифицированный алгоритм Ant Colony, БА, ГА, ЖА, КА и МО – бионический, генетический, жадный, квантовый и моделирования отжига алгоритмы размещения, оператор редукции корректирует размер популяции альтернативных решений, ЭС – экспертная система, определяющая дальнейший ход поиска. ИПА представляет собой кортеж: ИПА = .



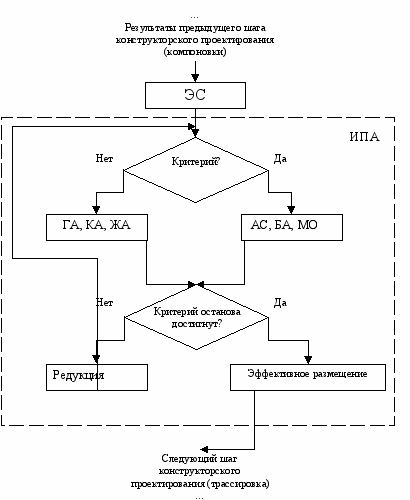
Рис.14. Архитектура комбинированного поиска

Для «борьбы с проклятием размерности» при переходе на проектирование изделий на кристалле в нанометровом диапазоне необходимо использовать технологию распараллеливания алгоритмов. Предлагается модифицированная стратегия распараллеливания на основе ИПА. Используется понятие «грубого» и «точного» параллелизма. В первом случае на основе клиент–серверной модели происходят соединения с серверами (в частном случае персональными компьютерами), где последовательно выполняются блоки алгоритма размещения. Во втором случае точными методами реализуется отдельные блоки алгоритма. Процесс размещения фрагментов БИС графовой модели коммутационной схемы при параллельном размещении будет осуществлен в 7 этапов: анализ, препроцессинг (построение начальной популяции), генетическое, бионическое, жадное и квантовое размещение, постпроцессинг.

В работе приведены алгоритмы определения инвариантов графовой модели принятия решений в задачах САПР. Построены квантовые алгоритмы раскраски, построения клик, гамильтоновых циклов и независимых множеств на основе графовых моделей. Это позволяет создавать новую архитектуру проектирования на основе комбинированных алгоритмов.

Для определения независимых подмножеств (стандартных IP-блоков) предлагается два варианта бионического алгоритма, отличающихся друг от друга методикой кодирования и нахождением значений целевой функции. Для выделения независимых подмножеств описан алгоритм, модифицированный с учётом знаний о решаемой задаче. На первом шаге алгоритма вводятся начальные данные и параметры алгоритма (вероятности кроссинговера, мутации, элитного и равновероятного отбора; размер популяции хромосом; количество генераций). Далее рассчитывается верхняя и нижняя оценка числа внутренней устойчивости и формируется начальная популяция. После этого начинается итеративный процесс применения операторов к исходной популяции. На каждой итерации с заданной вероятностью к хромосомам текущей популяции применяются разработанные операторы. Далее рассчитываются целевые функции хромосом, и производится их проверка на независимость. Независимые подмножества заносятся в отдельный список. После этого, в соответствии с заданной вероятностью, производится элитный или равновероятный отбор хромосом в новую популяцию. Процесс продолжается до тех пор, пока не будет выполнено условие останова – заданное число генераций.

Основными инвариантами графовой модели в САПР являются числа: цикломатическое, хроматическое, внешней и внутренней устойчивости, клик, полноты, ядер, планарности и т.д. Графовые деревья описывают модель неструктурированных знаний. В таких моделях важным является нахождение инвариантов. Инвариант графа G=(X,U), где |X|=n, а |U|=m, это число, связанное с G, которое принимает одно и то же значение на любом графе, изоморфном G. При определении клик графа найдем частичные решения, для каждой вершины графа рекурсивно расширяя “хорошие” решения и устраняя тупиковые решения.

Приведем описание алгоритма стандартной операции суперпозиции для определения клик графа и построения независимых подмножеств:

1. Выбирается первое частичное решение.

2. Данное решение последовательно или параллельно склеивается со всеми остальными решениями.

3. В «склеенных» решениях устраняются повторяющиеся вершины.

4. Аналогичные операции проводятся со всеми остальными вершинами, кроме повторяющихся вершин, пока не будет найдено полное решение, в противном случае выбор следующего частичного решения и переход на шаг 2.

5. Конец работы алгоритма.

Рассмотрим теперь решение раскраски графа на основе квантового поиска. Алгоритм основан на нахождении частичной раскраски для подмножеств вершин. Для определения полной раскраски производится рекурсивно расширение частичных окрасок с возвратом назад в случае тупиковых решений. Элементарный способ состоит в рассмотрении дерева поиска частичных решений заданной глубины. Решение по раскраске находится на “ветвях и листьях” этого дерева. Приведем эвристическое правило. При наличии нескольких возможных частичных альтернативных решений суперпозицию в квантовом алгоритме необходимо выполнять для подмножеств, имеющих наименьшее число совпадающих элементов.

В работе приведен модифицированный алгоритм квантового поиска, ориентированный на решение задачи определения гамильтонова цикла в графе.
  1. Начало.
  2. Ввод исходных данных.
  3. Проверка необходимых условий существования ГЦ в графе.
  4. Анализ математической модели и на его основе построение дерева частичных решений.
  5. Суперпозиция частичных решений на основе жадной стратегии и квантового поиска.
  6. В случае наличия тупиковых решений – последовательный поиск с пошаговым возвращением.
  7. Если набор полных решений построен, то переход к 7, если нет, то к 5.
  8. Лексикографический перебор полных решений и выбор из него оптимального или квазиоптимального решения.
  9. Конец работы алгоритма.

В работе предложены новые идеи определения максимальных паросочетаний в графовой модели на основе биоинспирированных алгоритмов, позволяющие находить наборы максимальных паросочетаний. Опишем модифицированную эвристику построения максимального паросочетания в двудольном графе. Паросочетанием (ПС) называется подмножество ребер M  U, не имеющих общих концов. Причем каждое ребро uiU смежно одному ребру из М. Также можно сказать, что паросочетание (ПС) - это множество независимых ребер. Максимальное паросочетание (МПС) – это паросочетание М, содержащее максимально возможное число ребер. Приведем эвристику построения МПС на основе анализа специальной матрицы смежности, и построения в ней «параллельных диагоналей». Каждая из таких диагоналей является паросочетанием исследуемого графа. Очевидно, при наличии всех единиц по главной диагонали матрицы - построено максимальное паросочетание. Полученные диагонали можно представить в виде амплитуды. Для дальнейших исследований оракул выберет оптимальную амплитуду и на основе суперпозиции с другими диагоналями будет построено максимальное паросочетание. Исходные данные алгоритма: двудольный граф G=(A,B;U), | A|, | B|, матрица смежности.
  1. Строится специальная матрица смежности.
  2. Определяются диагонали матрицы, соответствующие паросочетаниям графа.
  3. Строится квантовая амплитуда, и из нее оракул выбирает амплитуду с максимальным значением.
  4. Производится суперпозиция максимальной диагонали с другими, путем расширения специальной матрицы слева, справа, сверху и снизу.
  5. Определяется максимальное паросочетание.
  6. Конец работы алгоритма.

Сформулируем гипотезу. Главная диагональ матрицы R, полностью заполненная элементами, соответствует МПС. Суммарное число единиц соответствует суммарному числу ребер МПС. Каждая единица главной диагонали определяет ребро МПС. Доказательство следует из способа построения специальной матрицы по заданному двудольному графу, т.к. каждой вершине из X1 главной диагонали ставится в соответствие одна и только одна вершина из X2. Отметим, что перед работой алгоритма необходимо упорядочить вершины двудольного графа по возрастанию элементов. На основе этой гипотезы построен алгоритм определения МПС в двудольном графе.
  1. Определить вершины подмножеств X1 и X2 двудольного графа G.
  2. Упорядочим вершины X1 и X2.
  3. Построить специальную матрицу R и определить в ней главную диагональ.
  4. Если главная диагональ заполнена элементами полностью, то построено МПС и переход к шагу 7. Если нет, то переход к 5.
  5. В матрице R определить все диагонали и выбрать диагональ с наибольшим числом элементов. Если таких диагоналей несколько, то выбирается любая.
  6. Выполняется процедура агрегации и преобразования на основе генетических операторов. В результате строится МПС.
  7. Конец работы алгоритма.

Время работы алгоритма зависит от размера анализируемой матрицы. В задачах на графах размер входа часто измеряется не одним числом, а двумя (число вершин n и число ребер m графа). Время работы разработанных алгоритмов в лучшем случае имеет порядок роста n т.е. О(n).

В пятом разделе приведены результаты вычислительного эксперимента при испытании СППР в САПР. Сформулированы цели экспериментального исследования. Описана созданная инструментальная среда СППР. Описаны структурные схемы алгоритмов, компоненты разработанного программного обеспечения. Проведены экспериментальные исследования алгоритмов принятия решений на графах. Определено влияние динамических параметров на принятие решений. Приведены практические оценки эффективности разработанных алгоритмов для определения квазиотимальных и оптимальных решений в СППР. Описаны количественные и качественные оценки разработанных алгоритмов при проведении различных серий испытаний. Произведено сравнение разработанных алгоритмов с существующими стандартными решениями, известными из литературы, и по сведениям ведущих фирм мира.

Для комплексного тестирования различных бионических алгоритмов конструкторских задач САПР была реализована программная среда. Основное её предназначение заключается в получении, при помощи различных методов анализа, интегральных численных оценок эффективности набора алгоритмов для принятия решений. Для тестирования комплекса алгоритмов необходимы три основные компонента: генератор параметров задачи; решатель задачи; анализатор, тестирующий алгоритм и выдающий некоторую интегральную численную оценку его эффективности. Связь компонентов показана на рис.15.




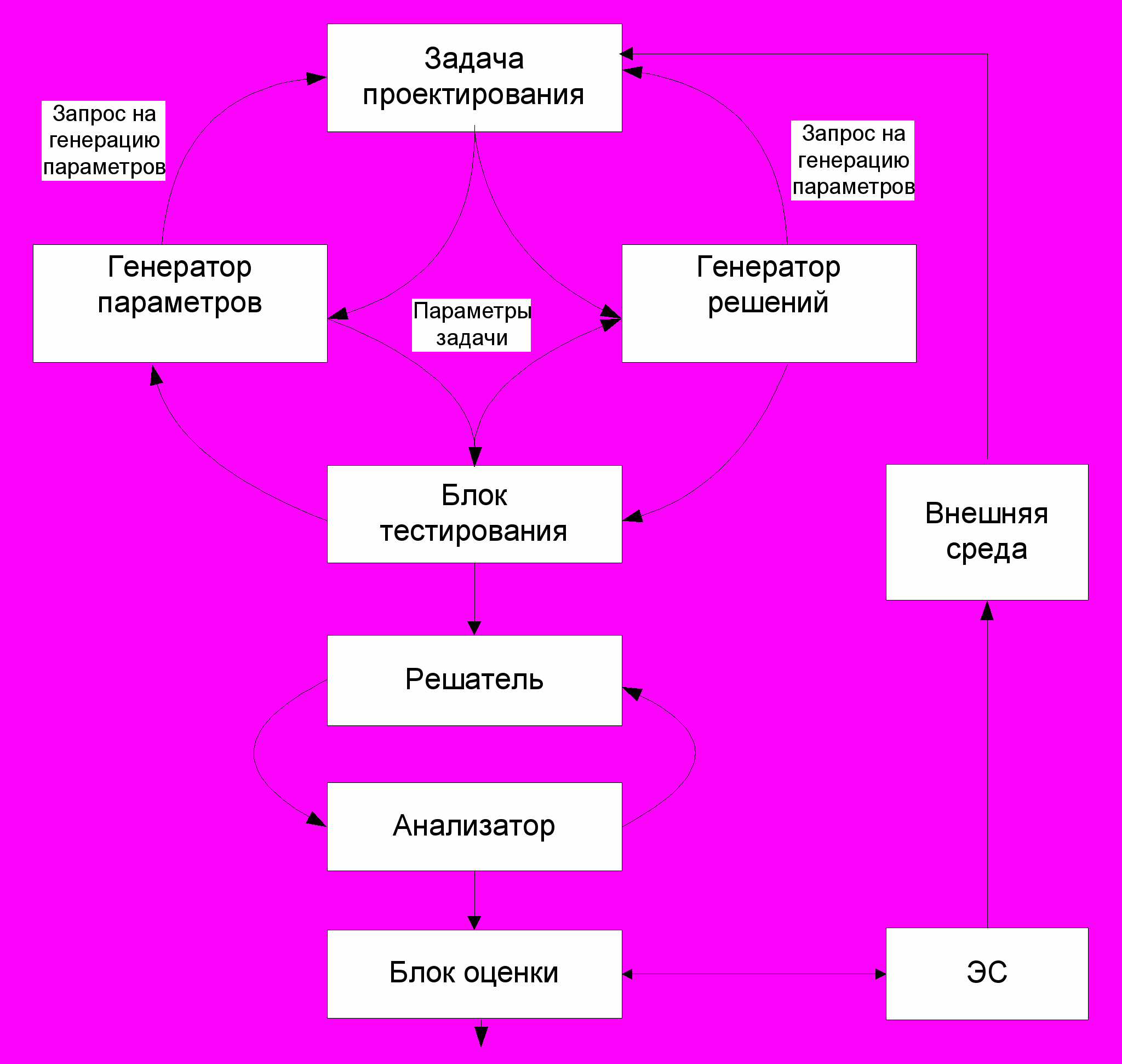
Рис.15.  Связь компонентов комплексного подхода выбора эффективного алгоритма

В работе приведена общая структурная схема инструментальной среды СППР на основе ИПА (рис. 16).



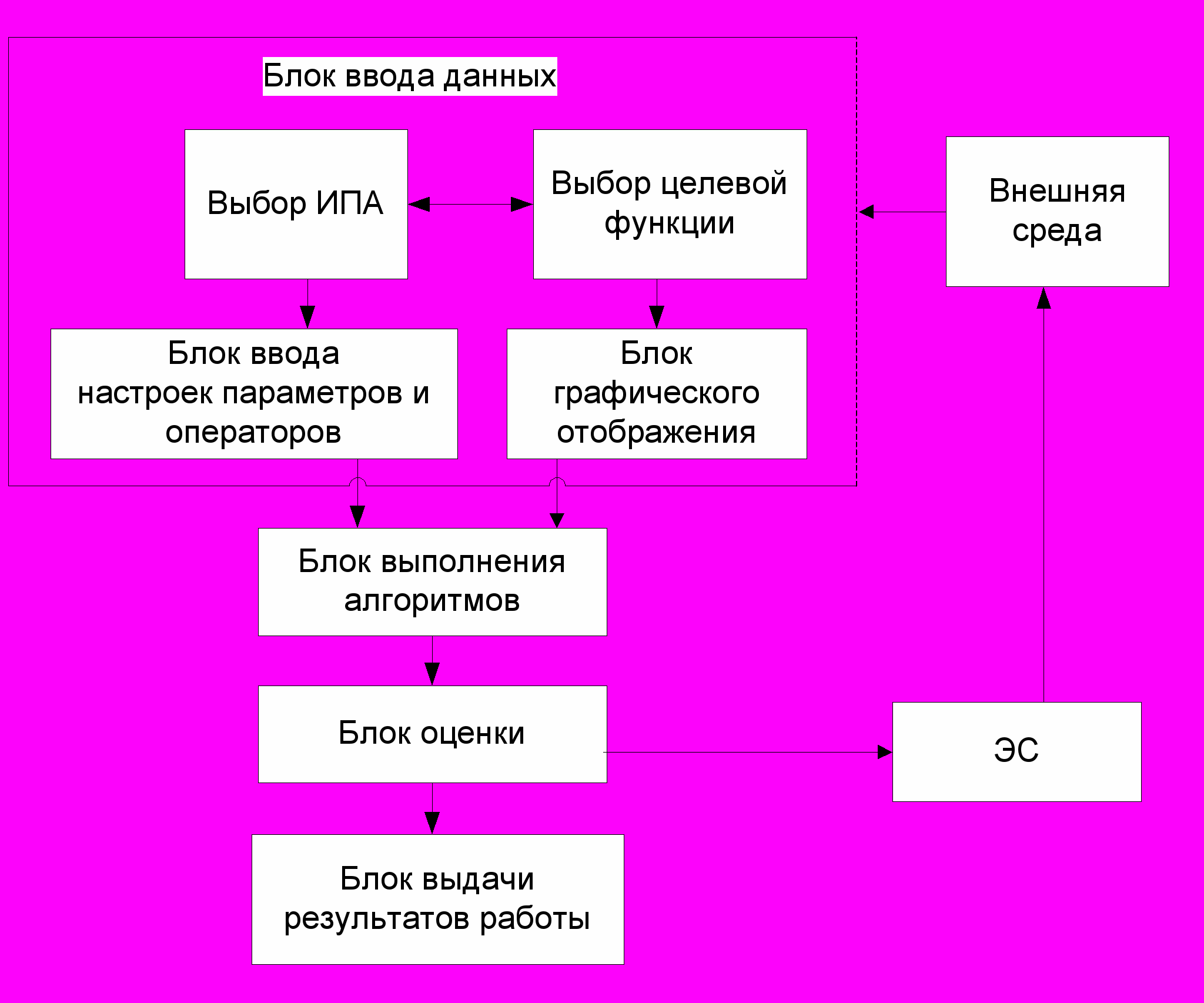
Рис. 16. Структурная схема инструментальной среды СППР на основе ИПА

Она состоит из следующих частей: блока выбора типа ИПА; блока выбора целевой функции; блок ввода настроек параметров и операторов; блока знаний, содержащей процедурные и декларативные знания о предметной области ПР; блока данных; блока ЭС; блока внешней среды; блока адаптации; блок работы выбранных алгоритмов с учетом настроек; блока выдачи результатов. Опишем теперь результаты экспериментальных исследований и приведем сравнительные количественные и качественные характеристики для всех приведенных задач принятия решений на графовых моделях в САПР. При построении комплекса программ использовались пакеты Borland C++, Builder, Visual C++. Отладка и тестирование проводилось на ЭВМ типа IBM PC c процессором Pentium-IV, с ОЗУ 2Гб. Для адекватного сравнения использовались стандартные оценки по производительности различных систем (бенчмаркам), представленными ведущими фирмами мира.

Эксперименты показали, что не всегда увеличение вероятностей операторов в БА повышает качество найденных решений. Очевидно, что существует определенное значение вероятности операторов, соответствующее оптимальному значению ЦФ.

Проанализируем зависимость времени работы алгоритма и значения ЦФ от числа элементов модели для серии опытов конструкторского проектирования. При этом вероятность всех операторов остается постоянной. Проведем эксперименты на десяти случайно сгенерированных схемах с количеством вершин и рёбер от 500 до 5000. Построим таблицу (см. таблицу 1). В таблице приведены данные для компоновки блоков схем на кристалле. В первом столбце указывается количество элементов схемы. Далее на каждом шаге эксперимента фиксируется значение ЦФ и время работы t. Размер популяции фиксирован и равен количеству элементов рассматриваемой модели, согласно стратегии генерации стартовой популяции. Далее подсчитаем среднее значение ЦФ, а также среднее время работы для каждой схемы.

Таблица 1. Зависимость времени работы алгоритма и значения ЦФ от числа элементов модели.

|X|=|U|
БА, Ni = 400
ЦФср


tср




N зап.
1
2
3
4
5
6
7
8
9
10

500
ЦФ
10
11
10
12
12
10
10
12
10
12
10,9

tраб., с
2,172
2,235
2,172
2,266
2,172
2,204
2,266
2,328
2,406
2,406
2,63

2000
ЦФ
70
69
70
72
67
70
69
74
69
73
70,3

tраб., с
12
8,156
8,203
8,253
10,78
8,297
9,453
8,719
8,156
8,188
9,021

3000
ЦФ
117
115
108
117
114
110
111
114
107
114
112,7

tраб., с
20,74
16,58
17,41
19,17
18,16
16,89
18,22
17,39
19,69
18,36
18,261

4000
ЦФ
160
153
157
153
150
153
157
153
160
158
155,4

tраб., с
30,16
30,03
30,55
32,83
29,79
28,91
29,2
30,66
36,79
28,88
30,78

5000
ЦФ
203
200
196
204
206
203
202
202
194
202
201,2

tраб., с
46,13
46,14
46,11
45,89
45,97
46
46
45,99
45,86
46,69
46,078

Из экспериментов следует, что время решения при компоновке практически линейно зависит от числа элементов. При этом временная сложность алгоритмов (ВСА), полученная на основе экспериментов, практически совпадает с теоретическими исследованиями, и для рассмотренных тестовых задач компоновки в лучшем случае ВСА ~ O(n).

Опишем исследование бионического алгоритма размещения.

В качестве изменяемых параметров выступают вероятности операторов, численность общей популяции, число итераций поиска. После нескольких запусков алгоритма получаем окончательное размещение. Графики работы бионического алгоритма размещения показаны на рис.17,18.



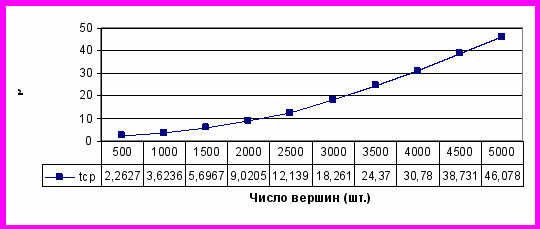
Рис.17. График зависимости времени решения от числа элементов



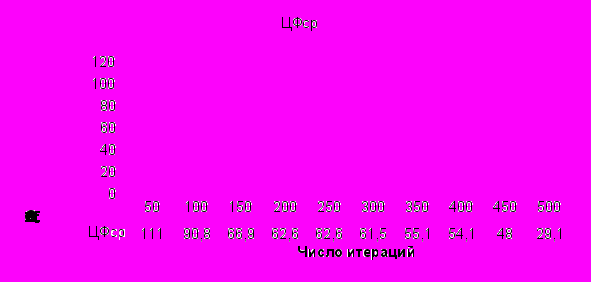
Рис.18. График зависимости значения ЦФ от числа итераций

Из графиков следует, что время решения находится в полиномиальной (близкой к квадратичной) зависимости от числа вершин и итераций БА. Помимо результата работы бионического алгоритма дается статистика: число элементов схемы, общая длина цепей (начальная и конечная), время работы алгоритма.

Анализ экспериментов позволяет отметить, что бионические алгоритмы требуют больших затрат времени, но позволяют получать набор локально-оптимальных решений и, в частном случае, оптимальных решений. Экспериментальные исследования показали, что разработанные алгоритмы по скорости совпадают с итерационными и несколько хуже последовательных. В отличие от всех рассмотренных алгоритмов, БА позволяют получать набор квазиоптимальных и оптимальных результатов. При этом с большой вероятностью среди этих решений может быть найден глобальный экстремум. Из приведенных статистических данных следует, что в общем случае время решения линейно зависит от количества генераций и ВСА подтверждает теоретические предпосылки ~ O((nlogn) - (n3)). Следует заметить, что с увеличением числа итераций время решения, конечно, повышается, но это повышение незначительно и компенсируется получением множества локально-оптимальных решений. Причем разработанные алгоритмы конструкторского проектирования имеют большее быстродействие, чем метод ветвей и границ, метод моделирования отжига и другие аналогичные методы.

В приложении даны копии актов использования и внедрения.