Учебно-методическое пособие по выполнению дипломной работы для студентов очной, очно-заочной, заочной форм и дистанционного обучения по специальностям 080504 «Государственное и муниципальное управление»

Вид материала

Учебно-методическое пособие

Содержание Нормальная устойчивость Неустойчивое финансовое состояние Кризисное финансовое состояние Собственные оборотные средства Текущие активы – Расходы будущих периодов Текущие активы – Текущие пассивы Основные пути финансового оздоровления предприятий К внешним источникам Экономико-математическое моделирование

Подобный материал:

• Реферат как форма самостоятельной работы студента: методическое пособие по выполнению, 325.87kb.
• Учебное пособие для студентов очной, очно-заочной и заочной форм обучения (дистанционное, 929.04kb.
• Методические указания по написанию курсовой работы для студентов очной, заочной и очно-заочной, 318.34kb.
• Вопросы к зачету по дисциплине «международное право» для студентов специальности «Юриспруденция»,, 35.21kb.
• Учебно-методический комплекс по циклу дисциплин сд. 04 Для студентов очной и заочной, 382.23kb.
• Методические рекомендации по выполнению практических работ по курсу «Экология» для, 474.71kb.
• Темы (задания) курсовых работ и методические указания по их выполнению для студентов, 578.18kb.
• В г. Красноярске муниципальное право российской федерации Учебно-методический комплекс, 730.54kb.
• Методические указания к курсовой работе по дисциплине «Стратегический менеджмент» для, 76.01kb.
• Гражданское право, 165.36kb.

Х

Рис. 22. Зависимость между объемом реализации продукции, ее себестоимостью и суммой прибыли

1. Абсолютная устойчивость финансового состояния встречается редко. Она задается системой условий: излишек (+) собственных оборотных средств или равенство величин собственных оборотных средств и запасов;
   
2. Нормальная устойчивость финансового состояния, гарантирующая его платежеспособность: недостаток (-) собственных оборотных средств, излишек (+) долгосрочных источников формирования запасов;
   
3. Неустойчивое финансовое состояние характеризуется нарушениями платежеспособности, при котором, тем не менее, сохраняется возможность восстановления равновесия за счет пополнения собственного капитала, а также за счет дополнительного привлечения долгосрочных кредитов и заемных средств;
   
4. К
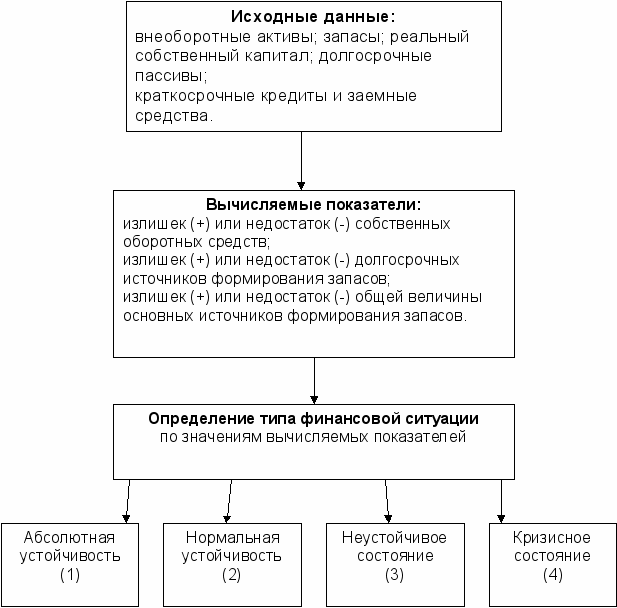
   ризисное финансовое состояние, при котором предприятие находится на грани банкротства: недостаток (-) собственных оборотных средств; недостаток (-) долгосрочных источников формирования запасов.
   

Рис. 23. Схема алгоритма идентификации типа финансовой ситуации


Устойчивость финансового состояния может быть повышена путем:

• ускорения оборачиваемости капитала в текущих активах, в результате чего произойдет относительное его сокращения на рубль оборота;
  
• обоснованного уменьшения запасов и затрат (до норматива);
  
• пополнения собственного оборотного капитала за счет внутренних и внешних источников.
  

Поэтому при внутренним анализе осуществляется углубленное изучение причин изменения запасов и затрат, оборачиваемости оборотных активов, наличия собственного оборотного капитала.

Наряду с абсолютными показателями финансовую устойчивость характеризуют также финансовые коэффициенты:

1. Коэффициент маневренности:
   

собственные оборотные средства

К₁=

реальный собственный капитал


Этот коэффициент показывает, какая часть собственного капитала находится в мобильной форме, позволяющей относительно свободно маневрировать капиталом. Высокие значения этого коэффициента положительно характеризуют финансовое состояние. Оптимальный уровень: 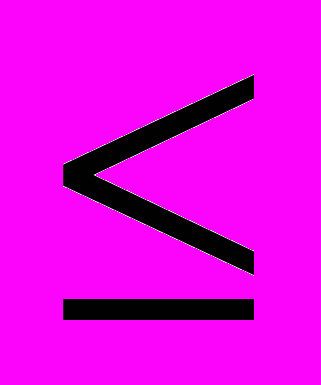0,5.

2. Коэффициент автономии источников формирования запасов:
   

Собственные оборотные средства

К₂=

Общая величина основных источников

формирования запасов

Рост этого коэффициента отражает тенденцию к снижению зависимости предприятия от заемных источников финансирования и оценивается положительно.

3. Коэффициент обеспеченности запасов собственными источниками:
   

Собственные оборотные средства

К₃=

Запасы

для промышленных предприятий оптимальный уровень К₃ 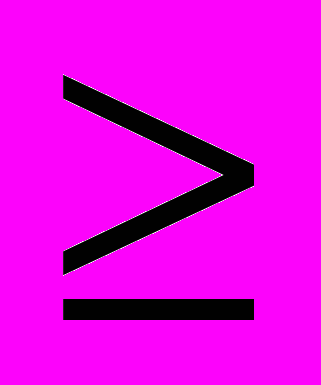0,6+0,8.

4. Коэффициент обеспеченности собственными средствами:
   

Собственные оборотные средства

К₄ =

Оборотные активы

Оптимальный уровень: К₄ 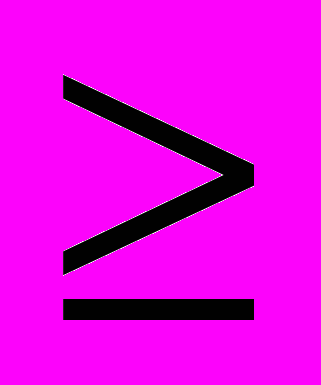0,1.

Если коэффициент обеспеченности собственными средствами на конец отчетного периода менее 0,1, то структура баланса считается неудовлетворительной, а само предприятие – неплатежеспособным.

В качестве критериев для оценки неудовлетворительной структуры баланса неплатежеспособных предприятий используются следующие показатели:

― общий коэффициент ликвидности;

― коэффициент обеспеченности предприятия собственными оборотными средствами;

― коэффициент восстановления платежеспособности.

Основанием для признания структуры баланса неудовлетворительной, а предприятие неплатежеспособным является наличие одного из условий:

а) если общий коэффициент ликвидности на конец отчетного периода имеет значение ниже нормативного (1,5);

б)если коэффициент обеспеченности собственными оборотными средствами имеет значение ниже нормативного (0,3).

Общий коэффициент ликвидности рассчитывается:

Текущие активы – Расходы будущих периодов

К_л =

Текущие пассивы – Доходы будущих периодов

Коэффициент обеспеченности собственными оборотными средствами равен:

Текущие активы – Текущие пассивы

К₀ =

Текущие активы

В случае если общий коэффициент ликвидности ниже нормативного, а доля собственного оборотного капитала в формировании текущих активов меньше 0,3 (норматив), но имеется тенденция роста этих показателей, рассчитывается коэффициент восстановления – платежеспособности.

Выводы о признании структуры баланса неудовлетворительной, а предприятие неплатежеспособным делаются при отрицательной структуре баланса и отсутствии у него реальной возможности восстановить свою платежеспособность.

Известно, что одним из критериев банкротства является неудовлетворительная структура баланса, определяемая по коэффициенту текущей ликвидности, коэффициенту обеспеченности текущих активов собственными средствами и суммой деловых обязательств к собственному капиталу. В этом случае, ввиду реальной угрозы утраты предприятием платежеспособности оно ставится на соответствующий учет в специальных подразделениях Мингоскомимущества по делам о несостоятельности (банкротстве) предприятий.

Банкротство – подтвержденная документально неспособность субъекта хозяйствования платить по своим долговым обязательствам и финансировать текущую основную деятельность из-за отсутствия средств.

Основным признаком банкротства неспособность предприятия обеспечить выполнение требований кредиторов в течение трех месяцев со дня наступления сроков платежей. По истечении этого срока кредиторы получают право на обращение в арбитражный суд о признании предприятия – должника банкротом.

Банкротство предопределено самой сущностью рыночных отношений, которые сопряжены с неопределенностью достижения конечных результатов и риском потерь.

В соответствии с действующим законом «О банкротстве» предприятие признается неплатежеспособным при наличии одного из следующих условий:

• Коэффициент текущей ликвидности на конец отчетного периода ниже нормативного значения для соответствующей отрасли;
  
• Коэффициент обеспеченности предприятия собственными оборотными средствами на конец отчетного периода ниже нормативного значения;
  
• Коэффициент восстановления (утраты) платежеспособности < 1.
  

В зарубежных странах для оценки риска банкротства и кредитоспособности предприятий широко используется модель известного западного экономиста Альтмана, который с помощью многомерного анализа исследовал 22 финансовых коэффициента и выбрал 5 из них для включения в уравнение множественной регрессии:

Z=1,2X₁+1,4X₂+3,3X₃+0,6X₄+1,0X₅ , (37)

где:

Х₁ – собственный оборотный капитал / сумма активов;

Х₂ – нераспределенная прибыль / сумма активов;

Х₃ – прибыль до уплаты процентов и налогов/ сумма активов;

Х₄ – рыночная стоимость собственного капитала / заемный капитал;

Х₅ – объем продаж (выручка) / сумма активов.

Если значения Z<1,81, то это признак высокой вероятности банкротства, тогда как значение Z>3 свидетельствует о малой его вероятности.

По результатам анализа должны быть предложены конкретные меры по укреплению финансового состояния предприятия.

Однако следует отметить, что к использованию западных моделей нужно подходить с большой осторожностью. Тестирование некоторых предприятий по данным модели Альтмана показала, что она не в полной мере подходит для оценки риска банкротства Российских предприятий из-за разной методики отражения инфляционных факторов и разной структуры капитала, а также из-за различий в законодательной и информационной базах.

На практике, для оценки рейтинга субъектов хозяйствования и степени финансового риска довольно часто используются методы многомерного рейтингового анализа.

Основные пути финансового оздоровления предприятий

К предприятиям, которые признаны банкротами, применяются ряд санкций:

• Реорганизация производственно-финансовой деятельности;
  
• Ликвидация с распродажей имущества;
  
• Мировое соглашение между кредиторами и собственниками предприятия.
  

Реорганизационные процедуры предусматривают восстановление платежеспособности путем проведения определенных инновационных мероприятий. По результатам анализа должна быть выработана генеральная финансовая стратегия и составлен бизнес-план финансового оздоровления предприятия с целью недопущения банкротства путем комплексного использования внутренних и внешних резервов.

К внешним источникам привлечения средств в оборот предприятия относится факторинг, лизинг, привлечение кредитов под прибыльные проекты, выпуск новых акций и облигаций.

Одним из основных и наиболее радикальных направлений финансового оздоровления предприятия является поиск внутренних резервов по увеличению прибыльности производства и достижению безубыточной работы, за счет увеличения объемов производства и реализации товара, повышению его качества и конкурентоспособности, снижения себестоимости и более рационального использования материальных, трудовых и финансовых ресурсов. Особое внимание при этом необходимо уделять вопросам ресурсосбережения. Кроме того, большую помощь в выявлении резервов улучшения финансового состояния предприятия может оказать маркетинговый анализ по изучению спроса на рынках сбыта.

Экономико-математическое моделирование

Экономико-математическое моделирование в настоящее время один из инструментов экономического анализа. Использование экономико-математических методов и моделей позволяет получить новые качественные выводы об социально-экономических процессах и явлениях, изучить общие тенденции их развития. Это можно осуществлять, применяя специальные методы прогнозирования.

В зависимости от формы модели для анализа и прогноза используются различные подходы, алгоритмы, критерии.

Существует много методов прогнозирования, среди которых можно выделить метод анализа временных рядов. Он основан на допущении, согласно которому случившееся в прошлом дает достаточно хорошее приближение в оценке будущего.

При изучении в рядах динамики основной тенденции развития (тренда) решаются две взаимосвязанные задачи:

• выявление в изучаемом явлении наличия тренда с описанием его качественных особенностей;
  
• измерение выявленного тренда, то есть получение обобщающей количественной оценки основной тенденции развития.
  

На практике наиболее распространенными методами статистического изучения тренда являются: укрупнение интервалов, сглаживание скользящей средней, аналитическое выравнивание.

Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития Yt рассчитывается как функция времени: Yti = f(ti)

Определение теоретических уровней Yt производится на основе адекватной математической функции, которая наилучшим образом отображает основную тенденцию ряда динамики.

Важнейшей проблемой при применении метода аналитического выравнивания является подбор математической функции, по которой рассчитываются теоре­тические уровни тренда. От правильности решения этой проблемы зависят вы­воды о закономерностях тренда изучаемых явлений. На практике статистического изучения тренда различают следующие типы раз­вития социально-экономических явлений во времени:

1. Равномерное развитие. Для этого типа динамики присущи постоянные абсолютные приросты: Yt = Cоnst

Основная тенденция развития в рядах динамики со стабильными абсолютными приростами отображается уравнением прямолинейной функции:

Yt = а + bt, где

а и b – параметры уравнения; t – обозначение времени.

2. Равноускоренное (равнозамедленное) развитие. Этому типу динамики свойственно постоянное во времени увеличение (замедление) развития. Уровни таких рядов динамики изменяются с постоянными темпами прироста: Тпр = const

Основная тенденция развития в рядах динамики со стабильными темпа­ми прироста отображается функцией параболы второго порядка:

Y = а + bt + сt²

Значение параметров а и b идентичны параметрам, используемым в предыдущей функции. Параметр с характеризует постоянное изменение интенсивности развития (в единицу времени).

3. Развитие с переменным ускорением. Для этого типа динамики основная тенденция развития выражается функцией параболы третьего порядка:

Yt = a + bt + ct² + dt³

В данном уравнении параметр d отображает изменение ускорения.

4. Развитие по экспоненте. Этот тип динамики характеризует стабильные темпы роста: Тр = const

Основная тенденция в рядах динамики с постоянными темпами роста отображается показательной функцией: Yt = ab, где

а – темп роста (снижения) изучаемого явления в единицу времени.

5. Развитие с замедлением роста в конце периода. У этого типа динамики показание цепного абсолютного прироста сокращается в конечных уровнях ряда динамики: Yц 0

Основная тенденция развития в таких рядах динамики выражается полулогарифмической функцией: Yt = а + blgt

На практике целесообразно выбор функции осуществлять либо на основе анализа аналитических показателей ряда динамики, либо методом перебора ряда функций и выбора той, которой соответствует наименьшая средняя квадратическая ошибка и средняя ошибка аппроксимации.

Этапы моделирования:

1. Исходные и расчетные данные о динамике уровня ряда (объем выпуска продукции или оказания услуг, балансовая прибыль, выручка, численность работающих и т.д. за 8-10 лет) заносятся в таблицу. Для наглядного отображения зависимости строят график динамики уровня ряда. По виду графика принимается гипотеза, например, что модель описывается линейной зависимостью: Y=+x

3. Определяют параметры модели методом наименьших квадратов МНК, т.е. min Σе_i². Способ наименьших квадратов дает систему двух нормальных уравнений.
   

Система нормальных уравнений:

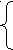
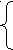n + х = x или  + x_ср = х_ср

х + х² = ух х_ср + x_ср² = у_срх_ср

у_i – фактические уровни из таблицы;

n – число членов ряда;

х – показатель времени (года, кварталы, месяцы и т.д.), который обозначается порядковыми номерами, начиная от низшего, например:

Год	2000	2001	2002	2003	2004
х	1	2	3	4	5

у - оценочные значения полученные из модели;

Коэффициенты регрессии:

 = у_срх_ср – у_ср * х_ср / x_ср² * x_ср²  = у_ср – х_ср

Особое значение имеет знак перед коэффициентом регрессии. Если перед  знак плюс, то с увеличением Х значение У возрастает. Если перед  знак минус, то с увеличением Х значение У уменьшается.

3. Оценка адекватности выбранного уравнения тренда:

Проверка адекватности моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии и корреляции..

Коэффициент корреляции: r_xy = у_срх_ср – х_ср * у_ср / _х * _у

Значение парных коэффициентов корреляции свидетельствует о сильной связи между отклонениями фактических уровней сравниваемых рядов от соответствующих им выравненных уровней, если r_xy > 0,7. Гипотеза о линейности верна с доверительной вероятностью р=0,95. Если коэффициент корреляции меньше 0,7, то гипотеза о линейности не подтверждается.

Значимость коэффициентов регрессии  и  и парных коэффициентов корреляции r_xy проверяется на основе t – критерия Стьюдента:

t_ =  / m_; t_ =  / m_ ; t_r = r_xy / m_rxy

Случайные ошибки аппроксимации ,  и r_xy:

m_ = (y_i – y_x)² / (n-2) / (х_i – x_{i ср})²

m_ = (y_i – y)² * х_i² / (n-2) * n(х_i – x_{i ср})²

m_{r xy} = 1 – r_xy² / (n-2)

Если все расчетные значения t- критерия больше tкр.- табличного, это свидетельствует о значимости коэффициентов регрессии и корреляции. Гипотеза о линейности верна.

Табличные данные t- критерия Стьюдента

При вероятности α = 0,05	При числе степеней свободы γ = х - 2
	5	6	7	8	9
	2,571	2,447	2,365	2,306	2,262

Коэффициент детерминации: R² = (y_ix – у_ср)² / = (y_i – у)²

показывает, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в многофакторную регрессионную модель. Изменяется в пределах от 0 до 1 и по определению положителен. Если коэффициент детерминации больше 0,9, то модель описывает наиболее существенные стороны рассматриваемого процесса.

Проверка адекватности всей модели, в т.ч. и значимости коэффициента детерминации, осуществляется с помощью расчета F–критерия и величины средней ошибки аппроксимации. Значимость уравнения регрессии на основе F–критерия Фишера-Снедекора.

Критерий Снедекора: F_ф = r_xy² * (n – 2) / (1 – r_xy²) .

Если все расчетные значения F - критерия больше Fкр.- табличного, это свидетельствует о значимости уравнения регрессии и подтверждает гипотезу о линейности. Моделью можно пользоваться.

Табличные данные F- распределения при вероятности α = 0,05

При числе степеней свободы γ
числителя знаменателя	2	3	4	5
4	6,94	6,59	6,36	6,26
5	5,79	5,41	5,19	5,05
6	5,14	4,76	4,53	4,39
7	4,74	4,35	4,12	3,97

γ -число степеней свободы, количество наблюдений в выборке минус число уровней связи, n –1.


Доверительные интервалы  и  - это проекция подынтегральной кривой, равной доверительной вероятности, решение интегрального уравнения. Интервал зависит от числа степеней свободы (m), доверительной вероятности (р) и разброса случайной величины.

При m → ∞ имеет место нормальный закон распредления.

Предельные ошибки ,  и r_xy: Δ = t_наб * m_; Δ = t_наб * m_; Δr = t_табл * m_r

Значение средней ошибки аппроксимации не должно превышать 12-15%.

Доверительные интервалы для определенных параметров:

L_{ min} =  – Δ; L_{ max} =  + Δ; L_{ min} =  – Δ; L_{ max} =  + Δ

4. Прогнозирование динамики на основе метода экстраполяции.

Прогнозное значение Y_p : Y_p =  + x_p определяется на основе экстраполяции линейной зависимости

Средняя квадратическая ошибка прогноза:

m_yp = _ост 1 + 1/n + (х_p – х_ср)² / (х_i – х_ср)², где

х_p – прогнозное значение, подставляемое вместо x_i

_ост = (y – y)² / n – 1

Доверительный интервал L – диапазон прогноза:

Ly_min = y_p – Δy_{p ;}Ly_max = y_p + Δy_p; Δy_p = t_табл * m_yp

Пример: Проанализировать динамику и определить перспективную выручку организации. Исходные и расчетные данные для определения параметров системы уравнения представлены в табл.18.

Таблица 18

Исходные и расчетные данные для определения параметров системы уравнения

n	X	Y	Xi*Yi	X2	Y2	Xi-Xср	Yi-Yср
1	2	3	4	5	6	7	8
1	1	1925	1925	1	3705625	-5	-13661.27
2	2	4039	8078	4	16313521	-4	-11547.27
3	3	7033	21099	9	49463089	-3	-8553.27
4	4	8930	35720	16	79744900	-2	-6656.27
5	5	10994	54970	25	120868036	-1	-4592.27
6	6	13757	82542	36	189255049	0	-1829.27
7	7	17072	119504	49	291453184	1	1485.727
8	8	20591	164728	64	423989281	2	5004.727
9	9	23995	215955	81	575760025	3	8408.727
10	10	28697	286970	100	823517809	4	13110.727
11	11	34416	378576	121	1184461056	5	18829.727
Итого:	66	171449	1370067	506	3758531575	0	0.272727

продолж.табл. 18

n	(Xi-Xср)2	(Yi-Yср)2	7*8	Y	Yi-Y	(Y-Yср)2	(Yi-Y) 2
1	9	10	11	12	13	14	15
1	25	186622921	68306.36	696	1229	221720222	1510441
2	16	133333209	46189.09	3172.7091	866	154096562	121104
3	9	73158474	25659.82	6276.1	757	86679316	572898
4	4	44305967	13312.55	9379.4909	-450	38524141	202042
5	1	21088969	4592.273	12482.882	-1489	9631035	2216769
6	0	3346239	0	15586.272	-1829	0	3346239
7	1	2207386	1485.727	18689.664	-1618	9631035	2616836
8	4	25047295	10009.45	21793.055	-1202	38524141	1444935
9	9	70706694	25226.18	24896.446	-901	86679316	812604
10	16	171898321	52442.91	27999.836	697	154096562	486037
11	25	354568900	94150	31103.227	3313	240775878	10974463
Ито го:	110	1.086Е+09	341374.4	172075.68	-627	1040358208	24304367

Расчёты производятся при помощи табличного редактора Excel по приведённым формулам.

Полученные результаты и коэффициенты:

X_ср = 6; Y_ср = 15586.27273; (X*Y)_ср = 124551.5455

Коэффициенты регрессии:

β = 3103,4 α = -3034.1

Уравнение регрессии: У = -3034,1 + 3103,4* Х

Среднеквадратические отклонения:

dx = 3,1623; dy = 9937,49; dо = 1486,43

Коэффициент корреляции: K_xy = 0,9876. Гипотеза о линейности модели верна, т.к. коэффициент корреляции больше 0,7 и равен 0,9876

Коэффициенты регрессии достаточно значимы, т.к.

Оценка значимости коэффициентов по t-критерию Стьюдента:

t_a = - 2, 855 t_b = 19,81 ; t_r = 18,349

t_ > tтабл. (2,855 > 2,26), t_ > tтабл. (19,81 > 2,26)

и t_r > tтабл. (18,349 > 2,26).

Модель линейная – надежна т.е. пригодна для практического применения.

Коэффициент детерминации: r²= 0,958 . Коэффициент детерминации больше 0,9, то модель описывает наиболее существенные стороны рассматриваемого процесса.

Критерий Фишера-Снедекора: Fф = 8,777 > Fтабл.= 6,94. Модель надежна и может быть использована для практического применения.

Случайные ошибки a, b и r_xy:

m = 156,684; m = 1062,682 mkxy = 0,05243

Средняя квадратическая ошибка прогноза

myp = 1770,16, при хр = 12

Предельные ошибки a, b и r_xy:

D_A = 2403,788; D_B = 354,4191

Доверительные интервалы для определенных параметров:

Lamin = -5437,86; Lbmin = 2748,972; Lamax = -630,285; Lbmax = 3457,81

Прогнозное значение Y_p

Yp12 = 34206,2; Yp13 = 37310.01; Yp14 = 40413,14;

Yp15 = 43516.79; Yp16 = 46620,18

На рис. 24 построены графики фактической и расчетной выручки от реализации продукции с прогнозом ее на конец 2003 года и 2004 гг.


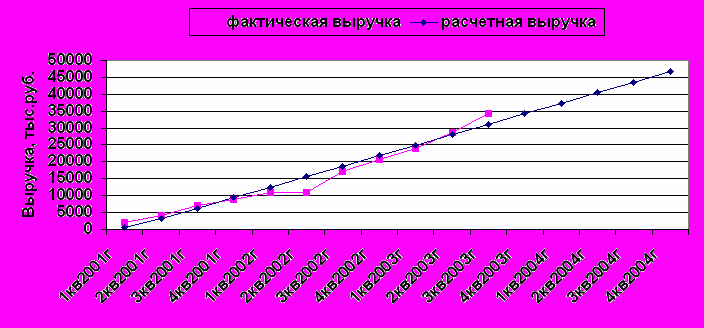
Y = - 3034.1 + 3103.4*X
Рис. 24. Динамика выручки от реализации продукции