Geum.ru

Rate Ring Model [2]. Вдоклад

Вид материалаДоклад

Содержание


Модель одной популяции.
Подобный материал:

ISBN 978-5-7262-1226-5. НЕЙРОИНФОРМАТИКА – 2010. Часть 1

А.В. ЧИЖОВ

Физико-технический институт им. А.Ф.Иоффе РАН, Санкт-Петербург

anton.chizhov@mail.ioffe.ru


БИОФИЗИЧЕСКИ ДЕТАЛЬНАЯ МОДЕЛЬ

ВЗАИМОСВЯЗАННЫХ НЕЙРОННЫХ ПОПУЛЯЦИЙ,

РАСПРЕДЕЛЕННЫХ ВДОЛЬ ПОВЕРХНОСТИ

ЗРИТЕЛЬНОЙ КОРЫ


На основе модели популяции реалистичных нейронов типа Ходжкина-Хаксли, сформулированной в терминах рефрактерной плотности, предлагается модель зрительной коры. Модель включает в рассмотрение континуум распределенных вдоль поверхности коры популяций нейронов, взаимодействующих посредством синаптических связей. Определенный набор параметров внутрикорковых связей и внешней таламической стимуляции (pinwheels) обеспечивает свойство коры выделять ориентацию стимула при различной степени его контраста. Модель реалистично воспроизводит стационарные и переходные режимы активности коры.


Введение. Нейроны первичной зрительной коры организованы в колонки- популяции клеток, отвечающие на стимул определенной ориентации (Hubel, Wiesel 1962, [1]). Простейшая модель, отражающая эффекты ориентационной селективности нейронов, основана на частотной модели одной популяции и рассматривает распределённые по кольцу популяции нейронов, предпочитающих стимул с определённый углом ориентации (Firing-Rate Ring Model) [2]. В докладе на прошедшей конференции «Нейроинформатика-2009» [3] было рассмотрено обобщение такой модели на случай связанных на кольце однотипных нейронов-пороговых интеграторов с мгновенной синаптической кинетикой. В настоящей работе предлагается много более детальная модель, все элементы которой, по мнению автора, необходимы для воспроизведения характерных ответов нейронов зрительной коры при зрительной или внеклеточной электрической стимуляции. В то же время, в нашей модели предполагается рассмотрение только значимых деталей нейросети, что отличает его от проектов по воспроизведению всех известных деталей, типа Blue Brain project, тем самым оно претендует на необходимость и достаточность всех компонентов модели. Однако следует заметить, что рассмотрение только двух типов нейронов в представленной здесь версии модели не является достаточным, а принято для простоты.

Модель одной популяции. Главным нововведением в нашей работе является применение недавно опубликованной модели одной популяции нейронов типа Ходжкина-Хаксли [4-6] для построения подробной 2-D распределенной модели взаимодействующих популяций зрительной коры. Основные идеи модели одной популяции таковы. Под популяцией понимается бесконечное число несвязанных нейронов, получающих общий входной сигнал (как ток, так и проводимость) и различный для каждого шум. Формально для описания такой популяции, как для статистического ансамбля частиц, можно применить формализм Фоккера-Планка (ФП) и перейти к описанию популяции в терминах функции плотности распределения в фазовом пространстве параметров состояния одного нейрона. Однако возникает проблема многомерности. С другой стороны, редуцированные модели обычно ограничиваются рассмотрением популяций нейронов типа нейронов-пороговых интеграторов, а наш подход применим к достаточно произвольным реалистичным аппроксимациям нейронов типа Ходжкина-Хаксли. В то же время он математически выражается в виде одномерных уравнений в частных производных (рис. 1), т.е. обладает высокой вычислительной эффективностью.



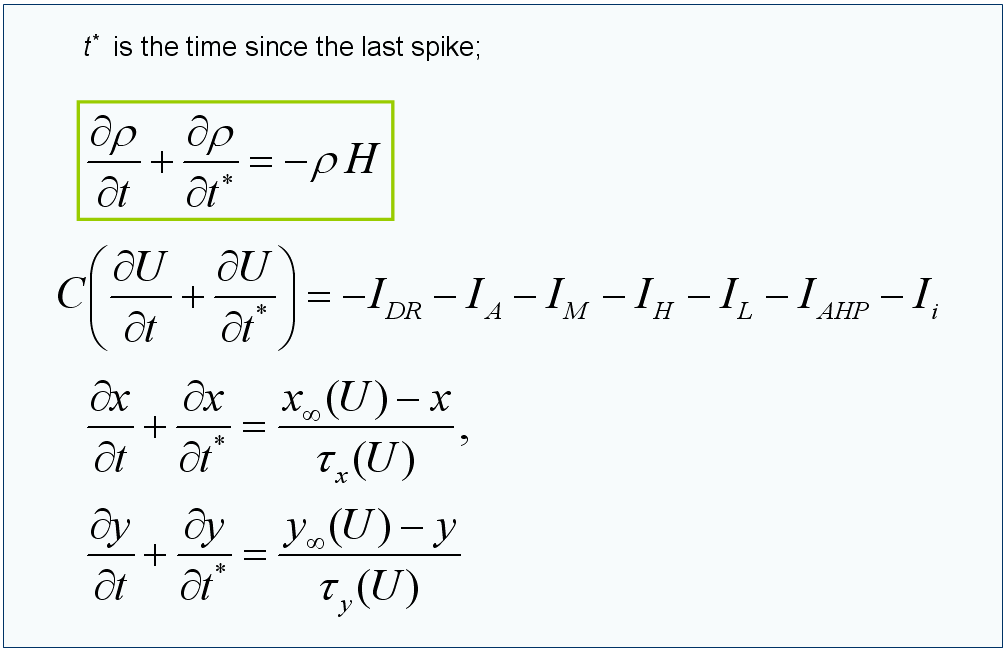
Рис. 1. Вид основных уравнений модели одной популяции нейронов. Здесь U(t,t*) – средний по реализациям шума мембранный потенциал; ρ(t,t*) – плотность распределения нейронов в пространстве t*; x(t,t*), y(t,t*) – переменные активации и инактивации ионных каналов (для каждого из каналов)





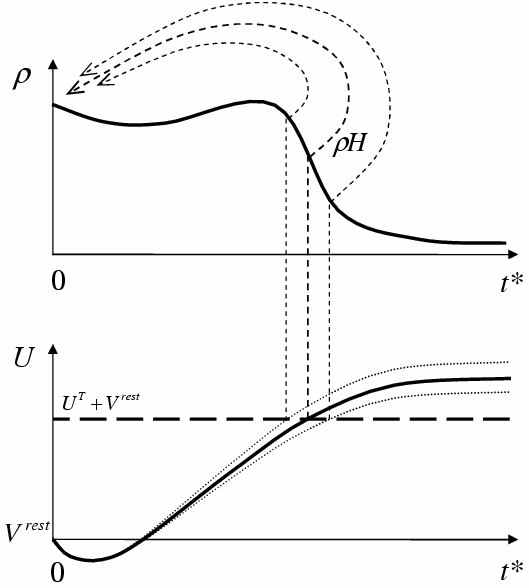
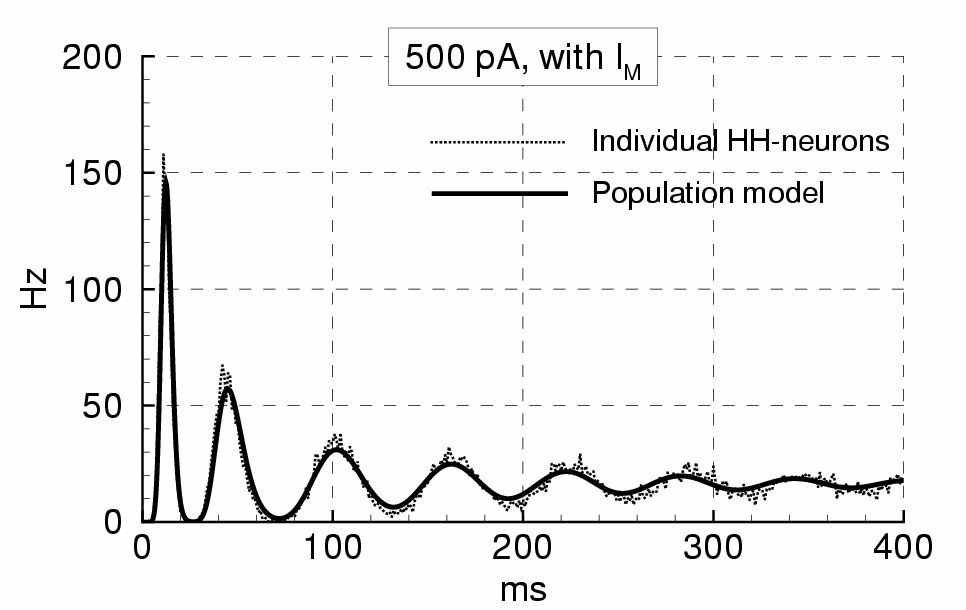
Рис. 2. Слева – схема эволюции нейронов в пространстве t* – времени, прошедшем от момента предыдущего спайка. Справа – частота спайков нейронов популяции в ответ на стимуляцию ступенчатым током [4]


Предложенный в [4-6] подход состоит в том, что в любой произвольный момент времени различие состояний нейронов одной популяции можно характеризовать только одним параметром – временем t*, прошедшим от момента генерации тем или иным нейроном импульса-спайка, при том, что само состояние каждого нейрона характеризуется несколькими переменными (потенциалом и переменными проводимостями ионных каналов). Тем самым, предполагается, что все переменные состояния можно параметризовать временем, прошедшим от момента генерации спайка, а распределение нейронов по этому параметру описывать функцией нейронной плотности ρ в одномерном фазовом пространстве t* (рис. 2).

Такой подход называется Refractory Density (RD) Approach – подход на основе рефрактерной плотности. Эволюция рефрактерной плотности описывается уравнением переноса в пространстве t*. Также к уравнениям переноса сводится параметризация переменных состояния средних по реализациям шума для нейрона в точке t*, если нейрон представим как пороговый. Пороговая модель отдельного реалистичного нейрона Ходжкина-Хаксли с учетом токов адаптации строится заменой быстрого натриевого тока пороговым условием генерации спайка, причём пороговый потенциал динамически зависит от временной производной от потенциала. По сравнению с полной моделью пирамидального нейрона, пороговая модель хорошо аппроксимирует временную последовательность моментов спайков и ход потенциала на межспайковых интервалах [5]. Таким образом, динамика нейронного континуума описывается множеством одномерных уравнений в частных производных для нейронной плотности ρ(t,t*), потенциала U(t,t*) и проводимостей всех ионных каналов, кроме натриевого канала (рис. 1). В источниковом члене уравнения для плотности стоит функция вероятности генерации спайка одним нейроном при заданном потенциале U, или, функция риска H. Зависимость H(U(t,t*)) полу-аналитически выводится из уравнения Фоккера-Планка для линеаризованного нейрона-порогового интегратора с белым [5] или цветным [6] шумом, управляемого средним потенциалом U(t,t*). Показано, что в случае произвольной стимуляции величина H(U(t,t*)) представима в виде суммы двух частных решений, автомодельного решения в случае медленного изменения потенциала U и замороженного стационарного решения при быстром изменении потенциала U. Ответы популяции нейронов в виде популяционной частоты спайков на стимуляцию ступенчатым током (рис. 2) и осциллирующим током хорошо согласуются с результатами моделирования большого числа отдельных нейронов. Предложенный RD-подход может быть эффективно использован для реалистичного моделирования активности связанных нейронных популяций.

Метод. Модель зрительной коры. Предлагаемая модель зрительной коры рассматривает континуум нейронных популяций, распределенных в 2-D пространстве вдоль коры и получающих стимуляцию из таламуса в соответствии с архитектурой типа pin-wheels [7] (рис. 3). Каждая популяция описывалась системой уравнений, вид которых представлен на рис. 1 и детально разобранных в работе [6] для пирамидальных нейронов и в [8] для интернейронов. Кроме того, учитывался эффект электротонического проведения по дендритному дереву пирамидных нейронов, согласно [9,4]. Кинетика возбуждающих AMPA- и тормозных GABA-A-рецепторных синаптических проводимостей описывалась обыкновенными дифференциальными уравнениями второго порядка, управляемых частотой спайков пресинаптической популяции [4]. Пространственная структура связей внутри коры задавалась изотропной, с экспоненциально убывающим распределением синаптических весов в зависимости от расстояния между пре- и постсинаптическими популяциями и с фиксированной задержкой аксонного распространения спайков.




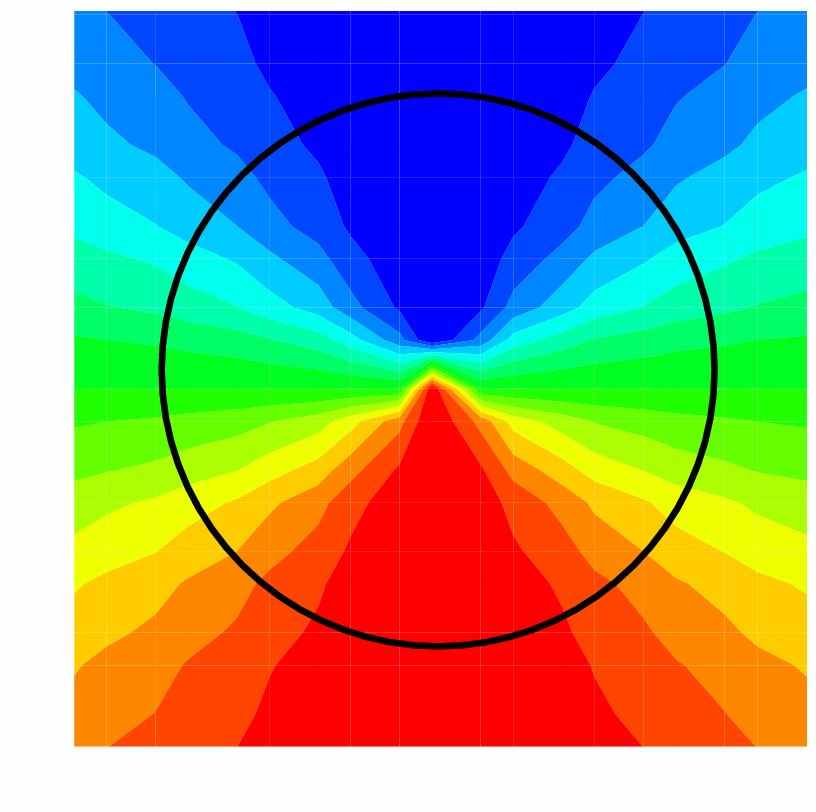
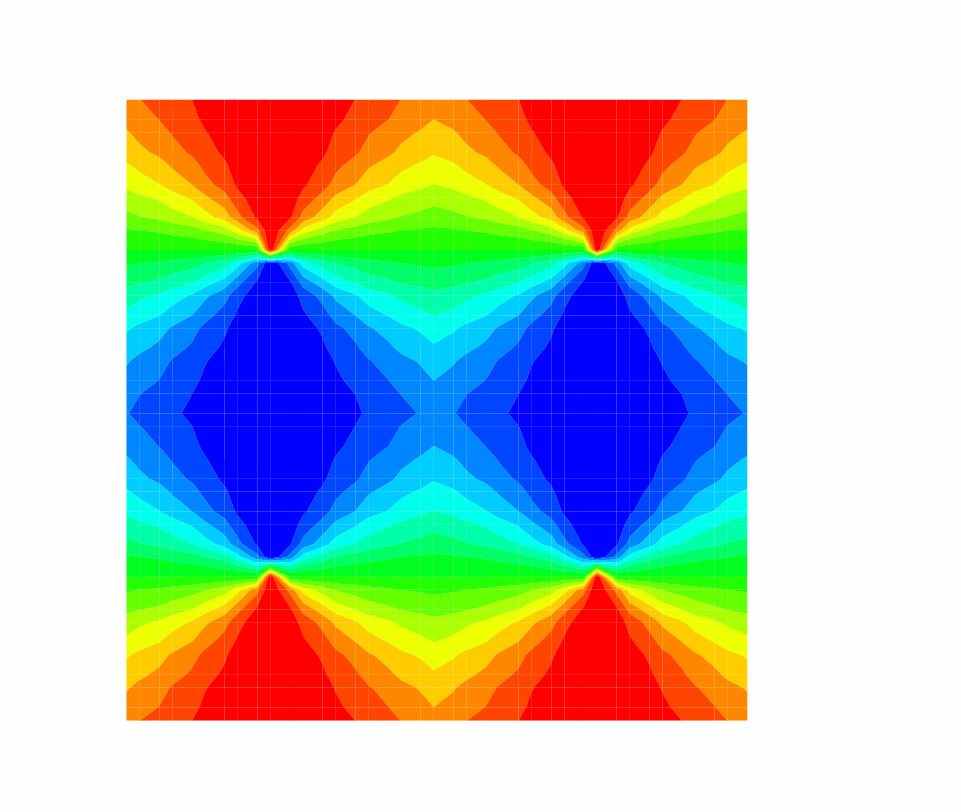
Рис. 3. Схематичное представление ориентационной гиперколонки (ГК, pin-wheel) и четырёх ГК, представляющих 1мм2 первичной зрительной коры. Каждый сектор ГК – колонка – получает преимущественно стимул определенной ориентации. Множество ориентаций составляет кольцо


Результаты. Активность четырёх ГК в один из моментов времени показана на рис. 4. Видна выраженная активность в колонках с предпочитаемой ориентацией, соответствующей ориентации стимула.

На рис. 5 демонстрируется переходный режим активности, когда зрительный стимул-полоса с горизонтальной ориентацией начинает предъявляться в момент времени t=0, а с момента t=100 мс ориентация меняется на вертикальную. В начальный момент активность характеризуется синхронной для большинства нейронов популяции вспышкой спайковой активности, которая затем снижается и постепенно устанавливается профиль, локализованный в пространстве угла ориентации. В установлении этого профиля выражается эффект выделения ориентации стимула зрительной корой. Форма этого профиля приближенно сохраняется при изменении контрастности стимула (данные не показаны), что соответствует поведению простейшей модели ГК (contrast invariance effect [2]). После изменения ориентации стимула максимум активности сначала наблюдается у колонок с ориентацией более удалённой от первоначальной, что соответствует проявлению иллюзии типа tilt after-effect [10], объясняющейся адаптивными свойствами нейронов.





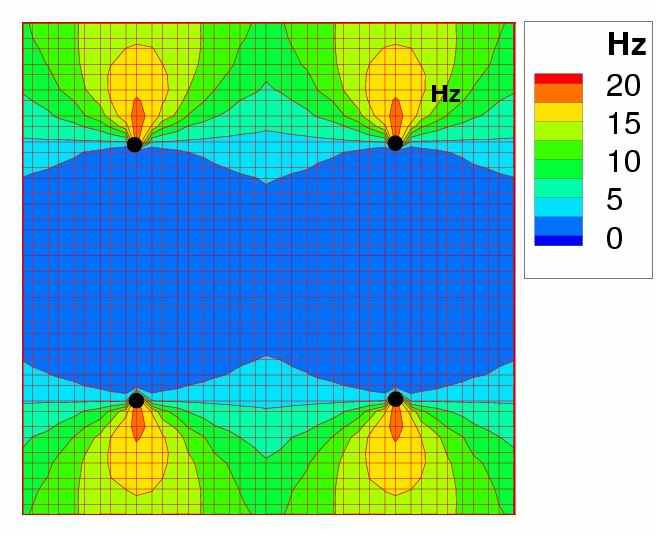
Рис. 4. Распределение спайковой активности пирамидальных нейронов по 1мм2-участку коры, содержащему 4 ориентационных гиперколонки в один из моментов времени предъявления зрительного стимула – вертикальной полосы, t=100 мс (см. рис. 5)





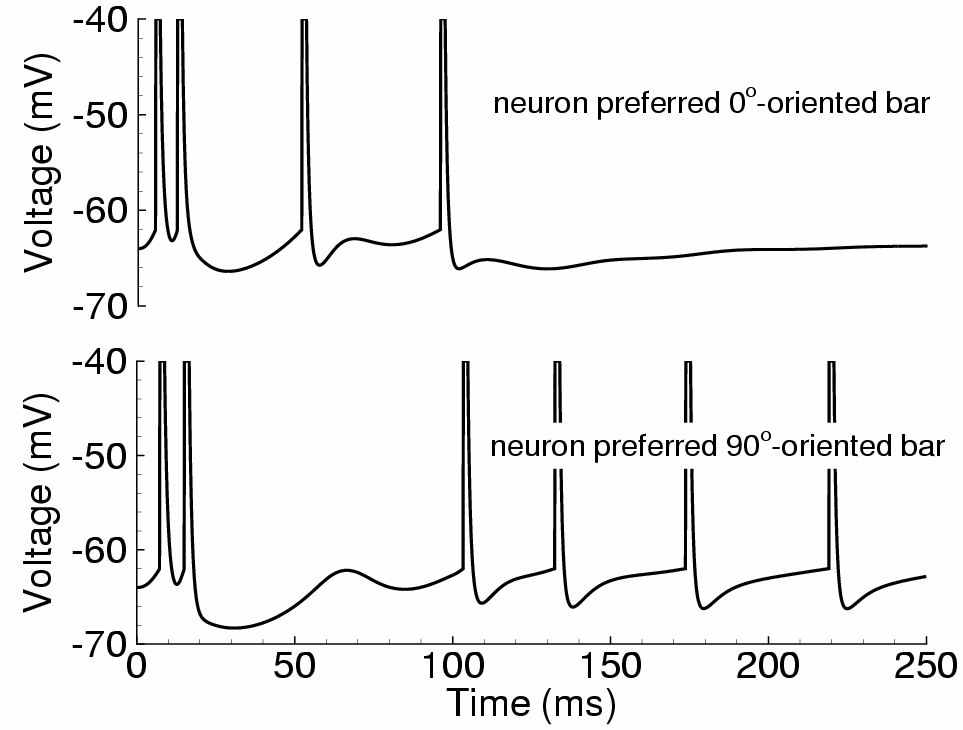
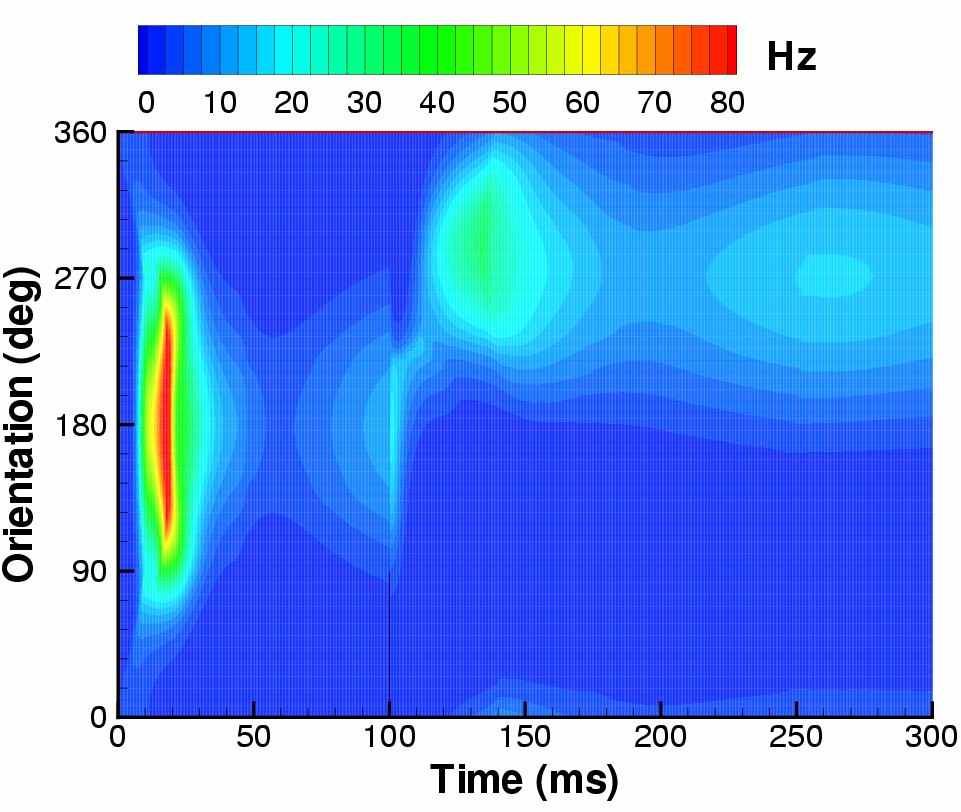
Рис. 5. Ответ зрительной коры на предъявление сначала горизонтального стимула-полосы (соответствует 0O наклона стимула и 180O угловой координаты колонки в ГК) в период времени от 0 до 100мс, а затем – вертикального стимула (соответствует 90O наклона стимула и 270O угловой координаты колонки в ГК). Слева сверху – ответа нейрона, предпочитающего горизонтальный стимул, слева снизу – вертикальный. Справа – эволюция распределения активности пирамидальных нейронов, расположенных на кольце (см. рис. 3)


Представленные результаты показывают, что построенная модель может служить полезным инструментом для анализа упрощенных моделей зрительной коры, сравнения математических моделей с экспериментальными данными и постановки экспериментов на основе предсказаний модели.

Работа поддержана грантом РФФИ-НЦНИ 07-04-92167a.


Список литературы


1. Hubel D.H.,Wiesel T.N. (1962) Reception fields, binocular interaction and functional architecture in the cats visual cortex. J. Physiol.Lond. 160:106–154.

2. Hansel D., Sompolinsky H. (1998) Modeling feature selectivity in local cortical circuits. In C. Koch & I. Segev (Eds.), Methods in neuronal modeling: From synapses to networks (2nd ed., p. 499–567). Cambridge, MA: MIT Press.

3. Смирнова Е.Ю., Чижов А.В. Ориентационная избирательность суперколонки нейронов зрительной коры: модели кольца в нестационарном режиме // Нейроинформатика-2009. XI всероссийская научно-техническая конференция. Сб. научн. трудов. – М.: МИФИ, 2009. Ч.1, с.118-124.

4. Чижов А.В. Модель популяций нейронов как элемент крупномасштабной нейросети // Нейрокомпьютеры: разработка, применение. No.2-3, с.60-68, 2004.

5. Chizhov A.V., Graham L.J: Efficient evaluation of neuron populations receiving colored-noise current based on a refractory density method // Phys Rev E 2008, 77: 011910.

6. Chizhov A.V., Graham L.J. Population model of hippocampal pyramidal neurons, linking a refractory density approach to conductance-based neurons // Phys. Rev. E 2007, 75: 011924.

7. K. Kang, M. Shelley and H. Sompolinsky. Mexican hats and pinwheels in visual cortex // PNAS, vol. 100(5), 2848–2853, 2003.

8. Chizhov A.V., Graham L.J., Turbin A.A. Simulation of neural population dynamics with a refractory density approach and a conductance-based threshold neuron model // Neurocomputing, v.70, p.252-262, 2006.

9. Чижов А.В. Связь постсинаптических потенциалов и токов, измеряемых полувнутриклеточно (методом patch-clamp) // Биофизика, 49(5), с.877-880, 2004.

10. Cortes J., Marinazzo D., Oram M., Series P., Sejnowski T., vanRossum M. Heterogeneous effects of adaptation on visual population coding efficiency (in preparation).


УДК 004.032.26(06) Нейронные сети