Geum.ru

Сматривается дифференциальная модель Эрроу-Дебре динамики цен и модифицированная модель Уилсона Баумоля-Тобина управления товарными запасами и денежной массой

Вид материалаДокументы

Содержание


Белгородский университет потребительской кооперации
Подобный материал:
Сучков В.К.,

к.ф.- м. н., доцент кафедры

естественнонаучных дисциплин

Белгородского университета

потребительской кооперации



МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДИНАМИКИ ЦЕН

И УПРАВЛЕНИЯ ЗАПАСАМИ РЕСУРСОВ


В статье рассматривается дифференциальная модель Эрроу–Дебре динамики цен и модифицированная модель Уилсона – Баумоля–Тобина управления товарными запасами и денежной массой.


Финансовая деятельность хозяйствующего субъекта в условиях рыночной экономики являются сложной и многообразной. В условиях дефицита и конкуренции постоянно приходится принимать решения, направленные на минимизацию как производственных, так и управленческих издержек. Математические методы принятия таких решений при этом играют существенную роль и важное место среди них имеют методы дифференциального и интегрального исчисления.

Спрос, предложение и цена являются основными категориями рыночной экономики, они являются индикаторами состояния рынка.

Пусть Х(p) = X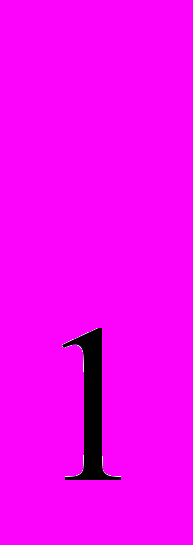(p) + X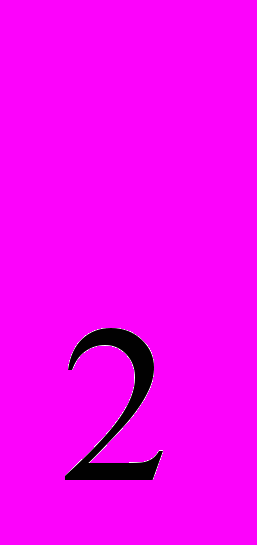(p) +…+ X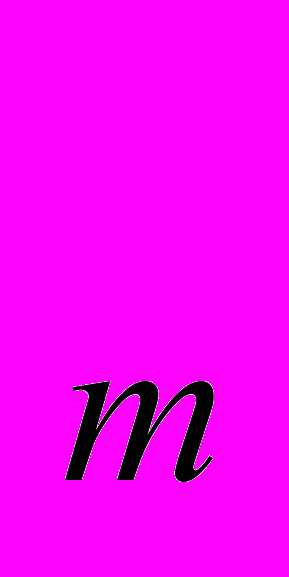(p) – совокупный рыночный спрос , а Y(p) = Y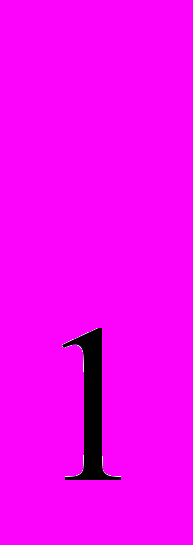(p) + Y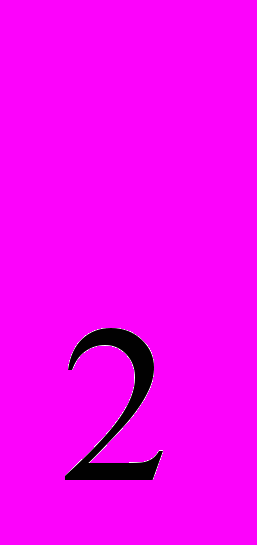(p) +…+ Y 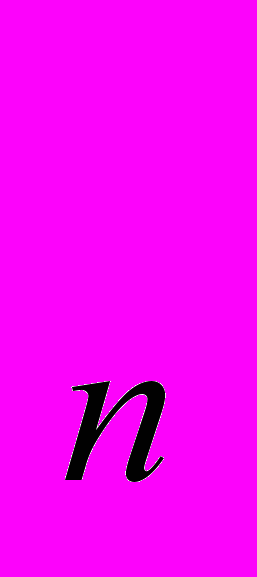(p) – совокупное рыночное предложение . Тогда F(p) = X(p) – Y(p) – избыточный спрос при ценах 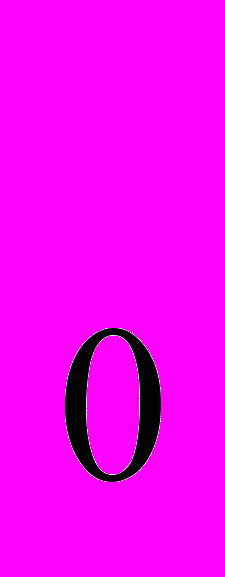p = (p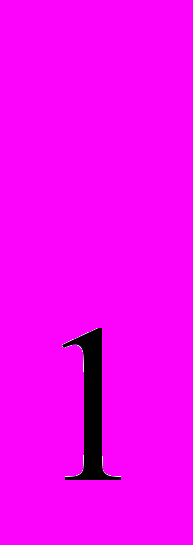 + p + p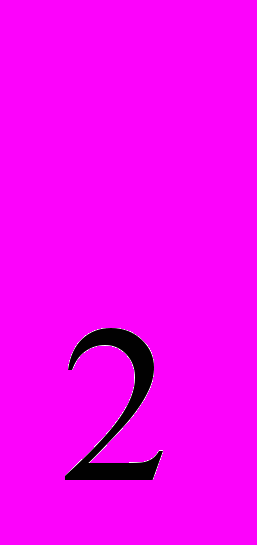 + …+ p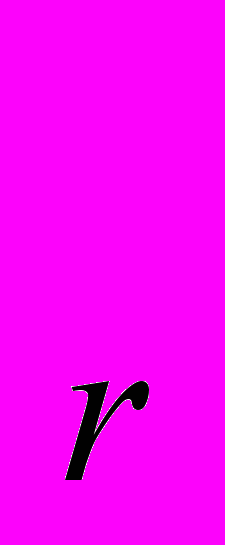). Предполагается, что спрос и предложение являются однородными функциями нулевой степени, поэтому и F(p) будет однородной функцией нулевой степени. Цены, спрос, предложение зависят от времени t. Если F(p(t)) > 0, то цена p(t) на продукт с номером k должна расти и значит производная . Если же F(p(t)) < 0, то цена p(t) на продукт с номером k должна убывать и поэтому производная . Если считать, что избыточный спрос F(p(t)) на продукт с номером k (k = 0,1,2,…r) изменяется во времени пропорционально скорости изменения цен, т.е. производной , то приходим к системе обыкновенных дифференциальных уравнений (модель Эрроу-Дебре)

= aF(p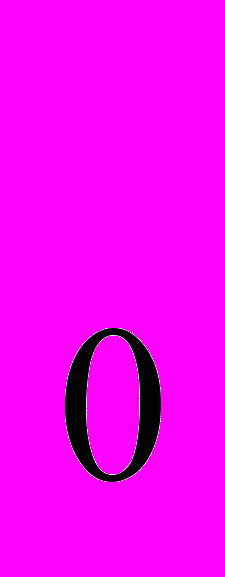(t) + p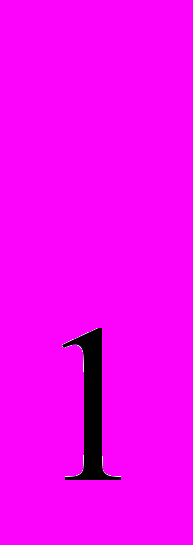(t) + p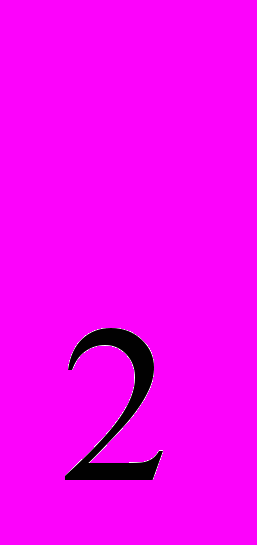(t) + …+ p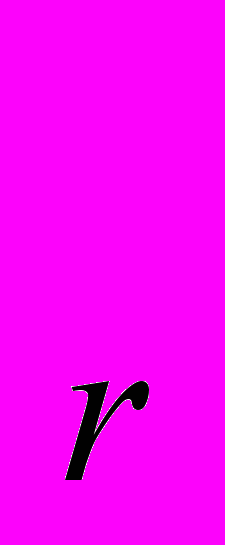(t)), k = 0,1,2,…r.

При дополнительных начальных условиях из этой системы получаем траекторию p(t) роста и падения рыночных цен.

Задача управления товарными или денежными ресурсами состоит в их использовании наилучшим образом, т.е. с наибольшей выгодой.

Пусть х - размер товарного запаса; у - издержки на обеспечение и реализацию товарного запаса х; Q - спрос на товар (он же товарооборот в плановом периоде Т); К - издержки по организации заказа и доставки одной партии товара, независящие от размера партии; С - издержки по хранению единицы товара в течение всего планового периода; А – издержки по организации продажи товара покупателю. Найдем зависимость между х и у при следующих допущениях:
  1. планируются запасы только одной товарной группы;
  2. уровень запасов снижается равномерно в результате равномерной продажи;
  3. в тот момент, когда все запасы исчерпаны, подается и немедленно исполняется заявка на поставку товара в количестве х;
  4. издержки управления запасами складываются только из издержек по завозу, хранению товара и организации его продажи покупателю;
  5. величины Q, K, C, А не изменяются в течение всего планового периода Т.

Ввиду того, что уровень запасов снижается равномерно, издержки по хранению текущего запаса составляют С 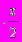денежных единиц. Так как общая потребность в товаре в плановом периоде равна Q, а х - размер одной поставки товара, то 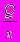- количество поставок.

В силу допущения 4) имеем модифицированную математическую модель

у = С 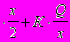+ А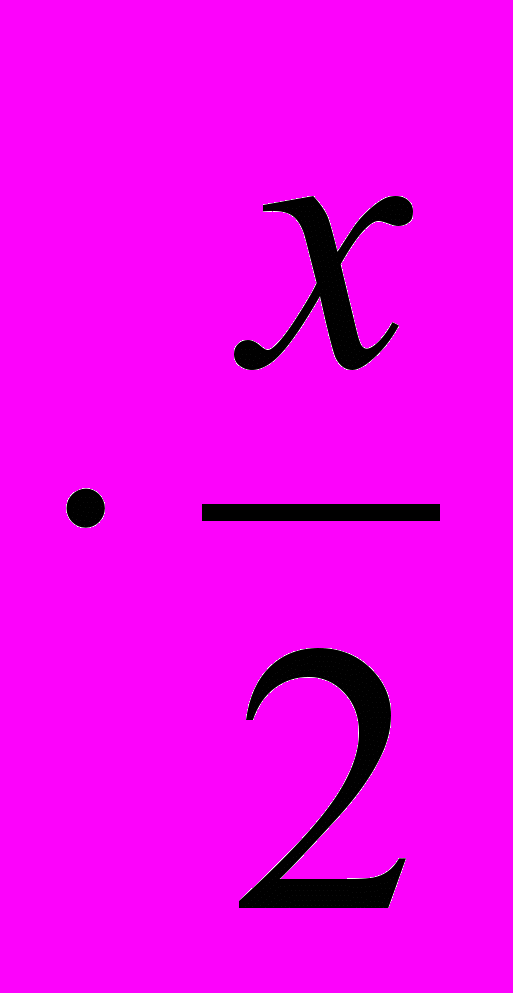, отличающуюся от модели Уилсона добавлением слагаемого А.

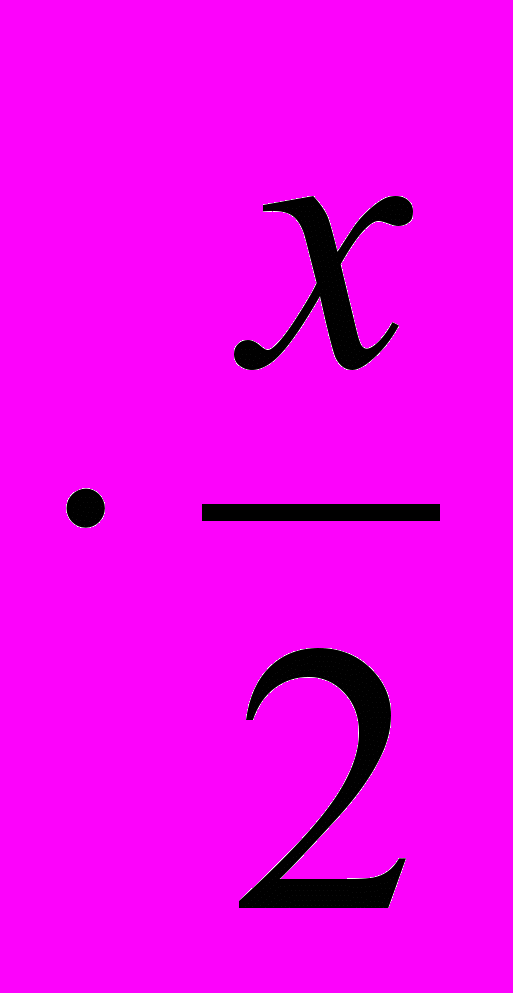Найдем наименьшее значение у с помощью производной:

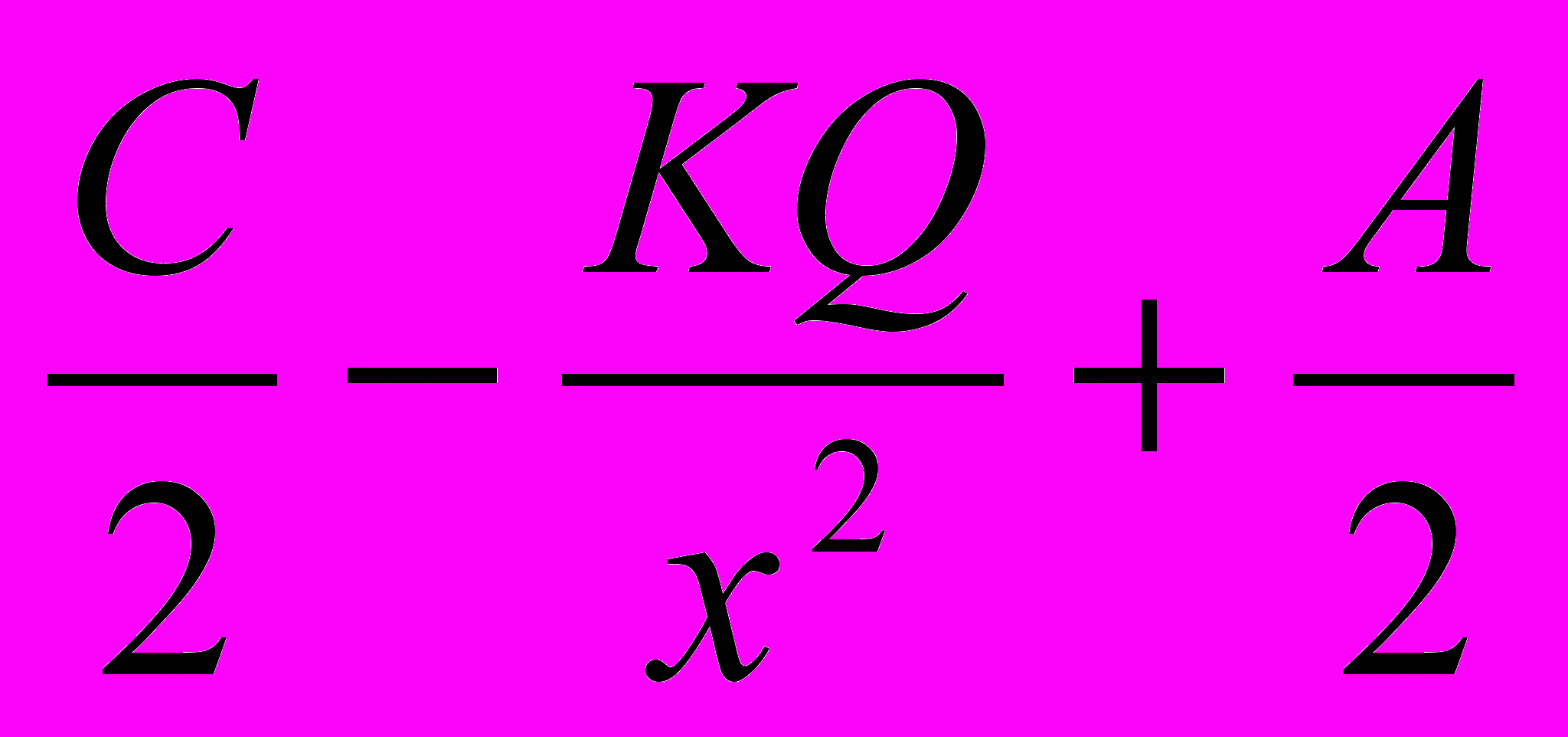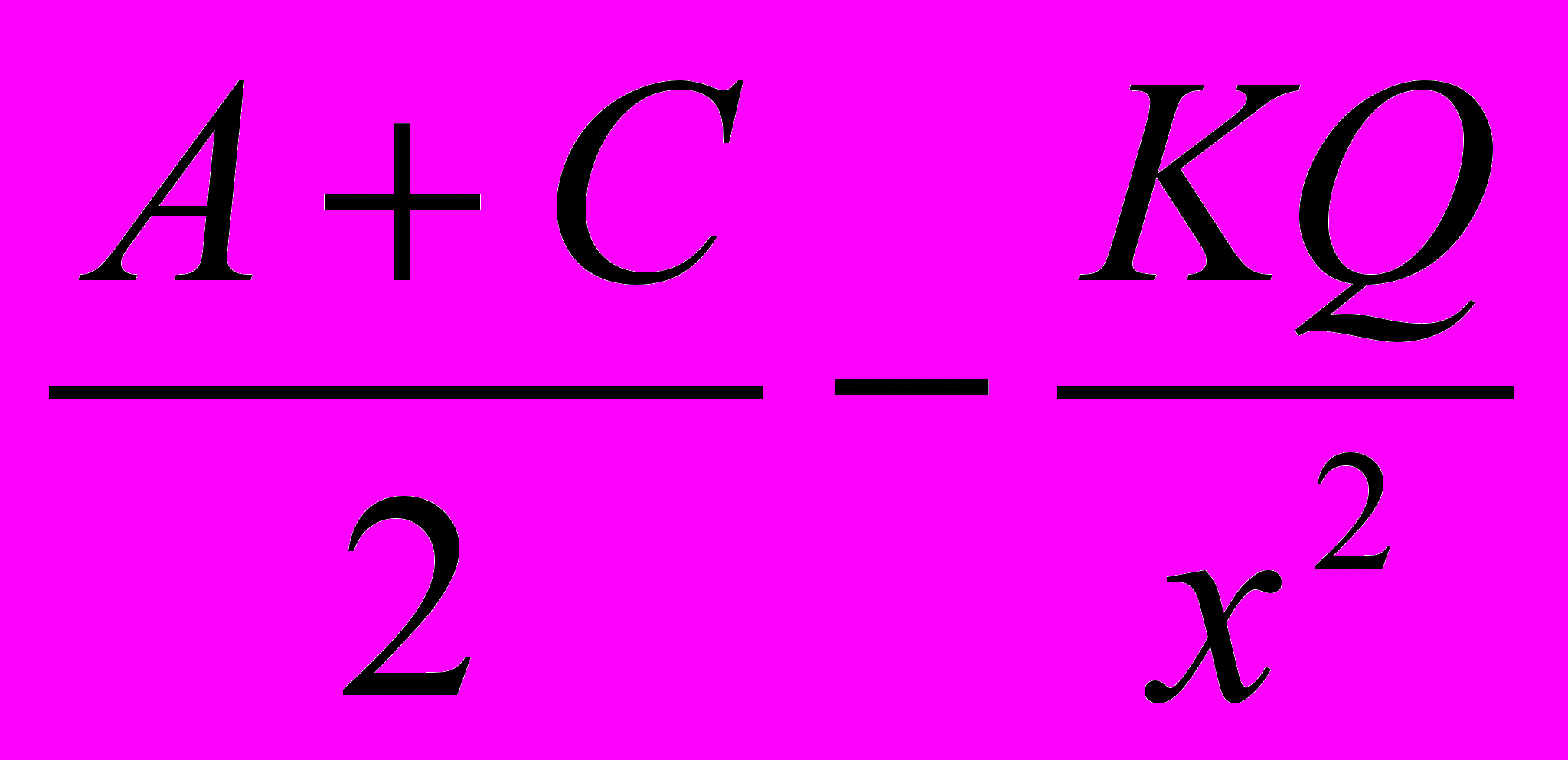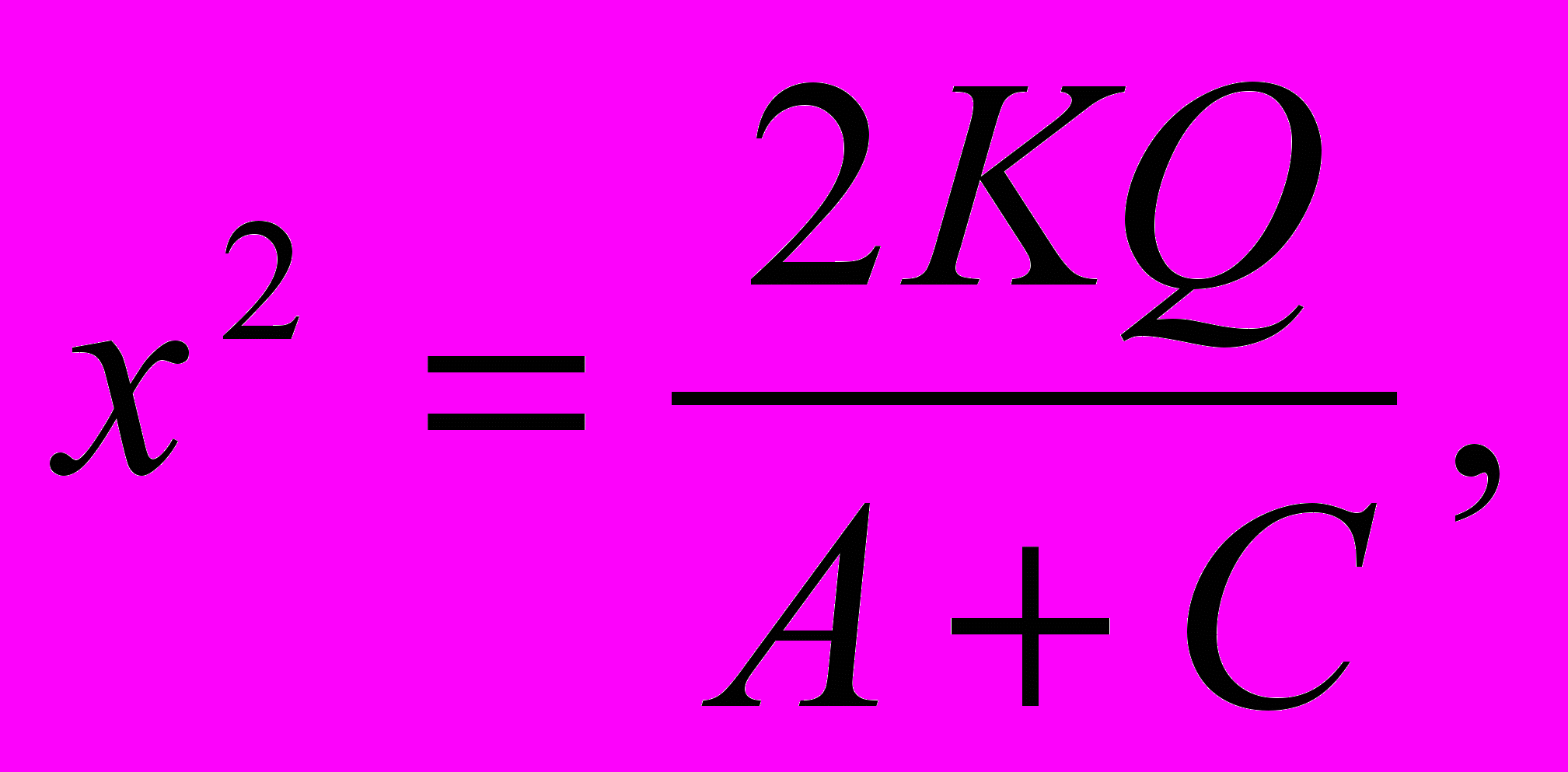
у(х) = = , 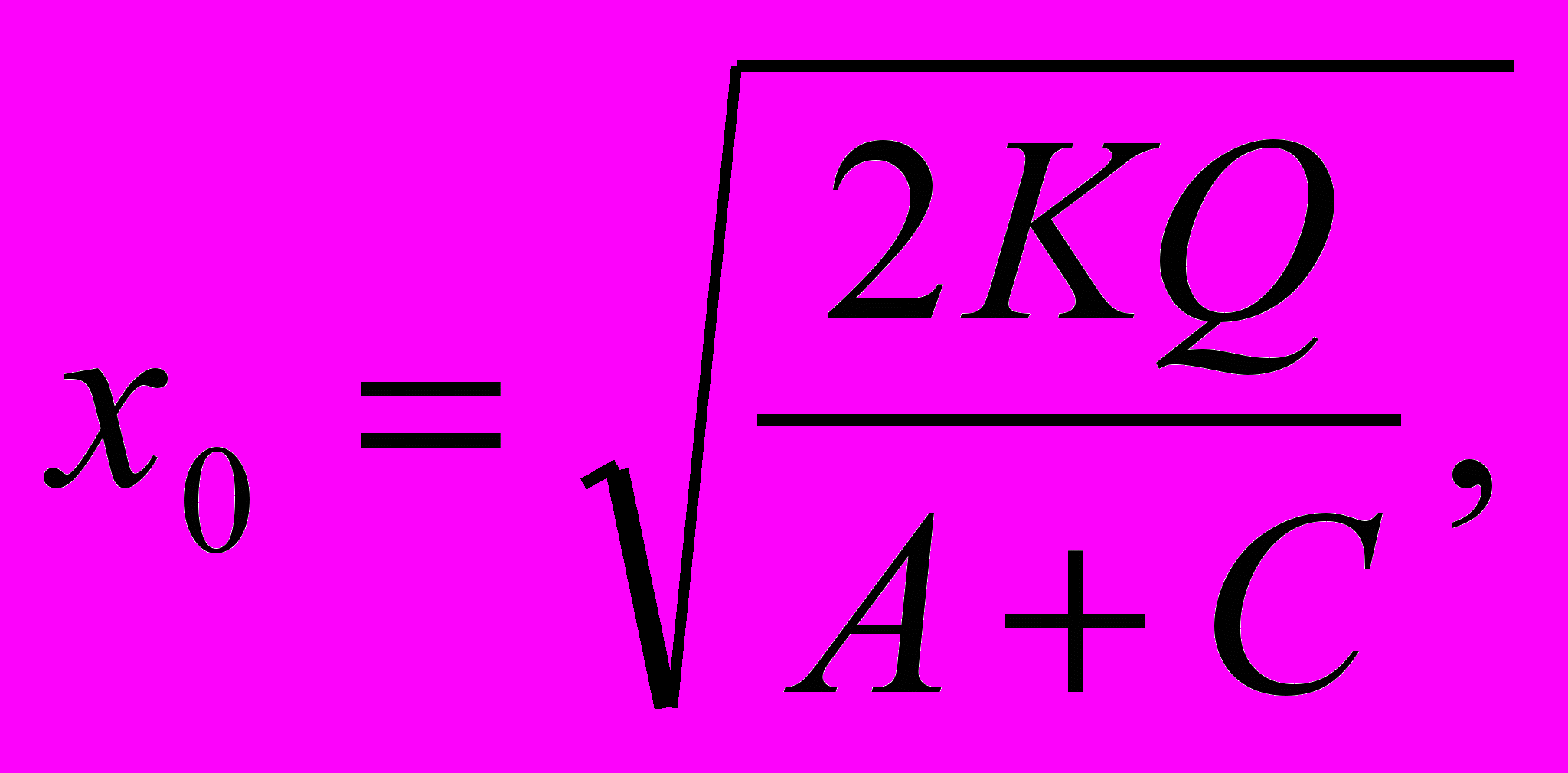у =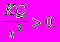

Следовательно, 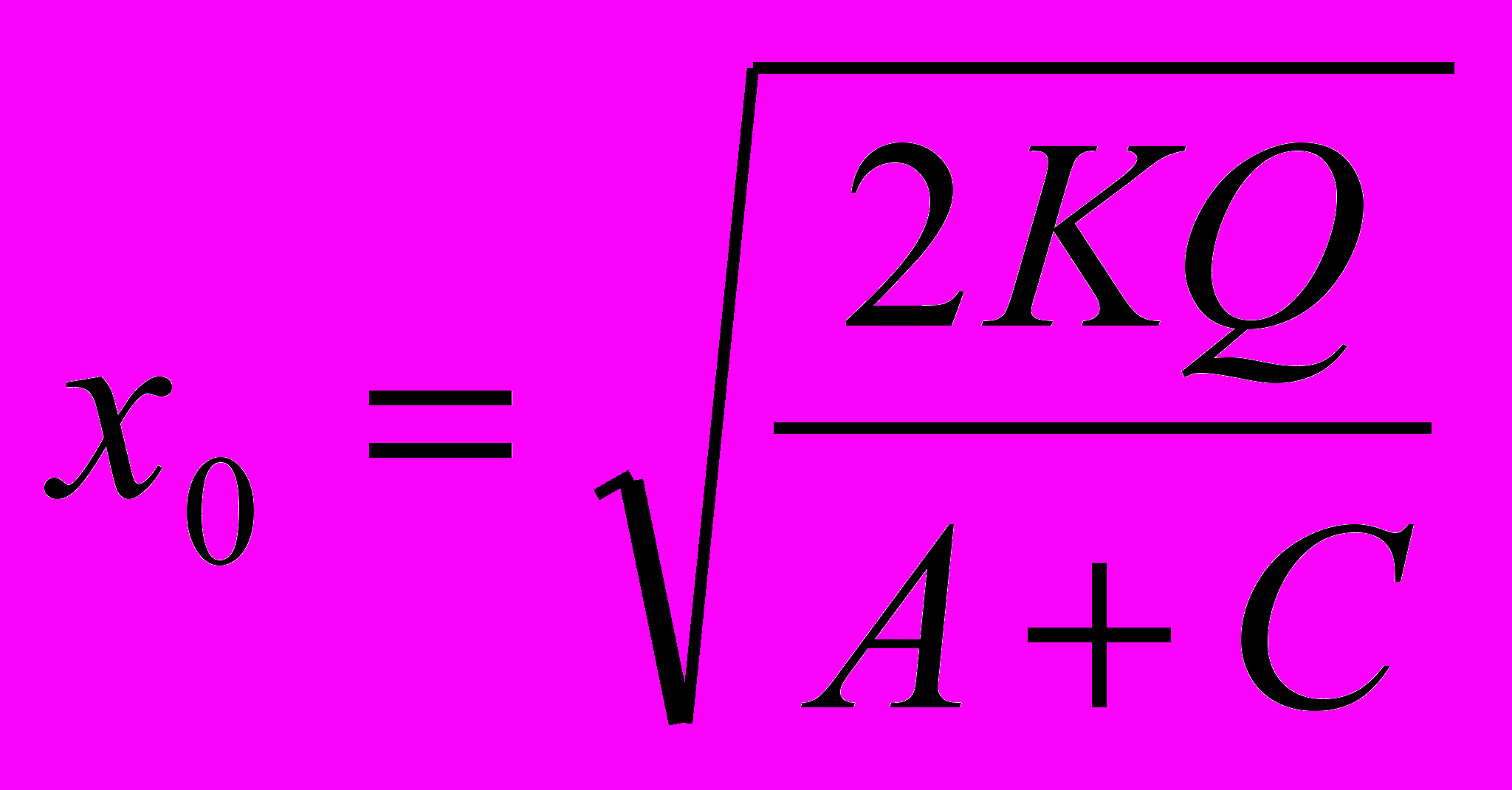- оптимальный размер одной поставки, при котором издержки у принимают наименьшее значение. Теперь можно найти и другие параметры управления запасами:

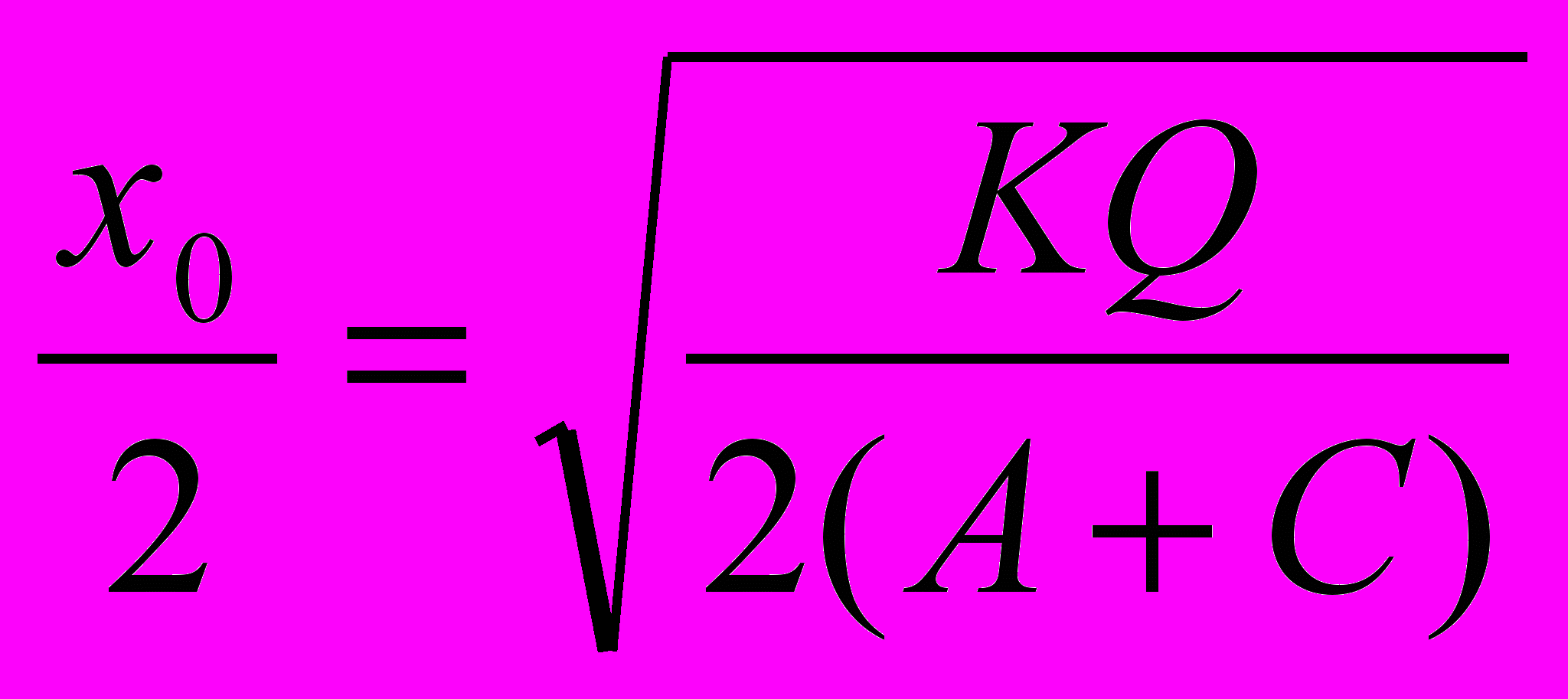- оптимальный средний текущий запас,

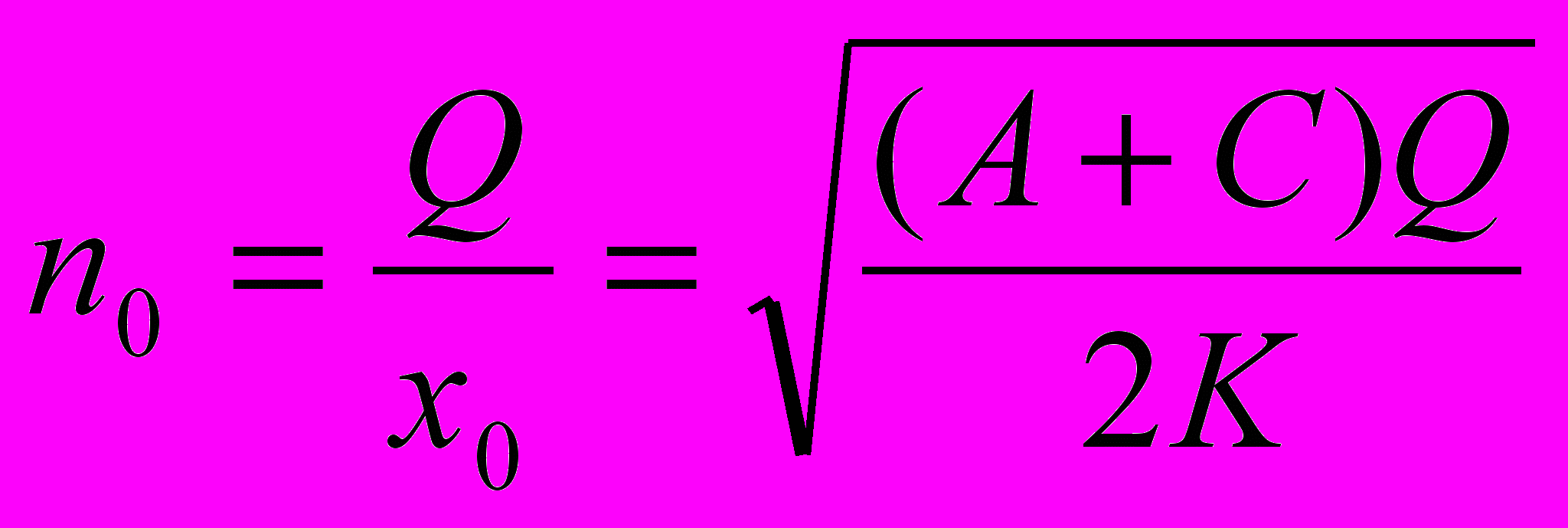- оптимальное число поставок товара,

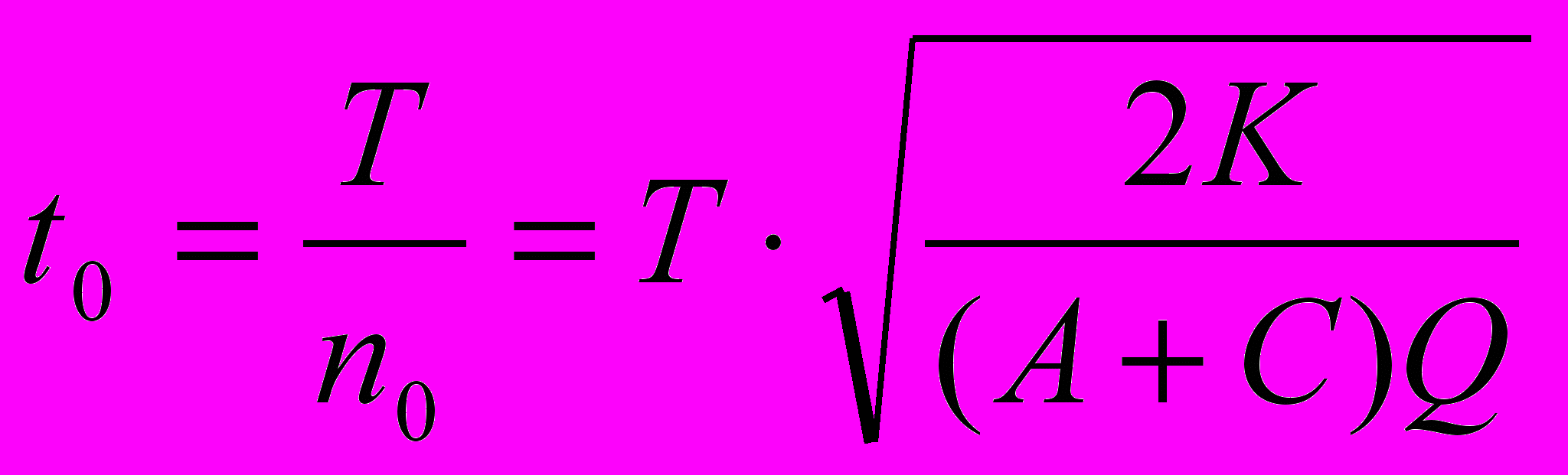- оптимальный интервал между поставками,

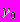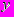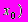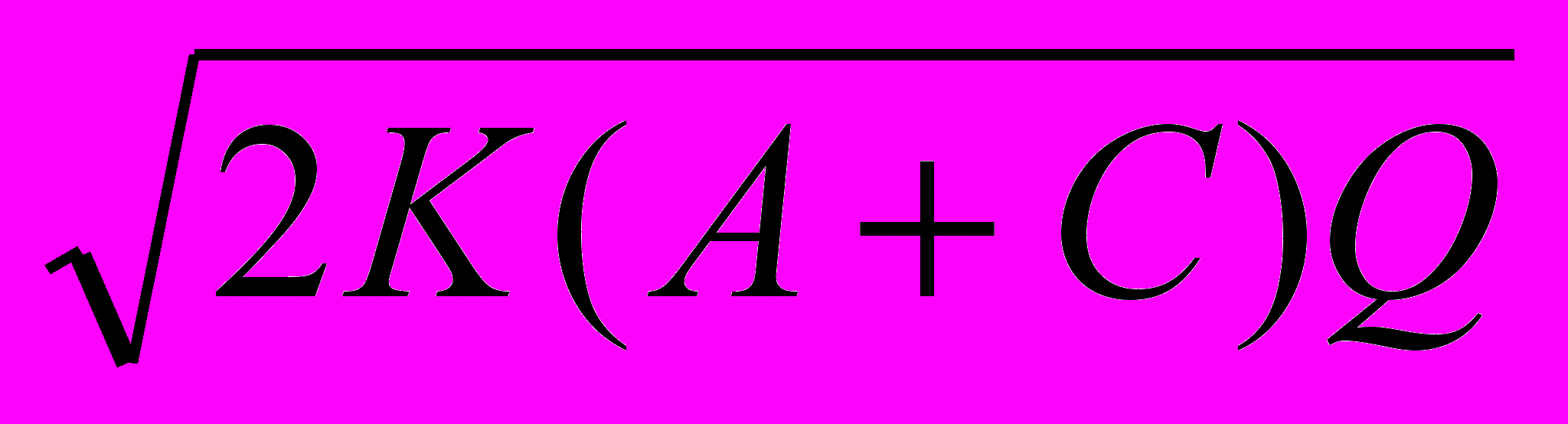= ( = - наименьшие издержки.


Модифицированная модель Баумоля - Тобина формально совпадает с модифицированной моделью Уилсона, различие только в том, что ее параметры имеют другой смысл.

Сформулируем модифицированную задачу Баумоля - Тобина.

Пусть Q – количество денег, которое положил в банк некоторый гражданин. Эти деньги равными долями х в течение времени Т он собирается брать из банка для покупки определенного товара в магазине, при этом половину их он расходует в тот же день, а вторая половина переходит на следующий день (находится у него в кошельке). Пусть К – издержки гражданина на одноразовое посещение банка, независящие от х; С – издержки (потери) гражданина, связанные с тем, что он мог бы получить проценты в банке на один рубль денег за время Т, которые он держал в кошельке; А – издержки по организации покупки единицы товара в магазине за время Т; у – общие издержки гражданина. Требуется найти зависимость между х и у при условии, что величины Q, K, C, А не изменяются в течение всего планового периода Т и минимизировать общие издержки. Решение этой задачи, как и выше, состоит в минимизации функции у = С 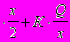+ А.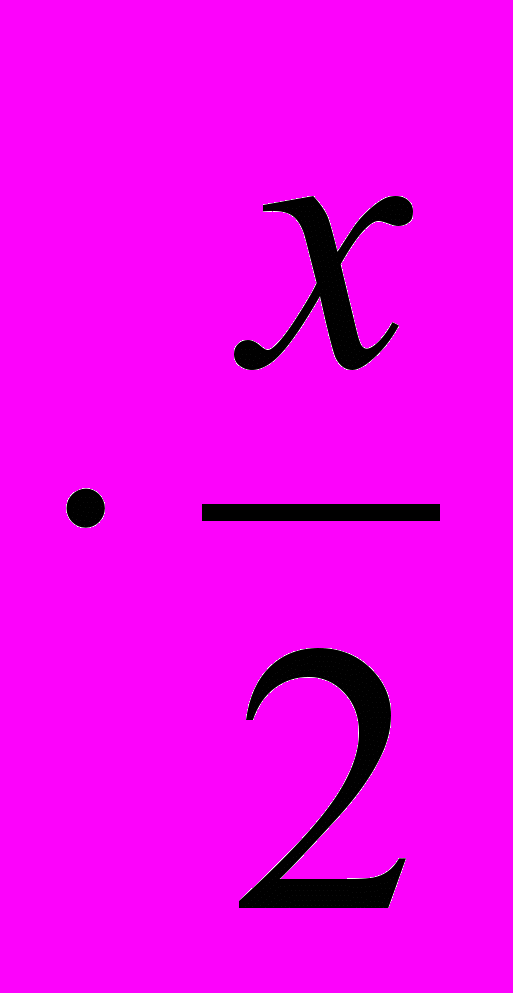


Список литературы

  1. Черемных Ю.Н. Микроэкономика. Продвинутый уровень: Учебник. – М.: ИНФРА-М, 2008. 844 с.



АНКЕТА

участника международной научно-практической интернет-конференции профессорско-преподавательского состава, аспирантов и студентов высших учебных заведений «Инновационные технологии: приоритетные направления развития»

12-14 апреля 2011 г.

Фамилия
Сучков

Имя
Владилен

Отчество
Константинович

Место работы (учебы)
Белгородский университет потребительской кооперации

Должность
доцент кафедры естественнонаучных дисциплин

Ученое звание, ученая степень
кандидат физико - математических наук, доцент

Название доклада
Математические модели динамики цен и управления запасами ресурсов

Номер секции
№1

Телефон
8-908–787–37–77

e-mail