Geum.ru

Учебное пособие по макроэкономике Для подготовки к лабораторным работам и экзаменам

Вид материалаУчебное пособие
39. Модель экономического роста Домара.
40. Модель экономического роста Харрода.
Подобный материал:
1   ...   17   18   19   20   21   22   23   24   25

39. Модель экономического роста Домара.



МОДЕЛЬ ЭКОНОМИЧЕСКОГО РОСТА ДОМАРА — про­стая кейсианская модель экономического роста, исследую­щая двоякую роль инвестиций в увеличении совокупного спроса и в увеличении производственных мощностей сово­купного предложения во времени.

В экономической литературе модель экономического ро­ста американского экономиста Е. Д. Домара и модель анг­лийского экономиста Р. Ф. Харрода часто рассматривают вместе как одну модель, именуемую моделью Харрода—До­мара. Однако, несмотря на их сходство, они в значительной мере отличаются друг от друга как объектом исследования, так и своим экономическим значением.

Домар не ставил задачу систематически разработать теорию экономического роста. Он ставил целью выдвинуть проблему полной занятости в долгом периоде. Основной вклад Е. Домара в теорию экономического роста заключа­ется в том, что он обратил внимание на необходимость уче­та обоих элементов инвестиций (мультипликатора и аксе­лератора).

Модель Домара является основным отправным пунктом для современной теории экономического роста.

Модель Е. Домара, предложенная в конце 40-х гг. XX в., исходила из следующих предпосылок:

а) технология производства представлена в ней произ­водственной функцией Леонтьева;

б) на рынке труда существует избыточное предложение, вызванное негибкостью цен;

в) выбытие капитала отсутствует, отношение К/У и нор­ма сбережений стабильны;

г) выпуск зависит только от одного ресурса — капитала;

д) рынок благ сбалансирован;

е) инвестиционный лаг равен нулю.

Инвестиционные расходы, являясь элементом совокуп­ного спроса, увеличивают общий спрос.




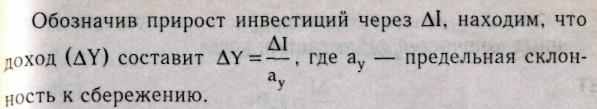
В коротком периоде модель Домара не учитывает, что уве­личение инвестиций ведет к увеличению производственных мощностей, эффект от которых невелик в коротком периоде, но в долгом периоде, когда проявляется экономический рост, следует принимать во внимание их роль в росте произ­водственных мощностей.

На вопрос: если инвестиции увеличивают производст­венные мощности и ведут к дополнительным доходам, то как должны увеличиваться инвестиции, чтобы темп прироста дохода был равен темпу прироста производственных мощно­стей? Домар ответил уравнением, в котором одна часть пред­ставлена темпом прироста производственных мощностей, а другая часть — темпом прироста дохода. Решение данного уравнения позволяло определить нужный темп роста.

Приведем условный пример.

Предположим, что каждый доллар инвестиций (I) вызы­вает рост производственных мощностей 6 долл. в год. На­пример, для производства $ 2000 выпуска в год требуется $ 6000 капитала. В этом случае 6 составит одну треть, или 33 % в год. Символом 8 обозначается капиталоемкость (от­ношение прироста инвестиций к приросту выпуска продук­ции). Исходя из этого, производственные мощности возрастут на 18, что и является эффектом от инвестиций и выступает стороной предложения в уравнении.

Чтобы занять дополнительные мощности, спрос должен увеличиться на эту же сумму. Что касается стороны спроса в уравнении, то в соответствии с теорией мультипликатора при любой предельной склонности к сбережению (av) прирост национального дохода выступает функцией не от инвестиций, а от абсолютного годового прироста инвестиций (AI). В этом случае абсолютный годовой прирост дохода составит



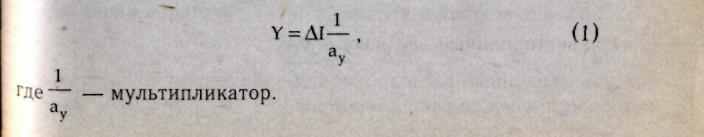
Условие равенства темпов прироста дохода и производственных мощностей соблюдается, когда



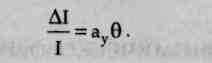
В левой части уравнения находится годовой темп рост инвестиций, которые, чтобы обеспечить полную занятости посредством роста производственных мощностей, должен увеличиваться с годовым темпом ау0. Что касается дохода, то он должен увеличиваться тем же темпом.


40. Модель экономического роста Харрода.



МОДЕЛЬ ЭКОНОМИЧЕСКОГО РОСТА ХАРРОДА —

модель, выявляющая механизм сбалансированного роста, опираясь на анализ психологических мотивов поведения предпринимателей и на уравнения, выражающие функциональные связи в экономике.

Модель Харрода разработана раньше (1939 г.), чем мо­дель Домара. Харрод поставил задачу заложить основы об­щей теории экономического роста.

Р. Ф. Харрод в свою модель включил эндогенную функ­цию инвестиций (в отличие от экзогенно заданных инвести­ций в модели Домара) на основе принципа акселератора и ожиданий предпринимателей.

Особое внимание Харрод уделяет темпу роста нацио­нального дохода, чтобы удовлетворить условию кейнсианс-кой экономической теории:

сбережения (St) = инвестиции (It), (1)

где t — период времени.

В модели Харрода St зависит от национального дохода:

St = sYt , (2)

где s — средняя склонность к сбережению и предельная склонность к сбережению,

Уравнение (2) означает, что сбережения в каждый дан­ный период времени зависят от дохода этого же периода.

Инвестиции во времени It зависят от скорости измене­ния дохода от одного периода до следующего периода. Если доход в текущем периоде обозначим (Yt), а доход в предыдущем периоде (Yt - 1), то

It = а(Yt - Yt – 1), (3)
где а — акселератор.

При данных сбережениях и инвестициях условие равновесия, представленное в уравнении (1), может быть выражено таким образом:

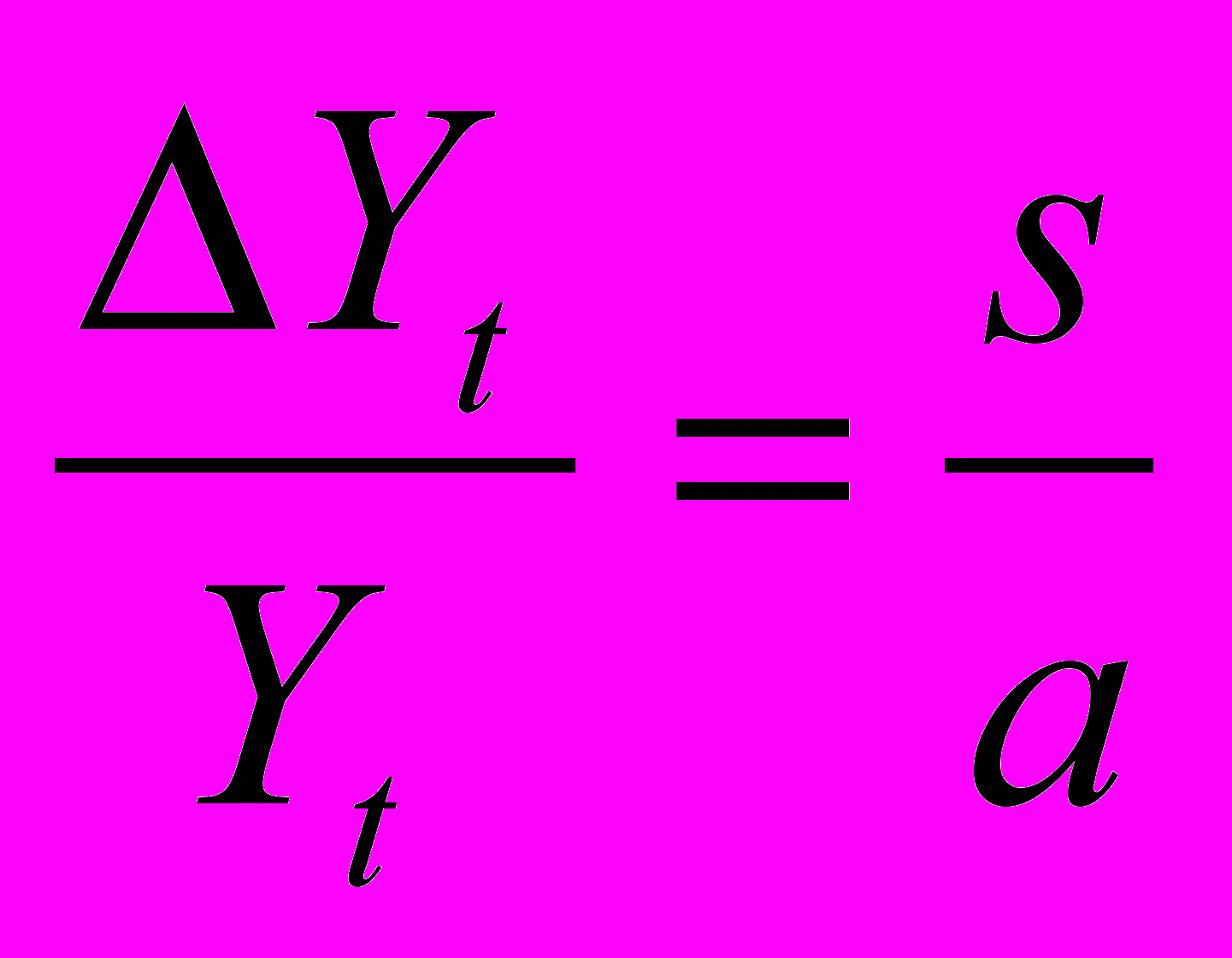, (4)

где Yt = Yt - Yt – 1.
Левая часть выражения (4) показывает процентное изменение дохода. В правой части в числителе находится предельная склонность к сбережению, в знаменателе — акселератор. В связи с тем, что данное уравнение Харрод вывел из условия сохранения равновесия в каждый период времени, то он назвал скорость изменения дохода гарантирован­ным темпом роста, при котором предприниматели удов­летворены своими решениями.

Уравнение (4) определяет гарантированный темп роста. Действительный темп роста определяется в модели темпом роста рабочей силы и темпом роста производительности. Допустим, что численность рабочей силы увеличивается со скоростью 2 %, а производительность труда — 4 %. Действительный достижимый темп роста национального дохо­да и производства равен, следовательно, 6 % в год.

Харрод вводит понятие естественного темпа роста как максимального темпа, допускаемого ростом активного на­селения и техническим прогрессом.

В том случае, когда естественный темп роста выше га­рантированного, экономика отклоняется от гарантирован­ного темпа роста, при этом доход увеличивается быстрыми темпами, выступая причиной долгосрочного подъема. Напро­тив, когда естественный темп роста ниже уровня гарантиро­ванного темпа, наблюдается долговременная стагнация.

Если действительный (фактический) темп роста равен гарантированному, и экономическая система развивается вполне удовлетворительно для предпринимателей, то такое положение нельзя назвать оптимальным, ибо, если гаранти­рованный темп роста ниже естественного темпа роста, эко­номическое развитие в таких условиях оставляет часть тру­довых ресурсов в состоянии вынужденной безработицы.

Идеальное развитие экономической системы достигает­ся только при равенстве действительного (фактического), гарантированного и естественного темпов роста. Поскольку, такое положение никогда не достигается, то динамическое равновесие в условиях экономического роста неустойчиво. Поэтому Е. Домар и Р. Харрод приходят к выводу о необхо­димости государственного вмешательства в регулирование экономики.