Geum.ru

Методические разработки для управляемой самостоятельной работы по астрономии Минск 2011 Тема №1

Вид материалаМетодические разработки
Методы определения масс небесных тел
Возмущающая сила и возмущающее движение.
Приливы и отливы
Приливное действие Луны
Подобный материал:
1   2   3   4   5   6   7

Методы определения масс небесных тел


Закон всемирного тяготения Ньютона позволяет измерить одну из важнейших физических характеристик небесного тела - его массу.

Массу можно определить:

а) из измерений силы тяжести на поверхности данного тела (гравиметрический способ),

б) по третьему уточнённому закону Кеплера,

в) из анализа наблюдаемых возмущений, производимых небесным телом в движениях других небесных тел.

1. Первый способ применяется на Земле.

На основании закона тяготения ускорение g на поверхности Земли:



где m - масса Земли, а R - её радиус.


,

где g и R измеряются на поверхности Земли. G = const.

С принятыми сейчас значениями g, R, G получается масса Земли: m = 5,976 . 1027 г = 6 .1024 кг. Зная массу и объём, можно найти среднюю плотность. Она равна 5,5 г/см3.

2. По третьему закону Кеплера можно определить соотношение между массой планеты и массой Солнца, если у планеты есть хотя бы один спутник и известны его расстояние от планеты и период обращения вокруг неё.

,

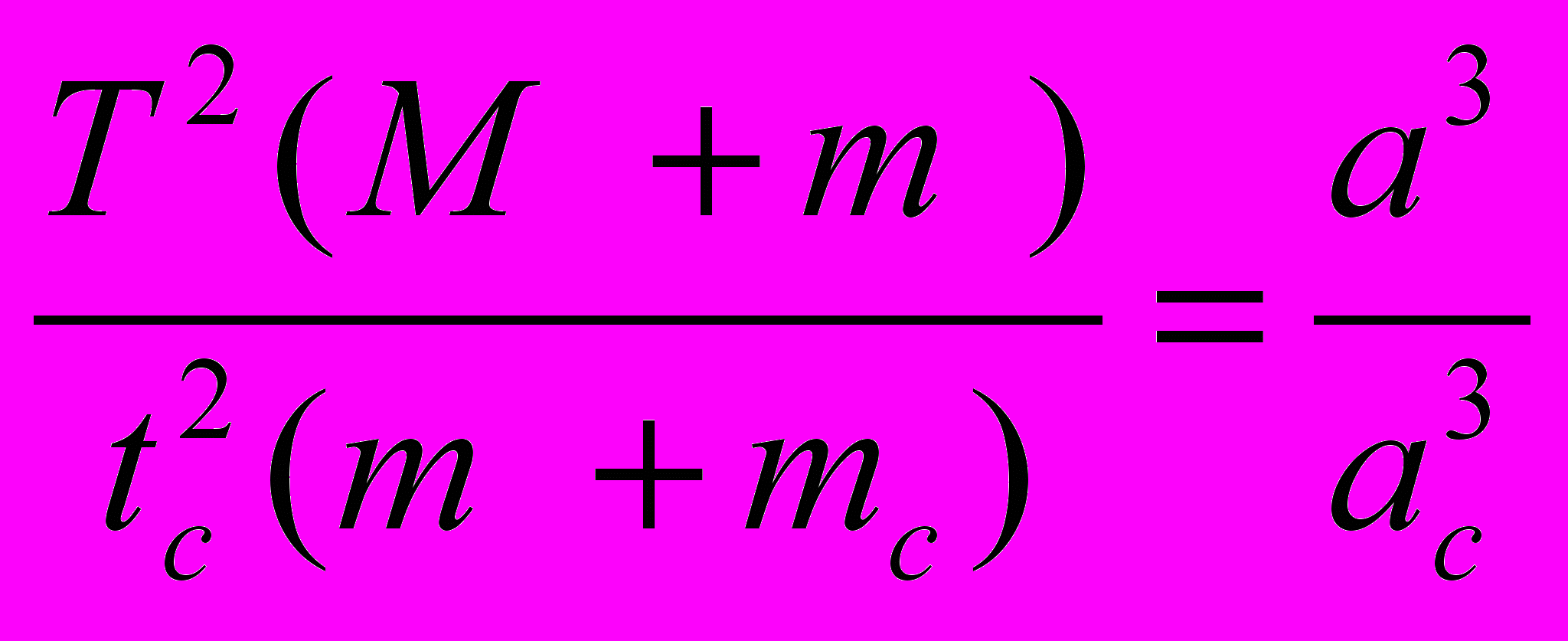где M, m, mc - массы Солнца, планеты и её спутника, T и tc - периоды обращений планеты вокруг Солнца и спутника вокруг планеты, а и ас - расстояния планеты от Солнца и спутника от планеты соответственно. Из уравнения следует:

.

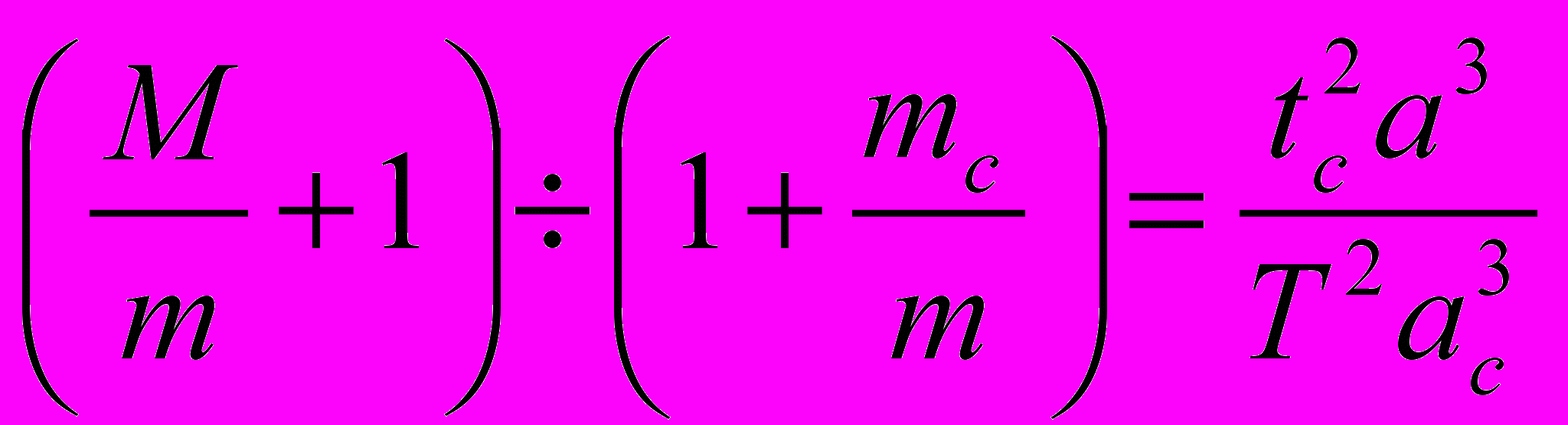Отношение М/m для всех планет очень велико; отношение же m/mc, очень мало (кроме Земли и Луны, Плутона и Харона) и им можно пренебречь. Соотношение М/m можно легко найти из уравнения.

Для случая Земли и Луны нужно сначала определить массу Луны. Это сделать очень сложно. Решается задача путём анализа возмущений в движении Земли, которые вызывает Луна.

3. По точным определениям видимых положений Солнца в его долготе были обнаружены изменения с месячным периодом, называемые "лунным неравенством". Наличие этого факта в видимом движении Солнца указывает на то, что центр Земли описывает небольшой эллипс в течение месяца вокруг общего центра масс "Земля - Луна", расположенного внутри Земли, на расстоянии 4650 км от центра Земли.

Положение центра масс Земля-Луна было найдено также из наблюдений малой планеты Эрос в 1930 - 1931 гг. По возмущениям в движениях искусственных спутников Земли отношение масс Луны и Земли получилось 1/81,30. В 1964 году Международный астрономический союз принял его как const. Из уравнения Кеплера получаем для Солнца массу = 2.1033г., что в 333000 раза превосходит земную.

Массы планет, не имеющих спутников, определены по возмущениям, которые они вызывают в движении Земли, Марса, астероидов, комет, по возмущениям, производимым ими друг на друга.

Возмущающая сила и возмущающее движение.


Если бы тела двигались вокруг Солнца только под действием его силы притяжения, то движения описывались бы законами Кеплера. Такое движение называется невозмущённым. В реальности все тела Солнечной системы притягиваются друг другом. Отклонения в движениях тел от законов Кеплера называются возмущениями, а реальное движение тел - возмущённым движением.

Возмущения имеют очень сложный характер и их учитывать очень трудно. Значения возмущений невелики, так как общая масса всех планет меньше массы Солнца примерно в 700 раз. Возмущения можно рассматривать как различие между положениями светила при возмущённом и невозмущённом движениях, а возмущённое движение тела представлять как движение по законам Кеплера с переменными элементами орбиты.

Изменения элементов орбиты тела вследствие притяжения его другими телами, помимо центрального, называются возмущениями, или неравенствами элементов. Возмущения элементов делятся на вековые и периодические.

Вековые возмущения тел Солнечной системы зависят от взаимного расположения их орбит, которое в течение очень больших промежутков времени меняется очень мало.

Вековым возмущениям подвержены долгота восходящего узла  и долгота перигелия .

Периодические возмущения зависят от относительного положения тел на орбитах, которое при движении тел по замкнутым орбитам повторяется через определённые промежутки времени. Этим возмущениям подвержены почти все элементы орбит.

Приливы и отливы


Прилив – это любая из циклических деформаций одного астрономического тела, вызванная гравитационными силами другого.

Размеры Земли не бесконечно малы по сравнению с расстоянием до Луны и Солнца. Силы лунного и солнечного притяжения на разные точки Земли неодинаковы. Поэтому появляется возмущающая сила, действующая на различные детали поверхности Земли по-разному. В твёрдых массивах действие силы вызывает натяжение, большие массивы воды же увлекаются силой притяжения и перетекают с места на место. Приливное воздействие на атмосферу выражается в появлении атмосферных потоков.

Водные приливы и отливы известны с давних времён. Географ Страбон (род. - 66 г.) рассказывает, что финикияне хорошо знали о приливах и отливах. В Средиземном море эффект малый, но финикияне проходили через Геркулесовы столбы и наблюдали его в океане. Они указывали, что приливы зависят от фаз Луны и особенно интенсивны в полнолуния и новолуния. Итальянский иезуит Кабео (1585 - 1650) предполагал, что Луна производит на морском дне какое-то спиртное вещество, которое и вызывает прилив. Стевин объяснял прилив притяжением Луны, но горб на обратной стороне Земли объяснял существующей там ещё одной притягивающей точкой. Галилей объяснял приливы центробежной силой, отвергая тяготение. Некоторые исследователи предполагали, что Луна производит изменения в давлении воздуха, что влияет на уровень моря.

Наиболее верное объяснение явлению приливов и отливов дал Исаак Ньютон, с помощью теории гравитации. Он писал, что Луна оттягивает воду от Земли на одной стороне и оттягивает Землю от воды на другой.

Если земная поверхность со всех сторон покрыта океаном, то каждая капля воды имеет ускорение, пропорциональное квадрату расстояния между частицей и и центром Луны.

Равнодействующая ускорений, сообщаемых твёрдым частицам проходит через центр Земли Т и равна:


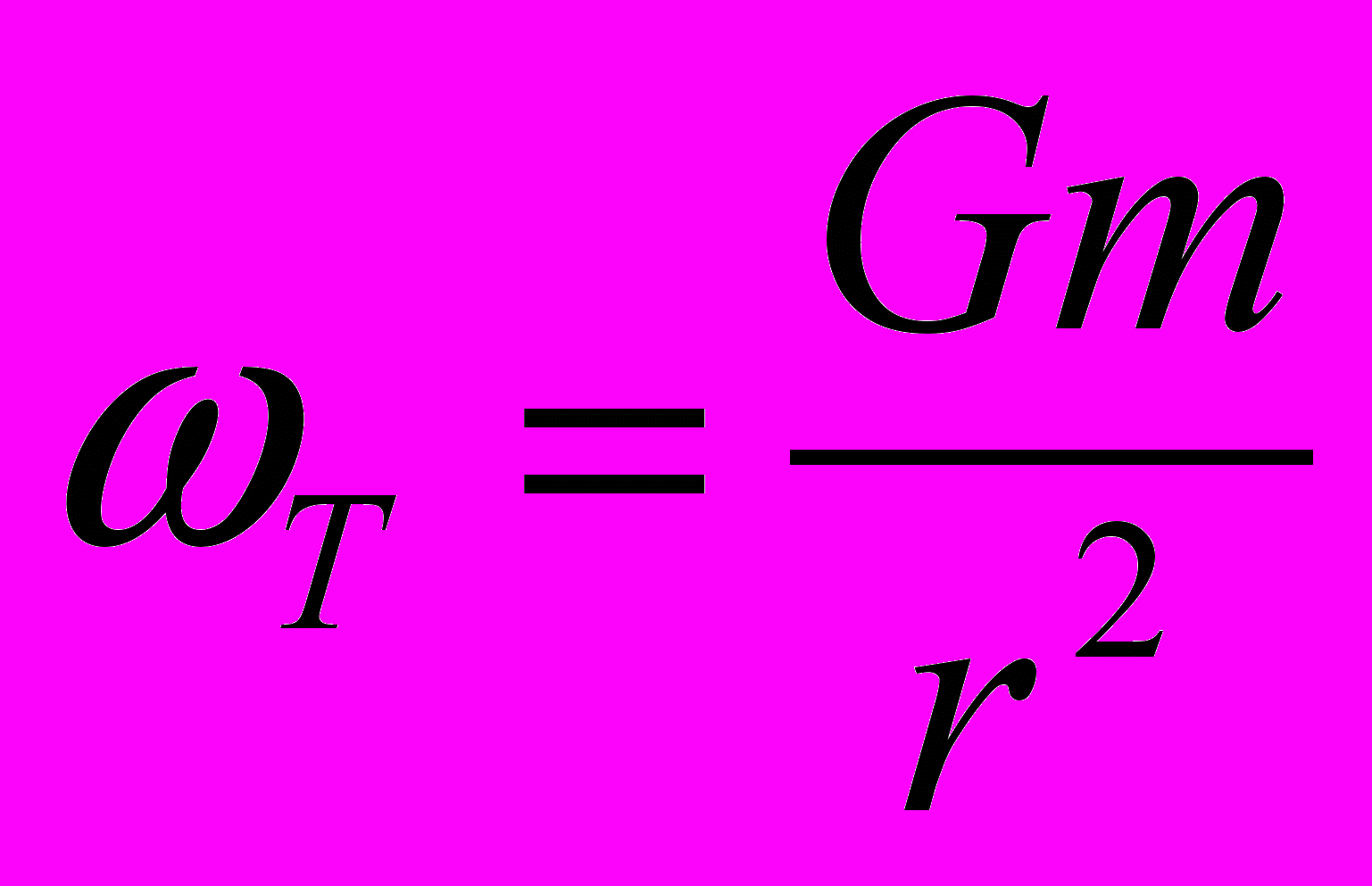
Приливное действие Луны
,

где m - масса Луны, r - расстояние центра Луны от центра Земли.

Для воды океана ускорение в точке А больше, чем T, а в точке В меньше, чем T, так как:

и ,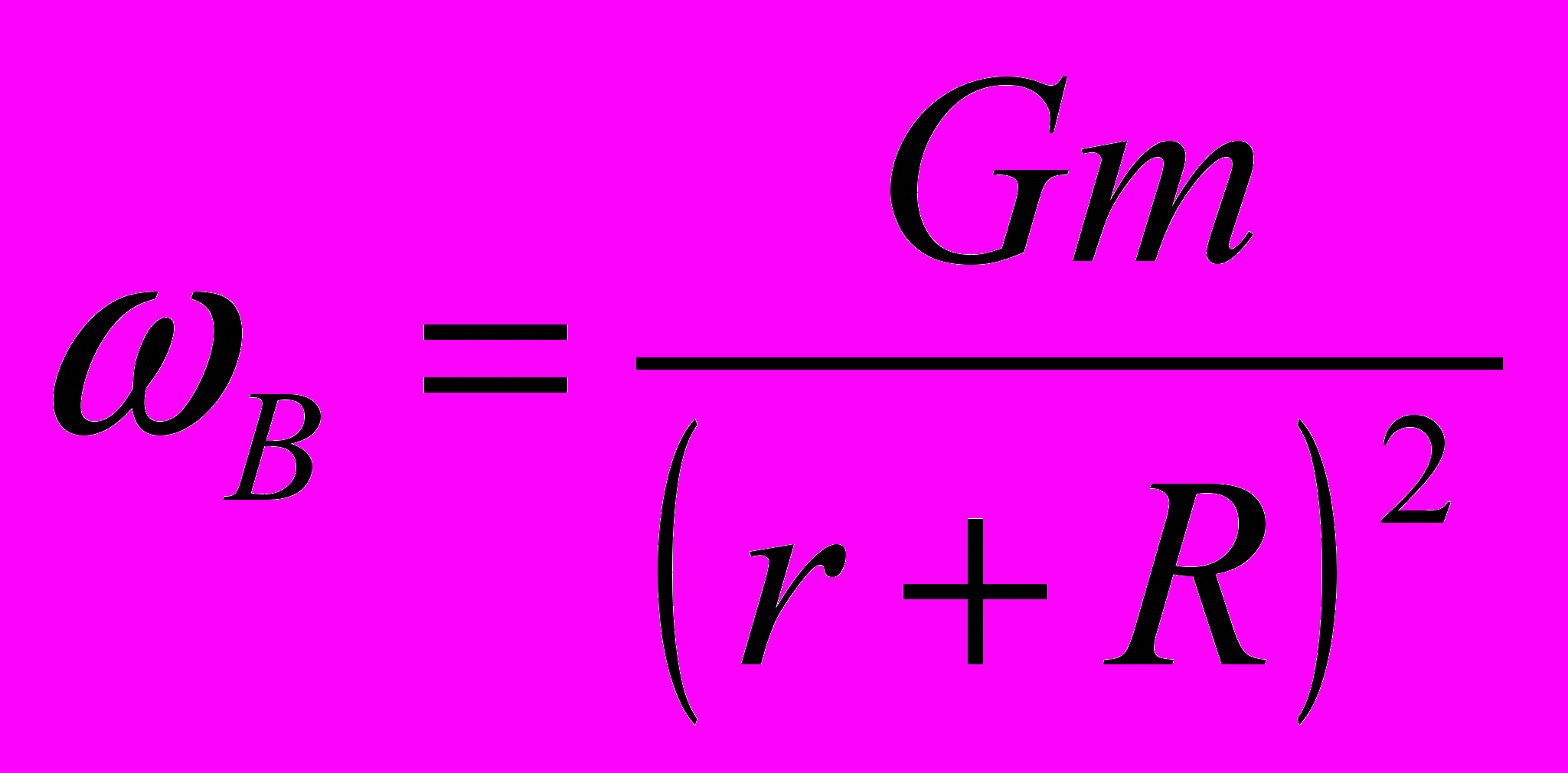

где R - радиус Земли.

Относительное ускорение (относительно центра Земли) в точке А равно:

.

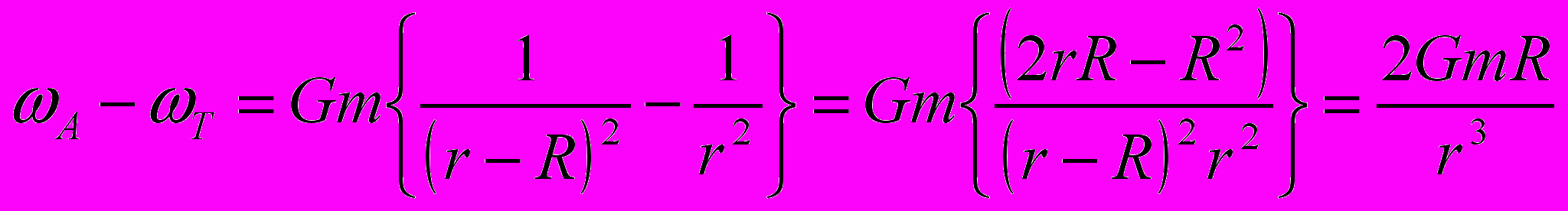Пренебрегаем малым членом R2, и вместо (r - R) оставляем r. Эта разность ускорений направлена от центра Земли.

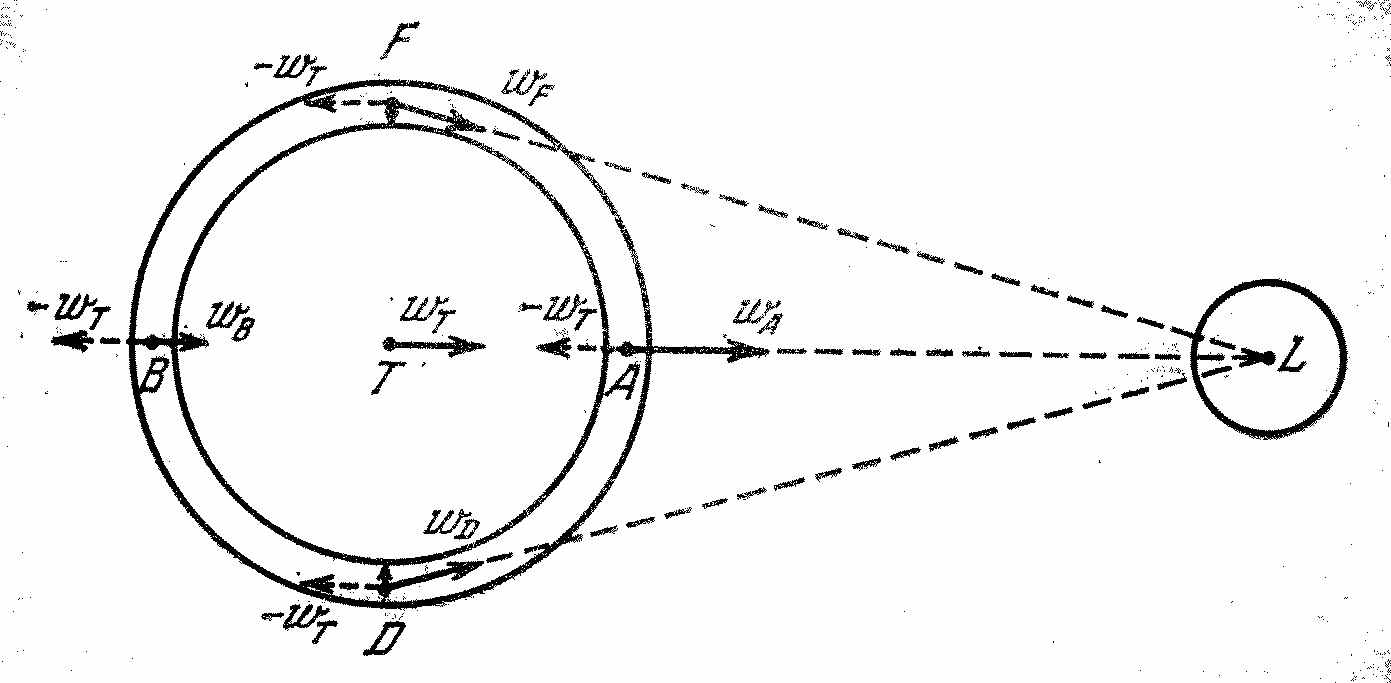
В точках А и В действие Луны ослабляет силу тяжести на Земной поверхности. В точках F и D действие Луны увеличивает силу земной тяжести.

Действие ускорений в промежуточных точках приводит к тому, что вода в океане стремится на одной половине Земли к точке А, где Луна находится в зените, на другой половине к точке В - где Луна находится в надире. Под действием Луны водная оболочка Земли принимает форму эллипсоида, вытянутого по направлению к Луне. Вблизи точек А и В будет прилив, а у точек F и D - отлив.

За промежуток времени между двумя последовательными кульминациями Луны, равный 24ч52м, приливные выступы обойдут вокруг Земли, и в каждом месте будет по два прилива и два отлива. Под действием солнечного притяжения водная оболочка Земли испытывает приливные силы меньше лунных в 2,2 раза. Солнечные приливы отдельно не наблюдаются, они только изменяют величину лунных приливов. Во время новолуний и полнолуний силы складываются и приливы больше обычных, в квадратуры на лунный прилив приходится солнечный отлив, силы вычитаются и приливы меньше.

В реальности Земля не везде покрыта водой, дно морей и океанов обладает сложным рельефом, приливная волна испытывает большое трение. Момент прилива поэтому не совпадает с моментом кульминации Луны и запаздывает до шести часов. Этот промежуток времени называется прикладным часом.

Высота прилива в Чёрном море равна нескольким сантиметрам, в заливе Фанди на Атлантическом побережье Канады - 18 метрам. Трение приливной волны о твёрдые части Земли вызывает систематическое замедление её вращения. Приливы и отливы сказываются на изменениях атмосферного давления.