Лекции по теории ценных бумаг Селищева А. С

Вид материала

Лекции

Содержание V/P). (1) Возрастание реального дохода (y Проанализируем эту формулу при изменении факторов, ее составляющих. Изменение реального дохода (y). Изменение уровня цен (Р). А.2.2. Предложение ЦБ. Факторы, от которых зависит реальное предложение ЦБ M/P). Реальный доход (у) Ставка процента (r). Реальные денежные балансы (М/Р). Процентная ставка (r). Реальный доход (y). Денежные балансы (M/P). Изменение уровня цен (рис. А.2.9). Изменение ликвидных предпочтений. А.2.4.1. Линия IS: равновесие на рынке благ. Модель IS строится на основании хорошо известного принципа равенства сбережений и и C), спрос на инвестиции (I Изобразим линию (BB) графически. Математическое доказательство того, что линия ВВ проходит исключительно через квадранты I и III сводится к двум действиям. А рисунка 1 при процентной ставке (r) и (у

Подобный материал:

• Лекции Селищева А. С. по курсу «Теория ценных бумаг», 1514.54kb.
• А. С. Селищева Последнее обновление 28. 01. 2012 = Приложения «Г» к лекции, 3466.33kb.
• Сообщение о сведениях, которые могут оказать существенное влияние на стоимость ценных, 27.95kb.
• Задачи: дать студентам понимание сущности и видов ценных бумаг; познакомить с профессиональной, 14.72kb.
• 2. Законодательство рф, регламентирующее функционирование рынка ценных бумаг, 495.27kb.
• Вопросы для подготовки к экзамену по курсу «Рынок ценных бумаг», 270.17kb.
• Сообщение о сведениях, которые могут оказать существенное влияние на стоимость ценных, 26.96kb.
• Учебная программа по курсу «управление портфелем ценных бумаг» Специальность, 48.16kb.
• Основные темы лекций: инфраструктура рынка ценных бумаг; раскрытие информации на рынке, 17.89kb.
• Сообщение о сведениях, которые могут оказать существенное влияние на стоимость ценных, 22.27kb.

Приложение «А» к лекции 2








Zài dòuzhēng zhōng fāzhăn

zhuàngdà măkèsīzhǔyì-de lĭlùn dùiwǔ


В борьбе формировать крепкие

марксистские теоретические группы




Содержание:

А.2.1. Модель IS-LM-BB ………………………………………………..……………….. 1


А.2. Модель IS-LM-BB




А.2.1. Спрос на ЦБ. Построим простую модель спроса на ЦБ, сведя всё многообразие совокупности ЦБ к облигациями (bonds – B). Допустим также, что реальный (то есть с учетом уровня цен P) спрос на ЦБ формируется только домашними хозяйствами (household sector):


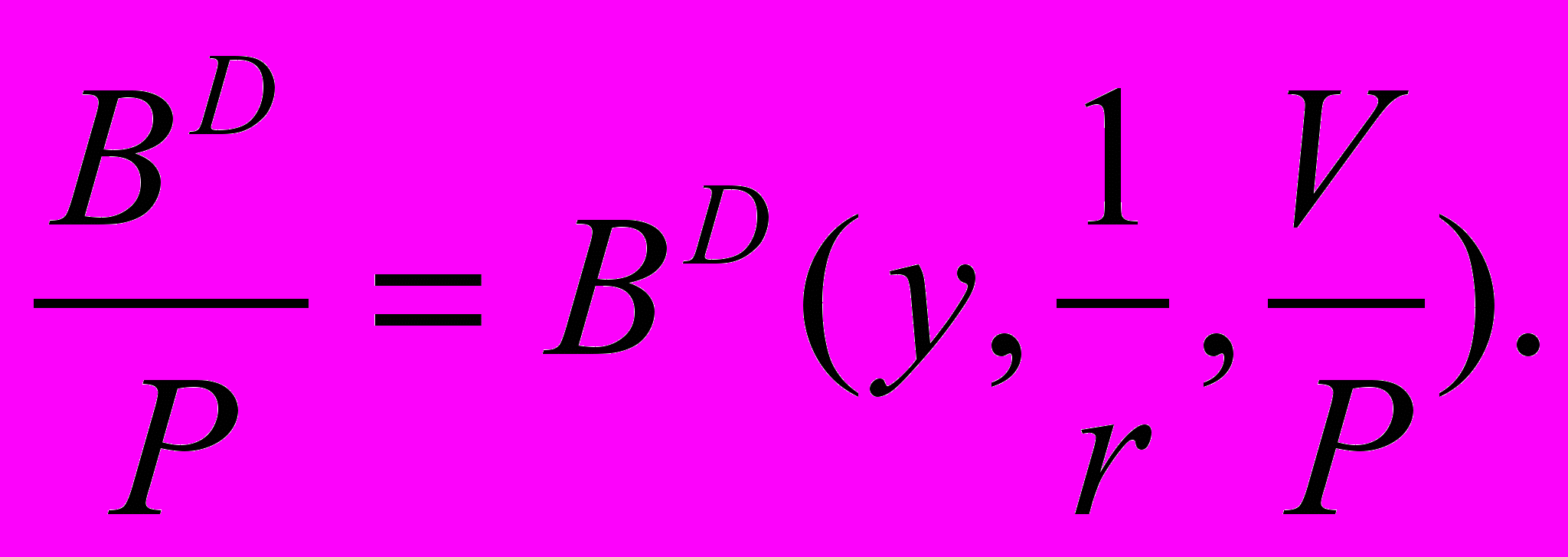(А.2.1)


Левая сторона уравнения представляет реальный спрос на ЦБ. Он равен количеству запрашиваемых ЦБ – B^D, деленное на уровень цен Р:

Факторы, от которых зависит спрос на ЦБ:

■ реальный доход (y),

■ цена ЦБ (B_P = 1/r )

■ реальные активы ( V/P).


(1) Возрастание реального дохода (y), способствует увеличению сбережений (S), при этом спрос на ЦБ также растет. Итак, спрос на ЦБ прямо зависит от изменения реального дохода (y) (+).

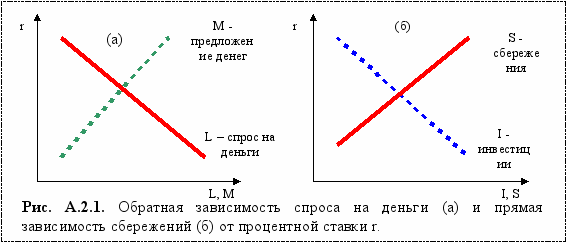
(2) При возрастании цены ЦБ (B_P = 1/r ↑), то есть при уменьшении ставки процента (r↓), начинают действовать два фактора, которые снижают спрос на ЦБ. Во-первых, сокращаются сбережения (S↓), во-вторых, домашние хозяйства избавляются от ЦБ в пользу денег (B↓ → L↑): см. рис. А.2.1.

При падении цены ЦБ (B_P = 1/r↓), имеет место противоположная тенденция: ставка процента (r↑) растет, спрос на ЦБ растет (В↑), сбережения возрастают (S↑), домашние хозяйства избавляются от денег в пользу ЦБ (L↓ → B↑). Итак, цена ЦБ (B_P = 1/r) и объем спроса на ЦБ (B^D) связаны обратной функциональной зависимостью (-).





(3) При возрастании реальных активов (V/P), спрос на ЦБ возрастает, и наоборот. То есть, зависимость между спросом на ЦБ и реальными активами является прямой (+).

Геометрически, удобно изобразить количество запрашиваемых ЦБ B^D как функцию их цены: 1/r. Преобразуем соответствующим образом формулу (А.2.1) и получим:

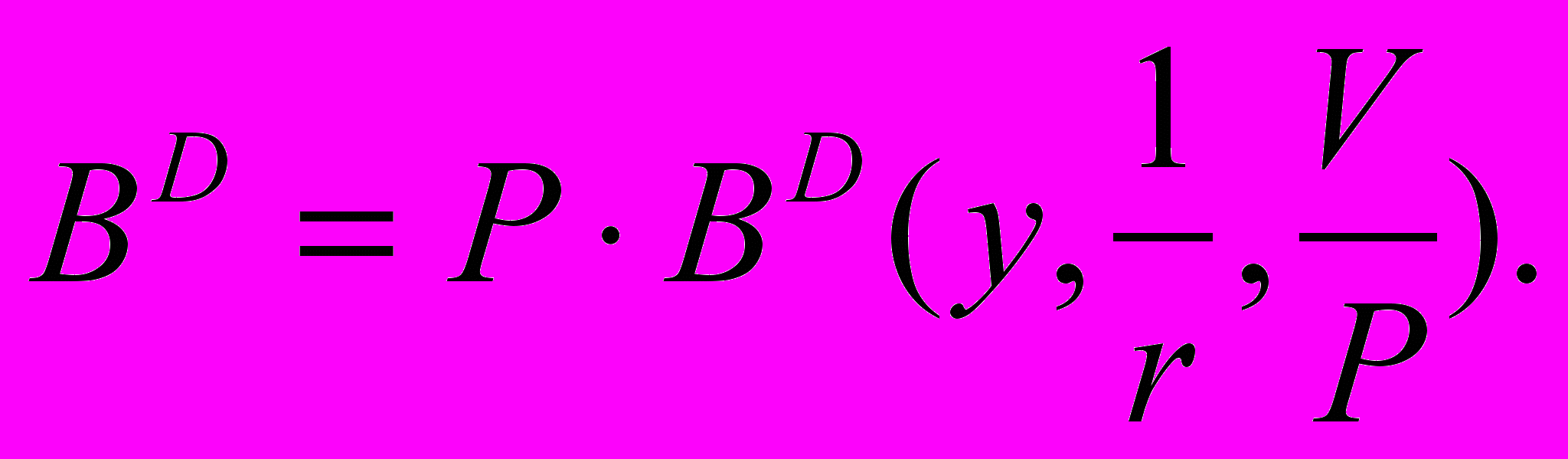(А.2.2)


Проанализируем эту формулу при изменении факторов, ее составляющих.

Изменение процентной ставки (r). Как B^D будет влиять на изменения процентной ставки при прочих равных условиях?





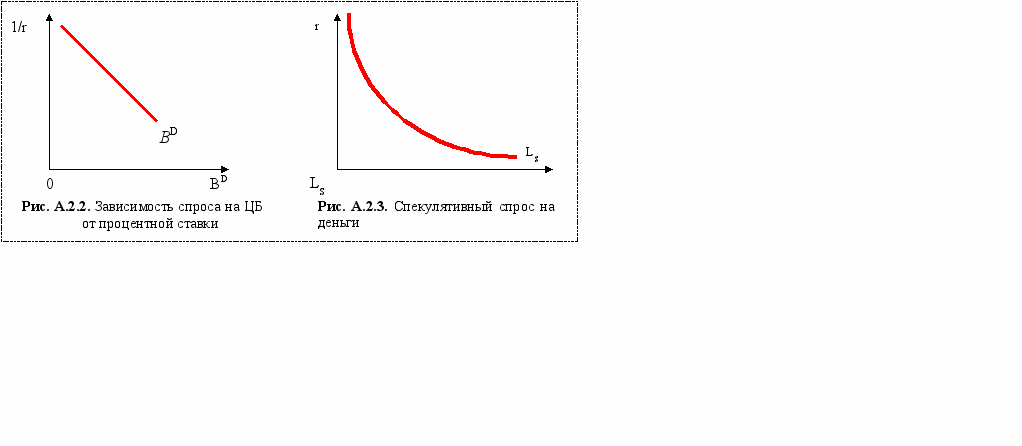
При возрастании процентной ставки (цена ЦБ падает), возрастает спрос на ЦБ. Таким образом, если мы изобразим графически количество запрашиваемых ЦБ как функцию их цены, то мы получим кривую спроса на ЦБ с отрицательным наклоном, которую обозначим B^D на рис. А.2.2.

Заметим, что зависимость спроса на ЦБ связана, прежде всего, с кейнсианским спросом на деньги по спекулятивному мотиву (L_S) о чем речь шла в пятой теме нашего курса «Деньги. Кредит. Банки» - «Спрос на деньги». Тогда мы отмечали, что при падении ставки процента (r) индивид переводит свои ЦБ в деньги и спекулятивная касса увеличивается (L_S). При росте процентной ставки, напротив, спекулятивная касса уменьшается, экономические субъекты покупают ЦБ. Итак, сформулируем общий вывод.


Вывод: изменение процентной ставки (r) определяет отрицательный наклон линии спроса на ЦБ.

Изменение реального дохода (y). При росте реального дохода (у₀) до (y₁) при прочих равных условиях реальный спрос на ЦБ возрастает (B^D) увеличивается. Это приведет к сдвигу кривой спроса на ЦБ вправо в положение B^D’ (рис. А.2.4).




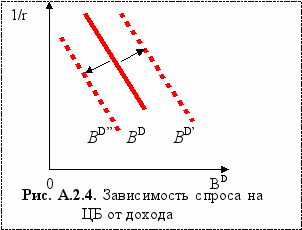
Напротив, снижение реального дохода сдвинет кривую B^D влево в положение B^D’’. Сформулируем общий вывод.


Вывод: увеличение реального дохода (у) сдвигает линию спроса на ЦБ вправо, а снижение - влево.

Изменение уровня цен (Р). Уровень цен (Р) присутствует в уравнении (А.2.1) дважды. Во-первых, вне скобок, и это означает, что, например, удвоение уровня цен, увеличит в два раза и объем спроса на ЦБ.

Во-вторых, показатель уровня цен присутствует еще и в скобках в знаменателе, определяя величину реального богатства (V/P). При росте Р (если считать при этом, что V остается неизменным) реальное богатство уменьшается, что, как известно, приводит к некоторому снижению объема спроса на ЦБ. Таким образом, можно сделать общий вывод: наличие Р вне скобок и внутри скобок в формуле А.2.1. приводит к тому, что, например, удвоение уровня цен Р увеличит объем спроса на ЦБ, но, меньше, чем в 2 раза (рис. А.2.5). Точно также, снижение уровня цен в 2 раза приведет к тому, что объем спроса на ЦБ снизится меньше, чем в 2 раза.





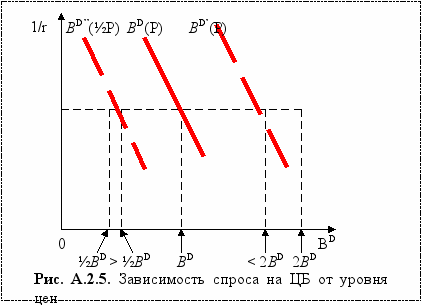
Сформулируем общий вывод.


Вывод: изменение уровня цен (Р) сдвигает линию спроса на ЦБ в том же направлении, как изменяется уровень цен, но менее интенсивно.


Итак, мы рассмотрели основные факторы, влияющие на наклон и положение линии спроса на ЦБ. Теперь рассмотрим функцию предложения ЦБ.


А.2.2. Предложение ЦБ. Предположим, что предложение ЦБ формируется предпринимательским сектором. Реальное предложение ЦБ равно предлагаемому объему ЦБ (B^S), деленному на уровень цен (Р), то есть (B^S/ P). От чего зависит эта величина? Когда фирмы предлагают облигации они, тем самым, берут в займы.

Факторы, от которых зависит реальное предложение ЦБ:

■ реальный доход (y);

■ цена ЦБ (B_P = 1/r ) или ставка процента (r);

■ реальные денежные балансы ( M/P).

Реальный доход (у). Известно, что уровень планируемых инвестиций фирмы прямо связан уровнем реального дохода (у). То есть существует прямая зависимость между предложением ЦБ и реальным доходом.


Вывод: увеличение реального дохода (у) сдвигает линию предложения на ЦБ вправо, а уменьшение – влево.


Ставка процента (r). Известно, что уровень планируемых инвестиций изменяется обратно пропорционально ставке процента. При снижении ставки процента (цена ЦБ растет), плановые инвестиции увеличиваются. Дополнительное финансирование требует увеличения объема капитала, что приводит к увеличению займов. Таким образом, реальное предложение ЦБ будет увеличиваться при снижении ставки процента (цена ЦБ растет) и снижаться при увеличении ставки процента. Таким образом, можно сделать вывод о том, что реальное предложение ЦБ прямо пропорционально связано с ценой ЦБ и определяет положительный наклон кривой предложения.


Вывод: положительный наклон линии предложения ЦБ прямо связан с соответствующим изменением ставки процента (r).

Реальные денежные балансы (М/Р). Еще одним фактором, который влияет на реальное предложение ЦБ, являются реальные денежные балансы фирмы (M/P). Фирмы формируют свой спрос на реальные денежные балансы для финансирования собственных транзакций. Фирма, не обладающая достаточными реальными денежными балансами должна сокращать свои контрактные обязательства, либо обратиться к заимствованиям, сопряженным с определенными издержками.

Таким образом, формулу реального предложения ЦБ можно выразить следующим образом:

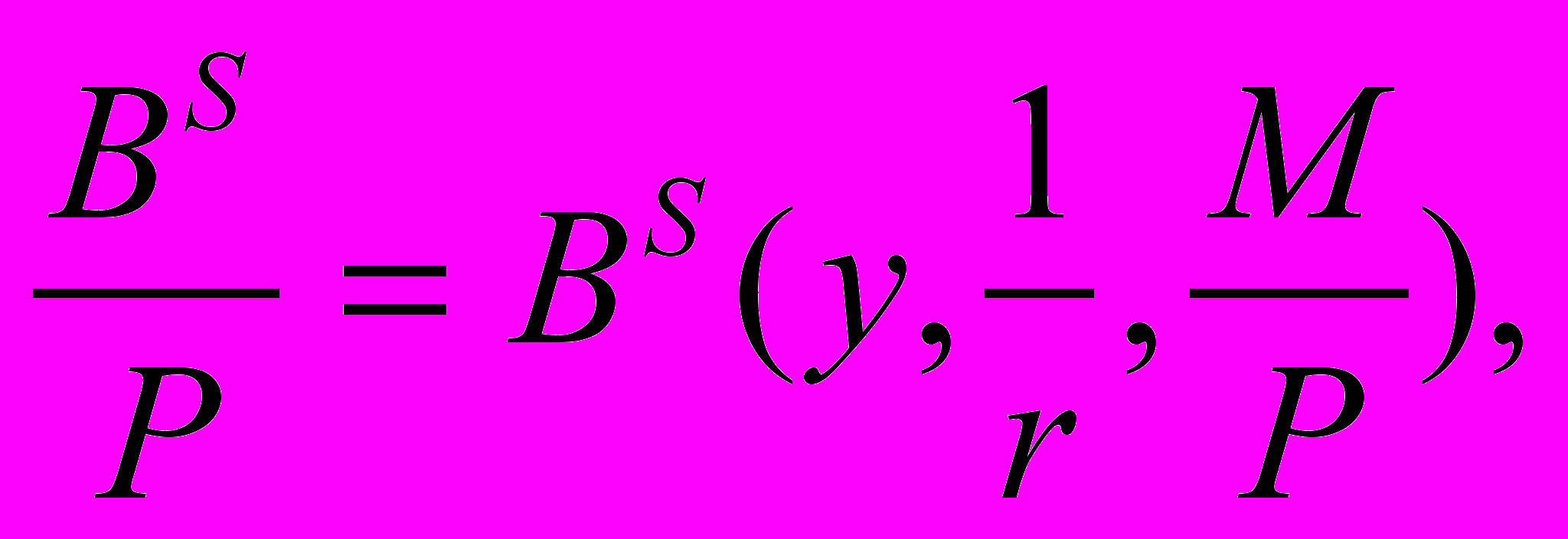(А.2.3)


Преобразуем это уравнение следующим образом:

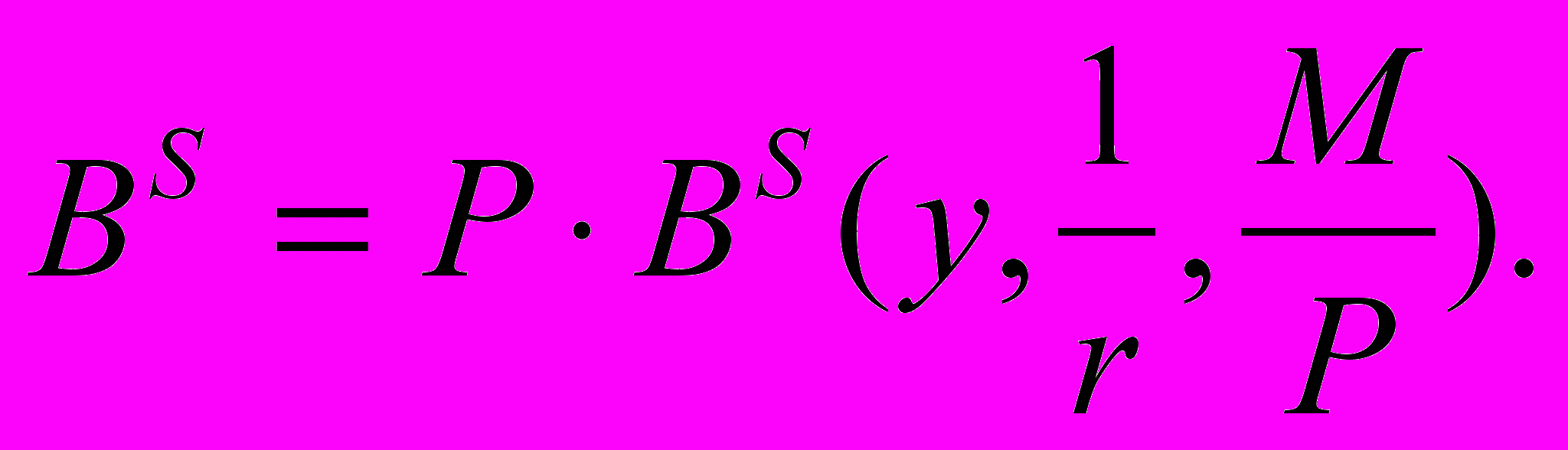(А.2.4)


Это уравнение иллюстрирует предложение количества ЦБ, как функциональную зависимость.

Проанализируем эту формулу при изменении факторов, ее составляющих.




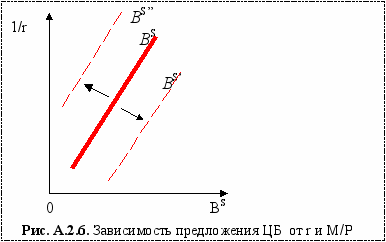
Процентная ставка (r). Каким образом будет изменяться предложение ЦБ при изменении процентной ставки? Падение процентной ставки (увеличение цены ЦБ) вынуждает фирму больше заимствовать, чтобы инвестировать больше в свое оборудование и поэтому увеличивать количество предлагаемых ЦБ. Поэтому линия предложения ЦБ на рис. А.2.6 имеет положительный наклон.


Вывод: изменение процентной ставки (r) определяет положительный наклон линии предложения ЦБ.

Реальный доход (y). Из уравнения А.2.4 следует, что увеличение реального дохода сдвигает кривую B^S вправо в положение B^S’, и в влево (B^S’’), если реальный доход снижается.

Денежные балансы (M/P). При увеличении денежной массы (М↑), реальные денежные балансы (M/P↑) возрастают, и фирмы используют дополнительные реальные балансы, для того, чтобы выкупить свои ЦБ. Поэтому на рис. А.2.6 показано, что при (M/P↑) линия предложения ценных бумаг B^S сдвигается влево в положение B^S’’.

Напротив, если денежная масса уменьшается (М↓), реальные денежные балансы также уменьшаются (М/Р↓), и фирма стремится восстановить свои реальные денежные балансы, выпуская больше ценных бумаг. Поэтому линия предложения ценных бумаг (B^S) на рис. А.2.6 сдвигается вправо в положение B^S’.




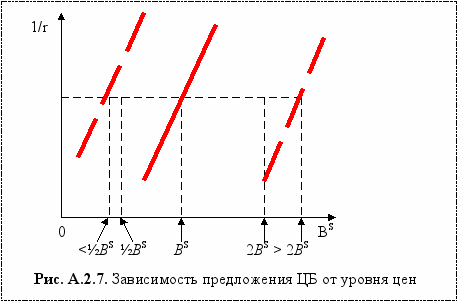
Уровень цен (Р). Воздействие изменения уровня цен на предложение ЦБ носит более сложный характер, так как Р появляется дважды в уравнении (А.2.4). Положение Р вне скобок указывает на прямо пропорциональную зависимость на предложение ЦБ: например, если Р удваивается, то и B^S должно удваиваться. Однако уровень цен имеется внутри скобок в выражении реальных балансов (М/Р). Но снижение реальных балансов при росте цен вынуждает фирмы эмитировать больше ЦБ, чтобы восстановить свои денежные балансы. Поэтому при росте общего уровня цен предложение ценных бумаг увеличивается в возрастающих масштабах. Это изображено на рис. А.2.7.

Точно также, при снижении уровня цен, предложение ценных бумаг уменьшается более быстрыми темпами.


А.2.3. Достижение равновесия на рынке ценных бумаг. Равновесие на рынке ценных бумаг можно записать при помощи уравнения:


B^D = B^S (А.2.5)


Рынок ценных бумаг в целом иллюстрирован на рис. А.2.8. Для данного уровня реального дохода (у), и уровня цен (Р) реальные активы (V/Р) для домашних хозяйств и (М/Р) для фирм, равновесная цена ЦБ равна (1/r)*.





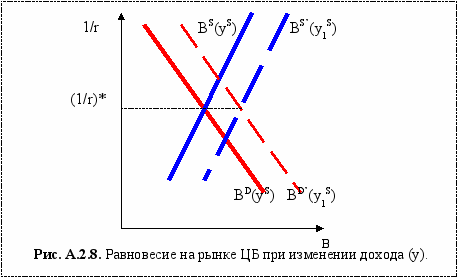
Если реальный доход изменяется, то и линия спроса, и линия предложения ЦБ смещаются в одном направлении, и (при прочих равных условиях) на одну величину, при этом процентная ставка остается неизменной.


Вывод: при изменении реального дохода процентная ставка остается неизменной, а объем продаж ЦБ изменяется прямо пропорционально величине дохода.


Изменение уровня цен (рис. А.2.9). При изменении уровня цен линии спроса и предложения на ЦБ также изменяются в одном направлении, но с разными скоростями.

Так, если уровень цен возрастет в 2 раза, и линия спроса, и линия предложения сдвинутся вправо, но при этом линия предложения сдвинется больше, чем линия спроса, и цена ЦБ снизится (ставка процента возрастет).

Если, напротив, уровень цен упадет в 2 раза, то линии спроса и предложения сдвинутся влево, но при этом линия спроса сдвинется больше, чем линия предложения, цена ЦБ возрастет, а ставка процента упадет.




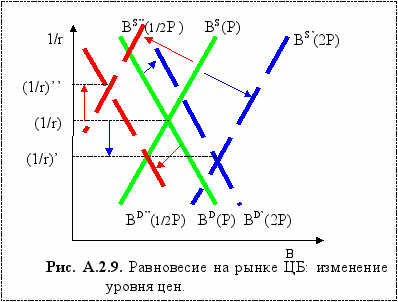
Вывод: рост уровня цен повышает процентную ставку, падение уровня цен снижает процентную ставку.





Изменение финансовых активов (рис. А.2.10). При изменении финансовых активов линии предложения и спроса сдвигаются в противоположных направлениях, поэтому и процентная ставка движется в противоположном направлении относительно движения финансовых активов. Так, если денежные балансы растут, то линия спроса сдвигается вправо, а линия предложения влево. Поэтому цена ЦБ растет, а процентная ставка снижается.

Изменение ликвидных предпочтений. Ликвидные предпочтения имеют место в том случае, если существует склонность к изменению держания объемов денег и ЦБ при неизменном реальном доходе, процентной ставке и реальных активах.

Увеличение ликвидных предпочтений. Если экономические субъекты начинают проявлять повышенные предпочтения к деньгам, и меньше – к ЦБ, то кривая спроса на ЦБ сдвигается влево (домашние хозяйства запрашивают меньше ЦБ), а кривая предложения ЦБ сдвигается вправо (фирмы хотят больше держать денег, а потому стремятся продать ЦБ). Результатом будет падение цен ЦБ и рост ставки процента.

Снижение ликвидных предпочтений. Напротив, если ликвидные предпочтения снижаются, то кривая спроса на ЦБ сдвигается вправо (домашние хозяйства хотят держать больше ЦБ), а линия предложения ЦБ сдвигается влево (фирмы не хотят держать деньги, поэтому избегают эмиссии ЦБ). Цена ЦБ будет расти, а ставка процента упадет.


А.2.4. Модель IS-LM-BB. Первоначально следует вспомнить построение моделей IS-LM и их формулы.

А.2.4.1. Линия IS: равновесие на рынке благ. Модель IS строится на основании хорошо известного принципа равенства сбережений и инвестиций (I = S).

Известно, что кейнсианская функция сбережений имеет следующий вид:


S =  C^a + (1 – C_y)y


Простую функцию инвестиций, зависящую лишь от ставки процента, изобразим так:


I = I(i)


Так как S = I, то:


 С^a = (1 – С_y) = I(i)


Когда плановые инвестиции (которые являются функцией ставки процента), превышают плановые сбережения, экономическое поведение фирм и домашних хозяйств является причиной повышения равновесного уровня дохода. Равновесие будет действительно достигнуто лишь тогда, когда планы экономических субъектов – домашних хозяйств (формирующих сбережения) и предпринимателей-инвесторов будут реализованы и вновь сравняются по своей величине. Изобразим это на рис. А.2.11.

Построение модели IS начинается с квадранта (а), на котором расположена функция инвестиций, зависящая от ставки процента. Возьмем на линии этой функции любую точку (а). Ей соответствует уровень процентной ставки (i₀) и объем инвестиций (I₀). Вспомним, что наша модель отражает равновесное состояние экономики, а поэтому I=S. Проецируем значения точки (а) вертикально вверх до пересечения с биссектрисой (S=I) в квадранте (b). Координаты точки (а) равны: абсцисса  I₀, ордината  S₀.

Теперь из точки (а) проводим горизонтальную линию в квадрант (с) до пересечения с функциональной линией сбережений (S), и получаем точку (а), с координатами: доход  у₀ и сбережения  S₀ .

Осталась последняя операция: из точки (а) проводим вниз вертикальную линию в квадрант (d). Мы получили точку (А) с координатами (у₀) и (i₀), которая характеризует равновесие на рынке благ.

Подобным образом получим точку (В), которая характеризует равновесие на рынке благ, но уже со значениями дохода и ставки процента соответственно: (у₁) и (i₁).





S S S=I

(c) (b)


S

S₁ b S₁ b


S₀ a S₀ а


y₀ y₁ y I₀ I₁ I








i i


A i₀ а





 B

(d) i₁ b (a)

IS

I(i)





y₀ y₁ y I₀ I₁ I

Рис. А.2.11. Построение линии IS


Таким образом, мы можем получить бесконечное множество точек с равновесными значениями дохода и процентной ставки. Однако для нашего исследования достаточно и двух: (А) и (В). Соединив их, получим простейшую линию модели IS.


Линия IS отражает всевозможные комбинации процентной ставки (i) и дохода (у), при которых сбережения (S) равны инвестициям (I), а то есть комбинации, которые соответствуют равновесным значениям на рынке благ.

А.2.2.4.2. Линия LM: равновесие на рынке денег. Линия IS не способна продемонстрировать полной картины равновесной экономики. В самом деле, мы позволили изменяться процентной ставке (i), определяя тем самым объем инвестиций (I) и равновесный уровень дохода (y). С другой стороны, из курса «Макроэкономика» известно, что ставка процента (i) зависит от уровня дохода (y). К тому же процентная ставка определяет транзакционный спрос на деньги.

В свою очередь, транзакционный спрос на деньги зависит от величины дохода. Совокупность транзакционного и спекулятивного спроса на деньги, а также предложение денег определяют равновесную ставку процента. Ставка же процента оказывает влияние на сбережения и инвестиции, и соответственно, уровень дохода. Таким образом, мы можем представить нашу простую экономическую модель как взаимосвязанную систему совместного равновесия, в которой взаимодействие, как рынка благ, так и рынка денег создает единый уровень ставки процента и дохода. Для того чтобы уяснить денежную сторону этого взаимодействия, кратко повторим принципы функционирования рынка денег.

Спрос на деньги состоит из двух компонентов. Прежде всего, деньги держат по причине их транзакционных свойств. Транзакционный спрос на деньги может быть выражен как функция реального дохода:


L_T = L_T (y)


Уравнение это можно переписать и так:


L_T = k (y)


В данном уравнении величина (k – кембриджский коэффициент), определяет пропорцию, в которой изменение спроса на деньги зависит от изменения дохода (L_T/y); при этом подразумевается, что данная величина больше нуля. Величина (k) в краткосрочном периоде предполагается постоянной. При этом она определяется такими институциональными факторами, как сложившиеся привычки платежа публики и наличие финансовых посредников. Все это, естественно, с течением времени подвержено изменениям, но, в краткосрочном временном периоде величину (k) можно считать постоянной. Вспомним, что спрос на деньги по мотиву предосторожности (L_P) мы включили в состав транзакционного спроса.

Вторым, и исключительно кейнсианским компонентом спроса на деньги, является спрос по спекулятивному мотиву. Он может быть выражен следующим образом:


L_S = L_S(i)


При этом предполагается, что (L_S/i) < 0.




i i LM


(c)


B

i₀ i₀


i₀ i₀ A


L_S




L_S1 L_S0 L_S y₀ y₁ y


L_T L_T




L_T=M₀


(b) (a)


L_T




L_T1 L_T1


L_T0 L_T0







k

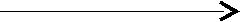L_S

L_S1 L_S0 L_S=M₀ y₀ y₁ y

Рис. А.2.12. Построение линии LM


Поэтому в сумме:


L = L_T + L_S

Или, что то же самое:

L = L(y, i)


Для анализа равновесия на рынке денег, мы, естественно, должны рассмотреть еще один элемент: предложение денег.

Предложение денежной массы выразим так:


M = L_T + L_S,


что означает, что данное предложение денег удовлетворяет транзакционные и спекулятивные мотивы спроса на деньги.

С помощью следующего графика (рис. А.2.12) мы можем проанализировать взаимодействие между совокупным спросом на деньги (L) и совокупным предложением денег (М), и на основе этого  получить кривую LM. Так как в нашем предположении цены постоянны и равны единице, то постоянная величина (М) соответствует реальному предложению денег. Уровень дохода (y₀) и данная величина (k), создадут некую величину трансакций и тем самым  определенный спрос на деньги (L_T0), как это отражено в квадранте (а) нашего рисунка А.2.12.

Предложение денег обозначено (М₀) в квадранте (b). Если все деньги предназначены для транзакционных целей (М₀ = L_T), то предложение денег (М₀) расположено на оси ординат в квадранте (b). Напротив, если все деньги предназначены для спекулятивных целей (М₀ = L_S), то предложение денег (М₀) расположено на оси абсцисс.

Линия, соединяющая указанные точки на оси абсцисс и оси ординат представляет собой все возможные сочетания между L_T и L_S, при этом наклон данной линии равен минус единице. Само собой разумеется, что увеличение денежной массы сдвигает данную линию вправо, а уменьшение – влево. При объеме транзакционного спроса (L_T0) должно также остаться определенное количество денег для спекулятивных целей. Но спекулятивное предложение денег определяется функцией спекулятивного спроса на деньги (L_S) в квадранте (с) и равно (L_S0) при ставке процента (i₀). На панели (а) данной ставке процента будет соответствовать уровень дохода (у₀). Тем самым мы получили точку (А) линии LM в квадранте (d).

Более высокий уровень дохода (к примеру,  у₁) даст нам точку (В) на линии LM. Уровень дохода (у₁) увеличит транзакционный спрос на деньги (L_T1), который (при данном предложении денег  М₀) будет способен удовлетворить спекулятивный спрос (L_S1).

На рис. А.2.12 видно, что это уменьшенное спекулятивное предложение отражает функциональную зависимость (L_S) при более высокой ставке процента (i₁). Новому, более высокому уровню дохода будут соответствовать более высокая ставка процента. Если мы теперь проследим все подобные комбинации ставки процента (i) и дохода (у), то получим общий вид модели LM.

Таким образом, мы подошли к определению кривой LM.


Линия LM отражает всевозможные комбинации ставки процента (i) и дохода (y), при которых общий спрос на деньги (L) равен общему предложению денег (М). Таким образом, эти комбинации соответствуют равновесию на рынке денег.


Следует отметить, что кривая (LM) также как и кривая (IS), не является функциональной зависимостью дохода от ставки процента. Линия LM показывает всевозможные комбинации дохода (у) и ставки процента (i), при которых рынок денег находится в равновесии.





Теперь возможно подумать о статусе рынка ценных бумаг. На пересечении в точке А на рис. А.2.13 в соответствии с законом Вальраса должно быть равновесие.

Но этот закон ничего не говорит об условиях на рынке при других комбинациях ставки процента и дохода. Потому что в любой из этих точек рынок денег и рынок благ не могут одновременно находиться в равновесии. Чтобы определить равновесие на рынке ценных бумаг, в других точках, кроме точки А, необходимо исходить из того, что совокупное предложение равно совокупному спросу:


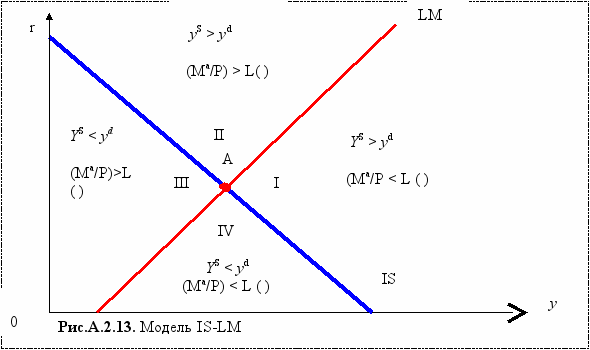
y + 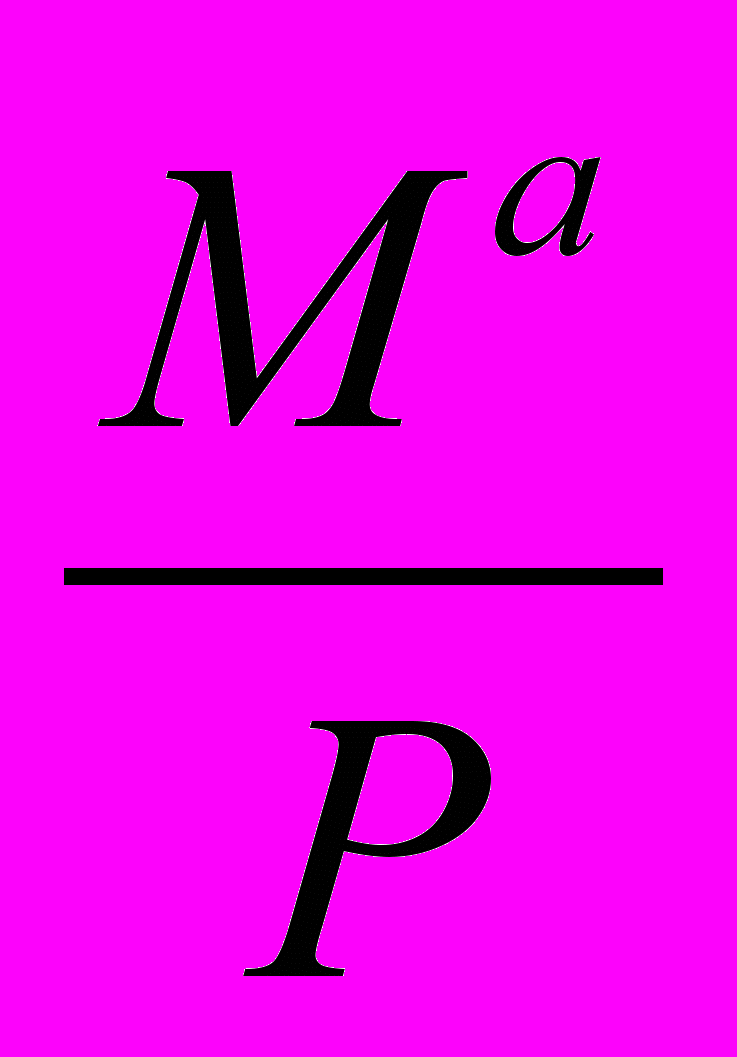+ B^s = D (y, r) + L(y, r) + B^d (А.2.6)


Здесь B^s и В^d отражают соответственно предложение и спрос на реальные ценные бумаги.

Перепишем теперь это уравнение (А.2.6) в следующем виде:


B^d – B^s = [y - D(y, r)] + [ 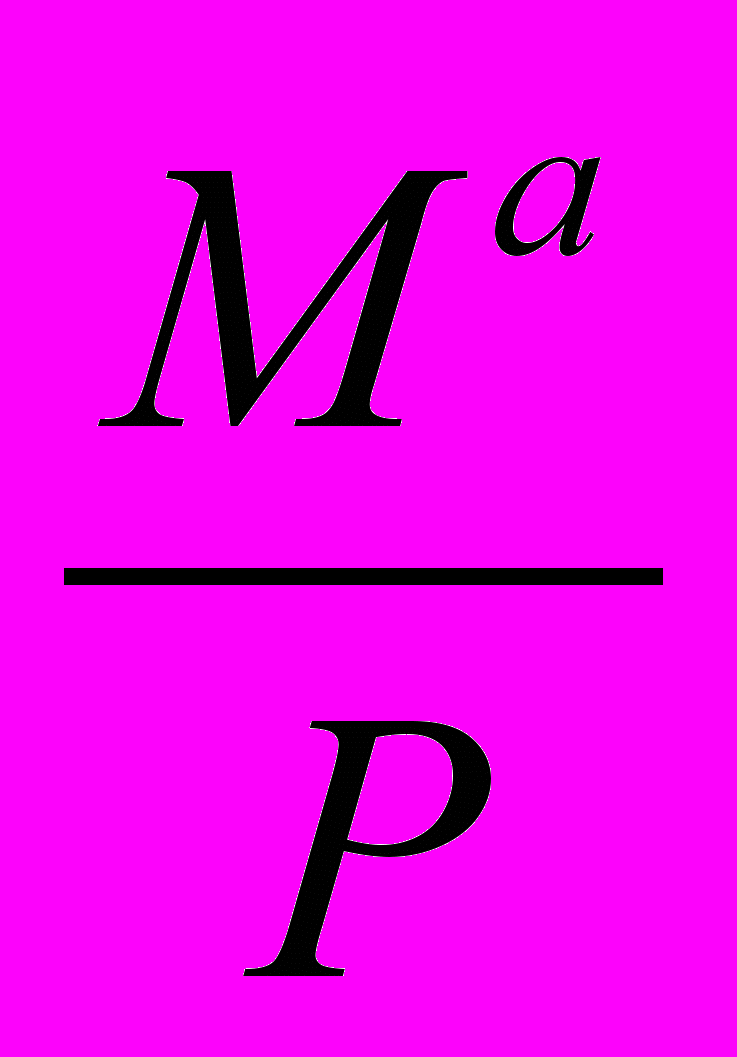- L(y, r)] (А.2.7)

В левой части данного уравнения изображено превышение спроса над предложением на ценные бумаги.

В правой части уравнения в первых квадратных скобках изображено превышение предложения благ над спросом благ; во вторых квадратных скобках изображено превышение предложение денег над их спросом.

При данной комбинации в экономике процента и дохода, необходимо, чтобы спрос и предложение, как ценных бумаг, так и благ и денег были равны. Этому состоянию соответствует точка А на рис. А.2.13.

Для всех других точек пространства для равновесия необходимо, чтобы избыток спроса на ценные бумаги точно равнялся избытку предложения на блага и деньги.

Квадрант II на рис. А.2.13 демонстрирует превышение предложения благ и денег. Соответственно, бюджетное ограничение требует, чтобы в этом же квадранте был избыток спроса на ценные бумаги.

В квадранте IV избыток спроса на товары и деньги подразумевают избыток предложения ценных бумаг.

В квадрантах I и III – противоположная картина. И условия для существования здесь рынка ценных бумаг сомнительны. На самом же деле – это не так. В соответствии с бюджетным ограничением, равновесие рынка ценных бумаг требует, чтобы:

0 = [y – D(y, r)] + [ 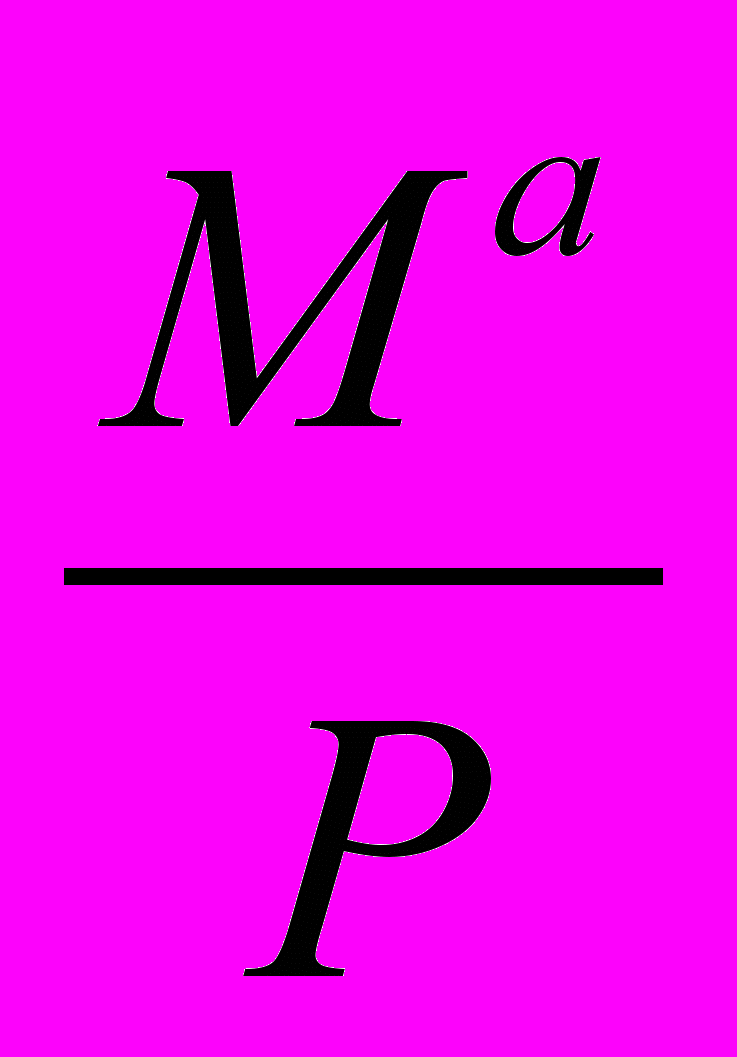- L(y, r) (А.2.8)

Развернем эту формулу, то есть более подробно распишем совокупный спрос на блага и совокупный спрос на деньги и получим:

(C + I + G) - y = 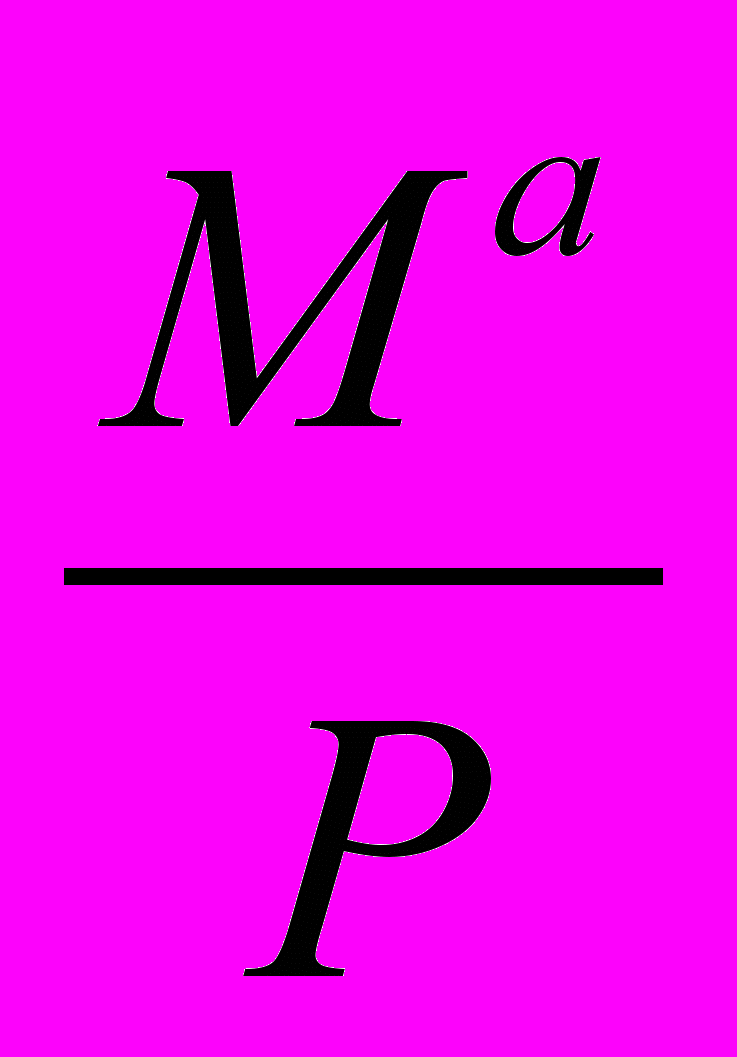- [ky + (L^a – mr)]. (А.2.9)

В этой формуле совокупный спрос на блага расписан на составляющие: потребительский спрос домашних хозяйств ( C), спрос на инвестиции (I) и спрос государственного сектора (G). При этом предполагается, что экономика закрыта, то есть отсутствует чистый экспорт (E_N).

В правой части уравнения совокупный спрос на деньги расписан на составляющие: транзакционный спрос (ky), где k – кембриджский коэффициент и спекулятивный спрос (L^a – m r), где m > 0 – чувствительность спекулятивного спроса по ставке процента.

Теперь распишем более подробно формулу спроса домашних хозяйств и спроса на инвестиции на блага:

C = C^a + C_y y^d (А.2.10)

y^d = y – T (А.2.11)


где Т – чистые налоги (т.е. налоговые поступления минус трансфертные выплаты). Отсюда


T = T^a + T_y y (15.12)


где Т^а – автономная часть налогов (например, подушная подать); 0 < T_y y <1 – ставка подоходного налога: T_y = T_x /Y.

I = I^a – I_r r, (А.2.13)


где I_r > 0 – предельная норма инвестирования по процентной ставке;


Напашем теперь формулу ВВ. Выразим ее через r. Для этого в формулу А.2.4 вставим значения формул (А.2.10), (А.2.11), (А.2.12) и (А.2.13).

Получим:


r = - 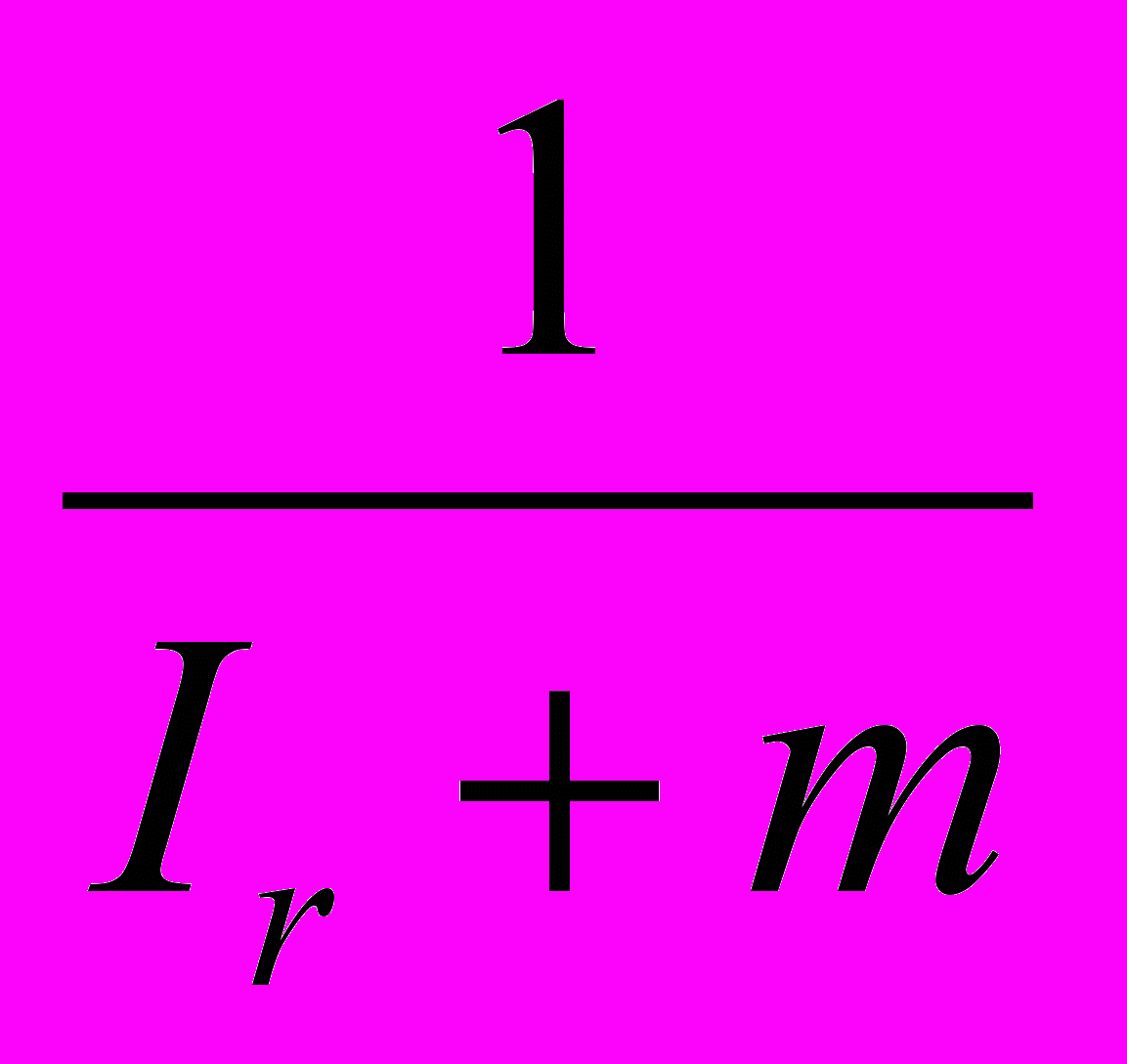( 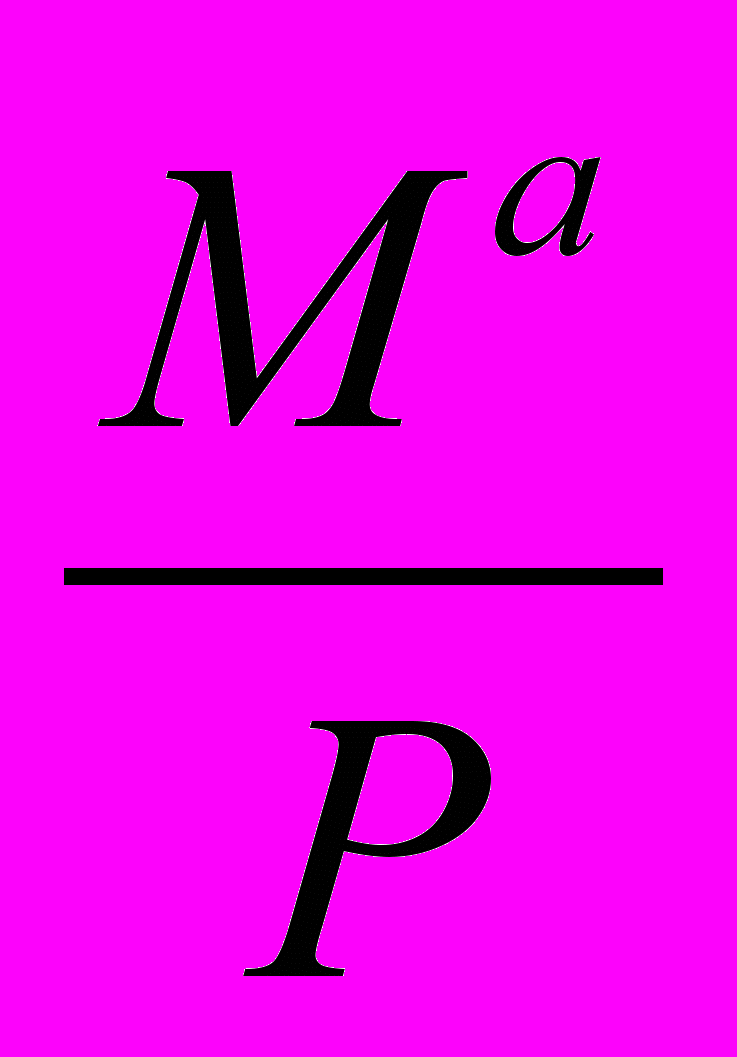- L^a) + 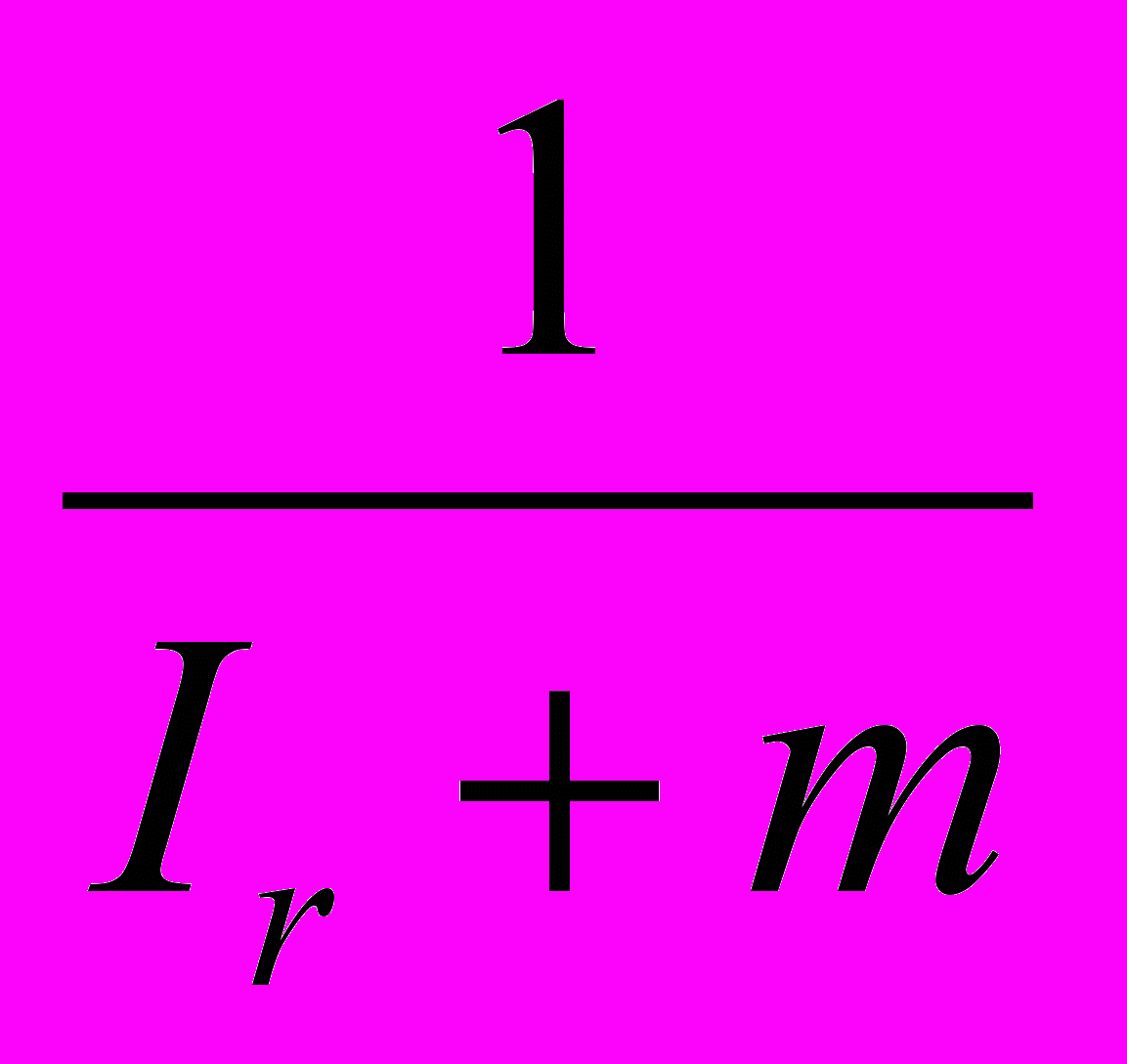(C^a + I^a + G^a – C_yT^a) –


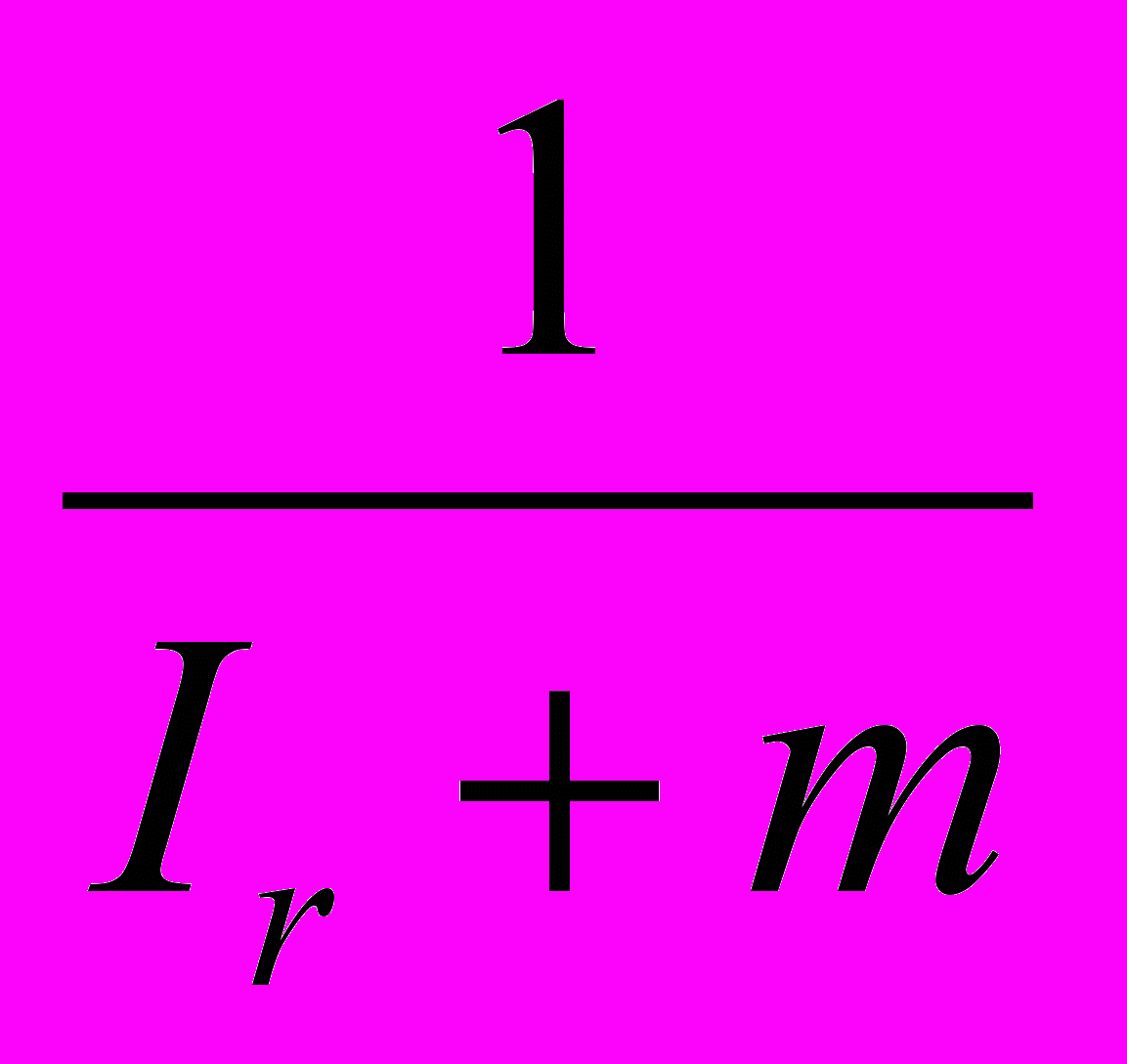- [1 – C_y(1 - T_y) – k] y (А.2.14)

Итак, формула (А.2.14) выражает линию ВВ через процентную ставку (r). Конечно, можно эту линию выразить и через доход (у).

В точной аналогии с выражениями IS и LM, данное выражение указывает все комбинации процентной ставки и дохода, которые необходимы для поддержания равновесия на рынке ценных бумаг.

Изобразим линию (BB) графически. Она должна проходить через квадранты I и III. Рассмотрим, почему это так.

Рассмотрим любую пару процентной ставки и дохода, которая уравновешивала бы рынок благ. Из формулы (А.2.14) следует, что рынки благ и денег должны быть уравновешены. Если эти два рынка не сбалансированы, тогда превышение спроса на одном из них должно точно перекрываться превышением предложения на другом.

Теперь позволим процентной ставке (r) расти, оставив доход (у) без изменения. При этом спрос на блага D ( ) и на деньги L ( ) падает и приводит рынки благ и денег в состояние на них избыточного предложения. Ценные бумаги, поэтому, должны показать избыточный спрос над линией ВВ. Напротив, избыточное предложение ценных бумаг будет ниже линии ВВ.

Если бы линия ВВ проходила через квадрант II, то она разбила бы этот квадрант на две части, при чем одна из них имела бы превышение предложения на всех трех рынках. Но такого быть не может. Значит, линия ВВ не может проходить через квадрант II.

Аналогично, если бы линия ВВ проходила бы через квадрант IV, то она разбила бы этот квадрант на две части, причем на одной из них было бы превышение спроса на всех трех рынках. Но такого также быть не может.

Математическое доказательство того, что линия ВВ проходит исключительно через квадранты I и III сводится к двум действиям.

Первое действие заключается в том, что в точке А рисунка 1 при процентной ставке (r) и (у) существует равновесие (формула А.2.14) и 0 = 0.

Второе действие показывает, что наклон линии ВВ лежит между IS и LM, а именно:


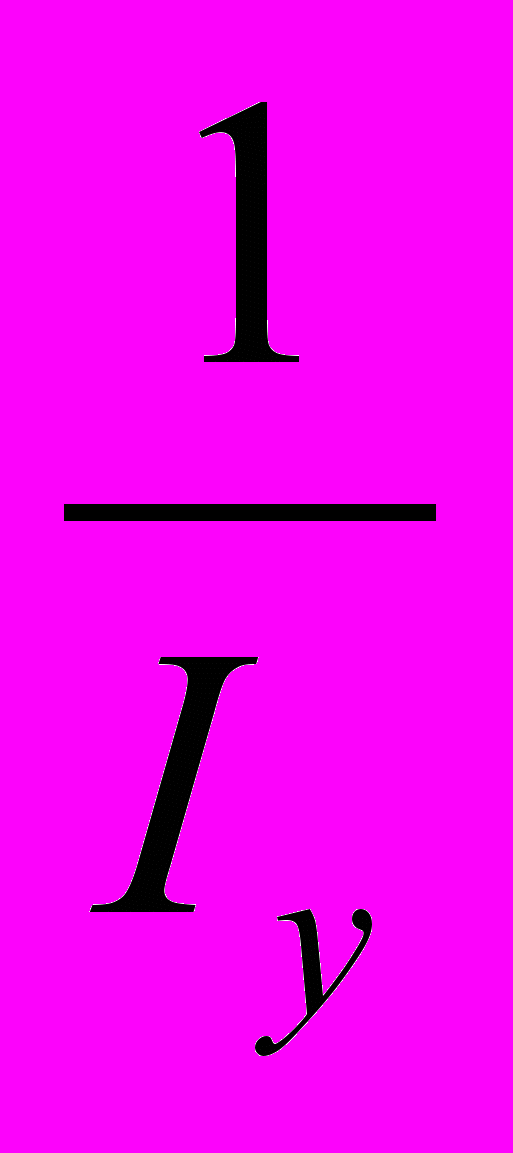[ C_y (1 – T_y) – 1] < 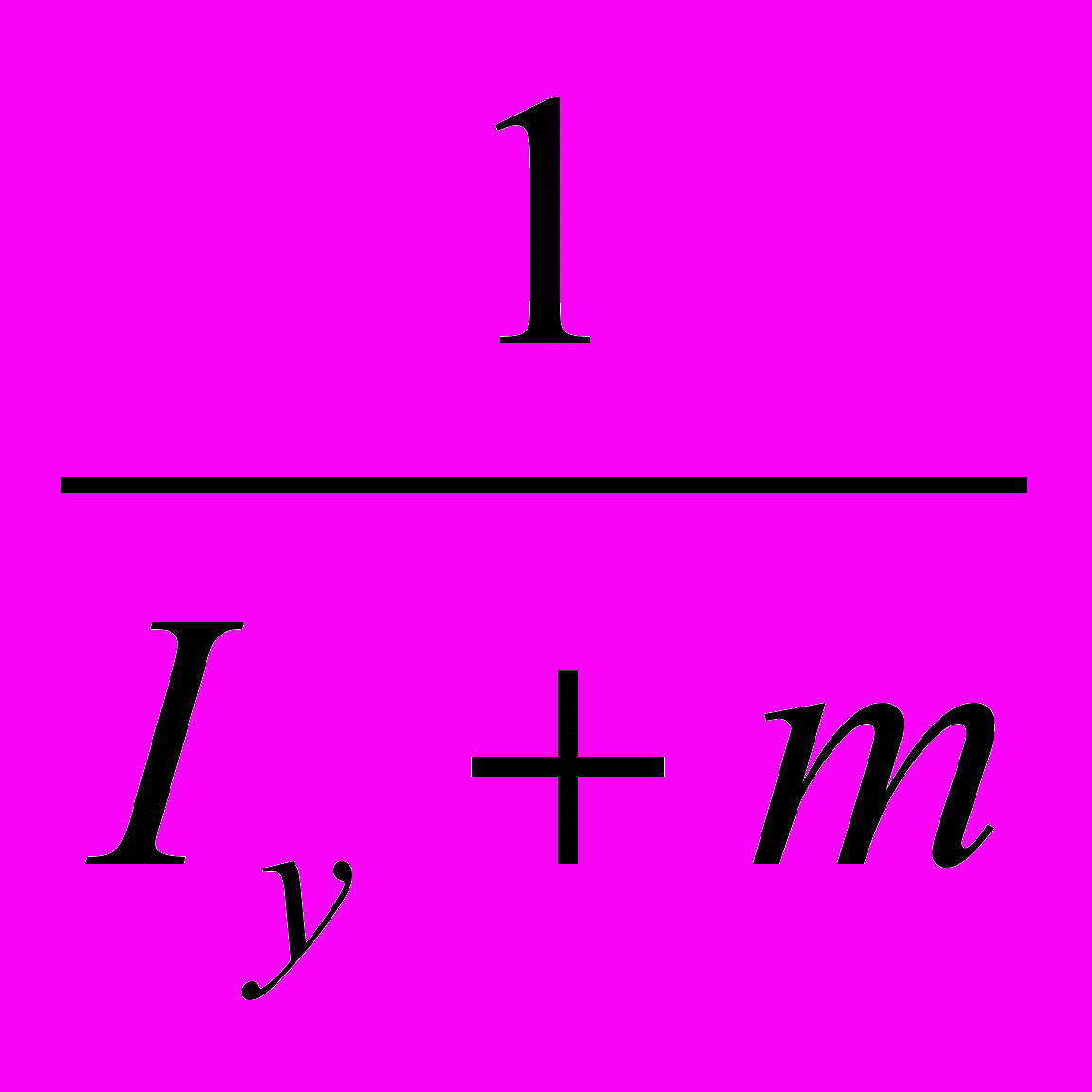[C_y(1 – T_y) – 1 + k] < 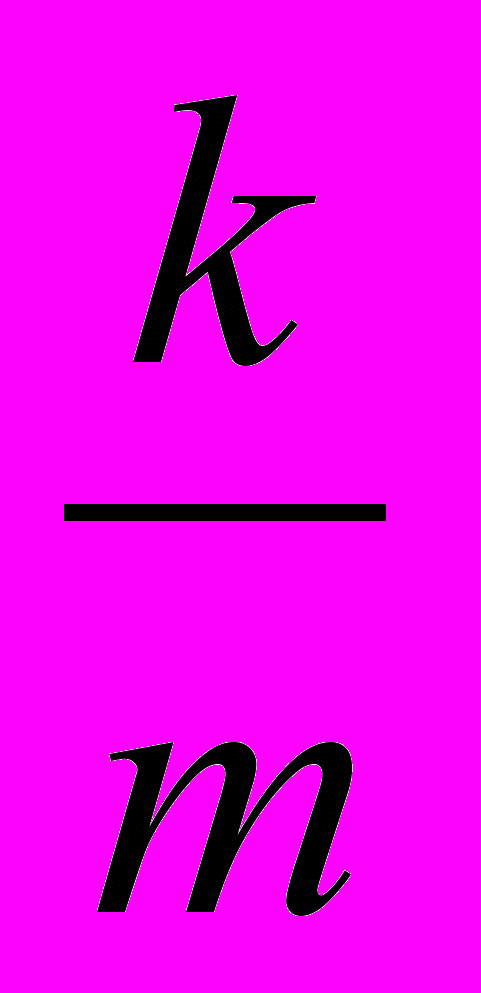(А.2.15)

В этом неравенстве левое выражение показывает наклон линии IS, так как формула линии IS представляет собой вид:


r = 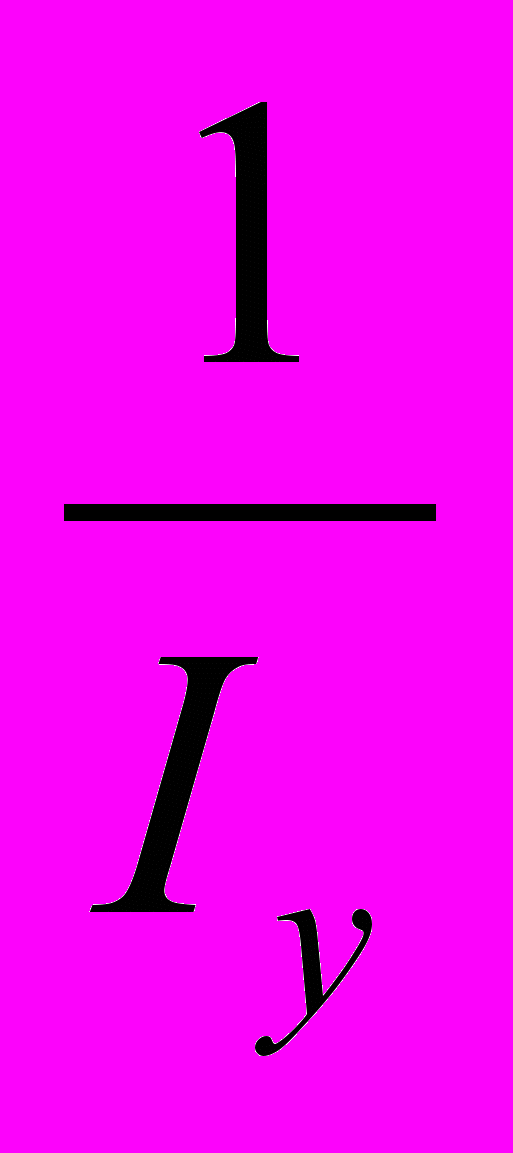(C^a + I^a + G^a – C_yT^a) + 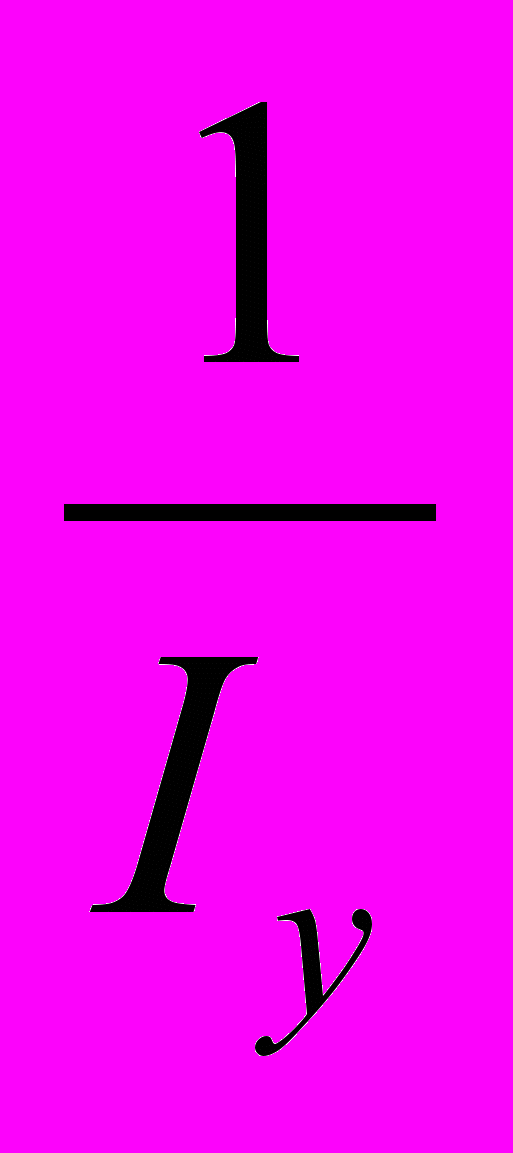[C_y(1 – T_y) – 1] y (А.2.16)

Центральное выражение показывает наклон линии ВВ (см.: уравнение А.2.14), а правое выражение показывает наклон LM, так как формула линии LM представляет собой вид:


r = - 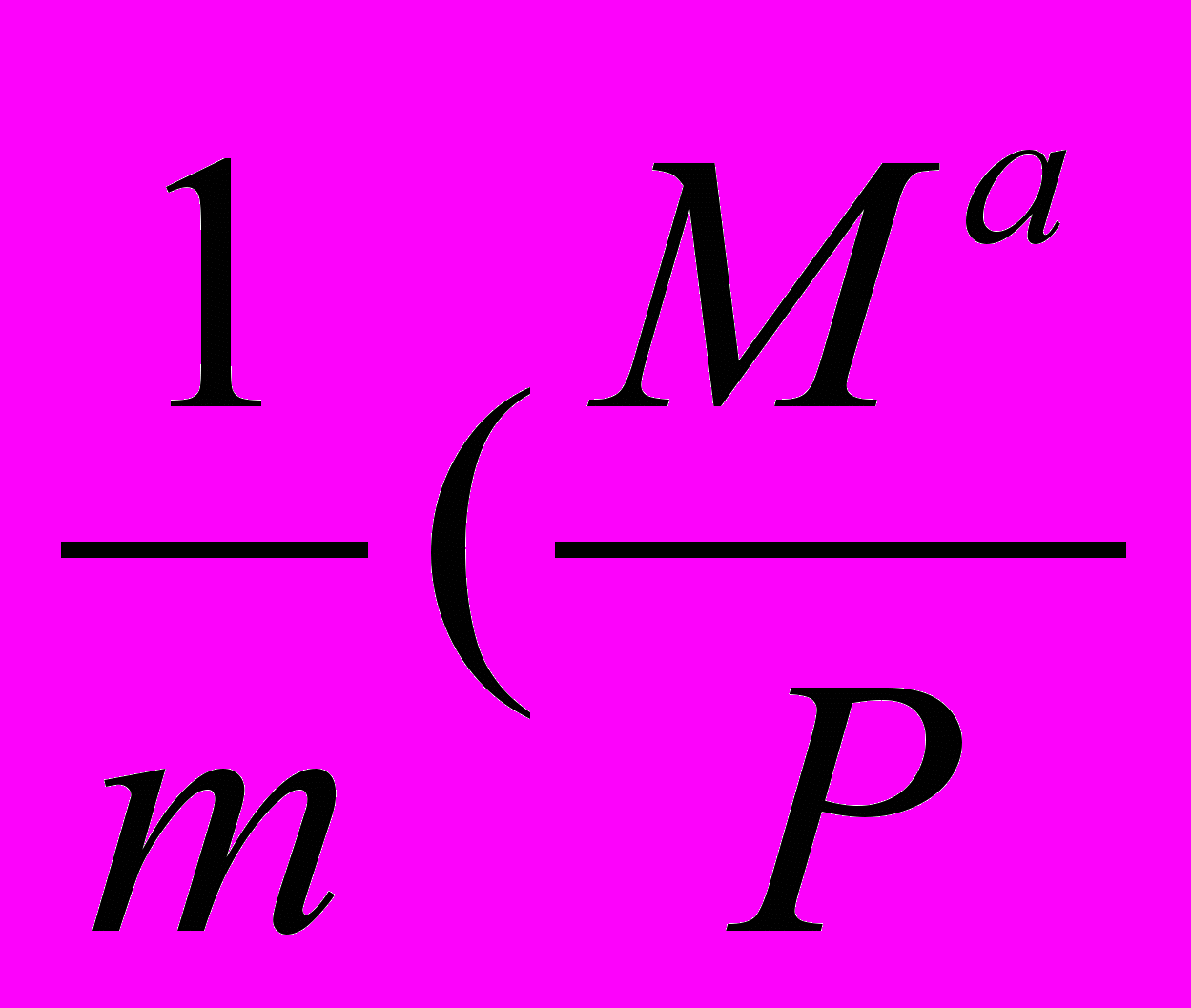- L^a) + 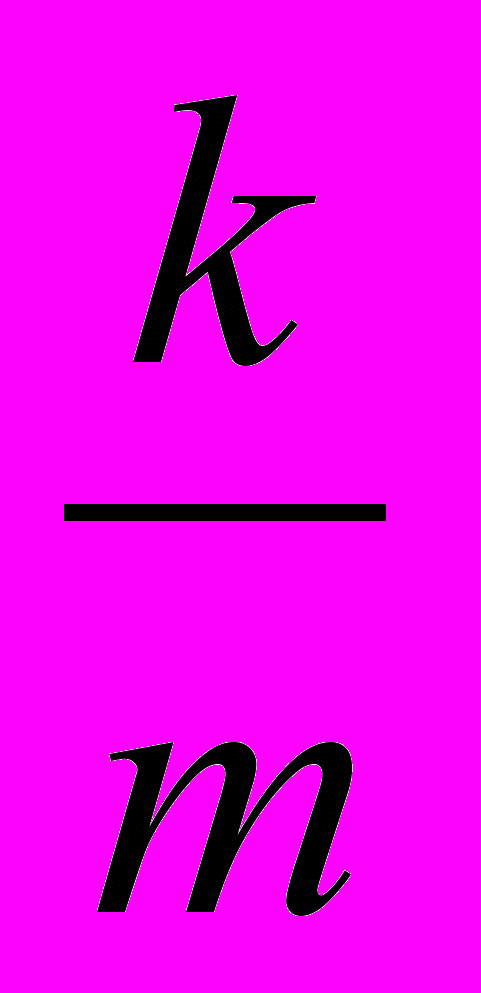y (А.2.17)

Перепишем выражение наклона линии ВВ, которое выглядит так: [C_y(1 – T_y) – 1 + k]/(I_y + m) следующим образом:


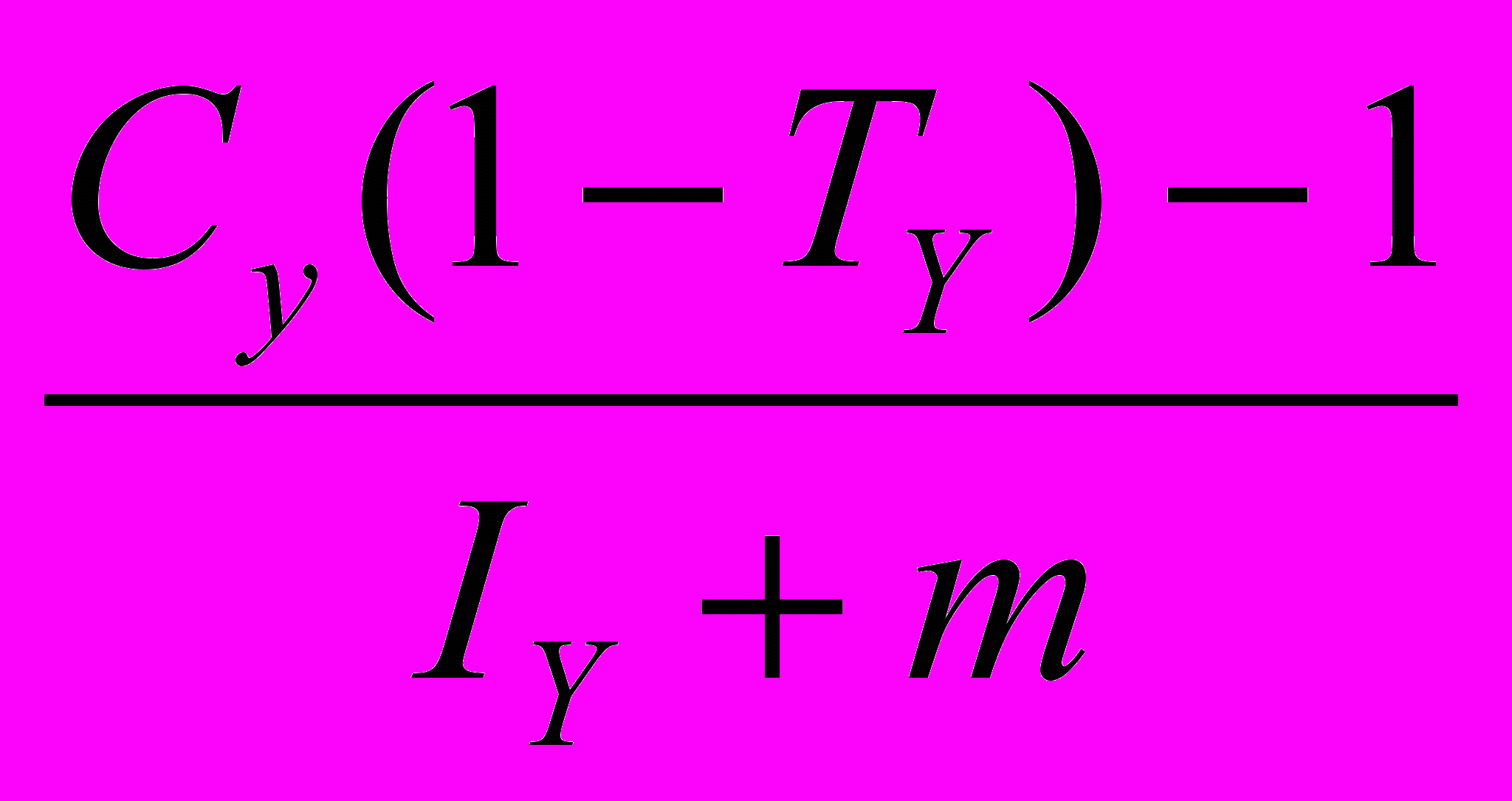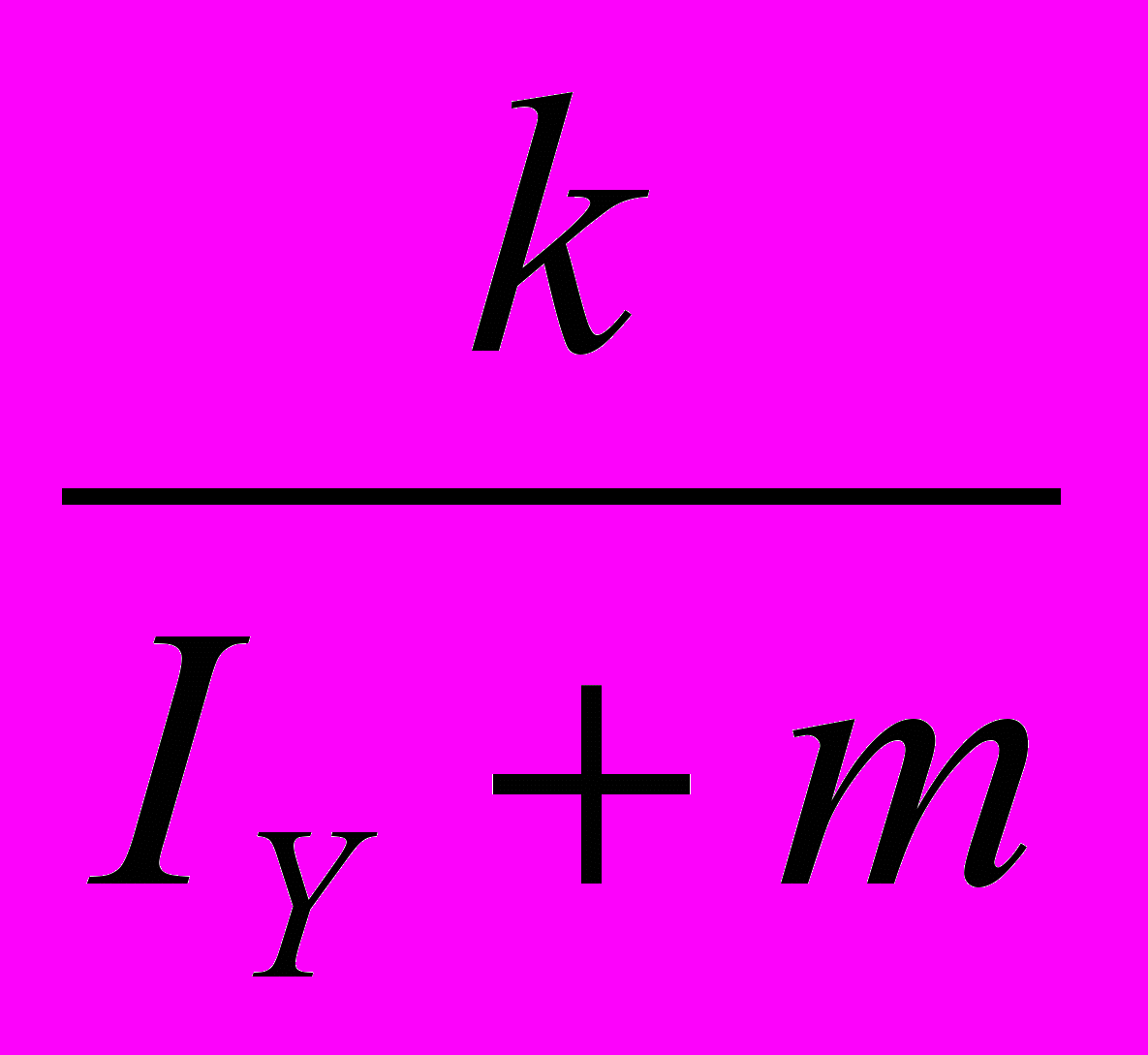+ (А.2.18)

Первое (или левое) выражение данной формулы наклона линии ВВ имеет меньший отрицательный наклон, чем у линии IS. А наклон линии IS, как мы знаем, равен (см. формулу А.2.15): [C_y (1 - T_y ) – 1]/I_y. Поэтому левое неравенство формулы (А.2.15) справедливо.

Более того, правая часть из формулы (А.2.18) меньше, чем k/m, в то время, как первая часть формулы (А.2.18). Поэтому правое неравенство формулы (А.2.15) справедливо.

Почему относительная величина выражения 1 – С_y(1 – T_y) и k определяют знак наклона линии ВВ? Предположим, что первоначально все рынки находятся в равновесии и доход увеличился на единицу, а ставка процента осталась прежней. Тогда выражение 1 – С_y( 1 – T_y) представляет собой чистое увеличение предложения благ; это означает превышение предложения благ. k представляет избыточный спроса на деньги.

Когда 1 - C_y(1 – T_y) = k, избыток предложения благ точно совпадает с избыточным спросом на деньги, и поэтому новый более высокий уровень дохода не влияет на рынок благ при данной ставке процента. Но когда 1 – C_y(1 – T_y) > k, превышение предложения благ превышает превышение спроса на деньги при данной ставке процента: блага и деньги в комбинации демонстрирует превышение предложения. Тогда, чтобы рынок ценных бумаг оставался в равновесии, ставка процента должна упасть, чтобы увеличить спрос на блага (снизить, тем самым, избыточное предложение) и увеличить спрос на деньги (увеличить превышение денежного спроса). В этом случае ВВ демонстрирует отрицательный наклон. Этот же аргумент справедлив для 1 – C_y(1 – T_y) < k, если бы линия ВВ имела положительный наклон.





Осталось определить каким все-таки является наклон линии ВВ: положительным, отрицательным или горизонтальным. Чтобы сделать это, предположим вновь, что доход увеличился при неизменной ставке процента. Экономика увеличилась на один процент, значит, на одну единицу увеличится совокупный спрос. При этом спрос на блага увеличится на C_y(1 – T_y) единиц [так как, C = C^a - C_yT^a + C_y (1 – T_y)y]. Для того чтобы получить эту формулу в квадратных скобках, подставим выражение А.2.11 и А.2.12 в А.2.10.

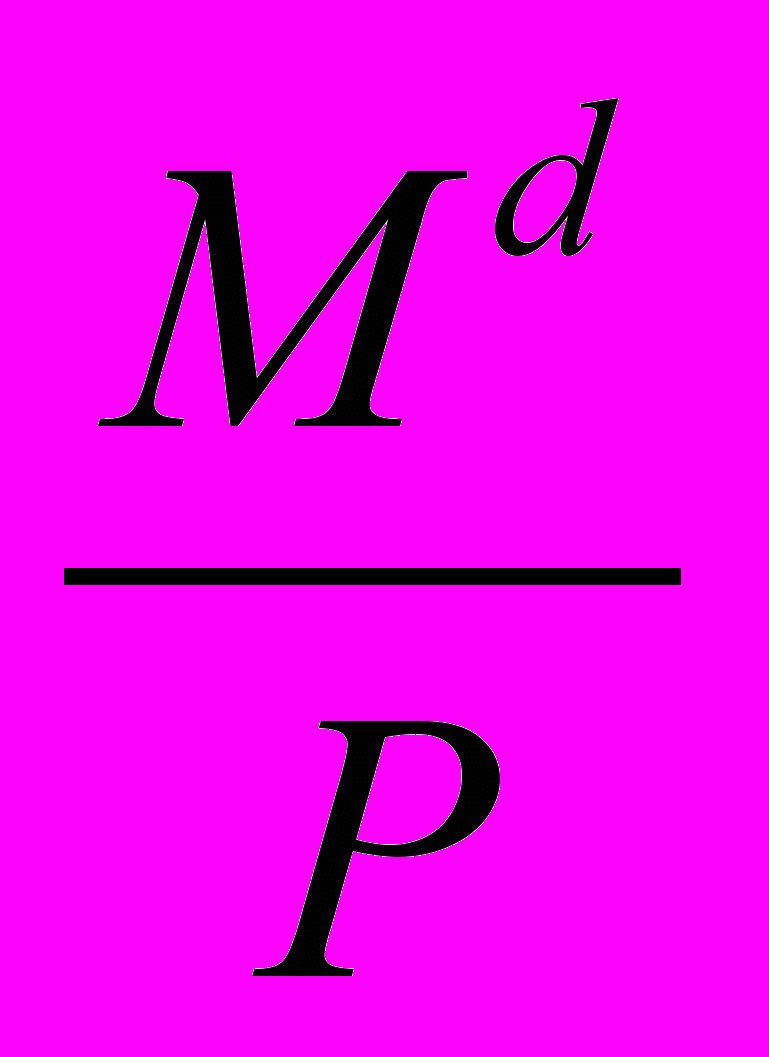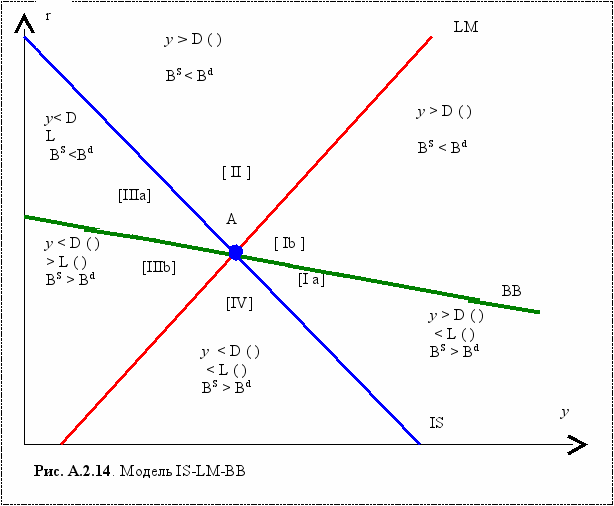
Спрос на реальные деньги увеличится на k единиц [так как спрос на деньги равен = ky + (L^a – mr)].

Соответственно, спрос на реальные ценные бумаги должен измениться на 1 – С_y( 1- T_y) – k единиц, потому что только тогда совокупный спрос увеличиться ровно на одну единицу. Подобно благам и реальным деньгам, реальные ценные бумаги являются нормальным благом. Спрос на них возрастает прямо пропорционально с доходом, и поэтому выражение 1 – С_y(1 – T_y) – k является положительным. Отсюда следует, что линия ВВ имеет отрицательный наклон. Полная модель IS-LM-BB изображена на рис. А.2.14.


А.2.4.3. Графическое построение модели ВВ. Вернемся к началу главы. Тогда мы полагали, что спрос и предложение на ценные бумаги зависит от уровня цен (Р), Процентной ставки (r) и дохода (у). Модель IS-LM строилась из предположения, что Р величина постоянная. При построения графической модели ВВ будем исходить из того же предположения (А.2.15).





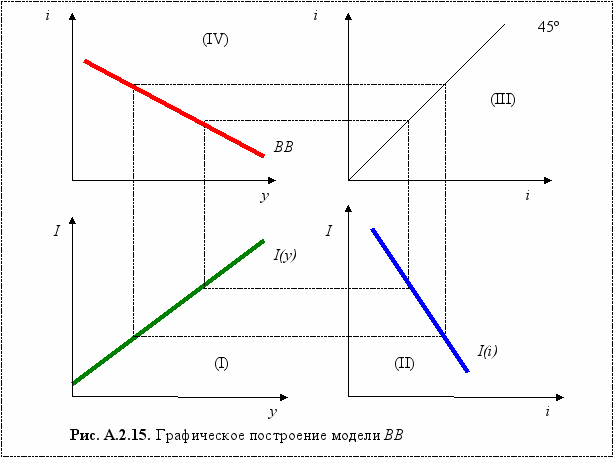
В квадрате (I) изображена функция инвестиций по доходу¹:


I = I^a + I_y y


В квадранте (II) – функция инвестиций по процентной ставке ²:


I = e + I_i i.


Квадрант (III) – чисто технический (i = i).

В квадранте (IV) строится линия ВВ.





 Литература

1. Селищев А.С. Микроэкономика. 2-е изд. СПб. 2003.
   
2. Селищев А.С. Макроэкономика. 3-е изд. СПб. 2005.