Применение формализма гибридных систем Вмоделях управления переключаемыми производственными процессами (с приложениями к заДачам горной промышленности)

Вид материала

Задача

Содержание S). Согласно соотношениям (23), при заданном начальном качественном состоянии d Пусть в задаче (39) функции F Таблица 1. Состав добычных блоков с позиций формирования товарного продукта Таблица 2. Характеристики задач управления в зависимости от технологии

Подобный материал:

• Внастоящее время, работы, которые ведутся в области автоматизации производственных, 107.41kb.
• Программа вступительного экзамена по специальности 05. 13. 06 " автоматизация и управление, 128.46kb.
• В наш компьютерный век человечество все в большей степени старается облегчить свою, 6.49kb.
• Курсовая работа по химии на тему: «управление химическими процессами», 382.99kb.
• Задачи профессиональной деятельности выпускников б производственно-технологическая, 83.52kb.
• Как наладить производство гибридных систем альтернативной энергетики, 210.52kb.
• Учебно-тематический план программы повышения квалификации «Методология сетевого планирования, 258.58kb.
• Катаргин Дисциплина "Сетевое моделирование и задачи управления запасами", 9.32kb.
• Учебный план №606. 1 «Эксплуатация автоматических систем диспетчерского контроля, 26.49kb.
• Составлена Международной Высшей Школой Управления для подготовки менеджеров высшей, 215.12kb.

сценарием процесса S). Согласно соотношениям (23), при заданном начальном качественном состоянии d(1) сценарий определяет дискретную траекторию d=(d(1),…, d(N+1)). При фиксированном сценарии совокупность соотношений (17), (20), (21), (23), (25) (27) определяет модель M₀ дискретного процесса со смешанными ограничениями, имеющую то отличие от традиционных моделей дискретных процессов, что неравенства (20) являются строгими; в этой модели в качестве управления для этапа и процесса удобно принять соответственно v (k)= (u(k), t(k)), v=(v(1),…, v(N)). Но это отличие неудобно для применения итерационных методов оптимизации, поскольку множество V₀(S) всевозможных управлений, удовлетворяющих вместе с порождаемыми ими траекториями условиям модели, незамкнуто. Поэтому вместо модели M₀, как правило, удобнее использовать модель M₁, отличающуюся от M₀ заменой (21) на

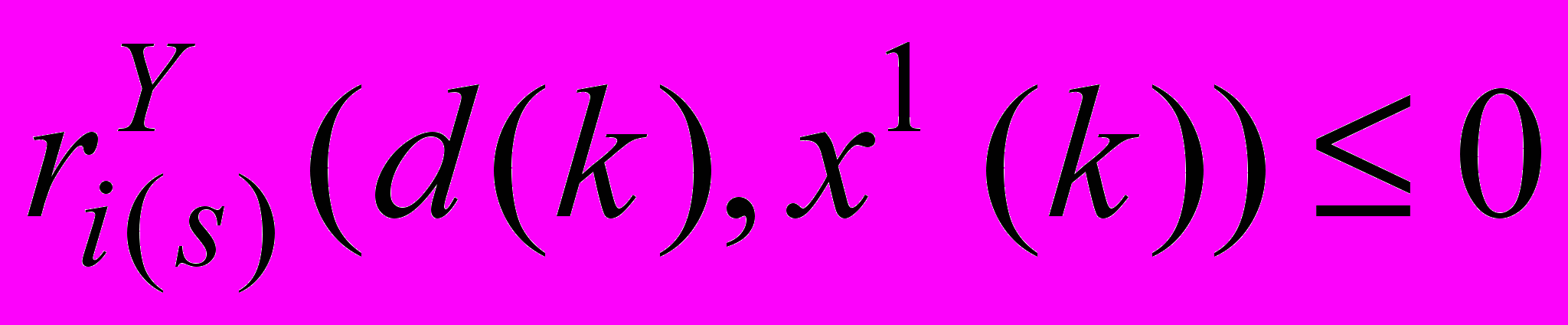, sS(k). (33)

Для совокупности соответствующих модели M₁ управлений используется обозначение V₁(S). Условие (33) слабее, чем (21), поэтому всегда V₁(S)V₀(S). Связь между моделями M₀ и M₁ определяется следующей теоремой:

Теорема 2.3. Если сценарий S некоторого N-этапного процесса таков, что для k-го этапа dim(S(k))>1, то для любого разбиения S(k) на непересекающиеся множества S₁(k),…, S_m(k) для произвольного управления vV₁(S) можно определить (N+m–1) этапный измененный процесс со сценарием S_A и управлением 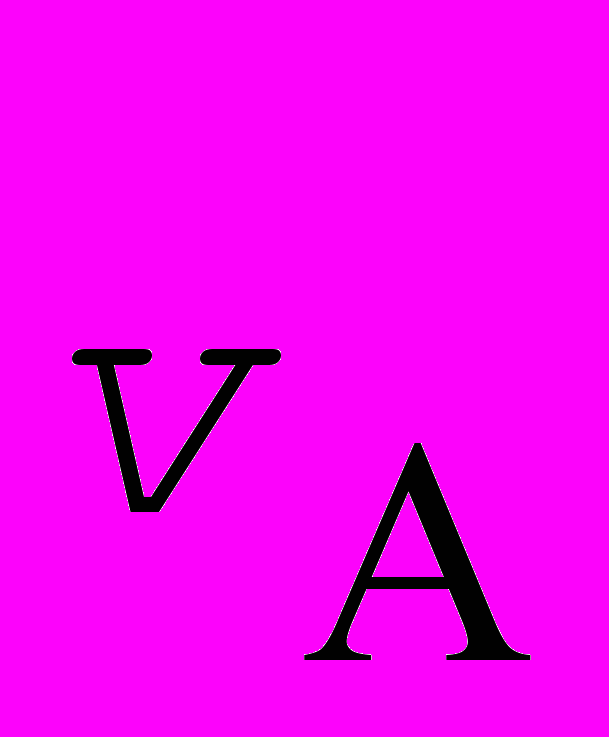, в котором после k-го этапа идут "вставные" этапы нулевой длительности, для которых

d_A(k)=d(k); S_A(k)=S₁(k); S_A(k+j)=S_j+1(k),  d_A(k+j)=D(S_j(k), d_A(k+j–1)),

u_A(k+j)U₀(d_A(k+j)), 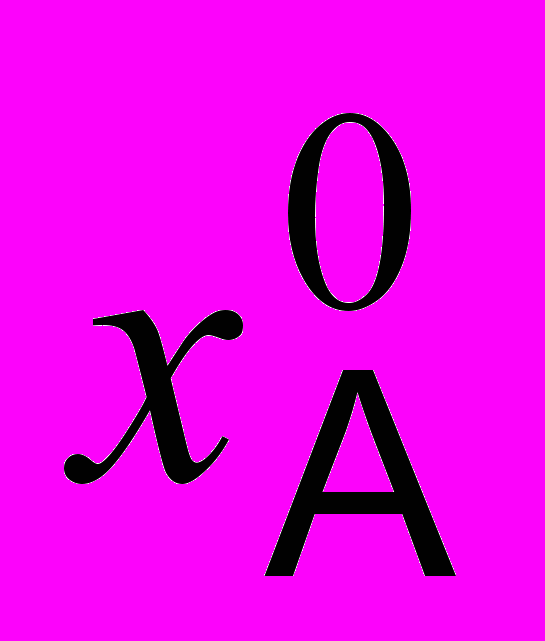(k+j)=X(S_j(k), d_A(k+j–1),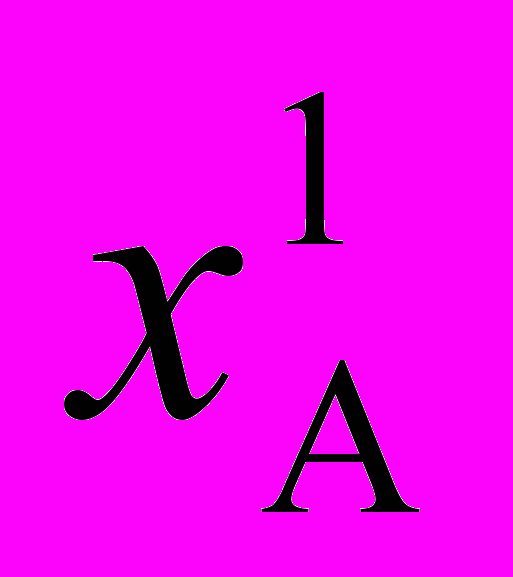(k+j-1)), (34)

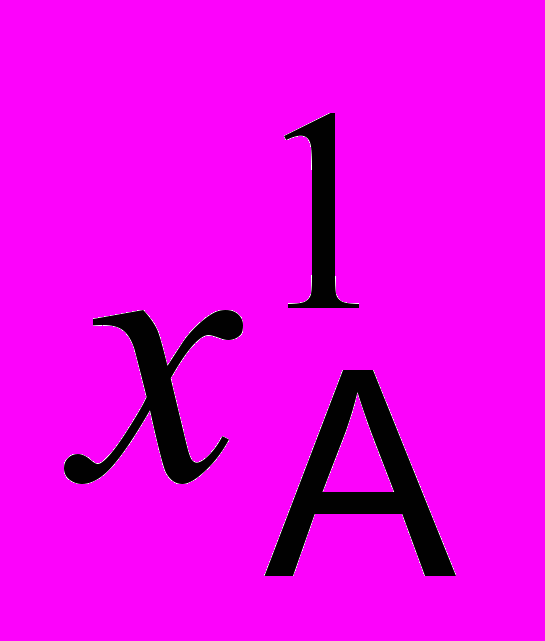(k+j)=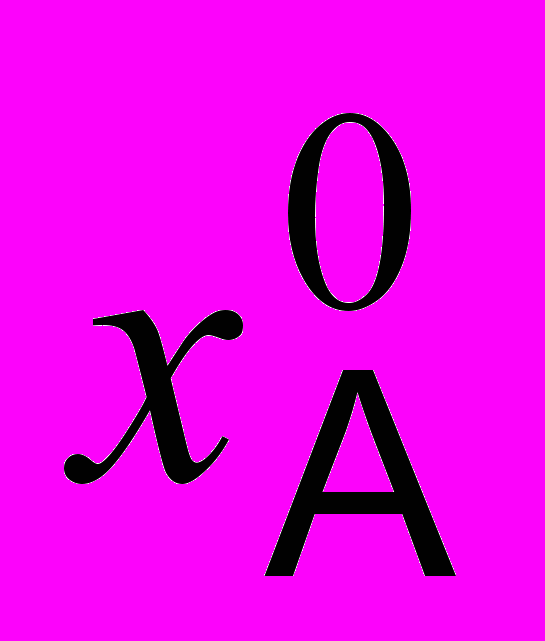(k+j),   j=1,…, m–1.

На остальных этапах (с точностью до нумерации) векторы управления и состояния на измененном процессе те же, что и на исходном. Тогда 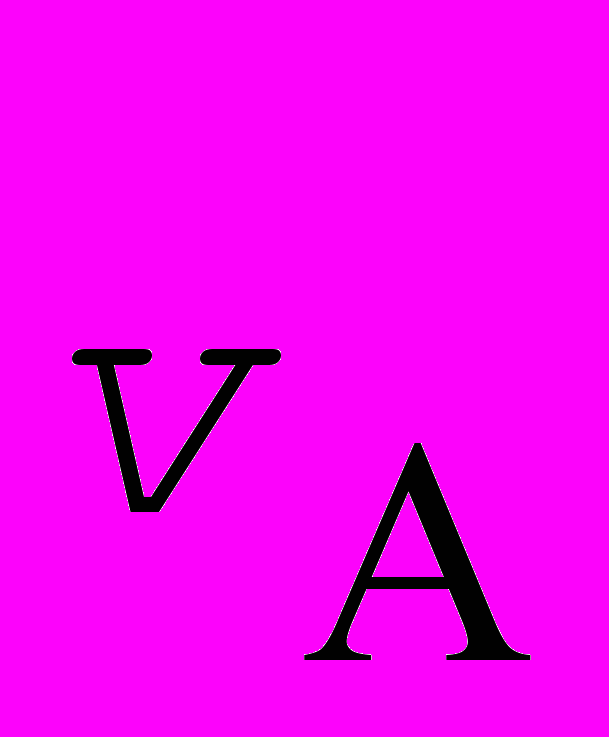V₁(S_A).

Качественное исследование введенного класса моделей выполнено в третьей главе. Анализ свойств конкретных соотношений моделей переключаемых процессов показывает, что выполняется следующее условие:

Условие 3.1. При любом dA_D, xRⁿ, u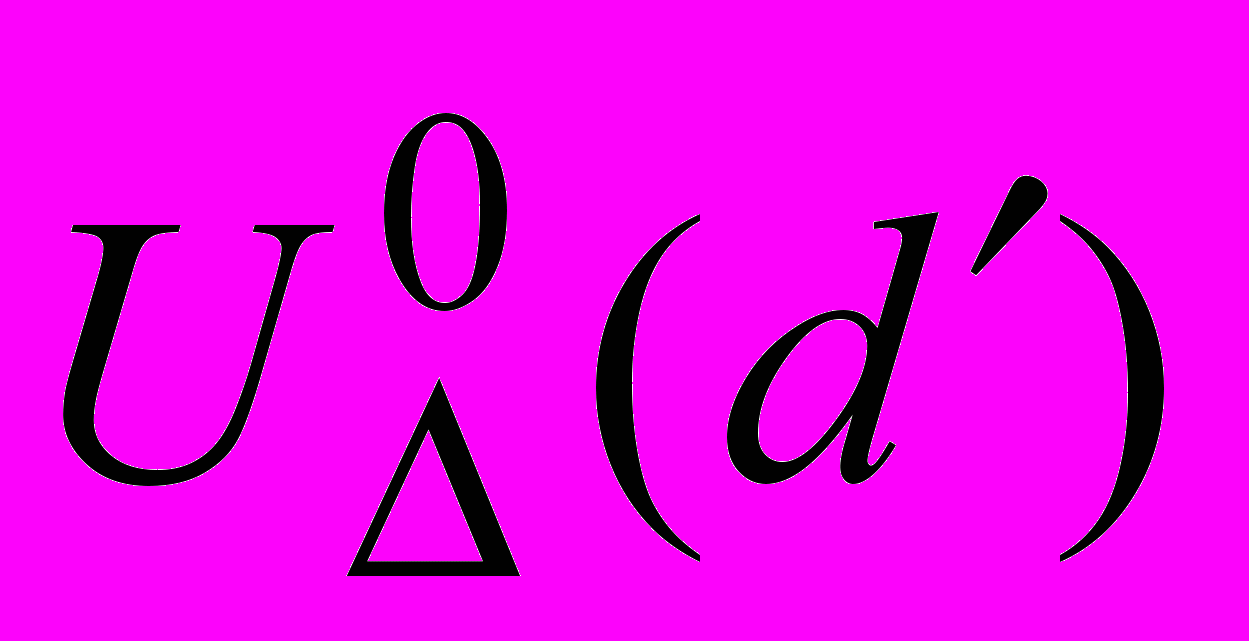, где 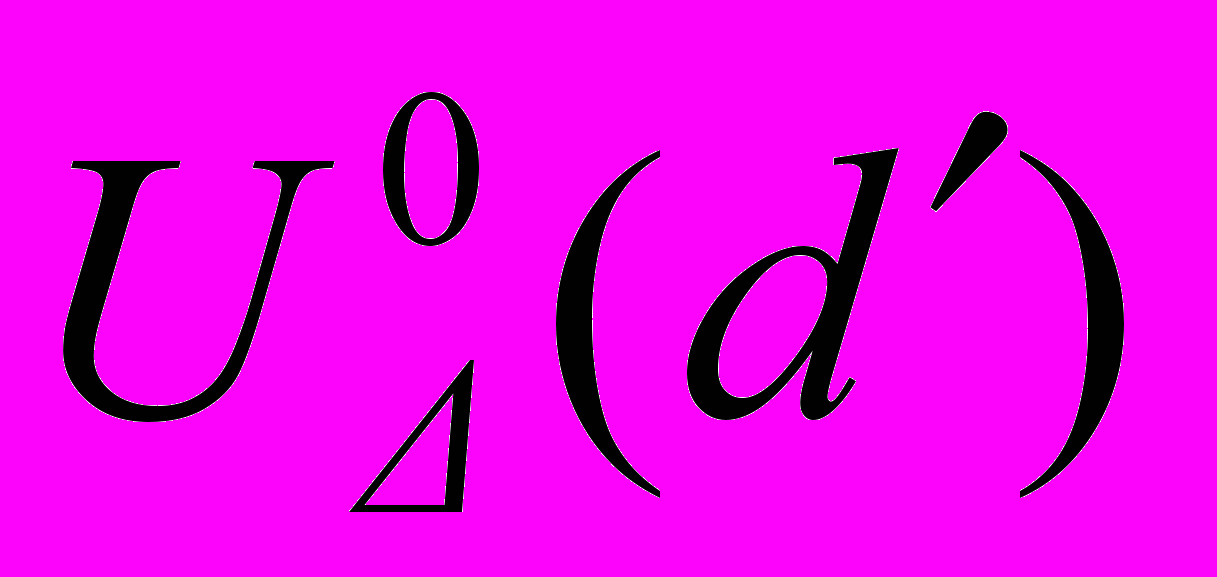—  окрестность U₀(d),  — положительная константа, функции f_i(d, x, u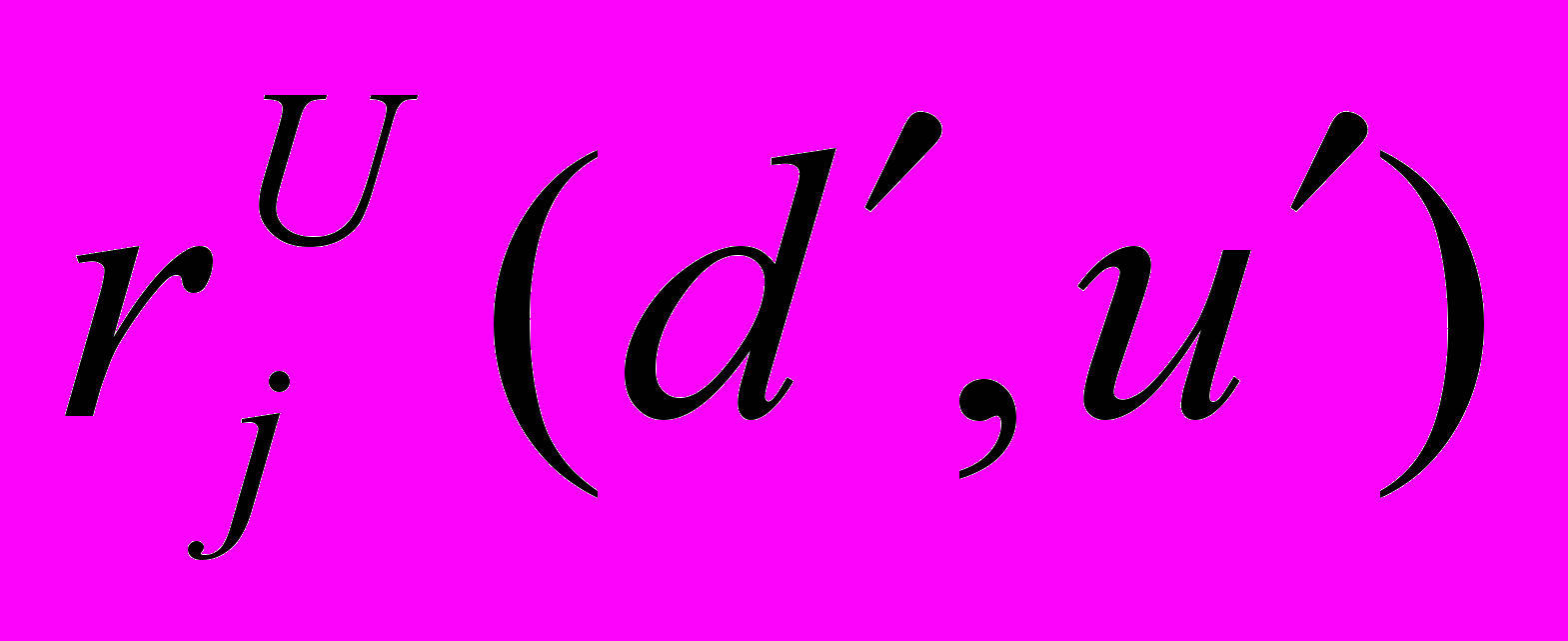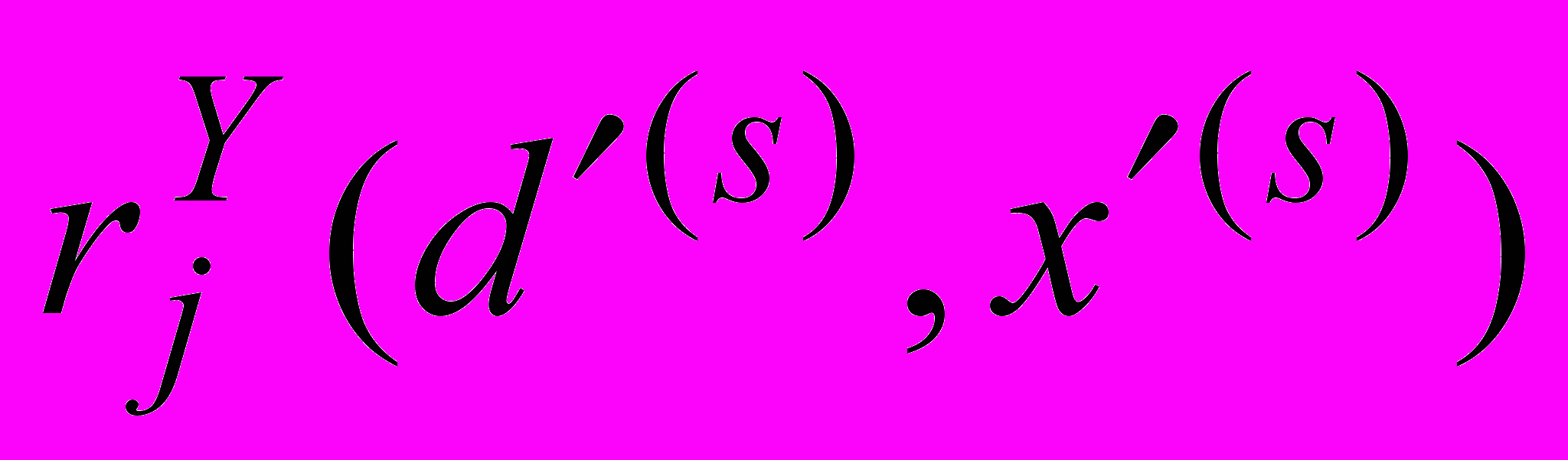), , определены, непрерывно дифференцируемы по x, u и для их производных справедливо обобщенное условие Липшица вида |g(y) g(y)|K||y y||^, где y=(x, u), а K>0, (0, 1] — константы, не зависящие от функции.

Справедливы также следующие условия, которым должна подчиняться модель, чтобы в ней имели место свойства реальных производственных процессов — конечность количества переключений и ограниченность множества траекторий.

Условие 3.2. Существует T_1max>T₁ и функция 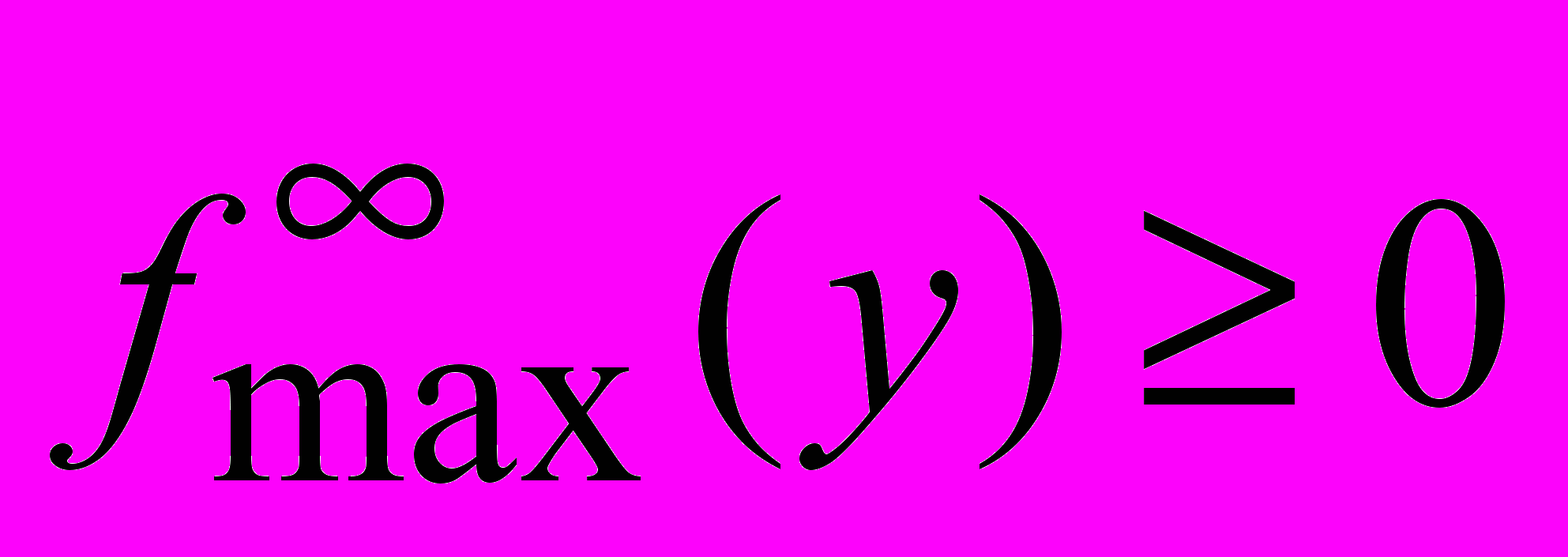, такая, что при любых dA_D, xRⁿ, uU₀(d) справедливо 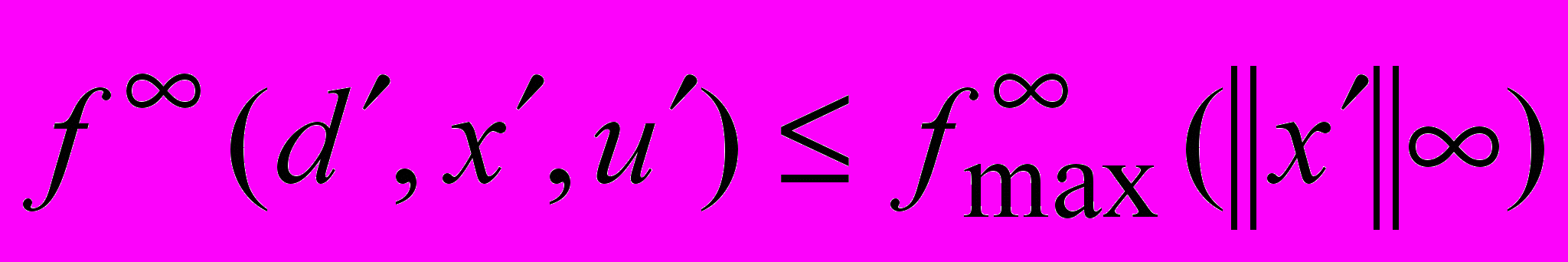и решение задачи Коши для уравнения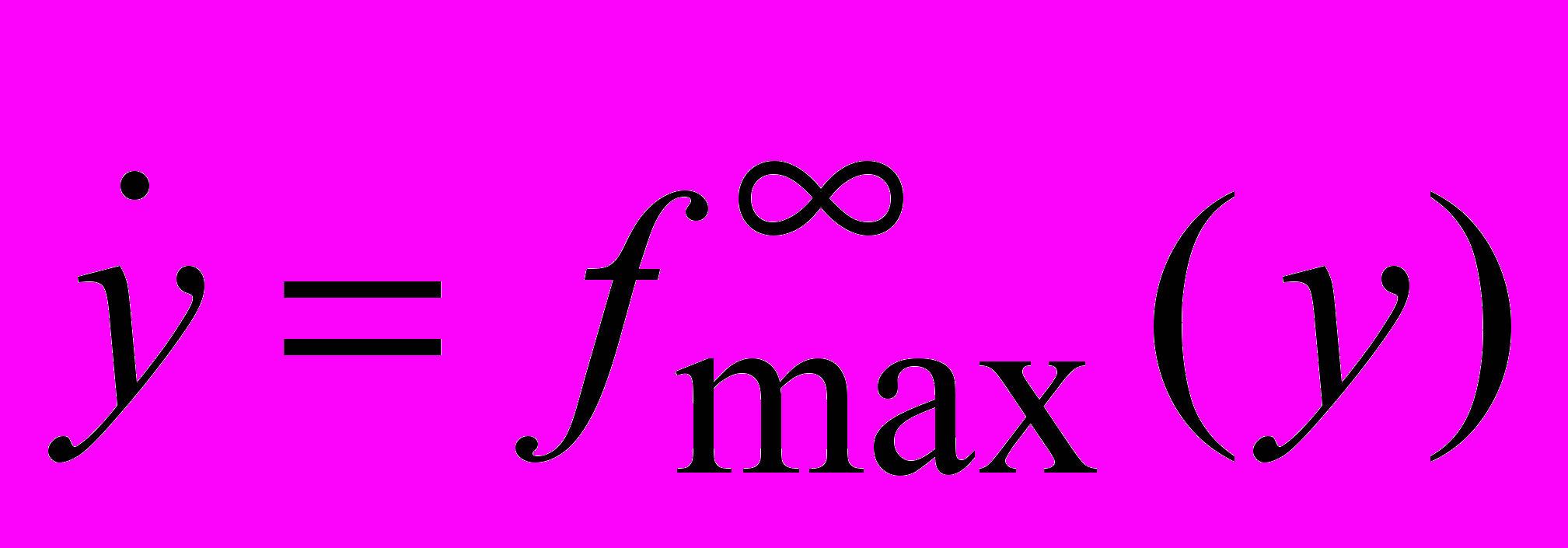



с начальными данными t=0, y(0)=y₀[0, ]_, существует и единственно на интервале [0, T_1max].

Условие 3.3. Существуют такие положительные константы K_X1, K_X2, что при любых S{1,…, L}, dA_D, xRⁿ , для которых



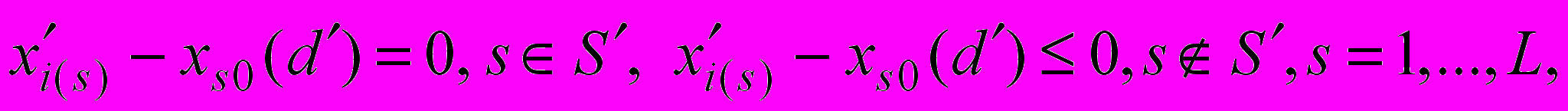
при любом sS.справедливо

K_X2x_s0(D_is(d(k))–X_i(s) s(d(k), x¹(k)), |X_is(d(k), x¹(k))|K_X1, iI_Xs.

Теорема 3.1. Пусть выполнены условия 3.1–3.3 и соотношения (24) и для начального состояния справедливо ||x⁰(1)||K_X0. Тогда существуют константы K_X и N_max, такие, что для любого такого процесса количество этапов не превышает N_max и при любом k=1,…, N справедливо ||x(t, k)||K_X при t[T(k), T(k+1)].

Невязки в ограничениях (21), (33), (26)–(27) можно обозначить F_j(v, S), а множества ограничений — неравенств и равенств — I₁(v, S), I₂(S). При 0 для vV₁(S) вводятся множества –активных ограничений I_1(v, S)={jI₁(S) | F_j(v, S)}, I_(v, S)= I_1(v, S)I₂(S).

Условие 3.5 (условие регулярности). Для любого возможного сценария S для любого vV₁(S) градиенты F_j(v, S), jI₀(v, S), линейно независимы. При любых dA_D, uU₀(d) векторы 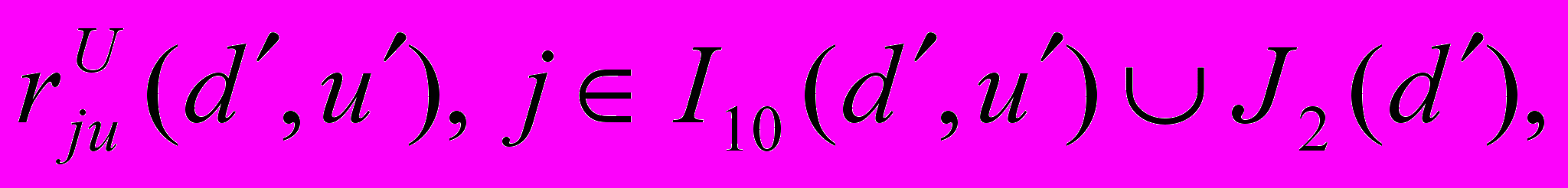линейно независимы, где .

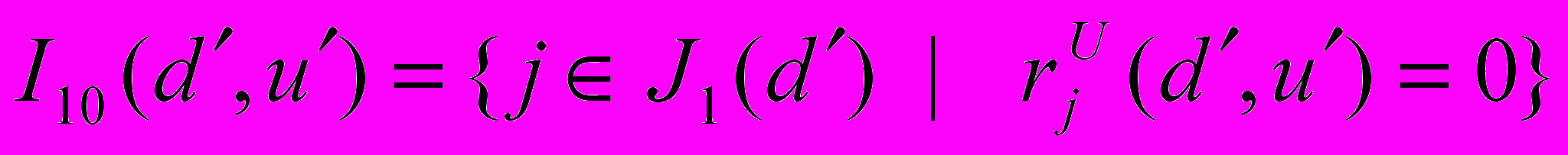Возможность изменения порядка переключений утверждается теоремой 3.3.

Теорема 3.3. Пусть выполнены условия 3.1–3.3, 3.5. Пусть S=(S(1),…, S(N)) — сценарий, для которого при некотором k dim(S(k))>1. Пусть S(k) разбивается на непересекающиеся множества S₁(k),…, S_m(k), при k=k+1,…, k+m–1 векторы d_A(k), u_A(k) удовлетворяют соотношениям (34). Определим сценарий S_A=(S(1),…, S(k-1), S₁(k),…, S_m(k), S(k+1), …, S(N)). Существуют положительные константы ₀ и a, так что:

1. если vV₁(S), то для любого , 0<₀ и для произвольно определенных при k=k+1,…, k+m 1 векторов v_A(k)=(u_A(k), t_A(k)), где u_A(k)U₀(d_A(k)), а t_A(k) удовлетворяет неравенству 0<t_A(k), существует v_AV₁(S_A), для которого
   

||v_A(k) v(k)||a, k=1, …, k, ||v_A(k) v(k+1-m)||a, k=k 1+m, …, N 1+m; (35)

2. если v_AV₁(S_A), для которого при некотором , 0<₀ при k=k+1,…, k+m 1 справедливо 0<t_A(k), существует vV₁(S), для которого справедливы соотношения (35).
   

Получены условия оптимальности событийно-переключаемого процесса.

Теорема 3.8. Если выполнены условия 3.1–3.3, 3.5 и управление vV₁(S) оптимально при фиксированном сценарии S, то для любой совокупности вариаций управления u(k), удовлетворяющих соотношениям

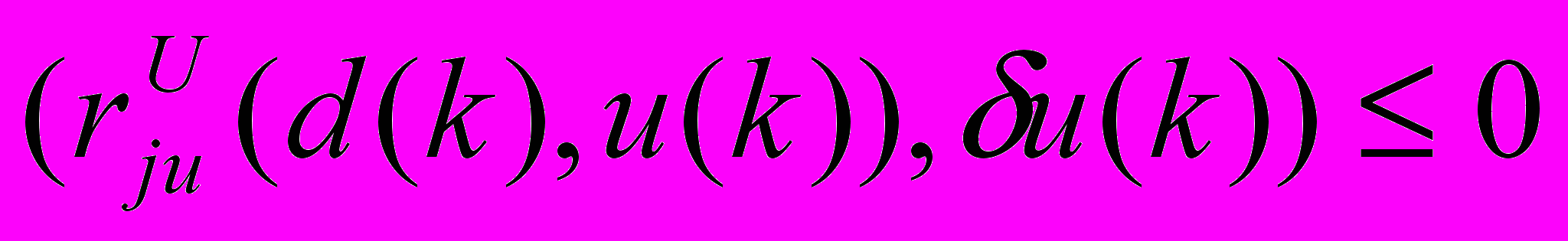, jJ₁(d(k))I₁₀(v, S), 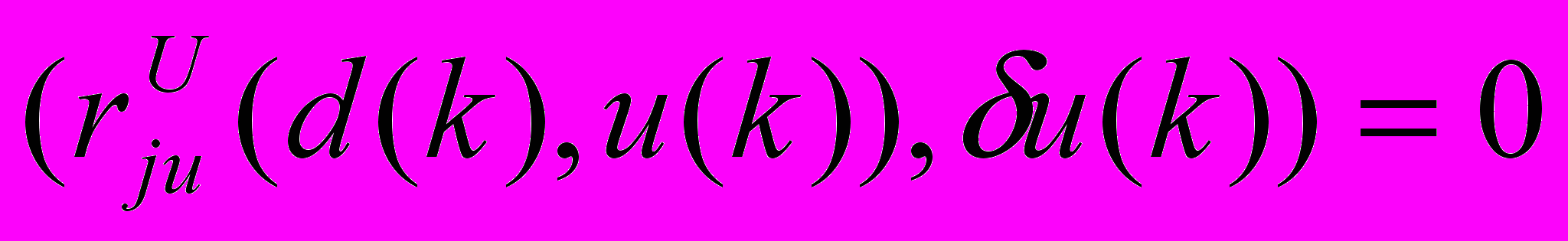, jJ₂(d(k)),

и вариаций продолжительностей этапов t(k), неотрицательных для этапов нулевой продолжительности, порождающих решение уравнения в вариациях для фазового вектора

x¹(k)=Y_x(d(k), x⁰(k), u(k), t(k))x⁰(k)+Y_v(d(k), x⁰(k), v(k))v(k),

x⁰(k+1)=X_x(S(k), d(k),  x¹(k))x¹(k),

для которых выполнены условия для вариаций невязок фазовых ограничений

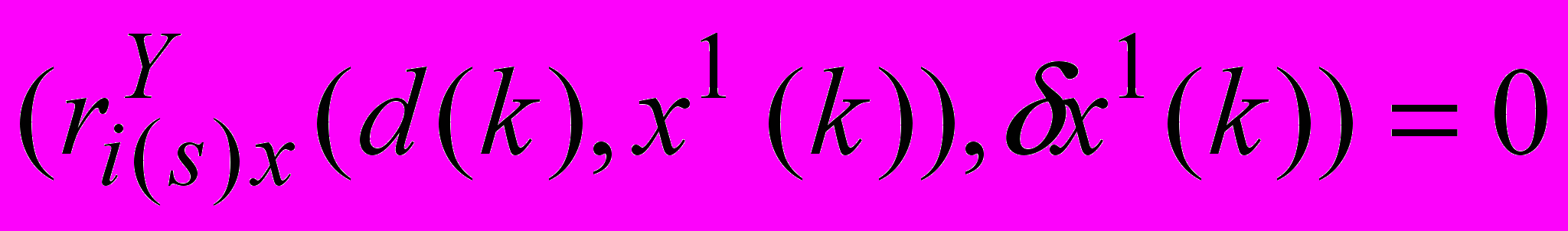, sS(k), 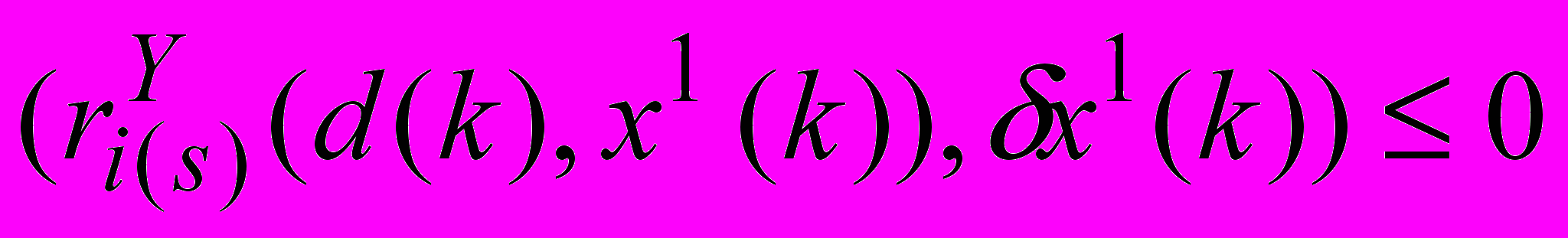, sS(k),

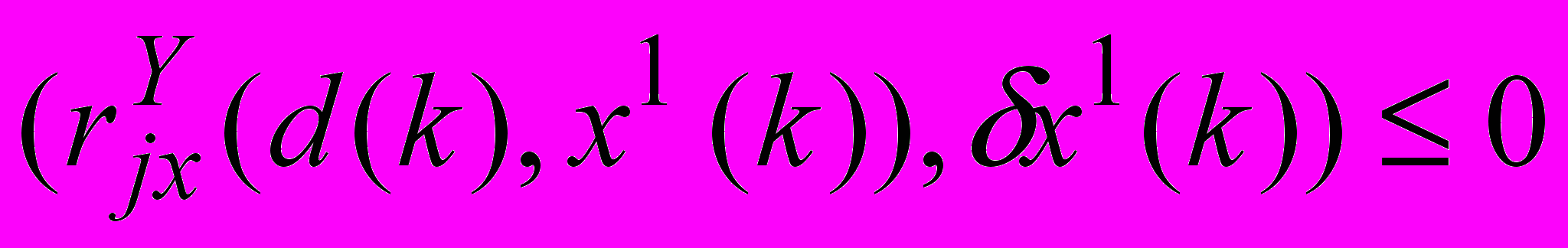, jK₁(s)I₁₀(v, S), sS(k), k=1,…, N; T(N+1)=0,

справедливо неравенство

(F_0x(x¹(N)), x¹(N))0. (36)

При совпадении хотя бы двух событий такое условие является недостаточно сильным, т.к. оно исключает сопоставление с управлениями, соответствующими другим сценариям. Пусть dim(S(k))>1 и S₁S(k), S₁. Тогда после k ого этапа, завершающегося набором событий S₁, согласно теореме 3.3 может следовать "вставной" этап, завершающийся набором событий S(k)\S₁.

Для этого случая формулируется второе необходимое условие оптимальности.

Теорема 3.9. Если выполнены условия 3.1–3.3, 3.5 и управление vV₁(S) оптимально, то для каждого k, для которого dim(S(k))>1, для любого непустого S₁S(k) существует вектор z₀(k; u, S, S₁), такой, что для любого u_INS(k)U₀(d_INS(k)), где d_INS(k)=D(S₁, d(k)), 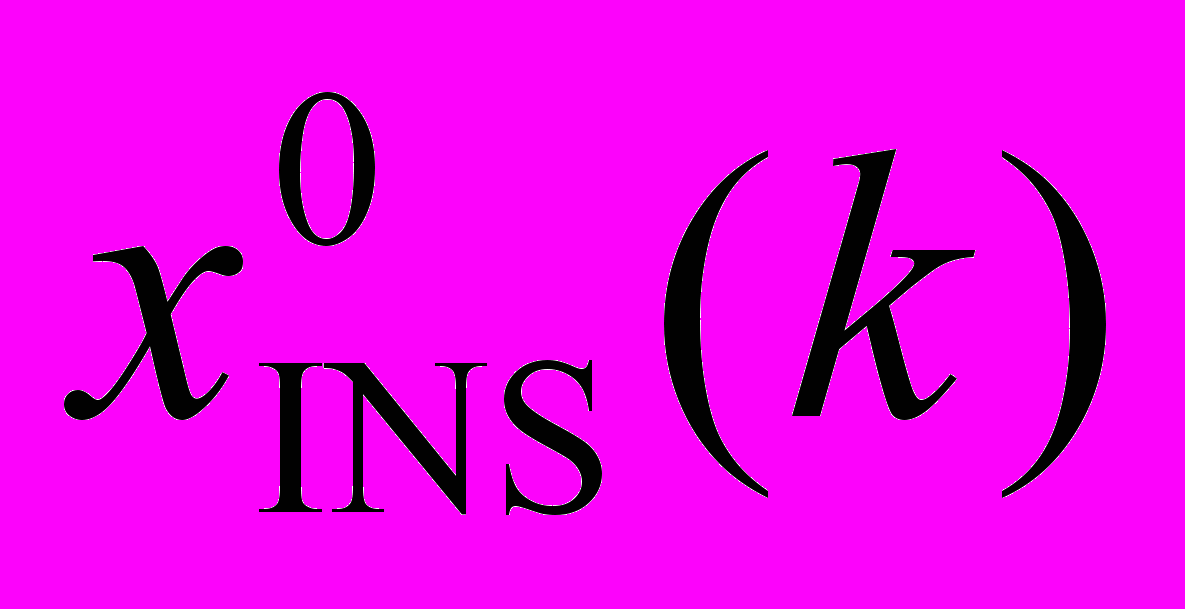)=X(S(k), d(k),  x¹(k)), справедливо

(z₀(k; v, S, S₁), Y_t(d_INS(k), 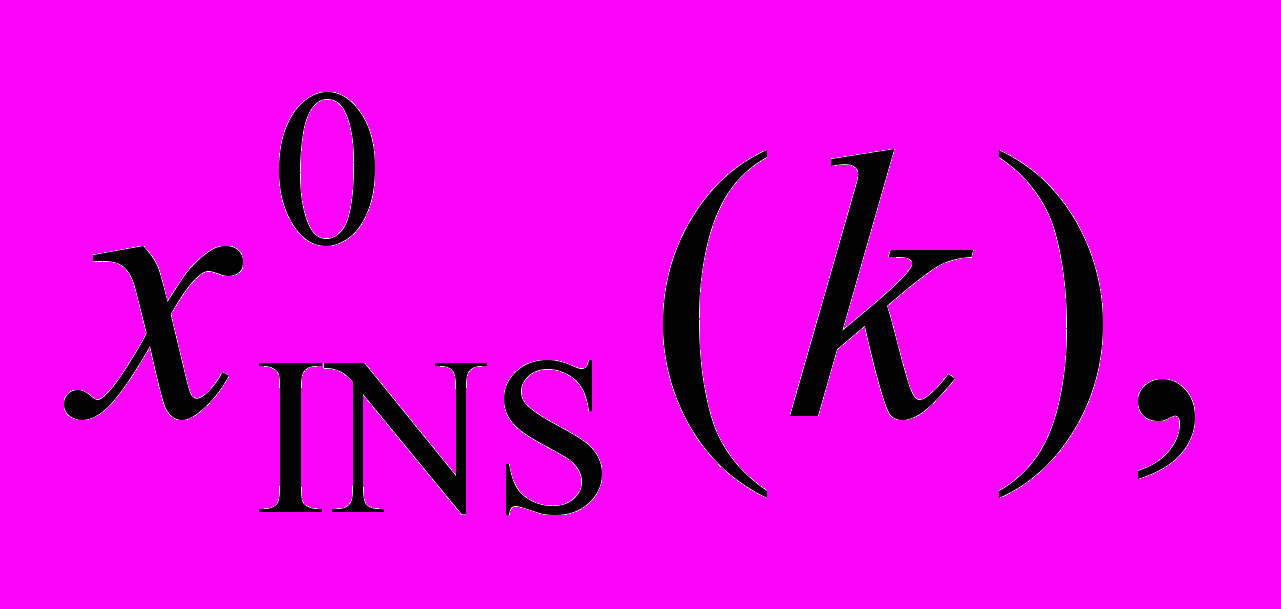u_INS(k), 0))0. (37)

Практически важным частным случаем модели (17)–(29) является модель распределения ресурсов-мощностей при выполнении комплекса взаимосвязанных работ. В этой модели сценарий определяется условиями предшествования работ:

d_i=0, если d_j<2, jP_i. (38)

Множества d, возможных по условию (38), определяются как D₀={d{0,1,2}ⁿ | d_i>0, если d_j=2, jP_i, иначе d_i=0}, а множества x, соответствующих d, — как X(d)={x(R₊)ⁿ | x_i=0, если d_i=0, x_i=x_Ti, если d_i=2, иначе 0<x_i<x_Ti}. Функция Беллмана W(x,d) определяется для состояний dD₀, xX(d) в начале этапов и в конце процесса. Установлено, что функция Беллмана — непрерывная кусочно-линейная функция x, выражаемая соотношениями: при l=1,…, n_L(d)

W(x, d)=C_X0l(d)x+C_0l, если C_Xlr(d)x+C_lr0, r=1,…, n_l(d).

В диссертации описан принципиальный алгоритм вычисления W(x, d).

Управление, оптимальное для заданного сценария, является решением задачи динамического линейного программирования (ДЛП), получаемой из исходной заменой переменных u_i(k) на x_i(k)=u_i(k)t(k), —

T(N)min; T(0)=0; T(k)=T(k 1)+t(k), k=1,…, N;

x(0)=0; x_i(k)=x_i(k 1)+x_i(k), iI₁(k), где I_s(k)={i | d_i(k)=s};

u_mini t(k)x_i(k)u_maxi t(k),  iI₁(k); x_i(k)=0, iI₁(k);

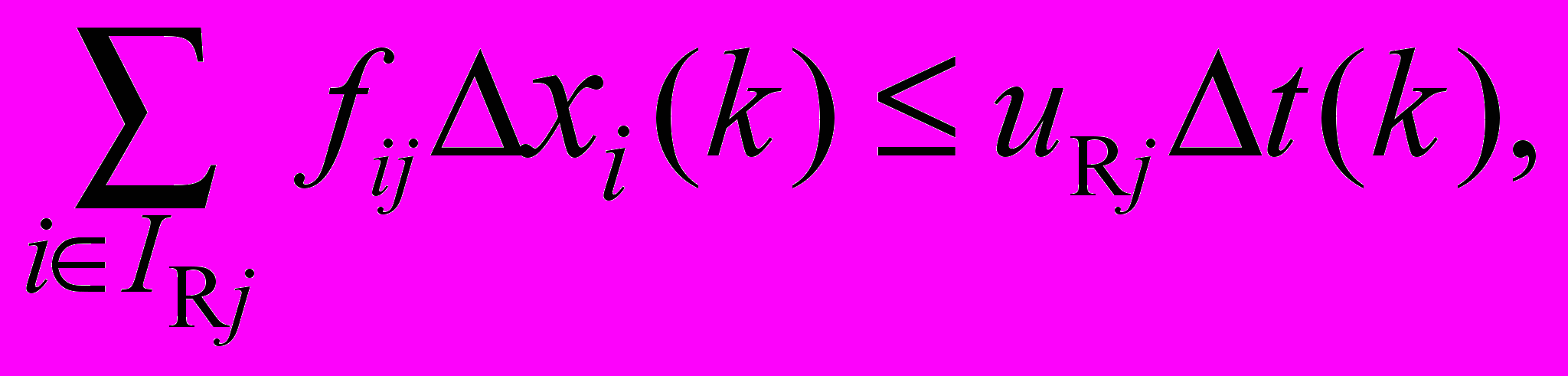  j=1,…, m; t(k)0; x_i(k)=x_Ti iI₂(k+1).

Условия оптимальности теорем 3.8 и 3.9 являются для данного класса моделей достаточными.

Опыт решения линейных и нелинейных задач оптимизации дискретных процессов с фиксированным сценарием показывает плодотворность декомпозиционного подхода при реализации прямых методов оптимизации, обеспечивающего не только резкое уменьшение объема вычислений, но и повышение устойчивости и уменьшение вычислительной погрешности. В силу структуры ограничений моделей положений горных работ он может быть применен и к рассматриваемым в работе статическим задачам оптимального годового планирования для карьеров, являющимися задачей нелинейного программирования обобщенной динамической структуры

u=(u₁,…, u_m), F₀(u)min, F_i(u₁,…, u_k)0, iI_1k,  F_i(u₁,…, u_k)=0, iI_2k, k=1,…,N. (39)

Преобразование формы условий оптимальности теоремы 3.8, конструктивное вычисление векторов z₀(k; v, S, S₁) и решения систем уравнений (35), обеспечивающих смену сценария, также успешно выполняется с развитием этого подхода в форме концепции декомпозиции по множеству ограничений в задаче вида (39). Рассматриваемые декомпозиционные схемы основаны на разбиении набора  активных ограничений I_(u)={iI₁ | F_i(u) }I₂ для допустимого управления u на подмножества J₁, …, J_L и представлении произвольного возможного направления в виде

w=H₁y₁+…+H_Ly_L,

где матрицы H₁,…,H_L определены из условия: для любого вектора w

(F_iu(u), w)=(F_iu(u), H_ly_l), iJ_l.

Определение 3.1. Пусть управление u является допустимым в задаче (39) , а набор ограничений JI₀(u). Совокупность матриц H₁,…,H_L задает декомпозиционную схему на u, если:

1) множество J разбивается на L непересекающихся подмножеств J₁,…, J_L, так что

F_iu^T(u) H_l=0, iJ_l;

2) при l=1,…, L матрицы H₁,…,H_L имеют полный ранг, а количество M_l столбцов H_l не меньше числа элементов J_l;

3) матрица H=[H₁H₂…H_L] имеет полный ранг.

При использовании таких декомпозиционных схем необходимые условия оптимальности первого порядка (выраженные теоремой 3.8 и другими подобными ей теоремами) преобразуются в условия следующего типа:

Теорема 3.7. Если J-регулярный вектор u*R^M является решением задачи (39) и совокупность матриц H₁(u^*,J),…,H_L(u*,J)(u^*,J) задает декомпозиционную схему на u*, то при любом l=1,…, L(u*,J) для произвольного вектора y_s, удовлетворяющего неравенствам

(F_iu*(u^*), H_l(u^*,J)y_l)0, iJ_lI₁₀(u^*), (F_iu*(u^*), H_l(u^*,J)y_l)=0, iJ_lI₂(u^*),

справедливо

(F_0u*(u^*), H_s(u^*,J)y_s)0.

Упрощается также построение управления, строго соответствующего измененному сценарию, сводящееся к решению системы (35) итерационным методом, сходящимся линейно или сверхлинейно.

Четвертая глава содержит описание методов решения задач оптимизации переключаемых производственных процессов. В разделе 4.1. описываются конкретные вычислительные конструкции схем декомпозиции по системе ограничений. Их построение сводится к совокупности следующих операций: выделения из матрицы R (полного ранга) максимальной квадратной подматрицы W⁺(R) и оставшихся столбцов W (R); объединения столбцов матриц (или векторов) R¹R²; сложения, умножения и обращения матриц.

Вычисление оптимального управления при фиксированном сценарии, также как и решение задачи оптимального годового планирования, возможно с помощью предложенного автором гибридного метода (с чертами методов возможных направлений и проекции градиента) с применением декомпозиции по ограничениям. Принципиально алгоритм ₁ получения улучшенного управления u' по известному u (при заданных положительных значениях параметров ₀, f_ (1>f_>0), c_, _H, K_F) состоит в следующем:

1. Положить =₀. Вычислить _min=min{–F_i(и) | iI₁\I₁₀(u)}.

2. Положить J=I_(u). Вычислить S(J), Н=Н(u, J)=[Н₁ |...|H_S(J)], векторы d₁,..., d_S(J), построить множества J₁,…, J_S(J). Ес­ли ||H||>c_ / или ||d_s||>c_/ при некотором s, то если _min, поло­жить =c_/||H||, иначе положить =f_ и перейти к пункту 2, в против­ном случае перейти к пункту 3.

3. Вычислить ₁=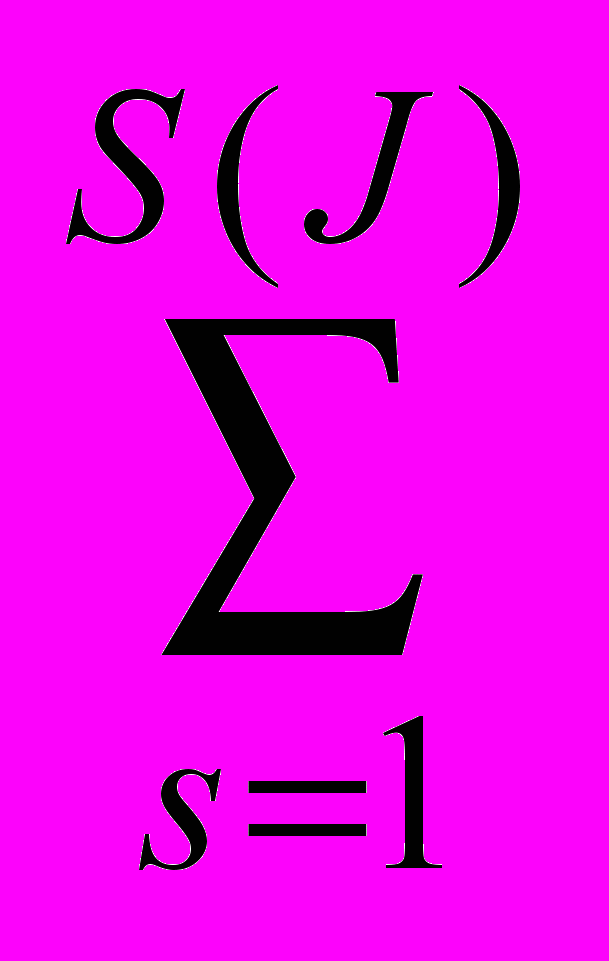(F_0u(u), H_sd_s).

4. При s=l, ..., s(j) найти число _0s и вектор y_s из решения за­дачи

_0s=( F _0u(u), H_sy_s)min, F _i(u)+(F _iu(u), H_sy_s)0, iJ_1s, (F_iu(u), H_sy_s)=0, iJ_2s,

-1y_si1, i=1,…, N(s).

5. Положить =1/(2max{₁, 1}), =₀(1+₁). При s=1,... , S(J) положить y_s=y_s+d_s.

6. Положить =_H.

7. Вычислить u'=u+Hy. Если для u' справедливо:

F_0u(u)F_0u(u)+/2–||₂(u+Hy)||; F _iu(u)–||₂(u+Hy||, iI₁, ||G||K_F(||Hy||+2||G|| ||₂(u+Hy)||)^l/2

(где ₂(u) — вектор невязок ограничений-равенств), перейти к п. 8, иначе положить =f_ и перейти к пункту 7.

8. Положить u^(1,0)=u. При k=0, 1, ... полагать u^(1,k+1)=u^(1,k)+G₂(u^(1,k)).

Положить u'=lim u^(1,k).

k

Сформулирован «реализуемый» вариант алгоритма, в котором операция восстановления ограничений-равенств выполняется приближенно. При отсутствии нелинейных неравенств вычисления упрощаются, восстановления связей не требуется. Предложен и второй алгоритм, отличающийся способом построения возможного направления — из решения задачи

_0s=(F _0u(u), H_sy_s)min, (F _iu(u), H_sy_s)0, iJ_sI_1(u) ,

(F_iu(u), H_sy_s)=0, iJ_sI₂, –1y_si1, i=1,…, N(s),

в котором выбирается значение , для которого при заданных с_,  выполнено неравенство _—с_^_. Предложен также алгоритм для минимаксной задачи, с помощью которого можно решать также задачу поиска допустимого плана. Для всех предложенных алгоритмов доказаны теоремы о сходимости следующего вида:

Теорема 4.2. Пусть в задаче (39) функции F_i(u)0, i{0}_I_1I₂ определены и непрерывно дифференцируемы при некотором >0 на замкнутом множестве приближенно-допустимых управлений U_={uR^M | F_i(u), iI₁, |F_i(u)|, iI₂}, их градиенты удовлетворяют обобщенному условию Липшица ||F_iu(u) F_iu(u)|K_F||u u||^ и в любой точке uU_ векторы F_iu(u), iI₀(u), линейно независимы. Пусть существуют константы n_H0, n_H0, такие, что для любого uU_ и любого J, для которого векторы F_iu(u), iJ, линейно независимы, декомпозиционная схема выражается матрицей H(u, J), имеющей невырожденную квадратную подматрицу полного ранга H₀(u, J), и выполнены условия ||H(u, J)||<n_H, ||H₀(u, J)^-1||<n_H0, и пусть K_F(_Hn_H)^1+. Пусть {u^(r)} — последовательность точек, построенных согласно алго­ритму ₁. Тогда предел u*() любой сходящейся ее подпоследова­тельности {u^(r), r} удовлетворяет необходимым условиям оптимальности в задаче (39).

Кроме того, в предположении двукратной непрерывной дифференцируемости соотношений, определяющих задачу, и незначительного усиления необходимых условий оптимальности доказана локальная линейная скорость сходимости второго алгоритма при значении =1/2. Наконец, предложен двухфазный метод, первая фаза которого выполняется по алгоритму описанного типа, а вторая — по алгоритму типа метода двойственных направлений и обладает сверхлинейной сходимостью.

Для линейных задач предложен вариант алгоритма, отличающийся лишь определением множеств активных ограничений и иным способом вычисления значения . Данный алгоритм дает решение за конечное количество итераций.

Если для сценария S при любом k dim(S(k))=1 и для предельной точки минимизирующей последовательности все t(k)>0, полученное управление является точкой локального минимума и процесс не имеет другого сценарного представления. Таким образом, имеет место локальная оптимальность безотносительно к сценарию. В противном случае требуется проверить условия теоремы 3.9 в отношении иных сценарных представлений процесса, вычисляя z₀(k; v, S, S₁) и решая задачи минимизации величины

(z₀(k; v, S, S₁), Y_t(d_INS(k), 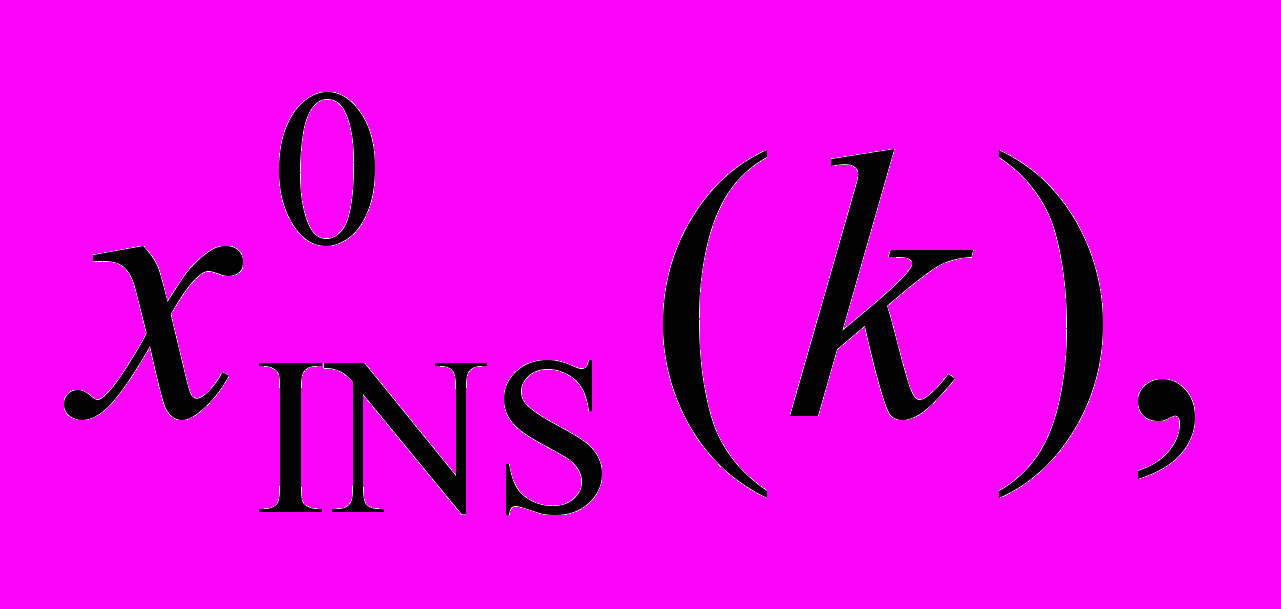 u_INS(k)))

при ограничениях (26). Если искомый минимум отрицателен в одной из этих задач, следует перейти к новому сценарию, решая систему уравнений (35) и затем выполнить минимизацию по этому сценарию. Для организации дерева решений построен метод поиска с возвратом (близкий к методу ветвей и границ), создающий возможности для нелокальной оптимизации.

Вычислительный опыт решения задач текущего и оперативного планирования добычных работ с фиксированным сценарием на основе описанного метода, а также проводившееся сравнение результатов решения ряда таких задач по методу автора и по методам штрафных функций и модифицированных функций Лагранжа, реализованным в разработанной в Вычислительном центре РАН диалоговой системе оптимизации ДИСО (подсистема оптимального управления), подтверждает вывод, что метод автора является вполне адекватным решаемым оптимизационным задачам и для них имеет преимущество перед более общими методами, проявляющееся как в большем быстродействии и вычислительной устойчивости, так и в единстве вычислительных построений, выполняемых при оптимизации в пределах сценария и при переходе к новому сценарию. Опыт решения линейных минимаксных задач оптимизации парка сельскохозяйственной техники, отличающихся сходной структурой ограничений и размерностью с рядом рассматриваемых задач, показал вычислительную эффективность декомпозиционного метода для линейного случая. Рост количества итераций от количества этапов (или уступов) N с порядком не выше N^3/2 показывает возможность получения оптимальных решений при любых размерностях реальных задач.

Пятая глава посвящена моделированию функционирования производственной системы с учетом возмущений и методам их компенсации. В работе рассмотрены основные виды случайных факторов — внутренних, вызванных ограниченной надежностью работы как отдельных механизмов, так и людей, управляющих ими, и внешних факторов — экономических (рыночная конъюнктура), а для природно-технологических систем также и природных, в частности погодных. По своей форме случайные факторы представляют собой:

• временные ряды случайных отклонений фактических значений показателей работы элементов системы от заданных;
  
• случайные ряды значений факторов, косвенно определяющих моменты наступления событий качественного изменения состояния отдельных элементов системы;
  
• случайные временные ряды моментов качественного изменения состояния среды;
  
• случайное распределение показателей природной среды в пространстве;
  

Для описания возмущений для предстоящих этапов, известных (или прогнозируемых) на момент начала фактического l го этапа, вводятся векторы e(k, l). Возмущения проявляются в уравнениях динамики, записываемых в виде

dx(t, k, l)/dt=f(d(k, l), e(k, l), x(t, k, l), u(k, l)),

и в ограничениях

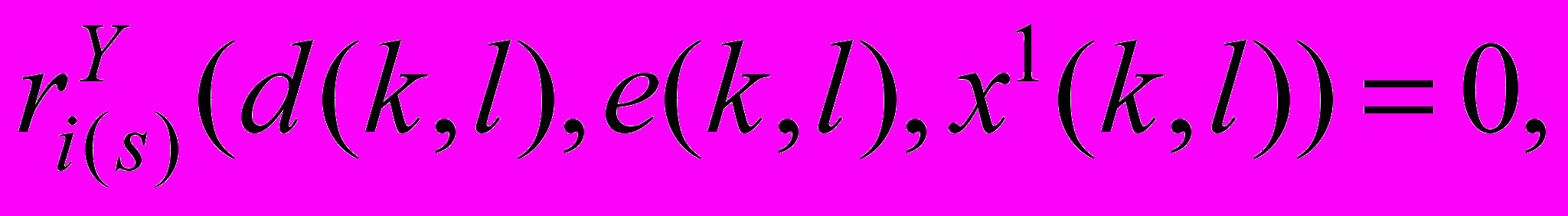sS(k, l),

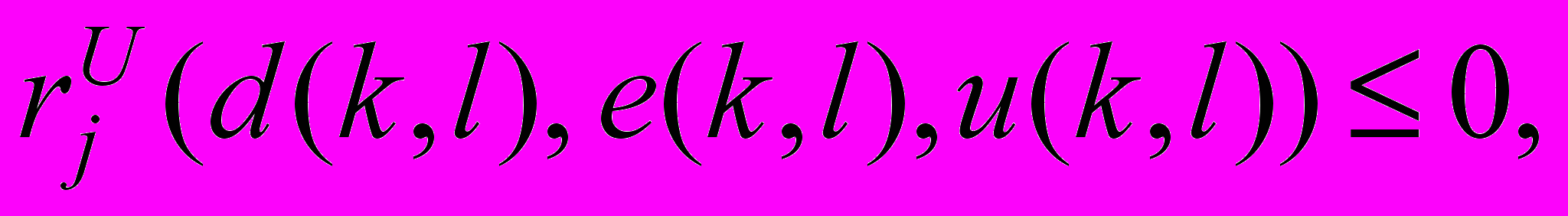jJ₁(d(k, l), e(k, l)),

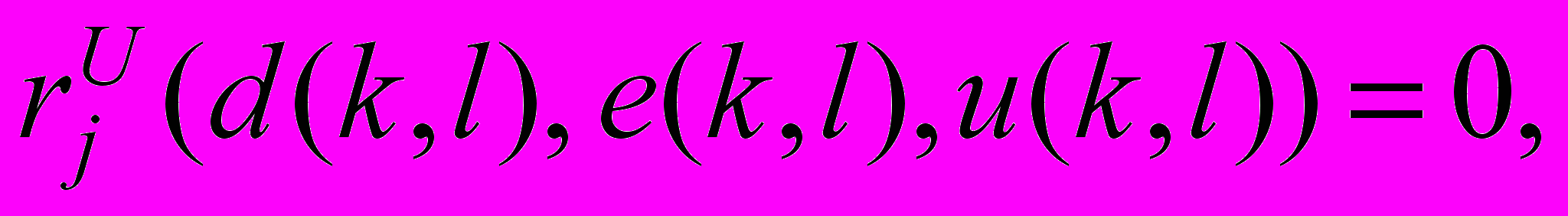jJ₂(d(k, l), e(k, l)),

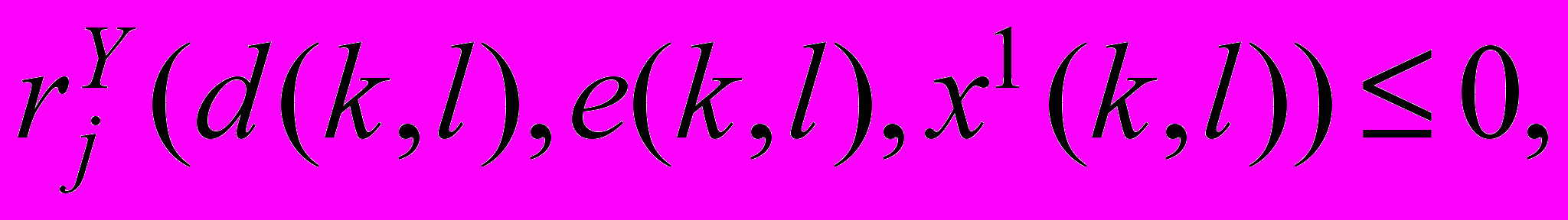jK₁(s), s S(k, l).

Метод инвариантного синтеза, разработанный для управляемых систем, описываемых как дифференциальными, так и разностными уравнениями, способен (при наличии адекватных резервов по переменным управления) полностью компенсировать влияние регистрируемых возмущений на конечные значения целевых показателей. С учетом разработанной модификации метода требуется, чтобы сумма количества целевых показателей и активных ограничений не превышала минимального количества переменных управления, значения которых можно менять как в меньшую, так и в большую сторону.

Модификация оригинального метода В.В.Величенко, рассматривающего процессы без ограничений на переменные состояния, заключается, в частности, в том, что прогноз последующего функционирования производственной системы на остаток планового интервала от текущего возмущенного положения строится не на основе неизменного планового управления, а на основе планового управления с компенсационными добавками, позволяющими не нарушить основные ограничения. Эти компенсационные добавки соответствуют декомпозиционной схеме метода локальных сечений, используемой и при вычислении оптимального плана, что позволяет использовать для задачи регулирования готовые программные блоки. Кроме того, управление доопределяется стандартным образом в виде зависимости u^0DE(d, e) от качественного состояния d и возмущения e для этапов, отсутствовавших в плановом сценарии.

Итак, производственный процесс при принятом плане характеризуется некоторой последовательностью этапов K(S)={1,…, N(S)}. Целевые показатели при известном сценарии S относятся к этапам из K₀(S)={k₁(S),…, k_M(S)(S)}K(S) и зависят от порядкового номера этапа в последовательности K₀(S). Интервальные ограничения на значения целевых показателей приводятся к виду

F_iT(x¹(N))0, iI_0T, F_im(x¹(k_m(S)))0, iI₀(m), m=1,…, M(S). (40)

В соотношениях (40) имеются в виду рассчитываемые по прогнозной модели значения векторов состояния x¹(k_m(S)) при известном фактическом состоянии x⁰(l,l)=y⁰(l) на начало фактического l го этапа процесса и значениях наблюдаемых возмущений для l го и ряда последующих этапов. Источником нарушения ограничений (40), соблюденных для расчетного состояния x⁰(l, l 1) на начало фактического l го этапа, является как наличие новых наблюдаемых возмущений, так и проявление ненаблюдаемых возмущений на предшествующем (l 1) м этапе, выражающееся в расхождении между x⁰(l, l 1) и y⁰(l).

Рассмотрим однопараметрическое семейство траекторий с состоянием на начало фактического l го этапа x⁰(l, l 1)(1 )+y⁰(l) и возмущениями e¹(k,l), [0,1]. При =0 имеем рассчитанную на предыдущем этапе траекторию, для которой ограничения (40) соблюдены, при =1 — искомую траекторию. Переход от =0 к =1 проводим с соблюдением соотношений (40) по аналогии с методом инвариантного синтеза, решая при каждом значении  относительно du(k, l, )/d систему уравнений, полученную из (40):

dF_iT(x¹(k_M(S(l, ))))/d=0, iI_0T, если F_iT(x¹(k_M(S(l, ))))=0, (41)

dF_im(x¹(k_m(S(l, ))))/d=0, iI₀(m), если F_im (x¹(k_m(S(l, ))))=0, m=1,…, M(S). (42)

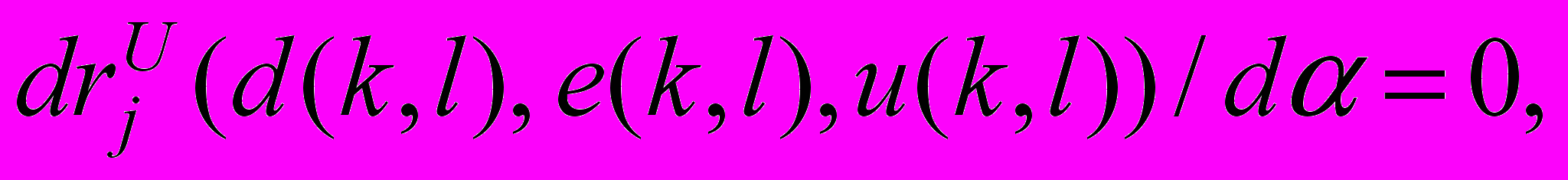jJ₁₀(d(k,l), e(k,l)) J₂(d(k,l), e(k,l)),

k=l,…, 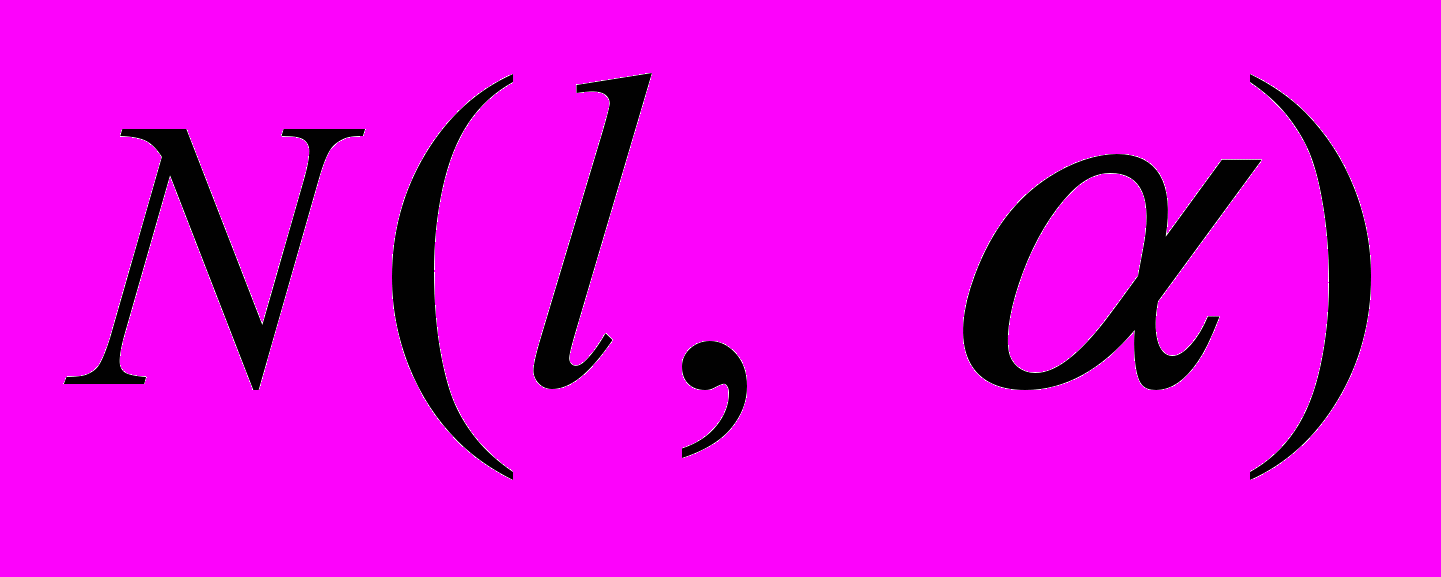, (43)

представляющую собой недоопределенную систему линейных алгебраических уравнений с блочно-диагональной матрицей. Метод ее решения аналогичен вычислениям, выполняемым при построении декомпозиционных схем.

При накоплении возмущений сценарий может измениться. В этом случае для некоторого  осуществляется один из случаев:

1. для некоторого предстоящего этапа 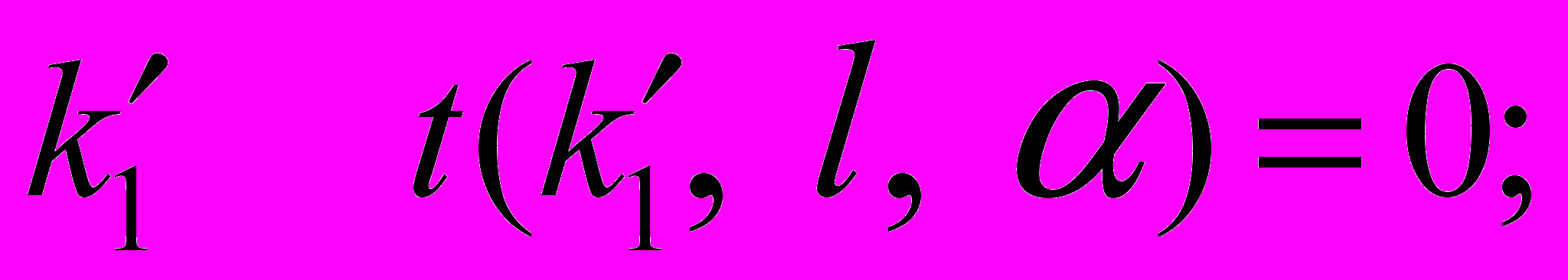в этом случае события 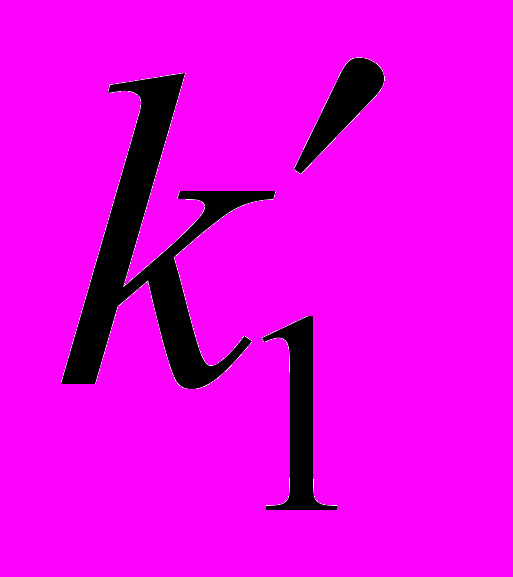и 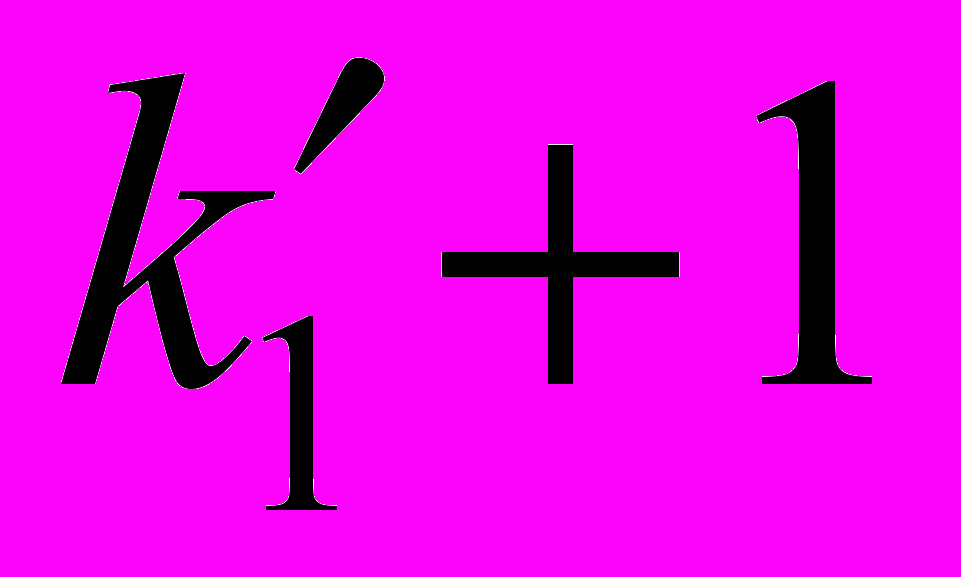поменяются местами; полагаем
   

u(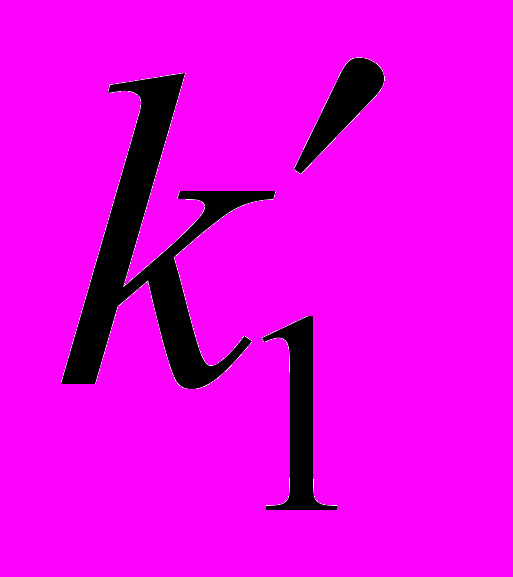, l, +0)=u^0DE(d(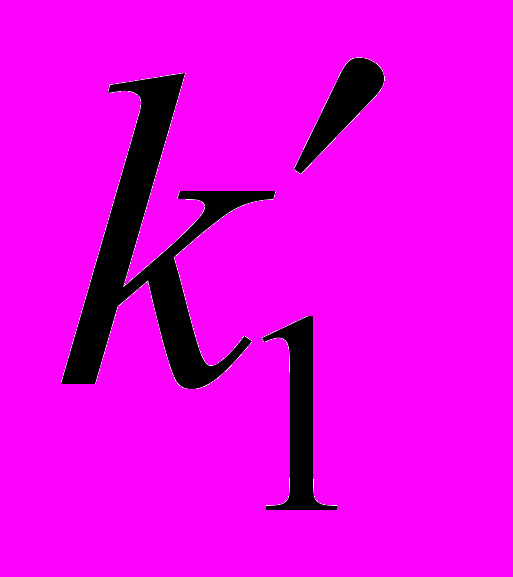, l), e(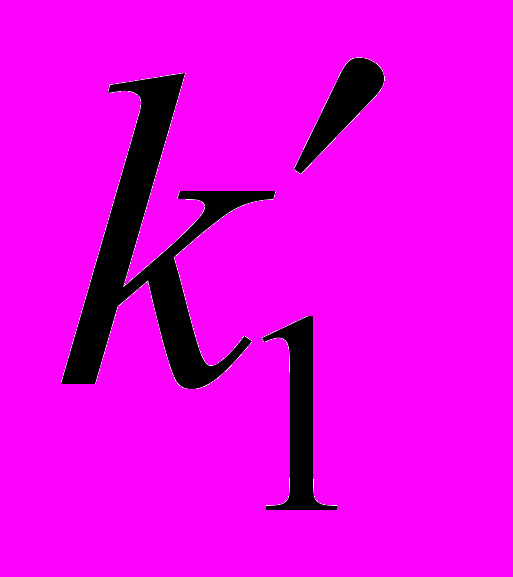, l, )); (44)

2. T(N(l, ), l,)=T₁; в этом случае
   

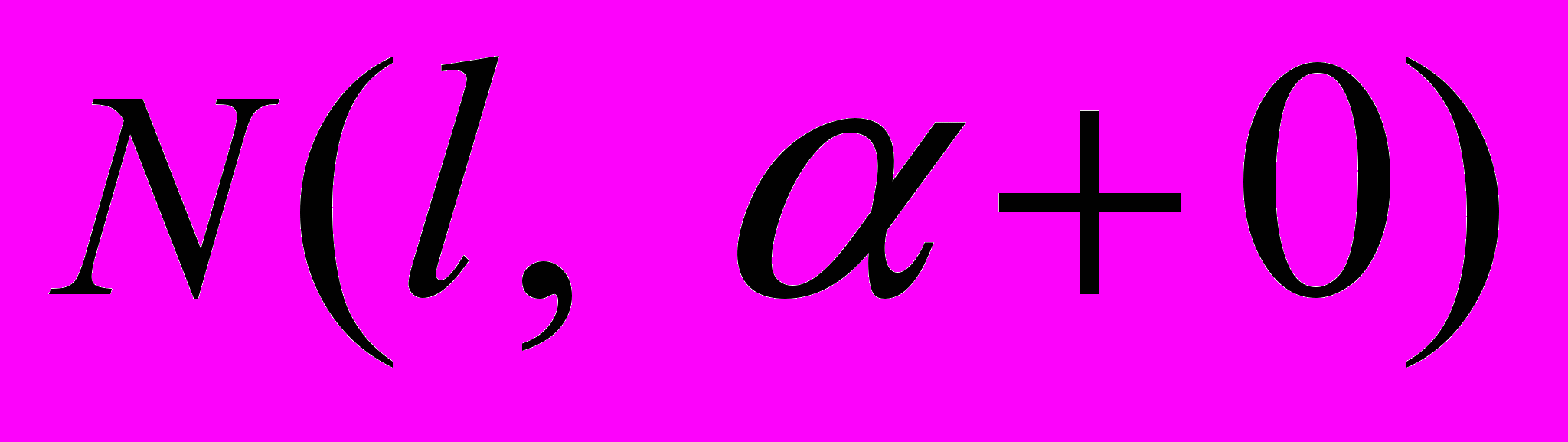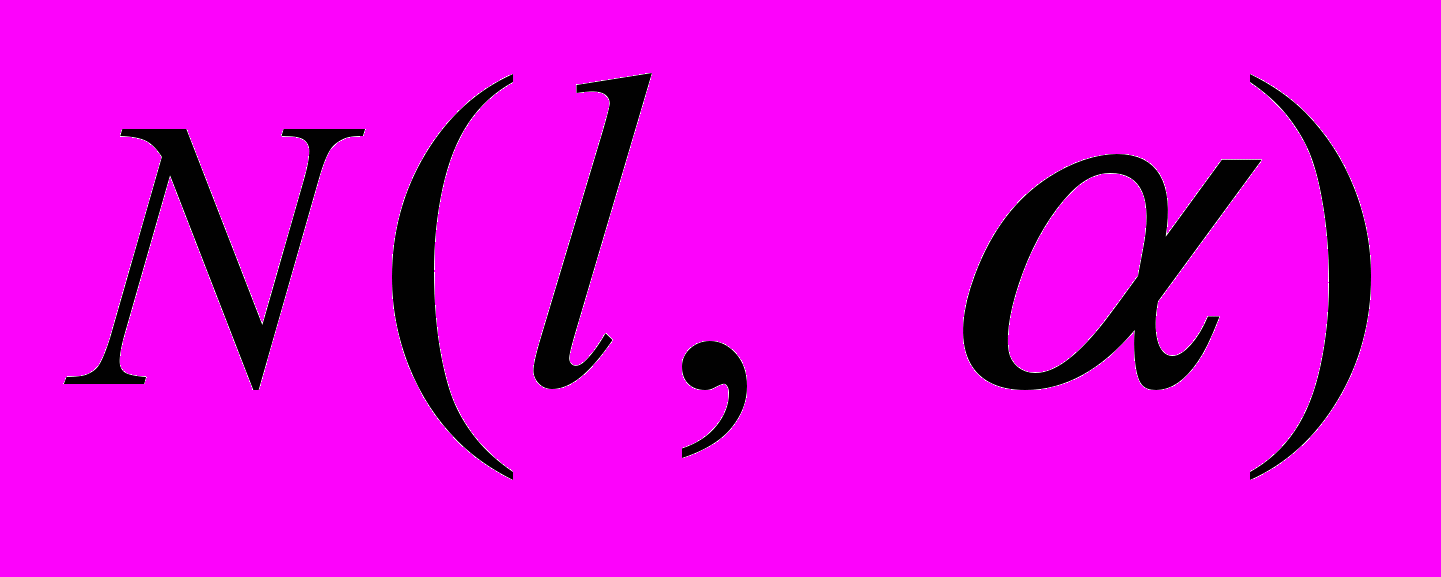=–1; (45)

3. T(N(l, )+2, l,)=T₁; в этом случае
   

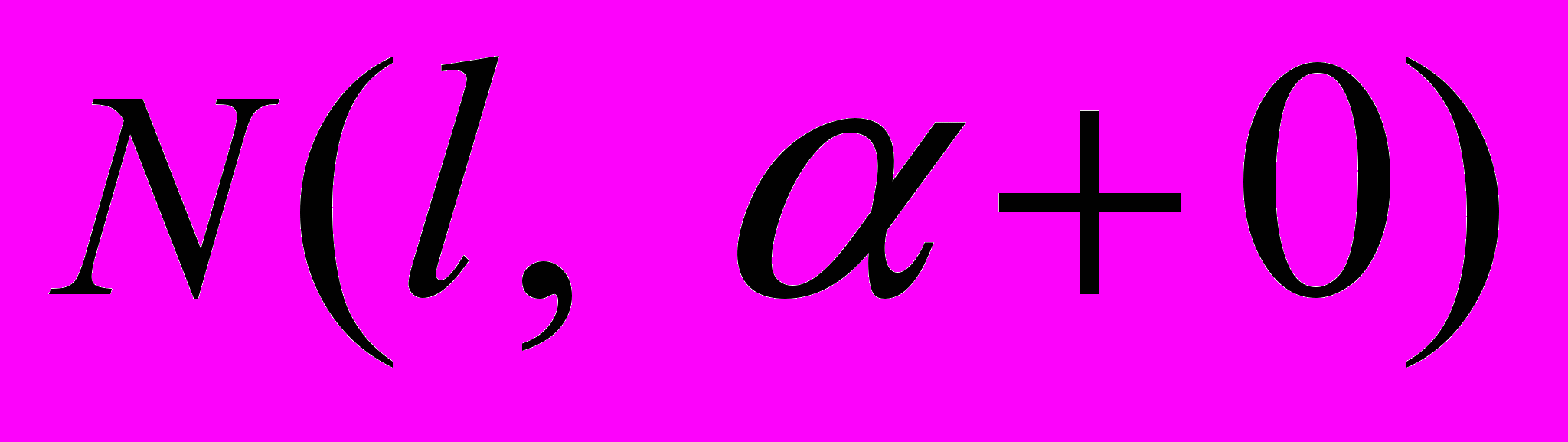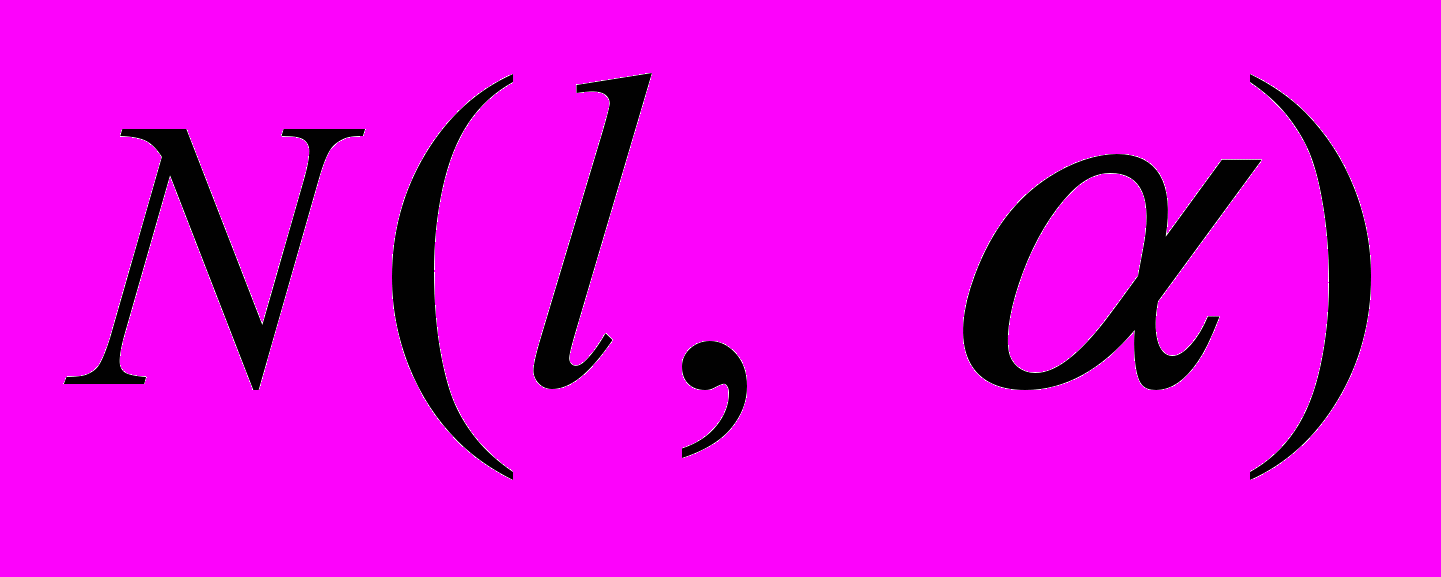=+1; (46)

u(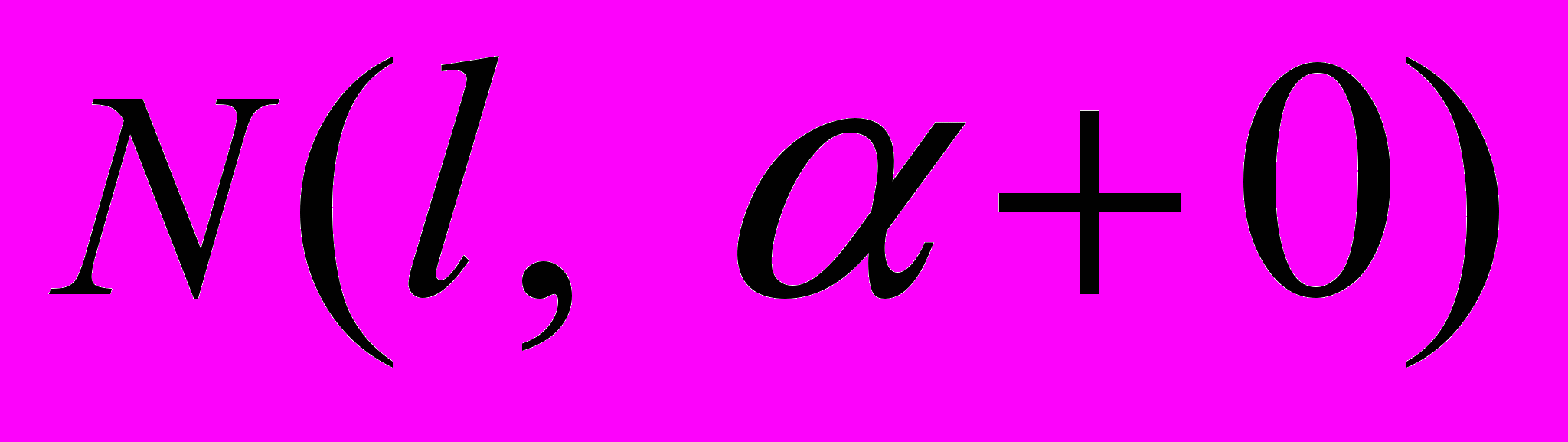, l, +0)=u^0DE(d(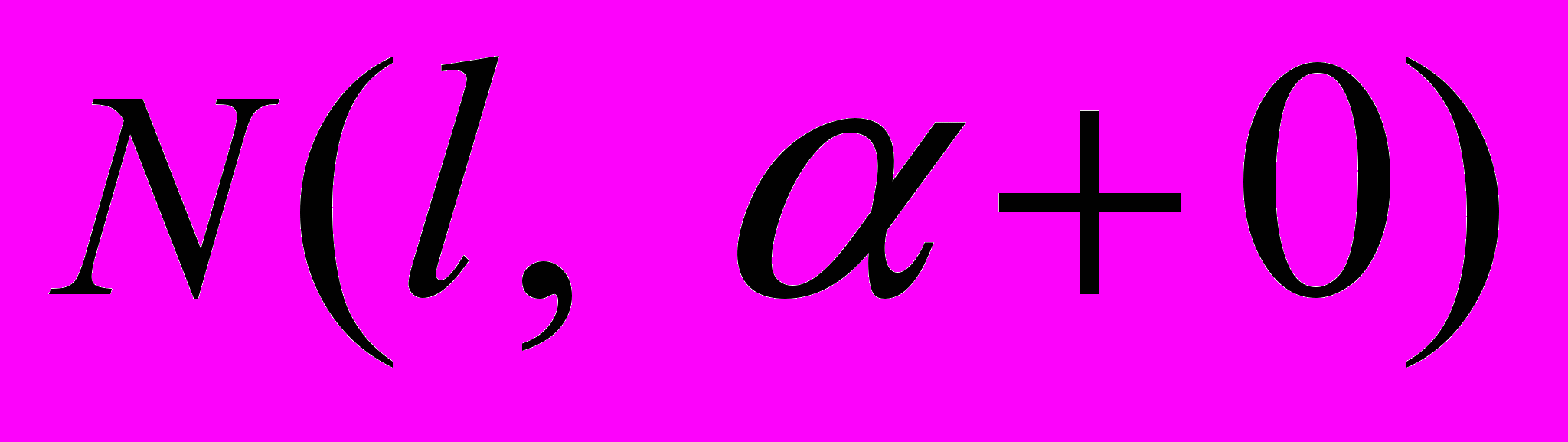, l), e(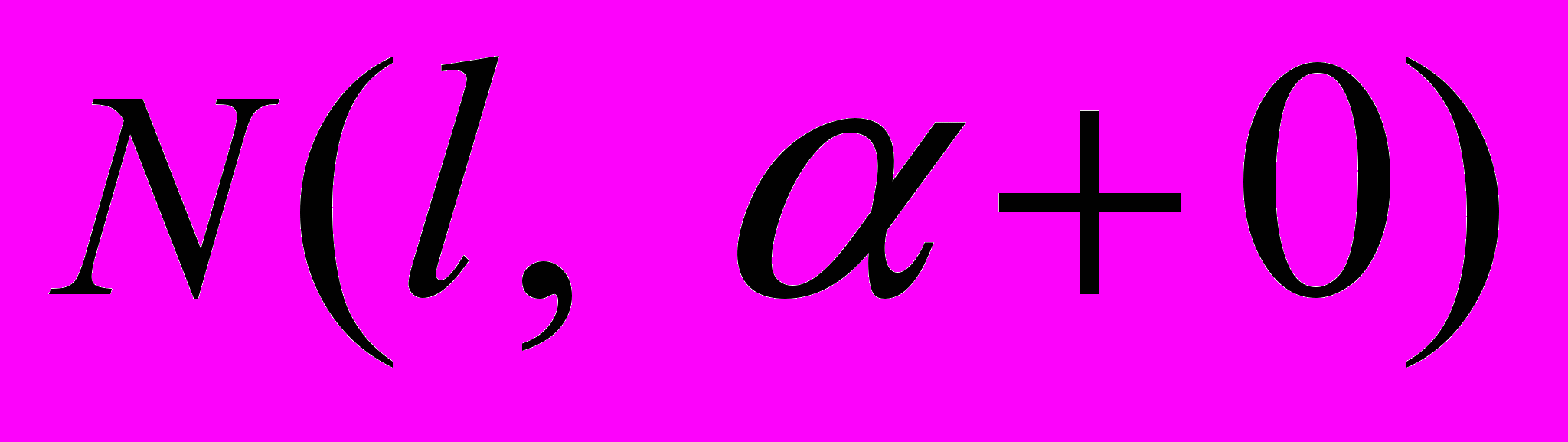, l, )). (47)

Принципиальный алгоритм вычисления скорректированного управления для l го фактического этапа формулируется следующим образом:

1. Определить тип переключения, начинающего этап. Если требуется, определить количество этапов и N(l, 0) и управления u(k, l, 0), k=l,…, N(l, 0) по формулам N(l, 0)=N(l 1)+2, u(l, l, 0)=u^0DE(d(l, l), 0); u(l+1, l, 0)=u(l 1, l 1); u(k, l, 0)=u(k 2, l 1), k=l+2,…, N(l, 0), иначе положить N(l, 0)=N(l 1), u(k, l, 0)=u(k, l 1), k=l,…, N(l, 0).

2. Изменяя  от 0 до 1:

• определять значения g(k, l, )=du(k, l, )/d, k=l,…, N(l, ), решая систему линейных алгебраических уравнений (41)–(43);
  
• интегрировать системы обыкновенных дифференциальных уравнений du(k, l, )/d= g(k, l, ), k=l,…, N(l, );
  
• если выполнено одно из условий изменения сценария, применить в зависимости от ситуации (44), или (45), или (46)–(47).
  

Результативность модифицированного метода инвариантного синтеза гарантирована (в определенном диапазоне возмущений) при соблюдении условий регулярности в возмущенной задаче, которые могут быть сформулированы аналогично условию 3.5.

Общий порядок имитационных расчетов для анализа возможных реализаций календарного плана состоит в следующем:

1. Породить представительный набор совокупностей реализаций случайных факторов, рассматриваемых как наблюдаемые и ненаблюдаемые возмущения производственного процесса;
   
2. Для каждой совокупности реализаций случайных факторов рассчитать процесс функционирования в виде чередования трех операций:
   

• расчета момента очередного переключения (окончания l го фактического этапа или планового периода) и фактического состояния в момент переключения по модели фактического функционирования;
  
• определения параметров прогнозной модели, исходя из значений наблюдаемых возмущений на рассматриваемой реализации для предстоящего этапа;
  
• решения задачи коррекции управления (на текущий этап и, быть может, до окончания планового периода) по прогнозной модели.
  

Шестая глава посвящена моделированию задач управления горным производством и результатам решения ряда сформулированных задач для отдельных предприятий, в первую очередь разрезов (угольных карьеров).

Проведена систематизация условий задач внутригодового планирования для разрезов и на ее основе предложена методика построения математических моделей производственного процесса для конкретных условий. В основу классификации положены характеристики выходных углепотоков и способы их формирования (табл. 1 и 2).

Особенностями моделей планирования горного производства являются:

1) ограничения на положение горных работ (и, возможно, состояния отвалов);

2) содержание компонентов полезного ископаемого, помимо его количества, характеризует состояние накопителей (запасов отдельных участков и складов), причем для первых определяются также зависимости мощности, типа (сорта) руды или угля от положений забоев;

3) ограничения на содержание компонентов накладываются на партии отгружаемой потребителям продукции (в составе текущих партий и с начала периода) и находящихся на усреднительных и (или) подшихтовочных складах сортов товарного угля.

Таблица 1.

Состав добычных блоков с позиций формирования товарного продукта

Состав залежи	Формируемые грузопотоки (углепотоки)
С1. Одна марка угля приемлемого качества	Из каждого забоя один поток в формируемые партии и(или) на усреднительные и(или) подшихтовочные склады при их наличии
С2. Одна марка угля, пригодная при качестве выше минимального	Аналогично С1, дополнительно — некондиционный уголь — на отвалы
С3. Одна марка угля, разделяемая на сорта в зависимости от качества	Для каждого сорта угля, выделяемого по качеству, углепотоки аналогично С1.
С4. Несколько марок угля приемлемого качества	Из каждого забоя потоки угля каждого типа, аналогичные С1.

Критерий оптимальности формулируется по-разному в зависимости от того, реализуется ли продукция по фиксированным договорам или частично на свободном рынке. В первом случае в качестве критериев целесообразно использовать:

• минимум накопленных отклонений от плана горных работ на конец планового периода;
  
• максимум запаса надежности плана (выражаемого через сохраняемые резервы производительности и (или) резервы по качеству поставок, т.е. отклонения планируемых значений показателя качества от предельно допустимых).
  

Таблица 2.

Характеристики задач управления в зависимости от технологии

Тип условий	Тип ситуации	Переменные управления	Переменные состояния
Спо­соб выем­ки угля	В1. Валовой	Интенсивность отгрузки из забоя угля в каждый адрес разгрузки	Объем отгруженного в забое угля
	В2. Селектив­ный по длине заходки	Интенсивность отгрузки из забоя угля в каждый адрес разгрузки текущего типа угля	Объем отгруженного в забое угля (горной массы)
	В3. Выемка с селекцией по высоте	Интенсивность отгрузки горной массы из забоя; для С2 или С3 границы качества (если не фиксированы)	Аналогично В2
Спо­соб форми­рова­ния товарной продук­ции	Ф1. Прямая отгрузка	Дополнительных переменных нет	Объем и среднее качество отгруженного угля (по сортам)
	Ф2. Усреднение в складах всего угля (по сортам)	Дополнительно: интенсивность отгрузки со склада(-ов)	Дополнительно к Ф1 — текущий объем и качество в секциях склада(-ов)
	Ф3. Использова­ние подшихто­вочных скла­дов при прямой отгрузке	Аналогично Ф2	Дополнительно к Ф1 — текущий объем и качество в подшихтовочных складах
	Ф4. Комби­ни­рованный	Аналогично Ф2	Как для Ф2

Эти критерии могут объединяться в комбинированный критерий или выступать в качестве ограничений при выборе другого критерия. Во втором — максимум стоимости продукции (за счет увеличения объема или более высоких качественных показателей, если такие возможности допускаются потребителями продукции). В этом случае должны использоваться ограничения как на запас надежности, так и на отклонения от плана горных работ.

На основе предложенной классификации моделей решались задачи для отдельных разрезов. Для разреза "Тугнуйский" АО “Востсибуголь” сложная структура пластов вызывает относительно высокий показатель разубоживания, приводящий к тому, что в среднем качество сырого угля не удовлетворяет требованиям основных потребителей, которыми являются две крупных электростанции — "Гусиноозерская" и "Улан-Удэнская-2" — а также местное население. Главные показатели качества угля для электростанций — зольность и доля "видимой" (т.е. крупнее 25 мм) породы. В проекте освоения месторождения были разработаны две альтернативы. Согласно первой геологические блоки разделяются на два вида: блоки "чистого" и "грязного" угля. "Чистый" уголь не требует никакой обработки, "грязный" должен быть обогащен. Согласно второй эти виды смешиваются в основном усреднительном складе, состоящем из двух секций и по отдельности формируют секции подшихтовочного склада, предназначенные для "исправления" качества угля на основном складе, из разгружаемой секции которого уголь поставляется потребителю.

Для обоих проектных вариантов в рамках рассмотренного подхода сформулированы задачи текущего и оперативного планирования. В рамках предложенного подхода автором было проведено исследование эффекта текущего (внутригодового) планирования при порядке развития горных работ согласно проекту, разработанному проектным институтом “Востсибгипрошахт”. Для расчетных ситуаций брались как непосредственно проектные положения на начало каждого года разработки, так и положения, представляющие собой случайные отклонения от них (с нулевым математическим ожиданием и среднеквадратичным отклонением порядка месячного объема). Расчеты показали, что за исключением отдельных периодов (годы 7-й и 8-й от начала разработки), равномерная по месяцам нагрузка на экскаваторы не обеспечивает соблюдения требования потребителей по засоренности. Данные оптимизационных расчетов иллюстрируют возможность ликвидировать нарушение ограничений на засоренность товарного угля, которое по проекту следовало бы компенсировать за счет подшихтовки “чистого” угля. Постановка разнообразных задач планирования была осуществлена с помощью разработанных автором программно-информационных средств автоматического формирования задач планирования, описываемых в главе 7. Было также показано, что в условиях Тугнуйского разреза за счет оперативного планирования нагрузок на экскаваторы возможно снизить колебания по зольности на 44%, а по засоренности видимой породой — на 13,7%.

Экибастузское — крупнейшее каменноугольное месторождение, которое разрабатывается несколькими угольными разрезами, весьма различными по технологии и структуре комплексной механизации. С момента ввода в эксплуатацию на «Восточном» используется поточная технология с применением конвейерного транспорта, а на «Богатыре» — цикличная технология с применением железнодорожного транспорта. Соответственно, и задачи планирования для этих разрезов существенно различаются. В работе сформулированы и исследованы в вычислительных экспериментах: 1) задача составления месячного технологического плана-графика добычных работ для условий разреза «Богатырь» (усреднение в потоке, планирование планово-предупредительных ремонтов); 2) задача недельно-сменного планирования для условий разреза «Восточный» (селекция по длине стружки, усреднение в штабелях). Для разреза «Восточный» обосновано увеличение выхода электроэнергии на 1÷3% и снижение затрат по всему циклу получения электроэнергии на 2÷4%.

Нерюнгринское месторождение отличается совместным залеганием коксующегося угля марок К и КО (К9–К15) и энергетического угля марки 3СС. Ввиду того, что коксующийся уголь, добываемый на разрезе «Нерюнгринский», является лишь сырьем для получения концентрата, была рассмотрена задача совместного планирования показателей добычи и обогащения. Обосновано увеличение выхода конечной продукции на 0,5÷1,0%, повышение прибыли системы «карьер — обогатительная фабрика» на 2÷4%.

Для условий разреза "Нерюнгринский" решались также задачи оптимизации развития горных работ на 1999–2003 гг. Для выработки рациональных вариантов развития горных работ на период до четырех–пяти лет необходимо оценивать возможные годовые положения горных работ по множеству показателей, отнесенных как к одному году, так и ко всему периоду. К этим показателям относятся: объемы добычи угля в целом и отдельно коксующегося и энергетического угля; объемы вскрышных работ и горных работ в целом по всему разрезу и по отдельным зонам; коэффициент вскрыши; зольность угля и отдельных его типов; стоимость транспортирования вскрыши на отвалы. Результаты выполненных расчетов для ряда вариантов оптимизационной задачи получили практическое применение (см Щадов В.М. О развитии горных работ и техническом перевооружении технологического транспорта на разрезе «Нерюнгринский» // Уголь. — 2000. — №8 — С. 36–40).

В седьмой главе описаны принципиальные решения, реализация которых позволила создать исследовательский программный комплекс, обеспечивающий подготовку и массовое решение разнообразных и взаимосвязанных задач планирования и регулирования на моделях введенного класса, сохранение и статистическую обработку их результатов. Опираясь на опыт разработанных в ВЦ РАН диалоговой системы оптимизации (ДИСО) и пакета SOLVEX, автор положил в основу представления задач планирования не программное, а "языковое" их описание. В настоящее время подобные языки моделирования, но для других типов моделей, и средства их реализации поддерживаются рядом пакетов программ оптимизации, таких как LINGO 8.0, ASCEND IV, General Algebraic Modeling System (GAMS), MINOPT и AMPL. В диссертационной работе описание ориентировано на дискретно-непрерывные модели процессов с иерархической структурой данных и сравнительно простыми взаимосвязями между величинами, в которых, однако, соотношения между величинами могут быть как единичными, так и образовывать группы однотипных соотношений.

Путем исследования сформулированных в работе детерминированных и стохастических моделей планирования и функционирования выявлена характерная структура системы входящих в эти модели величин, основные черты и формы используемых для их описания зависимостей, предложен формат описания отдельной модели в общем виде, включающий секцию описания структуры входных, промежуточных и выходных величин и секцию описания групп зависимостей между ними, разработаны форматы представления системы входных и выходных величин и способ размещения всех переменных и параметров конкретного экземпляра заданной модели в оперативной памяти. Разработаны методы проверки (анализа) и интерпретации соотношений заданной модели в контексте различных решаемых задач, включая аналитическое дифференцирование зависимостей, составляющие методическую основу подсистемы интерпретации моделей. Разработаны методы автоматического порождения реляционной базы данных Visual FoxPro для хранения входных и выходных параметров отдельной модели, извлечения отдельного экземпляра данных из базы с преобразованием в текстовой файл входных данных требуемого формата и записи в базу данных выходных величин, записанных в текстовом файле формата выходных данных, а также способы передачи данных из одной базы данных в другую (для логически взаимосвязанных или имеющих элементы сходства в структуре моделей). Основные решения по пользовательскому интерфейсу позволяют выполнять ввод и коррекцию данных для расчета конкретных экземпляров рассматриваемых моделей, запуск на счет отдельных задач и серий задач, автоматическое порождение экземпляров данных по имитационным моделям, просмотр результатов расчета на экране в различных формах. Характеристики наборов таблиц баз данных отдельных моделей и полей этих таблиц для всех введенных в информационную систему моделей хранятся в системной базе данных и используются для обмена данными между базами данных моделей и расчетными программами и для автоматической настройки пользовательского интерфейса информационной системы на работу с определенной моделью.

Ввод модели в систему сопровождается вводом ее описания (используемого далее для выбора задачи) и проверкой ее корректности, выполняемой с помощью специальной программы, дающей необходимую диагностику в случае выявленных ошибок (рис. 1). Ввод новых данных и просмотр результатов выполняется с помощью взаимосвязанных экранных форм, отображающих смежные уровни структуры данных (рис. 2). Эти формы как таковые не привязаны к определенной структуре данных и лишь при загрузке настраиваются на нее. Кроме того, на сходных принципах разработана программа оптимизации рабочей зоны угольного разреза, решающая задачи, описываемые на специально разработанном языке описания моделей такого рода. Возможности программы подтверждены путем решения 10 типов задач годового и квартального планирования для разреза "Нерюнгринский", а также отдельных задач для рудника "Эрдэнэтийн-Овоо".



Рис. 1. Облик системы. Определение задачи.

На основе результатов работы были выполнены расчеты и исследования для ряда угольных разрезов: "Тугнуйский", «Нерюнгринский», разрезов «Богатырь» и «Восточный» на Экибастузском месторождении.



Рис. 2. Просмотр данных модели.