Применение формализма гибридных систем Вмоделях управления переключаемыми производственными процессами (с приложениями к заДачам горной промышленности)

Вид материала

Основное содержание работы
T1]. В результате совокупности одновременных переключений S
N определяется условием наступления момента достижения финального качественного состояния d

Подобный материал:

1 2 3 4

Основное содержание работы

Во введении дается общая характеристика работы: обосновывается актуальность темы, формулируются цель и задачи диссертационного исследования, его основные результаты, теоретическое и практическое значение работы, положения, выносимые на защиту.

В первой главе анализируются основные подходы к моделированию производственных процессов в задачах управления, модели и методы их расчета, и на этой основе обосновывается область исследования и нерешенные задачи. Систематизация моделей проведена в работах А.А. Первозванского и представителей научной школы ИПУ — ИСА РАН (А.Н. Дюкалова, Ю.Н. Иванова, В.В. Токарева, А.И. Пропоя, Н.А. Магницкого и др.), в которой активно развивались и методы расчета линейных задач их оптимизации (также в работах А.Е. Илютовича, В.Е. Кривоножко и др.), основанные, в частности, на разных вариантах декомпозиционного подхода. Родственные задачи моделирования динамики экономических систем решены школой А.А. Петрова (И.Г. Поспелов, А.А. Шананин, А.В. Лотов и др.). Отмечается, что в зависимости от типа производственных процессов и временных горизонтов управления выделяются три основных типа моделей. Модели объемно-календарного планирования, берущие начало от работ Л.В. Канторовича, формулируются, как правило, как модели оптимального управления в непрерывном или дискретном времени. Для задач планирования комплекса работ развиваются модели на основе обобщения задачи сетевого планирования (в частности, Б.С. Разумихин, Ю.П. Иванилов, Э.Г. Давыдов, С.А. Баркалов, Д. Филлипс), но точные методы их расчета известны только для модели дискретного распределения мощностей (В.С. Михалевич, А.И. Кукса, А.П. Уздемир). Наконец, развиваются модели и методы теории расписаний, основанные на дискретном представлении производственных процессов.

Применительно к области горного производства и ряда других природно-технологических комплексов актуальны модели, основными свойствами которых являются нелинейность, динамический характер (зависимость последующего поведения системы от предыдущего), наличие факторов неопределенности. Детерминированные модели такого рода были впервые введены на примере химической промышленности Л.Т. Фаном и Ч.С. Ванем и теоретически исследованы В.Г. Болтянским, А.И. Пропоем, Л.Т. Ащепковым. Помимо специализированных методов расчета таких моделей школой Ю.Г. Евтушенко выработан общий подход к модификации методов решения задач нелинейного программирования в динамических задачах.

В работе выделены типы производственных систем, для которых не адекватны ни модели управления по этапам фиксированной продолжительности, ни модели теории расписаний. Характерными чертами таких производств являются: ограниченность номенклатуры продукции; наличие небольшого количества агрегатов большой единичной мощности, производительность которых составляет значительную долю от выпуска продукции соответствующего типа всей производственной системой; продолжительность производственных циклов (выпуск партии продукции определенного типа, выполнение вспомогательных работ) находятся в пределах между продолжительностью календарного этапа и планового периода и не являются фиксированными величинами. На границах таких производственных циклов изменяется качественное состояние производственной системы, в частности система материальных потоков. Такие производства характерны для нефтепереработки и горной промышленности, причем последнюю отличает также тесная связь между сроками производственных циклов для агрегатов, работающих на пространственно смежных участках.

Другой тип переключаемого производственного процесса, характерный для строительства, представляется в виде совокупности работ экстенсивного типа (т.е. разбивающихся на однотипные порции), для которой между сходными работами возможно непостоянное во времени распределение ресурсов-мощностей. Переключаемый характер динамики производственного процесса может быть также связан с переключаемым характером обеспечивающих процессов управления финансами, закупками и запасами материалов, которые тесно связаны с производственными процессами. Динамика таких процессов является смешанной, т.е. характеризуется сочетанием непрерывных и скачкообразных изменений основных показателей, если имеют место: вложение свободных средств в срочные депозиты или облигации, взятие или возврат кредита; приобретение материалов или продажа продукции партиями с одномоментными платежами за партии приобретаемых материалов или выплатами потребителей за поставленные партии продукции, в особенности в сочетании с закономерными изменениями цен, предложения и спроса в течение планового периода (характерно для сельскохозяйственной продукции и стройматериалов); ограниченность сроков хранения отдельных видов материалов и продукции.

Для описания таких процессов наиболее адекватными представляются нам модели со смешанной дискретно-непрерывной динамикой, ныне объединяемые общим названием — «гибридные системы». Общие формализации принадлежат зарубежным ученым J. Aubin, G. Habbard, S. Sastry, J. Lygeros, C. Tomlin, P. Antsaklis, J. Yong, A. Van der Schaft, H. Schumacher, M.S. Branicky, V.S. Borkar, Mitter S.K. и др. Следует отметить, что модели гибридных систем, в свою очередь, являются частным случаем моделей «интеллектного управления» (С.Н. Васильев, Е.А. Федосов, Б.Е. Федунов). Новые классы моделей с позиций оптимального управления исследовались А.Б. Куржанским, В.А. Дыхтой, Б.М. Миллером, Е.Я. Рубиновичем, Р. Габасовым, Ф.М. Кирилловой. В данной области оказываются актуальными и модели управления трансформирующимися системами, развитые ранее В.В. Величенко, А.Т. Ащепковым и А.С. Филатьевым.

Гораздо менее разработанной является задача реализации плана в условиях реально действующих возмущений, вызываемых в т.ч. принципиальной неточностью моделей, в которых динамика осредняется по коротким производственным циклам. Концепция совместного выбора плана и метода регулирования (В.В.Токарев) трудно реализуема. Поэтому, рассматривая задачу управления производственным процессом для определенного временного периода, целесообразно разделить ее на задачу планирования и задачу регулирования, т.е. задачу коррекции плана при регистрации возмущений и отклонений. Однако построенные по аналогии с непрерывными процессами методы автоматического регулирования в дискретном времени (Я.З. Цыпкин), как правило, малоэффективны из-за дискретного характера управления, вызывающего длительные задержки между возмущением и его компенсацией. Поэтому регулирование должно быть по преимуществу регулированием по возмущениям, для чего представляется целесообразным перенести на вводимый класс моделей построения метода инвариантного синтеза (по версии Л.И. Розоноэра — В.В. Величенко).

Что касается ресурсов регулирования, для их обоснования целесообразным представляется использование метода имитационного моделирования, эффективность которого применительно к социально-экономическим и техническим процессам значительной временной протяженности подтверждена работами А.А. Петрова, И.Г. Поспелова, А.А. Шананина, Ю.Н. Павловского, Г.И. Савина. Такой комбинированный оптимизационно-имитационный подход рассмотрен в работах А.Д. Цвиркуна, Е.Н. Хоботова и др. Способ моделирования комбинированного воздействия различных независимых случайных факторов обоснован В.Е. Лихтенштейном.

Использование метода имитационного моделирования требует привлечения моделей отдельных случайных факторов. В целом предлагается использовать следующую систему моделей:

Детерминированная динамическая модель для планирования, использующая в качестве значений неопределенных параметров:

средние или наиболее вероятные значения для параметров уравнений динамики;
эффективные значения (с учетом коэффициента использования оборудования) для производительности машин;
верхние (нижние) границы вероятного диапазона для величин, ограниченных в модели сверху (снизу).

Прогнозная модель для регулирования, используемая при регистрации конкретного возмущения или отклонения. Отличается от модели для планирования учетом зарегистрированных возмущений/отклонений и включает соотношения, приближенно описывающие взаимосвязи, вытекающие из уже случившихся случайных событий (например, восстановление работоспособности агрегата после ремонта).
Частные модели статистически определенных независимых случайных факторов с описанием случайных факторов переменными, не зависящими от управления.
Модель фактического функционирования для исследования параметров системы управления, связывающая фактические значения переменных состояния и управления, наблюдаемые и ненаблюдаемые возмущения (в т.ч. ошибки измерения и прогнозирования).

Построению моделей производственных процессов в формализме гибридных систем посвящена вторая глава диссертации. Производственная система рассматривается как совокупность работ, используемых при их выполнении единиц производственной мощности (агрегатов), накопителей и материальных потоков. Переменные состояния делятся на два типа — качественные d_i(k) (состояние выполнения отдельной работы или стадия производственного цикла для агрегата) и количественные x_i(t,k) (текущий объем выполняемой работы или время с начала ее выполнения, запас в накопителе); последние могут скачкообразно изменять состояние в результате переключений. Значения переменных управления определяются для отдельных этапов; ими являются: u_i(k) — интенсивности выполнения работы (или текущей операции отдельным агрегатом); интенсивности отдельных грузопотоков u_F_f(k).

Проведена систематизация типовых соотношений моделей, которыми являются:

1) уравнения количественной динамики — для объемов работ, суммарных затрат материалов, запасов в накопителях (с учетом потерь) и суммарных затрат на хранение соответственно

dx_i(t,k)/dt=u_i(k), (1)

dx_i_p(t,k)/dt=a_i_pu_i(k), (2)

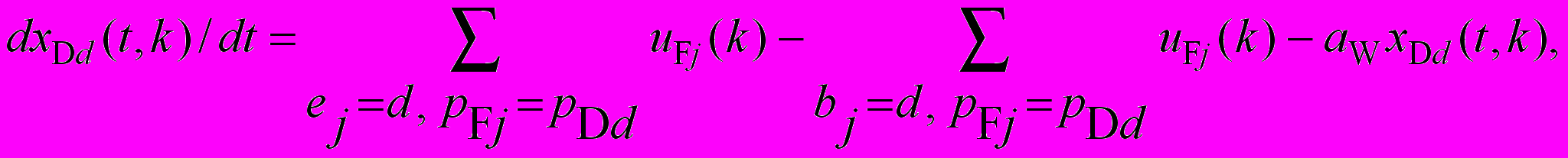(3)

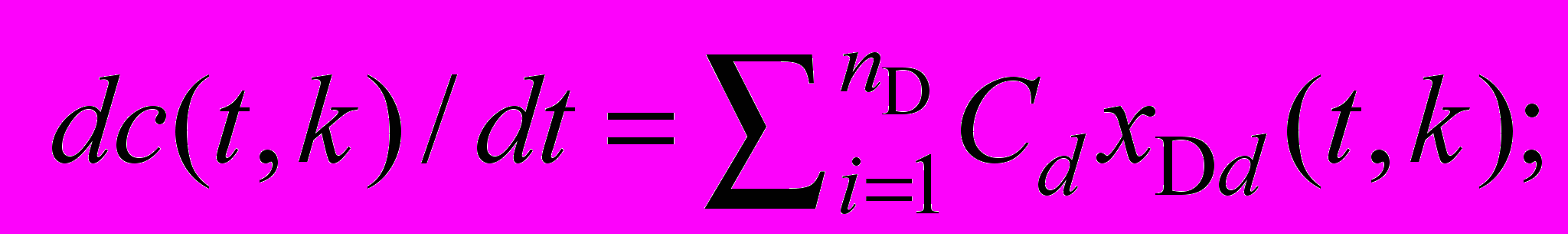(4)

2) балансовые соотношения (по материалам, выходным и промежуточным продуктам и компонентам и денежным средствам), в частности, для p-го продукта, образующегося в результате i-й работы, если он поступает непосредственно в выходной поток,

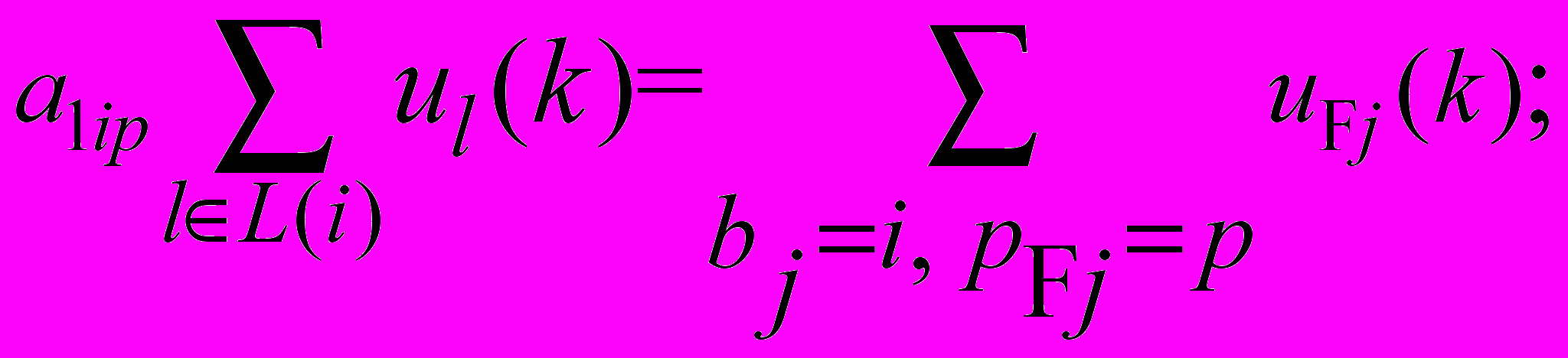(5)

3) ограничения на производительность (использование и разделение производственных мощностей между однотипными работами)

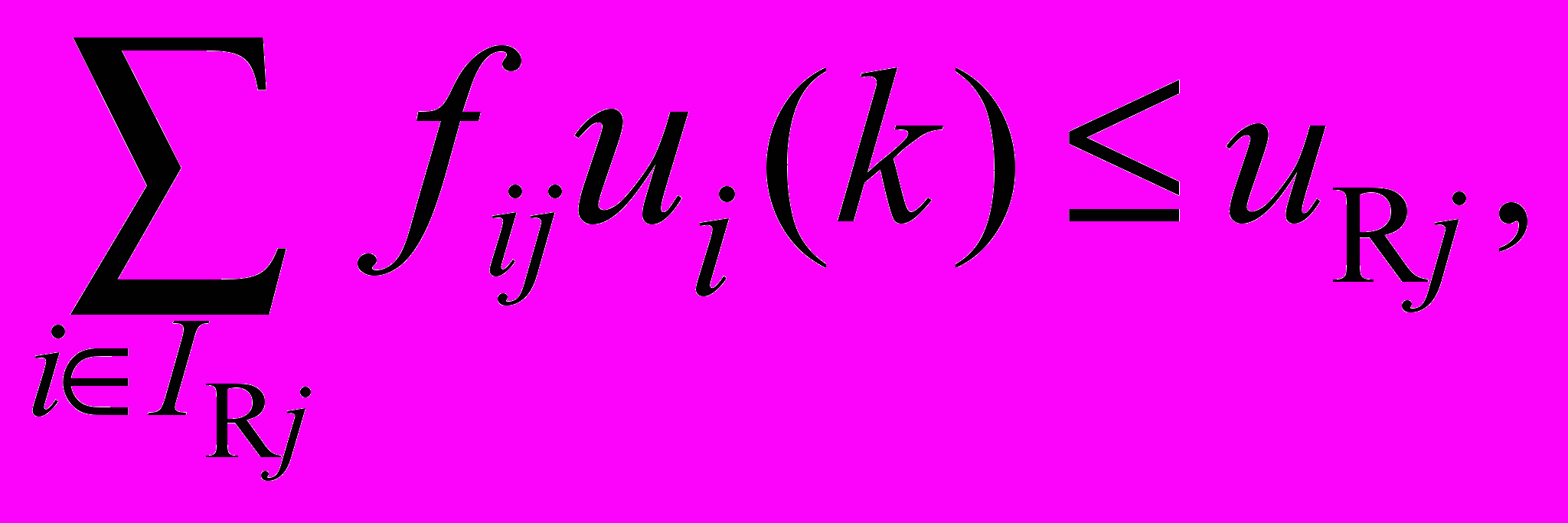j=1,…, m, (6)

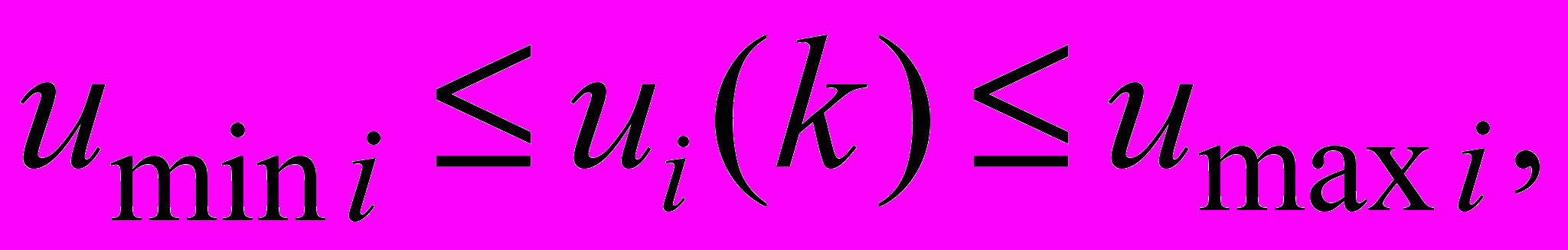если d_i(k)=1, иначе u_i(k)=0; (7)

4) ограничения по провозной способности участков транспортных коммуникаций

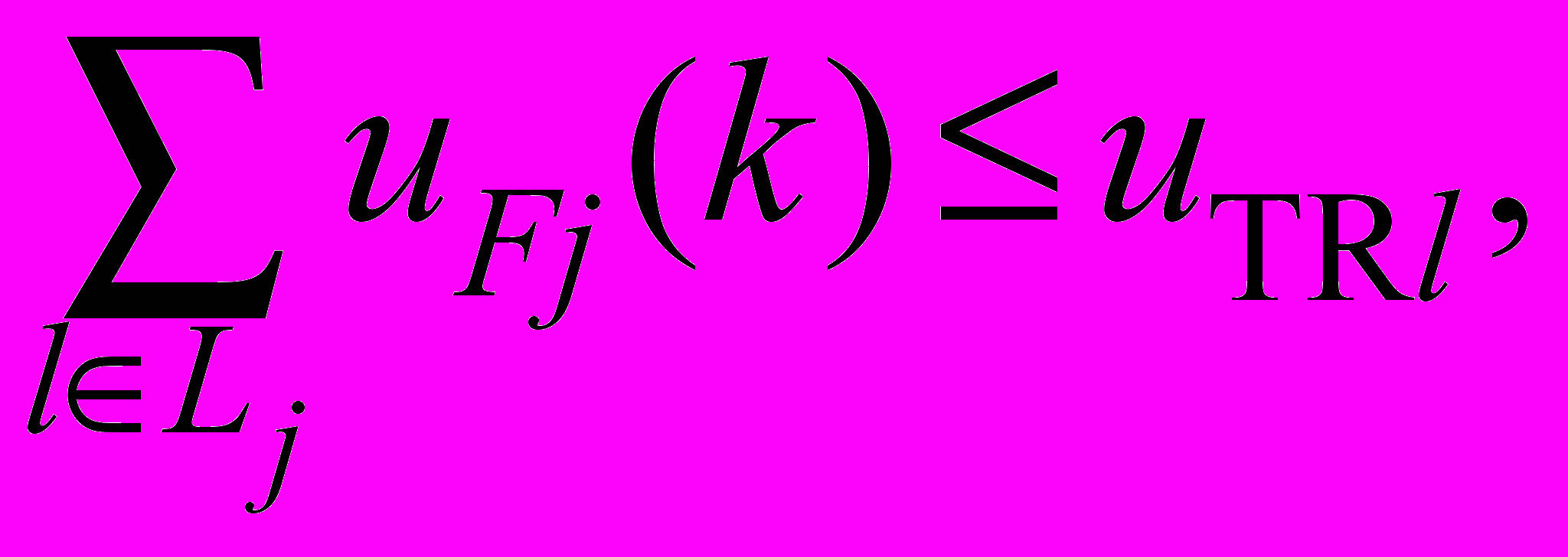l=1,…N_TR; (8)

5) ограничения на объем транспортной работы по совокупностям грузопотоков, обслуживаемых однотипным транспортом,

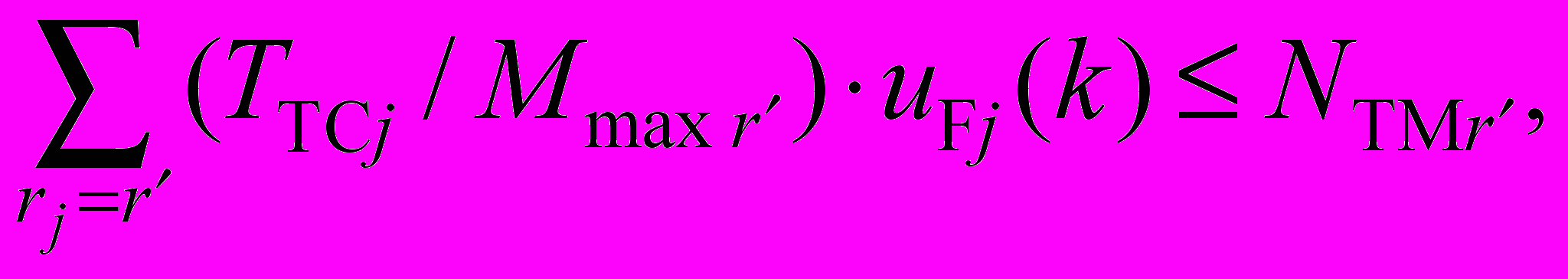(9)

где N_TM_r — общее количество единиц r-го вида транспорта, M_max_r — грузоподъемность;

6) условия окончания работы и начала последующих работ (определяющие момент окончания k го этапа T(k+1)) и соответствующие изменения их качественного состояния (d_i(k)Î{0;1;2}: 0 — "не начата", 1 — "выполняется", 2 — "завершена")

x_i(T(k+1), k)=x_T_i, (10)

d_i(k+1)=2, (11)

d_i(k+1)=1, если P_i₂(d(k))P_i и P_i₂(d(k+1))=P_i, (12)

где P_i — множество предшествующих работ для i-ой работы, P_i₂(d)={i | d_i=2};

аналогично для разгружаемого накопителя

x_D_d(T(k+1), k)=0, (13)

следствием чего является его одномоментное пополнение

x_D_d(T(k+1), k+1)=X_d (14)

или изменение состояния с «разгрузка» (d_i(k)=4) на «загрузка» (d_i(k)=3); аналогично для формируемой партии продукции, рассматриваемой как накопитель

x_D_d(T(k+1), k)=X_S_d; (15)

7) ограничения на взаимное положение взаимосвязанных работ i и j, которые достаточно рассматривать в моменты окончания этапов,

x_i(T(k+1), k)x_j(T(k+1), k)-x_i_j; (16)

8) ограничения на моменты времени начала и(или) окончания отдельных работ или их продолжительности, связываемые, следовательно, с моментами переключений.

Для горного производства, наряду с перечисленными, имеют место соотношения аналогичных типов (дифференциальные и функциональные уравнения), отличающиеся наличием нелинейных зависимостей, характеризующих пространственное распределение запасов и работ. В разделе 2.2 рассматривается пространственный аспект распределения ресурсов при планировании на карьерах, выполнено исследование адекватности и точности моделей геометрической формы борта и выработанного пространства (ВП) карьера, которые служат составной частью моделей производственного процесса. Ввиду того, что горные работы непрерывно изменяют форму карьера, а отдельные его элементы имеют существенно различный срок существования, адекватность этих моделей может пониматься только как соответствие порождаемых ими геометрических конфигураций усредненным конфигурациям карьера, называемых проектными положениями горных работ (ППГР). Сформулировано принципиальное математическое описание ППГР системой линий ограниченной кривизны — бровок уступов, предложены две формы аппроксимирующих полилинейных моделей (контурная и контурно-секторная) и установлены оценки погрешности аппроксимации в метрике Хаусдорфа, позволяющие выбирать размерность и параметры модели в зависимости от требуемой точности. Показано преимущество этих моделей в точности представления геометрической формы карьера перед известными. Предложены согласованные с ограничениями введенных моделей определения геометрических объектов — элементов карьерного поля, которые требуется определять при переходе от задач годового планирования к задачам внутригодового планирования, и алгоритмы их построения. Выведены формулы для значений геологических характеристик элементов карьерного поля в зависимости от организационно-технологических схем.

Для объединения вышеперечисленных элементов моделей задач планирования в работе введен новый класс гибридных систем, называемый далее классом событийно-переключаемых процессов. Событийно-переключаемый процесс есть N этапный процесс, в котором моменты окончания этапов определяются наступлением одного или нескольких событий окончания работ или частных процессов (для произвольного k множество событий S(k){1,…, L}, где L — количество типов событий). Для произвольного (k-го) этапа процесса, занимающего нефиксированный промежуток времени [T(k), T(k+1)), постоянны значения вектора качественного состояния d(k) (принимающего значение из конечного множества A_D) и управления u(k)R^m, а связь между конечным x¹(k)Rⁿ и начальным x⁰(k)Rⁿ состояниями и продолжительностью этапа t(k) имеет вид разностных уравнений

x¹(k)=Y(d(k), x⁰(k), u(k), t(k)), (17)

где Y(d(k), x⁰(k), u(k), t) — решение задачи Коши для системы

dx(t, k)/dt=f(d(k), x(t, k), u(k)) (18)

с начальными условиями t=0, x(0, k)=x⁰(k). Существует i(s)-я компонента вектора состояния x(t, k) (i(s)i(s) при s s), для которой

f_i₍_s₎(d(k), x(t, k), u(k))f_min_s>0. (19)

Условия окончания этапа выражаются в виде

, sS(k), (20)

, sS(k), (21)

первое из которых (20) есть условие наступления событий из множества S(k), а из второго вытекает, что внутри этапа событий не происходит, т.к. в силу (21) с учетом (19) наступление остальных событий происходит позже. Условие окончания определенного календарного этапа также имеет вид (20), если текущее время рассматривать в качестве переменной состояния x_n.

Кроме того, предполагается, что при любом s{1,…, L}

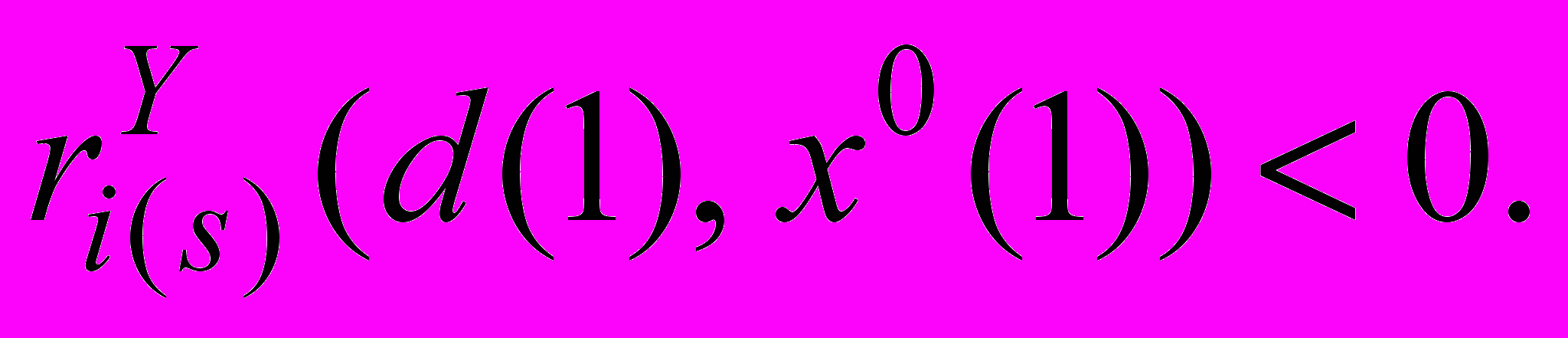(22)

Предположение (22) означает, что модель описывает производственный процесс и вне пределов интервала моделирования [0, T₁]. В результате совокупности одновременных переключений S(k) значения некоторых компонент дискретных и непрерывных векторов состояния (набор которых зависит от S(k), d(k)) изменяются:

d(k+1)=D(S(k), d(k)), x⁰(k+1)=X(S(k), d(k), x¹(k)), (23)

причем существует такая положительная константа K_X0, что при любых S{1,…, L}, sS, dA_D, xRⁿ

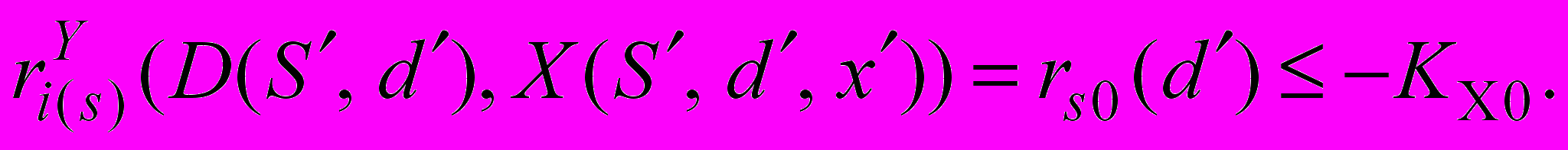(24)

Количество шагов процесса N определяется условием наступления момента достижения финального качественного состояния

d_i(N+1)=d_i_T, iI_T, (25)

которое при фиксированной продолжительности процесса T₁выводится из условия T(N+1)=T₁, имеющего форму (20) относительно текущего времени, выступающего в качестве фазовой переменной. Система ограничений, которой должен подчиняться процесс, состоит из нескольких типов ограничений: ограничений, относящихся к любому этапу и имеющих вид

, jJ₁(d(k)),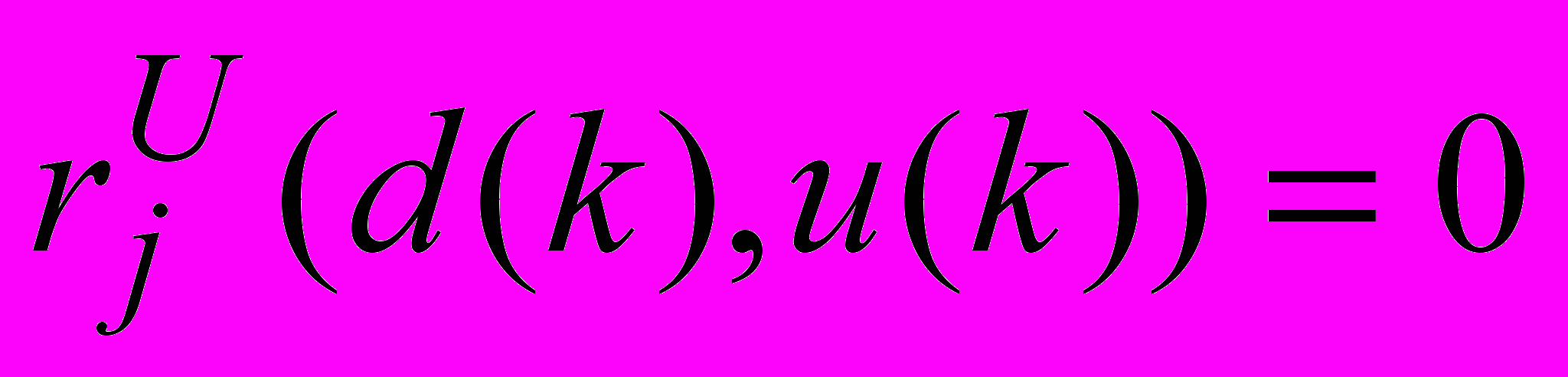

, jJ₂(d(k)), (26)

и ограничений, связанных с моментами событий определенного типа (включая ограничения на конечное состояние)

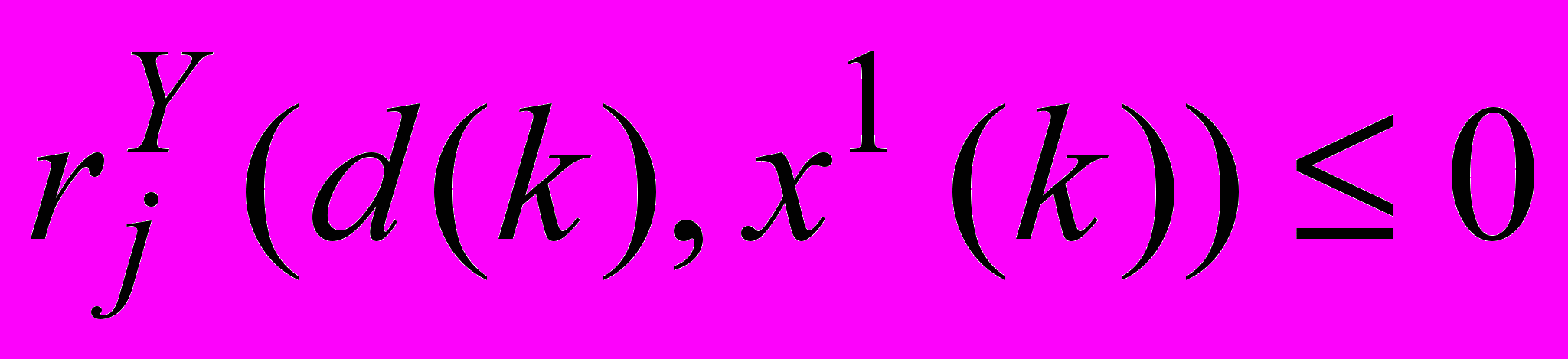, jK₁(s), sS(k). (27)

Предполагается, что при любом d(k)A_D множество U₀(d(k)) значений векторов u(k), при котором условия (26) совместны, не пусто и ограничено.

Задача планирования рассматривается как задача минимизации значения целевого функционала, который может быть задан в одной из форм:

F₀(x¹(N)), (28)

(29)

max{Y_j(d(k), x⁰(k), u(k), t(k)) | jJ₀(d(k)), k=1,…, N}. (30)

Далее предполагается, что при любых dA_D, xRⁿ, S₁, S₂{1,…, L}, S₁S₂=, справедливы следующие соотношения:

D(S₁S₂, d)=D(S₁, D(S₂, d)), (31)

X(S₁S₂, d, x)=X(S₁, D(S₂, d), X(S₂, d, x)). (32)

Справедливость данных соотношений согласуется с рассмотренными выше типовыми соотношениями моделей переключаемых производственных процессов.

Важнейшей характеристикой событийно-переключаемого процесса является последовательность S(1),…, S(N) (называемая, следуя В.В.Величенко,

Blog

Применение формализма гибридных систем Вмоделях управления переключаемыми производственными процессами (с приложениями к заДачам горной промышленности)

Основное содержание работы