Рекомендации по подготовке и проведению экзамена и оцениванию ответов
| Вид материала | Документы |
- Методические рекомендации по подготовке Ульяновск, 1747.38kb.
- Методические рекомендации при подготовке егэ-2012» 1 Методический сборник «Анализ результатов, 999.71kb.
- Методческие рекомендации по подготовке и проведению итогового государственного (междисциплинарного), 155.1kb.
- Методические рекомендации по подготовке и проведению егэ в пунктах проведения экзамена, 543.35kb.
- Методические рекомендации по организации и проведению самостоятельной работы, подготовке, 30.36kb.
- Рекомендации в помощь преподавателю при подготовке методических разработок, 229.22kb.
- Методические рекомендации по подготовке и проведению государственной (итоговой) аттестации, 908.06kb.
- Рекомендации по оцениванию ответов на первый и второй вопросы. Отметка «5», 134.27kb.
- На помощь методическим комиссиям и жюри в составлении заданий для школьного этапа всероссийской, 517.23kb.
- Методические рекомендации для учителей русского языка по подготовке учеников к внешнему, 217.64kb.
Билет 2
1. Измерение информации: содержательный иалфавитный подходы. Единицы измерения информации.
Определить понятие "количество информации" довольно сложно. В решении этой проблемы существует два основных подхода. Исторически они возникли почти одновременно. В конце 1940 г. один из основоположников кибирнетиеи американский математик Клож Шенон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к "объемному подходу".
Количество информации как мера уменьшения неопределенности
(вероятностный подход)
С точки зрения отдельного человека, ценность информации определяется тем, насколько она проясняет для него какой-либо вопрос, то есть уменьшает неопределенность ситуации. При этом количество одной и той же информации может быть оценено различными людьми по-разному. Для объективного измерения количества информации необходимо формализовать задачу.
Будем считать события равновозможными, если мы не располагаем заранее никакой информацией (статистическими данными, логическими умозаключениями и т.д.), о том, что шансы одного из событий выше или ниже, чем шансы любого другого. При этом имеется в виду, что в результате опыта обязательно наступит какое-либо событие и притом только одно.
Так, например, при подбрасывании монеты выпадение орла или решки можно считать равновозможными событиями, предполагая монету идеальной, то есть исключив из рассмотрения возможность других исходов ("зависла в воздухе", "встала на ребро"), а также влияние на исход опыта чеканки на сторонах монеты, отклонения формы реальной монеты от правильной и т. д.
Чем больше равновозможных событий, тем больше неопределенность ситуации. Минимальный размер сообщения о том, что произошло одно из двух равновозможных событий, равен одному биту. Информацию о том, что произошло первое событие, можно закодировать в двоичном алфавите нулем, а о том, что произошло второе событие – единицей.
Для уменьшения неопределенности в два раза (вместо двух возможных событий – одно реально произошедшее) требуется один бит информации. Иначе говоря, сообщение, уменьшающее неопределенность ситуации в два раза, несет один бит информации. Если его длина, подсчитанная с использованием алфавитного подхода, больше, значит сообщение несет избыточную, с точки зрения уменьшения неопределенности, информацию.
Пример. С точки зрения уменьшения неопределенности, сообщение о исходе опыта бросания идеальной монеты (два равновозможных события) несет один бит информации.
Можно рассчитать длину сообщения в двоичном алфавите, необходимую для передачи информации. Для уменьшения неопределенности ситуации в 2n раз необходимо n бит информации.
Пример. С точки зрения уменьшения неопределенности, сообщение о исходе опыта бросания двух идеальных монет (четыре равновозможных события: орел-решка; решка-орел; орел-орел; решка-решка) несет два бита информации. Действительно, 2n в данном случае равняется четырем, следовательно n = 2.
Задача нахождения n по известному значению k = 2n решается нахождением логарифма числа k по основанию 2, поэтому, для того, чтобы закодировать информацию, уменьшающую неопределенность в k раз, необходимо log2k бит информации. Приведем таблицу некоторых двоичных логарифмов, являющихся целыми числами. n log2k

Пример. С точки зрения уменьшения неопределенности, сообщение о исходе опыта бросания точечного объекта на шахматную доску (равновозможные события - попадания в одну из 64 клеток) несет 6 бит информации. Действительно, k в данном случае равняется 64, log264 = 6. Минимальная длина двоичного сообщения также будет равна 6. Подробнее: номер клетки доски по вертикали можно закодировать целым числом от 0 до 7. Для этого требуется 3 двоичных разряда (см. Системы счисления). Еще 3 разряда нужны для того, чтобы закодировать номер клетки доски по горизонтали, 3+3=6. Можно также просто пронумеровать все клетки числами от 0 до 63. Для этого опять-таки потребуется 6 разрядов.
Если используется алфавит, состоящий не из двух, а из 2p знаков, то каждый знак может нести информацию, уменьшающую неопределенность ситуации в 2p раз. Таким образом, сообщение из m знаков позволяет уменьшить неопределенность в (2p)m = 2pm раз, то есть его информационный объем равен m·p бит, что согласуется с результатом, полученным при использовании алфавитного подхода.
Пример. Пусть для кодирования сообщения о попадании точечного объекта на клетку шахматной доски используется алфавит из 8 символов (2p = 8, следовательно p = 3). Сообщение уменьшает неопределенность в 64 раза, следовательно 2pm = 23m = 64, отсюда 3m = log264 = 6; m = 2, то есть для кодирования информации попадании точечного объекта на клетку шахматной доски потребуется сообщение из двух знаков восьмисимвольного алфавита. Действительно, в первом знаке сообщения можно закодировать, например, информацию о горизонтали клетки, а во втором — о вертикали. В общепринятой шахматной нотации фактически используется указанный способ именования клеток, только для удобства чтения первый символ сообщения записывается как буква, а второй - как цифра. С математической точки зрения ничто не мешает обозначать клетки a1 и h8 как aa и hh или 11 и 88, используя только 8 символов.
Алфавитный подход
Если информация представлена в виде дискретного сообщения, то логично считать количеством информации его длину, то есть общее число знаков в сообщении. Но длина сообщения зависит не только от содержащейся в нем информации. На нее влияет мощность алфавита используемого языка. Чем меньше знаков в используемом алфавите, тем длиннее сообщение. Так, например, в алфавите азбуки Морзе всего три знака (точка, тире, пауза), поэтому для кодирования каждой русской или латинской буквы нужно использовать несколько знаков, и текст, закодированный по Морзе, будет намного длиннее, чем при обычной записи.
Пример: Сигнал SOS: 3 знака в латинском алфавите;
11 знаков в алфавите Морзе: ··· пауза – – – пауза ···.
Для упорядочивания измерений информационный объем сообщений принято измерять в битах. Один бит соответствует одному знаку двоичного алфавита. Итак, чтобы измерить длину сообщения, его нужно представить в двоичном виде и подсчитать количество двоичных знаков – битов. При этом совсем не обязательно уметь интерпретировать сообщения.
Пример: Пусть сообщение в двоичном алфавите выглядит следующим образом: 000100010001. Мы не знаем, какая информация была заложена в этом сообщении, но можем легко подсчитать его длину – 12 двоичных знаков, следовательно, его информационный объем равен 12-ти битам.
Такой способ измерения количества информации называется алфавитным подходом. При этом измеряется не содержание информации с точки зрения его новизны и полезности, а размер несущего информацию сообщения. Мы уже убедились, что при алфавитном подходе к определению количества информации одни и те же сведения, закодированные по-разному, будут иметь различный информационный объем. Сообщения одинаковой длины могут нести совершенно как совершенно бесполезные сведения, так и нужную информацию. Пример: Применяя алфавитный подход, получаем, что информационный объем слов “фыырпбьощ” и “компьютер” совершенно одинаков, а слов “ученик” и “учащийся” – различен.
Если алфавит содержит 2n знаков, то каждый из его знаков можно закодировать с помощью n знаков двоичного алфавита. Таким образом, объем информации, содержащейся в сообщении длиной m при использовании алфавита мощностью 2n, равен m·n бит.
Пример:
Найдем информационный объем слова SOS, записанного в компьютерной кодировке. При кодировании букв в компьютере используется либо алфавит ASCII (American Standard Code for Information Interchange — американский стандартный код обмена информацией), состоящий из 28=256 знаков, либо алфавит Unicode, мощность которого 216 = 65536. В слове SOS три буквы, следовательно, его информационный объем 3·8=24 или 3·16=48 бит, в зависимости от используемой кодировки.
Алфавитный подход удобен при подсчете количества информации, хранимого, передаваемого и обрабатываемого техническими устройствами. Действительно, устройствам нет дела до содержательной стороны сообщений. Компьютеры, принтеры, модемы работают не с самой информацией а с ее представлением в виде сообщений. Оценить информационные результаты их работы как полезные или бесполезные может только человек.
Единицы измерения информации
Для удобства, помимо бита используются более крупные единицы измерения количества информации. Вот соотношения между ними:
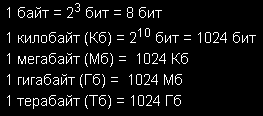
То, что отношения между единицами измерения кратны степеням 2, объясняется большим теоретическим и практическим значением двоичного кодирования в информатике.
2. Создание и редактирование текстового документа (исправление ошибок, удаление или вставка текстовых фрагментов), в том числе использование элементов форматирования текста (установка параметров шрифта и абзаца, внедрение заданных объектов в текст).
Билет 3
1. Дискретное представление информации: двоичные числа; двоичное кодирование текста в памяти компьютера. Информационный объем текста.
Кодирование информации
Представление информации происходит в различных формах в процессе восприятия окружающей среды живыми организмами и человеком, в процессах обмена информацией между человеком и человеком, человеком и компьютером, компьютером и компьютером и так далее. Преобразование информации из одной формы представления (знаковой системы) в другую называется кодированием.
Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.
В процессе обмена информацией часто приходится производить операции кодирования и декодирования информации. При вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на клавиатуре происходит кодирование знака, то есть преобразование его в компьютерный код. При выводе знака на экран монитора или принтер происходит обратный процесс - - декодирование, когда из компьютерного кода знак преобразуется в его графическое изображение.
Двоичное кодирование информации
В компьютере для представления информации используется двоичное кодирование, так как удалось создать надежно работающие технические устройства, которые могут со стопроцентной надежностью сохранять и распознавать не более двух различных состояний (цифр):
- электромагнитные реле (замкнуто/разомкнуто), широко использовались в конструкциях первых ЭВМ;
- участок поверхности магнитного носителя информации (намагничен/размагничен);
- участок поверхности лазерного диска (отражает/не отражает);
- триггер (см. п. 3.7.3), может устойчиво находиться в одном из двух состояний, широко используется в оперативной памяти компьютера.
Все виды информации в компьютере кодируются на машинном языке, в виде логических последовательностей нулей и единиц.
Цифры двоичного кода можно рассматривать как два равновероятных состояния (события). При записи двоичной цифры реализуется выбор одного из двух возможных состояний (одной из двух цифр) и, следовательно, она несет количество информации, равное 1 биту.
Даже сама единица измерения количества информации бит (bit) получила свое название от английского словосочетания BInary digiT (двоичная цифра).
Важно, что каждая цифра машинного двоичного кода несет информацию в 1 бит. Таким образом, две цифры несут информацию в 2 бита, три цифры — в 3 бита и так далее. Количество информации в битах равно количеству цифр двоичного машинного кода.
Представление числовой информации с помощью систем счисления
Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами. Например, в десятичной системе счисления числа записываются с помощью десяти всем хорошо известных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.
Римская непозиционная система счисления. Самой распространенной из непозиционных систем счисления является римская. В качестве цифр в ней используются: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).
Значение цифры не зависит от ее положения в числе. Например, в числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину - число 10, три числа по 10 в сумме дают 30.
Позиционные системы счисления. Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, то есть в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе - 60 минут).
В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и так далее.
В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе.
Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание.
Двоичное кодирование текстовой информации
Начиная с конца 60-х годов, компьютеры все больше стали использоваться для обработки текстовой информации и в настоящее время большая часть персональных компьютеров в мире (и наибольшее время) занято обработкой именно текстовой информации.
Традиционно для кодирования одного символа используется количество информации, равное 1 байту, то есть I = 1 байт = 8 битов.
Для кодирования одного символа требуется 1 байт информации.
Если рассматривать символы как возможные события, то можно вычислить, какое количество различных символов можно закодировать:
N = 2 I = 2 8 = 256.
Такое количество символов вполне достаточно для представления текстовой информации, включая прописные и строчные буквы русского и латинского алфавита, цифры, знаки, графические символы и пр.
Кодирование заключается в том, что каждому символу ставится в соответствие уникальный десятичный код от 0 до 255 или соответствующий ему двоичный код от 00000000 до 11111111. Таким образом, человек различает символы по их начертаниям, а компьютер - по их кодам.
При вводе в компьютер текстовой информации происходит ее двоичное кодирование, изображение символа преобразуется в его двоичный код. Пользователь нажимает на клавиатуре клавишу с символом, и в компьютер поступает определенная последовательность из восьми электрических импульсов (двоичный код символа). Код символа хранится в оперативной памяти компьютера, где занимает один байт.
В процессе вывода символа на экран компьютера производится обратный процесс — декодирование, то есть преобразование кода символа в его изображение.
Важно, что присвоение символу конкретного кода — это вопрос соглашения, которое фиксируется в кодовой таблице. Первые 33 кода (с 0 по 32) соответствуют не символам, а операциям (перевод строки, ввод пробела и так далее).
Коды с 33 по 127 являются интернациональными и соответствуют символам латинского алфавита, цифрам, знакам арифметических операций и знакам препинания.
Коды с 128 по 255 являются национальными, то есть в национальных кодировках одному и тому же коду соответствуют различные символы.
К сожалению, в настоящее время существуют пять различных кодовых таблиц для русских букв (КОИ8, СР1251, СР866, Mac, ISO), поэтому тексты, созданные в одной кодировке, не будут правильно отображаться в другой.
В настоящее время широкое распространение получил новый международный стандарт Unicode, который отводит на каждый символ не один байт, а два, поэтому с его помощью можно закодировать не 256 символов, а N = 2 16 = 65536 различных символов.
С развитием IBM PC международным стандартом стала таблица кодов ASCII:
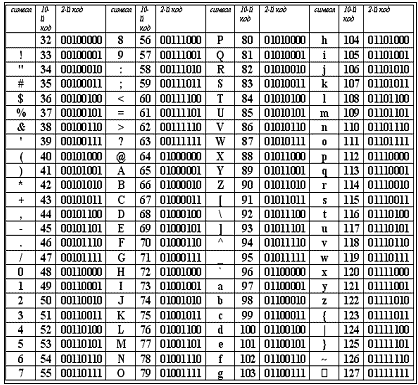
Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов.
В этом случае легко подсчитать объем информации в тексте. Если 1 символ алфавита несет 1 байт информации, то надо просто сосчитать количество символов, полученное число даст информационный объем текста в байтах.
Пусть небольшая книжка, сделанная с помощью компьютера, содердит 150 страни; на каждой странице - 40 строк, в каждой строке - 60 символов. Значит страница содержит 40 х 60 = 2400 байт информации. Объем всей информации в книге: 2400 х 150 = 360 000 байт.
Обратите внимание! Цифры кодируются по стандарту ASCII в двух случаях - при вводе-выводе и когда они встречаются в тексте. Если цифры участвуют в высилениях, то осуществляется их преобразование в другой двоичный код.
Возьмем число 57.
При использовании в тексте каждая буква будет представлена своим кодом в соответсвии с таблицей ASCII. В двоичной системе - это 00110101 00110111.
При использовании в вычислениях, код этого числа будет получен по правилам перевода в двоичную систему и получим - 00111001.
2. Создание и обработка графических изображений средствами графического редактора. Ввод изображения через сканер или с цифрового фотоаппарата. Простейшая обработка цифрового изображения.
Билет 4
1. Дискретное представление информации: кодирование цветного изображения в компьютере (растровый подход). Представление и обработка звука и видеоизображения. Понятие мультимедиа.
Кодирование информации в компьютере
Вся информация , которую обрабатывает компьютер, должна быть представлена двоичным кодом с помощью двух цифр — 0 и 1. Эти два символа принято называть двоичными цифрами, или битами. С помощью двух цифр 1 и 0 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организовано два важных процесса:
- кодирование, которое обеспечивается устройствами ввода при преобразовании входной информации в форму, воспринимаемую компьютером, то есть в двоичный код;
- декодирование, которое обеспечивается устройствами вывода при преобразовании данных из двоичного кода в форму, понятную человеку.
С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного
более простым, чем применение других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц, если представить эти значения как два возможных устойчивых состояния электронного элемента:
- 0 — отсутствие электрического сигнала или сигнал имеет низкий уровень;
- 1 — наличие сигнала или сигнал имеет высокий уровень.
Эти состояния легко различать. Недостаток двоичного кодирования — длинные коды. Но в технике легче иметь дело с большим числом простых элементов, чем с небольшим количеством сложных.
Вам и в быту ежедневно приходится сталкиваться с устройством, которое может находиться только в двух устойчивых состояниях: включено/выключено. Конечно же, это хорошо знакомый всем выключатель. А вот придумать выключатель, который мог бы устойчиво и быстро переключаться в любое из 10 состояний, оказалось невозможным. В результате после ряда неудачных попыток разработчики пришли к выводу о невозможности построения компьютера на основе десятичной системы счисления. И в основу представления чисел в компьютере была положена именно двоичная система счисления.
В настоящее время существуют разные способы двоичного кодирования и декодирования информации в компьютере. В первую очередь это зависит от вида информации, а именно, что должно кодироваться: текст, числа, графические изображения или звук. Кроме того, при кодировании чисел важную роль играет то, как они будут использоваться: в тексте, в расчетах или в процессе ввода-вывода. Накладываются также и особенности технической реализации.
Кодирование графической информации
Создавать и хранить графические объекты в компьютере можно мя способами — как растровое или как векторное изображение. Для каждого типа изображения используется свой способ кодирования.
Растровое изображение представляет собой совокупность точек, используемых для его отображения на экране монитора. Объем растрового изображения определяется как произведение количества точек и информационного объема одной точки, который зависит от количества возможных цветов. Для черно-белого изображения информационный объем одной точки равен 1 биту, так как точка может быть либо черной, либо белой, что можно закодировать двумя цифрами — 0 или 1.
Для кодирования 8 цветов необходимо 3 бита; для 16 цветов — 4 бита; для 6 цветов — 8 битов (1 байт) и т.д.
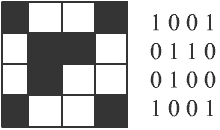
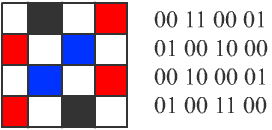
Кодирование звуковой информации
Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон. Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).
В процессе кодирования непрерывного звукового сигнала производится его временная дискретизация. Непрерывная звуковая волна разбивается на отдельные маленькие участки, причем для каждого такого участка устанавливается определенная величина амплитуды.Таким образом, непрерывная зависимость амплитуды сигнала от времени заменяется на дискретную последовательность уровней громкости.
Современные звуковые карты обеспечивают 16-битную глубину кодирования звука. В таком случае количество уровней сигнала будет равно 65536.
При двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала. Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, т.е. от частоты дискретизации. Чем больше количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования.
Количество измерений в секунду может лежать в диапазоне от 8000 до 48000, т.е. частота дискретизации аналогового звукового сигнала может принимать значения от 8 до 48 кГц - качество звучания аудио-CD. Следует также учитывать, что возможны как моно-, так и стерео-режимы.
Стандартная программа Windows Звукозапись играет роль цифрового магнитофона и позволяет записывать звук, т.е. дискретизировать звуковые сигналы, и сохранять их в звуковых файлах в формате wav. Также эта программа позволяет производить простейшее редактирование звуковых файлов.
Представление видеоинформации
В последнее время компьютер все чаще исползуется для работы с видеоинформацией. Простейшей такой работой является просмотр кинофильмов и видеоклипов. Следует четко представлять, что обработка видеоинформации требует очень высокого быстродействия компьютерной системы.
Что представляет собой фильм с точки зрения информатики? Прежде всего, это сочетание звуковой и графической информации. Кроме того, для создания на экране эффекта движения используется дискретная по своей сути технология быстрой смены статических картинок. Исследования показали, что если за одну секунду сменяется более 10-12 кадров, то человеческий глаз воспринимает изменения на них как непрерывные.
Казалось бы, если проблемы кодирования статистической графики и звука решены, то сохранить видеоизображение уже не составит труда. Но это только на первый взгляд, поскольку, как показывет разобранный выше пример, при использовании традиционных методов сохранения информации электронная версия фильма получится слишком большой. Достаточно очевидное усевершенствование состоит в том, что первый кадр запомнить целиком (в литературе его принято называть ключевым), а в следующих сохранять только отличия от начального кадра (разностные кадры).
Существует множество различных форматов представления видеоданных.
В среде Windows, например, уже боле 10 лет (начиная с версии 3.1) применятся формат Video for Windows, базирующийся на универсальных файлых с расширением AVI (Audio Video Interleave - чередование аудио и видео).
Большое рапространение получила технология под названием DivX (происходит от сокращения слова Digital Video Express). Благодаря DivX удалось достигнуть степени сжатия, позволившей вместить качественную запись полнометражного фильма на один компакт диск - сжать 4,7 Гб DVD-фильма до 650 Мб.
Что такое "мультимедиа"?
Мультимедиа – это собирательное понятие для различных компьютерных технологий, использующих динамические (движущиеся) изображения и звуковые эффекты. Само слово “мультимедиа“ происходит от двух латинских корней multi – много и media – средство. Использование видео- и аудиоэффектов обеспечивает наглядность представления информации, позволяет преподносить ее в более привлекательном с эстетической точки зрения виде. Примерами программных систем, широко использующих средства мультимедиа, являются системы подготовки презентаций, обучающие системы, в том числе компьютерные тренажеры и виртуальные лаборатории, компьютерные энциклопедии, фоно- и видеотеки, игры.
Основными объектами мультимедиа в настоящее время являются записи звука и динамических изображений, представленные в различных цифровых форматах.
Практически все программные системы, использующие мультимедиа-объекты, являются интерактивными, то есть ведущими интенсивный диалог с пользователем, поэтому для них очень важна возможность не только качественного, но и быстрого воспроизведения звука и изображений.
Широко распространены программы, служащие для воспроизведения объектов мультимедиа. Такие программы называются проигрывателями или плеерами (от английского «player»).
2. Работа с файловой системой, с графическим интерфейсом (выполнение стандартных операций с файлами: создание, копирование, переименование, удаление). Организация индивидуального информационного пространства (настройка элементов рабочего стола, проверка на вирусы, использование архиватора).
