Машинная программа. 9 Классификация вычислительных устройств. 11 Основные устройства компьютера, его архитектура. 13

Вид материала

Программа

Содержание 3.6. Операционная система UNIX. 4. Программирование на языке Паскаль. 4.1. Примеры алгоритмов

Подобный материал:

• Тест «Основные устройства икт» 1 вариант Вкакой строке перечислен минимальный набор, 31.4kb.
• Лекция Внешние устройства компьютера, 309.96kb.
• Назипов Рамиль Хайретдинович Назначение и устройство компьютера урок, 165.22kb.
• Архитектура персонального компьютера, 124.05kb.
• «Архитектура ЭВМ учитель информатики Юдина Наталия Сергеевна Тема: «Устройства персонального, 111.25kb.
• Оболочка Norton Commander. Windows и программа, 26.31kb.
• Лекция 12. Архитектура компьютера, 124.05kb.
• 1. Функциональная схема компьютера. Основные устройства компьютера, их назначение, 132.15kb.
• «Цифровые устройства и микропроцессоры», 23.44kb.
• Классификация и основные параметры, 145.52kb.

3.6. Операционная система UNIX.

Система UNIX имеет особенности, выгодно отличающие ее от других операционных систем. В ее основу положена концепция процессов. Процессом называется любой экземпляр запущенной программы (программой в UNIX называется просто файл откомпилированной программы). Каждый процесс с точки зрения UNIX представляет собой программу, выполняемую на своем виртуальном компьютере и использующую свою виртуальную память. Один процесс может запускать другой процесс (процесс-отец и процесс-сын). При этом совершенно неважно, на каком компьютере запускается тот или иной процесс и на каком носителе какого компьютера расположены данные, используемые данным процессом. UNIX имеет богатые возможности обмена информацией между процессами, позволяющие синхронизировать выполнение параллельных вычислений: сигналы, семафоры, межпроцессные каналы, очереди сообщений, разделяемую память.

Сигналы выполняют в среде процессов роль прерываний, посылаемых либо другим процессом, либо ядром операционной системы, либо пользователем за терминалом. При получении сигнала либо включается общесистемный обработчик сигнала, либо собственный обработчик процесса. Семафор внутри процесса приостанавливает или продолжает работу данного процесса. Изменение состояния семафора производится при получения соответствующего сигнала от другого процесса. Межпроцессные каналы представляют собой средство обмена информацией между процессами. Данные одного процесса записываются в канал, а затем читаются другим процессом. При этом другие процессы не имеют доступа к этим данным. В отличие от межпроцессных каналов, сообщения в очереди сообщений может прочитать любой другой процесс (при наличии доступа), то есть эта возможность обмена информацией является болеее гибкой. Наконец, разделяемая память – это возможность двум процессам иметь общую память для данных, то есть совместно обрабатывать одни и те же данные.

Операционная система UNIX состоит из ядра (Kernel), интерпретатора команд (Shell) и служебных программ – утилит. Утилиты UNIX делятся на пять групп:

• утилиты управления файловой системой;
  
• утилиты управления процессами;
  
• утилиты управления коммуникацией данных;
  
• библиотеки служебных подпрограмм;
  
• среда программирования.
  

Ядро в свою очередь можно условно разделить на четыре части:

• управление памятью;
  
• поддержка файловой системы;
  
• размещение системных ресорсов;
  
• обеспечение прав доступа.
  

Работа ядра основана на справочных таблицах, которые описывают всю структуру вычислительной сети: ресурсы сети, пользователей сети, организацию данных в сети, текущее состояние процессов сети и т.д. работа ядра состоит в сопоставлении данных в одних таблицах и внесении необходимых изменений в другие таблицы. Инструкции для выполнения этих действий поступают от пользователей и процессов в форме команд UNIX. Эти команды прочитываются интерпретатором команд, расшифровываются и затем вызывается соответствующая утилита UNIX.

4. Программирование на языке Паскаль.

4.1. Примеры алгоритмов

Прежде, чем анализировать принципы и приемы соствления алгорит­мов, приведем несколько примеров.

Пример 1. Вычисление расстояния между двумя точками на плоскости.

а). Блок-схема алгоритма.

б).Программа на Паскале.

program length;

var x1,x2,y1,y2,r: real;

begin readln (x1,y1,x2,y2);

r := (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);

r := sqrt (r);

writeln (r)

end.

Пример 2. Вычислить частную сумму ряда .

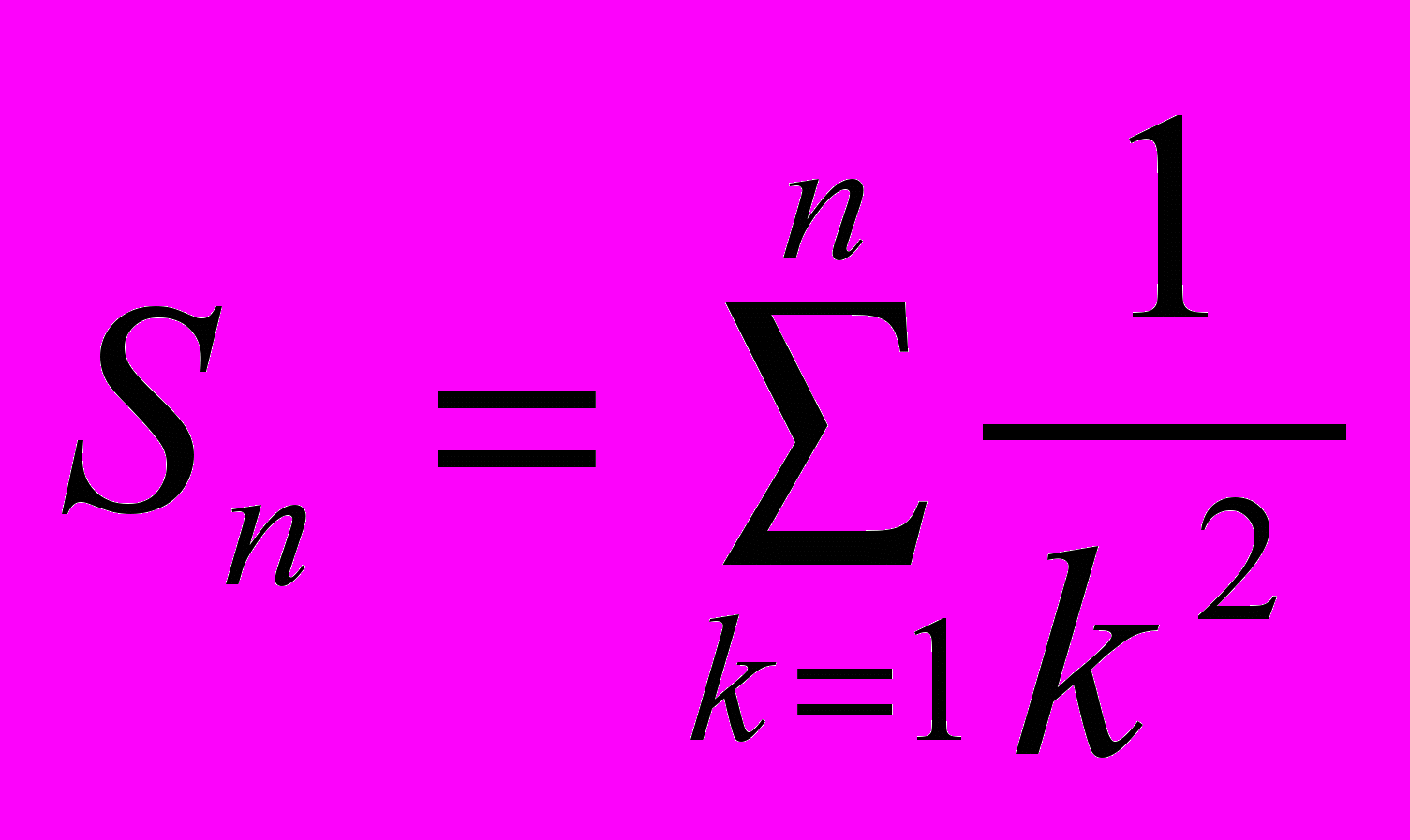а). Блок-схема алгоритма с предусловием.

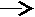k=1; s=0 kn ^да s=s+1/k²; k=k+1 результат в s

нет




б). Блок-схема алгоритма с постусловием.

_да

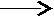
k=0; s=0 k=k+1 s=s+1/k² kn ^нет результат в s

в). Программа на Паскале с предусловием и безусловным переходом.

program summa;

var k,n: integer; s: real;

label m1,m2;

begin readln (n);

s := 0; k := 1;

m1: if k>n then goto m2;

s := s + 1/(k*k); k := k+1; goto m1;

m2: writeln (s)

end.

г). Программа на Паскале с постусловием и безусловным переходом.

program summa;

var k,n: integer; s: real;

label m1;

begin readln (n);

s := 0;

k := 0;

m1: k := k+1;

s := s + 1/(k*k);

if k<=n then goto m1;

writeln (s)

end..

д). Программа на Паскале с оператором цикла с предусловием, эквивалент­ная программе пункта в).

program summa;

var k,n: integer; s: real;

begin readln (n);

s := 0;

k := 1;

while k<=n do

begin s := s + 1/(k*k);

k := k+1;

end;

writeln (s)

end.

е). Программа на Паскале с оператором цикла с постусловием, эквивалентная программе пункта г).

program summa;

var k,n: integer; s: real;

begin readln (n);

s := 0;

k := 0;

repeat k := k+1;

s := s + 1/(k*k);

until k>n;

writeln (s)

end.

ж). Программа на Паскале с оператором цикла со счетчиком.

program summa;

var k,n: integer; s: real;

begin readln (n);

for k := 1 to n do s := s + 1/(k*k);

writeln (s)

end.

З). Другой вариант цикла:

program summa;

var k,n: integer; s: real;

begin readln (n);

for k := n downto 1 do s := s + 1/(k*k);

writeln (s)

end.

Пример 3. Поиск значения x в массиве a.

а). Блок-схема алгоритма (длина массива равна 100).

^нет

n=0 n=n+1 n>100 ^нет a[n]=x ^да Элемент имеет в массиве номер n

да

Элемент в массиве отсутствует

б). Фрагмент программы на Паскале.

var n,x: integer;

a: array [1..100] of integer;

label m1 ;

begin {Заполнить массив a}

readln (x);

for n:=1 to 100 do

if a[n] = x then goto m1;

n := 0;

m1: ...;

end.

Пример 4. Определение номера дня в невисокосном году по числу и месяцу (программа на Паскале).

function numerday (d,m: integer): integer; {d- день, m - месяц}

const a: array [1..12] of integer = (31,28,31,30,31,30,31,31,30,31,30,31);

b: array [1..12] of integer = (0,31,59,90,120,151,181,212,243,273,304,334);

begin if (m>=1) and (m<=12) and (d>=1) and (d<=a[m] )

then numerday := b[m]+d

else numerday := 0

end;


Пример 5. Определение дня и месяца в невисокосном году по номеру дня.

а). Процедура на Паскале.

procedure date (n: integer; var d,m: integer);

const b: array [1..12] of integer = (0,31,59,90,120,151,181,212,243,273,304,334);

var n: integer;

label m1;

begin for m:=1 to 11 do

if n<=b[m+1] then goto m1;

if n<=365

then m := 12

else m := 0;

m1: if m>0

then d := n - b[m]

else d := 0

end;

Пример 6. Установить, является ли данное целое число n простым.

а). Словесный алгоритм. Надо перебрать все натуральные числа k, меньшие квадратного корня из заданного числа n. Если для какого-то k число n делится на k нацело, то n составное, в противном случае оно простое.

б). Функция на Паскале.

function simple (n: integer): boolean;

var k,m: longint; b: boolean;

label m1;

begin b := true;

m := trunc (sqrt (n) );

for k:=2 to m do

if (n mod k)=0 then

begin b := false;

goto m1

end;

m1: simple := b

end;

Пример 7. Определить количество простых делителей в полном разложении заданного числа n.

а). Словесный алгоритм. Перебором в возрастающем порядке найдем наименьшее число k, на которое делится данное число n. Если k=n, значит число n простое и состоит из одного простого множителя. Если k
б). Рекурсивная функция на Паскале (функция, в которой один из операторов представляет собой вызов себя самой).

function fn (n: longint): integer;

var k,m: longint; p: integer;

label m1;

begin p := 1;

m := trunc (sqrt (n) );

for k:=1 to m do

if (n mod k)=0 then

begin p := 1+fn (n div k);

goto m1

end;

m1: fn := p

end;

Пример 8. Описать событие: “Карта К1 бьет карту К2, включая учет козырной масти”.

а). Функция на Паскале.

type

suit = (spades, clubs, diamonds, hearts);

value = (c7,c8,c9,c10,jack,queen,king,ace);

card = record s: suit; v: value end;

function beat (sc: suit; c1,c2: card): boolean;

begin

if c1.s=sc

then beat := ( (c2.s <> sc) or ( (c2.s = sc) and (c1.v > c2.v) ) )

else beat := ( (c1.s=c2.s) and (c1.v > c2.v) )

end;

Пример 9. Определение количества простых чисел, меньших или равных данному числу n.

а). Алгоритм (решето Эратосфена).

Сначала все числа от 2 до n считаются простыми. Затем, начиная с 2, для каждого числа k, для которого уже установлено, что оно простое, произво­дится следующая процедура: все числа, кратные k, считаются составными. Процедура заканчивается, когда k²>n. После этого подсчиты­ва­­ется число простых чисел.

б). Функция на Паскале.

function eratosphen (n: integer): integer; {n <= 255}

var

simple: set of 2..255; {Множество простых чисел}

k,m,p,s: integer;

begin

simple := [2..n]; {Сначала все числа от 2 до n считаются простыми}

m := trunc (sqrt (n) );

for k:=2 to m do

if (k in simple) then

begin

p := 2*k;

while p<=n do

begin

simple := simple - [p]; {Число p не является простым}

p := p+k

end

end;

s := 0;

for k:=2 to n do

if (k in simple) then s := s+1;

eratosphen := s

end;