Geum.ru

Електромеханічні системи та автоматизація

Вид материалаДокументы

Содержание


Материал и результаты исследований.
Подобный материал:

ЕЛЕКТРОМЕХАНІЧНІ СИСТЕМИ ТА АВТОМАТИЗАЦІЯ


УДК 62-83


СИНТЕЗ АДАПТИВНОГО ФИЛЬТРА-НАБЛЮДАТЕЛЯ
ДВУХФАЗНОГО СИГНАЛА

Потапенко Е.М., Потапенко Е.Е., Соломаха А.В.

Запорожский национальный технический университет



Введение. Современные электроприводы переменного тока (ЭП) в большинстве случаев содержат преобразователи частоты (ПЧ) с широтно-импульсной модуляцией (ШИМ). Выходные сигналы ПЧ с ШИМ (напряжения, токи) можно представить как суммы полезных сигналов (главных гармоник) и высокочастотных помех, причем амплитуды помех могут в десятки раз превысить амплитуды полезных сигналов. Кроме того, у напряжения помехи представляют собой прямоугольные импульсы малой длительности. Такая форма сигналов не позволяет путем числовой обработки достаточно точно выделить полезные сигналы, необходимые для применения в алгоритмах управления и идентификации. Во многих случаях частоты полезных сигналов неизвестны. Постановка обычных аналоговых фильтров приводит к недопустимому искажению полезных сигналов. Вследствие сказанного, в реализованных ЭП главные гармоники выходных напряжений ПЧ с ШИМ отождествляют с управляющими сигналами, подаваемыми на блок ШИМ. Однако такой подход приводит к погрешностям за счет падения напряжений на транзисторах, запаздываний при открытии и закрытии транзисторов блока ШИМ, а также за счет “мертвого” времени. Для оценки главных гармоник можно было бы попытаться использовать (см. работу [1] и библиографию к ней) ряд методов, таких как рекуррентный метод наименьших квадратов, расширенный фильтр Калмана, дискретное преобразование Фурье, метод Проуни и др. Однако, эти методы связаны с большим объемом вычислений и для этих методов в случае с ШИМ слишком велико отношение “шум/полезный сигнал”.

В работах [2–5] для измерения главных гармоник предложены простые адаптивные наблюдатели, содержащие различные непрерывные фильтры и дискретные компенсаторы искажений главных гармоник. Тот факт, что в цифровую часть алгоритмов сигналы поступают не непосредственно с выходов ПЧ, а с выходов аналоговых фильтров, позволяет существенно увеличить такт счета. Недостатком указанных наблюдателей является наличие дифференцирования сигналов для оценки частоты главных гармоник, снижающих помехозащищенность алгоритмов. Для восстановления помехозащищенности, сигналы вычисленных скоростей пропускают через фильтры, что приводит к появлению запаздываний в определении частоты, что, в свою очередь, приводит к снижению точности наблюдателей. При фильтрации выходных напряжений ПЧ с ШИМ этот недостаток можно устранить путем определения частоты главных гармоник не по выходным сигналам ПЧ с ШИМ, а по управляющим сигналам блока ШИМ ПЧ. К сожалению, для построения фильтров токов АД этого сделать нельзя.

Цель работы – синтез адаптивного фильтра-наблюдателя главных гармоник выходных сигналов (напряжений и токов) ПЧ с ШИМ, в котором отсутствует дифференцирование сигналов.

Материал и результаты исследований. Известно [6], что любой трехфазный вектор (напряжение, ток, потокосцепление, ЭДС и т.п.) можно привести к эквивалентному в том или ином смысле двухфазному вектору. Аналитические исследования и моделирование динамики ЭП с наблюдателями работ [2–5] показывают, что кинематика двухфазного вектора достаточно точно описывается векторно-матричным уравнением

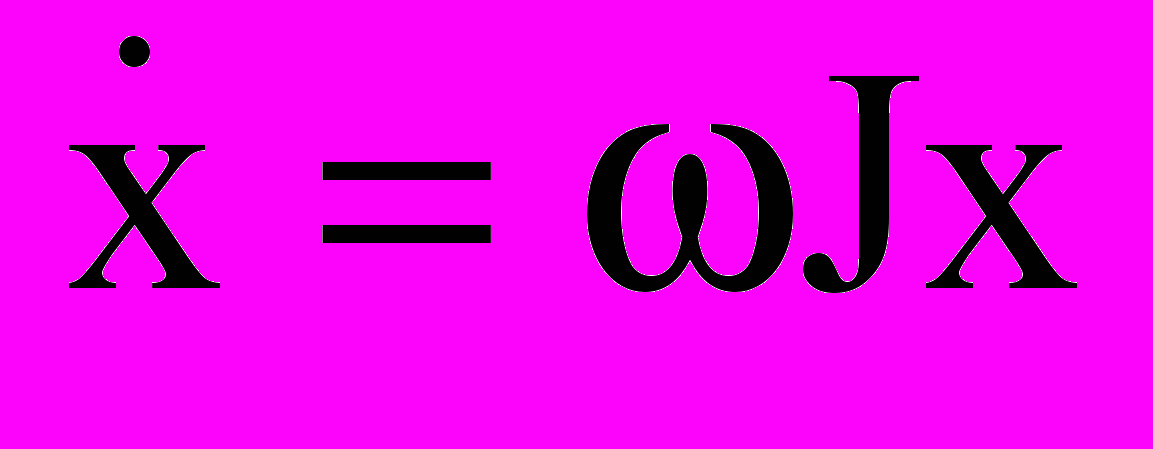, (1)

где – неизвестная скорость плоского вращения вектора 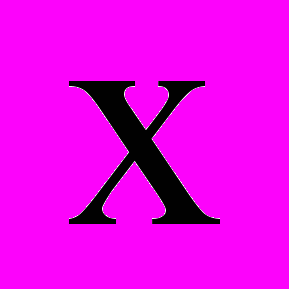, – кососимметричная матрица. Указанные вектор и матрица имеют вид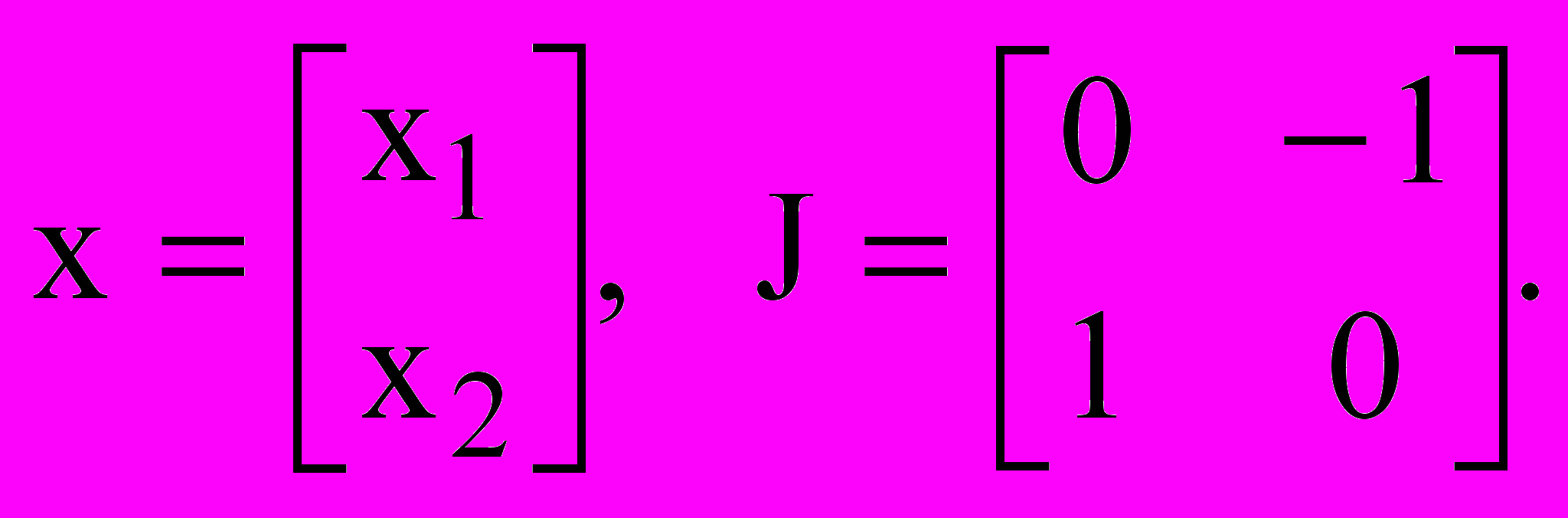

(2)

Пусть вектор 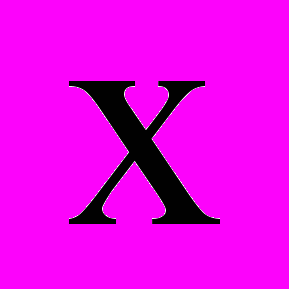соответствует главным гармоникам двух фаз двухфазного сигнала. На выходе ПЧ на главные гармоники налагаются высокочастотные шумы, обусловленные ШИМ, образующие вектор 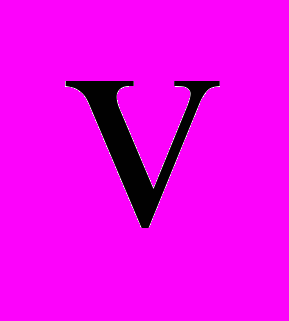. Таким образом, измерением будет вектор:

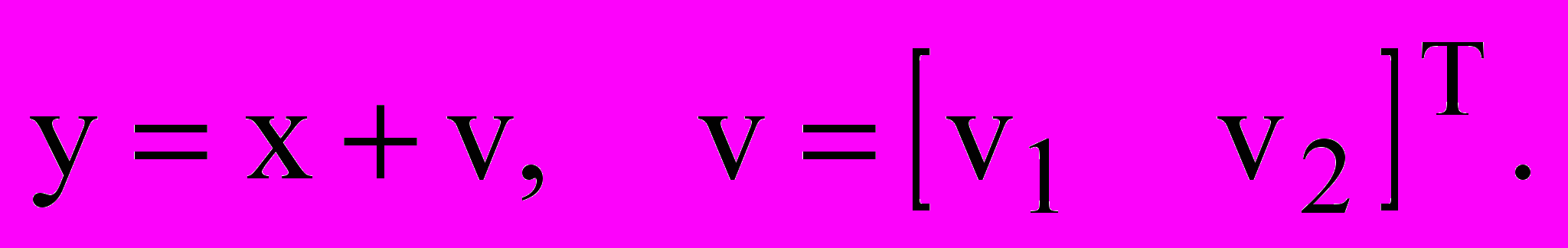(3)

Задачей является оценка вектора 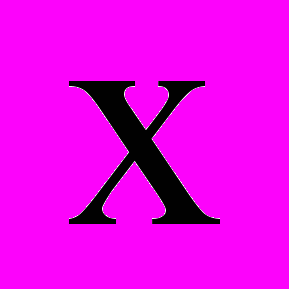и скорости . Для этого по уравнениям (2) и (3) составим наблюдатель [7, 8, 9] в виде: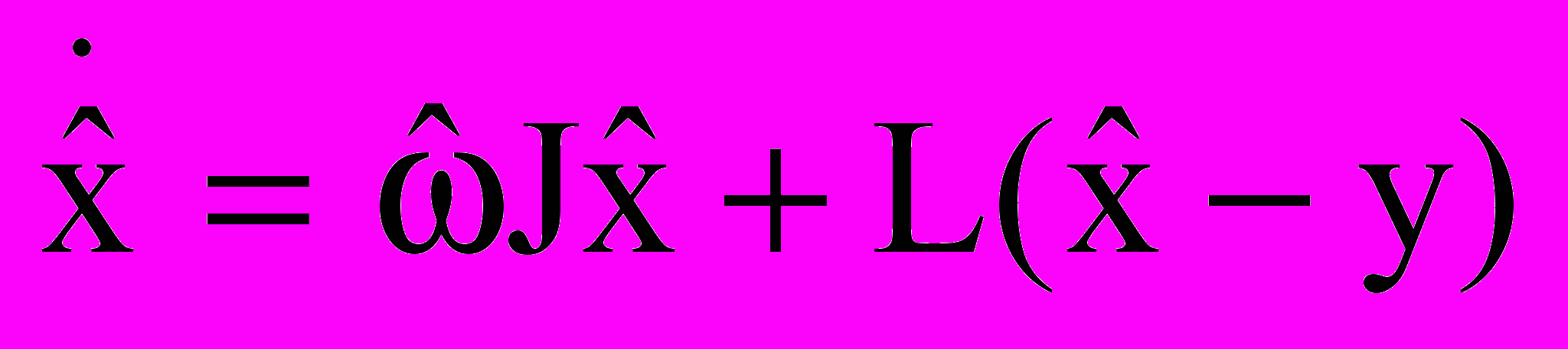

, (4)

где – матрица коэффициентов передачи наблюдателя, знаком “” обозначены оценки соответствующих переменных. Уравнение (3) с учетом (2) приводится к виду: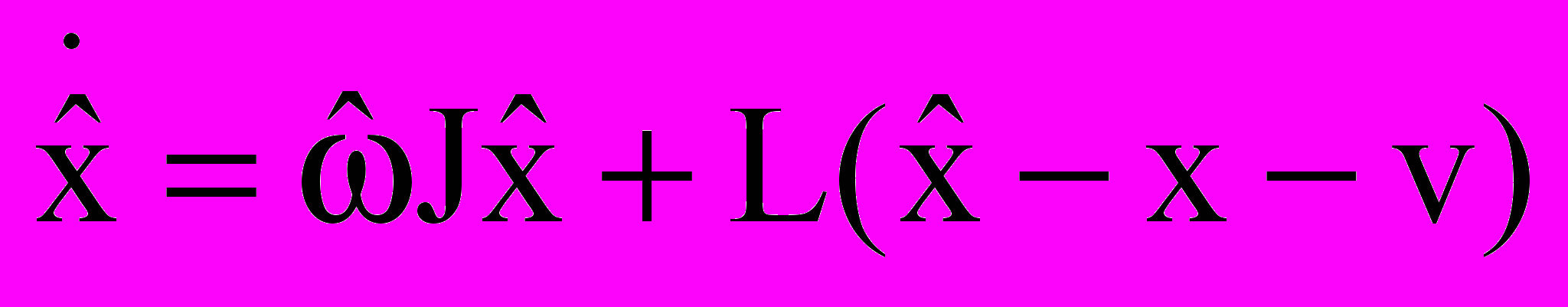

. (5)

Введем в рассмотрение ошибки наблюдателя:

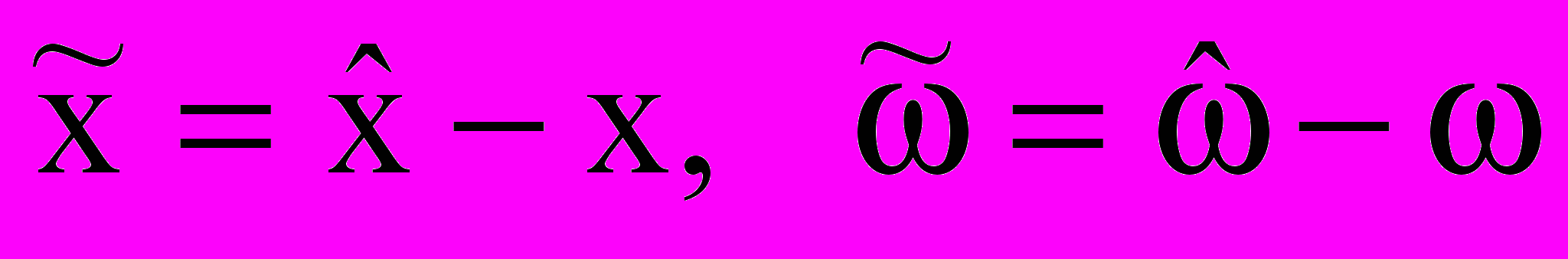. (6)

С помощью обозначений (6) уравнение (1) перепишется в виде:

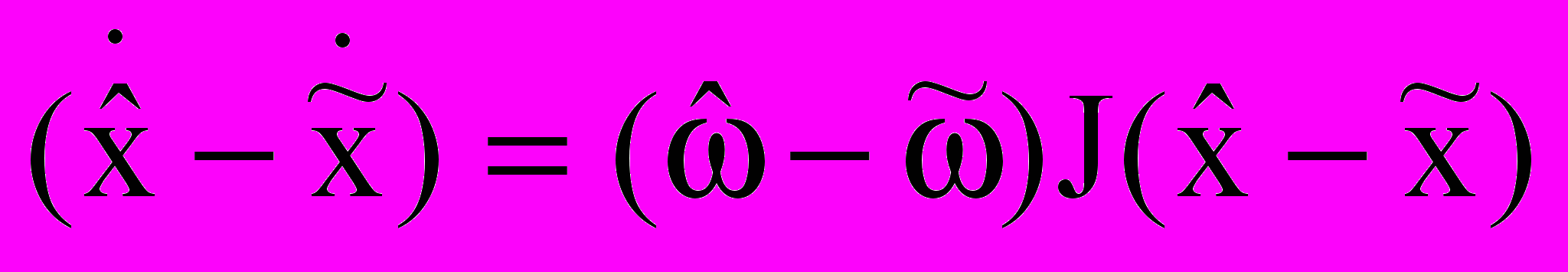. (7)

Вычитание из уравнения (4) уравнения (7) дает уравнение ошибки наблюдателя:

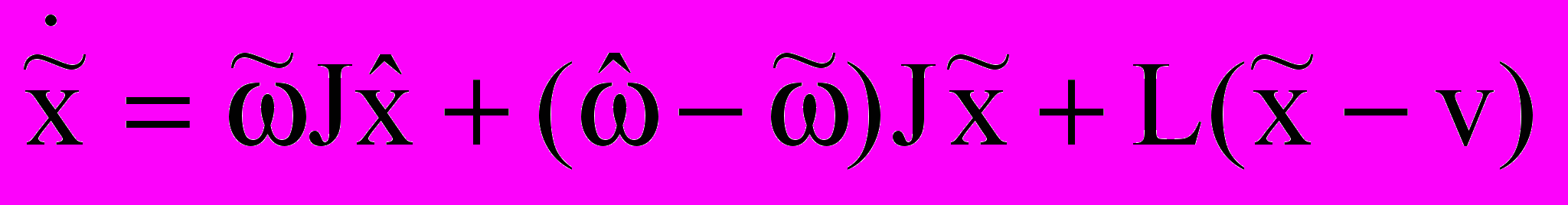. (8)

Найдем условия, при которых однородное уравнение, соответствующее уравнению (8), будет иметь асимптотически устойчивое нулевое решение. Для этого воспользуемся прямым методом В.М. Ляпунова. Для уравнения (8) при 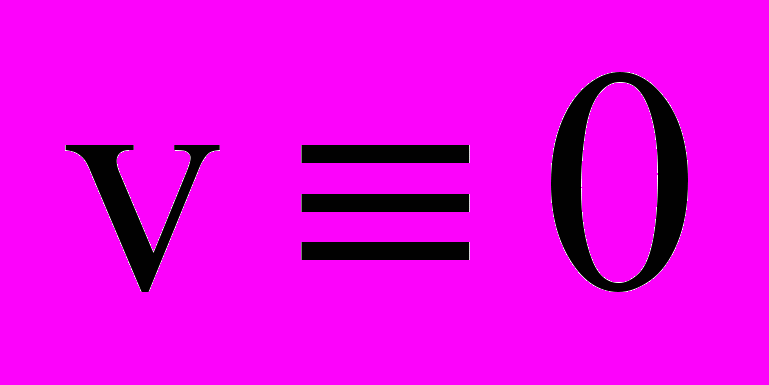составим функцию Ляпунова в виде:

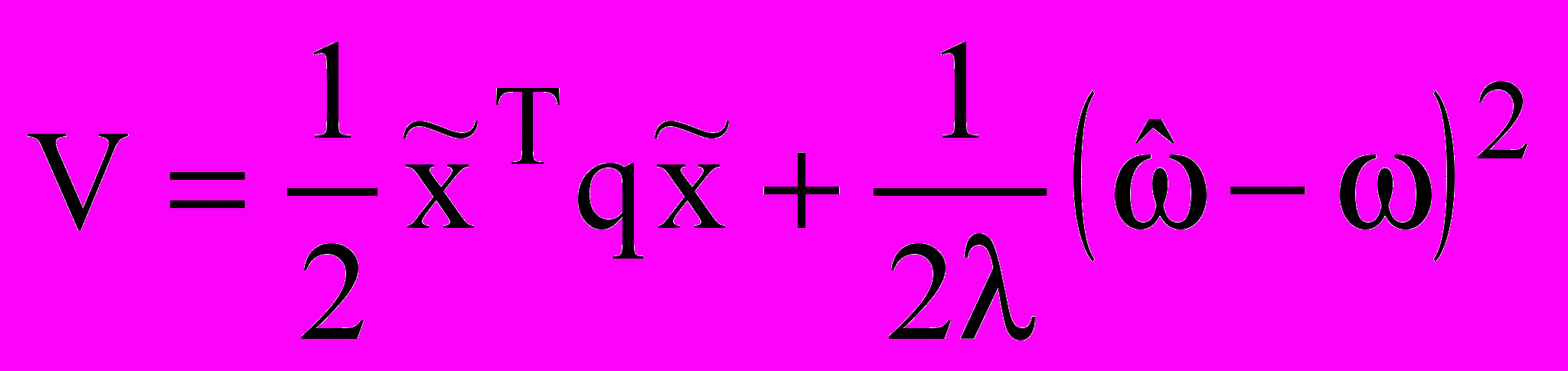, (9)

где коэффициенты .

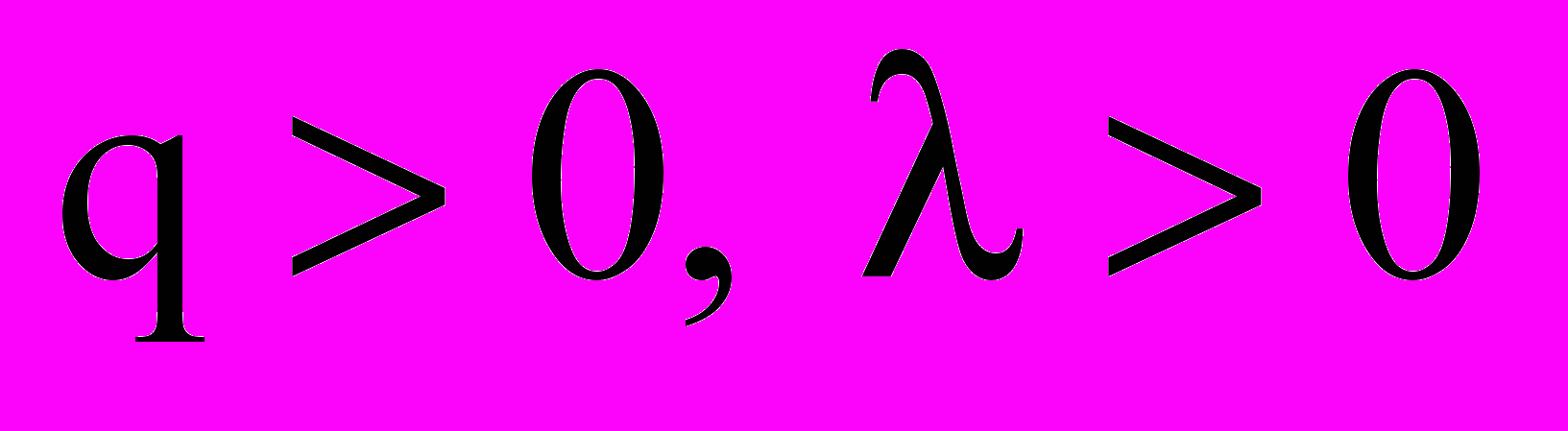Будем полагать, что меняется настолько медленно, что можно положить 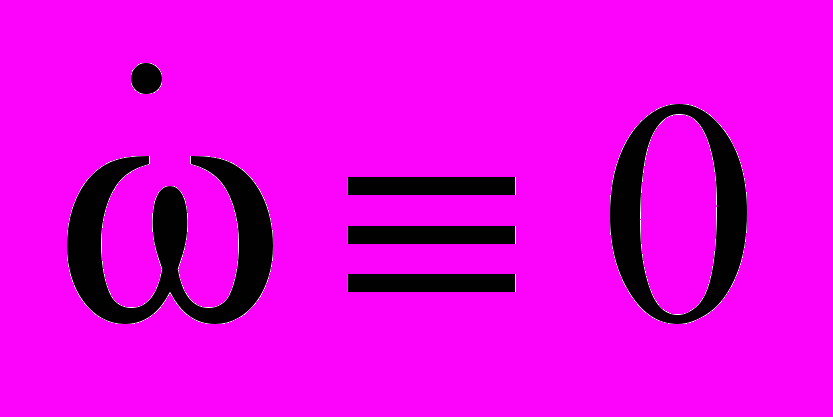. При этих условиях полная производная по времени функции 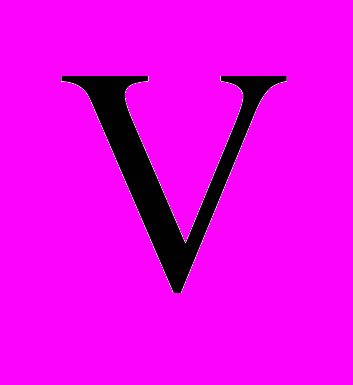с учетом уравнения (8) при 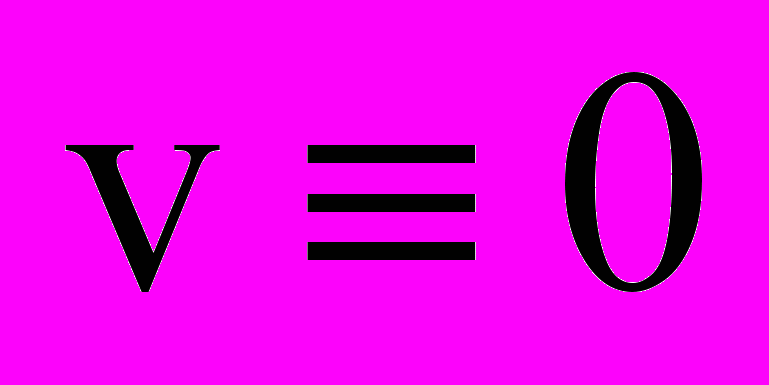примет вид:

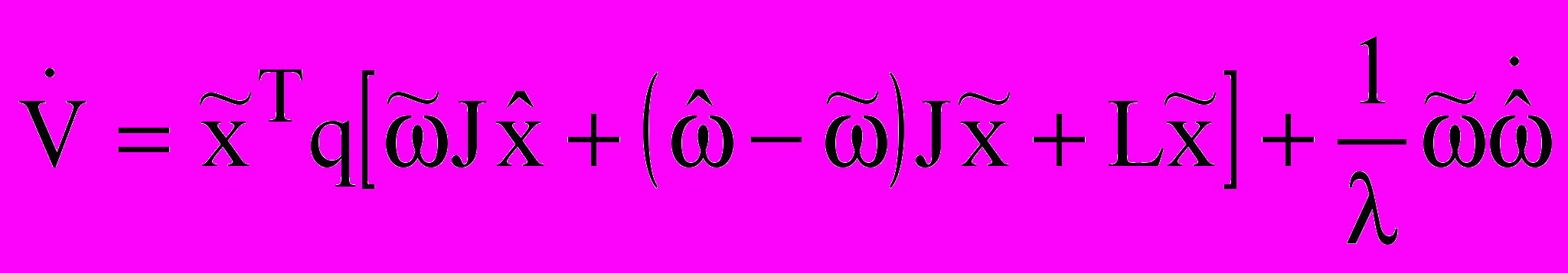. (10)

Положим, что в (10):

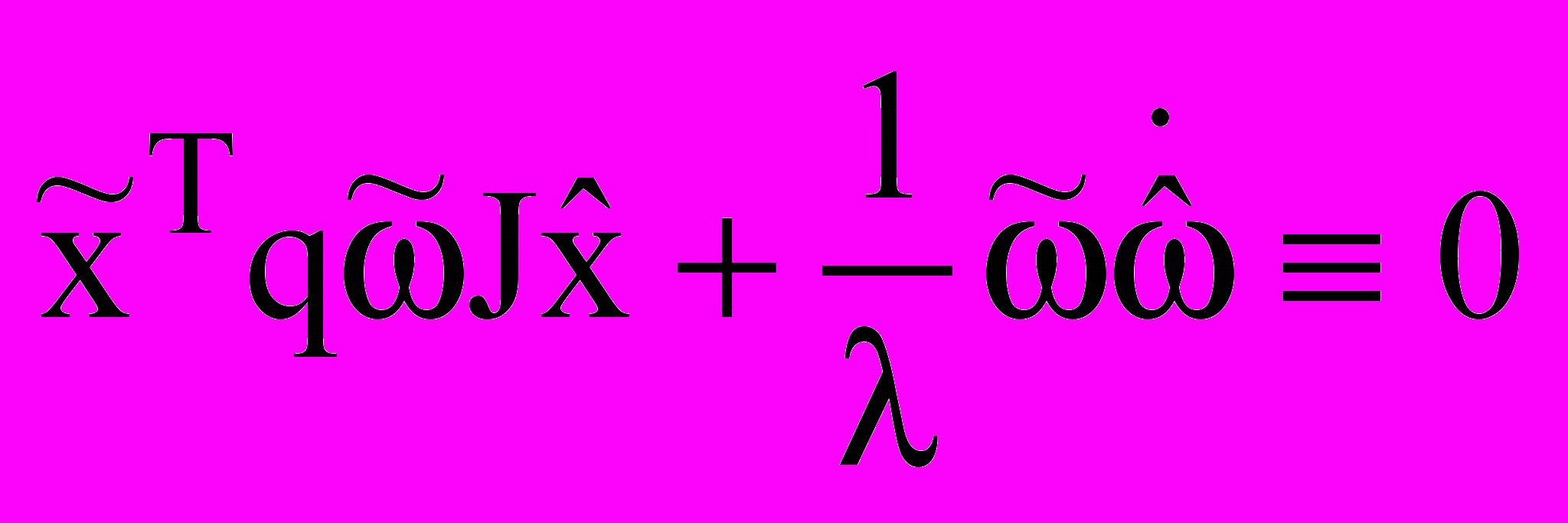. (11)

Из тождества (11) можно получить:

,

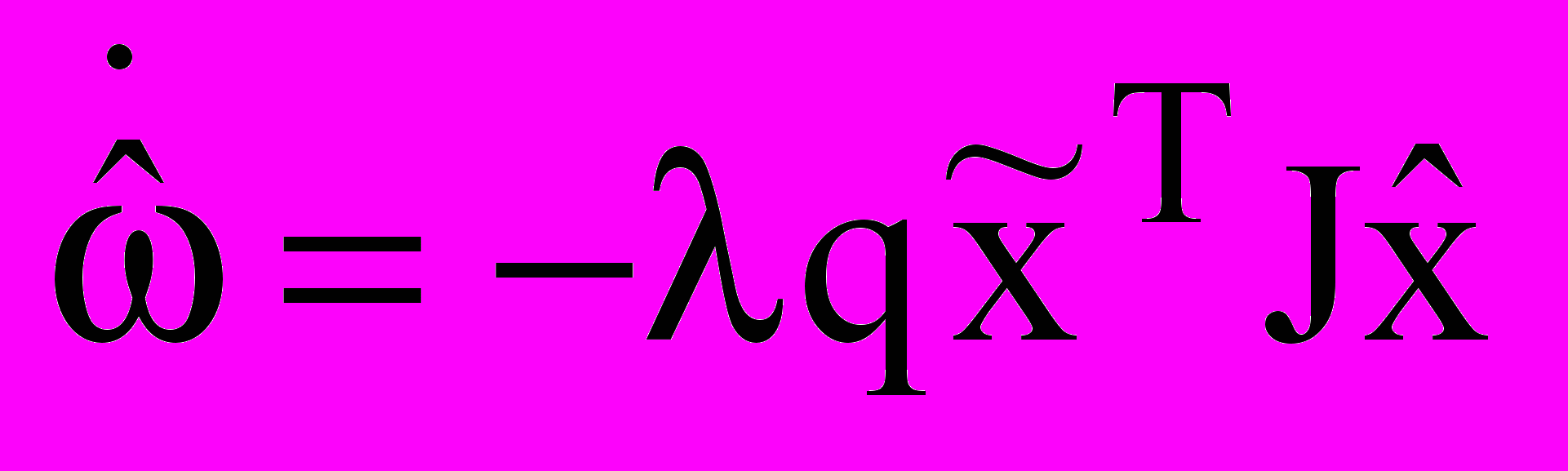откуда с учетом (6), (2) и обозначения 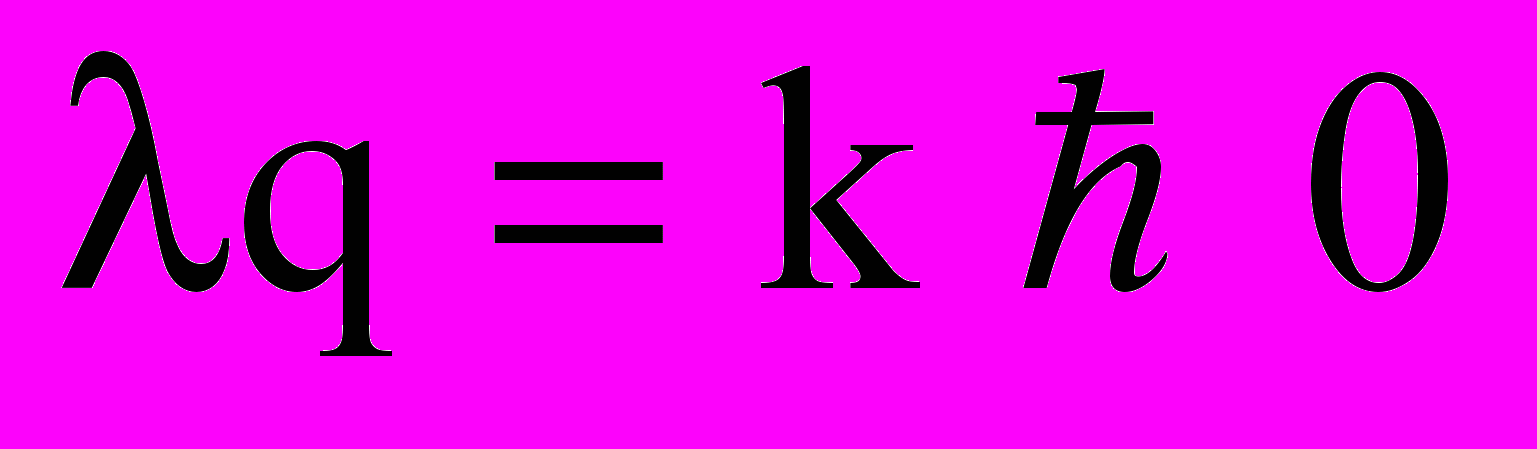следует:

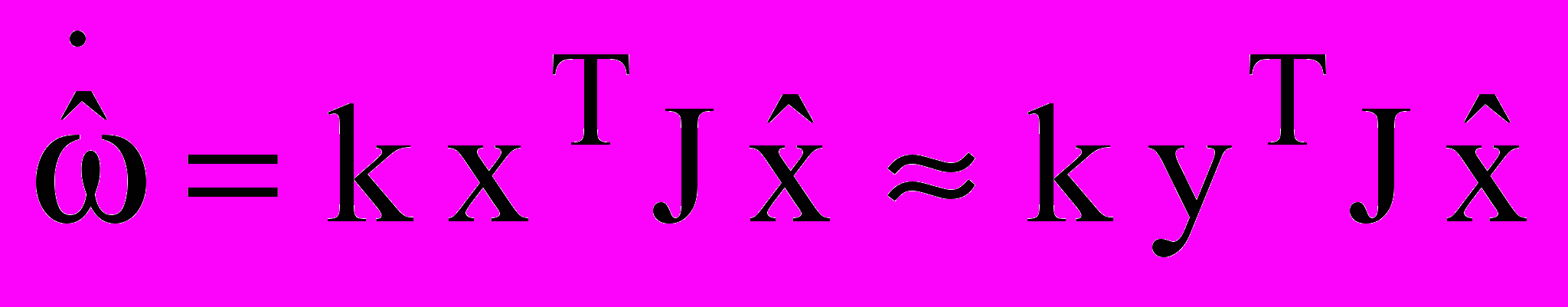. (12)

С учетом (11) и тождества 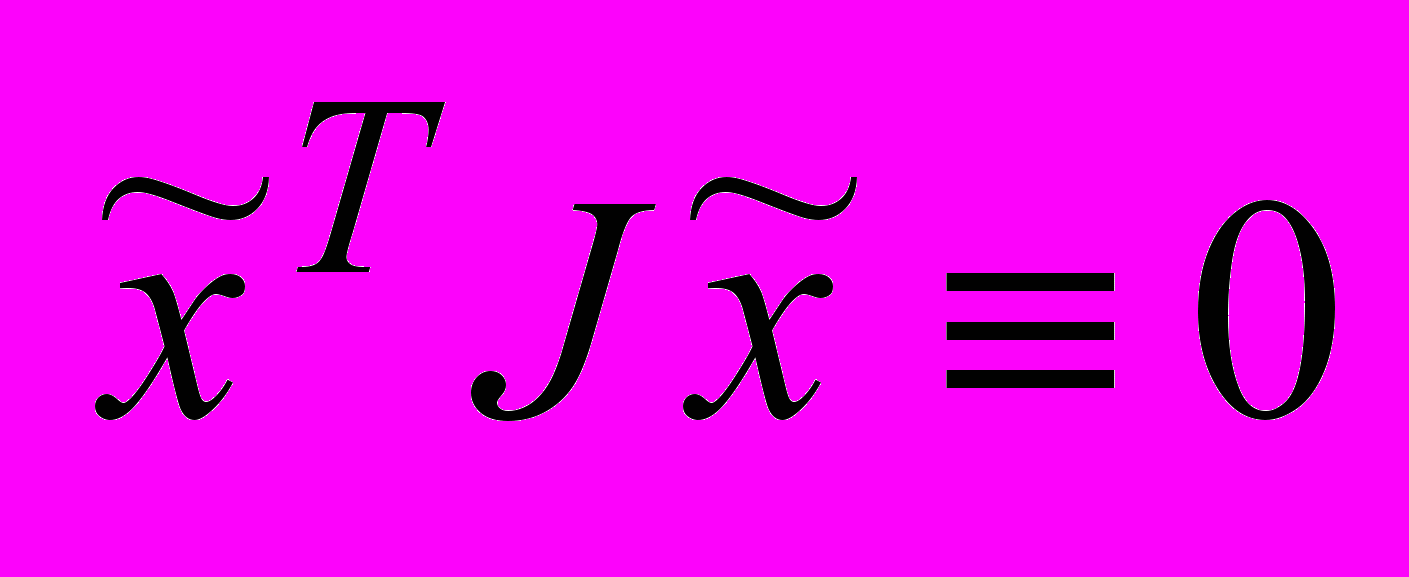выражение (10) упрощается до вида

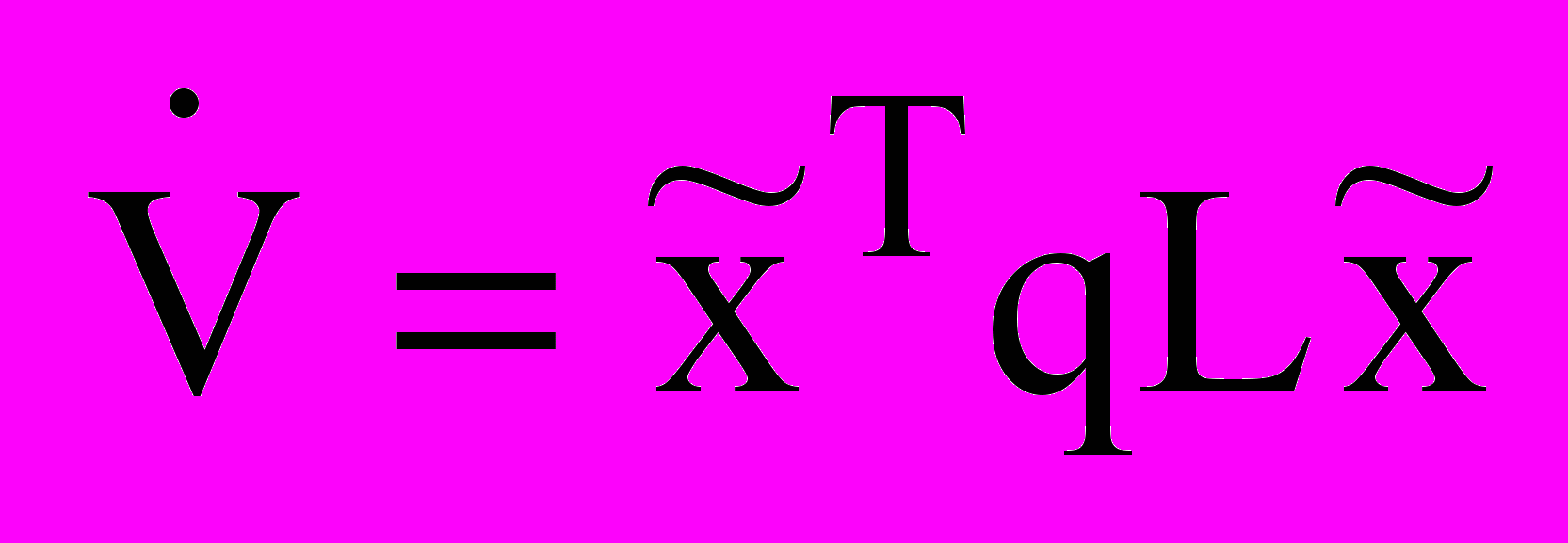. (13)

В том случае, когда 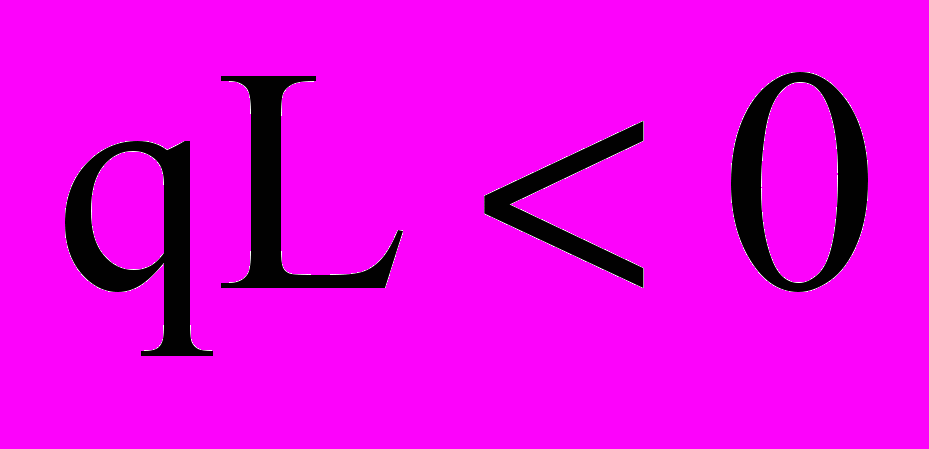(с учетом того, что 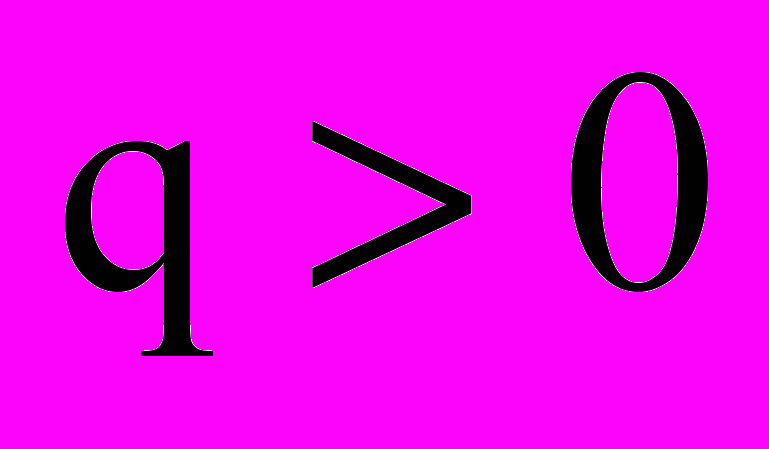, 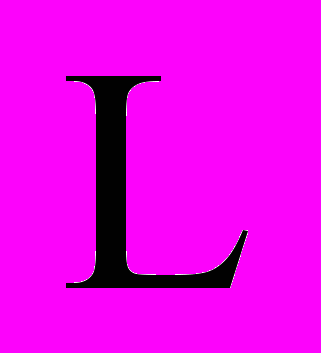– определенно отрицательная матрица), функция будет знакоотрицательной по отношению к уравнению (8) при 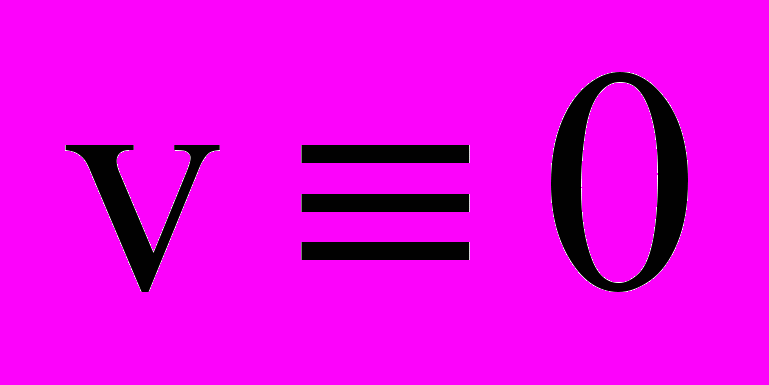. Подстановка 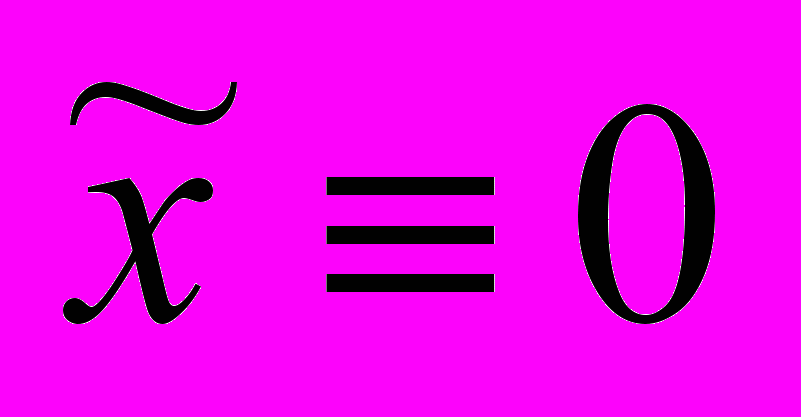в (8) при 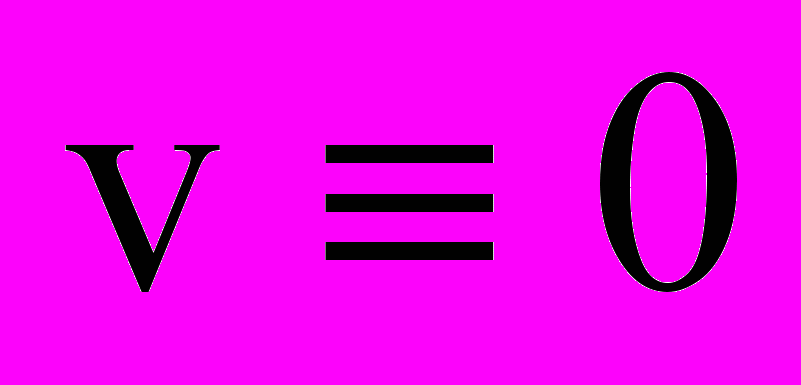дает 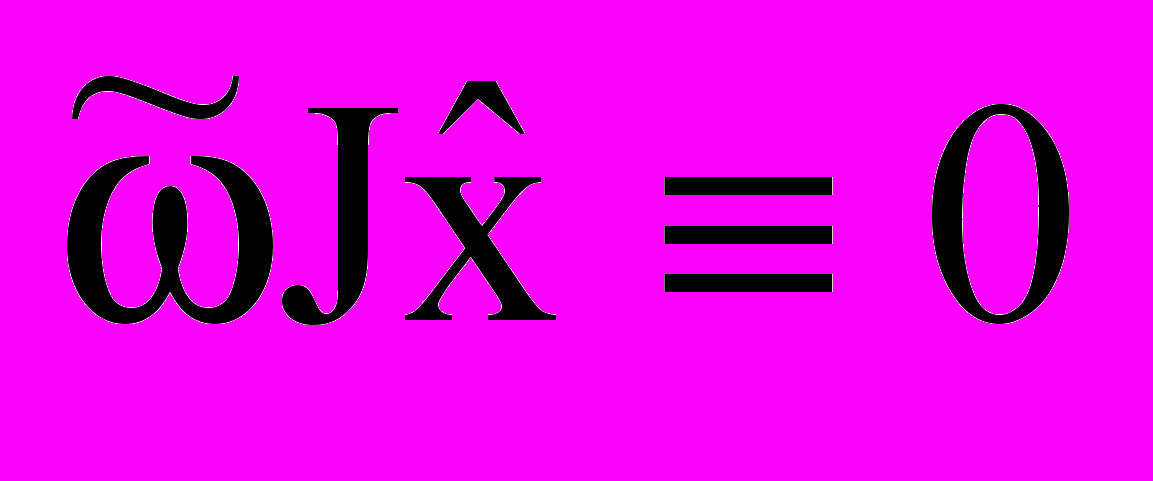, откуда следует, что при 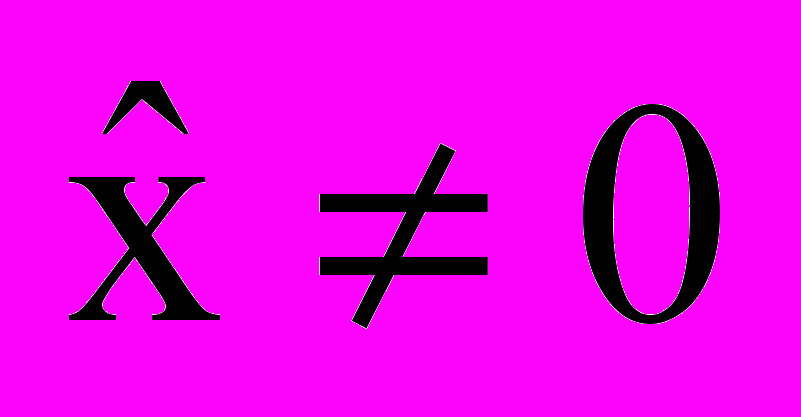ошибка 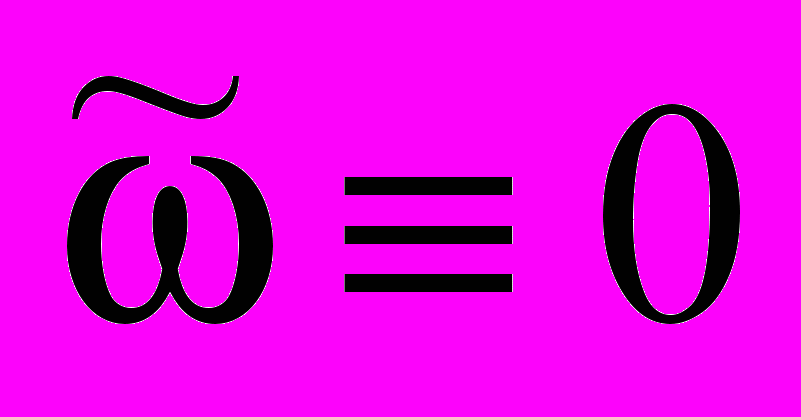. Сказанное означает, что при 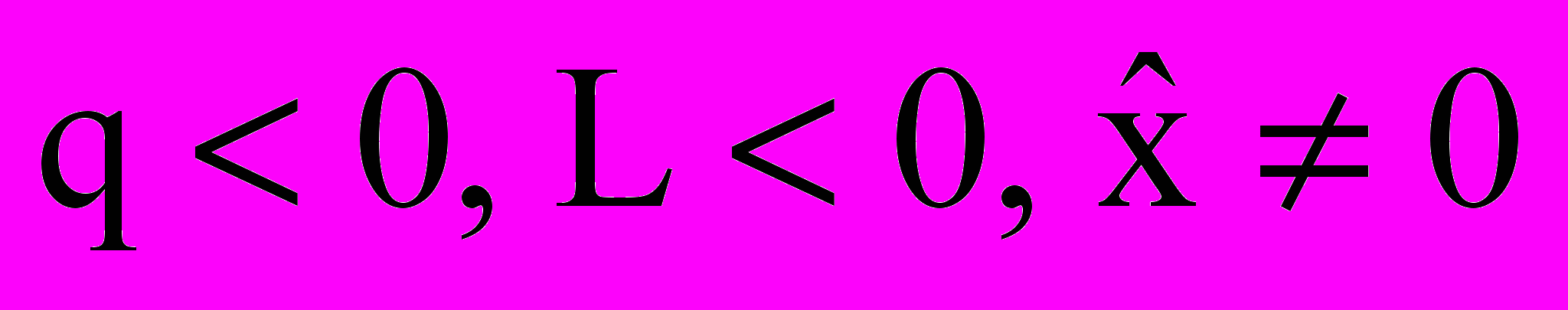, в соответствии с теоремой Барбашина-Красовского, решение уравнения (8) будет асимптотически устойчивым.

Как видно из уравнений фильтра (4), (12), дифференцирование измерения 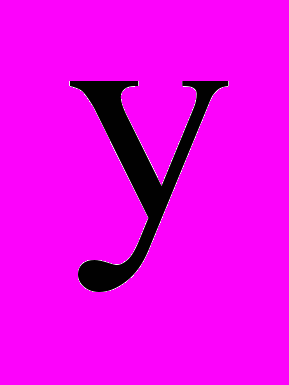отсутствует, и данный фильтр является более помехозащищенным по сравнению с фильтрами в [2–5].

Матрица 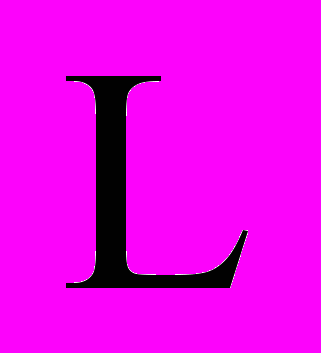имеет структуру

.

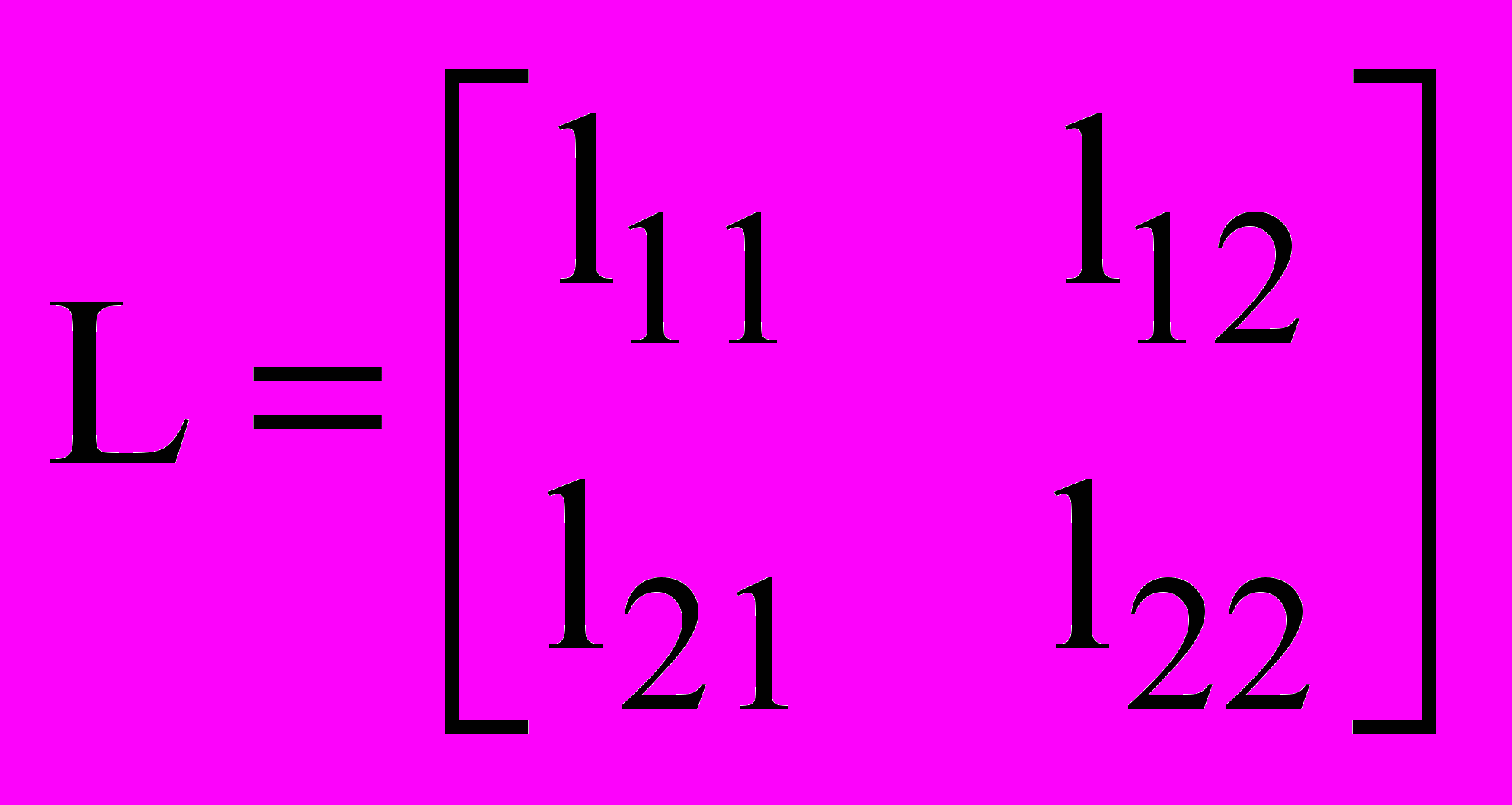Для выбора матрицы 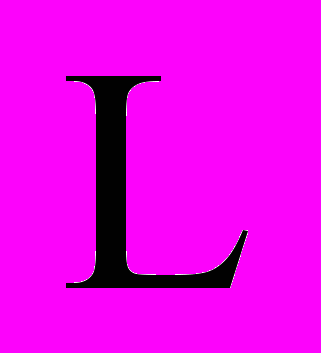составим характеристическое уравнение, соответствующее уравнению (8) при 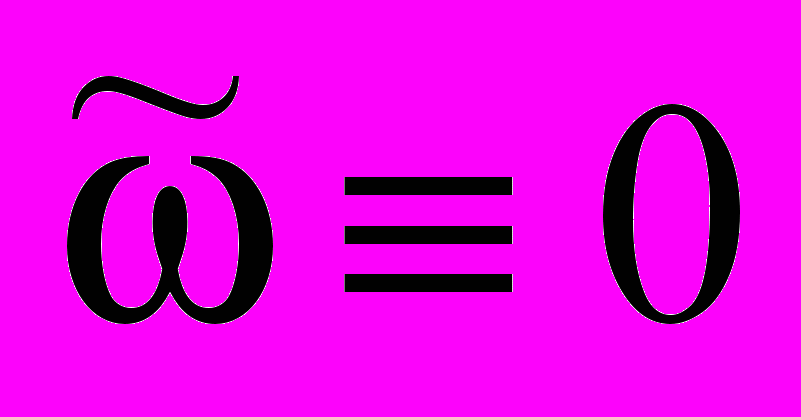. Это уравнение имеет вид:

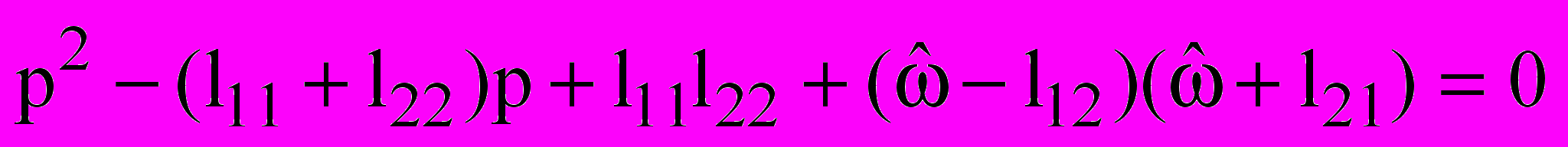. (14)

Исходя из аналогичности обоих скалярных уравнений, соответствующих уравнению (8), а также с учетом условий асимптотической устойчивости, будем полагать:

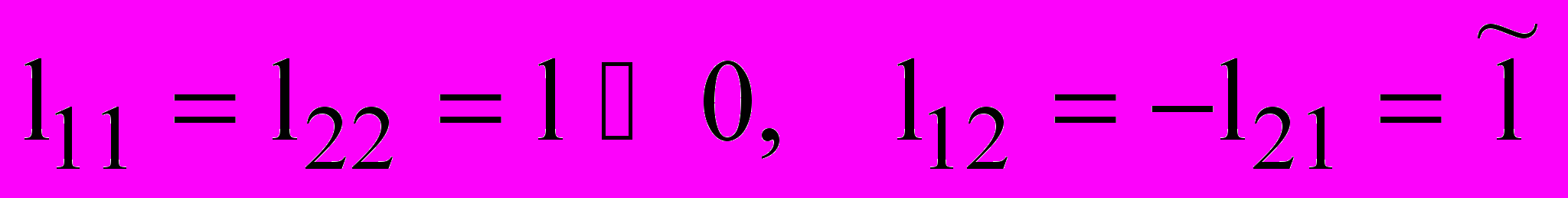. (15)

В этом случае уравнение (14) принимает вид:

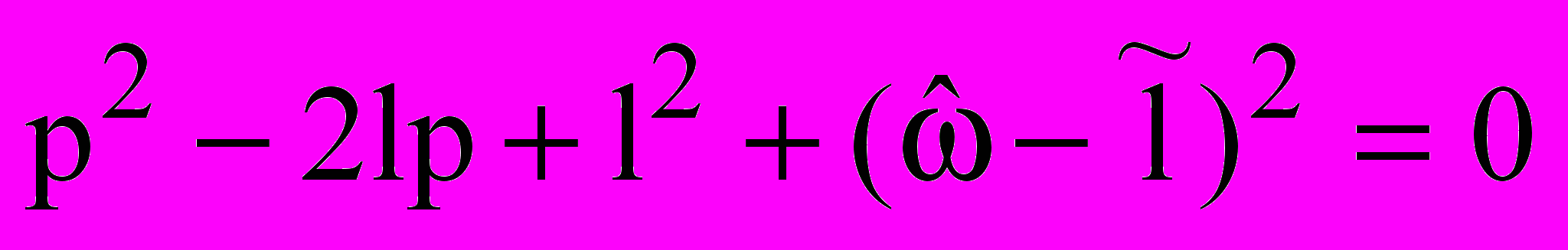. (16)

Представляются интересными два случая:

.

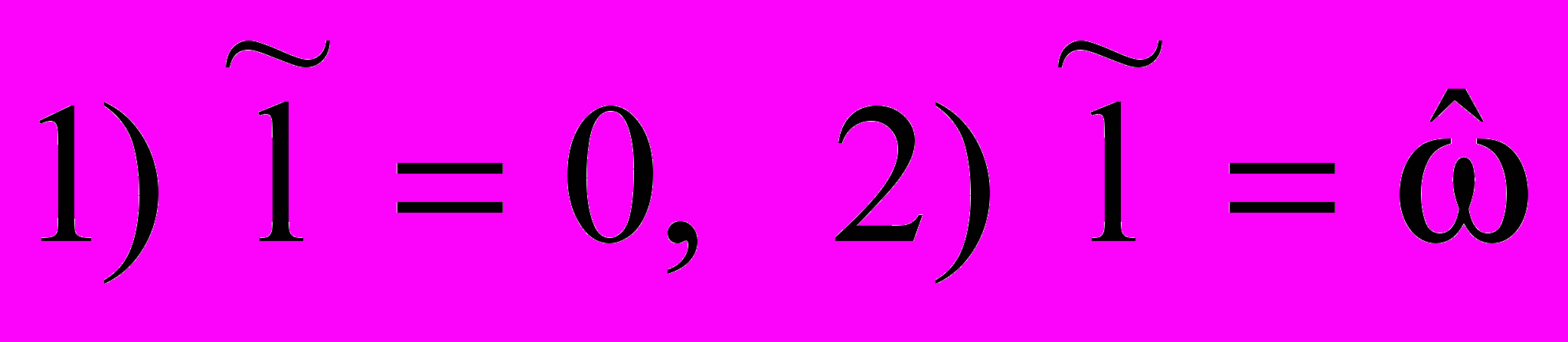Моделировался процесс фильтрации двухфазного сигнала 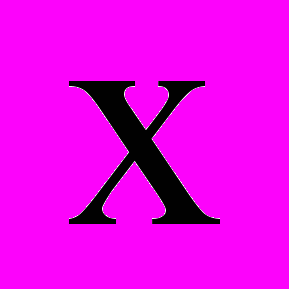с переменными амплитудой и частотой, описываемый уравнениями (3), (4), (12). Сигнал 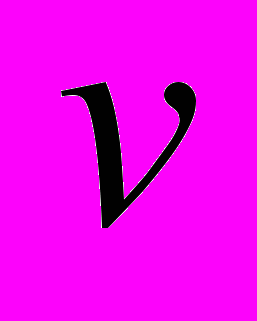представлялся синусоидой с амплитудой 75 и частотой 24000 с-1. На рис. 1, 2 представлены входной сигнал 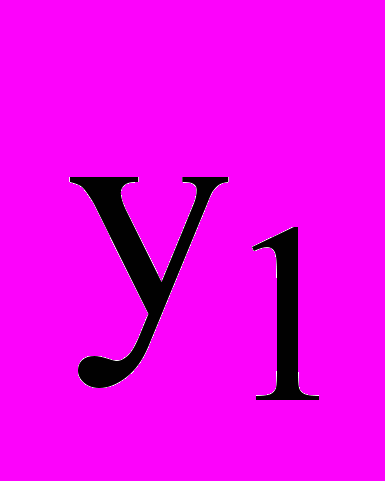, главная гармоника 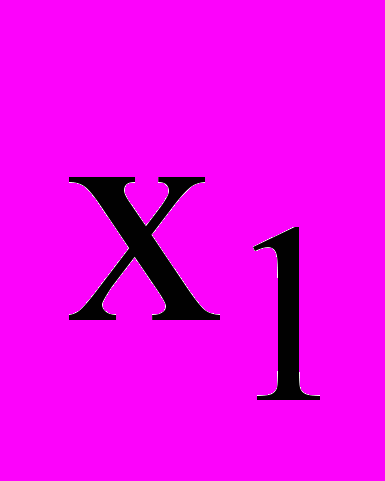, ее оценка 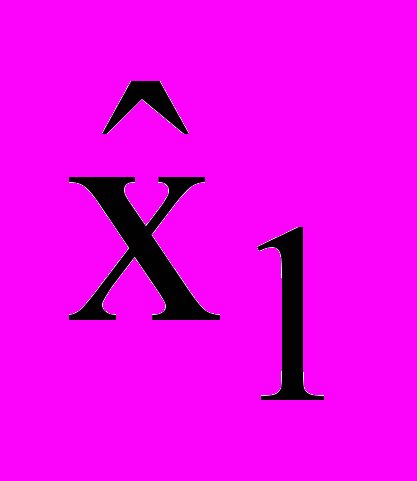, частота сигнала 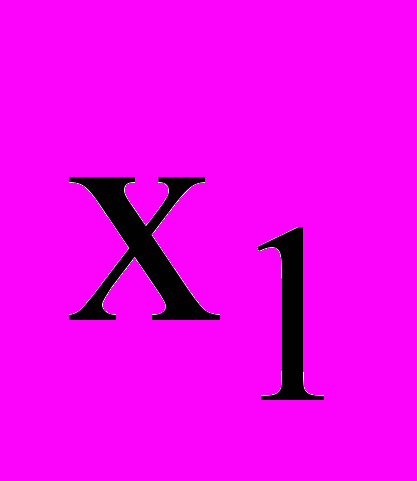и ее оценка .



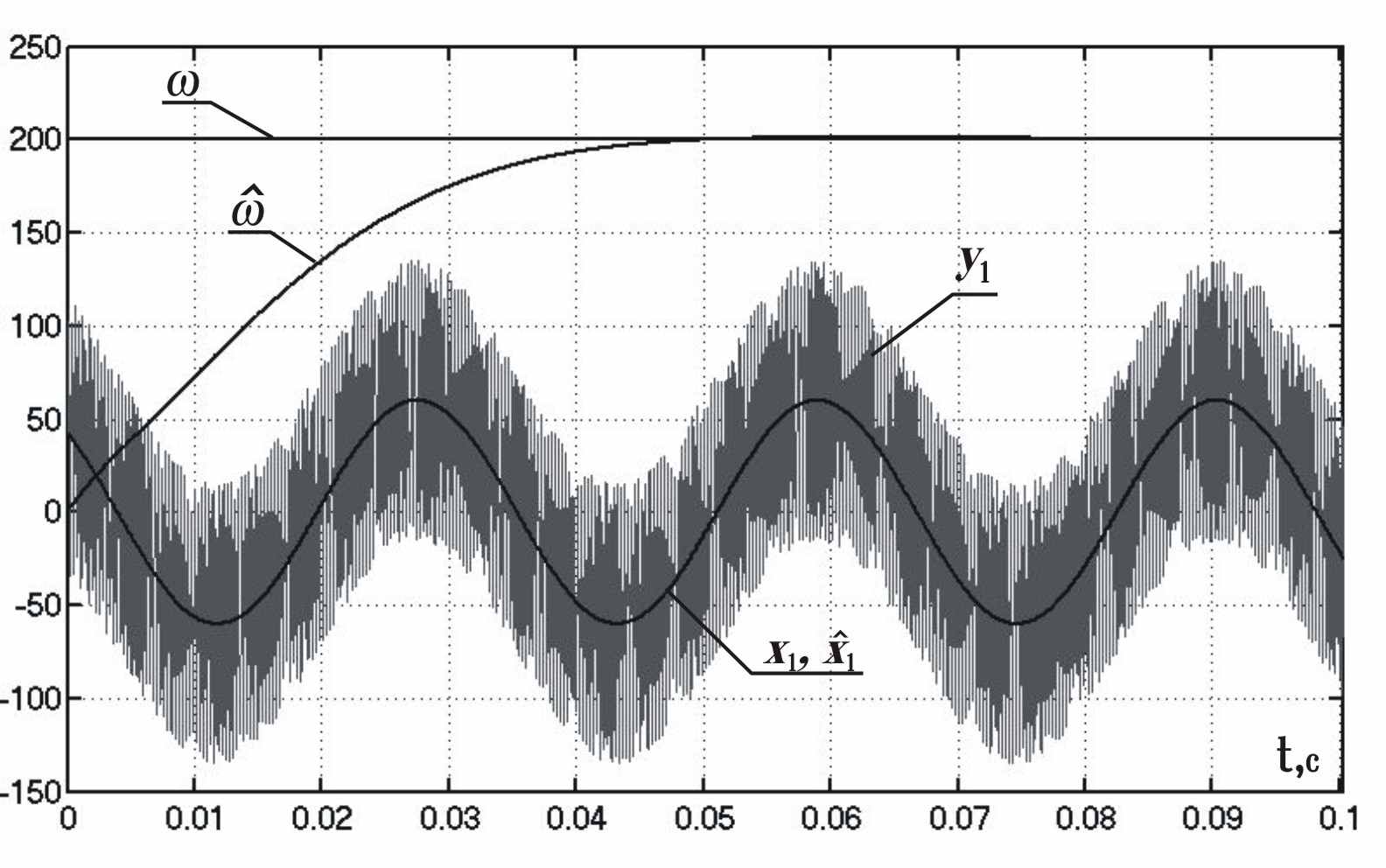
Рисунок 1 - Входной сигнал 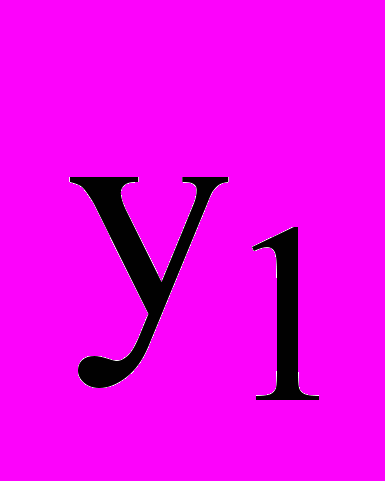, главная гармоника 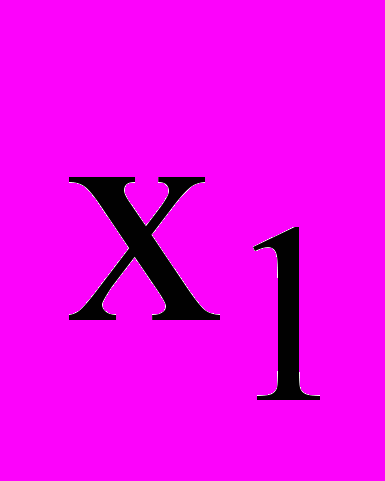, ее оценка ,

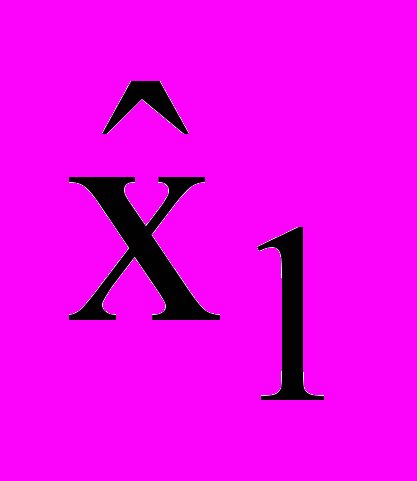частота сигнала 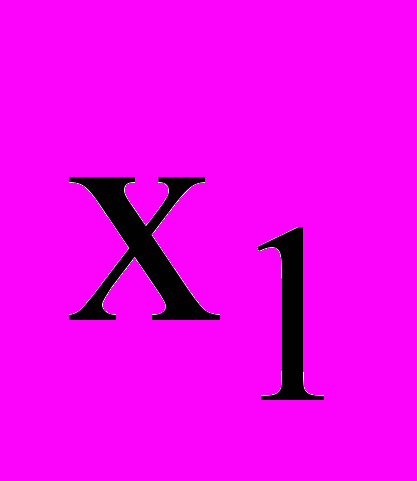и ее оценка



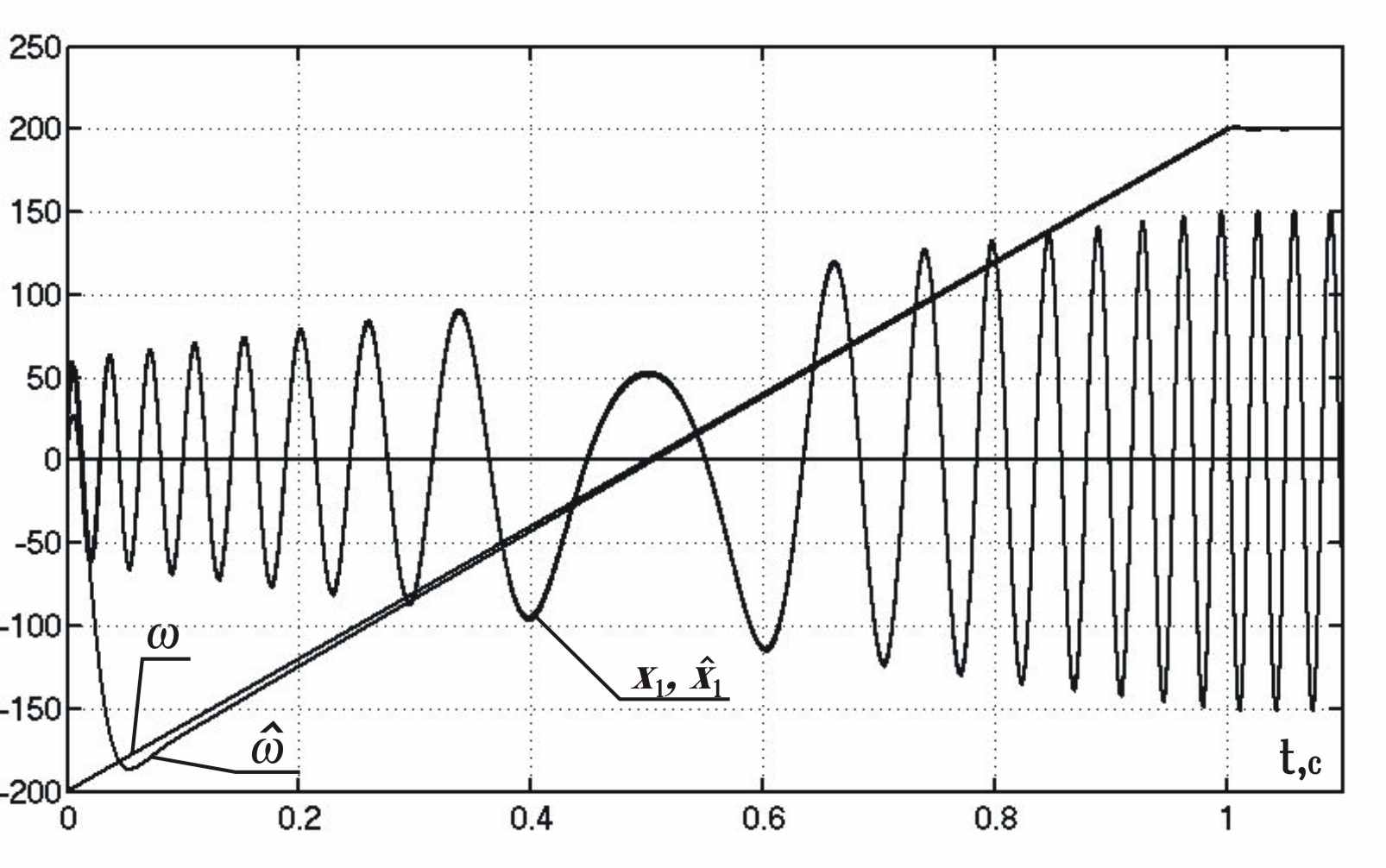
Рисунок 2 - Входной сигнал 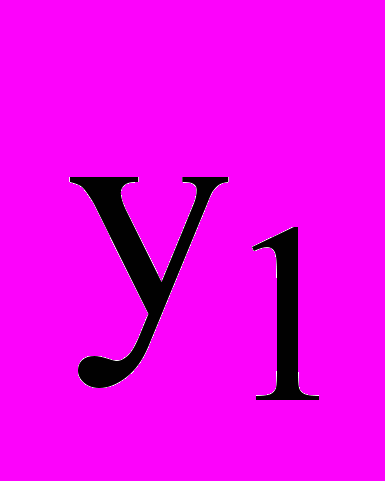, главная гармоника 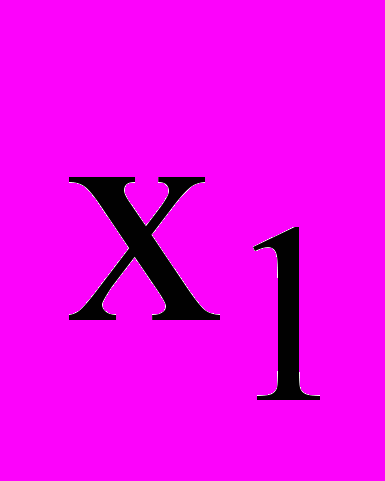, ее оценка ,

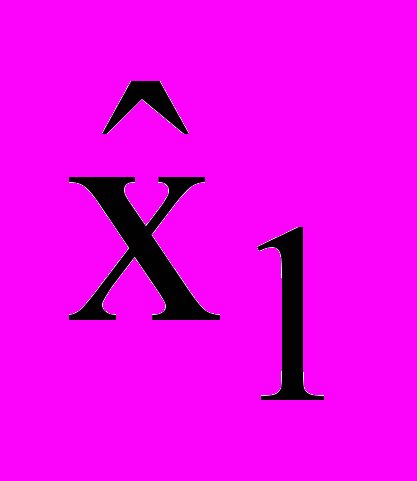частота сигнала 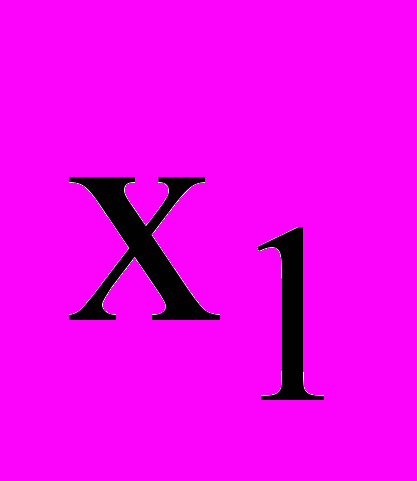и ее оценка




Выводы. Синтезирован адаптивный фильтр низких частот двухфазного гармонического сигнала, оценивающий главные гармоники фаз и частоту сигналов с приемлемой для практики точностью. Для дальнейшего улучшения фильтрующих свойств фильтра его можно комбинировать с фильтрами работ [3-5] с использованием в них оценки частоты из данного фильтра. В этом случае фильтр будет многокаскадным.


ЛИТЕРАТУРА
  1. Потапенко Е.Е. Определение скорости плоского вращения вектора, заданного его проекциями // Радиоэлектроника. Информатика. Управление. – 2002. – №1. С. 143-146.
  2. Потапенко Е.М., Потапенко Е.Е. Фильтрация многофазных нестационарных гармонических сигналов // Электротехника. – 2003. – №3. С. 55-57.
  3. Потапенко Е.Е. Синтез и анализ аналого-цифровых адаптивных наблюдателей многофазных неопределенных сигналов // Радиоэлектроника. Информатика. Управление. – 2003. – №1. С. 139-142.
  4. Потапенко Е.Е., Потапенко Е.М. Синтез и анализ компенсационных фильтров многофазных неопределенных сигналов // Вісник Національного технічного університету “ХПІ”. Збірник наукових праць “Проблеми автоматизованого електропривода. Теорія і практика”. – Харків: НТУ “ХПІ”. – 2003. – №10, т.2. С. 342-344.
  5. Ключев В.И. Теория электропривода: Учебник для вузов. – М.: Энергоатомиздат, 1985. – 560 с.
  6. Кузовков Н.Т. Модальное управление и наблюдающие устройства. – М.: “Машиностроение”, 1976. – 184 с.
  7. Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. – М.: “Мир”, 1977. – 650 с.
  8. Андреев Ю.Н. Управление конечномерными линейными объектами. – М.: Изд-во “Наука” гл. ред. физ.-матем. лит., 1976. – 424 с.



Стаття надійшла 15.04.2006 р.

Рекомендовано до друку

д.т.н., проф. Родькіним Д.Й.

Вісник КДПУ. Випуск 3/2006 (38). Частина 2