Численное моделирование и разработка комплекса программ исследования теплообмена и ламинарного течения в регулярных продольнооребренных коридорных структурах

Вид материала

Автореферат

Содержание Краткое содержание работы

Подобный материал:

• Д. Б. Сполдинг 1 и В. И. Артёмов, 482.05kb.
• Исследование и разработка комплекса программ для геомоделированиЯ размещения объектов, 286.89kb.
• Численное моделирование теплового процесса сварки полиэтиленовых труб при низких температурах, 251.39kb.
• А. С. Алешкин московский государственный университет приборостроения и информатики, 28.87kb.
• Математическое моделирование течения высоковязких жидкостей с маловязким пристенным, 225.73kb.
• Отчет по мероприятию 17. 4 Разработка и внедрение комплекса специализированных образовательных, 1122.44kb.
• Комплекс программ для исследования методов решения задачи о коммивояжере 05. 13., 360.23kb.
• Численное моделирование нелинейно-наследственного поведения пространственно-армированных, 22.15kb.
• Закономерности теплообмена и диагностика загрязнений термоанемометрической нити, 95.5kb.
• Название диссертации, 449.82kb.

КРАТКОЕ СОДЕРЖАНИЕ РАБОТЫ


Во введении обосновывается актуальность работы, проводится анализ существующего к настоящему времени состояния экспериментальных и численных результатов в области течения и теплообмена в круговых коридорных пучках труб поперечным потоком вязкой несжимаемой жидкостью, сформулированы цели и основные направления исследования. Учитывая современное состояние и практическую направленность, актуальность проблемы обтекания продольно оребренных пучков круглых труб поперечным потоком жидкости (газа) в ламинарном режиме изменения числа Рейнольдса как для симметричного, так и ассимметричного оребрения, позволили сформулировать тему исследования и решать проблему с помощью численного моделирования. В этой связи в работе ставится задача разработки вычислительного алгоритма расчета и комплексов программ для ЭВМ в регулярных коридорных структурах теплообменных устройств. Предлагаются подходы и методы решения поставленных задач.

Уделяется внимание вопросам сравнительной эффективности гладкотрубных и продольно оребренных пучков круглых труб, а также рекомендациям по использованию расчетных данных и установлению метода «среднего» Фурье проектировщикам теплообменного оборудования и их устройств в практике.


Отмечено, что значительный вклад в экспериментальные исследования течения и теплоотдачи продольно оребренных пучков труб кругового сечения внесли В.М. Антуфьев,

Г.С. Белецкий, В.Ф. Юдин, А.А. Жукаускас, Р,В. Улинскас, В.П. Исаченко, Я.Л. Полыновский, В.Г . Фастовский, Л.С. Тохтарова, А.И. Мицкевич, М.В. Кирпичев, Ю.В. Петровский, Д.Керн, А. Краус, В.А. Локшин, А.А. Гухман, В.Т. Буглаев, Л.А. Анисин, И.А. Белов, Н.А. Кудрявцев и др., которые сформулировали основные положения и разработали первые инженерные методики расчетов и установки исследований. Благодаря работам М.В. Кирпичева и его последователей М.В. Антуфьевым и В.Ф. Юдиным установлены критериальные зависимости коэффициентов сопротивления и теплопередачи для различных типов пучков (в том числе регулярных) и даны практические рекомендации для подсчета коэффициента теплоотдачи в условиях охлаждения и нагревания потоков газа. Экспериментальный материал обобщен и представлен в виде расчетных формул, графиков, номограмм, удобных для практического использования. Работы М.В. Кирпичева внесли также пионерские исследования по вропросам сравнительной эффективности теплообменных процессов пучках труб и развиты в работах В.М. Антуфьева, В,Ф. Юдина и др.

Существенно, что работы И.А. Белова, Н.А. Кудрявцева, С,А. Исаева дали новое, более перспективное направление численного моделирования процессов расчета течения и теплообмена поперечным потоком жидкости (газа) с помощью использования ЭВМ. Это направление сулит большую экономическую выгоду и переход к автоматизированным методам использования численных расчетов при проектировании ТА, ТЭУ и других их элементов.

Анализ результатов численного моделирования течения и теплдообмена в коридорном регулярном пучке труб с ассимметрично расположенным продольным оребрением полученного автором, говорит о целесообразности применения такого оребрения в практике.

В первой главе приводится анализ развития экспериментальных и численных методов течения и теплообмена в регулярных коридорных структурах поперечно обтекаемых и продольно оребренных пучках труб кругового сечения теплообменного оборудования в диапазоне ламинарного изменения числа Рейнлльдса, поиска путей совершенствования и повышения энергетической эффективности и надежности разного рода ТА. Делаются выводы о необходимости внедрения численного моделирования с целью экономии средств и перехода к автоматизированному проектированию ТА и их элементов. В этой главе приводится постановка задачи исследования, схемы расположения труб в пучке и их изображения , виды обтекания, вопросы выбора сетки в расчетных областях и их классификация (см. рис. 1); обзор экспериментальных исследований, вопросы развития поверхностей теплообмена и ее оценке при теплоотдаче.

Рисунки 1 и 2 иллюстрируют схемы расположения и конфигурации труб в пучке и их изображение, которые относятся к продольно оребренному и кольцевому оребрению.

Отмечается, что в связи с актуальностью развития численного моделирования процесса течения и теплообмена в симметрично и асимметричных пучках труб, впервые предпринята попытка исследования эффективности продольного оребрения. Расчетные исследования привели к новому методу получения результатов, названного методом «среднего» Фурье, который успешно может быть применим и в других областях знаний.

Рассчитывается плоское ламинарное течение несжимаемой вязкой жидкости и конвективный теплообмен в регулярном коридорном продольно оребренном пучке круговых труб, расположенных с продольными и поперечными шагами l и h (в нашем случае l = h = S₁ = S₂). Диаметр цилиндра d принят за линейный масштаб. В коридорном пучке выделяется расчетная ячейка (модуль) ABCDEF, на проточных границах BC и ED которого ставим периодические граничные условия. На границах CD и BE (рис. 3.а) – условие симметрии; на омываемой стенке AF - условия прилипания. Решение тепловой задачи рассматривается отдельно от динамической с использованием ранее рассчитанных полей скоростей. Число Re = 40,100, 250 и 500, а число Pr = 0,73. Геометрические размеры принимаются равными l = 1,25; 1,50 и 2,0, а также другие (см. рис.3.а; 6.г.).


Рисунок 4 иллюстрирует некоторые виды обтекания сечений и оребрения труб (продольного, кольцевого и мембранного). Конструктивная реализация вида пучка труб может иметь несколько вариантов варьируя продольный и поперечный шаги, способ оребрения и расположения труб в пучке.

Характерной особенностью работы является адресность проведения обзора литературных источников в главах. Первая глава является основополагающей в критическом обзоре работ. Обзор работ по пучкам труб и их оребрению изначально восходит от работ Н. Гребера, Е. Шмидта, С.Богерта и Р. Майера, Е. Нейля, О.Е. Власова, Л.Н. Ильина, М.А. Стриковича,

Харпера и Броуна, Т. Боша, Н. Деча, М. Ланга, благодаря чему можно продвинуться в решении задач теплообмена вообще и, в частности, оребренных трубчатых поверхностей при наличии удовлетворительных экспериментальных данных по коэффициентам теплоотдачи ребер и несущих их поверхностей нагрева. Отмечаются работы по повышению коэффициентов теплоотдачи и методам интенсификации тепловой активности, к которым следует отнести работы А.Е. Берглиса, Р.Л. Веба и других зарубежных авторов. Большой вклад отечественных исследователей: А.М. Антуфьева, В.Ф. Юдина, М.В. Кирпичева, А.И. Мицкевича и других. В развитие экспериментальных методов исследования течения и теплообмена привело к подходу сравнительной оценки поверхностей нагрева, при этом можно ее упрастить, что предлагается в данной работе, имея корреляционные зависимости чисел Рейнольдса, Эйлера и Нуссельта. Численные исследования пучков труб позволили сделать вывод о том, что экспериментальные данные, полученные названными авторами достаточно хорошо согласуются с расчетными, полученными с помощью численного моделирования. Следовательно, актуальность проблемы численного моделирования течения и теплообмена продольно оребренных пучков труб можно решать в плоской постановке, пренебрегая концевыми эффектами. Из всего отмеченного следует, что выбранный метод исследования течения и теплообмена, который основан на численном решении полных уравнений Навье – Стокса и энергии, содержание которого предложено П. Роучем и И.А. Беловым, А.С. Гиневским, Н.А. Кудрявцевым, С. Патанкаром и С.А. Исаевым, Е.Спэрроу является эффективным с версией реализации периодического характера течения и теплообмена. Эта методология получила развитие в приложениях к проектированию трубчатых ТА, контейнерному транспотру, аналитическому приборостроению, терморегулированию и экологическим вопросам.

Во-второй главе приводится математическая модель течения и теплообмена в пучках труб кругового сечения, с которой берет начало расчета течения и теплообмена в ламинарном диапазоне изменения числа Рейнольдса. В целях повышения устойчивости процесса численного решения и точности получаемых результатов, предлагается использовать дивергентную форму записи исходной системы дифференциалтных уравнений в полярной системе координат (см. рис.3.а,б). При решении задачи, учитывая дивергентную форму записи исходных уравнений Навье – Стокса и энергии с целью обеспечения оптимальной дискретизации расчетного модуля, используется метод контрольного объема (КО) . Обобщенное дифференциальное уравнение имеет вид:


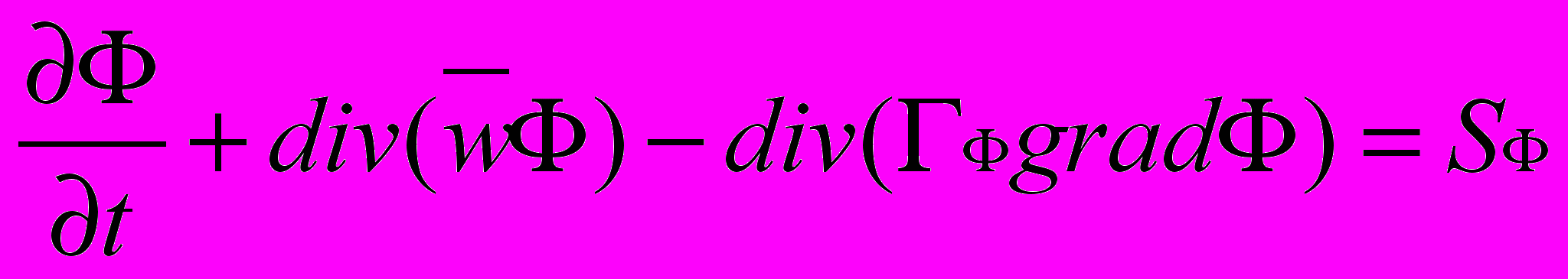, (1)


где 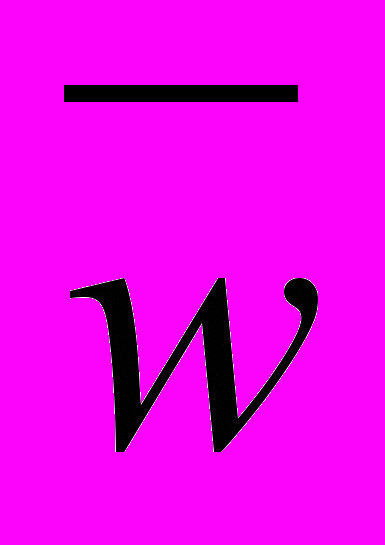- вектор скорости (u, v); Г_ф - коэффициент диффузии; t – время; Ф – зависимая переменная; S_ф – источниковый член. Уравнение (1) записано в нестационарном виде и включает в себя четыре члена: нестационарный, конвективный, диффузионный и источниковый.

Учитывая наложенные ограничения на характер течения, (1) запишем в виде:


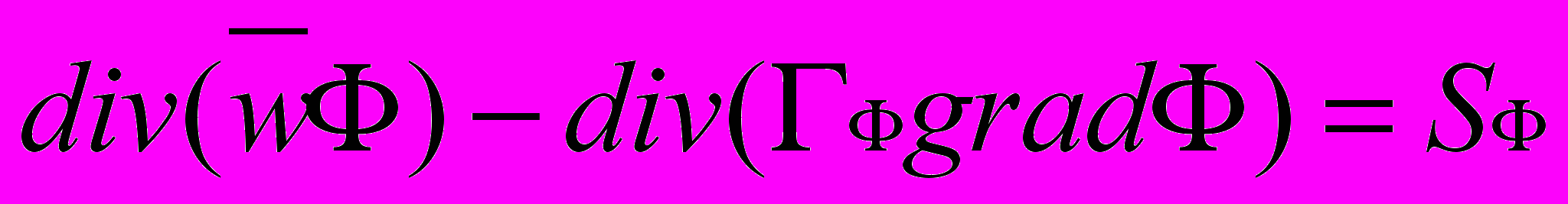, (2)


и включает три члена: конвективный, диффузионный и источниковый. Переменная Ф может принимать значения: 1; u или v, Т, где u и v – составляющие вектора скорости; Т – температура. Конкретный вид Г_ф и S_ф зависит как от Ф, так и от выбранной системы координат


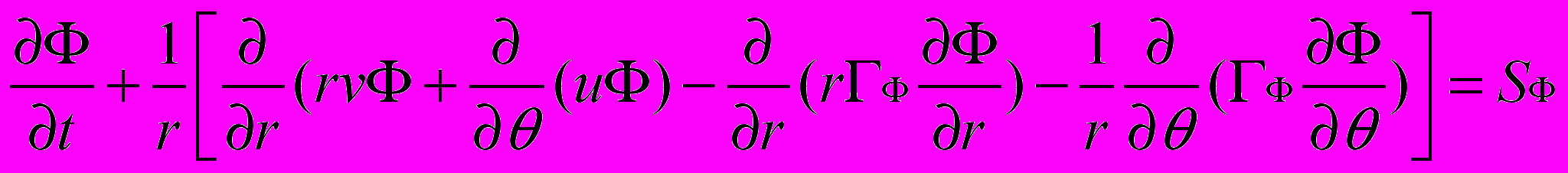, (3)


где r и v - радиальная и тангенциальная координаты; u и v - радиальная и тангенциальная составляющие скорости соответственно.

Уравнение (2) используется для расчета течения и теплообмена как в ламинарном, так и в турбулентном режимах течения, используя дополнительные режимные условия. Следовательно, в случае ламинарного режима течения переменная Ф обозначает составляющие скорости (u, v) и температуру Т.

В формуле (3) исходная система уравнений записывается в безразмерном виде следующим образом:

Ф= 1; Г_Ф = S_ф = 0 (4)

- уравнение неразрывности;

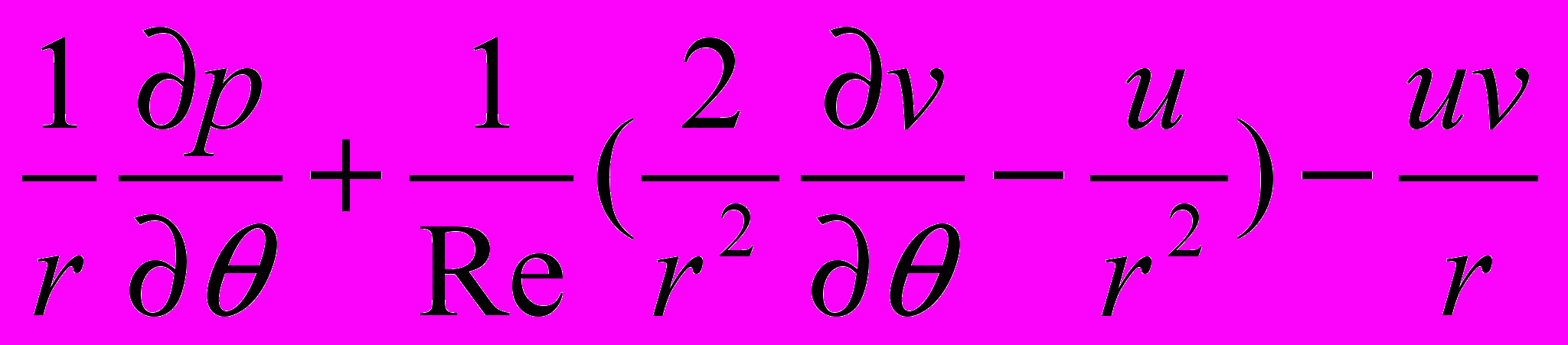
Ф=u: Г_u=1/Re; S_u=- (5)

- уравнение изменения количества движения в радиальном направлении;


Ф = v: Г_v = 1/Re; S_v= 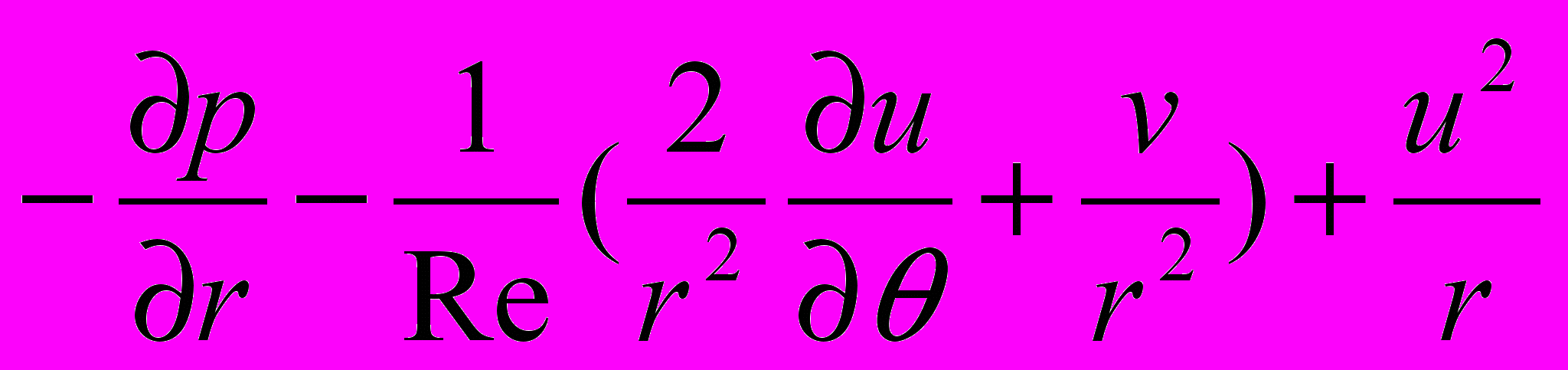(6)

- уравнение изменения количества движения в тангенциальном направлении;


Ф = Т: Г_Т = 1/ Re Pr ; S_Т = 0 (7)


- уравнение энергии. Здесь Re = u d/ v - характерное число Рейнольдса; Pr = v/a - число Прандтля; u - среднемассовая скорость в минимальном проходном сечении пучка АА^!

(см. рис.1.а); d – диаметр трубы; v - коэффициент кинематической вязкости; a - коэффициент температуропроводности. Система (3) - (7) может быть использована для расчета как стационарных, так и нестационарных течений в ламинарном диапазоне изменения числа Рейнольдса.

Обтекание пучка продольно оребренных труб кругового сечения поперечным потоком жидкости (газа) характеризуется неравномерностью распределения скорости, давления, температуры, локальных характеристик течения и теплообмена, сложностью геометрии расчетной области (см. рис.6.). При расчете таких течений С.А. Исаев, П.А. Баранов, Н.А. Кудрявцев, Т.А. Баранова в работе «Численное моделирование влияния чисел Рейнольдса» и

Прандтля на ламинарный теплообмен в коридорном пакете круговых труб различной плотности применяют базовую многоблочную сруктурированную сетку, состоящую из двух разномасштабных сеток различного типа: декартовой и полярной. В данной работе применяется полярная сетка, позволяющая упростить вычисления при расчетах. При расчете таких течений используется разностная аппроксимация исходных уравнений (3) - (7) . Учитывая дивергентную форму записи исходных уравнений, используют в этом случае метод контрольного объема (см. рис.7.а, б) , получают дискретный (разностный аналог системы).

Отметим, что свойства метода КО и детализация решения описаны в работах С.Патанкара, П.Роуча и И.А. Белова. Важным достоинством которого является обеспечение точного

интегрального выполнения физических законов для любой группы КО, следовательно, и для всей расчетной области. Разностная схема является консервативной по массе, количеству движения и энергии. Важным является и принцип построения сетки – размещение узлов сетки в расчетной области. От этого зависит точность информации и ее физическая достоверность. Используем сетку, в которой тангенциальная и радиальная составляющие скорости хранятся в узлах, смещенных относительно узлов хранения давления и температуры на полшага (см. рис.7.а, б.) . Значения переменной Ф_i можно определить, используя различные аппроксимационные схемы. В работе используется схема Леонарда против потока второго порядка точности. Численные эксперименты показывают, что схема Леонарда второго порядка точности близка по точности получения интегральных характеристик течения и теплообмена, а также по обеспечению устойчивости процесса численного решения. Рассматривая более общую задачу нестационарного обтекания и теплообмена, для способа аппроксимации нестационарного члена уравнений (3) – (7) можно на подобии уравнения (1) записать в следующем виде


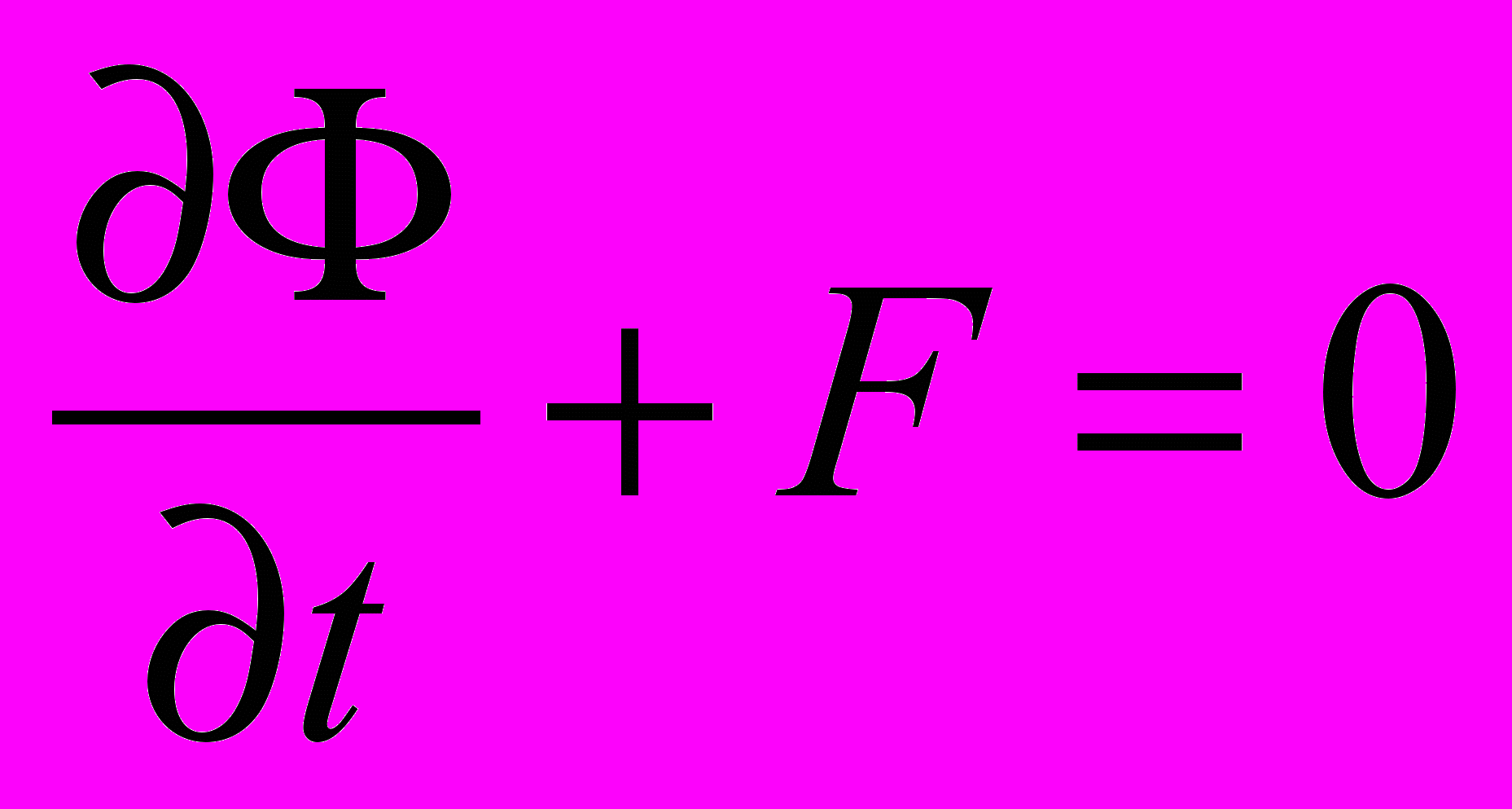, (8)


где F – стационарная часть, включающая в себя конвективные, диффузионные и источниковые члены. Практика расчетов показывает, что для обеспечения устойчивости и сходимости процесса численного моделирования выбирают неявные схемы, одну из которых рекомендует И.А. Белов – схему Перйе второго порядка точности по времени:


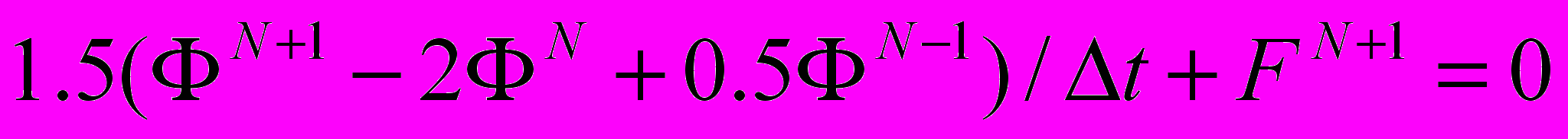, (9)


которая подавляет нефизические пульсации параметров течения и достаточно проста в алгоритмизации. Для обеспечения записи (9) стационарной части F на (N + 1) - м временном слое применяется итерационная процедура.

В общем виде разностный аналог конвективно-диффузионного уравнения представляется следующим образом (см. рис.5 и 7)


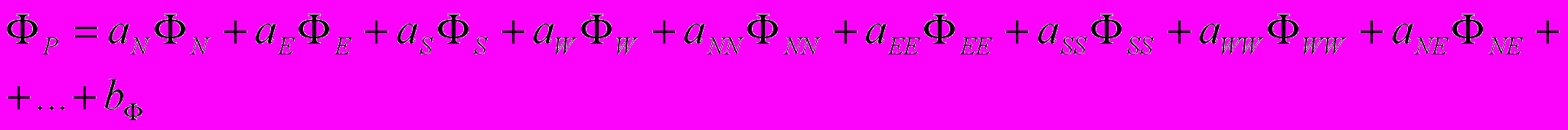, (10)


где Ф = u, v, Т; a_N, a_E, … - коэффициенты, определяемые способом нахождения конвективных и диффузионных потоков через грани КО; b_Ф - источниковая часть разностного уравнения. Учитывая факторы стабилизации окончательно получим, что


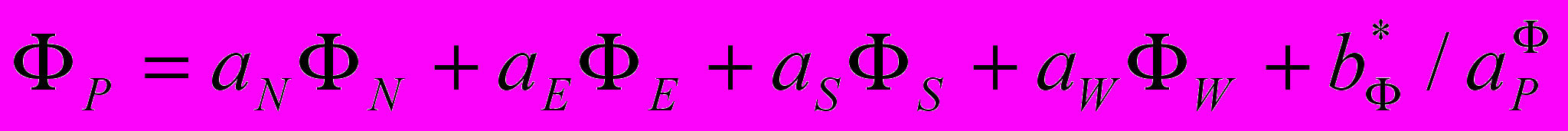, (11)


где 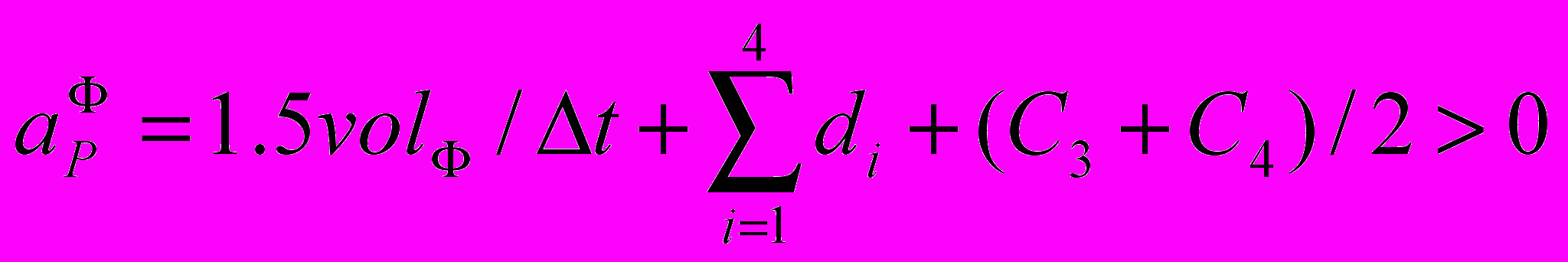; 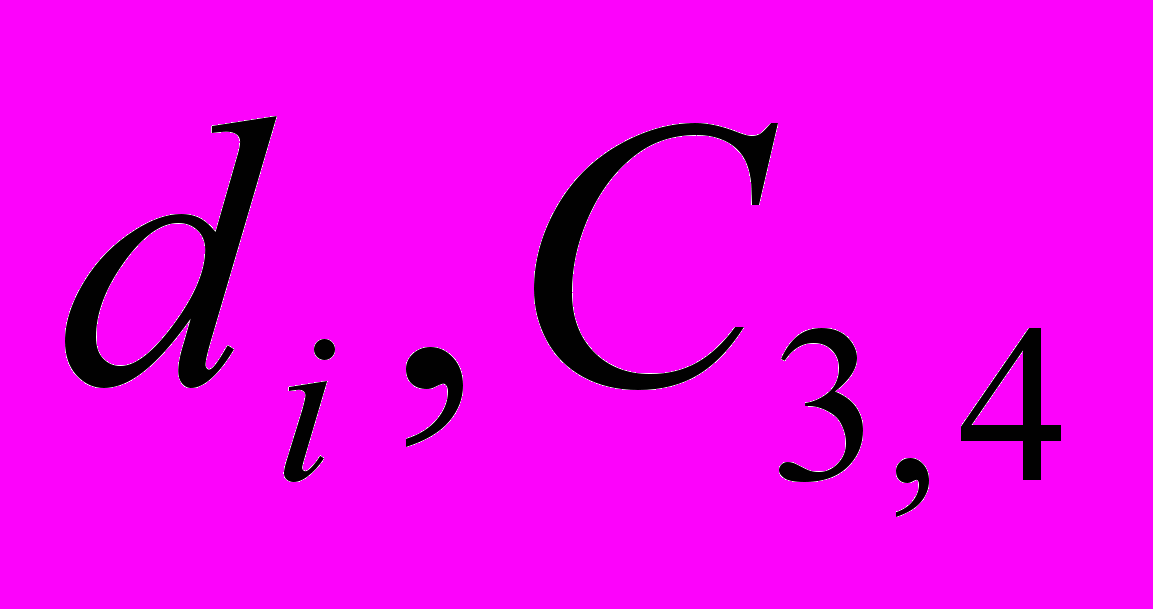- соответственно диффузионные и конвективные коэффициенты; vol _Ф - объем КО; - шаг по времени;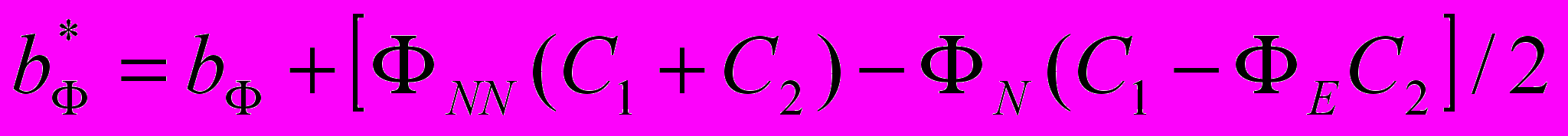


, (12)


Алгоритм решения конвективно-диффузионного уравнения (11) основан на LU - факторизации. Расчет давления основан на решении уравнения Пуассона для поправки давления, найдя которую можно определить и само давление, используя при этом процедуру SIMPLE.

Рисунок 7 иллюстрирует способ определения интерполяционных коэффициентов при заданных граничных условиях. Эти коэффициенты установлены автором в работе «Использование интерполяционных соотношений при нахождении параметров течения и теплообмена в расчетной области » можно также применять при разработке комплексов программ для построения многоблочного факторизованного алгоритма решения уравнений Навье – Стокса и энергии на базе структурированных пересекающихся сеток

На рисунке 8 приводится компьютерная графика, полученная по числовым полям скоростей и температуры решения динамической и тепловой задач в виде линий постоянных значений функции тока для регулярных коридорных и продольно оребренных пучков труб в варианте четырех и восьми ребер на поверхности несущей трубы. Данная визуализация позволяет сделать выводы о механизме течения в таких компоновках пучков труб.

В этой главе стоит отметить блок - схему (рис.9) решения нестационарной задачи в ламинарном диапазоне изменения числа Рейнольдса, а также вычислительный алгоритм и алгоритмическую блок-схему, предложенную автором. Роль этой схемы значительна в решении уравнения изменения количества движения для данного временного шага и уравнения Пуассона для поправки давления с целью его корректировки по найденной поправке. После чего проводят корректировку скоростей и находят их новое поле.

В третьей главе рассматривается численное моделирование стационарного обтекания и теплообмена регулярного коридорного пучка труб кругового сечения, а также обтекание изолированной трубы с результатами, полученными С.А. Исаевым как составного элемента пучков труб. Как и в случае стационарного, так и нестационарного течения используется для расчета q – расчетная область для исключения развития нестационарных процессов в межтрубном пространстве, ставя условия симметрии. Проводится сопоставление численных результатов с результатами, полученными другими авторами. Отмечается численный алгоритм, его реализация в программе «Коридор» и характерные особенности расчета. Расчеты сопротивления и теплоотдачи приведены в таблицах, делается заключение о хорошей корреляции расчетных результатов с имеющимися экспериментальными данными как по локальным, так и по интегральным характеристикам.

Анализ расчетных результатов также позволяет сделать вывод о том, что с уменьшением плотности регулярных коридорных пучков труб ведет к снижению уровня силовых нагрузок на глубинную трубу, продольная составляющая которых вносит основной вклад в сопротивление. Приводятся картины течения и температурного поля для компоновки 1,50 х 1,50 и Re = 40; 500, а также графики эволюции с ростом числа Рейнольдса поверхностного распределения давления. Результаты численных экспериментов и полученные с помощью метода «среднего» Фурье для регулярных пучков 2,25 х 2,25 и 2,50 х 2,25, говорят о том, что уменьшение плотности пучков труб за пределы компоновки 2,0 х 2,0 ведет к автомодельному процессу течения во всем диапазоне изменения чисел Re = 40…500 и величина Eu стабилизируется и находится в пределах 0,2 – 0,1 (рис.10). Представленные кривые на графиках распределения местного числа Нуссельта, напряжение трения, давления – топологически подобны для ламинарного режима течения (рис.11, рис. 12).

На основании проведенных исследований отмечается эффективность разработанного вычислительного алгоритма в связи с высокой степенью точности моделирования сложных динамических и тепловых процессов, развивающихся в межтрубном пространстве пучков; сравнение результатов расчета с другими говорит о допустимости использования более грубой сетки, а разработчикам конструкторам ТА рекомендуется использовать результаты численного моделирования и комплекс программ для ЭВМ «Коридор» в практике.

В четвертой главе представлены результаты численного моделирования стационарного поперечного ламинарного течения и теплоотдачи мембранных конвективных регулярных

коридорных пучках труб кругового сечения и их анализ, рассматривая мембраны как прямолинейные ребра – проставки.

Начиная с семидесятых годов ХХ столетия потребности государства в конструкторских и технологических разработках по промышленному освоению новых МКПН для парогенераторов поставили задачу исследований по расчету аэродинамического сопротивления и теплообмена. Большой вклад в экспериментальных исследованиях принадлежит Локшину В.А., Лисейкину И.Д., Аронову Д.И., Ленькову Ю.А., Назаренко В.С., Моргун А.В., Мигай В.К., Быстрову П.Г., Сотникову И.А.

Анализ результатов выявил расхождения при сравнении опытных данных с расчетными, что побудило автора работы к численным исследованиям для выработки рекомендаций. Следует обратить внимание на факт отсутствия сведений в литературных источниках по численному моделированию расчетов течения и теплообмена в МКПН, за исключением работы Костенко А.В. по использованию алгебраической блок-схемы при расчете аэродинамического сопротивления и теплоотдачи мембранного коридорного пакета труб. В данной главе все расчеты выполнены с использованием q – расчетной области (см. рис. 3). Проведен анализ расчетной информации, полученной по программе комплекса «Коридор» и методу «среднего» Фурье, разработанных автором. Приводятся картины течения и теплообмена, графики корреляционных зависимостей (см. рис.13 ) и др., а также использование результатов расчетов для практического применения их в практике проектирования ТА.

На рисунке 18 приведены изображения регулярного коридорного пучка труб, схема компоновки пучка и картина течения в виде линий постоянных значений функции тока при числе Re =40.

Среднее по периметру трубы пучка 2,0 х 2,0 значение Nu_m при всех режимах течения сведены в таблицу 1. Расчет значений Eu – динамической характеристике этого регулярного коридорного пучка труб в таблице 2. Расчетные данные сравнительной эффективности гладкотрубных и оребренных пучков, как пример для рассмотренного случая пучка 2,0 х 2,0 и Pr = 0.73 (Re =500), приведены в таблице 3.

На рисунке 20 а, б, в представлено влияние числа Рейнольдса на число Эйлера для регулярных мембранных коридорных пучков труб. Видно, что имеет место хорошее коррелирование расчетных и экспериментальных данных. Это позволяет говорить о качестве и надежности разработанного вычислительного алгоритма

В пятой главе представлены результаты исследований по применению рядов и комплексного интегрального преобразования Фурье с конечными пределами, которое базируется на работах Г.Е. Пухова «Комплексное исчисление и его применение» и автора настоящей работы, по свойствам, относящимся к комплексному исчислению как к предмету по интегральным преобразованиям. Эти результаты использованы в практике исследования течения и теплообмена регулярных структур ТА и их устройств для получения корреляционных зависимостей по сопротивлению и теплоотдаче и другим интегральным и локальным характеристикам. Метод названный методом «среднего» Фурье, так как доказательство его основано на достаточном признаке сходимости ряда Фурье (что представляет собой обратное преобразование Фурье).

Рис. 14.а - иллюстрирует динамику сходимости корреляционных зависимостей 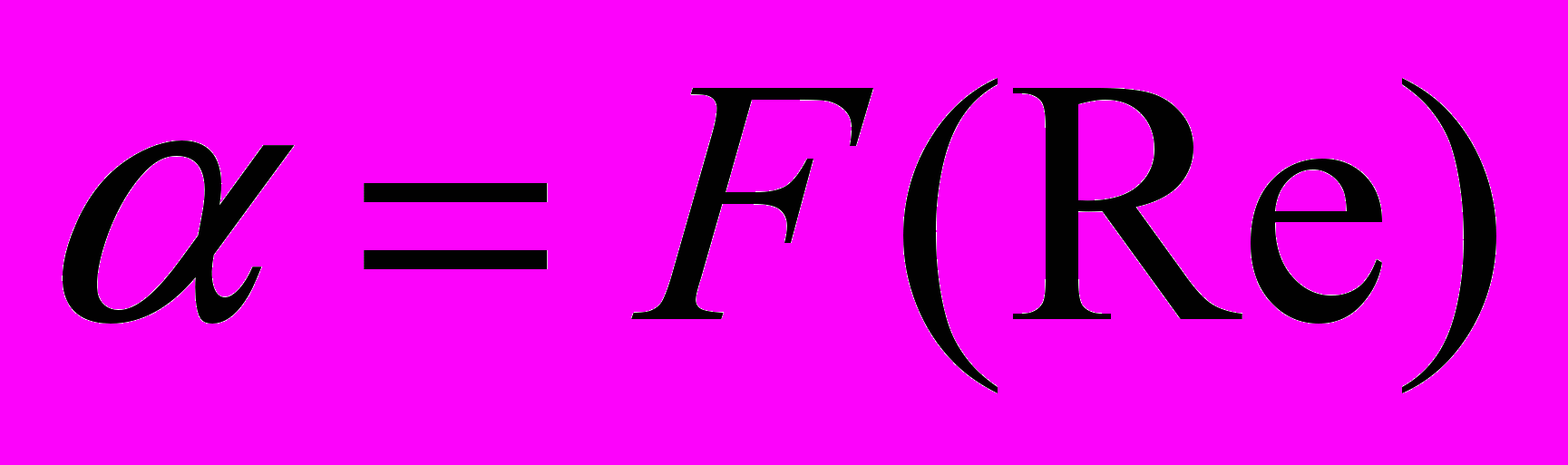по двум базовым к искомой зависимости. Рис. 14. б – показывает, в качестве примера

использование метода важный для практики проектирования ТА случай выбора корреляционной зависимости в переходном режиме течения, числа Нуссельта от числа Рейнольдса. Кривая 3 получен по методу «среднего» Фурье.

Для построения корреляционных зависимостей и построения их графиков автором создан вычислительный программный продукт «Корреляция Эйлер - Нуссельт».

Обращают на себя внимание содержание параграфов главы, относящихся к построению корреляционных зависимостей при исследованиях течения теплообмена, а также в других исследованиях, выполненных другими авторами.

Интерес представляют картины течения и теплообмена, графики распределения давления и трения, местного числа Нуссельта и другие.

Используя достаточные условия сходимости ряда Фурье по произвольной ортонормированной системе функций, заданной на промежутке < а, b > (в нашем случае таким промежутком может служить промежуток, представляющий собой диапазон ламинарного изменения чисел Рейнольдса) получают корреляционные зависимости с помощью преобразований Фурье, дающие наилучшие приближения. Каждая зависимость может быть получена с помощью физического или численного эксперимента или аналитически.

Получены формулы


αξн = 2αξс - αξв , (13)


αξв = 2αξс - αξн . (14)


Формулы (13) и (14) представляют математическую модель алгоритма построения «нижней» и «верхней» корреляционной зависимости, зная опорные (базовые). Зависимости, полученные в (13) и (14) позволяют дать значительную экономию во времени и затратах труда. В этой работе это обосновывается на наш взгляд впервые.

Глава содержит общие выводы и рекомендации для конструкторов-проектировщиков ТА и других устройств. Предложенные методы корреляционных зависимостей (13) и (14) могут пополнить по новым сведениям по теплообмену «Справочник по теплообменникам »: в 2 т. под редакцией Б.С. Петухова, В.К. Шикова. – М.: Энергоатомиздат, 1987.

В шестой главе представлены результаты численного моделирования обтекания и теплообмена продольно оребренных регулярных коридорных пучках круглых труб поперечным потоком жидкости в симметричной и асимметричной формах приводится сравнительная эффективность решений для гладких и оребренных трубных пучков. При конструировании ТА и их элементов необходимо добиться максимального уровня теплосъема развитой поверхности теплообмена при минимальных затратах мощности на перемещение теплоносителя через ТА или устройство. В связи с этим параметр, определяющий эффективность работы ТА, скажем η , должны входить средние по периметру трубы число Нуссельта и число Эйлера. Для этого η выразим простым соотношением(исходя из физического толкования задачи течения и теплообмена)


p

q

η = Nu_m / Eu , (15)


где p и q – вещественные числа. Кроме (15) возможны и другие более сложные функциональные зависимости. Этому вопросу и его освещению посвящены результаты работ А.И. Мицкевича, В.М. Антуфьева, В.Ф. Юдина, М.В. Кирпичева. Здесь ограничимся рассмотрением (15), предложенном автором данной работы для проведения предварительного качественного анализа эффективности продольного оребрения. Числа p и q должны зависеть от ряда факторов. Учитывая, что все предыдущие расчеты проведены при постоянном значении числа Прандтля Pr = 0,73 (отсюда следует подобие теплового и динамического пограничных слоев, что отражено в трудах Л.И. Седова, Б.С. Петухова, Л.Г. Генина, Л.Г. Лойцянского) примем p=q=1 зависимость (15) примет вид

η = Nu_m / Eu , (16)

При решении проблемы сравнительной оценки поверхности нагрева М.В. Кирпичев предложил использовать для оценки так называемый энергетический коэффициент. В настоящей работе предлагается делать заключение об эффективности поверхности нагрева с помощью геометрического смысла, построив прежде корреляционные зависимости для сравниваемых поверхностей. Для заданного режима течения и данной компоновки труб по графикам Nu = f (Re) найти отношение площадей , которое даст ответ о наивыгоднейшей поверхности нагрева. Так имея зависимости Nu = S₁ (Re) и Nu = S₂ (Re), коэффициент η эффективности трубного пучка определим соотношением :


η = S₁ (Re) / S₂ (Re) , (17)


где S₁ и S₂ – площади фигур , ограниченные зависимостями S₁ (Re) и S₂ (Re).

Таким образом, в общем случае


η =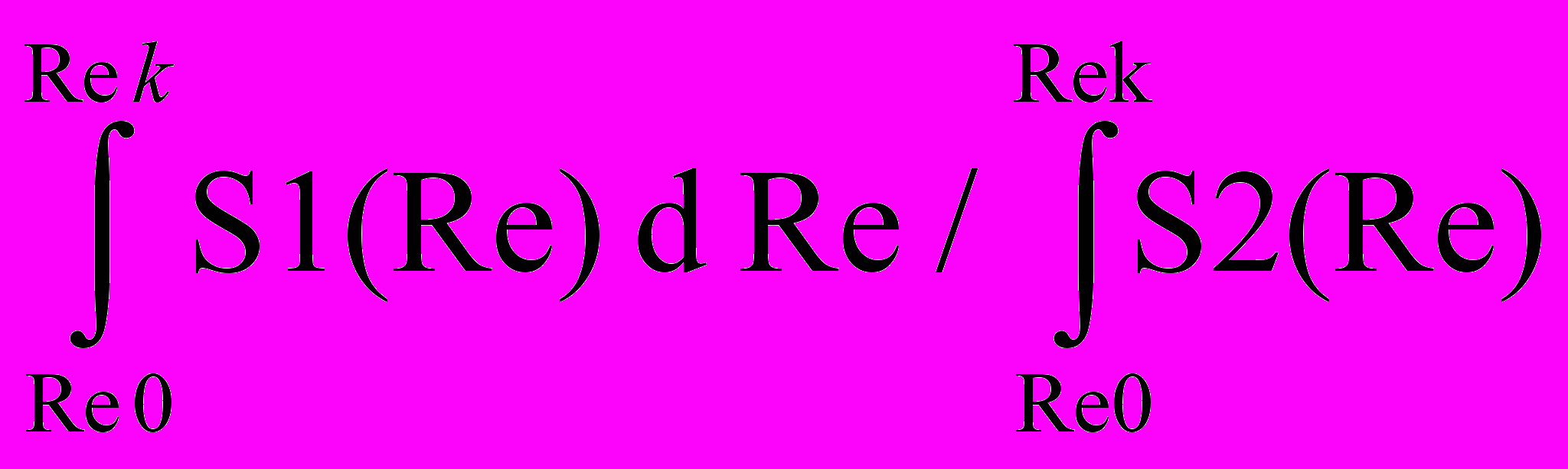d Re , (18)

где Re 0 и Re k - начальное и конечное значение числа Рейнольдса рассматриваемого режима течения.

Проведенные расчетные данные для коэффициента η для гладкотрубного и продольно оребренных пучков труб собраны в таблицу. Из данных таблицы сравнительной эффективности пучка 2,0 х 2,0 при Pr = 0,73 видно, что во всем диапазоне расчетных чисел Рейнольдса можно подобрать вариант оребрения пучка труб, при котором он будет эффективен, чем гладкотрубный пучок. В частности, при Re = 40 … 250 симметрично оребренный пучок с четырьмя ребрами дает выигрыш в эффективности в сравнении с гладкотрубным в среднем на 30%. В тоже время при числе Re = 500 наиболее эффективном является вариант ассимметричного оребрения (выигрыш 14%); а продольно оребренный пучок с восьмью ребрами дает выигрыш 50%, а дальнейшее оребрение приводит к падению по эффективности (начиная с варианта десяти ребер).

На рис. 16.а – представлены графики распределения коэффициента трения для четырех и восьми ребер, расположенных на поверхности трубы. Характерной особенностью распределения трения является факт наличия угловых точек в местах расположения ребер (здесь касательная резко меняет положение кривой распределения трения ).

На рис. 16.б – представлены распределения коэффициентов давления p_w на развитой поверхности для двух вариантов оребрения. Для случая четырех ребер наблюдается резкое падение давления по достижении абсолютного максимума, который с ростом Re смещается к передней критической точке. В тоже время для второго варианта оребрения характерно резкое падение давления в местах расположения ребер на поверхности трубы, причем видно, что месторасположение абсолютного максимума давления p_w зависит от числа Re. Зависимости коэффициента трения связаны с коэффициентом давления и геометрически.

На рис. 17.а – б - показано распределение числа Нуссельта для обоих вариантов оребрения. Отмечается, что наибольшее различие теплоотдачи оребренного и гладкотрубного пучков связано с наличием при оребрении большого числа локальных максимумов теплоотдачи (по числу ребер). Симметричное продольное оребрение приводит к более равномерной теплоотдаче поверхности трубы. В этой главе представлены также интегральные характеристики течения и теплообмена для продольного оребрения для обоих вариантов симметричного оребрения.

В итоге делаются выводы, из которых следует отметить, что:

- продольное оребрение является перспективным способом увеличения тепловой активности ТА при неизменной мощности на перемещение теплоносителя;

- вопрос о выборе оребрения, его геометрических параметров, количестве ребер должен решаться в конкретном случае, исходя из конструктивных особенностей ТА;

- вычислительные алгоритмы для продольно оребренных пучков в ламинарном диапазоне чисел Re как для стационарной, так и нестационарной постановке задачи позволяют эффективно получать информацию по локальным и интегральным характеристикам течения и теплообмена;

- снятие условий симметрии течения и теплообмена приводит к сближению расчетных результатов и экспериментальных данных;

- следствием асимметрии распределения коэффициентов давления и трения на поверхности несущей трубы является возникновение помимо лобового сопротивления и поперечной нагрузки - подъемной силы, о чем отмечено в работе А.И. Олейникова и А.В. Костенко;

- даны рекомендации для практики проектирования ТА использовать асимметричное и отказ от симметричного оребрения;

- вычислительные комплексы программ «Коридор», «Трубные пучки» использовать для перехода к автоматизированному проектированию ТА и их элементов.

В седьмой главе представлено использование результатов численного моделирования течения и теплообмена в продольно оребренных регулярных коридорных пучках труб кругового сечения и метода «среднего» Фурье в практике экспериментальных исследований, в задачах фильтрации, исследовании параметров центробежных малогабаритных насосов (МЦН), использующихся в аэрокосмической технике; литейного производства; сушильных установках; крупногабаритных переносных тепловых устройствах для сушки зерновой продукции; постройке преград через водные поверхности; использовании расчетных данных для создания аппаратов очистки нефтепереработки с целью сохранения экологически чистого пространства и обеспечения жизнедеятельности людей.

На рисунке 21 приведена процедура построения картин течения переменной  , в виде этапов и систематизации точек изолинии  = 0, отличающейся от предложенной П. Роучем в его книге «Вычислительная гидродинамика», введя понятие нормы сеточной ячейки.