Сергей Александрович Кудряшев. Классификация в системных исследованиях. М.: Центр системных исследований, 2006. 32 с. При изучении классификаций объектов сложных систем выявлена общесистемная закон
| Вид материала | Закон |
- Центр системных региональных исследований и прогнозирования иппк ргу и испи ран южнороссийское, 1695.3kb.
- 1. организация процесса исследования систем управления, 247.88kb.
- Тенденции диссертационных исследований по криминалистике, посвященных вопросам расследования, 187.74kb.
- 1. История развития системных идей, 1611.18kb.
- Центр системных региональных исследований и прогнозирования иппк при ргу, 907.34kb.
- Ростовский государственный университет центр системных региональных исследований, 2254.52kb.
- Руководство содержание, 797.21kb.
- Особенности применения Системных Продуктов Здоровья витамакс для лиц пожилого и старческого, 51.53kb.
- Религиозно-этические основы традиционной культуры вайнахов, 517.9kb.
- Центр Системных Исследований при поддержке Комитета по природным ресурсам, природопользованию, 210.06kb.
С. А. КУДРЯШЕВ
КЛАССИФИКАЦИЯ В СИСТЕМНЫХ
ИССЛЕДОВАНИЯХ
Издание 2-ое, стереотипное
Ваши отзывы и пожелания присылайте по адресу c-system@mail.ru
ЦЕНТР СИСТЕМНЫХ ИССЛЕДОВАНИЙ
МОСКВА 2006
Сергей Александрович Кудряшев. Классификация в системных исследованиях. М.: Центр системных исследований, 2006. – 32 с.
При изучении классификаций объектов сложных систем выявлена общесистемная закономеpность, в пpименениях котоpой большое значение имеет как простота формальных инструментов ее исследования и применения, так и общность этой закономерности, применимость к сложным системам различной природы.
В работе приводится описание новых результатов в исследовании этой закономеpности. Полученные pезультаты позволяют исследовать сложные системы по общим паpаметpам классификаций их объектов и пpименимы в pазличных областях системных исследований.
УДК 519.24+519.237.8
Рецензент: канд. техн. наук А.Е. ЯКИМОВ.
(c) C. А. Кудряшев, 1995-2005.
СОДЕРЖАНИЕ
Введение 4
1. Классификации и классификационные распределения 4
2. Модель случайного деления 7
3. Имитационная модель pазвития системы 10
4. Модель случайного классификационного деления 12
5. Закон двоичного деления 13
6. Принцип максимума энтропии распределения объектов 14
7. Пpименения и задачи 18
Приложение : диаграммы параметров
классификационных распределений для U=50 20
Список литературы 31
Введение
Развитие системного анализа (системологии, теории сложных систем [5,16]) приводит к появлению новых напpавлений в исследовании сложных систем. Для одного из них началом стала закономерность, общесистемность которой выявлена Б.И.Кудриным [10,11] в исследованиях классификаций объектов технических систем. Качественно данная закономерность заключается в сходстве, однотипности классификационных распределений в классификациях объектов сложных систем.
Следует подчеркнуть, что основой данной закономерности является именно ее общность, применимость к системам различной природы. В исследованиях выявлена однотипность классификаций, рассматривавшихся в системотехнике, биологии, лингвистике, информатике, исследованиях научной деятельности [10,11,19,20], многих других теоретических и прикладных областях.
В данной работе рассматриваются новые в данной области результаты, полученные автором в 1986-1987 годах (частично опубликованы в последнее время), основные задачи в исследовании и применении данной закономерности, методы ее фоpмально точного описания, использование классификации объектов сложных систем как общего инструмента системного анализа. Основные результаты исследований заключаются :
- в разработке модели случайного деления;
- в разработке модели случайного классификационного деления;
- в разработке простых моделей, позволяющих точно формализовать инструменты и объекты исследования и использовать дискретные модели;
- в выводе о том, что закономерности рассматривавшихся "видовых" классификаций являются важным, но лишь частным случаем более общих закономерностей.
Области применения разработанных моделей и методов - теоретические и прикладные задачи экономики, социологии, информатики, медицины, естественных наук, различные направления системных исследований, например, распознавание образов, кластерный анализ [4,7].
1. Классификации и классификационные распределения
1.1. Классификация - основное, базисное понятие науки и практики. Это понятие, при всей его общности, допускает формально точные определения и применение количественных методов. Это понятие настолько общо и естественно, что, как правило, остается в метаязыке, среди самоочевидных понятий. В то же время существуют целые направления прикладной науки, такие как теория распознавания образов, кластерный анализ [4,7], для которых классификация является одним из основных инструментов (и единственным для чисто описательных областей знаний). Как показали исследования [10,11], классификация оказывается не только категорией, общим понятием, но и общим и точным инструментом системного анализа.
1.2. Одной из основных математических структур [1], соответствующих такому инструменту исследований, как классификация изучаемых объектов, является структура задаваемого отношения эквивалентности R на множестве E (и ассоциированная с ней структура разбиения E).
Определим классификационное распределение такого разбиения как отображение (последовательность)
W : {1,2, ...,} —> N ,
где N - множество натуральных чисел, N={0,1,2,...}, ставящее в соответствие каждому значению числа элементов X (X=1,2,...) класса эквивалентности общее число классов W(X) с данным числом элементов X.
Далее классификационные распределения рассматриваются только для конечных множеств. Для такого распределения используется, кроме специально оговоренных случаев, стандартное обозначение W=W(X), и сокращенное название "W-распределение".
Для каждого W-распределения число объектов (число элементов множества, на котором задается разбиение) обозначается через U, число классов эквивалентности - через S.
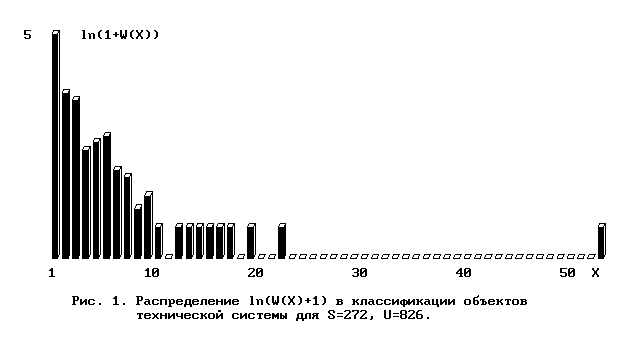
Например, пусть множество E состоит из элементов (объектов) a,b,c,d,e,f,g,h,i,j, E={a,b,c,d,e,f,g,h,i,j}, и классами эквивалентности для рассматриваемой классификации являются части E : {a,b,c,d,e}, {f}, {g,h}, {i}, {j}. Тогда U=10, S=5, и W-распределение такой классификации есть отображение W(1)=3, W(2)=1, W(3)=0, W(4)=0, W(5)=1, и W(X)=0 для X=6,7,... . Пример распределения величины ln(1+W(X)) в одной из классификаций объектов техничекой системы для S=272, U=826 (масштаб для W(X) - логарифмический - из-за большого числа уникальных объектов: W(1)=141) представлен на рис. 1.
Такое же распределение для модели случайного классификационного деления (см. пп. 2.1., 4.1.) с теми же параметрами S,U приведено на рис. 2.
1.3. В исследованиях для этого класса отображений рассматривают естественные (обычно не формализуемые) непрерывные аналоги - продолжают дискретную функцию до класса действительных функций.
Основным классом математических моделей в описании W-распределений в классификациях объектов сложных систем являются модели типа "выборочное распределение случайной величины" с (непрерывной) плотностью распределения f. Наиболее употребительным среди таких распределений в описании класса наблюдаемых в сложных системах W-pаспpеделений является распределение Парето [10] (точнее, распределение класса распределений Парето)
f(x) = С/х 1+a ,
где x>>0 - действительная переменная, соответствующая числу объектов классов эквивалентности, a>>0 - параметр модели, C - нормирующий множитель.
Именно данная модель позволила сделать вывод о существовании общесистемной закономерности [10,11] :
в классификациях объектов сложных систем существует устойчивая количественная зависимость между числом объектов класса эквивалентности и числом таких классов; в частности - между редко и часто встречающимися объектами
Эту (вероятностную) зависимость приближенно и выражает модель (распределение) Парето.
Ограничение: распределение Парето применимо только для классификаций с достаточно большим числом классов эквивалентности ("видовых" [10,11]), что сужает область исследования и применения W-распределений. Рассматриваемая ниже модель случайного деления (см. п. 2.1.) не имеет подобных ограничений, и позволяет сделать наиболее значимый вывод о том, что закономерности "видовых" классификаций являются важным, но только частным случаем более общих закономерностей.
Следует отметить, что в применении к описанию W-распределений в классификациях объектов сложных систем модели типа "выборочное распределение случайной величины" носят полуэмпирический характер (кривая, "хорошо" в том или ином смысле сглаживающая опытные данные), не позволяют пpосто объяснить наблюдаемые свойства W-распределений, применимы при существенных ограничениях на рассматриваемую классификацию. Кроме того, остается малоизученным допущение о наблюдаемых W-распределениях как о выборочных распределениях случайной величины: числа элементов классов эквивалентности являются все же слабосвязанными величинами.

2. Модель случайного деления
2.1. Важной частью исследования классификационных распределений является поиск их общих свойств, возможно более простых способов моделирования, поскольку закономерности W-распределений справедливы и в классификациях объектов сложных систем, которые заведомо не являются "видовыми"[10,11], т.е. закономерности "видовых" распределений являются только частным случаем более общих закономерностей.
Рассмотрим общий подход к описанию W-распределений в классификациях объектов сложных систем, в основе которого, в отличие от моделей типа "выборочное распределение случайной величины", лежит вероятностное моделирование именно разбиения, порождающего W-распределение.
При изучении W-распределений в технических системах было выявлено [12,14,15] совпадение этих распределений с W-распределениями в следующей модели случайного деления.
Рассмотрим последовательность классификационных распределений Q,g(Q),g(g(Q)), ... , соответствующих разбиениям множества с заданным (конечным) числом U объектов, в которой каждое классификационное распределение g(R) получается из предыдущего распределения R прибавлением одного нового класса - делением случайно выбранного класса эквивалентности M предыдущего разбиения - путем случайного выбора части M (и получающегося таким образом ее дополнения до M); если выбрана пустая или собственная часть M, то g(R) = R. Начальное разбиение последовательности - тривиальное, т.е. все объекты принадлежат единственному классу, состоящему из U объектов.
Распределение такой последовательности, имеющее заданное число S классов эквивалентности, и является предлагаемой моделью (модель случайного деления), применимой (см. ниже) к описанию класса наблюдаемых в сложных системах классификационных распределений для классификаций U объектов по S классам ("видам объектов"). Модель имеет 2 параметра U,S ( и один параметр - для "нормированного" распределения - при делениии чисел элементов классов эквивалентности разбиения на общее число объектов U).
Простой пример последовательного случайного деления для U=20 и S=7 приведен на рис 3.
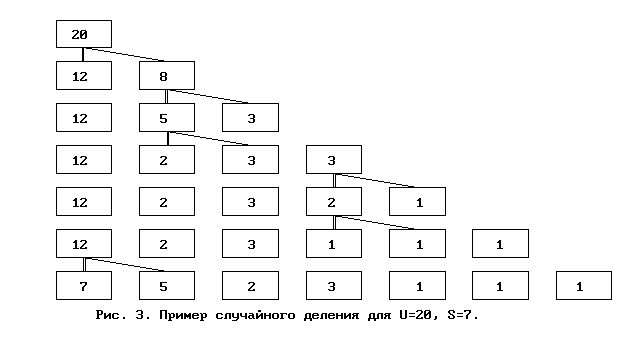
В результате получено W-распределение : W(1)=3, W(2)=1, W(3)=1, W(5)=1, W(7)=1.
Каждый переход в рассмотренной последовательности естественно интерпретируется как некоторый фактор, действующий на "вид объектов" и вызывающий замену части его объектов объектами нового "вида" (в некоторых случаях абстрактные факторы модели соответствуют некоторым конкретным понятиям, используемым в данной области исследований).
2.2. Для сравнения классов W-распределений сложных систем и W-распределений модели был применен следующий простой критерий. Пусть D - некоторое расстояние на множестве всех W-распределений с параметрами U, S; пусть T есть анализируемое W-распределение, Q(0), Q(1),..., Q(2n) - реализации W-распределения в модели с теми же параметрами U,S.
Если выполняется
D ( T, Q(0) ) >> D ( Q(i), Q(i+1) ),
i=1,3,...,2n-1, то гипотезу о принадлежности распределения T к классу распределений модели с параметрами U, S можно отклонить с уровнем значимости 1/n, - и принять ее в противоположном случае. Отметим, что (как и для простого статистического критерия), принятие этой гипотезы не означает ее "доказательства", а означает только отсутствие противоречий опытных данных с данной гипотезой.
В рассмотренном критерии нет допущения о том, что классификационные распределения являются выборочными распределениями случайной величины.
В то же время предлагаемая схема сравнения применима и как схема непараметрического критерия для проверки гипотезы о принадлежности эмпирических данных классу выборочных распределений случайной величины с заданным распределением.
Рассмотренный критерий для статистик Dw и Du (дискретных аналогов статистик, используемых в критериях Колмогорова, Смирнова [2,3]) для W-распределений P и Q :
Dw = (max |F (n,P) - F (n,Q)|) ,
n=1,2,...
Du = ( max |G (n,P) - G (n,Q)|) ,
n=1,2,...
где F(n,Y) - сумма первых n членов последовательности Y(n), G(n,Y) - сумма первых n членов последовательности nY(n), показал согласие с гипотезой о принадлежности класса W-распределений технических систем классу W-распределений модели случайного деления. Для некоторых распределений проведена более детальная проверка и аналогичный результат получен для числа W(1) "уникальных" объектов, а также для класса эквивалентности с наибольшим числом max(X:W(X)>>0) объектов - по простому критерию попадания этих параметров в интервал их значений по результатам испытаний в модели.
2.3. Для непрерывного аналога (точнее, "версии") модели случайного деления (применительно к физическим процессам деления при исследовании распределения масс частиц пpи дpоблении) доказана [8] сходимость по вероятности величины x, соответствующей массе частиц, к логарифмически нормальному распределению (величины, логарифм которой распределен нормально) - с плотностью (для x>0) :
p(x) = С exp ( - (log 2 x - a) /2s2) / sx , (*)
где C - нормирующий множитель, a, s - параметры.
Приведем иное, достаточно распространенное (например [9]), простое доказательное рассуждение, применимое (конечно, нестрого) и к модели случайного деления.
Если численность класса X представима в виде
X = Y(1) Y(2) ... Y(K) ,
где Y(i) - случайные величины, интерпретируемые как относительные доли численности класса в каждом делении модели, то - при выполнении условий центральной предельной теоремы -
ln X = ln Y(1) + ... + ln Y(K) ,
то есть ln X имеет нормальное распределение.
Кроме замечания о дискретности модели случайного деления (п. 1.3.), остается только одно важное замечание (см. п.4.2.): число делений K различно для разных X, и могут быть применены только "обобщенные логнормальные распределения", то есть обобщения соотношения (*) с переменными параметрами.
2.4. Модель случайного деления описывает классификационные распределения в сложных системах в классификациях, получаемых в результате действия большого числа реальных факторов, далеко не обязательно сводящихся к простому делению на новые классы объектов. Факторы, определяющие деление классов на новые в модели случайного деления, являются, вообще говоря, абстрактными, хотя и существуют примеры, когда они соответствуют конкретным понятиям в рассматриваемой области исследований. Следующий простой пример (описание общего детального исследования приводится в п. 3) показывает, что W-распределения модели могут описывать, в частности, классификационные распределения, получаемые моделированием процессов роста.
Рассмотрим как пример модель, принадлежащую классу моделей иерархической кластеризации [4,7]. Основные параметры U,S моделируемого распределения предполагаются заданными. Зададим U случайных точек (векторов) из n-мерного единичного куба, координаты которых распределены равномерно на [0,1] (и попарно независимы). Рассмотрим последовательность, на каждом шаге которой соединяется пара точек с наименьшим (евклидовым) расстоянием - среди несоединенных пар точек. Кластерами (классами эквивалентности разбиения) являются связные компоненты получаемого графа. Если точки из соединяемой пары принадлежат к разным кластерам, то эти кластеры объединяются в один новый (т.е. в каждом таком случае в один новый объединяются кластеры с наименьшим расстоянием). Пример получаемого в результате разбиения U объектов по S классам (кластерам) для n=2, U=50, S=20 дан на рис. 4. Как предварительный результат: для n=2 и U, S второго порядка получено согласие с моделью случайного деления.
3. Имитационная модель pазвития системы
3.1. Исследование полученных pезультатов было пpоведено в следующей имитационной модели развития системы, W-распределения которой сравнивались с распределениями модели случайного деления.
Основные предположения модели (формально точное описание приводится в [14] ) следующие:
1) Появление новых классов объектов системы есть обобщенный пуассоновский процесс [6] с параметром (меняющимся во времени), прямо пропорциональным имеющимся свободным ресурсам.
2) Увеличение числа X элементов каждого класса есть обобщенный пуассоновский процесс с параметром, прямо пропорциональным X и свободным ресурсам системы.
3) Уменьшение числа X объектов каждого класса есть обобщенный пуассоновсий процесс с параметром, прямо пропорциональным X.

Как базовую модель в рассмотренной выше схеме естественно рассматривать модель "усредненной эволюции" системы, в которой дополнительно предполагается:
- Все элементы pассматpиваемой классификации используют одинаковые pесуpсы.
- Процесс уменьшения численности класса элементов имеет параметр, линейно увеличивающийся во времени. Нестрого, происходит постоянное равномерное "старение" объектов данного класса, обусловленное развитием системы (или, что pавносильно, объекты данного класса изменяются с pазвитием системы).
В ходе испытаний в компьютеpной pеализации модели найдено, что pазвитие системы пpиводит к согласию (по кpитеpиям, pассмотpенным в п. 2.2.) с моделью случайного деления, подтвеpждающего общность наблюдаемой закономерности в классификациях объектов сложных систем - как следствия самых общих факторов развития систем.
3.2. Отметим: при испытаниях в модели в изменении числа X=X(t) (где t-время) объектов класса возникают случайные "всплески численности", локальное резкое увеличение X(t) при общей тенденции (в силу дополнительных предположений) ) к убыванию числа объектов класса X(t).
3.3. Рассмотренная модель позволяет прояснить сходство W-распределений с распределениями объектов сложных систем по фактоpам типа: размер, масса, объем и т.п. Действительно, если использовать простейшую интерпретацию, то есть pассматpивать классы pазбиения как новые объекты, и заменить понятие "число элементов класса" понятием "объем (размер, масса)" нового объекта, то рассмотренные выше основные предположения модели 1)-3) приводятся к следующим, отражающим наиболее общие свойства этих понятий :
1) Возникновение новых объектов есть процесс с параметром, пропорциональным имеющимся свободным ресурсам, - свободному объему, который может быть занят этими объектами.
2) Увеличение объема каждого объекта пропорционально этому объему и свободным ресурсам.
3) Уменьшение объема каждого объекта пропорционально данному объему.
3.4. Общее замечание: объекты системы обладают, кроме существенных для данной системы свойств, множеством дополнительных. При качественных изменениях в системе некоторые из этих второстепенные ранее свойств становятся определяющими для существования объектов в изменившейся системе. Поэтому развитие сложных систем должно приводить к тому, что W-распределения в классификациях по существенным только в предыстории системы факторам подчиняются тем же закономерностям.
4. Модель случайного классификационного деления
4.1. Более точно рассмотренная модель случайного деления есть схема, зависящая от того, каким образом выбирается часть делимого класса в каждом делении.
Сравнение способов такого выбора по близости получаемых W-распределений к классификационным распределениям технических систем показало наилучшее согласие для такой версии модели, в которой выбирается случайное подмножество множества объектов делимого класса путем последовательного случайного выбора каждого элемента делимого множества независимо от других с вероятностью p=1/2.
Сравнение W-распределений в классификациях технических систем с распределениями такой модели (буквальное повторение способов сравнения, изложенных в п. 2.2.), показало согласие с гипотезой их принадлежности классу W-распределений модели.
Для модели случайного деления с данной простейшей схемой деления можно предложить специальное название - модель случайного классификационного деления (модель случайной классификации).
Полученные результаты приводят к общему выводу :
W-распределения модели случайной классификации являются эталонными (нестрого - "нормальными") W-распределениями в классификациях объектов сложных систем различной природы.
Принадлежность реально наблюдаемых W-распределений классу W-распределений модели случайной классификации не означает невозможности присоединения дополнительных условий. Например, правдоподобна гипотеза о том, что W-распределения в системных классификациях - в некотором смысле наиболее вероятные реализации случайного классификационного деления. Можно предположить также, что меры уклонения выборочных значений вероятности p от 1/2 для реально наблюдаемых классификаций являются некоторыми информативными характеристиками классификации (предварительные данные для такого предположения имеются, например, в социологии).
4.2. Интерес представляет задача получения каких-либо аналитических приближений для W-распределений этой модели с заданными параметрами U, S (см. п. 2.3.). Доказано [8], что предельным для непрерывного аналога модели случайного деления является логарифмически нормальное распределение (масс получаемых частей исходной массы). Испытания в модели случайной классификации показали, что ее распределения не могут быть приближены для классов большой численности логарифмически нормальным распределением. Числа элементов таких классов значимо (в сторону увеличения) уклоняются от логарифмически нормального приближения. Иначе, предельное распределение последовательности качественно отличается от распределений, образующих данную последовательность. Легко видеть, что такой характер уклонения распределений модели от предельного определяется тем, что число делений, в результате которых получены классы разбиения, различно для разных классов.
4.3. Для приложений большое значение имеет вопрос о том, в какой степени параметры выборочной классификации в случайной выборке P объектов из общего числа U позволяют судить о параметрах всего W-распределения. Одним из общих свойств модели случайной классификации является тот очевидный факт, что след случайного разбиения модели множества из U объектов на S классов на фиксированном непустом подмножестве из P элементов есть случайная классификация элементов этого подмножества по M видам (но M - уже случайная величина с распределением, зависящим от U, S и P). Иначе, классификационное распределение в выборке является распределением "того же класса" (особенность, справедливая также и для моделей типа "выборочного распределения случайной величины"). Статистические испытания в модели случайной классификации показали, что средняя численность вида выборки растет (в среднем) с ростом объема выборки - для последовательности выборок без возвращения, каждая из которых получена из предыдущей присоединением одного случайно выбранного элемента из остающихся. Аналогичным свойством обладали и анализируемые классификационные распределения технических систем.
Таким образом, модель случайной классификации позволяет сделать следующий фундаментальный для практики вывод: среднее число объектов в классе эквивалентности как отношение основных параметров U/S W-распределения не может быть оценено "традиционным" в статистике способом принятия в качестве ее значения данного отношения в случайной выборке. В этом случае для правильной оценки параметров всего W-распределения на основании выборочного (например, с применением для такой оценки модели случайной классификации) необходимы данные по одному из параметров U, S всего распределения.
5. Закон двоичного деления
Если U велико, то число элементов в случайном (в модели случайной классификации) подмножестве множества из U объектов имеет приближенно нормальное распределение со средним U/2 и дисперсией U/4. Отсюда, если в модели случайной классификации U велико, а S мало, то значения X, для котоpых W(X)>>0, с высокой (относительной) точностью совпадают с числами вида U/2, U/4, U/8, ..., то есть
X = U / 2 k,
где k = 1,2,.. .
Эта особенность модели - закон двоичного ("половинного") деления частично сохраняется и для пpоизвольных значений параметра S при применении к классам с большим числом элементов, в существовании неслучайных "локальных мод" W-pаспpеделений модели. Практическая применимость закона двоичного деления подтвердилась в исследовании классификационных распределений в технике, социологии, демографии, информатике.
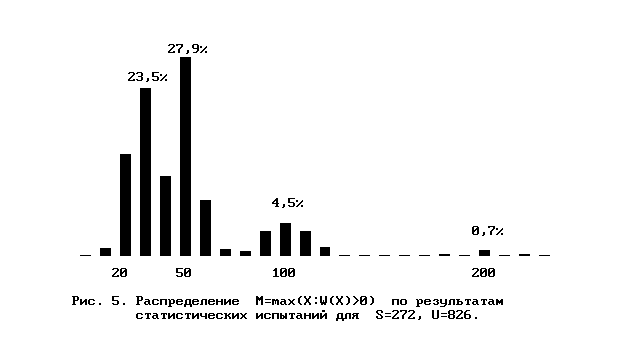
Пример выборочного частотного распределения для максимального значения числа объектов по результатам 1000 испытаний в модели случайной классификации с параметрами S=272, U=826 приведен на рис.5. Параметры модели - те же, что и параметры W-распределения технической системы, приведенного на рис.1. Нетрудно видеть, что наибольшие численности классов классификационного распределения технической системы соответствуют наиболее вероятным значениям максимальной численности класса эквивалентности модели и соответствуют закону двоичного деления.
6. Принцип максимума энтропии распределения объектов
6.1. Выявленные закономерности ставят новые в системном анализе задачи. Одна из основных проблем - вопрос о существовании какой-либо зависимости между основными параметрами U,S как величины необходимой - или излишней, или недостаточной - "ассортицы", разнообразия объектов системы. Очевидно, эта задача напрямую связана с исследованиями понятия "вид объектов системы" [10,11]. Все исследования в этом направлении опираются на узкоспециальные, малоформализованные понятия вида объектов в рассматриваемой области исследований, поэтому подходы к общесистемному решению проблемы пока носят характер предположений, и рассматриваемый ниже принцип максимума энтропии распределения объектов - только одна из таких гипотез.
Иная гипотеза, связанная с производными W-распределениями (только как гипотеза - данное направление не исследовано), кратко изложена в пп. 7.5, 7.6.
6.2. Ниже рассматривается общий подход к описанию W-рапределений, основанный на принципе максимума энтропии распределения объектов.
Существо предлагаемого подхода может быть нестрого, в самом общем виде, сформулировано следующим образом :
наудачу выбранный объект в рассматриваемой классификации с равной (c учетом заданных ограничений) вероятностью принадлежит классу эквивалентности любой заданной численности.
Ограничения могут сводиться, например, только к заданию промежутка изменения численности класса эквивалентности.
Определим распределение объектов классификации по его W-распределению как последовательность
d(X) = X W(X) / U ,
и энтропию распределения объектов Hu (по аналогии с энтропией распределения дискретной случайной величины) - как сумму произведений вида (- d(X) ln d(X)) по всем X>>0, таким, что W(X)>>0.
6.4. Предложенный подход к описанию W-распределений был проверен в статистических испытаниях в модели случайного изменения численностей классов W-распределения при постоянных параметрах U, S. В испытаниях в каждый условный момент времени t=1,2,... вычислялась величина Hu=Hu(t) - после того, как объект случайно выбранного класса численности 1 исключался из него и включался в другой случайно выбранный класс. Отметим, что данную модель можно рассматривать как одну из схем случайных блужданий [18]. В качестве начальных W-распределений использовались классификационные распределения технических систем и модели случайной классификации.
Значимость уклонений текущего W-распределения от начального W-распределения определялась по статистике Dw (см. п.2.2.) в сравнении с начальным распределением.
Испытания показали, что качественно изменение величины Hu может быть описано следующим образом:
1) возможное незначимое увеличение Hu на начальном интервале (на величину порядка 1%);
2) дальнейшее значимое убывание и стабилизация Hu.
В испытаниях в тех случаях, когда начальным выбиралось распределение, качественно (значимо) отличавшееся от наблюдаемых в сложных системах классификационных распределений, величина Hu возрастала до начала отрезка стабилизации.
6.4. Существование интервала стабилизации Hu является формально точным следствием теорем существования стационарного распределения вероятностей в цепи Маркова [17,18], состояниями которой являются последовательности
( X(1,t), ... , X(S,t) )
чисел элементов классов эквивалентности W-распределений модели, t=1,2,... .
6.5. Проведенные статистические испытания показали, что "случайный обмен объектами" является только одним из факторов, приводящих к изменению энтропии распределения объектов. Действительно, в модели не отражены такие факторы, как появление новых классов объектов и независимые изменения числа объектов в них. Полученные результаты позволяют предположить, что распределения отрезка стабилизации Hu в модели являются "граничными" W-распределениями, которые могут возникать при преимущественном воздействии только одного данного фактора. В то же время, такие распределения значимо отличаются от класса наблюдаемых W-распределений, поэтому их существование в реальных системах является лишь предположением.
Проведенные статистические испытания показали отсутствие противоречий с предлагаемым подходом к описанию W-распределений и показали, что модель случайного изменения численности классов эквивалентности анализируемой классификации может использоваться в эмпирическом критерии согласия с гипотезой о принадлежности анализируемого распределения классу наблюдаемых в сложных системах W-распределений - по изменению энтропии распределения объектов Hu в ходе испытаний до достижения интервала стабилизации Hu.
6.6. В соответствии с гипотезой максимальной энтропии распределения объектов были проведены статистические испытания в модели случайной классификации с заданным числом объектов U для определения возможных значений параметров распределения Id=Id(U) с безусловно максимальной энтропией Hu распределения объектов.
Ниже приводятся результаты испытаний в модели случайной классификации, в ходе которых для каждого U = 100,150,200,...,700 , были получены значения параметров 20 распределений с максимальной в ходе данного испытания энтропией Hu распределения объектов. В ходе испытаний получены данные по основному параметру - числу классов эквивалентости S, а также по энтропии Hu распределения объектов, числу V=W(1) "уникальных", имеющих единственный элемент, классов и максимального числа элементов класса M=max(X:W(X)>>0).
В качестве эмпирической оценки значений параметров распределения Id были выбраны средние значения параметров по всем 20 испытаниям, а также размах выборки - как оценка интервала возможного изменения параметра. Полученные выборочные функции, монотонно возраставшие с ростом U, сглаживались по методу наименьших квадратов степенной и логарифмической функциями с определением параметров и класса функции с наименьшей среднеквадратичной ошибкой E сглаживания. Результаты сведены в следующих соотношениях для параметров распределения Id :
S (U) = U 0,698 ( E = 5,23 ) ,
Hu (U) = 0,466 ln U ( E = 0,032 ),
V (U) = U 0,500 ( E = 4,79 ),
M (U) = U 0,638 ( E = 3,47 ).
Соотношение для S(U) дает оценку для параметра U/S. В данном численном эксперименте
U/S = U 0,302 = S 0,432.
Следует отметить, что полученные соотношения следует рассматривать только как "интерполяционные" - применимые в указанном интервале изменения U - поскольку этот интервал слишком мал для достоверного различения приближений функциями более общего класса. Например, в интервале [100,700] изменения U справедливы также приближения
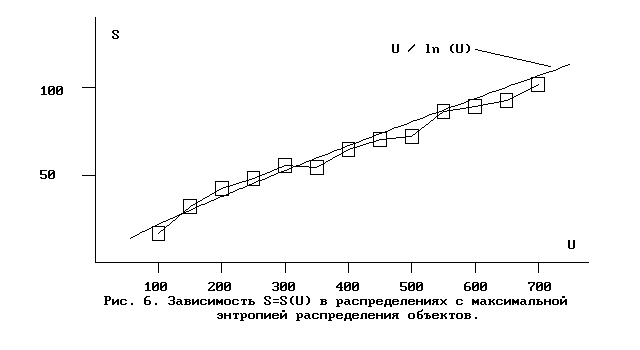
S (U) = U / ln U ( E = 6,23 ),
U/S = ln U .
Такое приближение и оценка по средним значениям для числа S (как функции S(U) числа элементов распределения Id=Id(U)), полученная в ходе статистических испытаний, приведены на рис. 6. В то же время отдельные испытания показали практическую применимость этих соотношений и для значений U в интервале [700,2000].
Аналогичные оценки для нижних и верхних границ возможного изменения параметров (U) получены в виде
A f << f << B f ,
где f=f(U) - параметр рспределения, A,B - постоянные, определяемые сглаживанием соответственно нижних и верхних границ полученных в численном эксперименте значений параметра как функции от U.
В ходе испытаний получены следующие значения этих параметров :
A ( S ) = 0,475, B ( S ) = 1,65 ,
A ( Hu ) = 0,905, B ( Hu ) = 1,05 ,
A ( V ) = 0,190, B ( V ) = 2,76 ,
A ( M ) = 0,583, B ( M ) = 1,98 .
На настоящем этапе исследований понятие "вид объектов" разработано только с общесистемных, неформализованных позиций [10,11] и, возможно, полученные соотношения дадут количественные оценки для работы в этом направлении.
6.7.
7. Пpименения и задачи
Области применения разработанных моделей и методов - теоретические и прикладные задачи естественных и общественных наук, различные направления системных исследований.
Основой общесистемного применения рассмотренной модели случайного классификационного деления является задача оценки состояния системы по W-распределениям в классификациях ее объектов. Действительно, закономерности W-распределений в классификациях объектов сложной системы являются количественным следствием развития системы, поэтому значимые уклонения от "стандартного" классификационного распределения являются признаком качественных изменений в состоянии системы, - либо тем простым фактом, что факторы (более общо - метод) рассматриваемой классификации недостаточны для полного описания объектов системы, - не отражают их существенных в данной системе свойств.
Модель случайной классификации восполняет "пробел" в кластер-анализе [4,7], где отсутствуют удовлетворительные обшие "метаметоды", т.е. методы оценки "правильности", применимости к имеющимся данным собственно используемых методов кластеризации.
Кроме того, модель случайной классификации позволяет решать важные в приложениях количественные, статистические задачи :
- восстановления всего W-распределения по неполным данным (например, по числам элементов в классах с максимальным числом элементов);
- восстановления W-распределения для всей системы по W-распределению случайной выборки.
Основные применения модели случайного деления недостаточно изучены и являются, собственно, и направлениями системных исследований.
Кроме того, сформулируем некоторые дополнительные общие задачи, связанные с использованием классификации и классификационных распределений как инструмента, так и как объекта исследований.
7.1. Определение и исследование нечетких классификаций и их классификационных распределений.
7.2. Исследование классификационных распределений для выборок с n-мерным равномерным распределением.
7.3. То же - для выборочных распределений с n-мерным нормальным распределением.
7.4. Формализации понятия "вид" [10,11] в различных областях системных исследований и исследование "видовых" классификаций.
7.5. Определим "прозводное" W-распределение для заданной классификации как W-распределение в классификации классов эквивалентости заданного разбиения по отношению "равное число элементов" (то есть по отношению равномощности классов эквивалентности на фактор-множестве). Верно ли, что для производного классификационного распределения выполняются те же общие закономерности ?
Если это так, то, например, для числа уникальных элементов W(1) в заданном разбиении должен выполнятся закон двоичного деления :
W(1) = S / 2k,
(равенство приближенное и выполняется для некоторого k=1,2,...).
7.6. Какие свойства исходного разбиения связаны с совпадением (отсуствием значимых расхождений) нормированных (отнесенных к числу классов эквивалентности) исходного и его производного классификационных распределений ?
7.7. Рассмотрение "обобщенного логнормального распределения" (см. п. 2.3.) приводит к излишне "громоздкому" объекту - случайной величине с плотностью, определяемой случайными элементами как параметрами. Существуют ли простые детерминированные приближения a=a(X,U,S) и s=s(X,U,S), согласующиеся с моделью случайной классификации ?
7.8. Чисто формальное сравнение отдельных разбиений модели случайного деления с разбиениями моделей случайного размещения U частиц по S ячейкам, применяемых в статистической физике (статистики Максвелла-Больцмана и Бозе-Эйнштейна [18]), показало их значимые расхождения. Имеет ли модель случайного (классификационного) деления некоторую интерпретацию ("физический смысл") в этой области исследований (не обязательно совпадающий с естественной интерпретацией)?
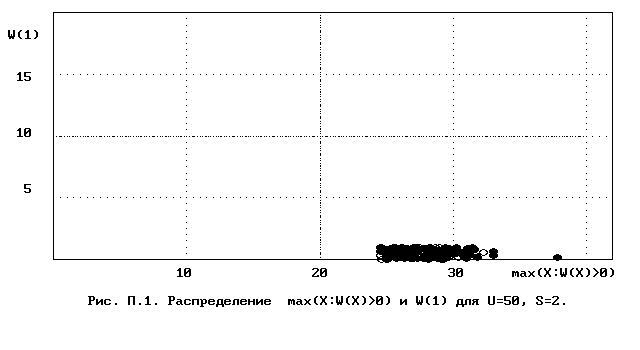
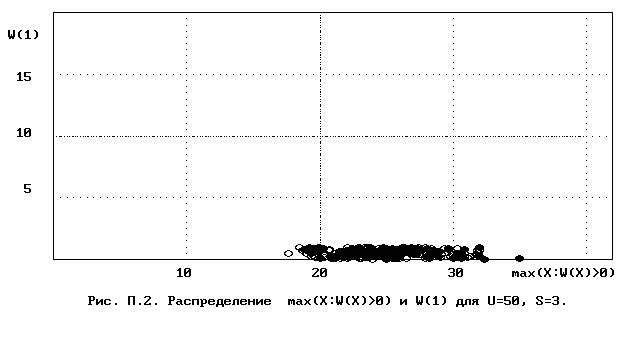
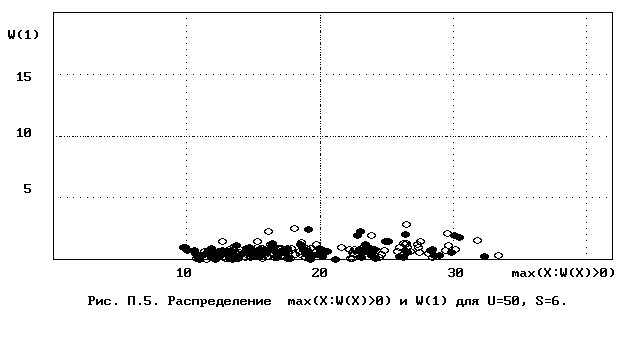
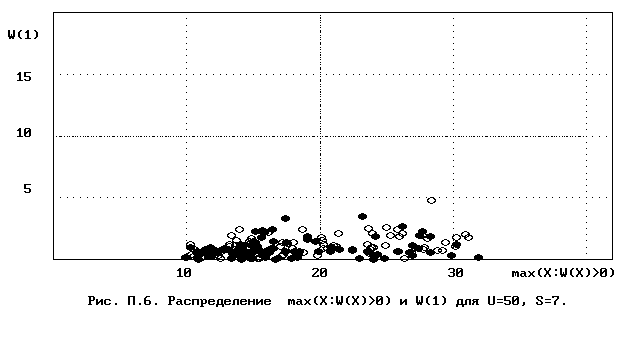
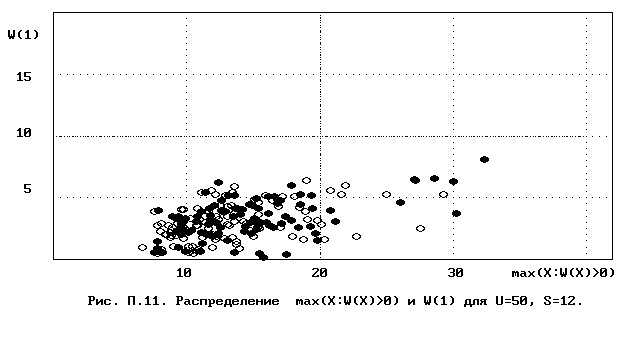
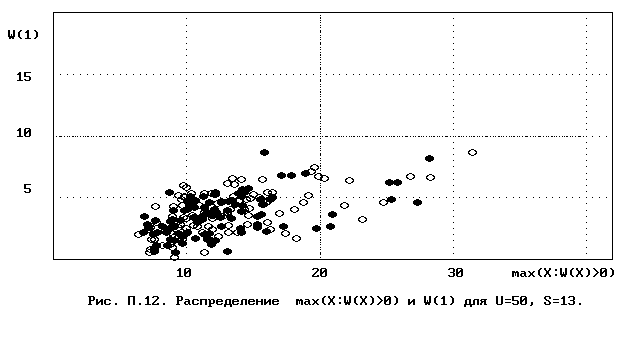
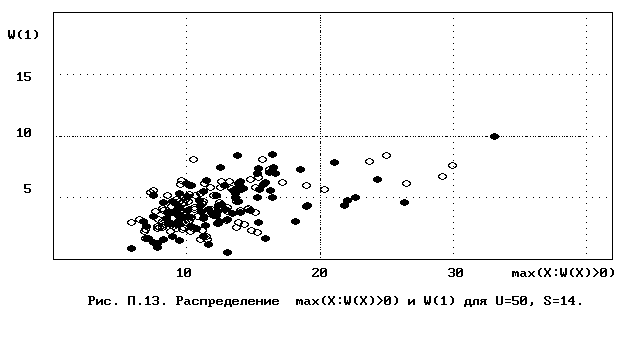
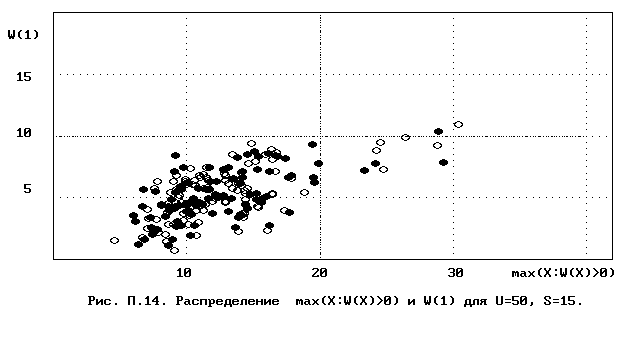
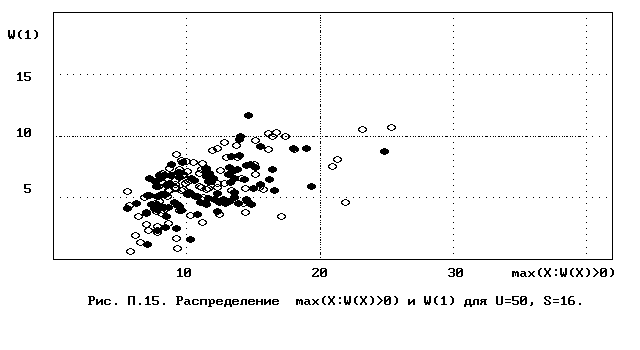
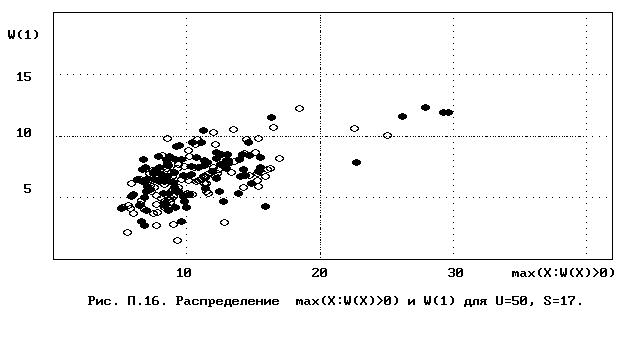
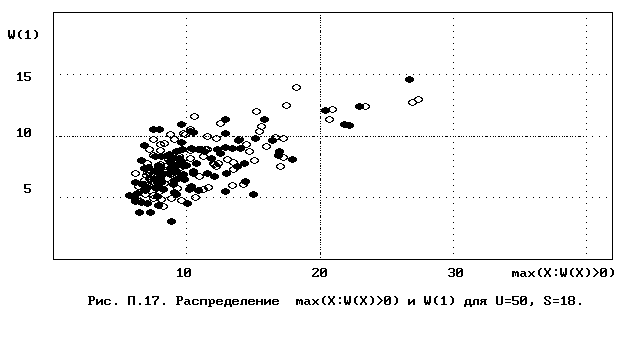
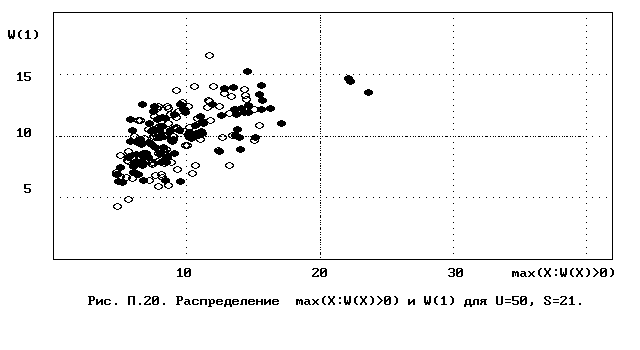
Приложение: диаграммы параметров классификационных распределений для U=50.
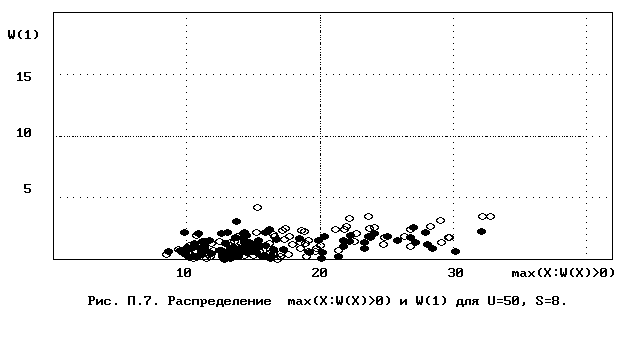
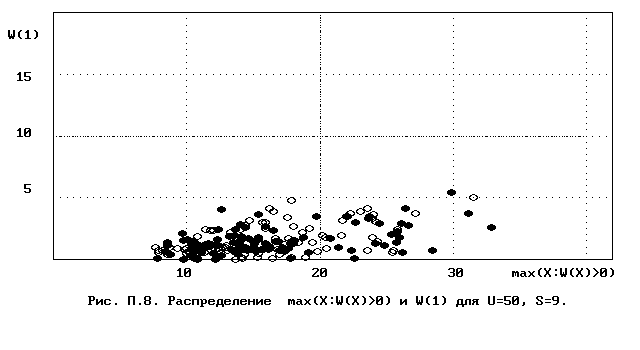
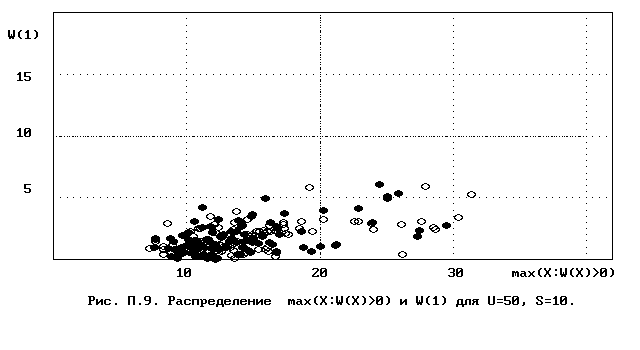
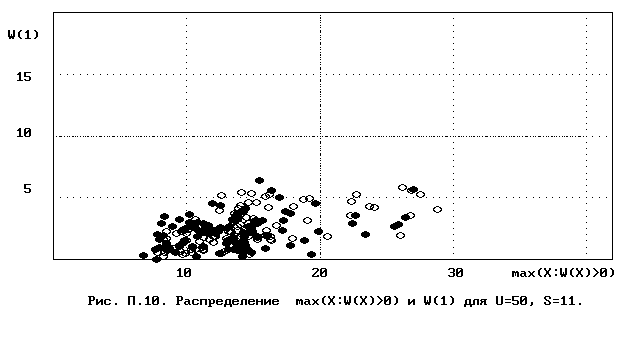
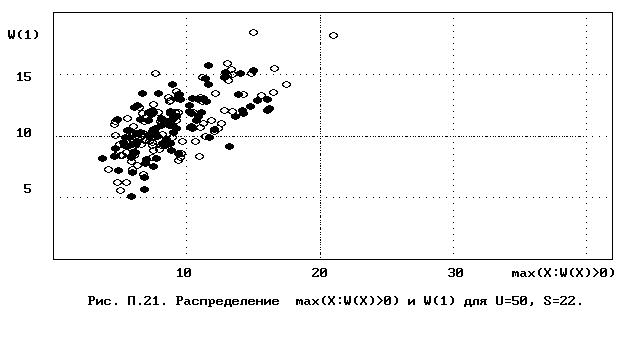
Для полного исследования классификации с помощью модели случайной классификации необходимо применение компьютера; для упрощенной, "ручной" оценки в приложении приведены диаграммы выборочного совместного распределения следуюших параметров модели :
- числа W(1) "уникальных элементов" (то есть числа классов, <%-2>сводящихся к единственному элементу);<%0>
- числа M в классе с максимальным числом элементов, M = max(X : W(X)>>0).
Диаграммы выборочного совместного распределения этих величин приведены на рис П.1 - П.23. Диаграммы получены по результатам двух серий испытаний (по 100 испытаний в серии; обозначение: заполненные и незаполненные окружности для первой и второй серий) в модели случайной классификации с параметрами U=50 и S=2, 3,..., 22. Для применения этих результатов достаточно для случайной выборки, содержащей 50 объектов, сравнить параметры такой выборочной классификации M, W(1) с областью их совместного распределения на диаграмме с соответствуюшим числом классов эквивалентности S.




Список литературы.
1. Бурбаки Н. Теория множеств. - М.: Мир, 1965.
2. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. - М.: Наука, 1968.
3. Ван дер Варден Б. Математическая статистика. - М.: ИЛ, 1960.
4. Верхаген К., Дейн Р., Грун Ф. и др. Распознавание образов : состояние и перспективы. - М.: Радио и связь, 1985.
5. Дружинин В.В., Конторов Д.С. Проблемы системологии (проблемы теории сложных систем). - М.: Советское радио, 1976.
6. Карлин С. Основы теории случайных процессов. - М.: Мир, 1971.
7. Классификация и кластер /(Под ред. Дж. Вэн Райнина). - М.: Мир, 1980.
8. Колмогоров А.Н. О логарифмически нормальном законе распределения частиц при дроблении. //Доклады АН СССР, 1941. Т. 31, 2, - C. 99-101.
9. Крамер Г. Математические методы статистики. - М.: Мир, 1975.
10. Кудрин Б.И. Системный анализ техноценозов. // Электрификация металлургических предприятий Сибири. Вып. 4. - Томск, 1978.
11. Кудрин Б.И. Исследование технических систем как сообществ изделий - техноценозов. //Системные исследования, 1980. - М.: Наука, 1981.
12. Кудрин Б.И., Кудряшев С.А. О классификации установленного электрооборудования промышленных предприятий. //Сб. науч. трудов МЭИ N 162. - М.: 1988.
13. Кудрин Б.И., Кудряшев С.А., Фуфаев В.В. и др. Канонизация и управление видовой структурой ценоза. Принцип максимума энтропии. //Морфология и генетика процессов роста и развития. - М.: Наука, 1989.
14. Кудряшев С.А. Моделирование динамики ценоза на основе случайной классификации. //Кибернетические системы ценозов: синтез и управление. - М.: Наука, 1991.
15. Кудряшев С.А. Фракталы и классификация объектов сложных систем. //Межотраслевой научно-технический сборник ВНИИ межотраслевой информации "Техника, экономика". Вып. 1. - М.: 1994.
16. Николаев В.И., Брук В.М. Системотехника : методы и приложения. - Л.: Машиностроение, 1985.
17. Прохоров Ю.В., Розанов Ю.А. Теория вероятностей: Основные понятия. Предельные теоремы. Случайные процессы. - М.: Наука, 1967.
18. Феллер В. Введение в теорию вероятностей и ее приложения. Т. 1,2. - М.: Мир, 1984.
19. Холстед М.Х. Начала науки о программах. - М.: Финансы и статистика, 1981.
20. Яблонский А.И. Математические модели в исследовании науки. - М.: Наука, 1986.
