Тезисы докладов

СЕССИЯ D

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = =

КУЛОНОВСКАЯ ЭНЕРГИЯ УЕДИНЕННОЙ ПЫЛЕВОЙ ЧАСТИЦЫ

В ПЛАЗМЕ

Паль А.Ф ., Старостин А.Н ., Филиппов А.В .

ГНЦ РФ ТРИНИТИ

Сообщаются результаты численного моделирования процесса формирования заряда уединенной пылевой частицы и образования объёмного заряда вокруг неё в плазме аргона, создаваемой внешним источником ионизации. Изучена зависимость кулоновской энергии системы от таких параметров задачи как напряженность внешнего однородного электрического поля, скорость ионизации газа и концентрация атомов аргона. Показано, что энергия взаимодействия заряженной пылевой частицы с объёмным зарядом плазмы значительно превышает энергию взаимодействия пылевых частиц друг с другом, также как и тепловую энергию пылевых частиц.

ПОТЕНЦИАЛ ВЗАИМОДЕЙСТВИЯ ЗАРЯЖЕННЫХ ПЫЛИНОК В ПЛАЗМЕ

И ЕГО ИСПОЛЬЗОВАНИЕ ДЛЯ РАСЧЕТА ХАРАКТЕРИСТИК ПЫЛЕВОГО КРИСТАЛЛА

Д.Н. Герасимов, О.А. Синкевич

(МЭИ)

Ранее в нашей работе [1] было получено аналитическое выражение для потенциала взаимодействия заряженных частиц, находящихся в частично ионизованной плазме. Полученный потенциал учитывает влияние на взаимодействия пылевых частиц плазменного окружения и существенно отличается от известного потенциала Юкавы - Дебая. Этот потенциал не монотонен, имеет минимум, соответствующий потенциальной яме, и удобен для аналитических и численных оценок. Наличие потенциальной ямы свидетельствует о возможности образования связанных состояний из твердых частиц, несущих одинаковый электрический заряд. Используя полученный нами потенциал можно рассчитать многие характеристики плазменного пылевого “кристалла”, включая определение границ образования “кристалла”. В работе [1] нами было получено условие образования плазменного пылевого “кристалла” отличное от известного критерия Линдемана. Позже, исходя из аналогичных физических представлений, похожее поведение потенциал взаимодействия двух заряженных пылинок в плазме было получено в работе [2] без ссылки на нашу работу, опубликованную в отечественной и и зарубежном изданиях. Несмотря на некоторое различие в представлении потенциала взаимодействия двух заряженных пылинок в плазме, положение минимума потенциальной энергии полностью совпадает и равняется r_min /r_D = 1 + 3^1/2.

Численные эксперименты, выполненные в рамках уравнений Власова для пылевой плазмы [3], учитывающие вклады различных механизмов взаимодействия, также подтвердили аналогичное не монотонное изменение потенциала взаимодействия заряженных твердых частичек в газовой плазме. В представленном докладе приводится сопоставления аналитических и численных результатов работ [1-3].

Д.Н. Герасимов, О.А. Синкевич. Образование упорядоченных структур в термической пылевой плазме. Теплофизика высоких температур, 1999, Т. 37, No 6, С.853 - 857.
A.S.Ivanov. Polarization’s interaction and bound states of like charged particles in plasma. PhysicsLetters, 2001, Vol.A290, P. 304–308.
Л.В. Иньков. Численное моделирование кинетических процессов в пылевой плазме. Диссертация канд.ф.-м.н., 2003, МФТИ.

ДАЛЬНОДЕЙСТВУЮЩЕЕ ВЗАИМОДЕЙСТВИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ КОНДЕНСИРОВАННОЙ ФАЗЫ В ТЕРМИЧЕСКОЙ ПЛАЗМЕ

В.И. Вишняков, Г.С. Драган

Одесский национальный университет им. И.И.Мечникова

pipeaes@te.net.ua

Термическая плазма характеризуется тем, что ее компоненты, как правило, имеют одинаковую температуру. Ионизационное равновесие в термической плазме достигается за счет столкновений газовых частиц. Поэтому термическая плазма, содержащая частицы конденсированной фазы (дымовая плазма) существенно отличается от пылевой плазмы.

Распределение потенциала в плазме описывается уравнением Пуассона

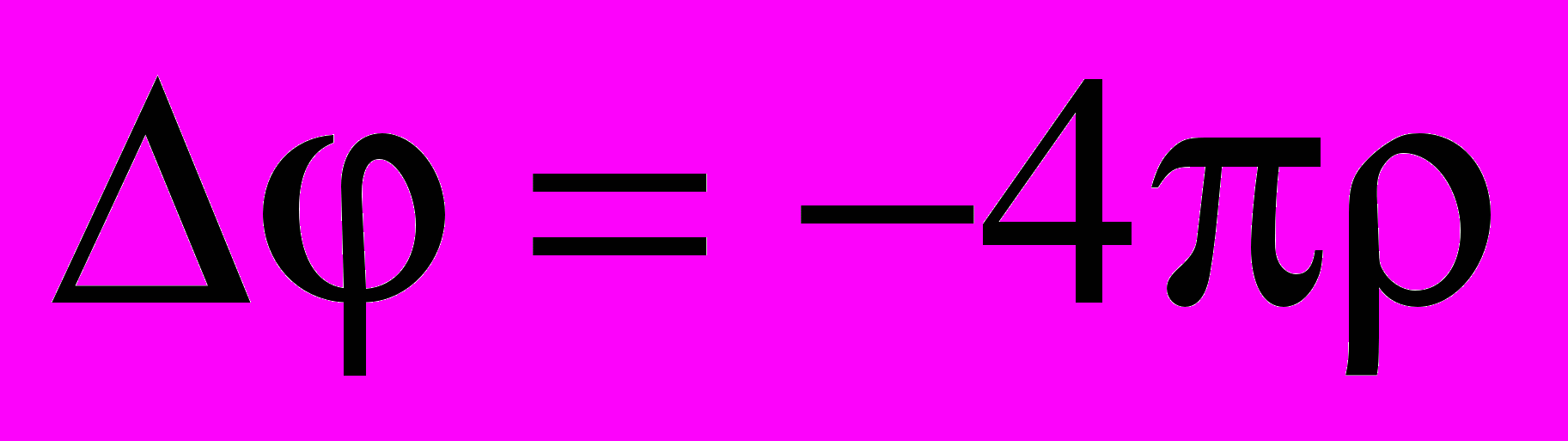(1)

Вопрос задания граничных условия для уравнения Пуассона (1) был рассмотрен Эйнштейном в работе [1]. Было показано, что потенциал необходимо отсчитывать от некоторого значения

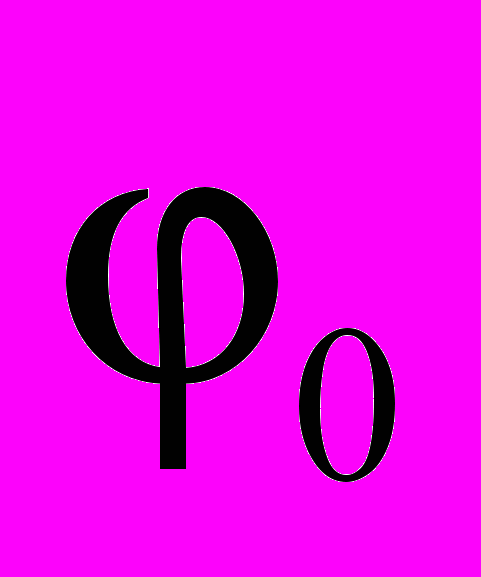, которое является тривиальным решением уравнения (1).

Для одиночной частицы, находящейся в равновесии с газовой фазой, плотность заряда в уравнении (1) задается в виде распределения Больцмана, а потенциал отсчитывается от потенциала плазмы

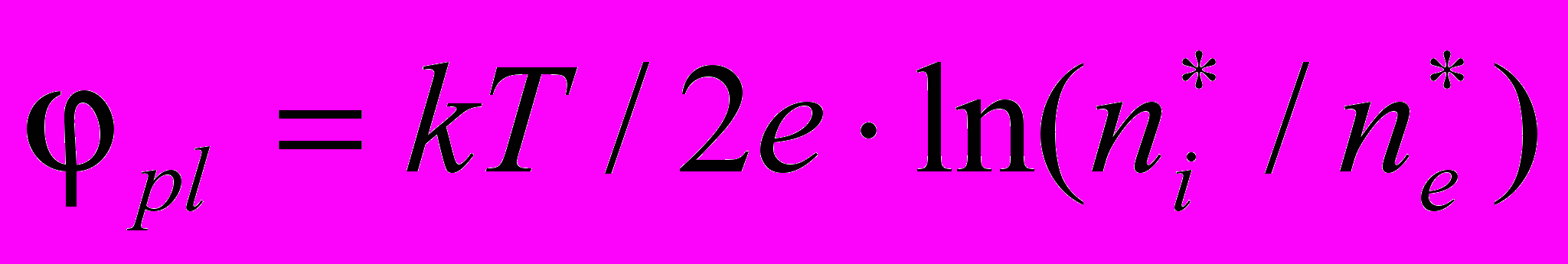. (2)

Здесь мы предполагаем, что где-то в объеме плазмы реализуется условие

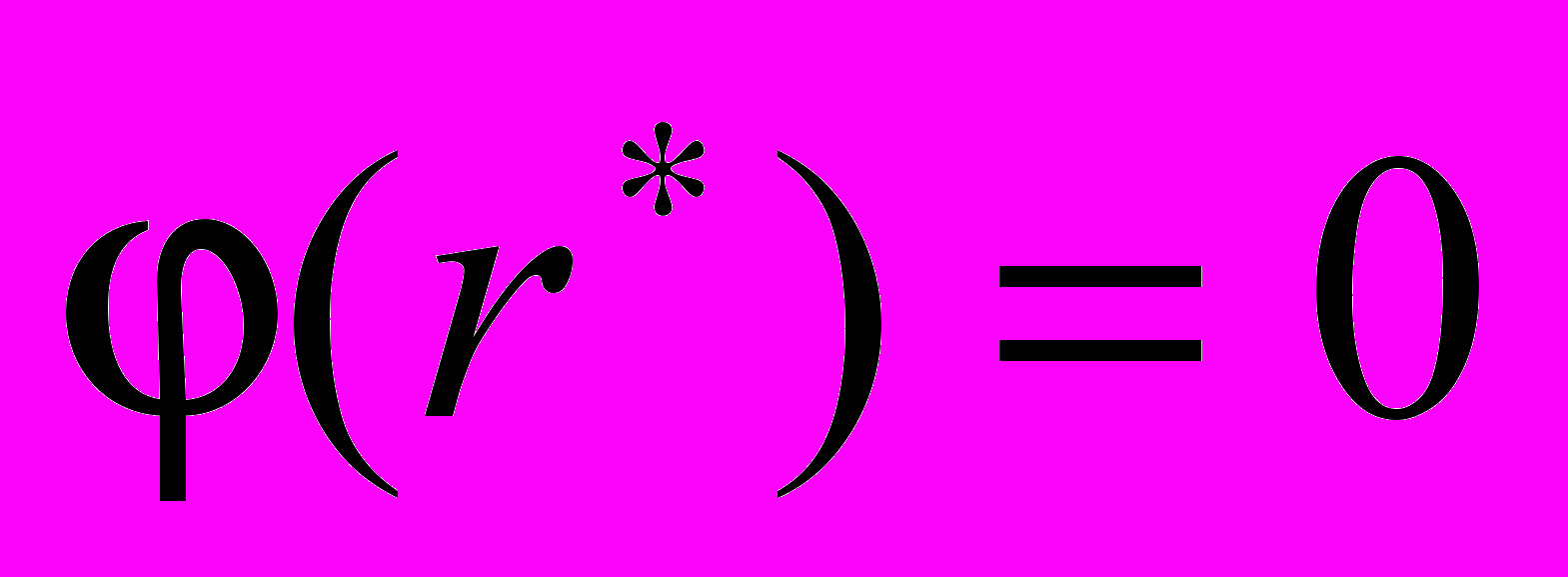и в окрестности точки r^* существуют некоторые значения концентрации электронов

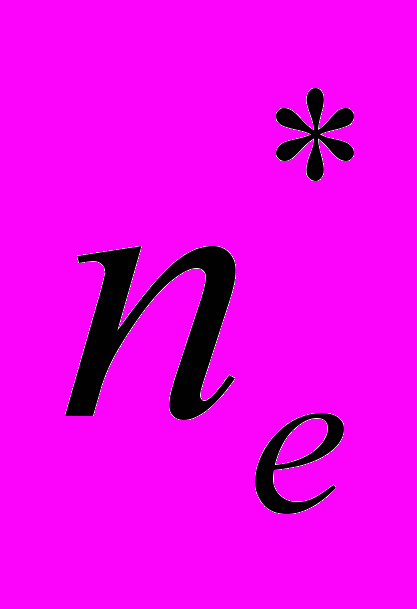и ионов

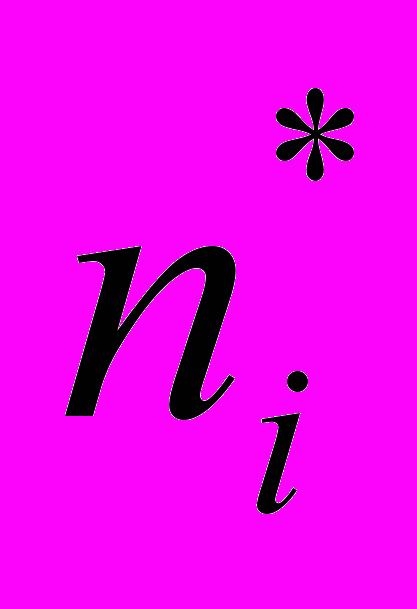. Все решения уравнения Пуассона-Больцмана должны быть симметричны относительно прямой (2). Потенциал плазмы линейно связан с параметром неравновесности:

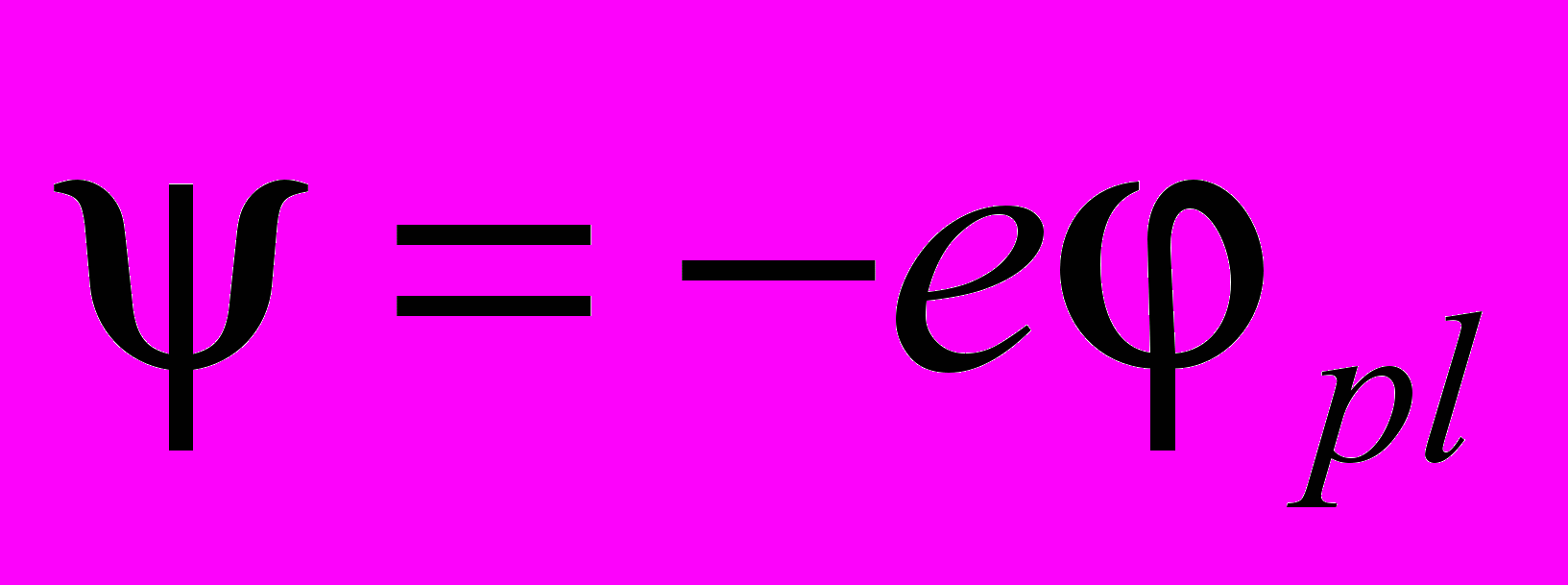(3)

Неравновесная ионизация у поверхности частицы является следствием равновесия на границе частица – плазма и не зависит от наличия других частиц и расстояния между ними. Однако градиент

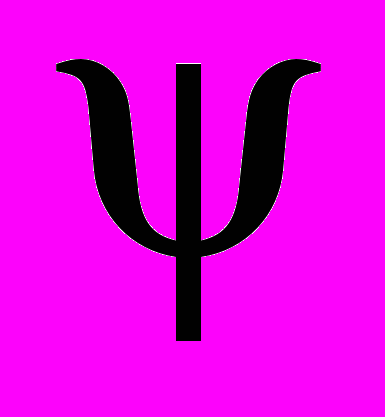, если он существует, может оказывать существенное влияние на процессы, происходящие в плазме.

Мы исходим из того положения, что локальные возмущения в плазме не распространяются на весь объем, а затухают по мере удаления от источника возмущений. Тогда возмущение ионизационного равновесия, вызываемое процессами на границе раздела фаз частица – плазма должны затухать по мере удаления от частицы.

Однако параметр неравновесности линейно связан с потенциалом плазмы. Обратимся к уравнению Пуассона. Заметим, что всеми свойствами тривиального решения уравнения Пуассона обладает любая функция, являющаяся решением уравнения Лапласа

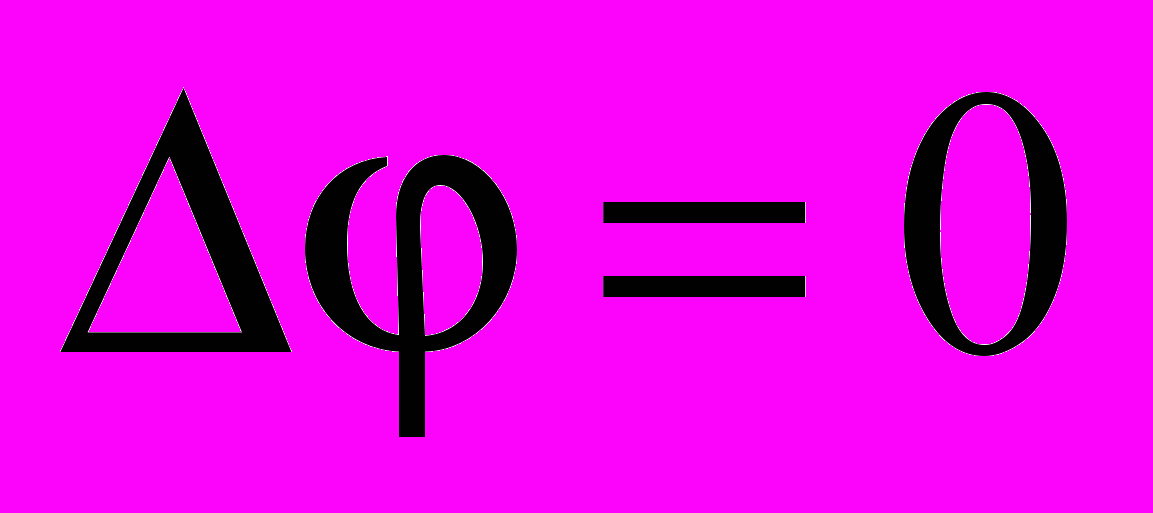. То есть в окрестности некоторой частицы радиуса

, возбуждающей в близи своей поверхности потенциал плазмы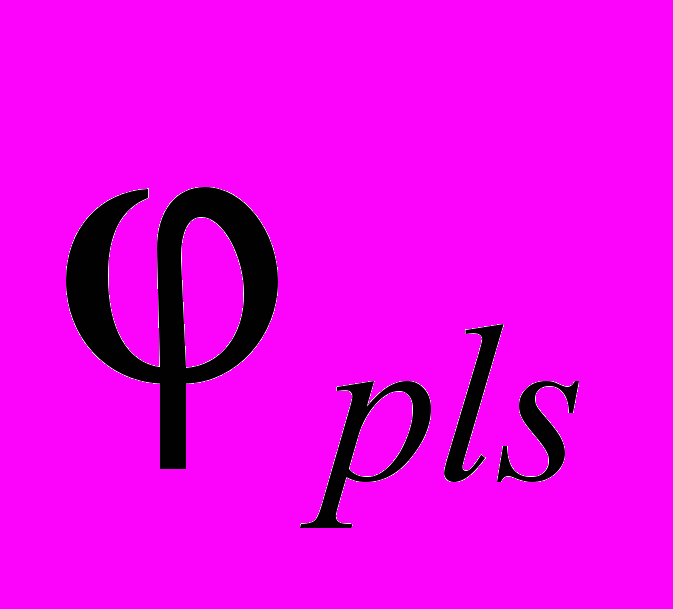

, распределение потенциала плазмы может иметь вид:

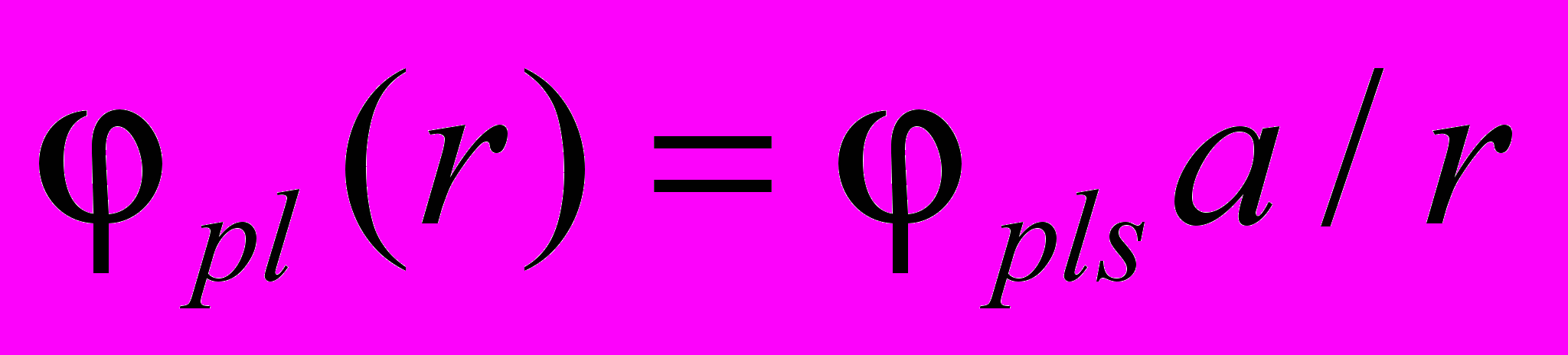, (4)

при этом везде, где измеряемое значение потенциала не отличается от значения

, плазма остается электронейтральной: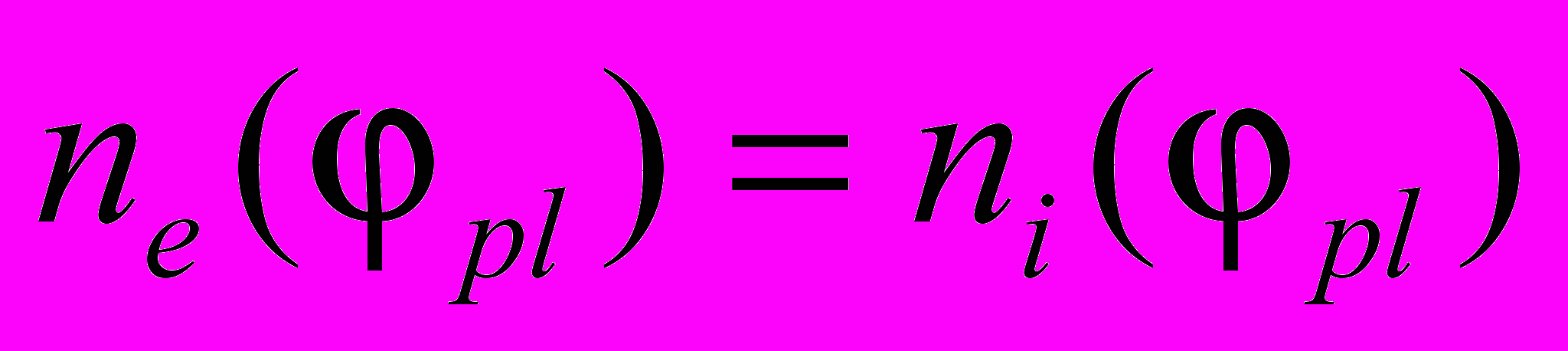

. (5)

Пространственная неоднородность потенциала плазмы и параметра неравновесности плазмы может быть причиной дальнего взаимодействия заряженных частиц конденсированной фазы.

1. А. Эйнштейн, в сб.: Альберт Эйнштейн и теория гравитации, Москва, Мир (1979) с.287

ВОЛНЫ БОЛЬШОЙ АМПЛИТУДЫ И УДАРНЫЕ ВОЛНЫ

В КОМПЛЕКСНОЙ ПЛАЗМЕ ТЛЕЮЩЕГО РАЗРЯДА ПОСТОЯННОГО ТОКА

В.Е. Фортов, О.Ф. Петров, В.И. Молотков, В.М. Торчинский, М.Ю. Пустыльник, А.Г. Храпак, В.Н. Наумкин, А.В. Чернышев

Институт теплофизики экстремальных состояний РАН

Получены волны большой амплитуды, состоящие из двух уплотнений, разделенных областью разрежения. Для возбуждения таких волн в пылевой плазме тлеющего разряда постоянного тока использовался газодинамический импульс. Полученная волновая структура имела ряд интересных особенностей, таких как сильное сжатие в одной из уплотнений, присутствие сверхзвуковых частиц в зоне разряжения, восстановление исходной плотности пылевых частиц после прохождения волны. Скорость возмущения порядка пылеакустической скорости. Предложен механизм генерации и распространения подобных возмущений.

В других экспериментах наблюдалось распространение скачка по плазменно-пылевой структуре со сверхзвуковой скоростью. Для возбуждения этого возмущения к плазменно-пылевой структуре, формирующейся в страте, прикладывается импульс магнитного поля. Этот импульс приводил к растяжению структуры. При восстановлении структуры в ней появлялось возмущение плотности. Наблюдалось укручение фронта этого возмущения, приводившее к образованию пылеакустической ударной волны.

ТРЕХЧАСТИЧНЫЕ КОРРЕЛЯЦИИ В НЕИДЕАЛЬНОЙ ПЫЛЕВОЙ ПЛАЗМЕ

Ваулина О.С., Петров О.Ф., Фортов В.Е., Чернышев А.В., Гавриков А.В, Шахова И.A. (Институт теплофизики экстремальных состояний ОИВТ РАН).

В настоящей работе впервые приведены результаты экспериментального исследования трехчастичной корреляции для макрочастиц в пылевой плазме. Выполнен анализ полученных трехчастичных корреляционных функций для экспериментальных и численных данных и их сопоставление с суперпозиционным приближением. Анализ экспериментальных результатов показал, что отличие суперпозиционного приближения от регистрируемой трехчастичной корреляционной функции может составлять ~ 30%. Наблюдалось формирование регулярных кластеров макрочастиц как в экспериментальных плазменно-пылевых системах, так и в моделируемых жидкостных структурах. Численные расчеты трехчастичной корреляции макрочастиц, взаимодействующих с экранированным потенциалом, показали, что формирование таких кластеров в моделируемых системах наблюдается с ростом эффективного параметра неидеальности Г*>25. Экспериментальные исследования трехчастичной корреляции макрочастиц позволяют получить дополнительную информацию о физических свойствах исследуемых плазменно-пылевых систем и могут использоваться для структурного анализа пылевой плазмы.

ДИНАМИКА ФАЗОВОГО ПЕРЕХОДА КРИСТАЛЛ-ЖИДКОСТЬ

В ПЛАЗМЕННО-ПЫЛЕВЫХ СТРУКТУРАХ

Шахова И.А., Чернышев А.В., Петров О.Ф., Фортов В.Е.

(Институт теплофизики экстремальных состояний ОИВТ РАН).

В данной работе впервые экспериментально исследована динамика фазового перехода в плазменно-пылевом слое (диаметр структуры превышает ее толщину  в 10 раз). Изучено движение межфазной границы (фронта плавления) плазменно-пылевой жидкости и кристалла, определена скорость фазового перехода. В результате анализа экспериментальных данных были получены распределения кинетических температур и концентраций частиц в плазменно-пылевой жидкости и кристалле, а также вблизи границы раздела фаз, определены значения межчастичных расстояний, коэффициентов самодиффузии и параметров неидеальности Г вблизи границы фазового перехода.

ВЯЗКОСТЬ ПЛАЗМЕННО-ПЫЛЕВОЙ ЖИДКОСТИ

Гавриков А.В.² Ворона Н.А.¹ Чернышев А.В.² Иванов А.С.³ Петров О.Ф.² Фортов В.Е.²

(¹МФТИ, ²ИТЭС РАН, ³РНЦ «Курчатовский Институт»)

В данной работе впервые экспериментально изучена вязкость плазменно-пылевой жидкости. Были проведены эксперименты с воздействием лазерного излучения на пылевую плазму (Г  30), в результате которого наблюдалось возникновение в ней ламинарного течения плазменно-пылевой жидкости. Пылевая структура формировалась в приэлектродном слое ВЧ-разряда ( W_RF = 10Вт, P = 35 Па) из монодисперсных МФ частиц диаметром 1,9 мкм. Течение плазменно-пылевой жидкости инициировалось излучением Ar⁺ лазера (мощность излучения W = 0,190 Вт,  = 514 нм, радиус пучка R = 1 мм). Из анализа распределения скоростей в поперечном сечении течения плазменно-пылевой жидкости был определен коэффициент сдвиговой вязкости, величина которого составила ^*= 2,0 × 10^-9 Па с. Данное значение существенно меньше коэффициента вязкости буферного газа (аргона) _ar=6·10^-5Па с в условиях эксперимента.

Низкочастотный Тензор Диэлектрической Проницаемости

Комплексной Плазмы с Учетом Дипольного Момента Гранул

В.Н. Мальнев¹, Е.В. Мартыш²

1 Киевский национальный университет им. Т.Г. Шевченко, физический факультет.

2 Киевский национальный университет им. Т.Г. Шевченко, радиофизический факультет

(malnev@i.com.ua; emart@mail.univ.kiev.ua).

Как известно из многих работ, посвященных физическим свойствам комплексной плазмы, гранулы могут иметь довольно большой отрицательный заряд q, который может достигать тысяч зарядов электрона. В целом ряде случаев эти гранулы не являются сферически симметричными частицами. Они скорее напоминают вытянутые эллипсоиды или даже иголочки. Соответствующие электрические дипольные моменты будут порядка d  qL (L – длина вытянутой частицы) [1]. Для L~1 дипольный момент гранулы будет около d~10⁴D. Такие диполи вращаются с тепловой частотой

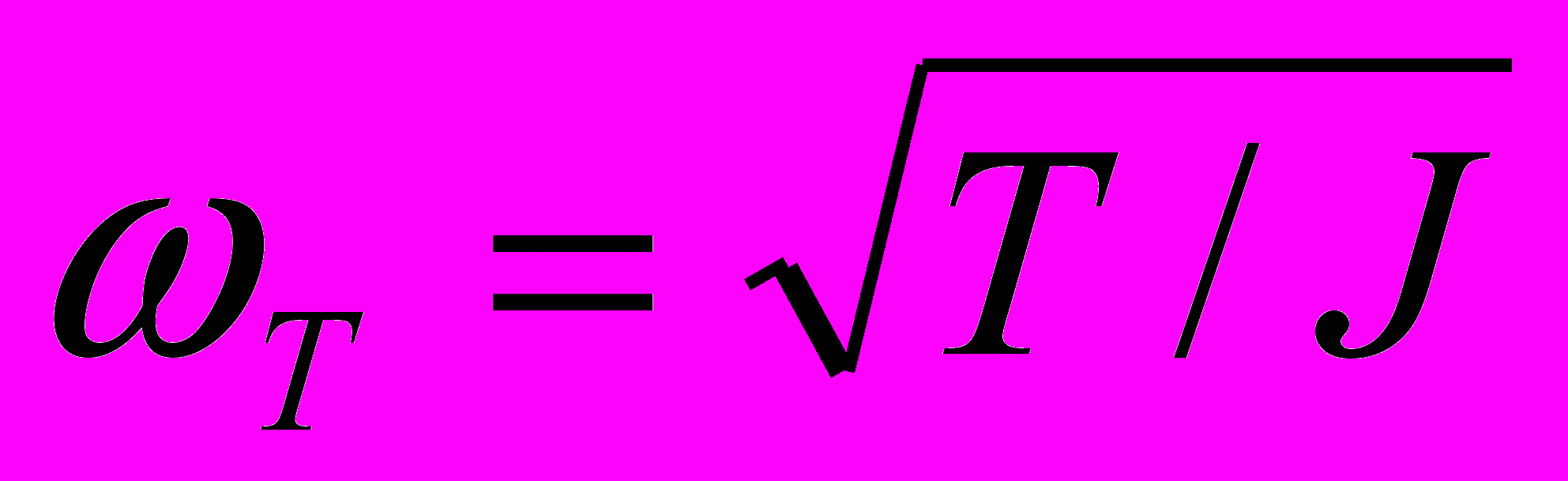( T- температура гранул, по порядку величины она равна температуре ионов или буферного газа; J – момент инерции гранулы, JML², M – масса гранулы). Если масса гранулы порядка M~10^-11- 10^-12г, то соответствующие _T ~10²-10³ Гц. Сообщалось [2], что такие частоты могут быть и порядка _T ~10⁴ Гц.

В этом сообщении представляются результаты вычислений низкочастотной части тензора диэлектрической проницаемости комплексной плазмы с заряженными гранулами, обладающими дипольным моментом. Для этого был рассчитан (с применением квантовой механики) тензор поляризуемости системы жестких ротаторов в переменном электрическом поле. Тензор диэлектрической проницаемости, связанный с вращением гранул, может быть получен в классическом пределе, т.к. разница между вращательными уровнями

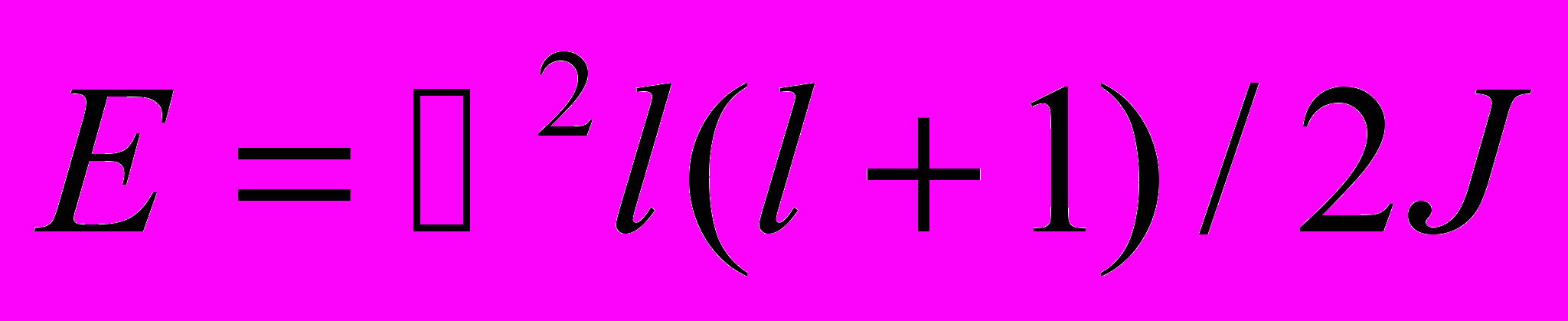всегда мала по сравнению с температурой Т.

Оказывается, что тензор диэлектрической проницаемости содержит мнимую часть, которая является специфическим затуханием Ландау, не зависящем от волнового вектора и имеющей вид:

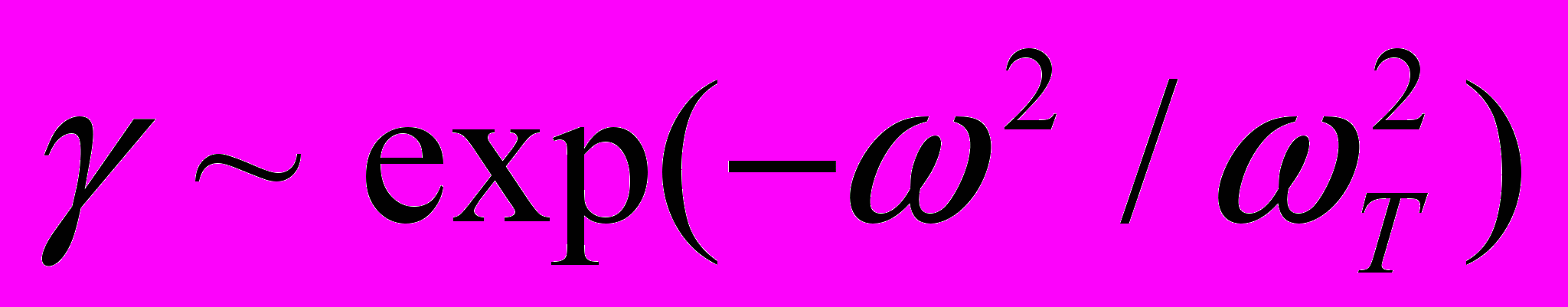. Этот тип затухания впервые был описан в [3], где был получен тензор диэлектрической проницаемости электрон-ионной плазмы с нейтральной компонентой в виде полярных молекул. Такое затухание должно приводить к заметному поглощению низкочастотного электромагнитного излучения вблизи частоты _T. Возможно также заметное подавление собственных колебаний комплексной плазмы в случае, если они близки к _T. С другой стороны, этот механизм затухания может быть инвертирован и использован для усиления низкочастотных колебаний в комплексной плазме. Это можно реализовать при наличии внешнего источника энергии, который создаст неравновесное заселение вращательных уровней (синхронное вращение некоторой части или большинства ротаторов) или ситуацию, когда средняя энергия вращения гранул становится выше температуры их поступательного движения.

References

1. D.D. Tskhakaya, P.K. Shukla, N.L. Tsintsadze, Electrodynamics and dispersion properties of a magnetized plasma containing elongated and rotating dust grains, Zh. Exp. Teor. Fiz., 120, 340 (2001).

2. P.K. Shukla, A.A. Mamun, Introduction to Dusty Plasma Physics, IoP Publishing, London, 2002.

3. Solomon.Mulugeta and V. Malnev, Thermodynamic properties and waves in a dipole plasma, J. Plasma Phys, 39, 475 (1988).

Магнитная Проницаемость Комплексной Плазмы

с Ферромагнитными Гранулами

В.Н. Мальнев¹, Е.В. Мартыш²

1 Киевский национальный университет им. Т.Г. Шевченко, физический факультет.

2 Киевский национальный университет им. Т.Г. Шевченко, радиофизический факультет

(malnev@i.com.ua; emart@mail.univ.kiev.ua).

В этом сообщении рассмотрены низкочастотные дисперсионные свойства комплексной плазмы с ферромагнитными гранулами. Последние могут иметь отрицательный заряд. Если предположить, что типичный размер гранул порядка 10^-4 – 10^-5 см, то это позволяет считать их однодоменными частицами. Все гранулы считаются одинаковыми и обладающими постоянным магнитным дипольным моментом d_mи моментом инерции J. Упоминание об экспериментальном изучении такого типа комплексной плазмы дано в [1]. Коллективные свойства электрон-ионной плазмы с парамагнитными атомами в качестве нейтральной компоненты исследованы в [2].

Вращательные степени свободы магнитных диполей обладают определенным запасом тепловой энергии, поэтому диполи вращаются с угловой частотой _T. Вычисления намагниченности единицы объема газа гранул приводят к определенному выражению для магнитной проницаемости (). Результат похож на полученный ранее тензор диэлектрической проницаемости  газа с электрическими диполями. В пределе  << _T получается хорошо известное выражение для ланжевеновского намагничивания. Если  >> _T_,то необходимо учитывать дисперсию намагничивания, которая связана с вращением магнитных моментов пылинок. Мнимая часть намагничивания даже при отсутствии столкновений дает специфическое «вращательное» затухание Ландау.

Исследовано и поведение намагниченности газа ферромагнитных пылинок во внешнем однородном постоянном магнитном поле. В этом случае, в соответствии с моделью Ланжевена, пылинки ориентированы вдоль магнитного поля. В этом случае частота _T будет частотой прецессии магнитных моментов вокруг силовых линий магнитного поля. Заметим, что появляется дополнительная собственная частота подсистемы пылинок, связанная с колебаниями магнитных моментов в постоянном магнитном поле

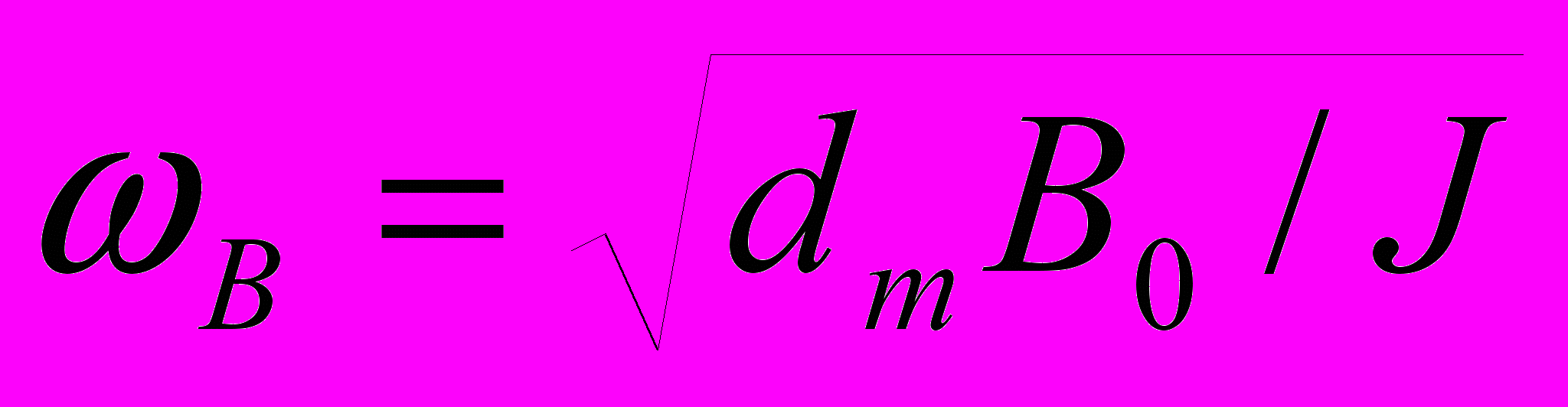, где B₀– индукция внешнего магнитного поля.

Рассмотрение распространения линейно поляризованной электромагнитной волны перпендикулярно к внешнему магнитному полю показало, что для частот  из диапазона

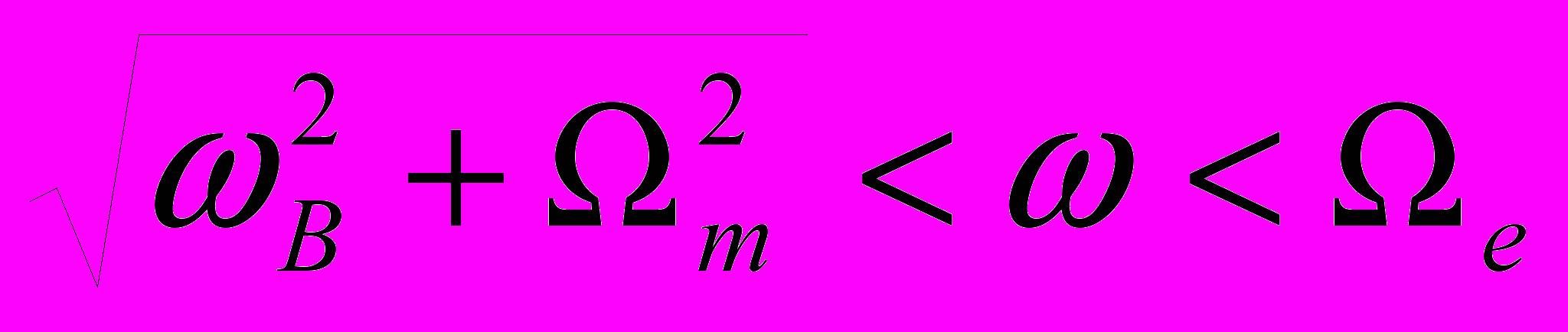, (где _m = (2N_gd_m²/J)^1/2, _e – плазменная частота электронов) возможно одновременное выполнение неравенств  < 0;  < 0. Такая среда, как известно [3], называется «левосторонней» и обладает рядом специфических электродинамических свойств. Экспериментальная реализация такой ситуации на других материалах показана в [4]. Заметим, что выражение слева в приведенном выше двойном неравенстве зависит только магнитных параметров пылинок и внешнего магнитного поля. Правая часть есть функция только электронной плотности. Таким образом, можно утверждать, что описанная выше плазма – хороший кандидат для «левосторонней» среды с управляемыми параметрами.

1. V.I. Molotkov, M.Yu. Pustyl’nik, V.M. Torchinskii, and V.E. Fortov, Plasma of DC current corona with dusty particles: selforganization and peculiarities of behavior, Proceedings of the Conference on Plasma Chemistry, Ivanovo, Russia, v.1, pp 51-54.,( 2002).

W. Bantikassegn and V.N. Mal’nev, Waves in a paramagnetic plasma, J. Plasma Phys, 45, 125 (1991).
V.G.Veselago, “The electrodynamics of substances with simultaneously negative values of  and ,”, Sov.Phys.-Usp.,v.10, #4, pp..509-514, 1968.

4. D. Smith, W.J. Padilla, D.C. Vier, e.a., Composite medium with Simultaneouasly Negative Permeability and Permittivity, Phys. Rev. Lett. V.84,#18 pp. 4184-4187 (2000).

ОБРАЗОВАНИЕ АЭРОЗОЛЬНОЙ ПЛАЗМЫ В ПРОЦЕССЕ ОБЪЕМНОЙ КОНДЕНСАЦИИ В ОБЛАКЕ ПРОДУКТОВ ПРИЗЕМНОГО ВЗРЫВА

Н. М. Корценштейн, Е. В. Самуйлов

ОАО «Энергетический институт им. Г. М. Кржижановского»

Аэрозольная плазма может образоваться в процессе объемной конденсации, если капли конденсационного аэрозоля способны в заметном количестве эмитировать электроны при температуре конденсации паров. В данной работе рассмотрены продукты приземного взрыва на стадии охлаждения. Объект исследования представляет собой гетерогенную смесь паров минеральных веществ грунта, неконденсирующихся газов и неиспарившихся частиц грунта. Выяснены причины, обеспечивающие наличие заряженных частиц в области температур, при которых происходит образование конденсационного аэрозоля из паров минеральных веществ. Рассмотрено взаимодействие неравновесных процессов электрон-ионной рекомбинации и объемной конденсации. Прослежен переход от ионной к гомогенной нуклеации в зависимости от концентрации ионов, определяемой скоростью охлаждения. Выяснено, что при определенной концентрации ионов функция распределения капель по размерам является бимодальной. С учетом обстоятельства, что для паров минеральных веществ температура кипения (в энергетических единицах) не мала по отношению к работе выхода электронов, сформулирована модель процесса объемной конденсации в облаке продуктов взрыва. Модель учитывает объемную конденсацию паров минеральных веществ грунта, взаимодействие зарождающихся капель с неиспарившимися частицами грунта и термическую эмиссию электронов с зародышей и капель. На основе сформулированной модели рассчитаны параметры конденсационного аэрозоля и концентрация электронов в продуктах приземного взрыва. Как показали результаты расчетов, вследствие термической эмиссии электронов образование высокодисперсного конденсационного аэрозоля обеспечивает существенное превышения концентрации электронов над фоновым значением, связанным с термической ионизацией молекул газа; низкотемпературный предел указанного превышения связан с образованием отрицательных ионов в газовой фазе. Получены расчетные зависимости концентрации электронов в продуктах взрыва от температуры, скорости падения температуры, а также концентрации неиспарившихся частиц грунта.

Работа выполнена при поддержке РФФИ (проект 03-02-16646).

РАСЧЕТ ЗАРЯДКИ ИГОЛОЧЕК В ИОННОМ ПОТОКЕ

С.А. Майоров

Институт общей физики им. А.М. Прохорова РАН, Москва

В настоящей работе, продолжающей работы [1 - 3], на основе вычислительного эксперимента исследовано формирование пространственного заряда вокруг структур протяженной формы в движущейся плазме. Ионная фокусировка существенным образом влияет на распределение области пространственного заряда вокруг пылинки и соответственно меняется плотность потока заряженных частиц плазмы на различные участки поверхности пылинки протяженной формы. Заряд на поверхности такой пылинки (иголочки) распределяется неравномерно, что приводит к появлению значительного дипольного момента у протяженных пылинок и усложняет характер их взаимодействия. Рассмотрены случаи с различным типом проводимости пылинок – металлическая и диэлектрическая (более точно – проводящая и непроводящая поверхности).

Постановка задачи позволяет самосогласованно учитывать процесс зарядки и флуктуации заряда макрочастицы. Кроме того, граничные условия позволяют более корректно, чем в предыдущих работах, моделировать течение плазмы вокруг пылинки при низких скоростях ионного потока, когда скорость потока сравнима или даже меньше тепловой скорости ионов. Полученные численные данные и их анализ позволяют сделать следующие выводы.

Во-первых, результаты расчетов показывают новый эффект – влияние ионной фокусировки на характер зарядки пылинок протяженной формы.

Во-вторых, продемонстрирована сильная зависимость зарядки пылинок от проводимости их поверхности. Строго говоря, для обеспечения эквипотенциальности поверхности нет необходимости в том, чтобы вся пылинка была проводящей (металлической). Конечной проводимости (даже довольно низкой) может быть достаточно для обеспечения эквипотенциальности. Так как поверхность материала, из которого изготовлены пылинки, подвергается интенсивному воздействию частиц плазмы, то вероятность образования у диэлектрика проводящей поверхности должна учитываться при интерпретации экспериментов.

Достаточно удивительным является также и то, что суммарный заряд пылинок для обоих типов поверхности отличается незначительно (у диэлектрика примерно на 2% выше), но характер распределения плотности заряда вдоль пылинки меняется радикально. У диэлектрической пылинки примерно половина заряда сосредоточена в ее начале, а далее идет область, у которой плотность заряда даже меняет знак. Этот эффект обусловлен фокусировкой в эту часть пылинки более значительного ионного потока и соответствующим уменьшением электронного потока из-за геометрического фактора.

Следующей интересной особенностью является то, что поток частиц плазмы на диэлектрическую пылинку оказывается примерно в два с половиной раза выше, чем на металлическую (при примерно равном суммарном заряде). То есть диэлектрическая пылинка из-за накопления заряда в ее носовой части более сильно фокусирует ионный поток на свой хвост. Соответственно, сила увлечения, действующая со стороны ионного потока на диэлектрическую пылинку протяженной формы выше, чем на проводящую.

[1] S.A. Maiorov, S.V. Vladimirov, and N.F. Cramer / Phys. Rev. E, 63, 017401 (2000).

[2] S. V. Vladimirov, S.A. Maiorov, and N.F. Cramer/ Phys. Rev. E, 67, 016407 (2003).

[3] С.А. Майоров, С.В. Владимиров, Н.Ф. Крамер / Физика плазмы, 28, №11, 1025 (2002).

Blog