Секция: математика

Вид материала

Документы

Содержание Паркеты с тремя многоугольниками в вершине В первом случае А еще одним многоугольником. Из нее видно, что один из углов при вершине В В вершине правильного паркета не могут сходиться три раз­личных многоугольника, у одного из которых нечетное число сторон Паркеты с пятью многоугольниками в вершине Неправильные паркеты ABCD (рис. 16) и рассмотрим симметричный ему относитель­но середины стороны АВ

Подобный материал:

• Xix всероссийская конференция, 249.97kb.
• 1 ноября в с. Табуны прошёл ежегодный молодёжный фестиваль «Табуния-2008». Внём приняли, 111.28kb.
• Секция «Математика и информатика» Руководитель секции, 115.57kb.
• Iii халықаралық ғылыми-тәжірибелік конференция Қазақстан Республикасы, Павлодар, 412.06kb.
• Итоги IV школьной научно-практической конференции «шаг в науку» Секция 1 (химия, биология,, 72.67kb.
• «Математика. Прикладная математика», 366.03kb.
• Программа подраздела «Философские проблемы математики», 94.9kb.
• Научные направления и секции конференции: Секция, 39.35kb.
• Расшифровка : Математика, 146.94kb.
• Секция: математика, 535.74kb.

XVIII Ставропольская краевая открытая научная конференция школьников


Секция: математика.


Паркеты


Автор работы: Холодова Оксана

Место выполнения работы: г. Пятигорск

МОУ СОШ №5с углубленным изучением отдельных предметов им. А.М.Дубинного

Научный руководитель:

Кравченко Анна Николаевна,

учитель математики высшей категории


Ставрополь, 2007


Содержание

1. Что такое паркет?
   
2. Правильные паркеты.
   
   • Паркеты с тремя многоугольниками в вершине.
     
   • Паркеты с четырьмя многоугольниками в вершине.
     
   • Паркеты с пятью многоугольниками в вершине.
     
   • Паркеты с шестью многоугольниками в вершине.
     

3. Замощение плоскости неправильными одинаковыми

многоугольниками.

4. Периодические замощения.

5. Непериодические замощения.

6. Рисунки голландского художника М. Эшера,

связанные с паркетами.


Уже пифагорейцам было известно, что име­ется только три вида правильных многоуголь­ников, которыми можно полностью замостить плоскость без пробелов и перекрытий, — тре­угольник, квадрат и шестиугольник (рис. 1). В каждом из этих замощений любые два мно­гоугольника имеют либо общую сторону, либо только общую вершину, либо вовсе не имеют общих точек.

Паркетом будем называть такое покрытие плоскости правильными многоугольниками, при котором имеют либо общую сторону, либо Общую вершину или совсем не имеют общих точек. Паркет производит приятное впечатление, если он достаточно симметричен. Фигура называется симметричной, если ее можно наложить на саму себя «не правильным» способом (т. е. не таким, когда все точки останутся на своем месте).

Паркеты из правильных многоугольников сами правильные в том смысле, что они «оди­наково устроены» относительно всех своих вершин и всех составляющих паркеты кусоч­ков-многоугольников. (Эти кусочки называ­ются гранями замощения или просто плитка­ми.) Другими словами, для любых двух вершин правильного паркета можно указать такое его самосовмещение, при котором одна из вершин попадает на другую. То же верно для любых двух плиток паркета.


а) б) в)


рис.1


Паркет называется правильным, если его можно наложить на самого

себя так, что любая заданная его вершин наложится на любую другую

заданную его вершину.

Самый простой из «правильных» паркетов — это разбиение плоскости на квадраты (рис. 1,б). Интересно вы­яснить, сколько есть еще пар­кетов, у которых к каждой вершине паркета примыкают четыре правильных мно­гоугольника и все вершины устроены одинаково (последнее означает, что паркет можно сдвинуть так, что любая его заданная вершина перейдет в любую другую заданную вершину, и все линии совпадут). Это — впол­не практическая задача.

Мы знаем, что сумма углов пра­вильного n-угольника равна 180°(n — 2), а его один угол равен



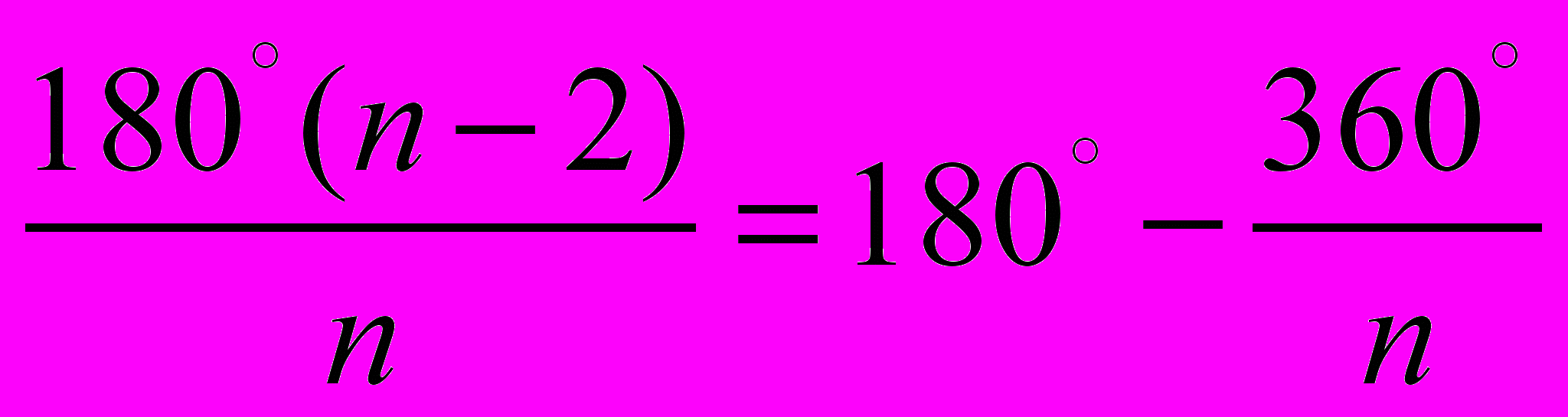
Пусть в вершине паркета сходятся углы четырех правильных много­угольников: p-угольника, q-угольника, r-угольника и s-угольника. Сумма этих четырех углов должна равняться 360°. Запишем это условие:



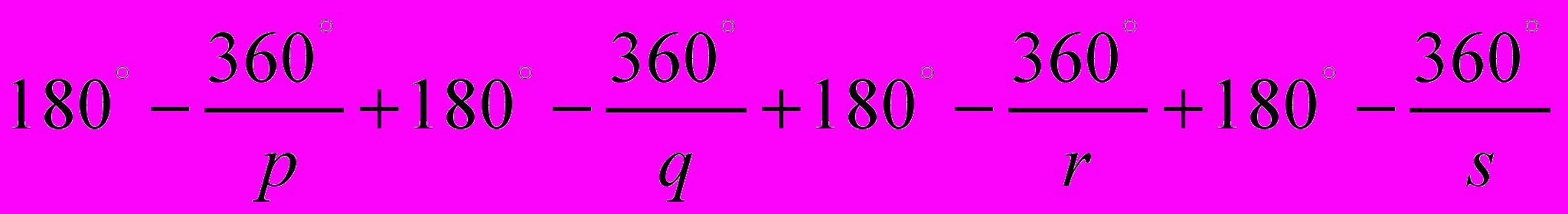
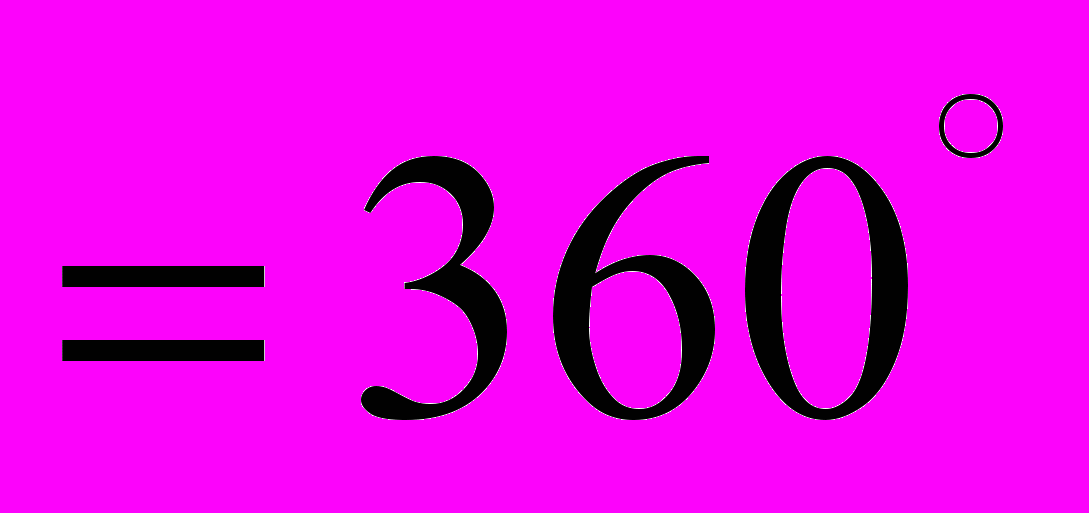
Это равенство приводит к соотношению



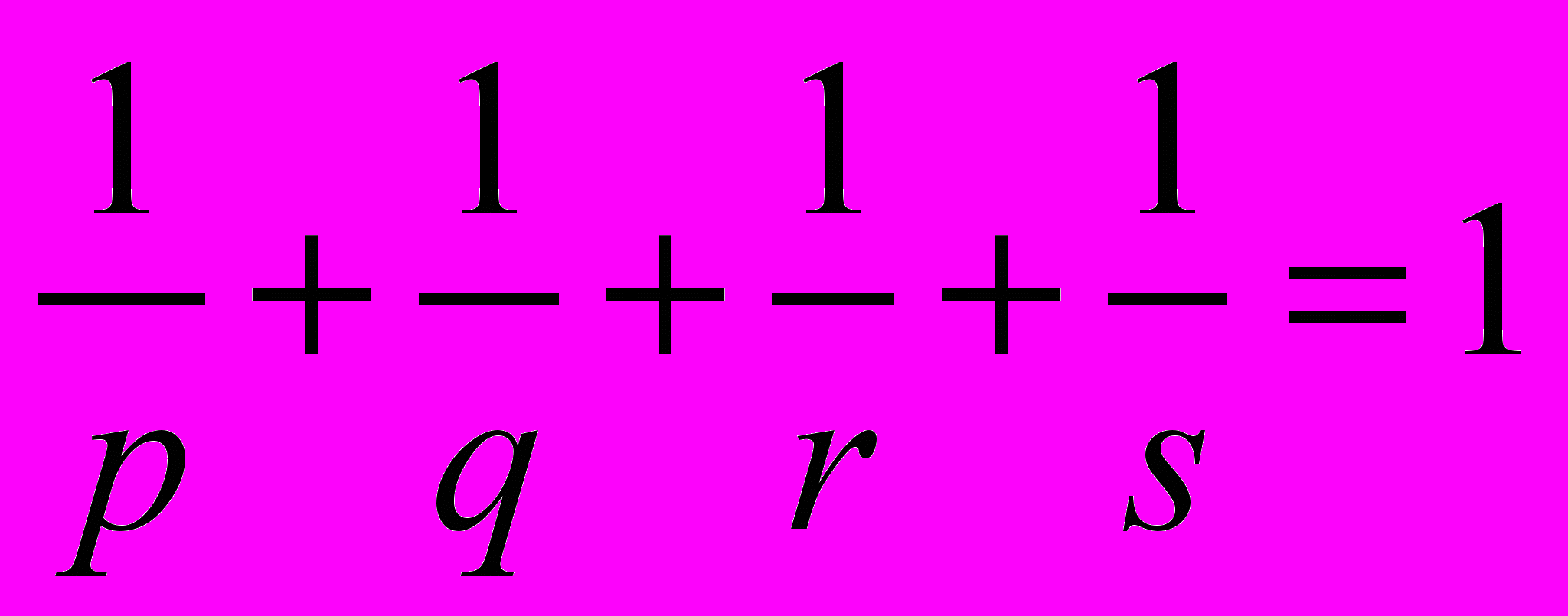
Если считать, что 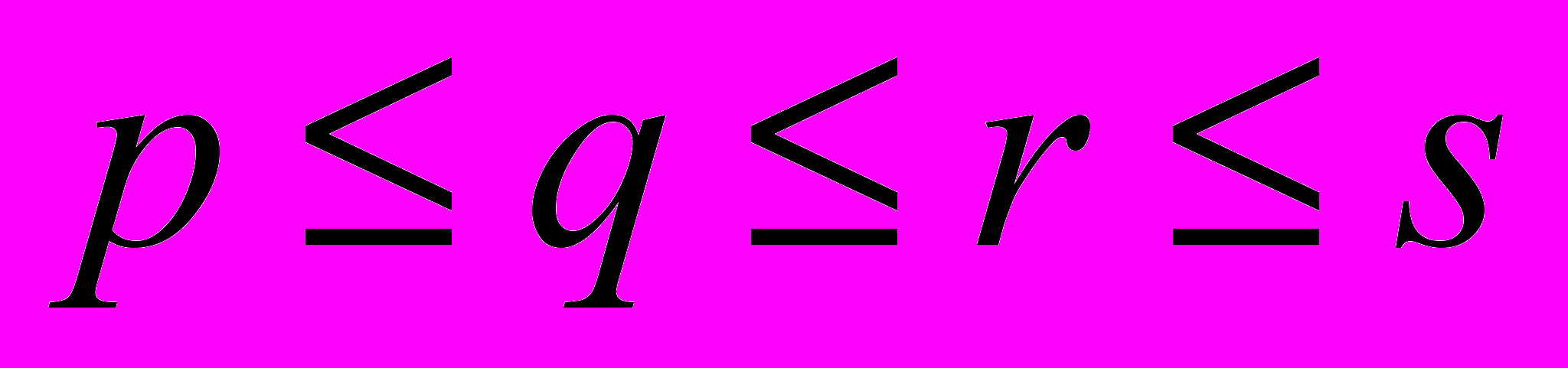, то, перебрав все возможности, убеждаемся в том, что существует 14 различных четверок (p, q, r, s). Вот они:

(2, 3, 7, 42); (2, 3, 8, 24); (2, 3, 9, 18); (2, 3, 9, 15); (2, 3, 15, 15);

(2, 4, 5, 20); (2, 4, 6, 12); (2, 4, 8, 8); (2, 5, 5, 10); (2, 6, 6, 6);

(3, 3, 4, 12); (3, 3, 6, 6); (3, 4, 4, 6); (4, 4, 4, 4).

Так как речь идет о много­угольниках, надо отбросить те четвер­ки, где р = 2. Останутся четыре чет­верки: (4, 4, 4, 4); (3, 4, 4, 6); (3, 3, 6, 6); (3, 3, 4, 12).

Первая четверка соответствует пар­кету из одинаковых квадратов (к каждой вершине примыкают 4 пра­вильных четырехугольника — см. рисунок 2).



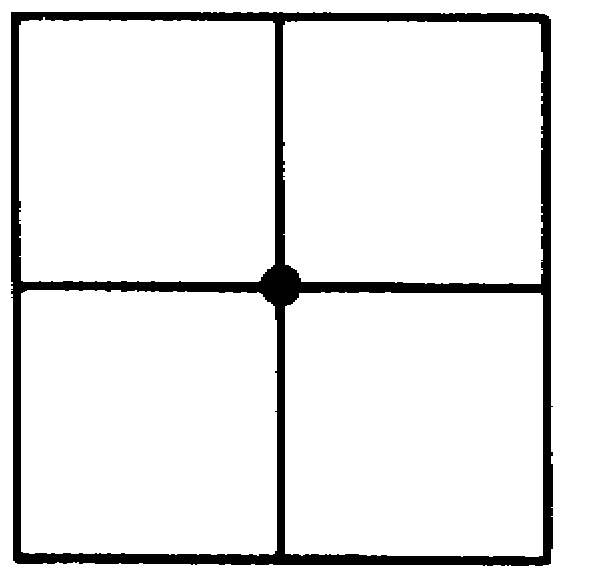
рис.2

Вторая четверка (3,4,4,6) представ­ляет две возможности для устройст­ва вершины (рис. 3, а, б), но до пра­вильного паркета удается достроить только паркет на рисунке 3, а — по­лучается рисунок 3, в.


в)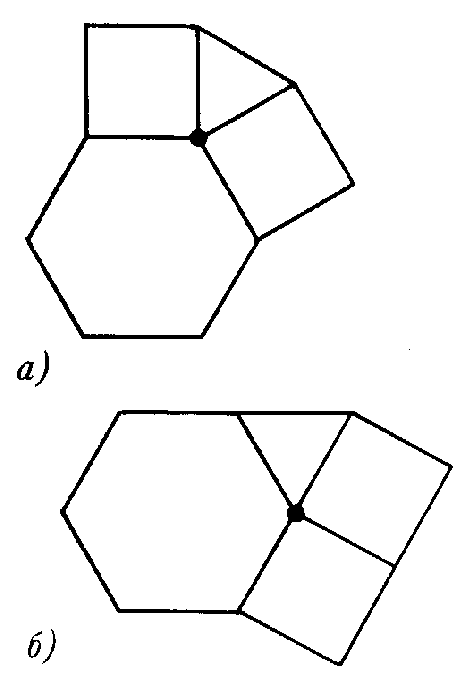

рис.3


Третьей четверке (3,3,6,6) также со­ответствуют два расположения многоугольников в вершине (рис. 4, а, б), и только второй случай, изображен­ный на рисунке 4, б, достраивается до правильного паркета (рис. 4, в)

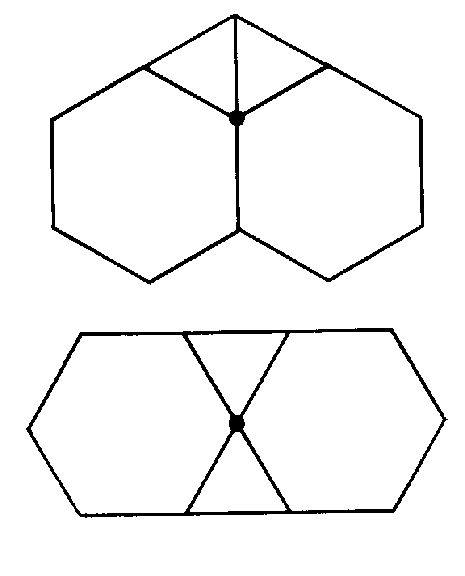
а) в)

б)

рис.4


Два рисунка (рис. 5, а, б), соот­ветствующих четвертой четверке (3,3, 4,12), до правильного паркета не до­страиваются.





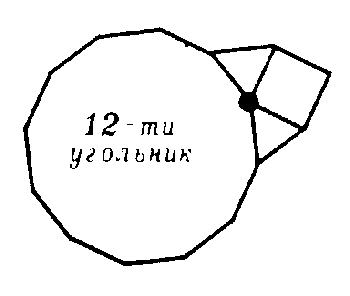
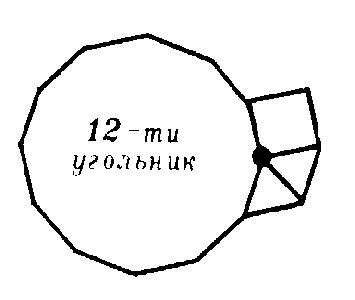
а) б)

рис.5


Сколько всего правильных парке­тов? Как они устроены? Наша зада­ча — ответить на эти вопросы.

Легко видеть, что вообще парке­тов — не обязательно правильных — существует бесчисленное множество (Два паркета мы считаем различ­ными, если не существует гомотетии плос­кости, переводящей один из этих паркетов в другой.). Од­нако, подобно тому как при бесчис­ленном множестве многогранников вообще существует лишь конечное число правильных многогранников, так и при бесчисленном множестве паркетов существует лишь конечное число правильных паркетов.

Решение нашей задачи естествен­но начать с исследования вершин паркета. Из определения правильно­сти сразу вытекает принцип эквивалентности вер­шин: любые две вершины устроены одинаково в том смысле, что звезды всех вершин одинаковы. (Звездой вершины называется фигура, обра­зованная всеми многоугольниками, содержащими ее.)

Обозначим через 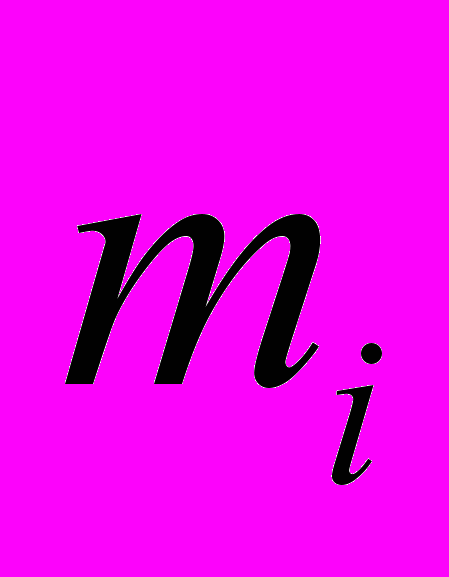число приле­гающих к вершине i-угольников, а че­рез a_i — величину внутреннего угла правильного i-угольника. Тогда в каждой вершине, очевидно, выпол­няется соотношение.


,

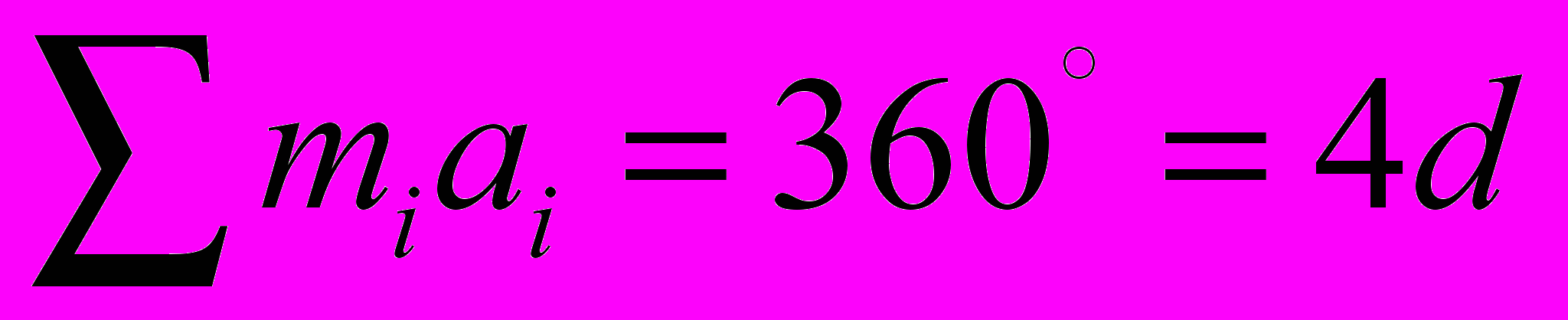где в сумму мы включаем все слагае­мые с номерами i, для которых к вер­шине примыкает хотя бы один i-угольник.

Подставляя в эту формулу извест­ное из геометрии выражение для a_i,

a_i =2(1 – 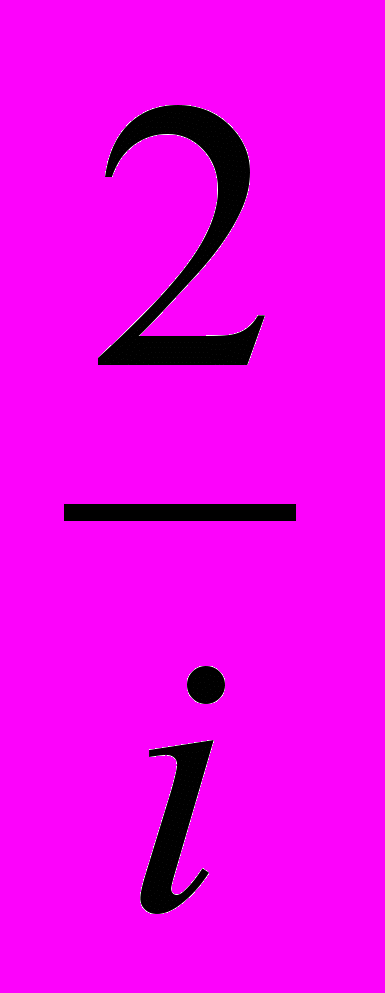)d, и сокращая на 2d, получим

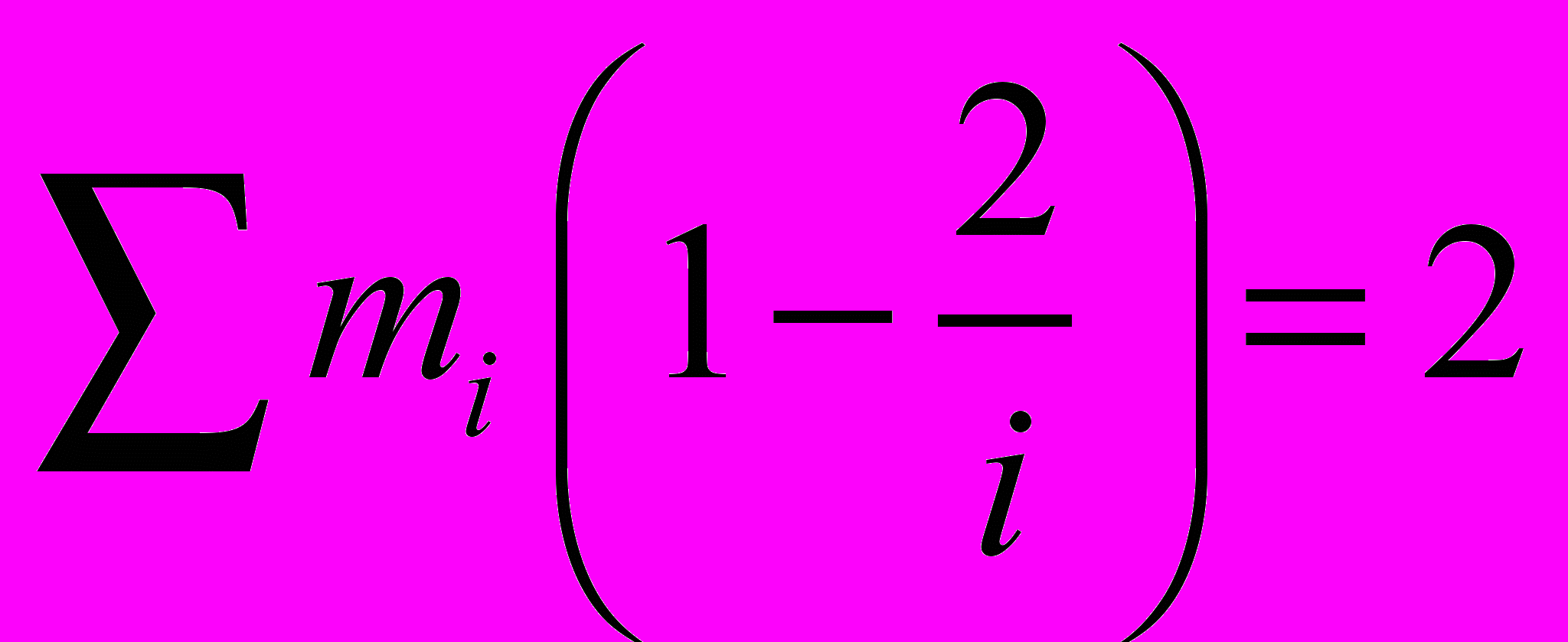(1)

Таким образом, числа 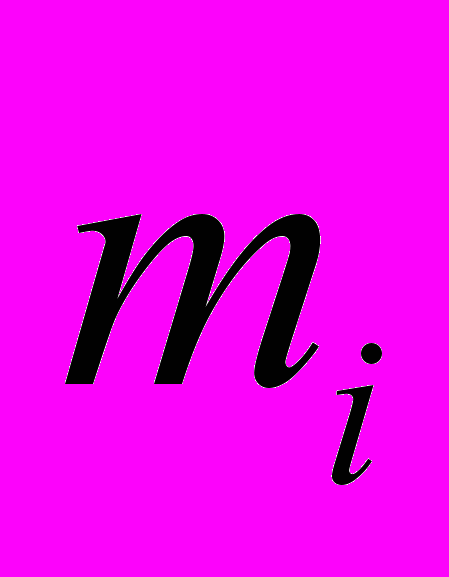являются целочисленными решениями уравнения (1) . Однако, как мы увидим ниже, не все целочисленные решения уравнения (1) реализуются правильными паркетами!

Далее, в вершине паркета может сходиться не более шести и не менее трех многоугольников. Действительно, при схождении в одной вершине семи или более многоугольников хотя бы один угол в правильном многоугольнике должен быть менее 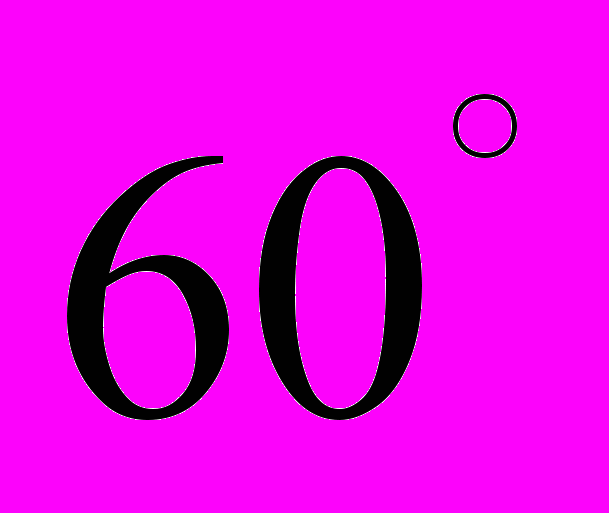, что невозможно (минимальный, угол - у треугольника - равен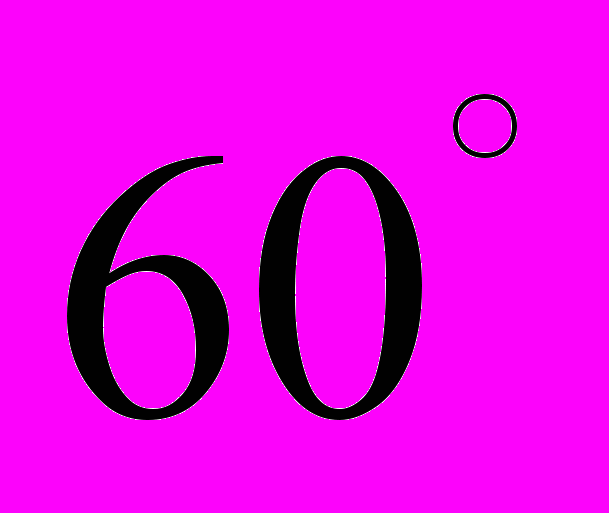). При схождении в одной вершине двух многоугольников у одного из них внутренний угол должен быть более 2d (180°), что, очевидно, также невозможно. Таким образом, реше­ние задачи распадается на анализ тех вариантов, когда в вершине паркета сходятся 3, 4, 5 и 6 правиль­ных многоугольников.


Паркеты с тремя многоугольниками в вершине

Здесь, в свою очередь, в принципе возможны три случая (в зависимости от набора многоугольников в каждой вершине):

1°. Три одинаковых многоуголь­ника.

2°. Два одинаковых и один отлич­ный от них.

3°. Три различных многоуголь­ника.

В первом случае сумма в уравне­нии (1) сводится к одному слагаемо­му, отвечающему трем одина­ковым n-угольникам, поэтому мы

получаем 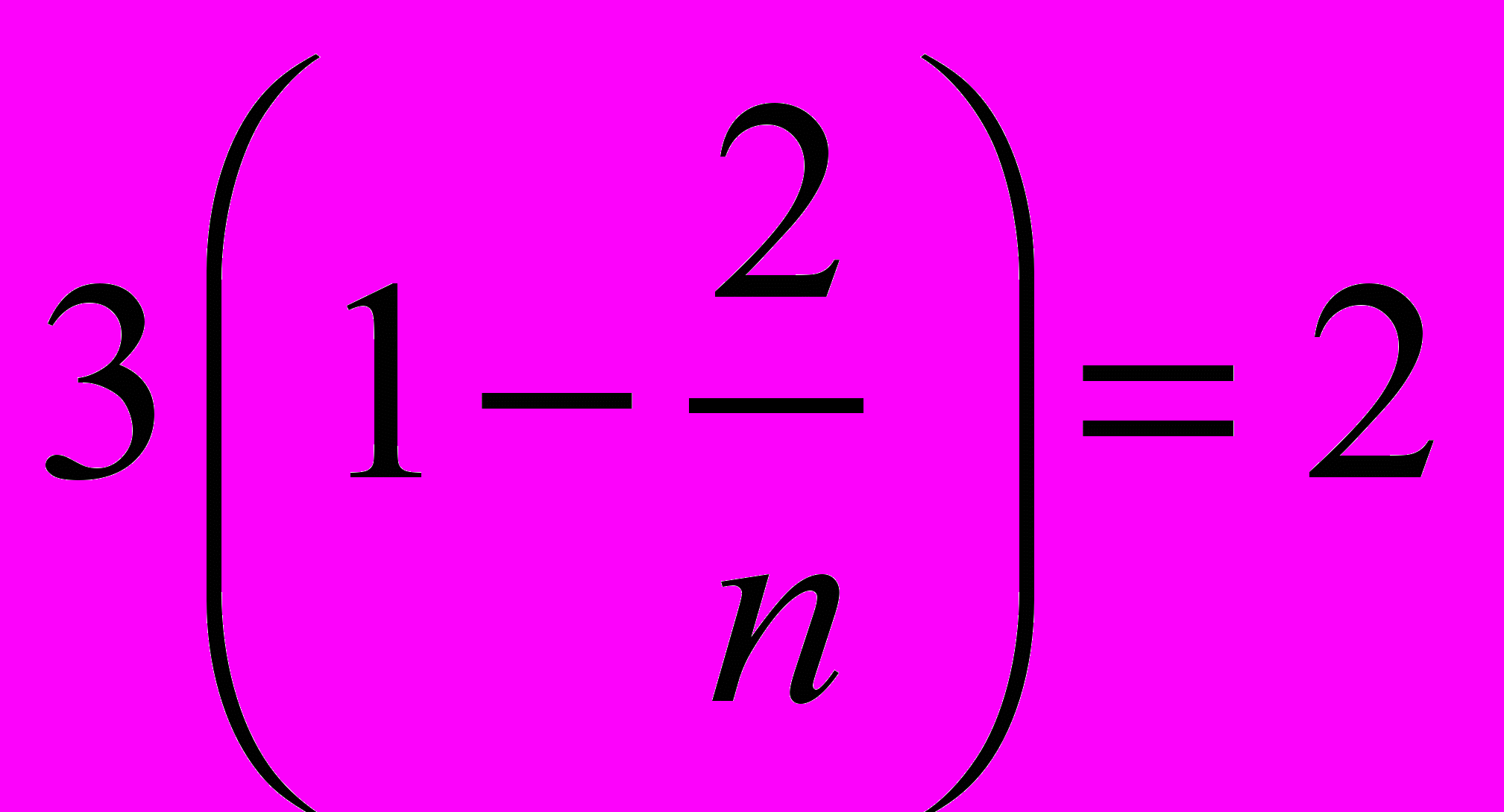или п = 6,

то есть к каждой вершине примыкает 3 шестиугольника. Это один из про­стейших правильных паркетов (рис.6).




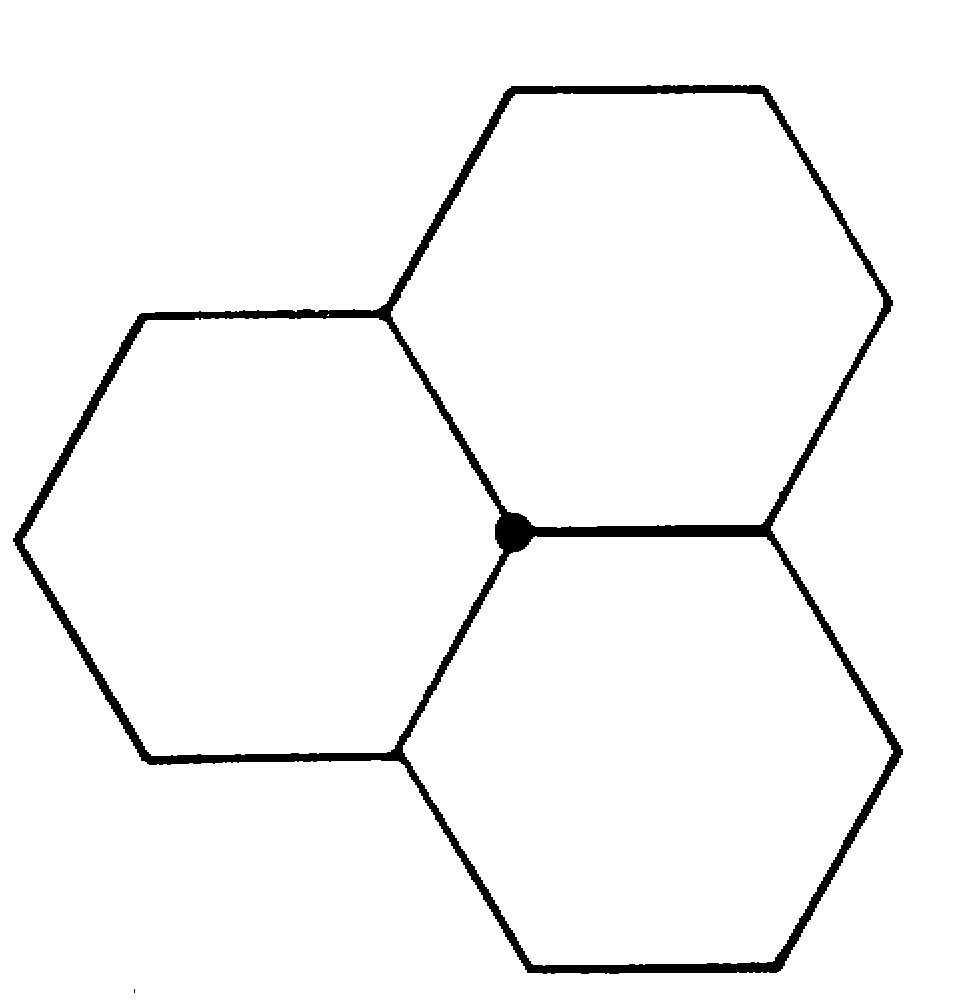
рис.6


Для второго случая (два k-угольника, один n-угольник) имеем


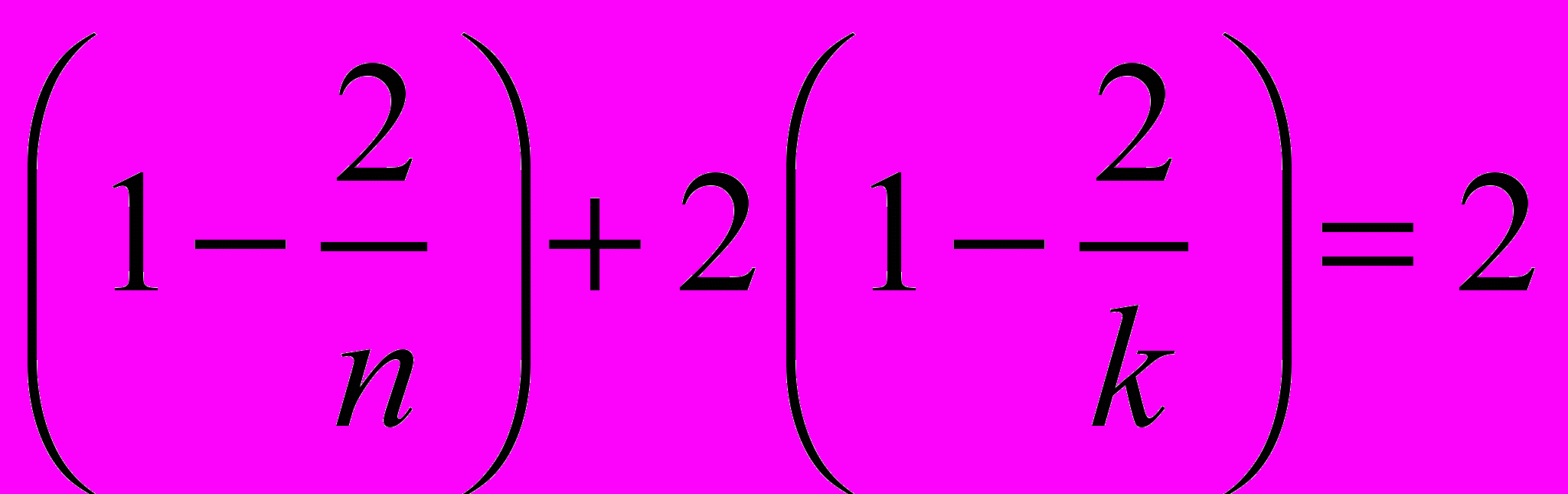или .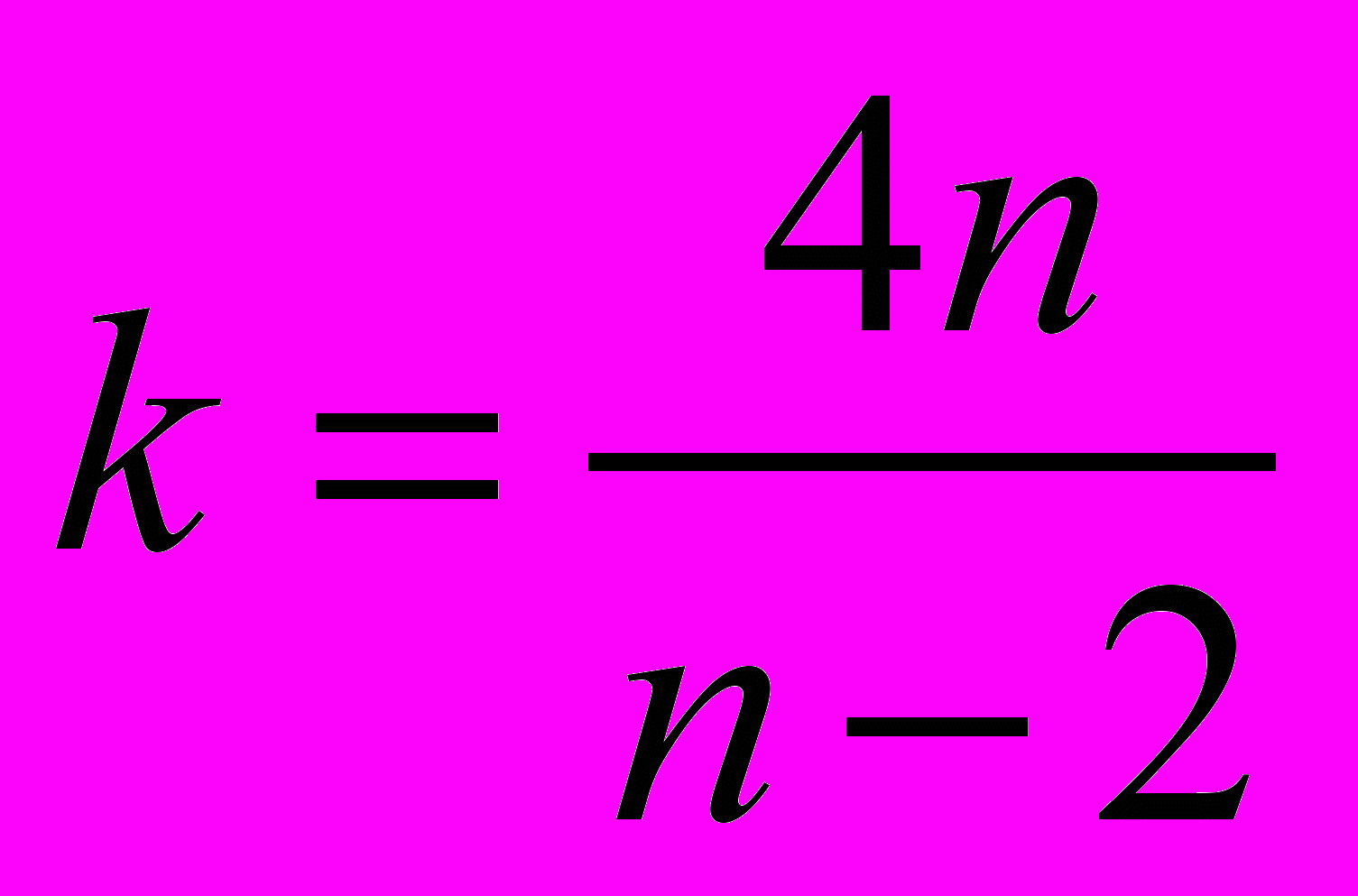


Целочисленные решения последнего уравнения проще всего найти

перебором различных значений:

N	1	2	3	4	5	6	7	8	9	10	11
K			12	8		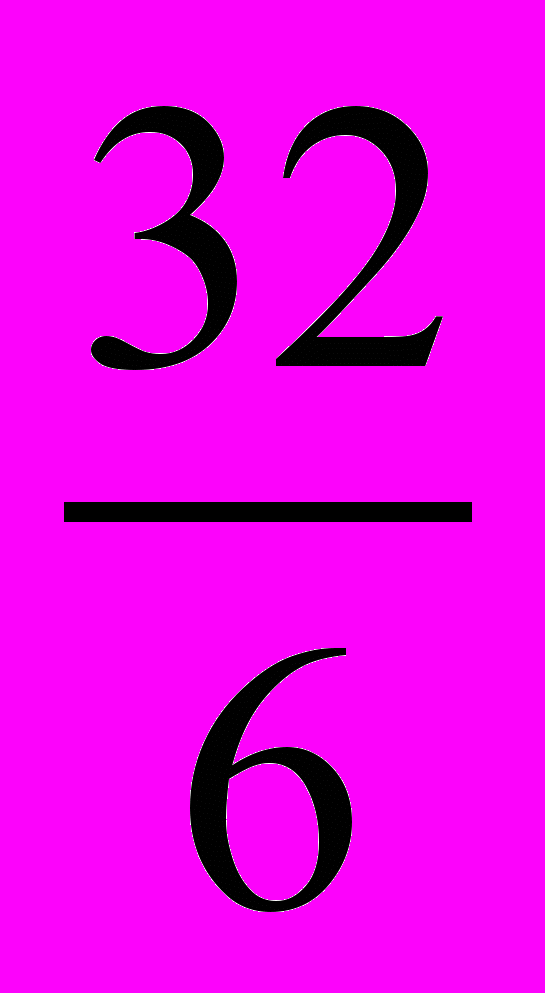6		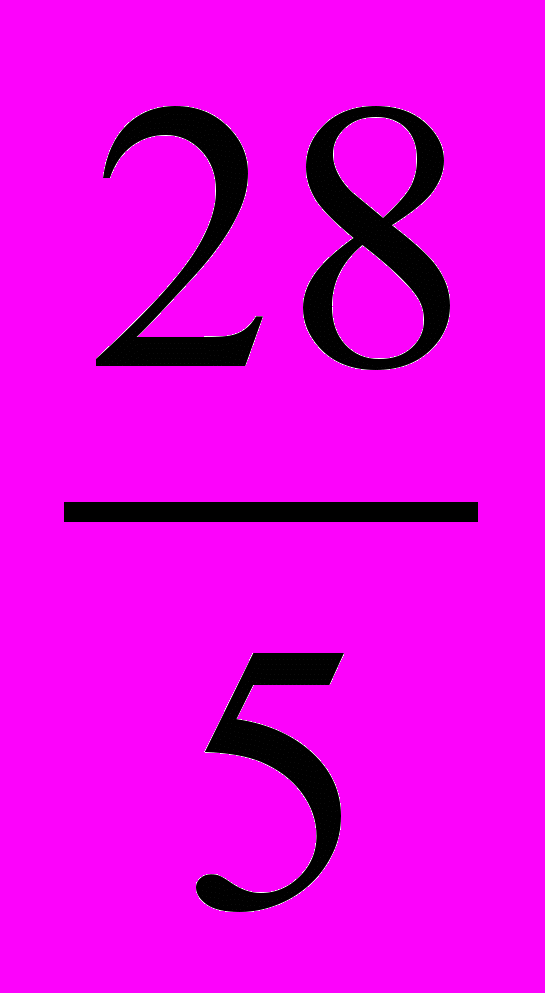		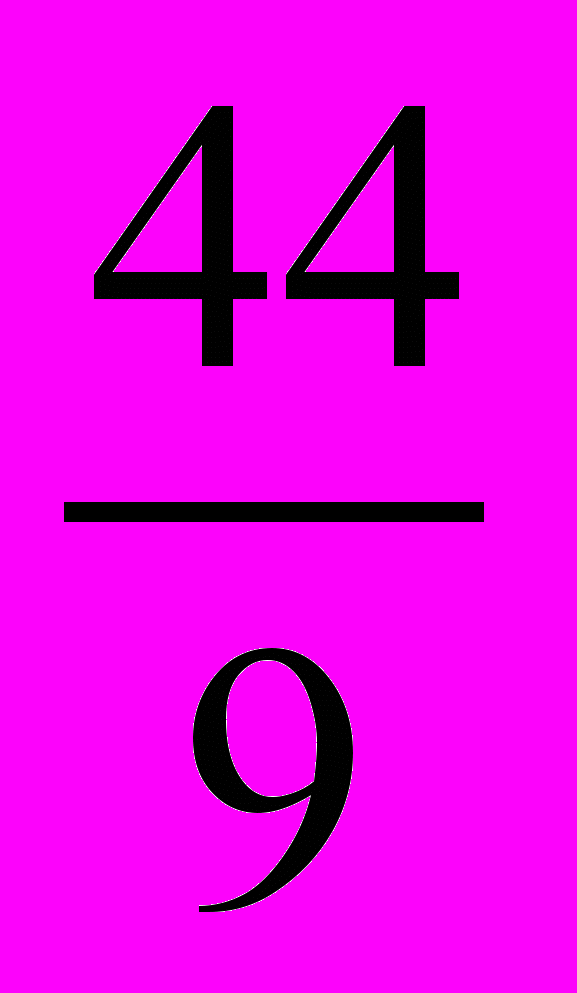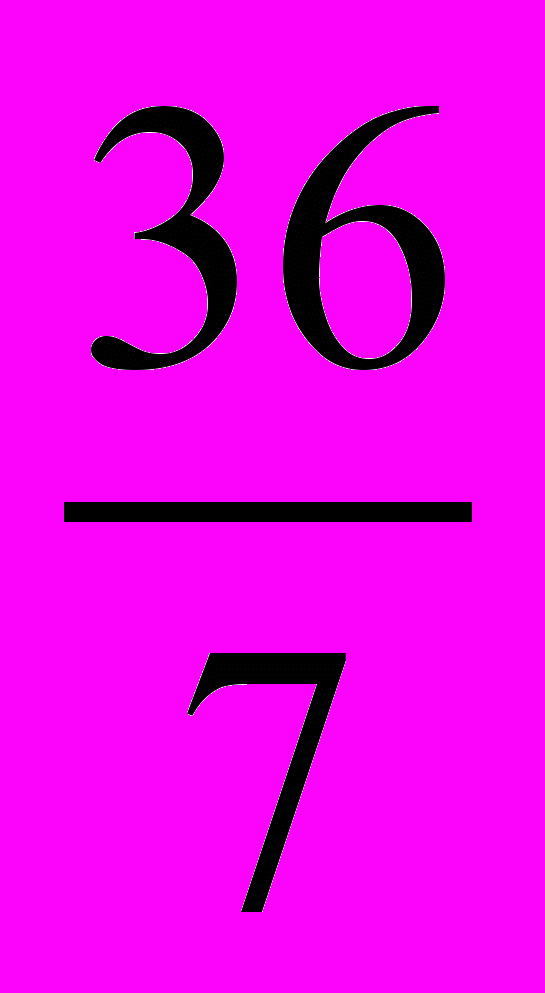5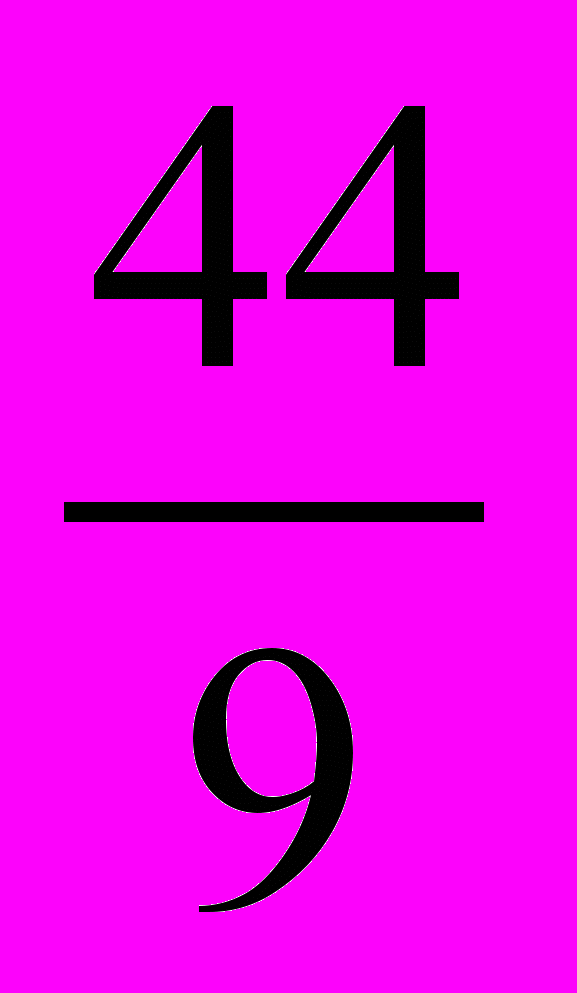

Продолжать перебор дальше нет смыс­ла, так как целочисленных k мы больше не получим: ,

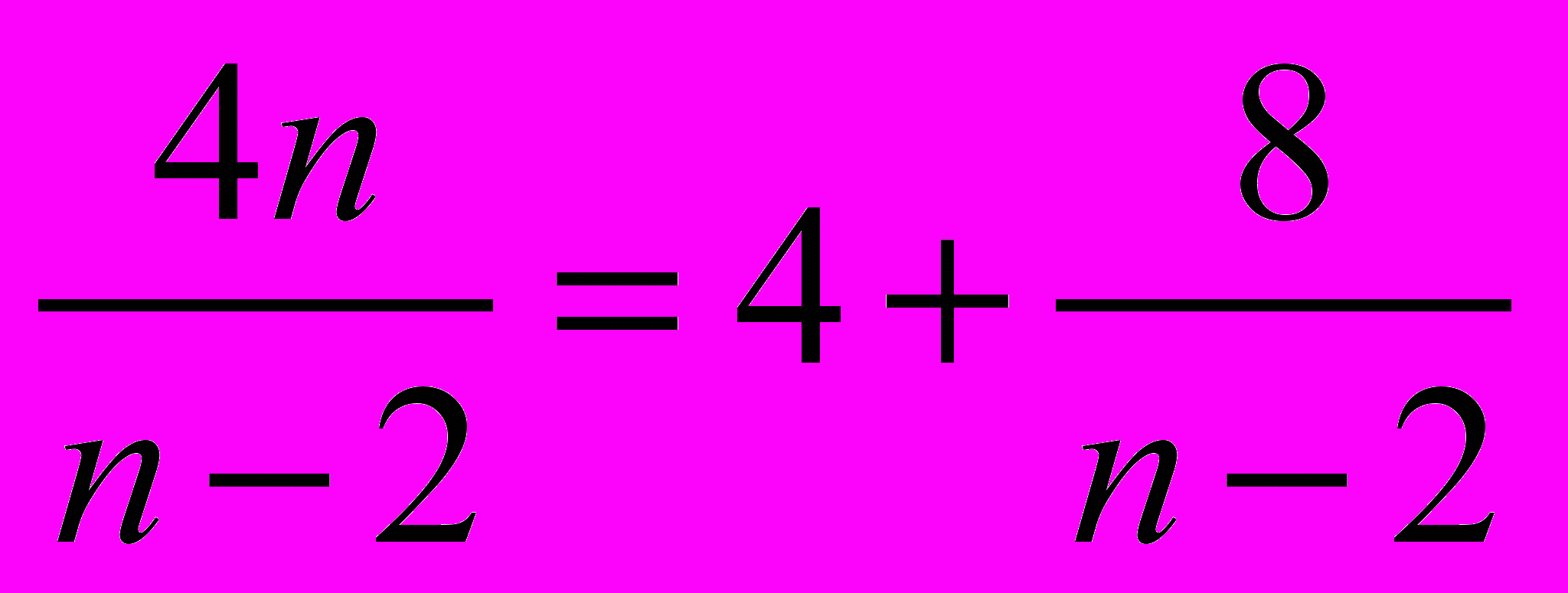а при n >10 последнее слагаемое не может быть целым.


Таким образом, кроме уже рас­смотренного случая n= k = 6 мы получили три решения, которые мы запишем в виде суммы углов в вершине:


; ; .


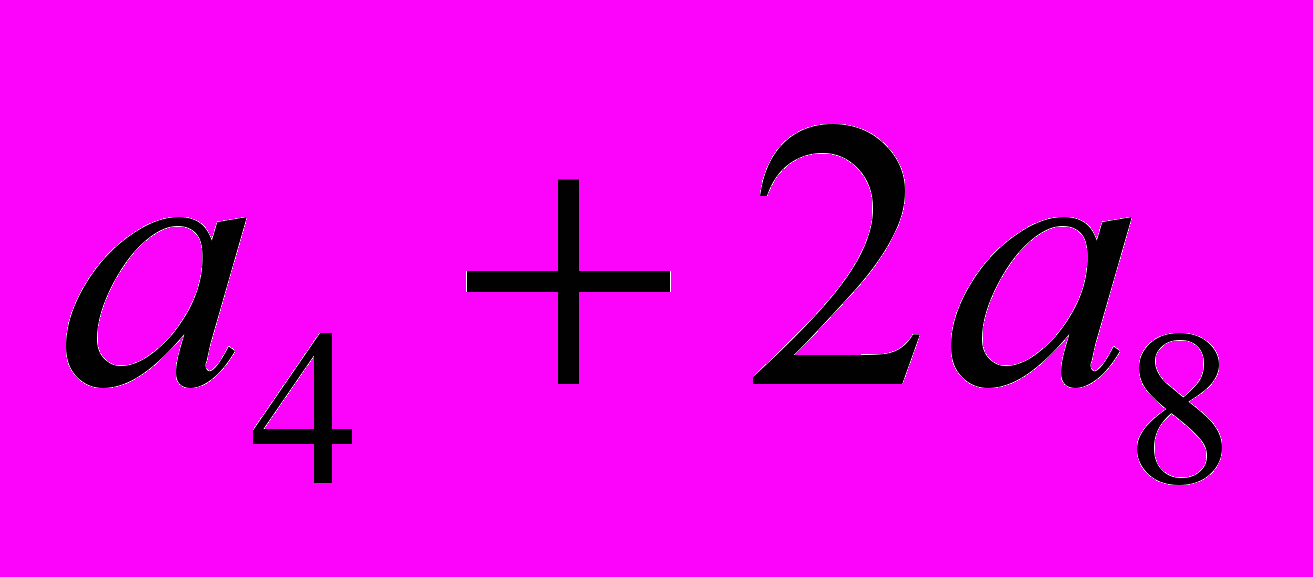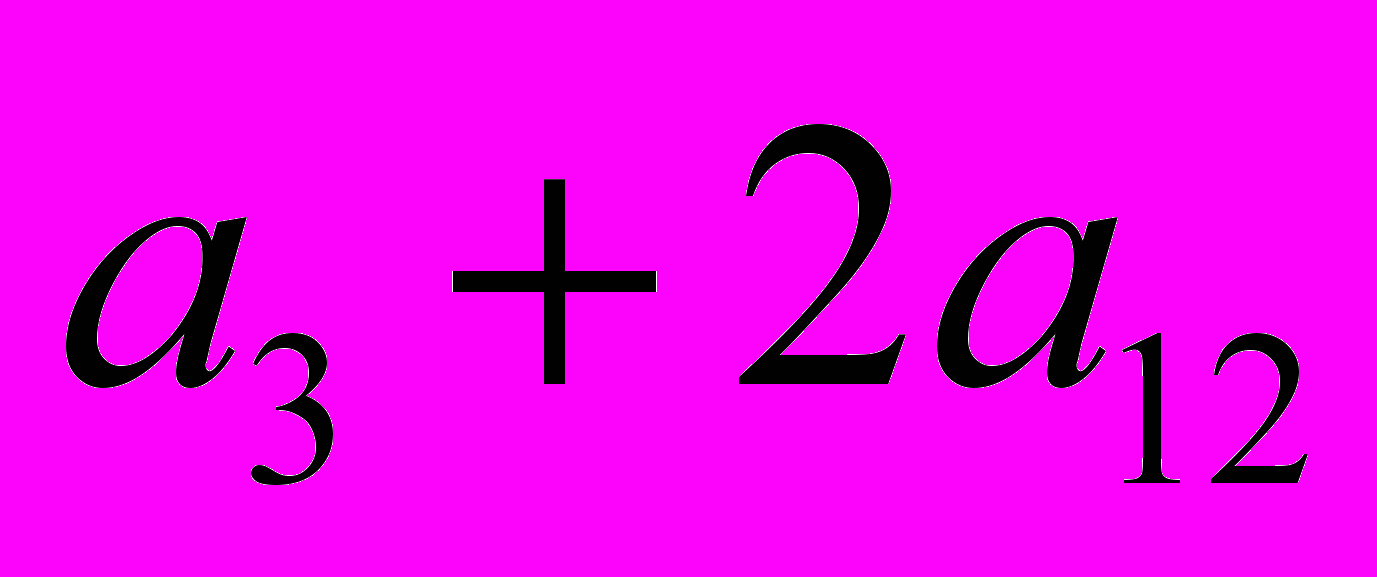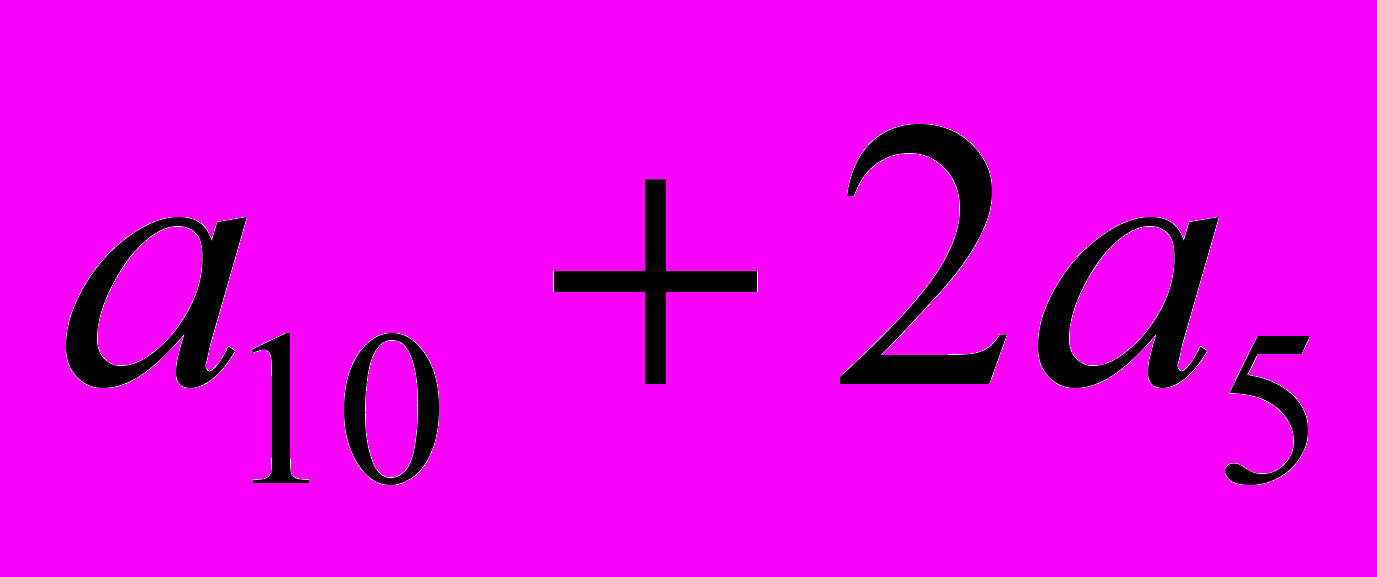Первому решению отвечает пар­кет, часто встречающийся на прак­тике (рис. 7).




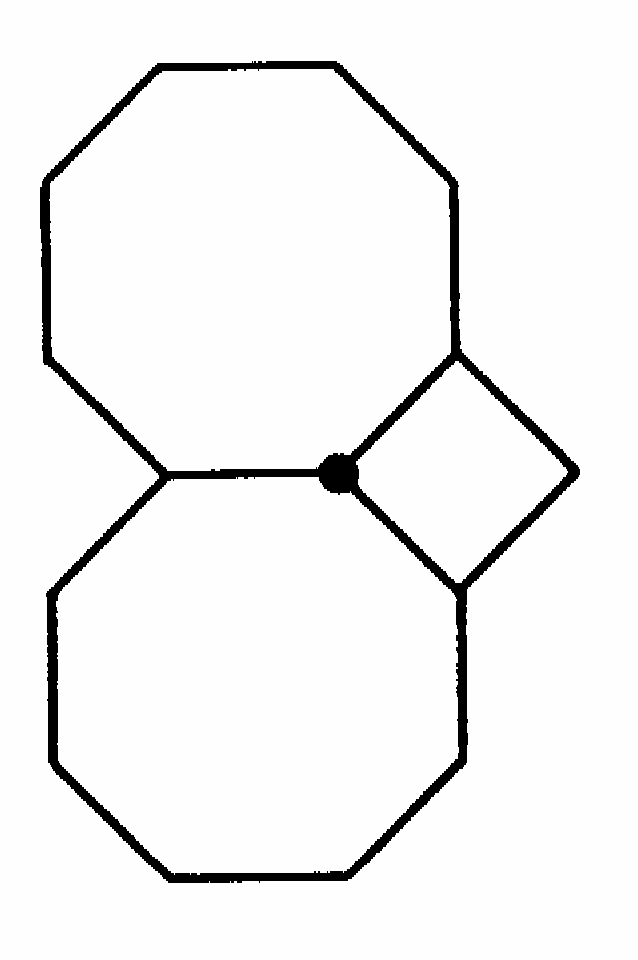
Рис. 7.

Менее обычный паркет, отвечающий второму решению, изо­бражен на рисунке 8.







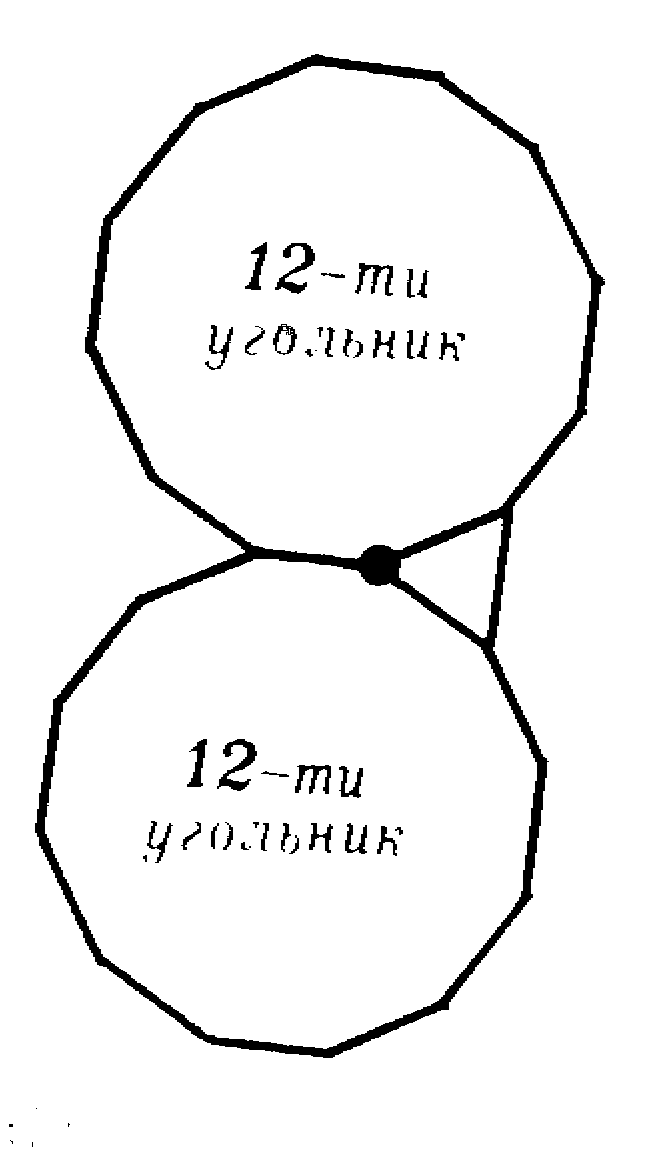
Рис.8

А 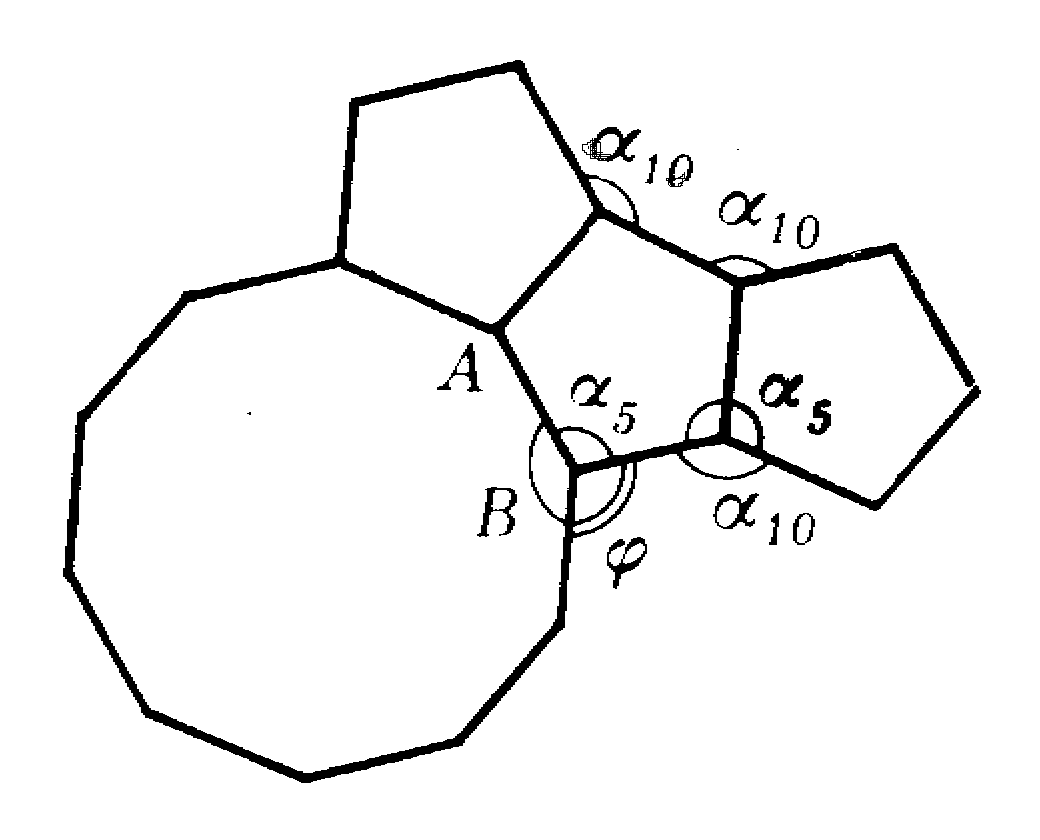вот комбинация 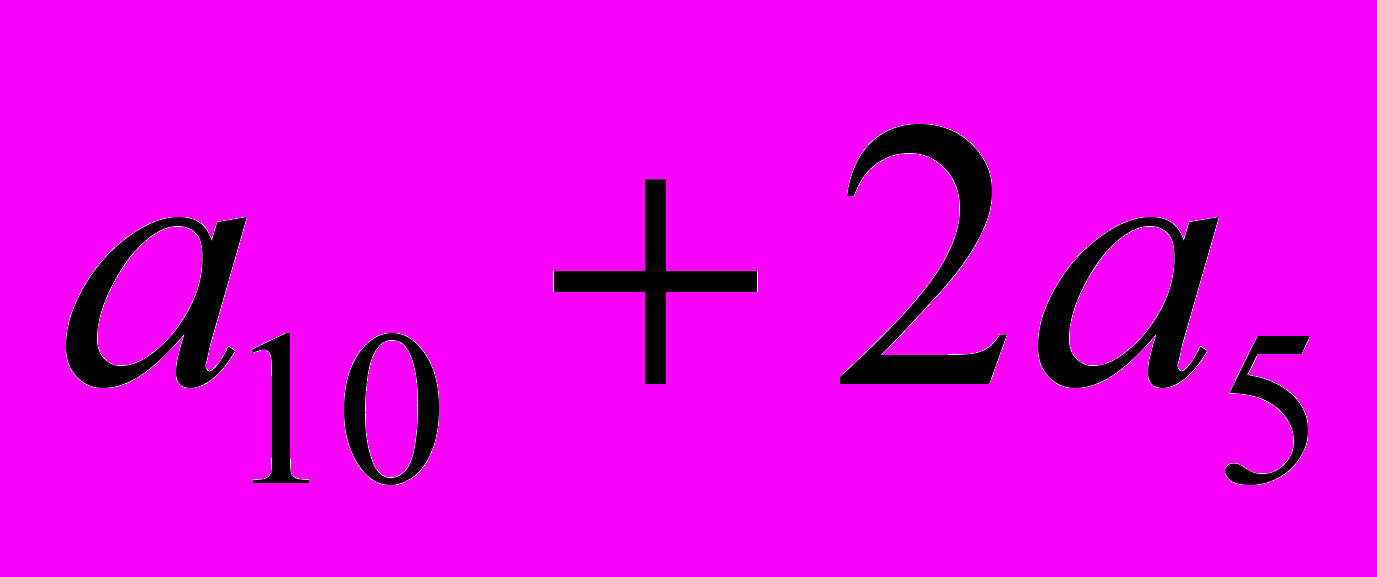, в отличие от ранее рассмотренных, пра­вильного паркета не образует. Убе­диться

в этом позволяет «достройка» (рис.9) окружения вершины А еще одним многоугольником. Из нее видно, что один из углов при вершине В (угол, обозна­ченный на рисунке 10 через 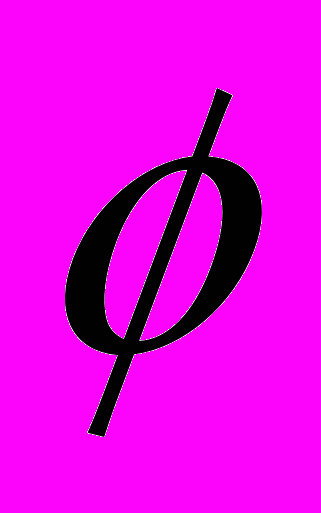), по принципу эквивалентности вершин, должен быть равен 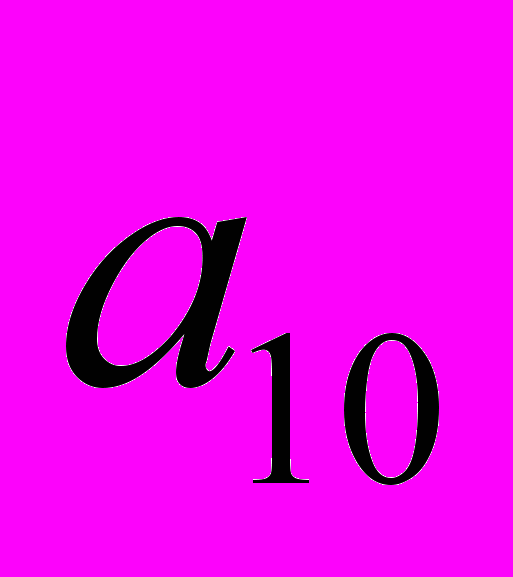. На самом же деле, угол 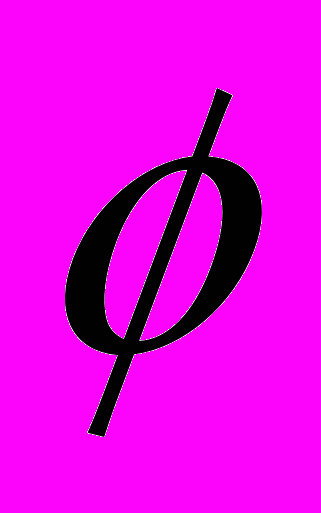равен . Рис. 9

Правильного паркета типа 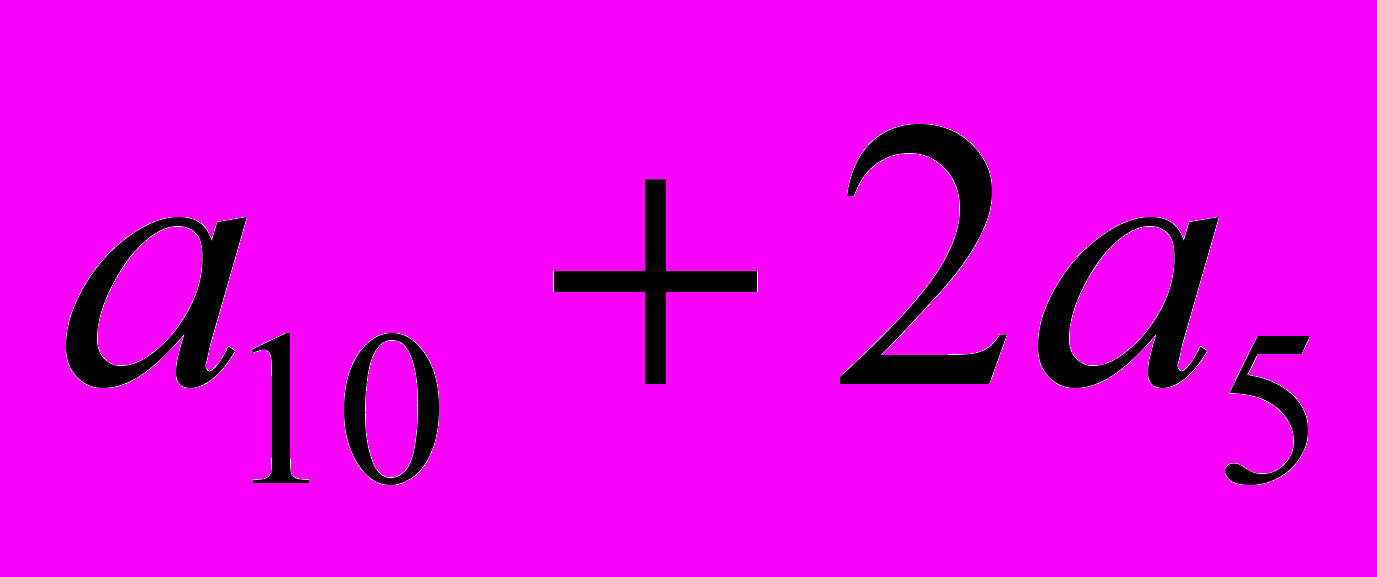не сущест­вует.


Для оставшегося, наиболее слож­ного, третьего случая (три разных многоугольника с n, т и k вершина­ми) уравнение (1) приводится к виду


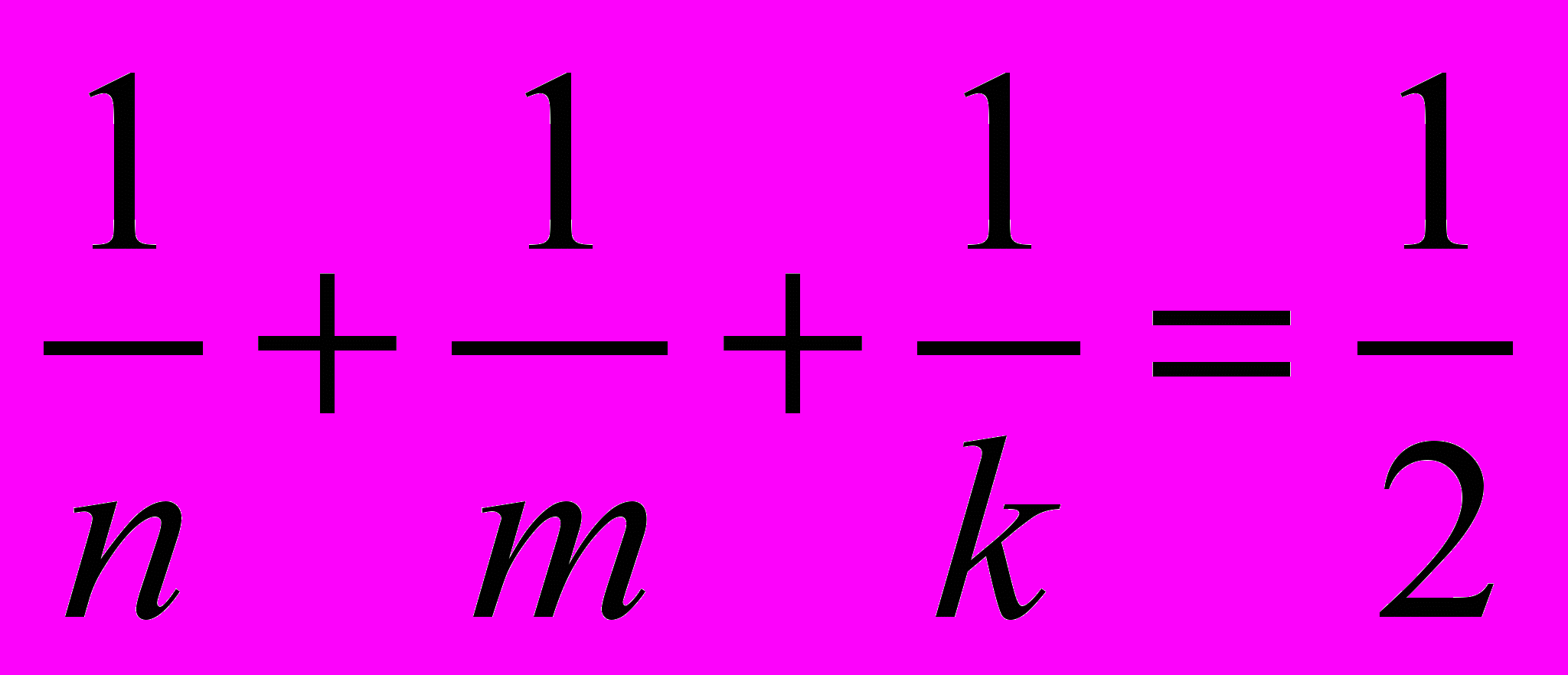. (2)


Чтобы не разбирать всех возможных числовых решений, нам будет нужна следующая

Лемма. В вершине правильного паркета не могут сходиться три раз­личных многоугольника, у одного из которых нечетное число сторон.


Доказательство.


Действительно, пусть такой пар­кет существует (рис. 10). Тогда вок­руг нечетноугольника оставшиеся т- и n-угольники должны идти че­редуясь. Поэтому при его обходе ря­дом окажутся два одинаковых мно­гоугольника, вопреки условию лем­мы.





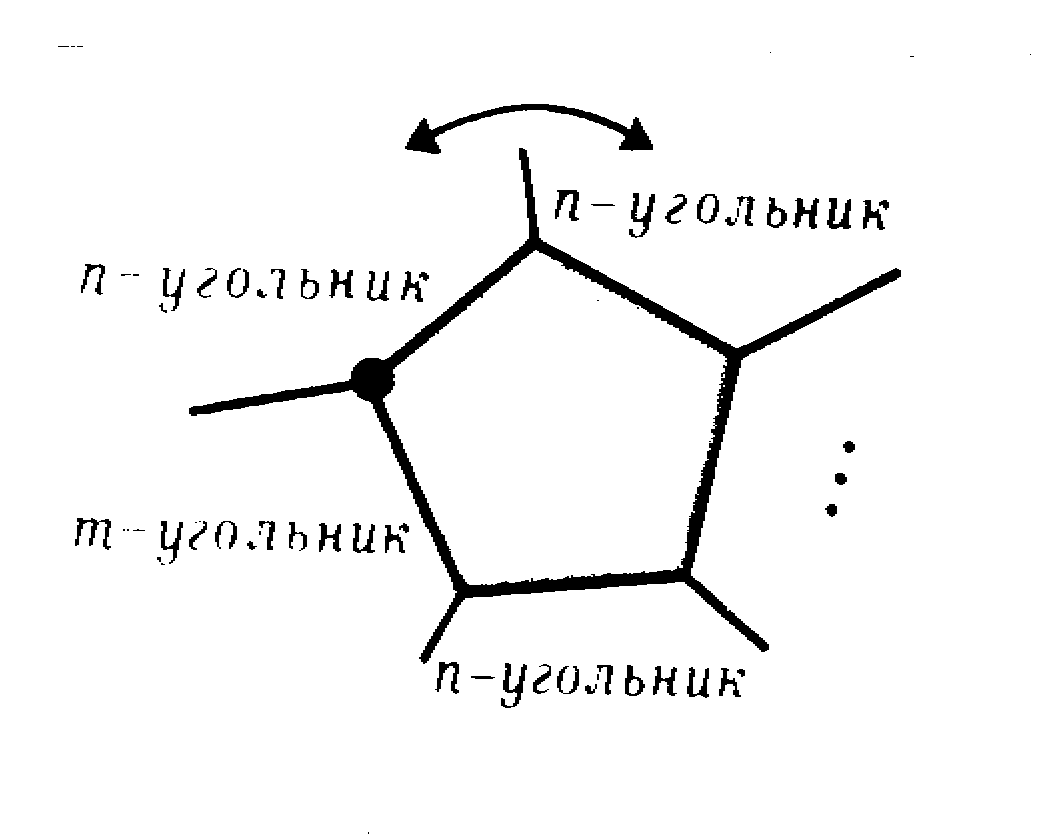
Рис.10


Благодаря лемме мы можем в (2) заменить k на 2k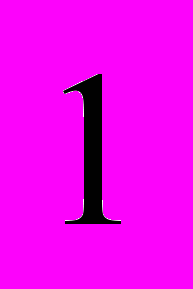, т на 2т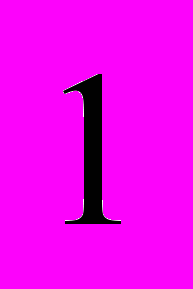,l на 21₁ и перейти к уравнению

.

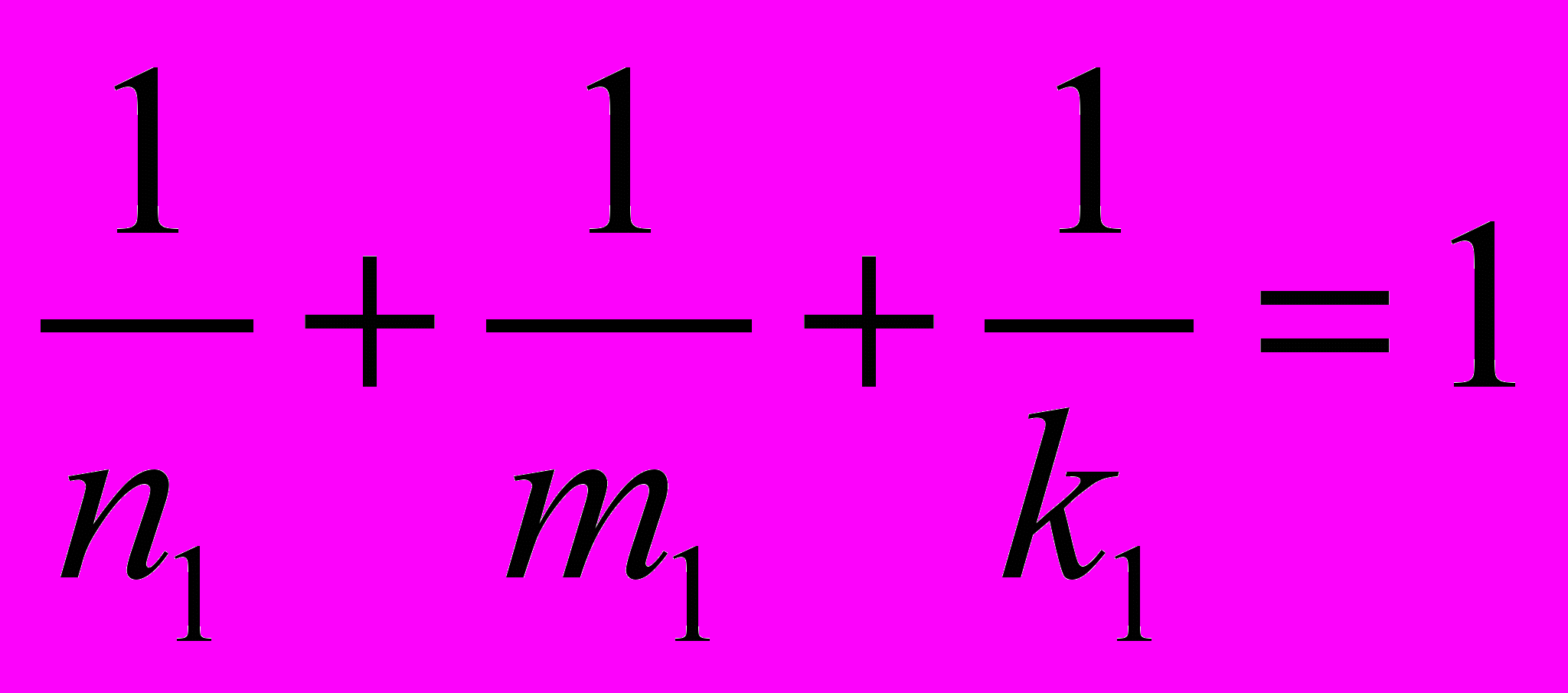Не нарушая общности, можно пред­положить, что k₁ < m₁ < n₁. Тогда


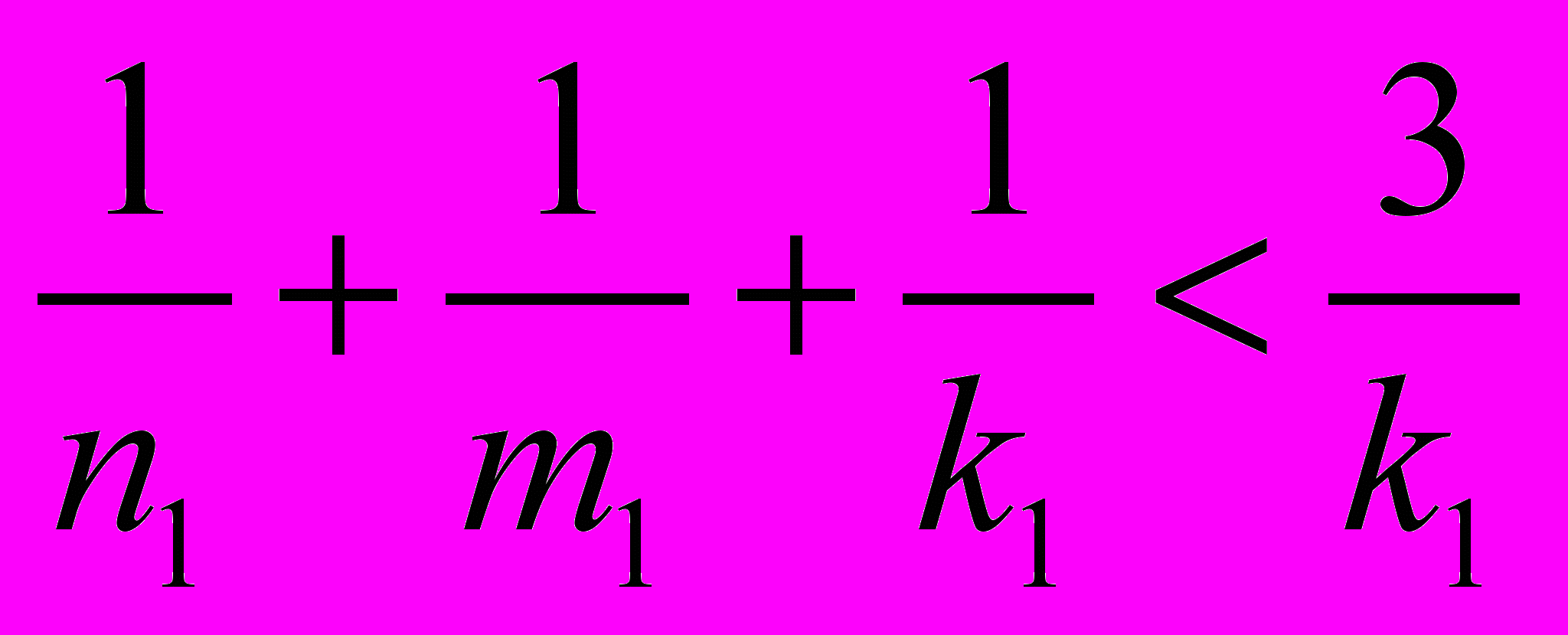, поэтому k₁= 2. Следовательно, 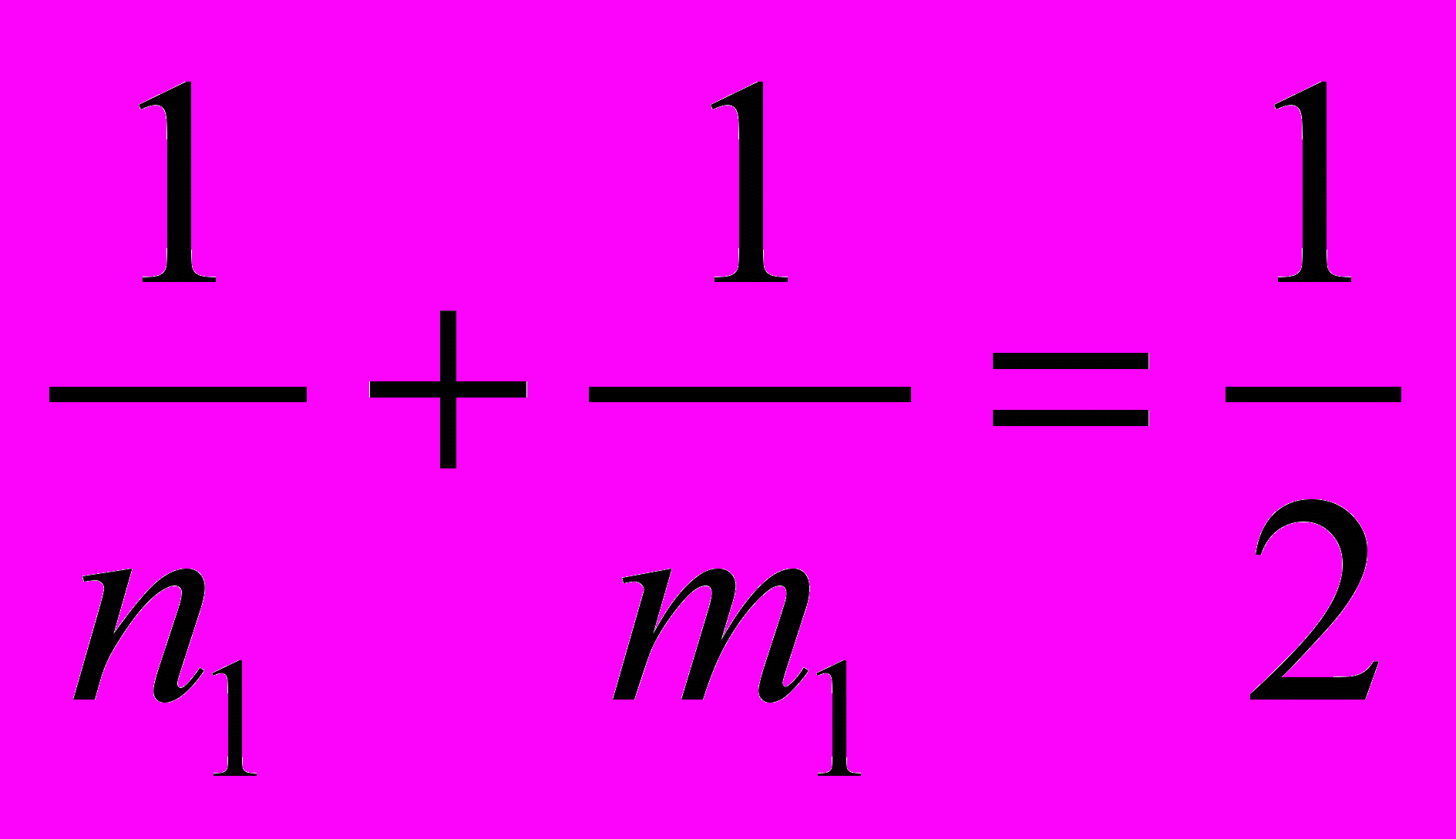, откуда


m₁ = 3, n₁ = 6 (если 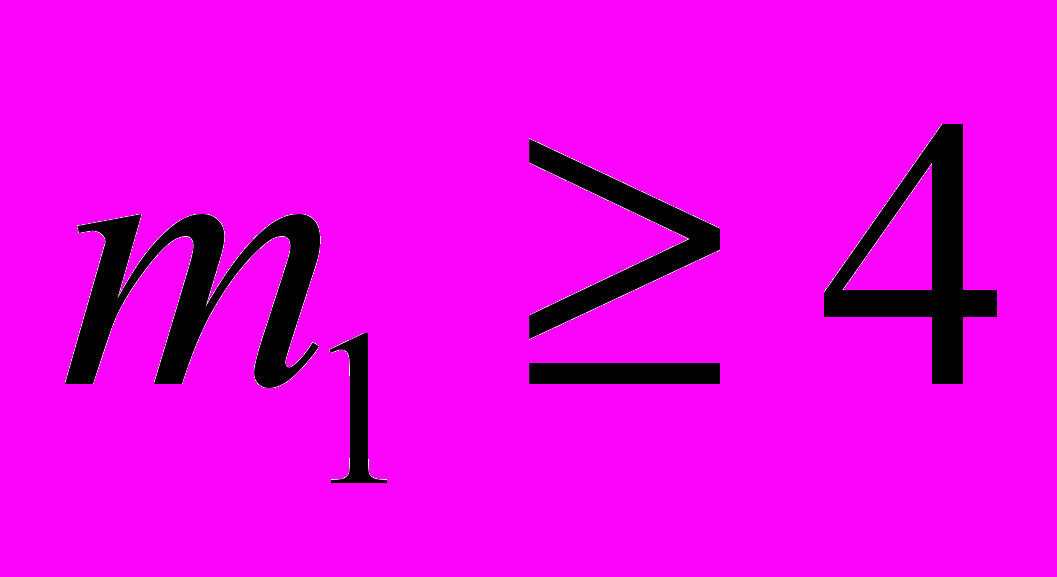, то 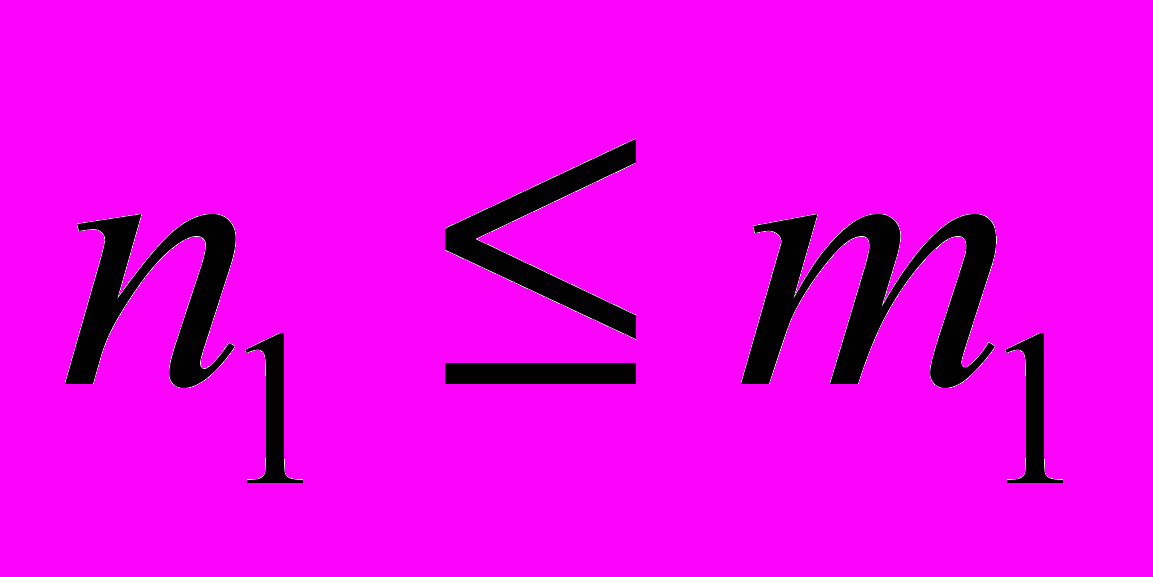). Полученное решение


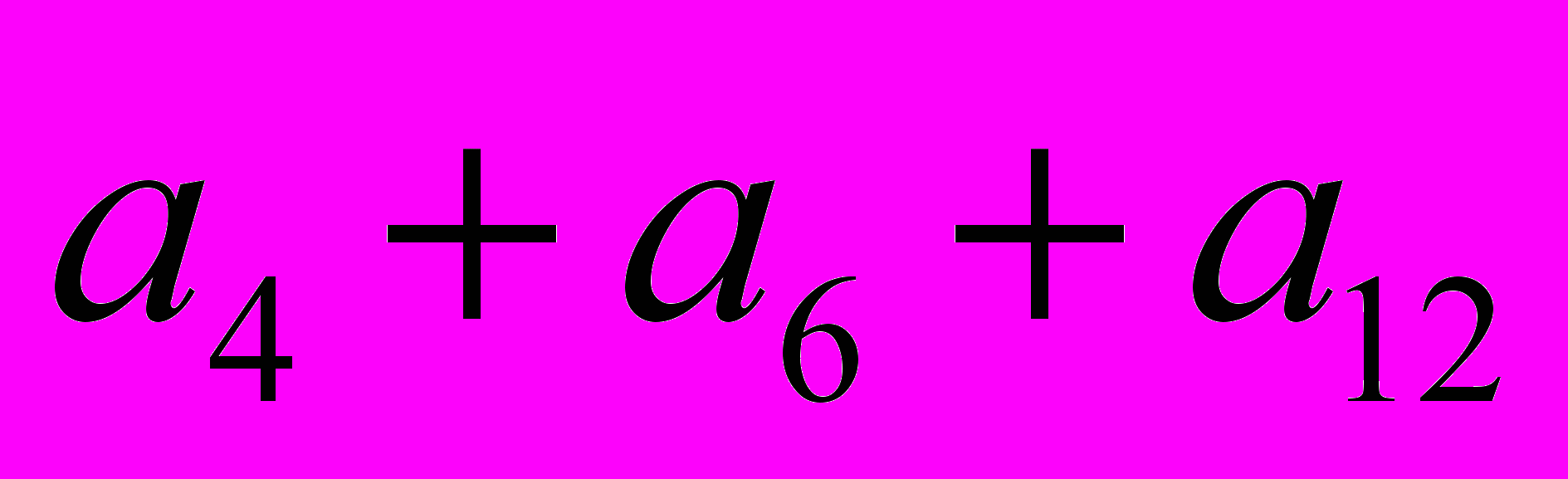дает нам очередной паркет (рис.11).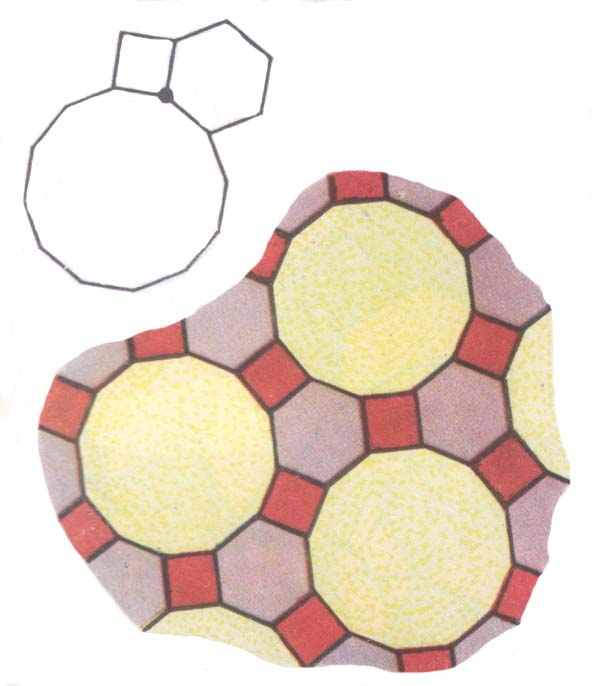





рис.11


Паркеты с четырьмя многоугольниками в вершине рассмотрены ранее, их три (рис.2, 3, 4).


Паркеты с пятью многоугольниками в вершине

В этом случае нужно найти решения уравнения

. (2)

Из него сразу видно, что j = k = l = 3 (мы считаем, что 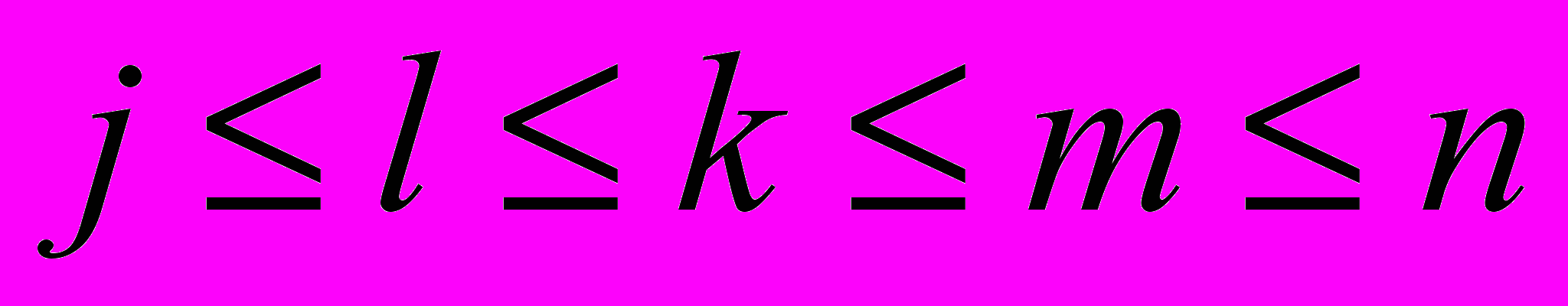). По­лучилось уравнение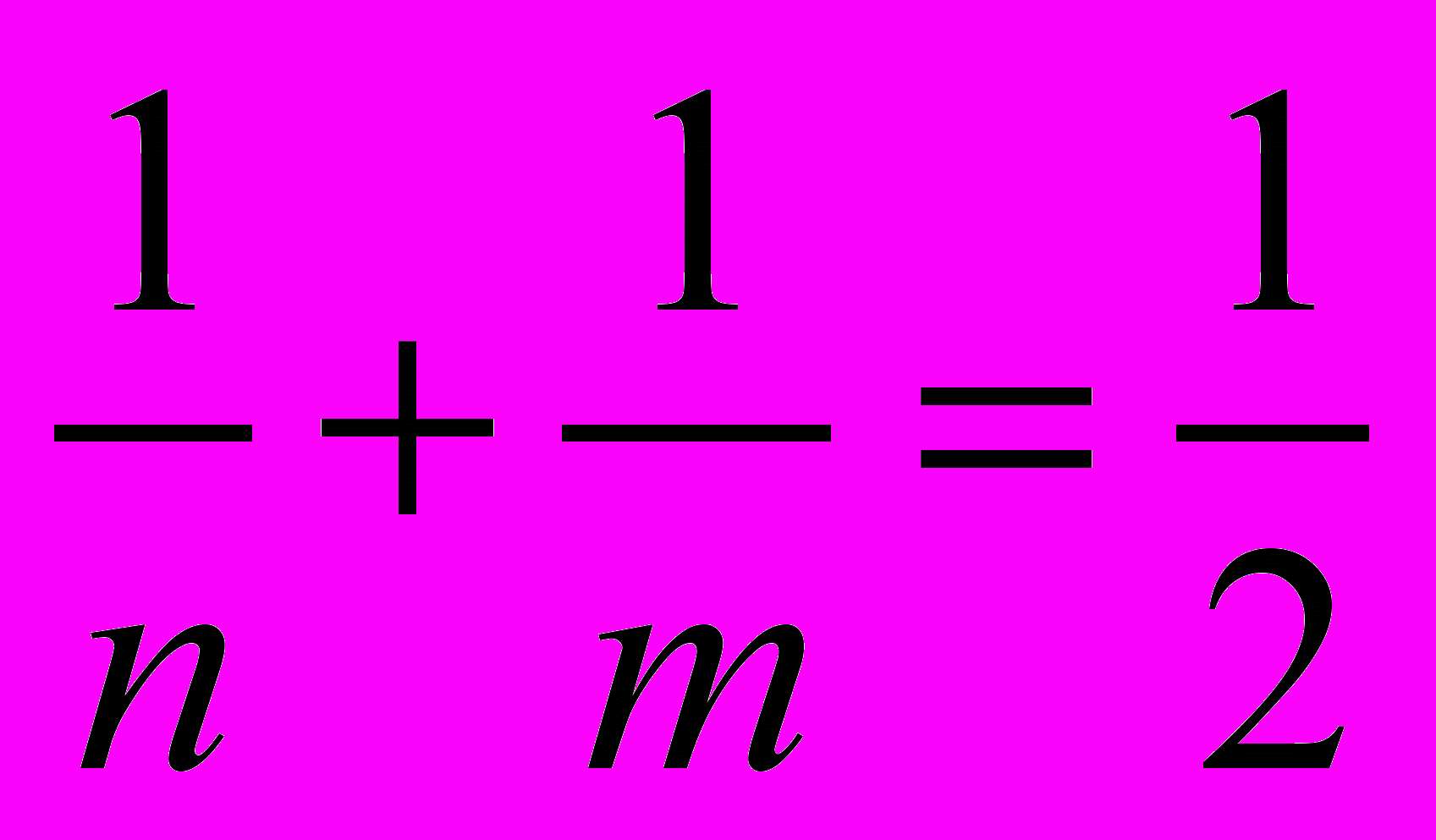

у которого два решения: т = 3, n = 6и m = 4, п = 4.

Остается теперь рассмотреть най­денные комбинаци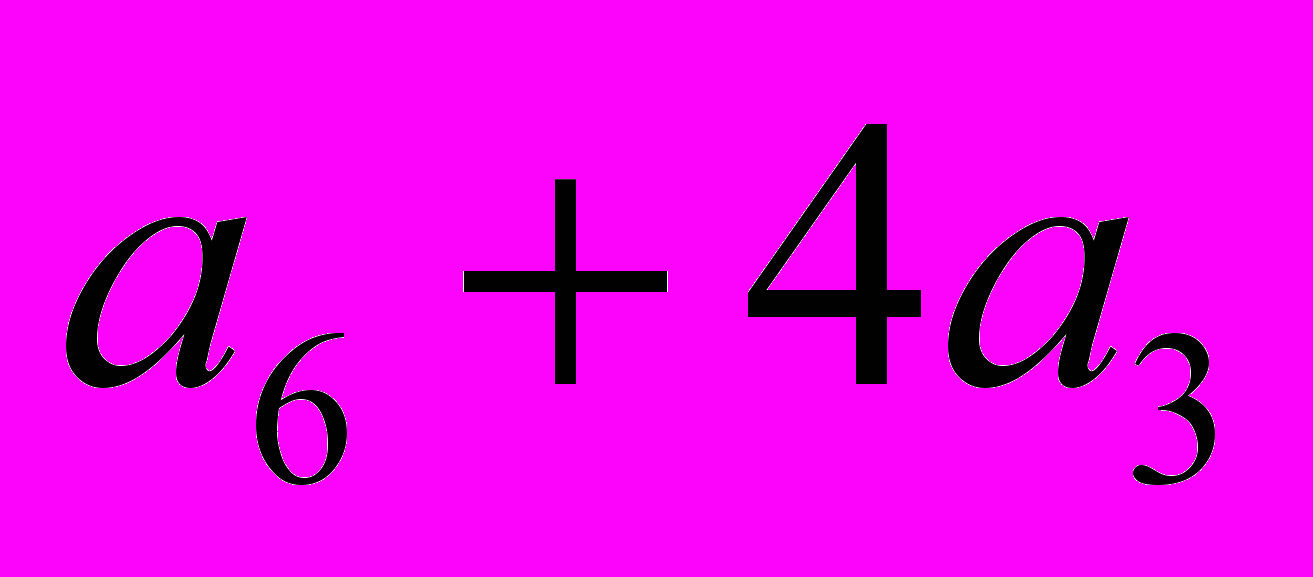и:

и .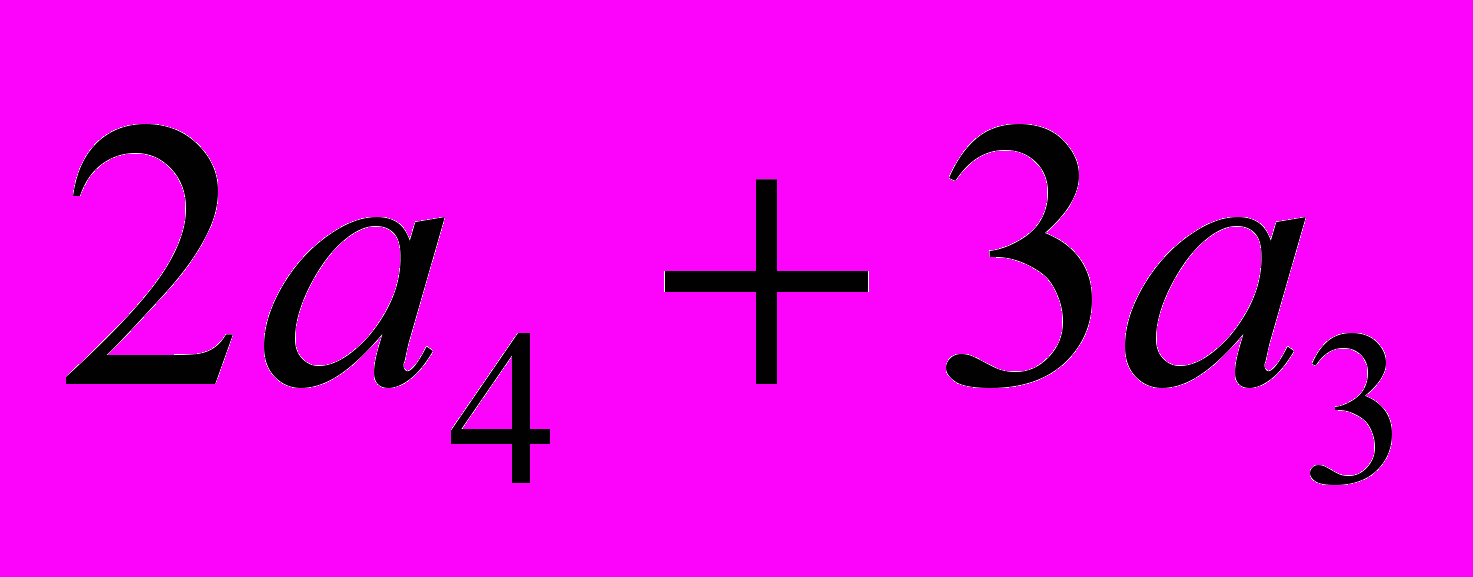

Первая из них дает единственный тип вершины и единственный правиль­ный паркет (рис. 12).





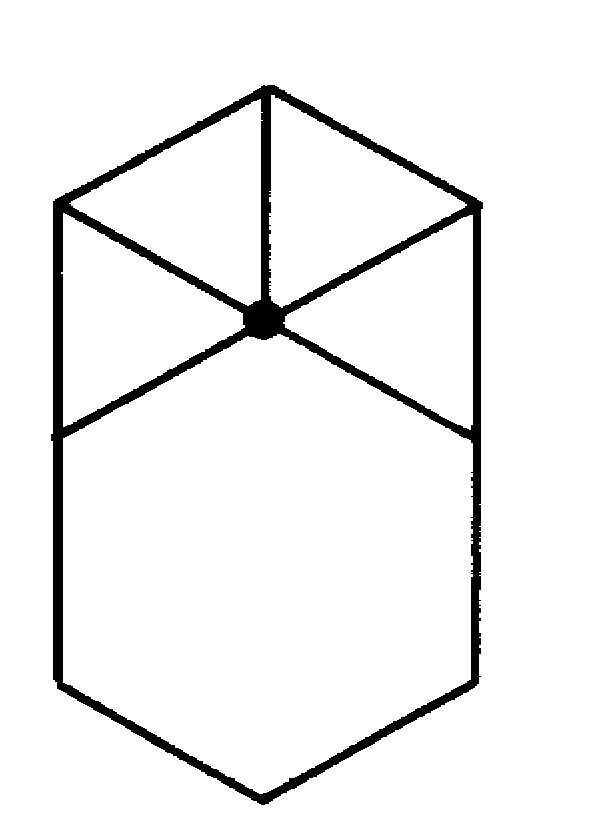
рис.12

Вторая комби­нация допускает две неэквивалент­ные вершины, причем каждая из них образует паркеты (рис. 13 и 14).




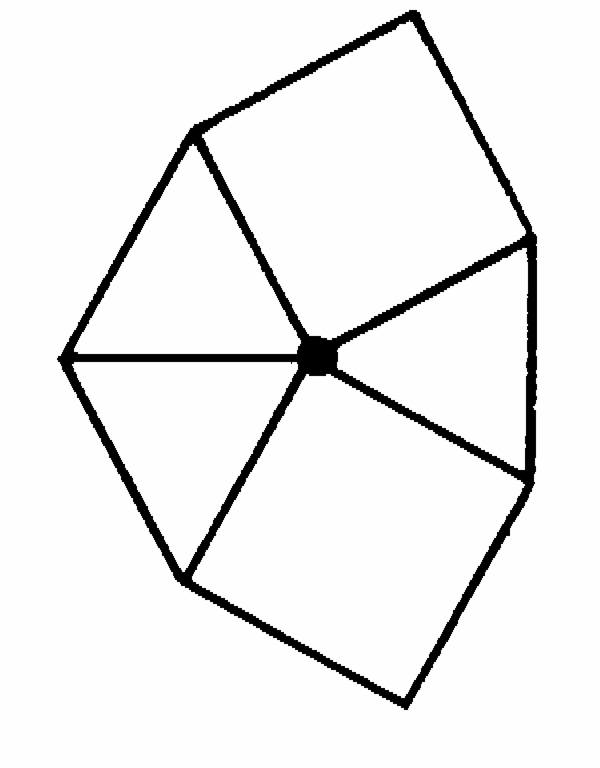
рис.13





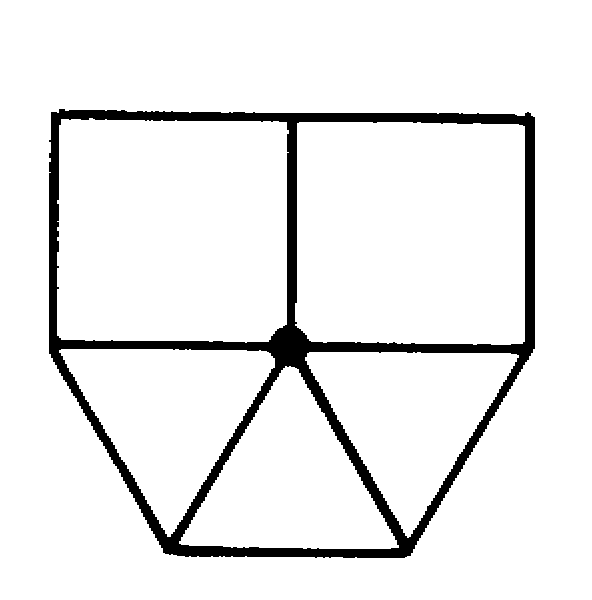
рис.14


Таким образом, «пятимногоугольных» паркетов три:

(); (); () .


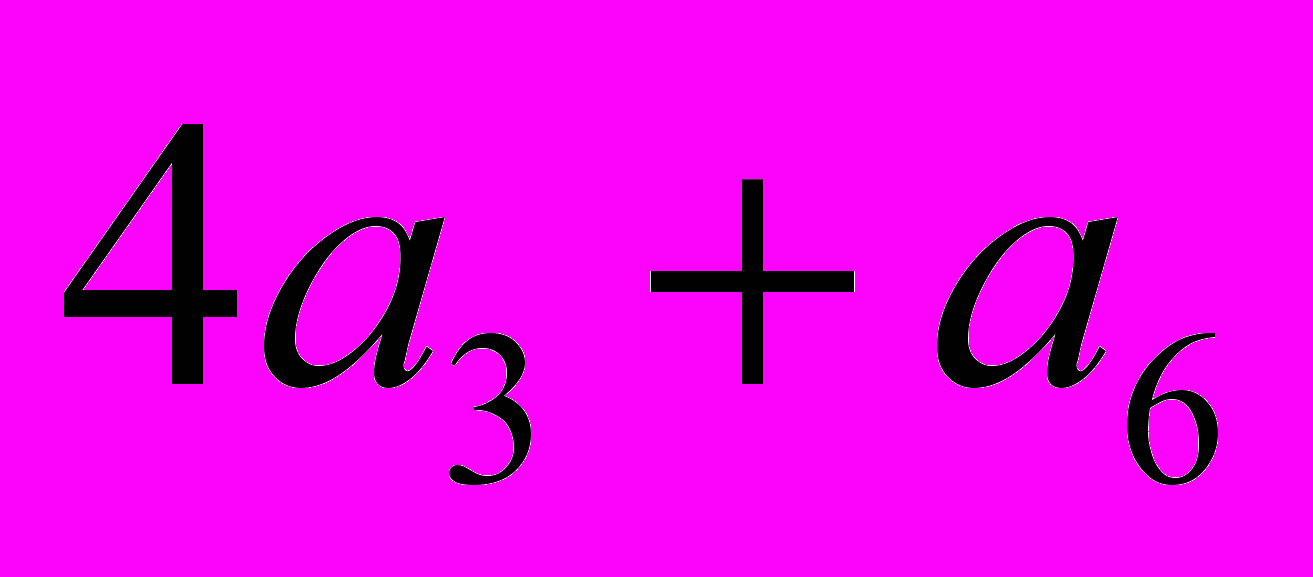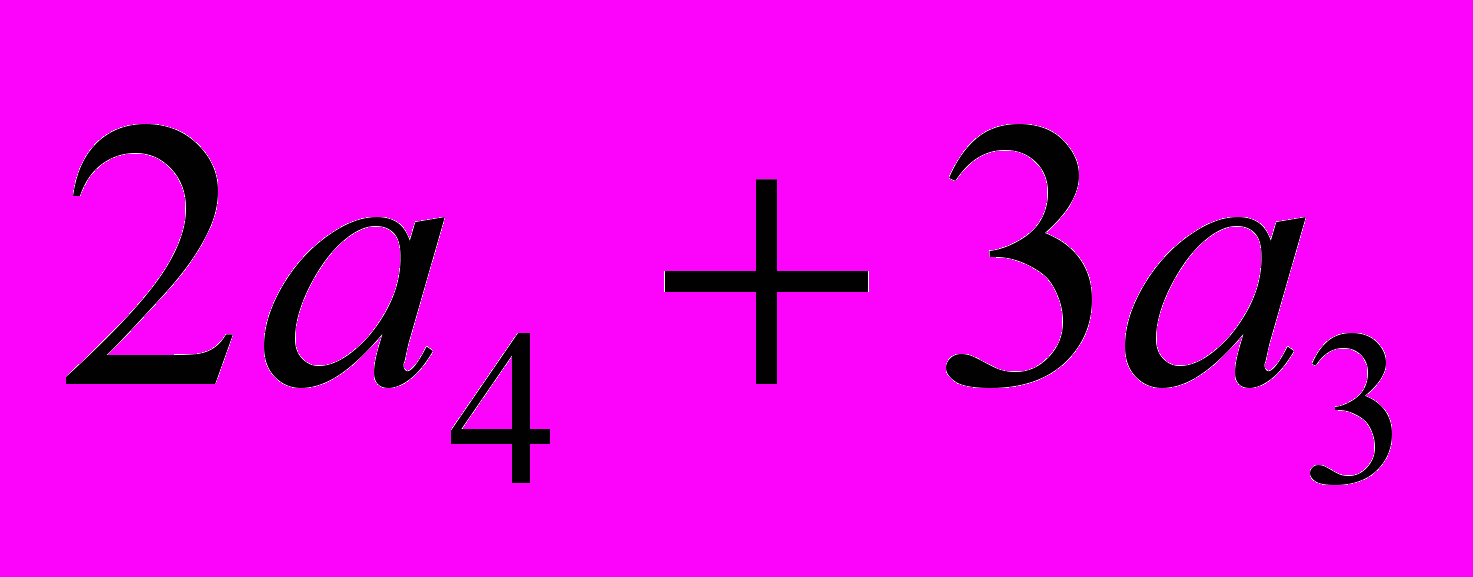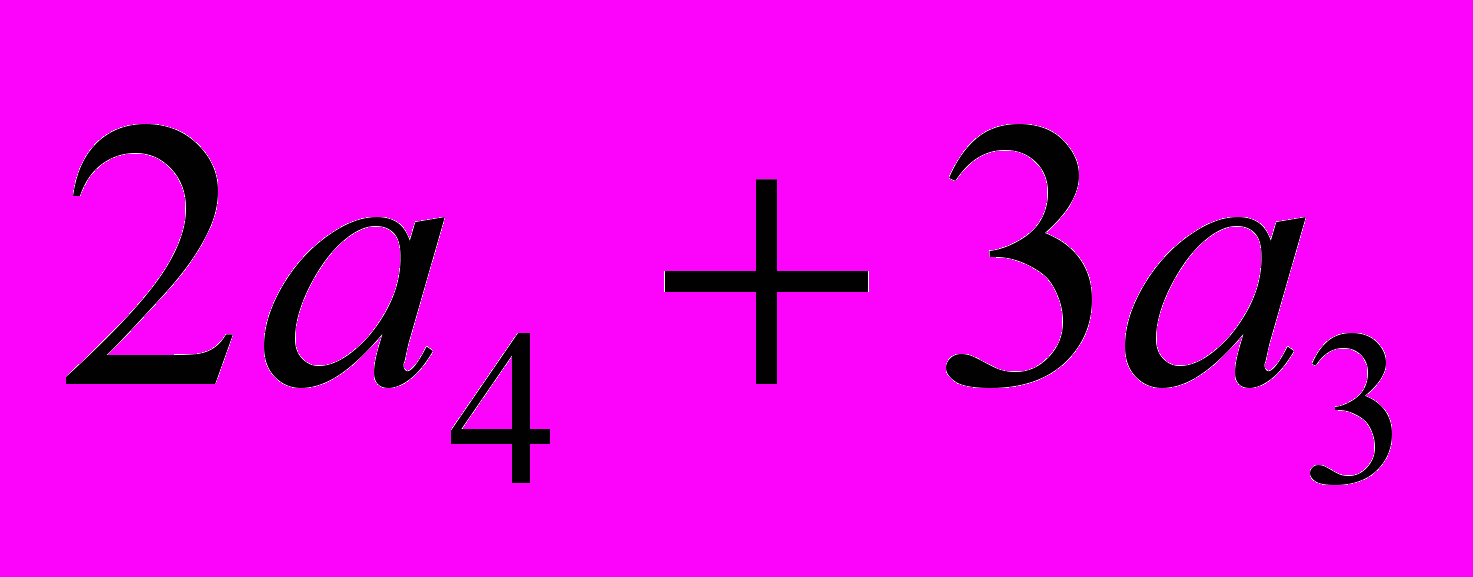Паркеты с шестью многоугольниками в вершине

Совершенно очевидно, что такой пар­кет (рис. 15)— единственный, по­лучающийся из комбинации .





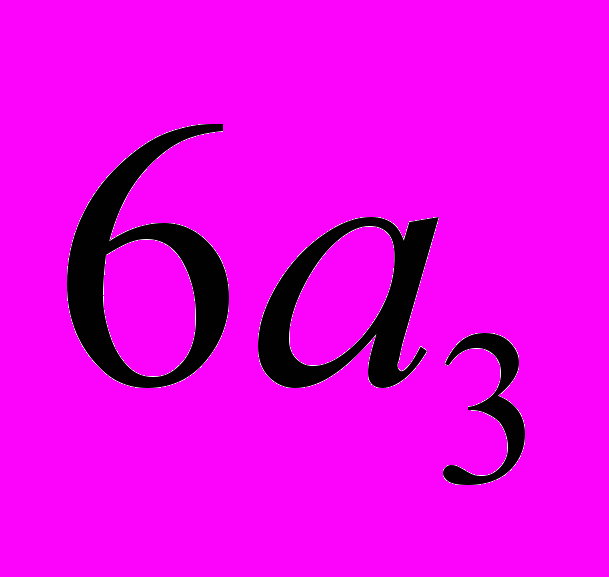рис.15


Перечисленными выше случаями исчерпывается все многообразие пра­вильных паркетов. Как видно из сказанного, общее число их — один­надцать.


Неправильные паркеты

Теперь займемся заполнением плоскости неправиль­ными одинаковыми многоугольниками и проверим ут­верждение о том, что для любого четырехугольника су­ществует паркет, состоящий из четырехугольников, рав­ных исходному. Иначе говоря, четырехугольником про­извольной формы можно заполнить всю плоскость без пробелов и наложений.

Возьмем произвольный четырехугольник ABCD (рис. 16) и рассмотрим симметричный ему относитель­но середины стороны АВ четырехугольник. Исход­ный четырехугольник ABCD обозначим цифрой 1, а симметричный — цифрой 2. Теперь четырехугольник 2 отразим симметрично относительно середины его стороны ВС. Полученный четырехугольник обозначим цифрой 3 и отразим его симметрично относи­тельно середины его стороны CD. Полученный че­тырехугольник обозначим цифрой 4. Четырехуголь­ники 1, 2, 3 и 4 примыкают к общей вершине углами А, В, С и D. А так как сумма углов четы­рехугольника равна 360°, то эти четырехугольники заполнят часть плоскости вокруг общей вершины. Такое же построение можно провести вокруг каждой новой вершины, что и даст искомое заполнение плос­кости.





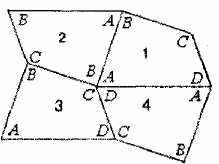
Рис.16


Отметим, что четырехугольник может быть и невы­пуклым. Соответствующий паркет приведен на рис. 17.




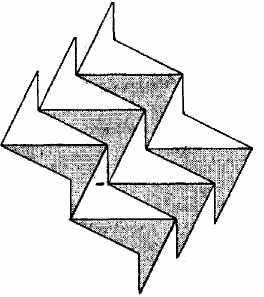
рис.17


Рассматривают и другое обобщение — пар­кеты из копий произвольного многоугольника, правильные «по граням» (т. е. допускающие самосовмеще-ния, которые переводят любую за­данную плитку в любую другую). Число таких паркетов — 46, включая и первые три (рис.1). Многоугольники, которые могут быть плитками в этих паркетах, называются планигонами. Ясно, что плоскость можно уложить копиями произволь­ного треугольника, но менее очевидно, что произвольный четырёхугольник — планигон (рис. 18, а). То же верно и для любого шести­угольника, противоположные стороны которого равны и параллельны (рис. 18, б).




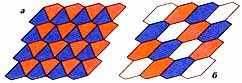
рис.18

Ещё пять примеров показаны на рис. 19.




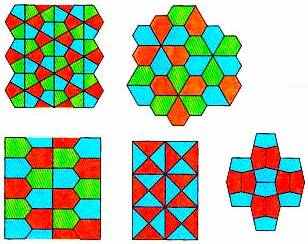
рис.19


Все рассмотренные выше паркеты перио­дичны, т. е. в каждом из них можно выделить (и даже многими способами) составленную из нескольких плиток область, из которой парал­лельными сдвигами получается весь паркет. Интерес учёных к таким конструкциям объяс­няется тем, что периодические замощения, особенно замощения пространства, моделиру­ют кристаллические структуры. Одно из простейших периодических замощений приведено на рисунке 20.



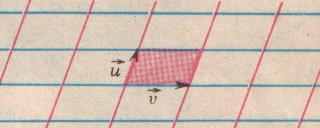
рис.20

Плоскость по­крыта параллелограммами, причем все параллелограммы одинаковы. Лю­бой параллелограмм этого замощения можно получить из розового парал­лелограмма, сдвигая последний на вектор 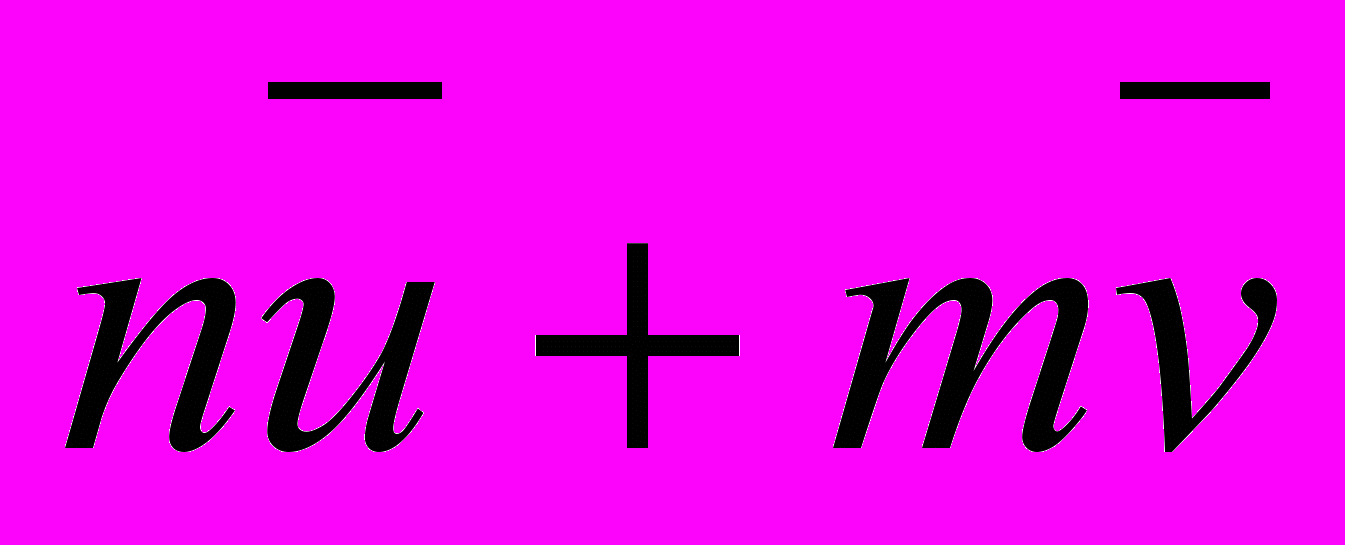(векторы и 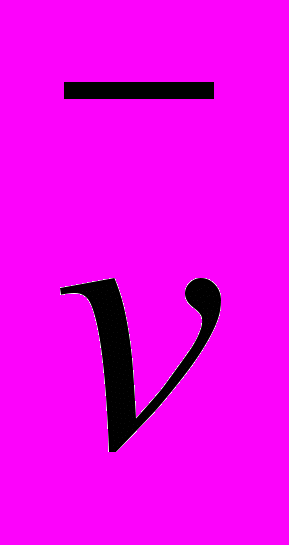оп­ределяются ребрами выделенного параллелограмма, п и т — целые чис­ла). Следует отметить, что все замо­щение как целое переходит в себя при сдвиге на вектор (или 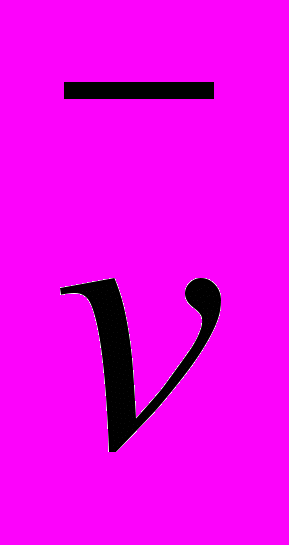). Это свой­ство можно взять в качестве определе­ния: именно, периодическим замоще­нием с периодами и 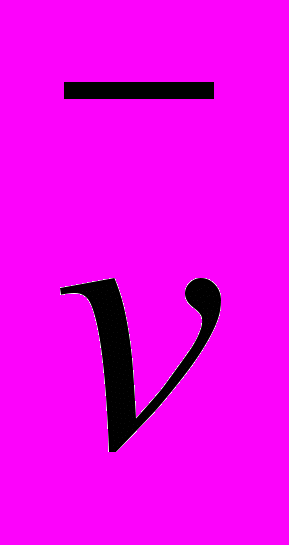назовем такое замощение, которое переходит в себя при сдвиге на вектор и на вектор 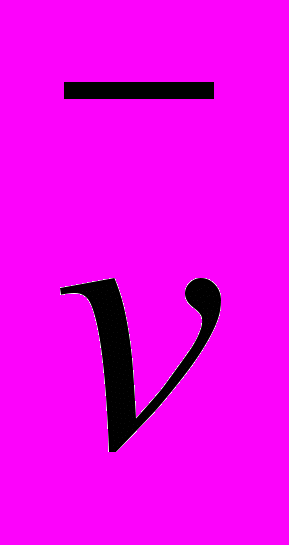. Как было показано выше, периодические замощения могут быть и весьма замысловатыми.


Существуют и интересные непериоди­ческие замощения плоскости. Долгое время предполагали, что не суще­ствует плиток и даже наборов из нескольких различных плиток, копии которых могли бы устилать плоскость только непериодически. Однако в середине 60-х гг. XX в. эта гипотеза была опровергнута, для чего понадобился набор из более чем 20 000 разных видов пли­ток. Шаг за шагом число плиток удавалось уменьшить, и, наконец, в 1974 г. англий­скому математику Роджеру Пенроузу удалось обойтись всего двумя очень простыми фигур­ками. Но при их выкладывании необходимо соблюдать некоторые простые правила соче­тания фигурок (вместо этого на краях фигурок делают специальные зазубрины, их совпадение обеспечивает соблюдение правил). Форма фи­гурок может быть различной, но все они связаны с правильным пятиугольником. Свойства этих за­мощений естественным образом обоб­щают свойства периодических.

Пример такого замощения приведен на рисунке 21. Рис. 21.

Вся плоскость покрыта ромбами. Между ромбами нет проме­жутков. Любой ромб замощения с по­мощью сдвигов и поворотов можно по­лучить всего из двух.

Это узкий ромб (36°, 144°) и широкий ромб (72°, 108°), показанные отдельно на рисунке 22. Длина сторон каждого из ромбов равна 1.





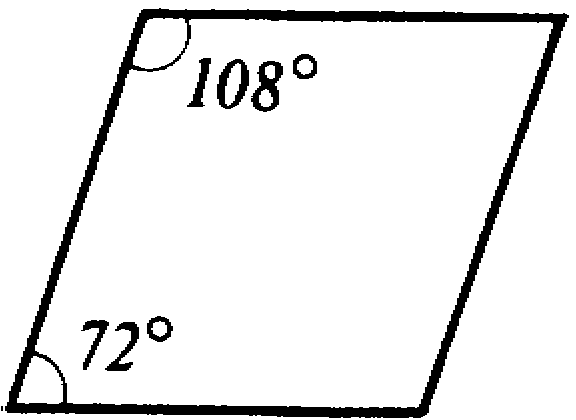
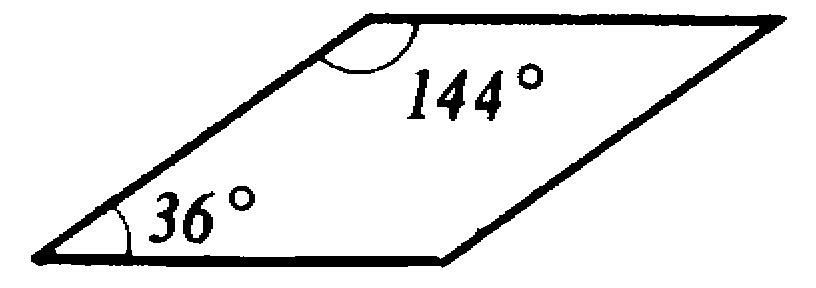
рис.22

Это замощение не является пе­риодическим — оно очевидно не пере­ходит в себя ни при каких сдвигах. Однако оно обладает неким важным свойством, которое приближает его к периодическим замощениям и застав­ляет называть его квазипериодическим. Дело в том, что любая конечная часть квазипериодического замоще­ния встречается во всем замощении бесчисленное множество раз.

Любопытно отметить, что это замо­щение обладает осью пятого порядка (переходит в себя при повороте на угол 72° вокруг некоторой точки), в то время как таких осей у периодиче­ских замощений не существует.


Другое квазипериодическое замо­щение плоскости, построенное Пенроузом, приведено на рисунке 23. Вся плоскость покрыта четырьмя много­угольниками специального вида. Это звезда, ромб, правильный пятиуголь­ник и «бумажный кораблик».





рис.23

Очень красивое спиральное замощение плос­кости девятиугольниками, придуманное в 1936 г. немецким математиком X. Фодербергом. рис.24

Оно составлено из большого числа конгруэнтальных девятиугольников. Эти девятиугольники невыпуклы, их неправильная форма напоминает латинскую букву S (рис.24). Оказывается, конфигурация может быть продолжена до бесконечности; при этом девятиугольники продолжают разворачиваться по

«двойной спирали» и заполняют всю плоскость (без пробелов и наложений друг на друга).

Но самое интересное заключается в том, что вскоре — уже через не­сколько лет после открытия квазипериодичес­ких замощений, вначале казавшихся не более чем игрой ума, — были получены вещества с квазипериодической структурой.


Для некоторых паркетов можно указать такие пре­образования плоскости, кото­рые переводят фигуры, сос­тавляющие паркет, друг в друга так, что сам паркет не меняется.

Для паркета, приведен­ного на рисунке 25, та­кими не меняющимися его преобразованиями будут по­ворот вокруг точки О на 60° и симметрия относительно пря­мой l.





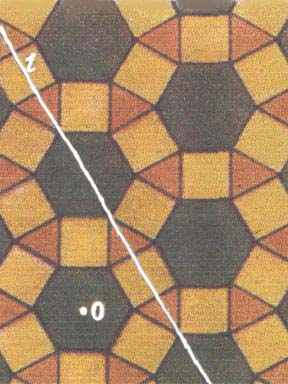
Рис. 25


Паркеты с древних времен привлекали к себе внимание людей. Им, в частности, посвящены многие замечательные картины голландского художника М. Эшера.





Рис. 26 М. Эшер. «Ящерицы»





Рис. 27 М. Эшер. «Летящие птицы».





Рис. 28 М. Эшер «Всадники»


А паркет на рисунке 29 замечателен тем, что одним из не меняющих его преобразований является увеличение вдвое всех рас­стояний относительно цент­ра (преобразование подобия). Поэтому, строго говоря, на рисунке изображено беско­нечное число уменьшающихся ящериц.





Рис. 29 М. Эшер. «Рептилии»


И, конечно, с паркетами мы встречаемся в повседневной жизни.


Список используемой литературы.

1. Геометрия: Учеб. для 7-9 кл. общеобразоват. Учреждений./ Смирнова И.М., Смирнов В.А..- М.: Просвещение, 2001.- с.175-179.
   
2. Гутенмахер В.Л.. Дроби - верблюды – паркеты./ Квант.-1989-№1- с.30-33.
   
3. Земляков А.. Орнаменты./ Квант.-1977-№3-с.20-27.
   
4. Колмогоров А. Н.. Паркеты из правильных многоугольников./ Квант.- 1970-№3-с.24-27.
   
5. Корепин В.Е.. Узоры Пенроуза и квазикристаллы./ Квант.-1987-№6- с.2-6.
   
6. Михайлов О.. Одиннадцать правильных паркетов./ Квант.-1979-№2- с.9-14.
   
7. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия 5-6 класс //Издательский дом «Дрофа» 1998 г. – с.142-147.
   
8. Энциклопедия для детей. Т. 11. Математика/ Глав. ред. Аксенова М.Д..-М.: Аванта+, 2002.- с.298-300.