Дисциплина: Инженерия знаний Доклад Генетические алгоритмы

Вид материала

Доклад

Содержание Рассмотрим общую задачу непрерывной оптимизации вида D - область поиска, D D и закодировать каждое возможное решение строкой s D нужно представить множество узлов пространственной решетки S 3. Т.е. отрезок [0,10] 1 (из всего 6), соответствуют комбинации: {0**, 1**, *0*, *1*, **0, **1}. 3. Функции пригодности 3.1. Функция пригодности в задаче о непрерывной оптимизации

Подобный материал:

• Дисциплина: Инженерия знаний Доклад Машинный перевод, 263.57kb.
• Генная инженерия как наука, 14.18kb.
• Доклад «Моделирование эволюции. Генетические алгоритмы», 75.42kb.
• Доклад на тему: "Модели эволюций и генетические алгоритмы", 155.74kb.
• Дисциплина «Инженерия знаний» Реферат Онтологии, 257.23kb.
• Доклад «Моделирование эволюции. Генетические алгоритмы», 108.9kb.
• Теоретические аспекты инженерии знаний, 680.47kb.
• Генетические алгоритмы. Мутация (обобщенный доклад), 124.68kb.
• Программа дисциплины «Нечеткая логика, генетические алгоритмы и экспертные системы, 228.23kb.
• Модели эволюции. Генетические алгоритмы, 361.44kb.

Рассмотрим общую задачу непрерывной оптимизации вида:

max f(x), где D = {x = (x₁, x₂, :, x_N) | x_i на [a_i, b_i], i=1, 2,:N}, где

x из D

f(x) - максимизируемая (целевая) скалярная многопараметрическая функция, которая может иметь несколько глобальных экстремумов;

прямоугольная область D - область поиска, D - подмножество R^N.

Предполагается, что о функции f(x) известно лишь то, что она определена в любой точке области D. Никакая дополнительная информация о характере функции и ее свойствах не учитывается в процессе поиска.

Под решением данного вида задачи понимается вектор x = (x₁, x₂, …, x_N). Оптимальным же решением задачи считается вектор x*, при котором целевая функция f(x) принимает максимальное значение. Исходя из того, что функция f(x) может иметь несколько глобальных экстремумов, оптимальное решение может быть не единственным.

В принятых ранее обозначениях под объектом понимается точка x в многопараметрическом пространстве O=D в R^N, а роль функции цели играет максимизируемая функция f(x).

Построение пространства представлений (S) под генетический алгоритм для задачи непрерывной оптимизации производится следующим образом.

Параметры x кодируются бинарной строкой s. Используя целевую функцию f(x) строится функция (s) - функция пригодности или, как она называется в генетических алгоритмах, функция приспособленности, отобразив, когда это необходимо, f на положительную полуось. Это делается для того, чтобы гарантировать прямое соотношение между значением целевой функции и приспособленностью решения, и затем такая модифицированная целевая функция рассматривается как функция приспособленности генетического алгоритма. Таким образом, каждое возможное решение s, имеющее соответствующую приспособленность (s), представляет решение x.

Обычно, переход из пространства параметров в хемминингово пространство бинарных строк осуществляется кодированием переменных x₁, x₂, …, x_N в двоичные целочисленные строки достаточной длины - достаточной для того, чтобы обеспечить желаемую точность. Желаемая точность в этом случае и будет тем отправным условием, которое определяет длину бинарных строк. Для этого пространство параметров должно быть дискретизировано таким образом, чтобы расстояние между узлами дискретизации соответствовало требуемой точности. Предположим, по условию задачи с функцией от двух переменных x₁ и x₂, определенной на прямоугольной области D = {0₁<1; 0₂<1}, требуется локализовать решение x* с точностью по каждому из параметров 10^-6. Для достижения такой точности пространство параметров дискретизуется равномерной сеткой с (b_i-a_i)/(10^-6)= 1/10^-6 = 1000000 узлами по каждой координате. Закодировать такое количество узлов можно l = 20 битами, где l определяется из условия 10⁶ < 2^l+1. Отсюда получается, что общая длина бинарной строки кодировки для двумерной задачи составит 2X20 = 40 бит.

При таком способе кодирования значения варьируемых параметров решений будут располагаться по узлам решетки, дискретизующей D. Соответственно, если кодировки двух решений будут совпадать, то будут совпадать и значения параметров обоих решений.

Во многих случаях такая естественная модель может оказаться неэффективной, т.к. она достаточно громоздка, а длинная кодировка повышает вероятность "преждевременной" сходимости, для борьбы с которой изобретаются различные уловки. Поэтому чаще всего применяется модификация символьной модели, которая позволяет, не применяя длинных кодировок, добиваться сравнимой точности.

Таким образом, чтобы провести дискретизацию пространства D и закодировать каждое возможное решение строкой s, "погружают" равномерную сетку в пространство параметров следующим образом.

Каждый интервал [a_i, b_i] разбивают на k отрезков равной длины:

h_i = (b_i - a_i) / k, i = 1, 2, …, N.

Благодаря этому, i-ый интервал [a_i, b_i] покрывается сетью s_i из (k+1) узла с постоянным шагом h_i:

x_i,j = a_i + j^.h_i, j = 0, 1, …, k.

Используя двоичный алфавит {0,1} каждому узлу сетки s_i присваивается уникальный бинарный код длины . Длина кода  выбирается таким образом, чтобы k < 2^. Доказано,что наиболее целесообразно и экономично использовать сетку с k = 2^-1.

Таким образом, чтобы построить символьную модель непрерывной оптимизационной задачи на гиперкубе D нужно представить множество узлов пространственной решетки S с помощью бинарных последовательностей (хромосом).

Отметим также, что здесь необходимо помнить, что генетический алгоритм оперирует строками фиксированной длины. Поэтому, чтобы применять генетический алгоритм к задаче, сначала выбирается метод кодирование решений в виде строки. Фиксированная длина (l-бит, l=*N) двоичной кодировки означает, что любая из 2^l возможных бинарных строк представляет возможное решение задачи. Такая кодировка соответствует разбиению пространства параметров на гиперкубы, которым соответствуют уникальные комбинации битов в строке - хромосоме. Для установления соответствия между гиперкубами разбиения области и бинарными строками, описывающими номера таких гиперкубов, используется либо обычная двоичная кодировка, либо рефлексивный код Грея. Код Грея предпочтительнее обычного двоичного тем, что обладает свойством непрерывности бинарной комбинации: изменение кодируемого числа на единицу соответствует изменению кодовой комбинации только в одном разряде.

Генетический алгоритм манипулирует имеющейся совокупностью бинарных представлений с помощью ряда генетических операторов для получения новых строк, т.е. перемещения в новые гиперкубики. Получив бинарную комбинацию для нового решения, формируется вектор (операция декодирования e^-1), со значениями из соответствующего гиперкуба, используя равномерное распределение.

Подводя итого можно сказать, что каждое решение генетического алгоритма в общем виде имеет следующую структуру:

• точка в пространстве параметров (фенотип): x = (x₁, x₂, : x_N) принадлежит D из R^N;
  
• бинарная строка s фиксированной длины, однозначно идентифицирующая гиперкуб разбиения пространства параметров (генотип): s = (₁, ₂, …, _l) принадлежит S, где S - пространство представлений - бинарных строк длины l.
  
• Скалярная величина , соответствующая значению целевой функции в точке х (приспособленность): = f(x).
  

В терминологии генетического алгоритма, такая структура называется особью. Предлагаемая модель обязательно включает в себя вектор со значениями из гиперкуба пространства параметров. Совокупность особей принято называть популяцией.


2.3. Конкретный пример задачи непрерывной оптимизации на основе символьной модели для генетического алгоритма.


Ознакомившись с общими положения в области постановки задачи поиска и общих подходов к решению задачи непрерывной оптимизации, приступим к рассмотрению конкретного примера.

В качестве примера рассмотрим непрерывную оптимизацию простой одномерной функции f(x) вида:

f(x)=10+x*sin(x),

определенной на отрезке [0, 10].

К
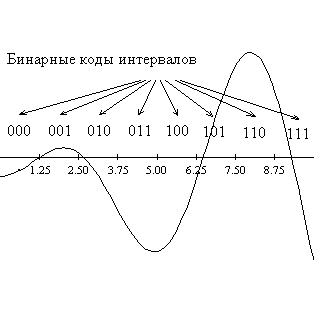
одирование будем осуществлять бинарными строками длины 3. Т.е. отрезок [0,10] нужно разбить на 2³ = 8 подинтервалов, каждому из которых будет соответствовать уникальная двоичная комбинация, получаемая переводом номера подинтервала, считая слева направо, в двоичную системы. Длина каждого такого интервала будет h=10:8=1.25. В результате получим следующее представление в евклидовом пространстве параметров:

Таким образом, как видно из выше приведенного рисунка, пространством поиска становится множество всех бинарных строк длины 3. Это пространство можно представить в виде трехмерного куба, вершинам которого соответствуют кодовые комбинации, расставленные так, что хэмминингово расстояние между смежными вершинами равно 1.


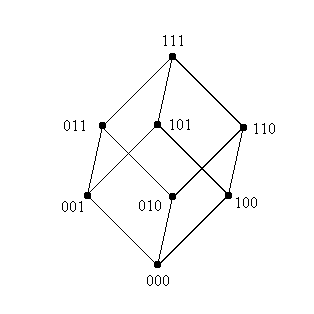
Таким образом, задача алгоритма поиска – непрерывной оптимизации - в том, чтобы, сводится к тому, чтобы, следуя некоторому правилу (кроссовер, мутация), перемещаться в новые вершины этого куба, что будет соответствовать исследованию новых подинтервалов в пространстве D.


2.4. Конкретный пример задачи непрерывной оптимизации на основе Шим для генетического алгоритма.


В выше описанном примере с одномерной функцией f(x)=10+x*sin(x) и 3-битными строками, как кажется на первый взгляд, вроде бы обрабатываются строки, хотя на самом деле при этом неявно происходит обработка шим (шима - это строка длины l (что и длина любой строки популяции), состоящая из знаков алфавита {0;1;*}, где {*} - неопределенный символ). Пространство поиска, как уже было выяснено выше, в этом случае представляет собой трехмерный куб. Поэтому интересным представляется графическая интерпретация шимы для рассматриваемой одномерной функции f(x)=10+x*sin(x).

Сначала исследуем шимы, чей порядок равен 3, т.е. все три бита в шаблоне определены. Очевидно, что, в данном случае, шимы порядка 3 будут соответствовать вершинам куба.

Шаблонам же порядка 2 соответствуют следующие комбинации:

2^o(H)C_l^l-o(H) = 2²C₃¹ = 12: {00*, 01*, 10*, 11*, 0*0, 0*1, 1*0, 1*1, *00, *01, *10, *11}.

Г

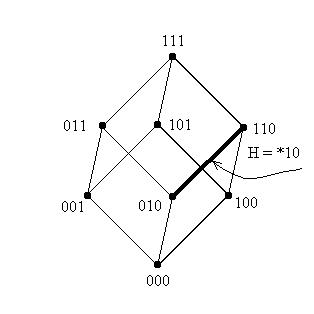
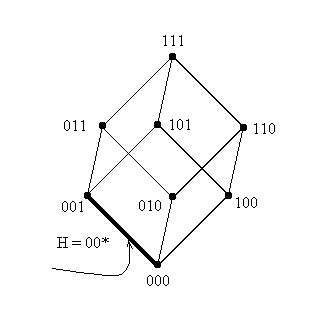
еометрически, все такие шаблоны описывают поверхности, размерность которых на единицу превосходит размерность точки - вершины куба, т.е. шимы порядка 2 длины 3 соответствуют ребрам куба. Так, графическая интерпретация шим H=(00*) и H=(*10) выглядит следующим образом:

Шаблонам же, чей порядок равен 1 (из всего 6), соответствуют комбинации:

{0**, 1**, *0*, *1*, **0, **1}.

В

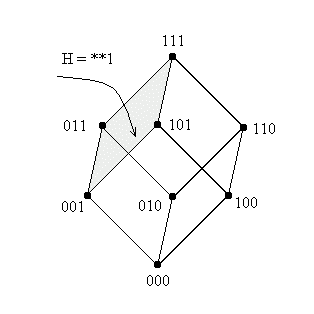
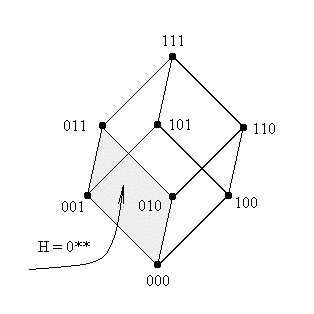
се они представляют поверхности, размерность которых на единицу больше размерности шим порядка 2, т.е. в нашем случае это грани куба. Вот, например, как выглядят шимы H=(**1) и H=(0**):


Если же рассматривать единственную шиму порядка 0, т.е. в ней нет определенных битов, то очевидно, что ее будет соответствовать весь куб

До сих про мы рассматривали то, как шимы представлены в пространстве бинарных строк. А чему они будут соответствовать в евклидовом пространстве параметров? Поскольку каждая шима определяет множество всех бинарных строк, имеющих в соответствующих позициях либо 0, либо 1, в зависимости от того, какой бит находится в соответствующей позиции самой шимы, то в пространстве параметров шиме будет соответствовать объединение подинтервалов, бинарные представления которых являются примерами этой шимы. Шимы с меньшим порядком будут задавать более многочисленное множество бинарных строк, поэтому в пространстве параметров они смогут охватить большую область.

3. Функции пригодности


Прежде всего необходимо отметить, что функция пригодности очень важна для реализации генетического алгоритма, т.к. каждая особь из совокупности “особей”, с которой работает генетический алгоритм, оценивается мерой ее "приспособленности" согласно тому, насколько "хорошо" соответствующее ей решение задачи. Наиболее приспособленные особи получают возможность "воспроизводит" потомство с помощью "перекрестного скрещивания" с другими особями популяции. Это приводит к появлению новых особей, которые сочетают в себе некоторые характеристики, наследуемые ими от родителей. Наименее приспособленные особи с меньшей вероятностью смогут воспроизвести потомков, так что те свойства, которыми они обладали, будут постепенно исчезать из популяции в процессе эволюции. Таким образом, от значения функции пригодности напрямую зависит “выживаемость” любого рассматриваемого объекта – потенциального решения – из области объектов определенной задачи.


3.1. Функция пригодности в задаче о непрерывной оптимизации


Как уже отмечалось выше, для реализации алгоритма поиска (генетического алгоритма для решения задачи о непрерывной оптимизации – задача поиска оптимума) в пространстве представлений - S - вводится функция оценки представлений, определенная на элементах из множества O - множество объектов или, так называемая, область поиска оптимального решения:

: S -> R,

где R – множество вещественных чисел.

С помощью  можно определить порядок в S таким образом, чтобы представителям лучших объектов в смысле f - функции цели - соответствовало большее значение . Т.е. если для любых двух объектов o₁, o₂ из O в S определены различными представителями s₁=e(o₁) и s₂=e(o₂), s₁ не равно s₂ и если f(o₁)>f(o₂), то (s₁)>(s₂). В общем случае функцией (s) может быть любая функция M, удовлетворяющая этому условию.

(s) = M(f(e^-1(s))) или (s) = f(e^-1(s))

Данная функция строится на основе целевой функции – f(x). При этом, когда это необходимо, f отображается на положительную полуось, т.е. скалярная величина , соответствующая значению целевой функции в точке х (приспособленность) – это: = f(x). Это делается для того, чтобы гарантировать прямое соотношение между значением целевой функции и приспособленностью решения, и затем такая модифицированная целевая функция рассматривается как функция приспособленности генетического алгоритма. Таким образом, каждое возможное решение s, имеющее соответствующую приспособленность (s), представляет решение x.


Для выше описанного примера, в котором рассматривалась задача непрерывной оптимизации простой одномерной функции f(x) вида:

f(x)=10+x*sin(x),

определенной на отрезке [0, 10], скалярная величина функции пригодности – пригодность -  - равна:

=f(x)=10+x*sin(x), а наилучшей степенью пригодности считается max()=max(f(x)), т.к.

(s)=f(e^-1(s))=e^-1(s)+ e^-1(s)*sin(e^-1(s)),

где s  S={000, 001, 010, 011, 100, 101, 110, 111}, s – это узел сетки дискретизации.


3.2. Функция пригодности в задаче оптимизации параметров пид-регулятора



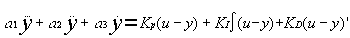
Рассмотрим модель замкнутой системы с объектом третьего порядка и ПИД-регулятором. Она описывается дифференциальным уравнением

правая часть которого описывает модель объекта третьего порядка, а левая - ПИД-регулятор. Решение этого уравнения при единичном скачке на входе определяет кривую переходного процесса в системе. Для оценки качества переходного процесса в инженерной практике нередко используются следующие параметры

• t_н - время нарастания, т.е. время, за которое переменная y(t) возрастает с 0.1 до 0.9 установившегося значения,
  
• S - выброс (максимальное превышение сигналом y(t) единичного уровня),
  
• t
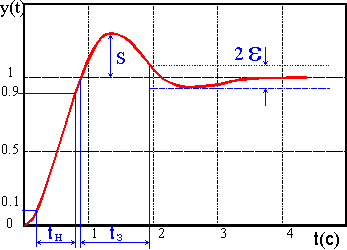
  _з - время затухания переходного процесса (время между моментом первого достижения сигналом y(t) единичного уровня и моментом, начиная с которого значения y(t) остаются внутри интервала [1,],  - некоторая постоянная).
  

Оценка переходной кривой по упомянутым выше параметрам (t _н, S, t _з) представляет собой многокритериальную задачу.

В
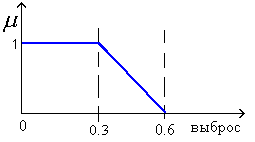
ведем лингвистические переменные: время нарастания, время затухания, выброс и определим на каждой из них терм - приемлемое значение как нечеткое множество с функцией принадлежности (x) трапецеидального вида.

К
онкретные значения параметров переходной кривой (t _н, S, t _з) могут быть охарактеризованы степенью принадлежности (x) каждого из параметров к терму - приемлемое значение, - соответствующей лингвистической переменной. В рассматриваемом нами случае представляется естественным принять в качестве оценки переходной кривой функцию

Структура простого генетического алгоритма для этого случая выглядит следующим образом. На протяжении к-ой итерации ГА сохраняет популяцию потенциальных решений (хромосом)



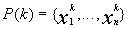
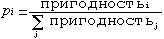
Каждое решение Xⁱ_r оценивается некоторой мерой пригодности (fitness). Затем формируется новое поколение ((k+1)-итерация) путем селекции решений в соответствии с мерой пригодности. Вероятность быть отобранным в следующее поколение выражается в виде

Некоторые решения из следущего поколения подвергаются действию генетических операторов (кроссовера и мутации) для образования новых решений. Кроссовер комбинирует характеристики пары решений для получения двух решений - потомков путем взаимного обмена сегментами родительских хромосом. Мутация произвольно изменяет один или несколько генов в выбранной хромосоме. Алгоритм завершает работу при достижении заданных значений пригодности либо по исчерпанию числа поколений.

Для оценки эффективности предложенного метода проведен подбор коэффициентов ПИД-регулятора в системе с объектом третьего порядка (T1=0.1с, T2=0.2с, T3=0.7с). Приняты трапецеидальные функции принадлежности терма приемлемое значение, характерные значения которых Х1 и Х2 для параметров t _н, S, t _з приведены в таблице:

	Х1	X2
t н	0.4	0.8
S	0.3	0.6
t з	1.5	2.0

В эксперименте использован генетический алгоритм со следующими параметрами:

• размер популяции - 10;
  
• число поколений - 20;
  
• вероятность кроссовера - 0.9;
  
• вероятность мутации - 0.001;
  
• точность вычислений - 0.0001.
  

Использовано представление возможного решения в виде хромосомы с тремя генами, соответствующими K_p, K_I и K_D. В отличие от простого генетического алгоритма в эксперименте использовано свойство элитизма, обеспечивающее обязательное сохранение в следующем поколении решения с наибольшей пригодностью из текущего поколения. Графики значений пригодности лучшего решения