Дисциплина: Инженерия знаний Доклад Генетические алгоритмы

Вид материала

Доклад

Подобный материал:

• Дисциплина: Инженерия знаний Доклад Машинный перевод, 263.57kb.
• Генная инженерия как наука, 14.18kb.
• Доклад «Моделирование эволюции. Генетические алгоритмы», 75.42kb.
• Доклад на тему: "Модели эволюций и генетические алгоритмы", 155.74kb.
• Дисциплина «Инженерия знаний» Реферат Онтологии, 257.23kb.
• Доклад «Моделирование эволюции. Генетические алгоритмы», 108.9kb.
• Теоретические аспекты инженерии знаний, 680.47kb.
• Генетические алгоритмы. Мутация (обобщенный доклад), 124.68kb.
• Программа дисциплины «Нечеткая логика, генетические алгоритмы и экспертные системы, 228.23kb.
• Модели эволюции. Генетические алгоритмы, 361.44kb.

(1) и средней пригодности в каждом поколении (2) выглядят следующим образом:






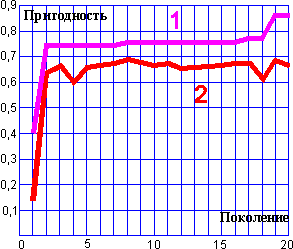
3.3. Функция пригодности в задаче оптимального дихотомического разбиения графа

Вообще, как говорилось ране, при взаимодействии особи с внешней средой ее генотип E() порождает совокупность внешне наблюдаемых количественных признаков (характеристик _i), включающих степень приспособленности () особи к внешней среде и ее фенотип ().

Приняв в качестве внешней среды критерий оптимальности 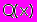, мы можем говорить, что степенью приспособленности () каждой особи является численное значение функции 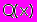, вычисленное для допустимого решения 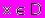с именем . В общем случае степень приспособленности 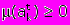можно задать с помощью следующего выражения:

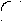
		Q2(x), если решается задача максимизации функции ;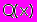
()=
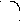		1/(Q2(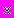)+1), если решается задача минимизации функции ;

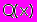Из данного выражения следует, что чем больше численное значение степени приспособленности (), тем лучше особь приспособлена к внешней среде. Следовательно, цель эволюции особей заключается в повышении их степени приспособленности.

Фенотипом () особи в рамках экстремальной задачи

,

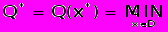
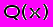являются численные значения вектора управляемых переменных 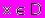и соответствующих ему характеристик .

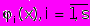Для задачи оптимального дихотомического разбиения графа G, сформулированной как экстремальная задача, в качестве особи выступает конкретное дихотомическое разбиение (Х₁,X₂), удовлетворяющее определенным условиям. В этом случае геном является бит в бинарной строке Е(Х₁,X₂), который определяет, к какой части разбиения Х₁ или Х₂ принадлежит вершина графа G, соответствующая этому биту. Линейная последовательность всех n битов составляет хромосому, в которой каждый ген определяет принадлежность вершины, соответствующей этому гену, одной из частей Х₁ или Х₂. Введенные гены обладают свойством диморфизма, т.к. каждый ген может иметь только две различающиеся формы аллели: “1”, если вершина х_i принадлежит части Х₁ и “0”, если вершина х_i принадлежит части Х₂.

Степень приспособленности () в данном случае просто совпадает с критерием оптимальности F(Х₁,X₂) - общей суммой весов ребер, входящих в подграфы G₁ и G₂: () = F(Х₁,X₂).