Курсовая работа по статистике на тему: «14. Виды рядов распределения. 24. Мода и медиана.»

Вид материала

Курсовая

Содержание Статистика – это самостоятельная общественная наука, которая изучает Ранжированный ряд Дискретный ряд Интервальный вариационный ряд Частота повторения 24. Мода и медиана 24.3. Соотношение между средней величиной, медианой и модой. 2.1 Задача №1 2.2 Задача №2 2.3 Задача №3 2.4 Задача №4 2.5 Задача №5 2.6 Задача №6 2.7 Задача №7 2.8 Задача №8 2.9 Задача №9 2.10 Задача №10 Товарооборот в фактических ценах Задача №3 Задача №10 ... Полное содержание

Подобный материал:

• Курсовая работа по дисциплине «Статистика» на тему "Аналитические показатели рядов, 396.09kb.
• Исследование по результатам решенных задач «Копилка методов и советов Мода Исследование, 391.12kb.
• Задачи и виды группировок Статистические ряды распределения Абсолютные показатели, 18.57kb.
• Курсовая работа по статистике на тему: «Использование статистических методов при анализе, 392.39kb.
• Курсовая работа по статистике на тему: «Использование статистических методов при анализе, 392.06kb.
• Понятие статистики. 2 История математической статистики. 3 Простейшие статистические, 108.95kb.
• Курсовая работа на тему "Прогнозирование временных рядов", 149.68kb.
• 1 курс Группа 17 Курсовая работа по дисциплине «Экономическая теория» на тему №67:, 303.3kb.
• Курсовая работа по дисциплине «Финансы предприятий» на тему «Анализ использования прибыли, 355.67kb.
• Курсовая работа на тему: «Лидерство в управлении», 508.7kb.

МЭИ ИББ

Курсовая работа по статистике

на тему:

«14.Виды рядов распределения.

24.Мода и медиана.»


Выполнил студент группы ИБ-03-05:

Чувиков Александр Владимирович


Проверила:

Демченко Наталья Леонидовна


Москва 2006

Содержание

Введение…………………………………………………………………3

Глава 1. Теоретическая часть.

14. Виды рядов распределения.

14.1. Виды рядов распределения……………………………………..5

14.2. Ранжированный ряд……………………………………………..5

14.3. Дискретный ряд………………………………………………….6

14.4. Интервальный вариационный ряд……………………………7

14.5. Частота повторения……………………………………………...8

24. Мода и медина.

24.1. Мода………………………………………………………………..9

24.2. Медиана…………………………………………………………..10

24.3 Соотношение между средней величиной, медианой и модой……………………………………………………………………12

Глава 2. Расчётная часть.

Задачи №1-№10……………………………………………………13-23

Заключение……………………………………………………………24

Список использованой литературы………………………………..27

Введение.

Статистика – это самостоятельная общественная наука, которая изучает

количественную сторону массовых явлений и процессов, исследует

закономерности общественного развития в конкретных условиях, места и

времени. Статистика изучает статистические закономерности, которые в

отличие от динамических проявляются только в массовых процессах.

Данная курсовая работа состоит из двух глав: теоретической и расчётной.

В теоретической главе я рассмотрел два вопроса, которые кажутся мне наиболее важными и интересными. В них мы подробно разберем важнейшую часть статистического анализа (а именно построение радов распределения), а также моду и медиану.

Статистические ряды распределения являются одним из наиболее важных элементов статистики. Они представляют собой составную часть метода статистических сводок и группировок, но, по сути, ни одно из статистических исследований невозможно произвести, не представив первоначально полученную в результате статистического наблюдения информацию в виде статистических рядов распределения.

Актуальность данной темы обусловлена тем, что статистические ряды распределения являются базисным методом для любого статистического анализа. Понимание данного метода и навыки его использования необходимы для проведения статистических исследований.

В статистике применяют два вида средних величин, которые определяются только структурой распределения. Такими величинами являются мода и медиана. Их используют как среднюю характеристику в тех совокупностях, где расчёт средне степенной невозможен или нецелесообразен. Мода – наиболее часто встречающееся значение признака у единиц данной совокупности. Мода применяется при изучении качества продукции, покупательского спроса, конструировании одежды, обуви и т. д.

Медиана – варианта, делящая ранжированный ряд на две равные части.

Вторая глава – расчетная. Она состоит из задач, которые включают в себя большой спектр заданий (расчёта среднего показателя, нахождение моды и медианы, метод постоянной средней и многое другое).


Глава 1.Теоретическая часть.

14.Виды рядов распределения.

14.1. Виды рядов распределения


Важнейшей частью статистического анализа является построение рядов распределения (структурной группировки) с целью выделения характерных свойств и закономерностей изучаемой совокупности. В зависимости от того, какой признак (количественный или качественный) взят за основу группировки данных, различают соответственно типы рядов распределения.

Если за основу группировки взят качественный признак, то такой ряд распределения называют атрибутивным (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.).

Если ряд распределения построен по количественному признаку, то такой ряд называют вариационным. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу).

Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд.



14.2. Ранжированный ряд


Ранжированный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.

Банк	Капитал (тыс. руб.)
СБ РФ	96007237
Внешторгбанк	47991724

Другие формы вариационного ряда - групповые таблицы, составленные по характеру вариации значений изучаемого признака. По характеру вариации различают дискретные (прерывные) и непрерывные признаки.


14.3. Дискретный ряд

Дискретный ряд - это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением (дискретные признаки). К последним можно отнести тарифный разряд, количество детей в семье, число работников на предприятии и т.д. Эти признаки могут принимать только конечное число определенных значений.

Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака, а во второй - число единиц совокупности с определенным значением признака.

Кол-во детей в семье	0	1	2	3	4
Кол-во семей	20	40	45	10	5

14.4. Интервальный вариационный ряд


Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд.

Групповая таблица здесь также имеет две графы. В первой указывается значение признака в интервале «от - до» (варианты), во второй - число единиц, входящих в интервал (частота).

Размер собственного капитала (тыс.руб.)	0 - 10000	10000 - 50000	Свыше 50000
Кол-во банков	20	40	10

При построении интервального вариационного ряда необходимо выбрать

оптимальное количество групп, самый распространенный способ по формуле

Стерджесса:

k 1 + 3,32 lg n= 1 + 1,44 ln n,

где k — число групп;

n — численность совокупности.


14.5. Частота повторения

Частота (частота повторения) - число повторений отдельного варианта значений признака, обозначается f_i , а сумма частот, равная объему исследуемой совокупности, обозначается



где k - число вариантов значений признака

Очень часто таблица дополняется графой, в которой подсчитываются накопленные частоты S, которые показывают, какое количество единиц совокупности имеет значение признака не большее, чем данное значение.

Частоты ряда f могут заменяться частностями w, выраженными в относительных числах (долях или процентах). Они представляют собой отношения частот каждого интервала к их общей сумме, т.е.:

 

При построении вариационного ряда с интервальными значениями прежде всего необходимо установить величину интервала i, которая определяется как отношение размаха вариации R к числу групп m:



где R = x_max - x_min ; m = 1 + 3,322 lgn (формула Стерджесса); n - общее число единиц совокупности.


24. Мода и медиана


24.1. Мода.


Бесспорно, важное значение имеет такая величина при­знака, которая встречается в изучаемом ряду, в совокупности чаще всего. Такую величину принято называть модой и обо­значать Мо. В дискретном ряду мода определяется без вычис­ления как значение признака с наибольшей частотой. Обычно встречаются ряды с одним модальным значением признака. Если два или несколько равных (и даже несколько различных, но больших, чем соседние) значений признака имеются в ва­риационном ряду, он считается соответственно бимодальным либо мультимодальным. Это говорит о неоднородности совокупности, возможно, представляющей собой агрегат нескольких совокупностей с разными модами.

Так и в толпе туристов, приехавших из разных стран, вме­сто одной, преобладающей среди местных жителей модной одежды можно встретить смесь «мод», принятых у разных на­родов мира.

В интервальном вариационном ряду, тем более при непре­рывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интерва­лом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи кото­рого плотность распределения, Т.е. число единиц совокупно­сти, приходящееся на единицу измерения варьирующего при­знака, достигает максимума. Это условное значение и счита­ется точечной модой. Логично предположить, что такая точеч­ная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в ин­тервале за другой границей модального интервала. Отсюда имеем обычно применяемую формулу :

Мо = хо + f_Mo - fMo - 1 • i,

(/Мо - f_mo-₁) + (/Мо - fMo+ 1)

где хо - нижняя граница модального интервала; fMo - частота в модальном интервале;

fMo - 1 - частота в предыдущем интервале;

fMo + 1 - частота в следующем интервале за модальным; i - величина интервала.

Вычисление моды в интервальном ряду весьма условно.

Приближенно Мо может быть определена графически .

В равно интервальном ряду при расчете моды следует использовать плотность распределения.

К изучению структуры вариационного ряда средняя ариф­метическая величина тоже имеет отношение, хотя основное значение этого обобщающего показателя другое.

24.2. Медиана.


При изучении вариации применяются такие характери­стики вариационного ряда, которые описывают количествен­но его структуру, строение. Такова, например, медиана - ве­личина варьирующего признака, делящая совокупность на две равные части - со значениями признака меньше медианы и со значениями признака больше медианы. На примере этих данных видно принципиальное различие между медианой и средней величиной. Медиана не зависит от значений признака на краях ранжированного ряда. Если бы капитал крупнейшего банка Санкт-Петербурга был в десять раз больше, величина медианы не изменилась бы. Поэтому часто медиану используют как более надежный показатель типичного значения признака, нежели арифметическая сред­няя, если ряд значений неоднороден, включает резкие откло­нения от средней. В данном ряду средняя величина собствен­ного капитала равна 394 млн руб., сложилась под влиянием наибольшей варианты. 80% банков имеют капитал меньше среднего и лишь 20% - больше. Вряд ли такую среднюю мож­но считать типичной величиной. При четном числе единиц совокупности за медиану принимают арифметическую сред­нюю величину из двух центральных вариант, например при 10 значениях признака - среднюю из пятого и шестого значе­ний в ранжированном ряду.

В интервальном вариационном ряду для нахождения ме­дианы применяется формула

Ме = Х_е + fi...L (~ - fMe - 1) ,

Ме где Ме - медиана;

Х_е - нижняя граница интервала, в котором находится медиана;

п - число наблюдений; .

!Ме -\ - накопленная частота в интервале, предшествующем медиан-

ному;

fMe - частота в медианном интервале; j - величина интервала.

Например, если имеется 100 наблюдений, то медианными,

Т.е. стоящими в середине ряда, являются: 100,,+ 1= 50,5 - 50-я

и 51-я единицы. В нашем примере имеется нечетное число значений: 143_+1= 72, Т.е. в середине ряда находится 72-е от

начала ряда значение урожайности. Как видно из ряда нако­пленных частот , оно находится в четвертом интер­вале. Тогда

Ме = 25 + 724135 . 5 = 29,5 цjгa.

При нечетном числе единиц совокупности номер медианы, как видим, равен не 'Lfj: 2, а ('Lfj + 1) : 2, но это различие несущественно и обычно игнорируется на практике.

В равно интервальном ряду медиана - это середина сред­него интервала при их нечетном числе или средняя арифме­тическая из границ двух средних интервалов при их четном числе.

В дискретном вариационном ряду медианой следует счи­тать значение признака в той группе, в которой накопленная частота превышает половину численности совокупности. На­пример, для данных табл. 5.1 медианой числа забитых за игру мячей будет два.


24.3. Соотношение между средней величиной, медианой и модой.


Различие между средней арифметической величиной, ме­дианой и модой в данном распределении невелико. Если рас­пределение по форме близко к нормальному закону, то ме­диана находится между модой и средней величиной, причем ближе к средней, чем к моде.

При правосторонней асимметрии х > Ме > Мо; при левосторонней асимметрии х < Ме < Мо.

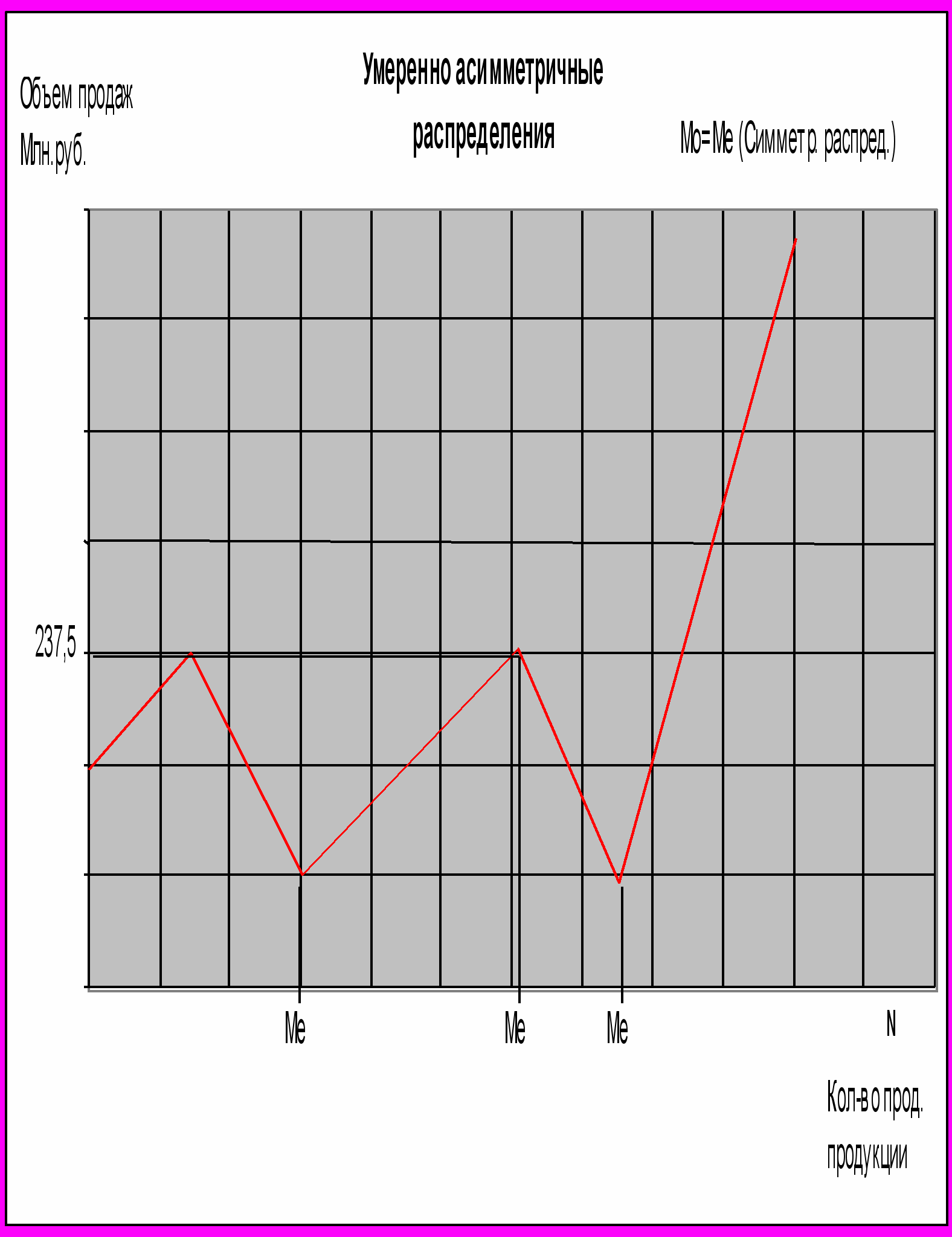Me=230 + 10 * ((51,5 – 32)/26)=237,5=Mo

Для умеренно асимметричных распределений справедли­во равенство: IMo - хl = 31Ме - xl.


Глава 2. Расчётная часть.

2.1 Задача №1

Выполнить расчёт средней выработки на одного рабочего в бригаде из 12 человек.

Выработка каждого рабочего представлена в следующей таблице:

Выработка одного рабочего деталей, штук
1	2	3	4	5	6	7	8	9	10	11	12
20	18	22	15	27	16	14	28	21	25	17	19

Решение:

Определим среднюю выработку по формуле средней арифметической:

__ ∑ Xi

Х = --------------

N

X = (20+18+22+15+27+16+14+28+21+25+17+19)/12 = 242/12 = 20,1(6) (штук)

2.2 Задача №2

Определить среднюю трудоёмкость работ по производству деталей.

Трудоёмкость одной детали, чел.час	5	7	9	4	8	12	14
Объём производства деталей, штук	30	15	35	27	29	30	34

Решение:

Для решения используем формулу средней арифметической взвешенной:


__ ∑ X_i*n_i

Х = --------------

∑ n_i

Х = (5*30+7*15+9*35+4*27+8*29+12*30+14*34)/ (30+15+35+27+29+30+34) = 1746/200 = 8,73 (мин.)

2.3 Задача №3

Определить среднюю выработку рабочего на предприятии. Известно, что норма на одного рабочего в смену составляет 20 деталей.

Удельный вес рабочих предприятия, %	74	15	3	4	2	1	1
Выполнение норма выработки рабочими предприятия (%)	100	95	90	85	80	75	70

Решение:

__ ∑ X_i*n_i

Х = --------------

100%

Х=(74*100+15*95+3*90+4*85+2*80+1*75+1*70)/100= 95,8 (%)

Х=0,958*20=19,16 (деталей)

2.4 Задача №4

Определить среднее время обработки одной детали в бригаде из 9 человек. Определить сколько деталей будет изготовлено бригадой за 8 часовой рабочий день по индивидуальным нормам выработки с использованием полученной средней величины затрат времени на изготовление одной детали членом бригады.

Число рабочих, чел.	2	3	1	1	1	1
Время обработки одной детали, мин.	3	4	5	6	7	8

Решение:

1) Используем формулу средней гармонической величины:

__ ∑ n

Х = --------------

∑ n/х

X= 9/(2/3 + ¾ + 1/5 + 1/6 + 1/7 + 1/8) ~ 4.56 (мин)

Тогда общее количество деталей, изготовленных бригадой из 9 человек за 8 часов, будет равно (480/4,88)*9 ~ 947,34 (дет).

2. Находим сколько деталей за 8 часов сделает каждый рабочий:
   

X₁ = 480/3 = 160 шт; X₂ = 480/3 = 160 шт; X₃ = 480/4 = 120 шт; X₄ = 480/4 = 120 шт; X₅ = 480/4 = 120 шт X₆ = 480/5 = 96 шт; X₇ = 480/6 = 80 шт; X₈ = 480/7 = 68,6 шт; X₉ = 480/8 = 60 шт;.

Просуммировав эти результаты, получаем, что вся бригада за 8 часов сделает:

Х = 160 +160 + 120*3 + 96 + 80 + 68,6 + 60 = 984,6 шт.

2.5 Задача №5

Определить средний коэффициент роста для динамического ряда данных об объёме выпуска продукции за 5 лет. Показать расчётно, что полученная средняя соответствует данным динамического ряда.

Год	1996	1997	1998	1999	2000
Объём выпуска продукции, млн. руб	3	24	60	120	156

Решение:

Используем формулу средней геометрической:

___________

Х = ^n-1√X₁*X₂*…*X_n


X = ⁴√(24/3)(60/24)(120/60)(156/120) = ⁴√52 ~ 2,68

Проверка: 4*2,68*2,68*2,68*2,68 ~ 206 => средний коэффициент роста не равен 2,68.

2.6 Задача №6

Определить Моду и Медиану для распределения рабочих сдельщиков по нормам выработки.

Выполнение норм выработки рабочими, %	100-110	110-120	120-130	130-140	140-150	150-160	160-170	170-180	180-190
Численность рабочих сдельщиков	12	19	37	47	45	22	11	6	2
Сумма накопленных частот	4	10	23	47	69	80	86	88	89

Решение:


Расcчитаем моду по формуле (модальный интервал - 130-140):

M₀=x₀+d(n₂-n₁)/((n₂-n₁)+(n₂-n₃))

M₀=130+10*(47-37)/((47-37)+(47-45)) ~130,08 (%)

Рассчитаем медиану по формуле:

M_е=x₀+d*(½*∑n – S_m-1)/n_m

Сумма накопленных частот в данном случае составит: 12+19+37+47+45+22+11+6+2=201 => Полусумма равна 100,5 => медианный интервал – 130-140. Отсюда, медиана равна:

M_е= 130 + 10*(100,5-23)/24 ~ 146,49 (%)

2.7 Задача №7

Выполнить расчёт средней трудоёмкости обработки деталей методом моментов.

Решение:

Решение можно записать в виде следующей таблицы:

Трудоёмкость обработки деталей, мин.	20-25	25-30	30-35	35-40	40-45	45-50	50-55	55-60	60-65
Число деталей, штук.	12	19	37	47	45	22	11	6	2
Среднее значение интервала ( X’)	22,5	27,5	32,5	37,5	42,5 (А)	47,5	52,5	57,5	62,5
(X’ – A)	-20	-15	-10	-5	0	5	10	15	20
Ci=(X’-A)/i	-4	-3	-2	-1	0	1	2	3	4
Ci*ni	-16	-18	-26	-24	0	11	12	6	4

Рассчитаем среднюю арифметическую:

__ ∑ c_in_i

С = --------------

∑ n_i

C=(-16-18-26-24+11+12+6+4)/(12+19+37+47+45+22+11+6+2)=-51/201 ~ -0,25

Тогда средняя трудоёмкость равна: X=(C*i + A)= -0,25*5 + 42,5 = 41,23 (мин.)

2.8 Задача №8

По данным о численности работников предприятия по годам определить показатели, характеризующие тенденцию развития дан­ного явления во времени:

1. Абсолютные приросты базисные (накопленные) и цепные (годовые).
   
2. Темпы роста базисные и цепные.
   
3. Темпы прироста базисные и цепные.
   
4. Абсолютное значение одного процента прироста; темп наращивания
   одного процента.
   
5. Средний абсолютный прирост; средний темп роста.
   
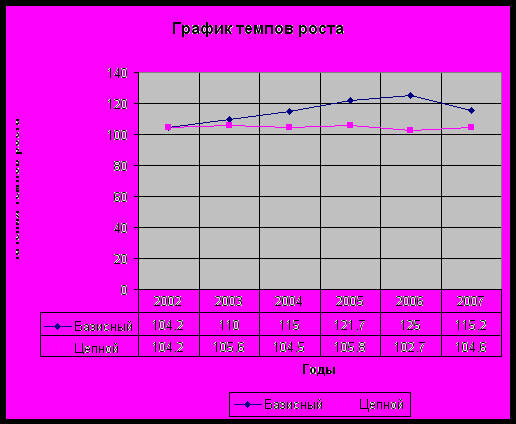
6. Постройте график базисных и цепных темпов роста.
   

На основании расчетов сделайте выводы о тенденции динамики числен­ности работников предприятия.

Расчет показателей выполнить в таблице

Решение:

Годы	Числен-ность работни-ков (чел.)	Абсолютные приросты (чел.)		Темп роста (%)		Темп прироста (%)		Абсолют-ное значе-ние 1% прироста	Темп наращивания одного процента
		Базис-ный	Цеп-ной	Базис-ный	Цеп-ной	Базис-ный	Цеп-ной
2002	1200	-	-	-	-	-	-	-	-
2003	1250	50	50	104,2	104,2	4,2	4,2	11,9	-
2004	1320	120	70	110	105,6	10	5,6	12,5	105
2005	1380	180	60	115	104,5	15	4,5	13,3	105
2006	1460	260	80	121,7	105,8	21,7	5,8	13,8	103,8
2007	1500	300	40	125	102,7	25	2,7	14,8	107,2
Среднее значение		182	60	115,2	104,6

Данные показатели рассчитаны следующим образом:

Абсолютный прирост = Численность рабочих за отчётный период – Численность рабочих за базисный период (или предыдущий, в случае цепного метода)

Темп роста = 100% * Численность рабочих за отчётный период / Численность рабочих за базисный период (или предыдущий, в случае цепного метода)

Темп прироста = Темп роста – 100%

Абсолютное значение 1% прироста = Абсолютный прирост / Темп прироста

Темп наращивания одного процента = Абсолютное значение 1% прироста за отчётный период / Абсолютное значение 1% прироста за базисный (или предыдущий) период

График базисных и цепных темпов роста выглядит следующим образом:

2.9 Задача №9

По данным об объеме реализованной продукции (млн. руб.) :

1. измерить сезонные колебания объема реализованной продукции, применяя соответствующую формулу индекса се­зонности;
   
2. показатели сезонной волны изобразить графически;
   
3. на основе синтезированной модели сезонной волны сделайте прогноз объемов реализованной продукции (млн. руб.) по месяцам 2007 г. возможного объема реализации в 1000 млн. руб.
   

Расчет выполнить в таблице.

Решение:

Период	Значения	Индекс сезонности	Прогноз на 2007 г.
Январь	30,8	0,87	72,5
Февраль	25,9	0,73	60,8
Март	29,1	0,82	68,3
Апрель	41,1	1,16	96,6
Май	35,2	0,99	82,5
Июнь	39,4	1,11	92,5
Июль	38,4	1,08	90,0
Август	35,3	0,99	82,5
Сентябрь	35,7	1,01	84,4
Октябрь	35,6	1,00	83,3
Ноябрь	36,3	1,02	85,0
Декабрь	42,7	1,20	100
Среднее значение	35,46		83,3

Индекс сезонности расчитывается по формуле: I_s = y_i/y_ср

Так как в 2007 году объём реализации планируется сделать равным 1000 млн. руб, то в среднем по месяцам этот показатель ссоставит 1000/12 = 83,3 млн. руб.

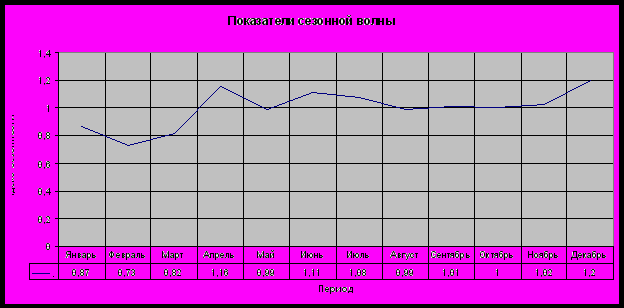
Показатели сезонной волны изображены на следующем графике:

2.10 Задача №10

По данным о продаже товаров на оптовом рынке, вычислите:

1) общий индекс цен;

2) общий индекс физического объема товарной массы;

3) общий индекс товарооборота в фактических ценах;

4) покажите взаимосвязь индексов в относительном и абсолютном выражениях.


Товарооборот в фактических ценах

Товары	Продано товаров в фактических ценах (млн руб.)		Индивидуальный индекс цен ip
	Базисный период poqo	Отчетный период p1q1
А	310	560	1,25
Т	470	780	1,46

Решение:

1) Общий индекс цен показывает изменение товарооборота засчёт изменения цены при неизменном количестве проданных товаров за отчётный период. Для нахождения общего индекса цен используется следующая формула: I_p = ∑p₁q₁/∑p₀q₁

Так как индивидуальный индекс цен i_p равен отношению цены за отчётный период к цене за базисный период, следовательно данную формулу можно преобразовать в следующую:

I_p = ∑p₁q₁/∑((p₁q₁)/i_p) = (560+780)/((560/1,25)+(780/1,46)) ≈ 1,14

Абсолютное же значение общего индекса цен будет равно:

∆I_p = 560+780-(560/1,25)-(780/1,46) = 1340 – 982 = 358 (млн. руб)

2) Общий индекс физического объёма товарной массы показывает изменение товарооборота засчёт изменения объёма выпуска при неизменной цене товаров. Для нахождения данного общего индекса используется следующая формула: I_q = ∑p₀q₁/∑p₀q₀

Так как индивидуальный индекс цен i_p равен отношению цены за отчётный период к цене за базисный период, следовательно данную формулу можно преобразовать в следующую:

I_q = ∑((p₁q₁)/i_p)/∑p₀q₀ = ((560/1,25)+(780/1,46))/(310+470) ≈ 1,26

Абсолютное же значение изменение индекса объёма товарной массы равно:

∆I_q = (560/1,25)+(780/1,46) - (310+470) = 982 – 780 = 202 (млн. руб)

3) Общий индекс товарооборота рассчитвается по формуле: I_pq = ∑p₁q₁/∑p₀q₀ =(560+780)/(310+470) ≈ 1,44

Абсолютное же значение общего индекса товарооборота составит:

∆I_pq = 560+780-310-470 = 560 (млн.руб)

4) I_pq=I_p*I_q = 1,14*1,26 ≈ 1,44

∆I_pq = ∆I_p + ∆I_q =358+202 = 560 (млн. руб)


Заключение.

Задача №3

После произведенных расчетов по этой задаче, мы получили, что средняя величина выработки составляет – 19,16 дет. Следовательно, учитывая предоставленные в условии данные, можно подытожить:

В связи с тем, что большинство рабочих в бригаде выполняет план, можно сделать вывод о том, что проблем с оборудованием и с сырьем нет; значит, что оставшиеся рабочие не выполняют норму из-за своей низкой квалификации, профнепригодности и возможно некоторых других факторов.

Можем сделать вывод, что нужно постоянно проводить переквалификацию работников. При этом все затраты, израсходованные при этой процедуре будут определенно меньше, чем убытки, вызванные недовыполнением нормы.


Задача №4

Среднее время обработки детали = 4,56 минут; За 8 часов работы бригада из 9 человек сделает 985 деталей. Следовательно, можно сделать вывод о том, что на данном заводе нет серьёзных проблем с квалификацией работников, с оборудованием. Значит, данные условия на производстве способствуют хорошей работоспособности и производительности труда.


Задача №5

Из условия этой задачи мы замечаем, что прослеживается постоянное увеличение выпускаемой продукции по сравнению с предыдущим годом. Проанализировав же полученные данные, становится видно, что коэффициент роста постепенно уменьшается. Так в 1997 году К_р был равен 8, а в 1998 году уменьшился до отметки в 2,5. В 1999 же году показатель изменился до 2, а в 2000 – коэффициент роста снова уменьшился, и на этот раз до 1,3. Следовательно, я могу сделать вывод о том, что наблюдается явная тенденция спада объема выпуска продукции. И можно предположить, что в последующие годы спад будет продолжаться.


Задача №6

По полученным данным на предприятии, изготавливающим чугунный прокат, в бригаде рабочих, средняя норма выработки, вычисленная по Медине, равна 130,08%. Это говорит о том, что рабочие-сдельщики, перевыполняют план. А средняя же, вычисленная по Моде равна 146,49%.Следовательно, на данном этапе, на этом предприятии не существует никаких проблем, и так как рабочие перевыполняют план – завод находиться в выигрышном положении.


Задача № 7

На данном предприятии средняя норма выработки одной детали составила 41,23 мин, исходя из того что расчет выполнен методом моментов, можно заметить, что такой показатель выполняют меньше рабочих, когда большая перекрывает этот показатель.

Учитывая это следует принять меры по повышению нормы выработки, путем либо найма новых и увольнением профнепригодных рабочих, либо повышать их квалификацию и стимулировать работу путем улучшения качества труда и поощрением при перевыполнения плана.


Задача №8

Среднее значение абсолютного прироста численности рабочих по базисному методу составляет 182 человек, по цепному – 60 человек. А среднее значение темпов роста по базисному методу составит 115,2 %, а по цепному - 104,6 %. Что говорит о том, что за всё время деятельности предприятия численность промышленного персонала увеличилась на 60 человек, что говорит о том, что предприятие развивается и увеличивает объёмы производства.

Задача №9

Полученные данные позволяют сделать следующие выводы:

1. Объём реализованной продукции возрастает к концу года по сравнению с его началом,
   
2. В течение первого квартала заметен резкий спад, который сменяется ростом к середине февраля,
   
3. В течение второго квартала отмечается резкий подъём показателя объёма реализованной продукции, который потом сходит на ноль к середине мая, но затем данный показатель продолжает расти.
   
4. В течение третьего квартала отмечается стабилизация объёма реализованной продукции ,
   
5. В течение четвёртого квартала отмечается резкий подъём показателя объёма реализованной продукции, начинающийся с ноября.
   

Задача №10

Полученные индексы свидетельствуют о том, что объём товарооборота увеличился на 560 млн. руб, в том числе на 358 млн. руб из-за увеличения цены товаров и на 202 млн. руб в следствие увеличения объёма выпускаемой продукции. В относительном выражении товарооборот увеличился на 44%, в том числе на 14% из-за увеличения цены и на 26% из-за увеличения объёма выпускаемой продукции.


Список использованной литературы.


1.Общая теория статистики: Учебник/ Под ред. И.И.Елисеевой. – 5-е изд., перераб. и доп. – М.: Финансы и статистика, 2006.

2.Статистика: Учеб. пособие/ А.В.Багат, М.М.Конкина, В.М.Симчера и др.; Под. ред. В.М.Симчеры. – М.: Финансы и статистика, 2006.

3. Статистика / Под ред. В. Г. Ионина. – М.: ИНФРА-М, 2006.

4. Яблочник А.Л. Общая теория статистики. – М.: Финансы и статистика, 2002.

5. t.msk.ru/16/29103b.htm