14 поняття про мову розмітки гіпертексту

Вид материала

Тема 15 основи алгоритмізації і програмування
Таблиця розрахунку заробітної платні
Тема 14 основи алгоритмізації і програмування
Тема 14 основи алгоритмізації і програмування

Подобный материал:

1 2 3 4 5

ТЕМА 15 ОСНОВИ АЛГОРИТМІЗАЦІЇ І ПРОГРАМУВАННЯ

УРОК 3 Способи подання алгоритмів

Для подання алгоритмів застосовуються різні способи. Кожний з них надає певні засоби для опису дій, які треба виконати, та встановлення послідовності їх виконання.

У повсякденному житті найчастіше застосовується словесний спосіб. У такий спосіб алгоритм подається як послідовність окремих занумерованих пунктів, кожний з яких містить команду на виконання певної дії. Команди записуються словами. Пункти виконуються один за одним у порядку зростання їх номерів, якщо немає спеціальної вказівки на перехід до виконання іншого пункту, номер якого задається. Словесний спосіб подання алгоритму є найбільш прийнятним для опису інструкцій побутового характеру, дій на випадок надзвичайної ситуації, фармакологічних чи кулінарних рецептів тощо.

Записом алгоритму можна вважати формулу, тому що з неї випливає порядок здійснення обчислень для здобуття числового результату. Якщо виконується серія розрахунків за однаковими формулами, то для запису алгоритму іноді використовується розрахункова таблиця, де визначаються всі етапи обчислень і фіксуються проміжні результати.

Таблиця розрахунку заробітної платні

№ п/п	Прізвище	Розмір місячної ставки	Кількість робочих днів у місяці	Денний заробіток	Кількість відпрацьованих днів	Заробітна платня за місяць	Сума податку (23%)	До видачі
1	2	3	4	5	6	7	8	9
(1)	(2)	(3)	(4)	(3):(4)	(6)	(5)х(6)	(7)хО,23	(7)-(8)
1	Асеев Б.	420	24	17,5	24	420	96,6	323,4
2	Волін О.	420	24	17,5	20	350	80,5	269,5
3	Котик І.	360	24	15.0	23	345	79,35	265,65

У наведеній таблиці верхній рядок містить найменування стовпчиків таблиці, наступний рядок — їх номери, рядок під ним — позначення дій, які треба виконати над даними у попередніх стовпцях (вказано їх номери) для здобуття значення у поточному стовпці. Так, для обчислення денного заробітку (5) треба розмір місячної ставки (3) поділити на кількість робочих днів у місяці (4), що умовно позначається як (3):(4).

Поширеним способом наочного подання алгоритму є блок-схема.

Блок-схема складається з геометричних фігур, які з'єднані напрямленими лініями. Зміст дій описується всередині геометричних фігур. Порядок виконання дій задається лініями.

Для подання алгоритму застосовуються геометричні фігури двох видів: прямокутники та ромби. У прямокутниках записують дії, які мають виконуватися, в ромбах — умови, які треба перевіряти. Перевірка умов потрібна для вибору тих чи інших подальших дій. Якщо прямокутник має один вхід і один вихід, то у ромба вхід один, а виходів — два. Коли перевіряється умова, записана в ромбі, то існує два

можливих варіанти: умова або виконується, або ні. На ці випадки («так» і «ні») і є два виходи з ромба, які спрямовують подальші дії виконавця алгоритму залежно від результату перевірки умови.

Наприклад, якщо в прямокутнику записано х = 2, то це не ствердження, а наказ надати х значення 2. Яким би не було раніше значення х, тепер воно дорівнює 2. Якщо в ромбі записано х = 2, то це читається як «х = 2?». Далі перевіряється, чи виконується ця рівність для поточного значення, і вибирається відповідна вихідна гілка — «так» або «ні». Значення х залишається таким, яким воно було до цієї перевірки.

Для того щоб алгоритми, подані блок-схемами, було зручно читати та виконувати, введено допоміжні елементи: овали, які застосовуються для позначення початку або кінця алгоритму, та паралелограми •— для введення або виведення даних.

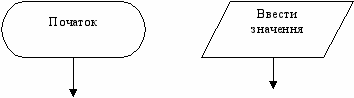
ТЕМА 14 ОСНОВИ АЛГОРИТМІЗАЦІЇ І ПРОГРАМУВАННЯ

УРОК 4 Види алгоритмів

Види алгоритмів розрізняють звичайно не за складністю виконуваних дій, не за їхньою.кількістю, а за складністю організації (або за управлінням, за логічною конструкцією) алгоритмічного процесу.

Алгоритми найпростішого виду — лінійні. Це такі алгоритми, в яких дії виконуються послідовно, одна за одною. Кожна дія лінійного алгоритму обов'язково виконується, і виконується тільки один раз:

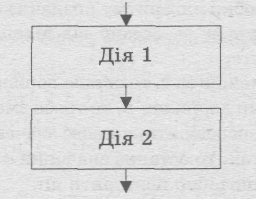
Наведена базова алгоритмічна конструкція називається слідуванням. Ця конструкція є замкненою в тому розумінні, що у неї є один вхід і один вихід, і інші можливості увійти всередину конструкцій чи вийти з неї виключені.

Якими б не були вхідні дані, лінійний алгоритм приписує виконання однієї й тієї самої послідовності дій.

Прикладом лінійного алгоритму може бути наведений вище алгоритм завершення роботи з комп'ютером.

Складнішими за організацією є алгоритми, в яких треба не просто виконувати всі підряд задані дії, а приймати рішення, які саме дії виконувати.

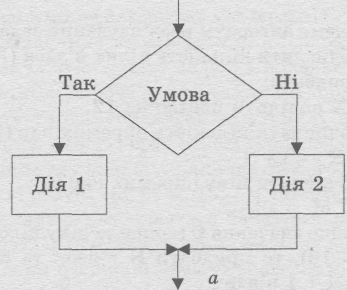
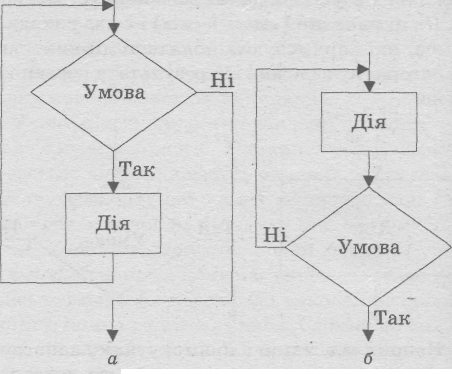
Алгоритм, який приписує здійснення тієї чи іншої дії в залежності від виконання заданої умови, називається алгоритмом з розгалуженням. Розрізняють повну і коротку форму розгалуження. В короткій формі при невиконанні умови ніякі дії не передбачаються. Повну форму розгалуження можна прочитати так:

«якщо умова виконується, то виконати дію 1, інакше виконати дію 2» (див. рис. а),

а коротку — так:

«якщо умова виконується, то виконати дію» (див. рис. б).

Так Ні

Дія

б

Наведена на рис. а базова алгоритмічна конструкція називається розгалуженням (на рис. б — п окремий випадок). Вона є замкненою: має один вхід і один вихід.

Приклад алгоритму з розгалуженням

У крамниці пара шкарпеток коштує 2 гривні, а в'язка (дванадцять пар) — 19 гривень. Визначити, скільки в'язок та пар шкарпеток вигідніше придбати, якщо потрібно X пар.

За таких умов очевидно, що замість 11 пар шкарпеток (22 гривні) і навіть 10 пар (20 гривень) вигідніше придбати в'язку (19 гривень) — буде затрачено менше грошей, і ви ще отримаєте додаткові шкарпетки. Але для дев'яти пар (18 гривень) знижка на в'язку вже не спрацює.

Розв'язання задачі ґрунтується на такому міркуванні. Треба порівняти за ціною всього два варіанти придбання шкарпеток:

перший — з округленням кількості шкарпеток до в'язки в менший бік і додаванням, якщо потрібно, окремих пар;

другий — з округленням кількості окремих пар, якщо такі є, до цілої в'язки.

Наприклад, якщо треба придбати 45 пар шкарпеток, то обов'язково треба купувати З в'язки і, порівнявши ціну 9 пар з ціною цілої в'язки, зробити висновок, що вигідніше докупити — потрібну кількість окремих пар чи цілу в'язку. У нашому прикладі дешевше докупити 9 пар.

Наведемо алгоритм розв'язування задачі:

1. Обчислити кількість цілих в'язок (N), які треба придбати:

N = X поділити націло на 12.

2. Обчислити кількість окремих пар (М) :

М = X — 12 N

3. Обчислити ціну окремих пар (С):

С = 2 М

4. Якщо значення С менше за ціну цілої в'язки (С < 19), то придбати N в'язок та М пар, інакше N + 1 в'язку.

Третій вид алгоритмів складають такі, які приписують неодноразове виконання певної дії (або декількох дій). Це циклічні алгоритми. Дії, які мають повторюватися, називаються тілом циклу. Умова, яка визначає кількість повторень циклу, називається умовою циклу.

Розрізняють два основні типи циклів: цикли, де умова перевіряється до виконання тіла циклу (цикли з передумовою), і цикли, де перевірка умови здійснюється після виконання тіла циклу (цикли з післяумовою, або постумовою). Двом типам циклів відповідають дві базові алгоритмічні конструкції повторення (див. рис. а, б), які подібно до інших базових конструкцій теж є замкненими, тобто мають один вхід і один вихід:

Тіло циклу з післяумовою, на відміну від циклу з передумовою, обов'язково виконується хоча б один раз — до першої перевірки умови.

У циклі з передумовою (рис. а) умова циклу формулюється так, щоб повторення тіла циклу здійснювалося за її виконанням. Через це такі цикли називаються ще циклами «поки»: поки умова виконується, виконується і тіло циклу. Якщо при черговій перевірці ця умова виявляється невиконаною, то відбувається вихід з циклу.

У циклі з післяумовою (рис. б) умова циклу формулюється таким чином, щоб повторення тіла циклу здійснювалося за її невиконанням, тому такі цикли називаються також циклами «до». Вихід з циклу «до» відбувається за виконання умови.

Зауважимо, що з розвитком мов програмування розширилися й види циклів, які можна застосовувати у програмах: так, наприклад, дозволяється у циклах з передумовою вживати умову «до», у циклі з післяумовою — умову «поки», комбінувати перевірку умов, використовуючи дві перевірки — і до, і після виконання тіла циклу і т.п.

Цикли є єдиним видом базових алгоритмічних структур, де передбачається повернення до вже виконаних дій.

Приклад циклічного алгоритму

Розробимо алгоритм знаходження остачі від ділення двох натуральних чисел, використовуючи лише операцію віднімання чисел.

Для розробки алгоритму позначимо через а та b задані числа,' г — остачу від ділення першого числа на друге.

Якщо а менше за Ь, то остача дорівнює а; якщо ж а більше чи дорівнює 6, то треба зменшити а на величину Ь і перевірити, чи нове значення а менше за Ь. Якщо так, то останнє значення а і є остачею, якщо ні — потрібно повторити дії.

Оскільки результатом роботи алгоритму має бути значення г, то доцільно одразу покласти г рівним а і подальші дії виконувати над г та Ь. У такому разі наш алгоритм не виявиться довшим, а вхідні значення а та й будуть збереженими, що завжди схвалюється як коректний стиль розробки алгоритму чи програми.

Зважуючи на те, що для випадку о < Ъ остача г дорівнює заданому значенню а і цикл не потрібно виконувати жодного разу, скористаємося для складання алгоритму циклом з передумовою.

Блок-схему алгоритму знаходження остачі від ділення двох натуральних чисел а, Ь подано на рис. а). На рис. б) наведено кроки виконання алгоритму для випадку а = 15, 6=7.

Крок 1. а=15,

r=a

Крок 2.

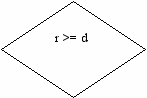Крок 3. Крок 5. Крок 7.

Ні 15

(так) (так) (ні)

r = r - b
Крок 4. Крок 6.

Крок 8

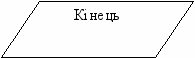r=1

a b

Алгоритм знаходження остачі від ділення двох натуральних чисел.

а — блок-схема алгоритму; б — кроки його виконання для а=15, Ь~7.

ТЕМА 14 ОСНОВИ АЛГОРИТМІЗАЦІЇ І ПРОГРАМУВАННЯ

УРОК 5 Структурний підхід до побудови алгоритмів

Одним із методів, який дозволяє поліпшити якість алгоритму в цілому, запобігти більшості логічних помилок і легко виявити ті, яких не вдалося уникнути, є структурний підхід до розробки алгоритмів. Він дозволяє забезпечити прозорість логічної будови алгоритму, його зрозумілість,

легкість сприйняття, простоту перевірки, зручність використання і модифікації (тобто внесення змін, перетворення з певною метою — наприклад, для пристосування до вирішення схожої задачі). Структурний підхід ґрунтується на трьох основних принципах:

• проектування алгоритму методом «згори вниз»;

• організація алгоритму у вигляді відносно незалежних частин — модулів;

• конструювання алгоритму з уніфікованих базових алгоритмічних структур (слідування, розгалуження, повторення). Структурне програмування - - це метод складання програм на засадах структурного підходу до побудови алгоритмів.

Технологія структурного програмування — це система методів, способів і прийомів реалізації ідей структурного програмування засобами конкретної мови програмування (докладніше див. тему «Мови програмування»).

Ефективним методом проектування алгоритмів у межах структурного підходу є метод «згори вниз» (йото називають також методом покро-кової деталізації, або методом послідовного уточнення). Ідея цього методу полягає у забезпеченні правильності алгоритму за рахунок самої процедури його розробки.

Проектування алгоритму має ієрархічну структуру і розпочинається з вершини ієрархії. Спочатку аналізують мету задачі і визначають основні етапи її розв'язку, тобто встановлюють загальну структуру алгоритму. Далі кожний етап, який у свою чергу також є задачею, піддають подібному аналізу: виявляють його основні функції і структуру і т.д. Таким чином, крок за кроком задача розбивається на все більш дрібні підзадачі, її структура уточнюється, деталізується, доки одержані врешті-решт підзадачі не виявляться настільки простими, що подальше уточнення стає непотрібним.

Таким чином, описаний метод проектування приводить до алгоритму деревоподібної структури, яка поступово зводить складний алгоритм до сукупності простих елементів:

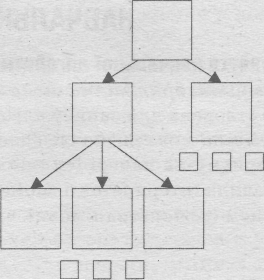
Таку структуру алгоритму називають також модульною, тому що кожна його підзадача становить собою модуль.

Модуль — це логічна частина алгоритму, яка є відносно незалежною, має певне цільове призначення і вирішує тільки одну чітко сформульовану задачу.

За сутністю модуль є функціональним блоком алгоритму. Щоб виконувати поставлену задачу, модуль має отримувати вхідні дані і повертати результати своєї роботи. Це відбивається у специфікації модуля. Така специфікація розробляється для кожного модуля і містить формулювання задачі, яку він розв'язує, і опис даних, якими він обмінюється з іншими модулями. Наявність специфікацій дозволяє здійснювати розподіл роботи з проектування, а далі і створення алгоритму між різними виконавцями, доручаючи кожному розробку свого модуля.

Модуль є відносно незалежною частиною алгоритму. Звичайно модуль обмінюється даними тільки з тим модулем, який відносно нього має наступний ступінь ієрархії, тобто інформаційна взаємодія обмежується контактом між модулем і його підмодулем. Обмін даними між модулями одного рівня або зв'язки далі наступного рівня виключаються (за можливістю). Щоб досягти мінімізації міжмодульної взаємодії, тісно пов'язані елементи намагаються розмістити в одному модулі, а непов'язані — в різних.

Незалежність модуля оцінюється впливом змін у цьому модулі на інші частини алгоритму. Якщо будь-які зміни в модулі, але такі, що він, як і раніше, сприймає ті самі дані і видає ті самі результати, не впливають на роботу інших частин алгоритму, то такий модуль вважається незалежним.

Високий ступінь незалежності модулів і мінімальний зв'язок між ними, які характерні для алгоритмів, спроектованих за методом структурного підходу, сприяють тому, що наслідки

можливої помилки локалізуються — шляхи п проникнення в інші частини алгоритму максимально обмежені.

Після завершення проектування структури алгоритму розпочинається процес створення алгоритмів для кожного модуля. Спочатку алгоритм розробляється для головного модуля, при цьому вважається, що алгоритми для модулів нижчого рівня вже існують і працюють відповідно до своїх специфікацій. Потім створюються алгоритми для модулів наступного рівня, і так до самого низу.

За методом структурного підходу розробка алгоритмів має здійснюватися виключно із застосуванням базових алгоритмічних конструкцій слідування, розгалуження та повторення. Теоретично доведено, що алгоритм будь-якої складності піддається опису за допомогою тільки таких простих базових конструкцій, де кожна з них може виступати складовим елементом будь-якої іншої (теорема про структурування, Bohm С., Jacopini G., 1972 p.).

Уніфікованість базових конструкцій зумовлює стандартизацію прийомів їх реалізації засобами мов програмування, що сприяє зменшенню помилок у програмах.

Замкненість базових конструкцій має наслідком і замкненість побудованих на їх основі алгоритмів. Це дозволяє значно спростити і полегшити складні процеси аналізу, тестування та модифікації алгоритму, які можна здійснювати окремо для кожного модуля.

Логічна простота базових конструкцій у поєднанні з модульною організацією структури алгоритму забезпечують його читабельність (алгоритм не перевантажується переходами та зв'язками, а послідовно простежується згори вниз) і зручність використання.

Всі позитивні властивості структурних алгоритмів переходять у корисні якості розроблених на їх основі програм.

Blog

14 поняття про мову розмітки гіпертексту