Самостоятельная работа 2 часа в неделю всего часов

Вид материала

Содержание

лабораторные занятия нет
проблем передачи и обработки информации 02 июня 2008 года

Подобный материал:

министерство образования и науки российской федерации

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Московский физико-технический институт

(государственный университет)

УТВЕРЖДАЮ

проректор по учебной работе

д.т.н. Е.В. Глухова

«___» _____________ 200__ г.

П Р О Г Р А М М А

курса АЛГЕБРАИЧЕСКИЕ КОДЫ

по направлению 010600 «Прикладные математика и физика»

по магистерским программам 010656, 010674

факультет РТК

кафедра проблем передачи и обработки информации

курс III, IV

семестры 6 (весенний), 7 (осенний)

лекции 66 часов Экзамен 7 семестр (осенний)

семинары нет Зачёт нет

лабораторные занятия нет

самостоятельная работа 2 часа в неделю

ВСЕГО ЧАСОВ 66

Программу составил: профессор, д.т.н. Сагалович Ю.Л.

Программа обсуждена на заседании кафедры

проблем передачи и обработки информации

02 июня 2008 года

Заведующий кафедрой

чл.-корр. РАН А.П. Кулешов

1. Теория сравнений.

1.1. Определение.

1.2. Свойства сравнений, полная и приведенная системы вычетов.

1.3. Теоремы о свойствах систем вычетов.

2. Функция Эйлера.

2.1. Определение.

2.2. Мультипликативность и вычисление функции Эйлера. Теоремы Эйлера и Ферма.

2.3. Пример применения в криптосистемах с открытым ключом.

3. Первообразные корни и индексы.

3.1. Показатель, которому принадлежит число по некоторому модулю.

3.2. Связь сравнимости чисел со сравнимостью их показателей.

3.3. Показатели чисел по модулю m, как делители функции Эйлера.

3.4. Первообразные корни.

3.5. Модули, по которым существуют первообразные корни.

3.6. Число первообразных корней.

3.7. Индексы.

3.8. Аналогия между индексами и логарифмами.

3.9. Основные теоремы об индексах.

4. Группа.

4.1. Определение группы.

4.2. Единичный и обратный элементы.

4.3. Порядок группы, порядок элемента группы.

4.4. Показатель группы.

4.5. Циклическая группа и порядки ее элементов.

4.6. Примеры групп.

4.7. Когда приведенная система вычетов является циклической группой?

5. Подгруппа.

5.1. Примеры подгрупп.

5.2. Смежные классы.

5.3. Разложение группы по подгруппе.

5.4. Фактор-группа.

5.5. Теорема Лагранжа.

5.6. Нормальные делители.

5.7. Изоморфизм и гомоморфизм групп.

6. Кольца и поля.

6.1. Определение кольца.

6.2. Делители нуля.

6.3. Область целостности.

6.4. Определение поля, характеристика поля.

6.5. Подполе.

6.6. Примеры колец и полей.

6.7. Идеал. Примеры идеалов.

6.8. Идеалы поля.

7. Поля Галуа.

7.1. Определение поля и построение поля по модулю неприводимого многочлена.

7.2. Расширение поля, степень расширения.

7.3. Мультипликативная группа поля.

7.4. Элементы поля, как корни многочлена

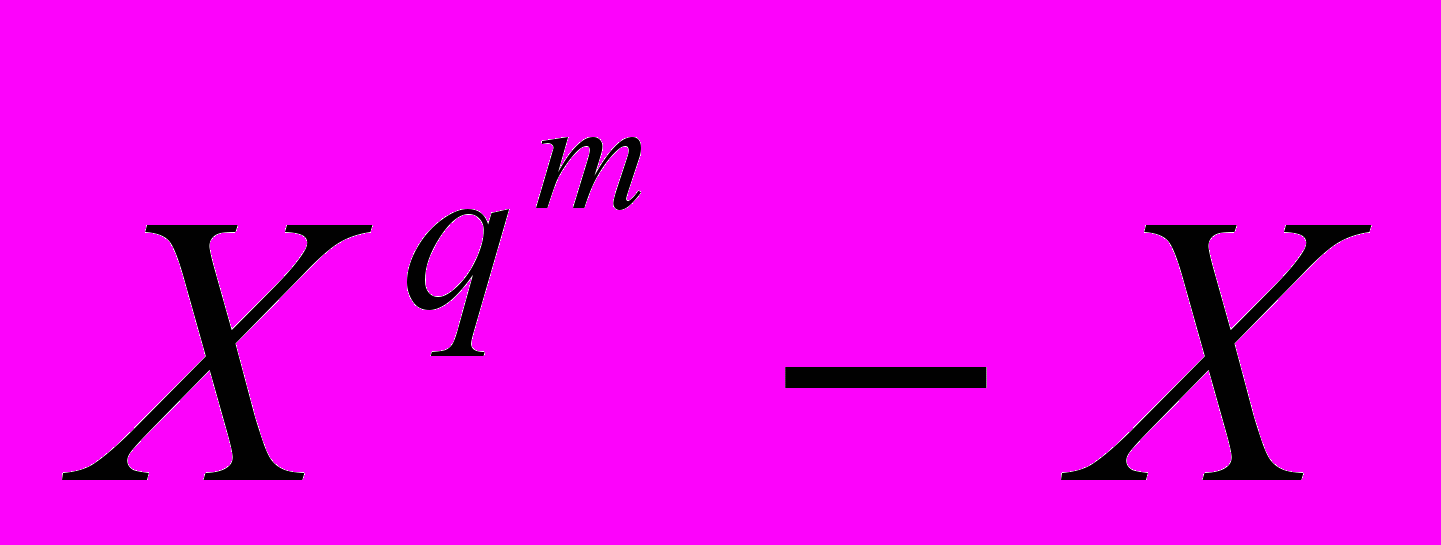. Теоремы Эйлера и Ферма.

7.5. Теорема Вильсона.

7.6. Цикличность мультипликативной группы поля.

7.7. Аддитивная группа поля.

7.8. Поле как векторное пространство.

7.9. Базис поля.

8. Теоремы о полях Галуа.

8.1. Минимальный многочлен; неприводимость, делимость на минимальный многочлен.

8.2. Существование минимального многочлена для произвольного элемента поля.

8.3. Делимость многочлена

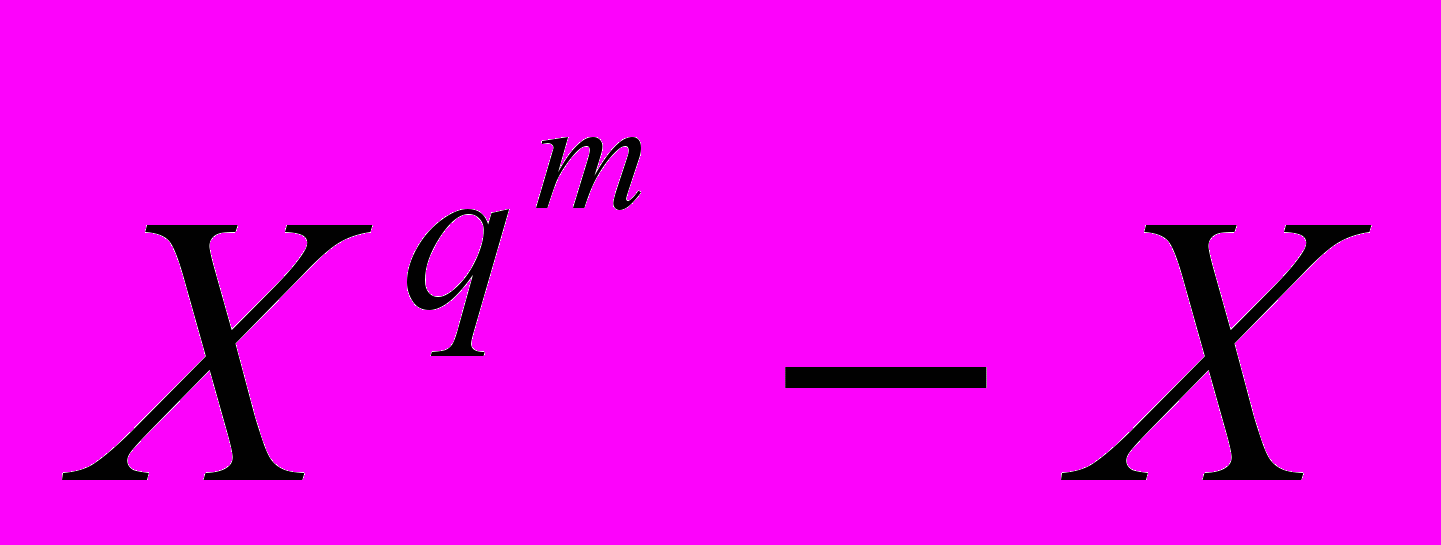на неприводимый многочлен над

.

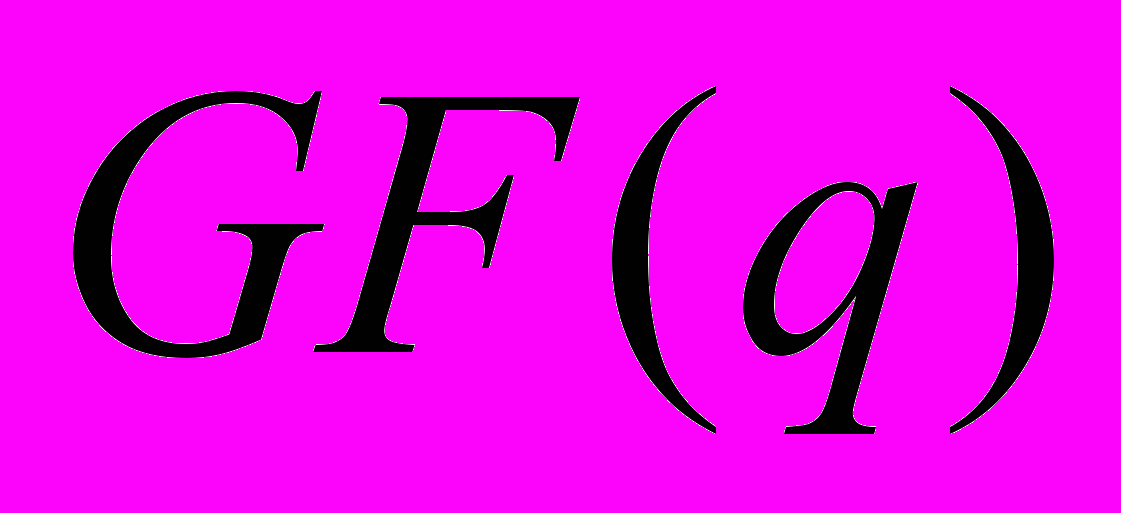8.4. Делимость многочлена

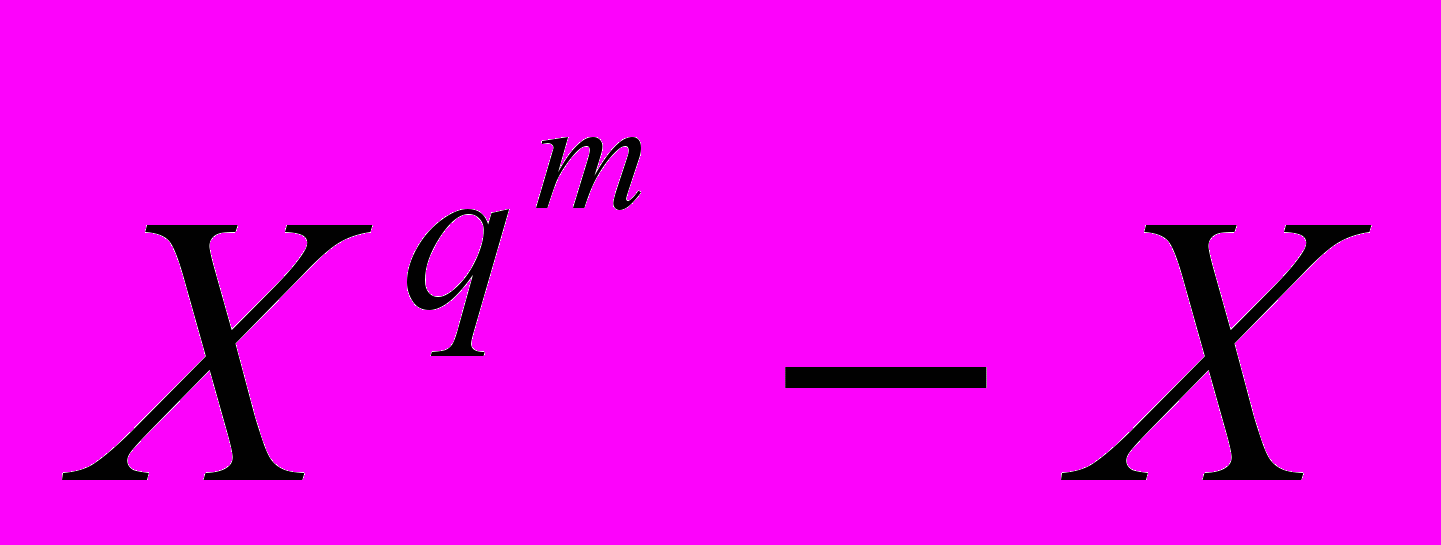на многочлен

.

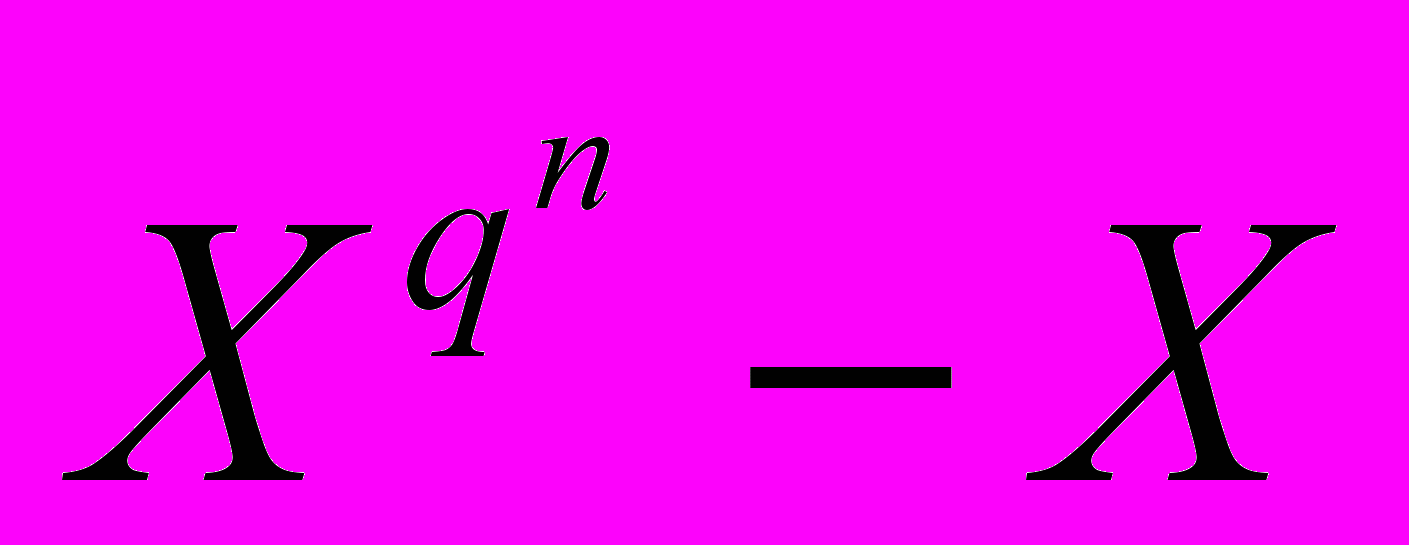8.5. Элементы 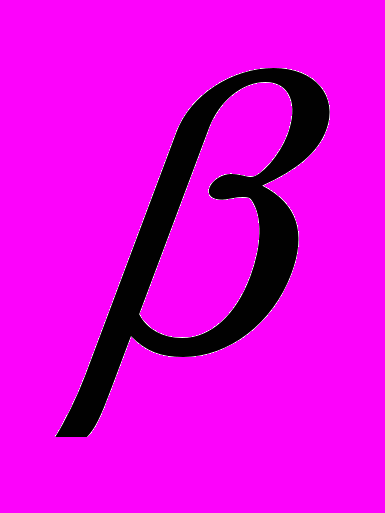и 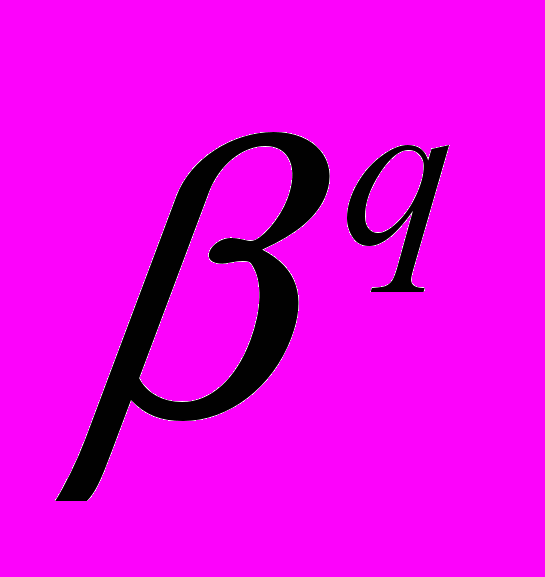как корни одного и того же многочлена.

8.6. Сопряженные элементы поля Галуа.

8.7. Циклотомические классы.

8.8. Подполе поля

.

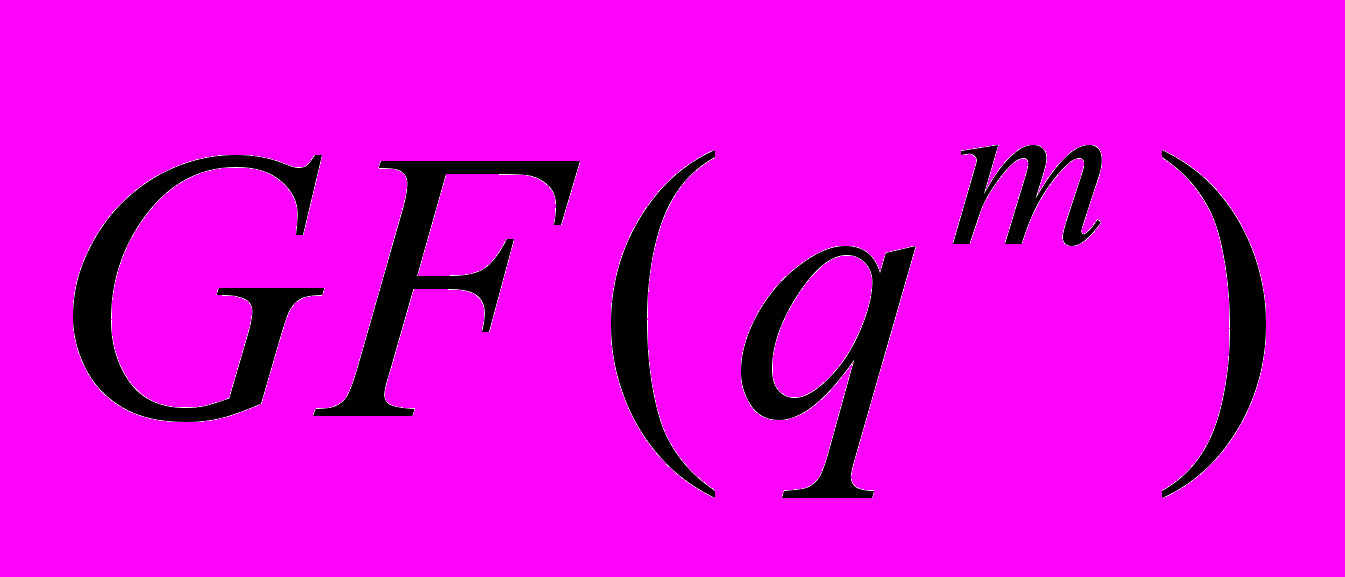8.9. Степени неприводимых делителей многочлена

.

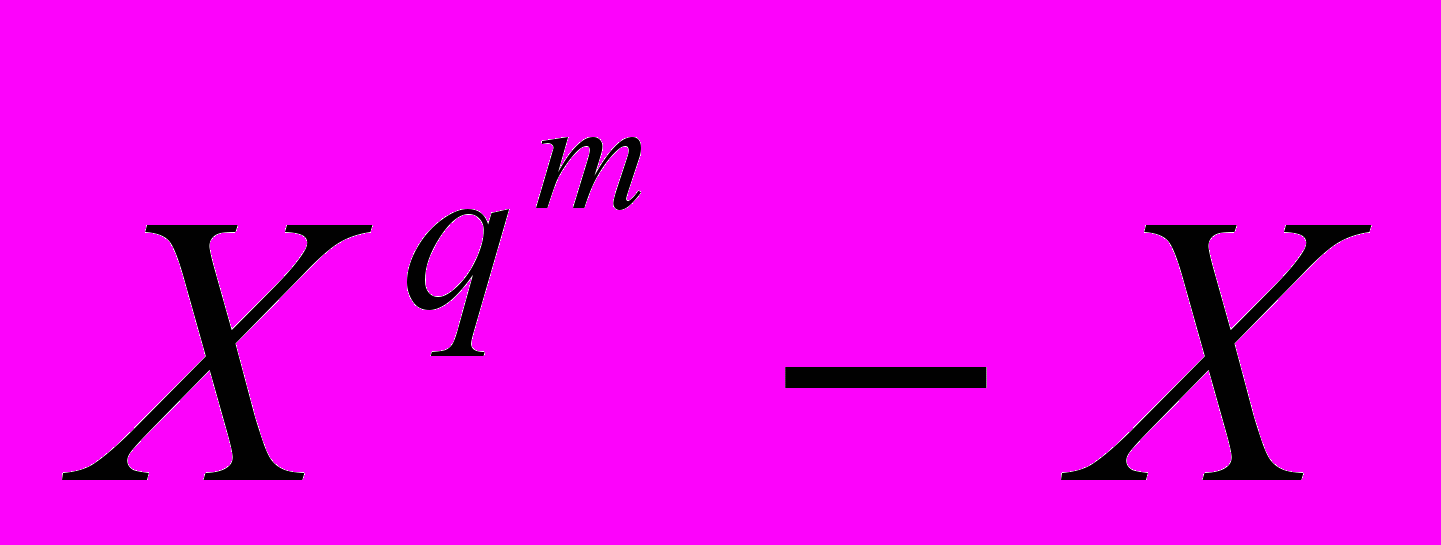8.10. Порядок корней неприводимого многочлена и порядок неприводимого многочлена.

8.11. Примитивный многочлен.

8.12. Изоморфизм полей

8.13. Автоморфизмы поля Галуа.

8.14. Группа автоморфизмов (группа Галуа) поля Галуа.

8.15. Порядок группы Галуа.

8.16. Связь между подгруппами группы автоморфизмов с подполями поля Галуа.

9. Введение в теорию кодирования.

9.1. Двоичный симметричный и стирающий каналы.

9.2. Кодовое расстояние.

9.3. Исправление и обнаружение ошибок.

9.4. Исправление стираний.

9.5. Граница Гилберта (вывод для нелинейного кода). Метод исчерпания.

9.6. Код Хэмминга.

9.7. Декодирование и сложность вычислений при декодировании.

10. Линейные коды.

10.1. Определение линейного кода как подпространства.

10.2. Ортогональные подпространства.

10.3. Минимальное расстояние и минимальный вес кода.

10.4. Порождающая и проверочная матрицы кода, их приведённо-ступенчатые формы и связь между ними.

10.5. Информационные и проверочные символы кода.

10.6. Связь проверочной матрицы линейного кода с минимальным расстоянием d.

11. Кодирование и декодирование линейного кода.

11.1. Информационный вектор и его умножение на порождающую матрицу.

11.2. Синдром. Синдромы и смежные классы в разложении пространства по кодовому подпространству

11.3. Стандартное расположение, лидеры смежных классов.

11.4. Совершенные коды.

12. Операции над кодами.

12.1. Удлинение, укорочение линейного кода.

12.2. Выкалывание.

12.3. Расширение линейного кода.

12.4. Пополнение и выбрасывание.

13. Границы параметров кодов.

13.1. Граница Варшамова-Гилберта (вывод для линейных кодов).

13.2. Границы Синглтона, Хэмминга, Плоткина и Элайса.

13.3. Другие границы.

13.4. Оценка сумм биномиальных коэффициентов, асимптотическая форма границ.

14. Коды, построенные на основе матриц Адамара.

14.1. Мощность и корректирующая способность.

14.2. Построение матриц Адамара.

14.3. Матрицы Адамара и граница Плоткина.

15. Мажоритарное декодирование.

15.1. Разделенные проверки.

15.2. Реализация кодового расстояния.

16. Коды, двойственные кодам Хэмминга.

16.1. Кодовое расстояние и мажоритарное декодирование.

17. Коды Рида-Маллера.

17.1. Порождающая матрица.

17.2. Порядок кода Рида-Маллера.

17.3. Кодовое расстояние.

17.4. Кодирование и декодирование.

17.5. Сложность декодирования.

18. Циклические коды.

18.1. Кольцо

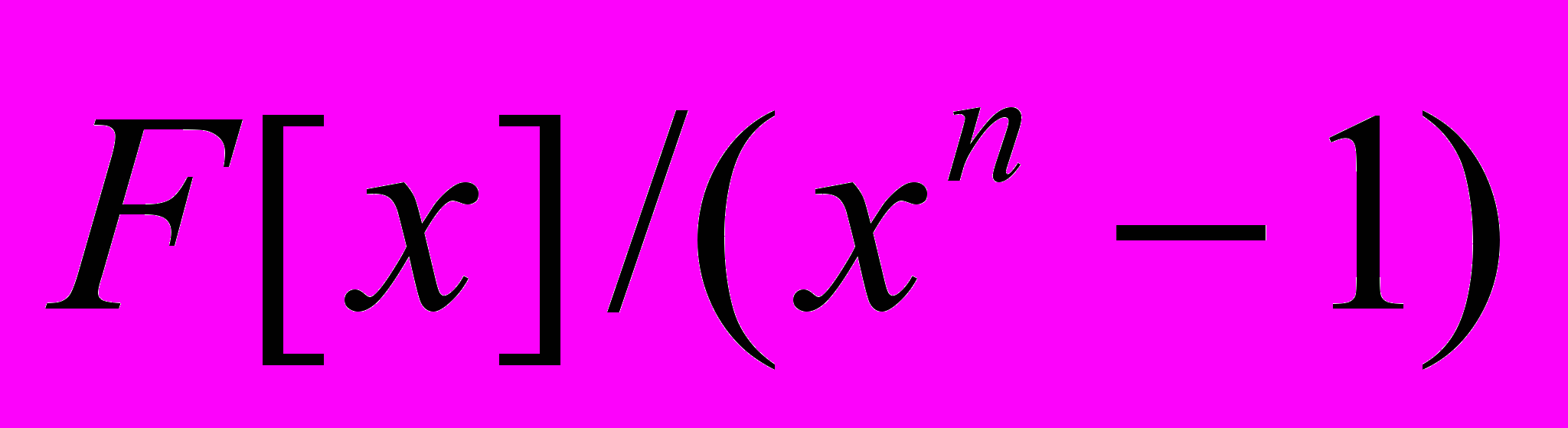многочленов по модулю многочлена

.

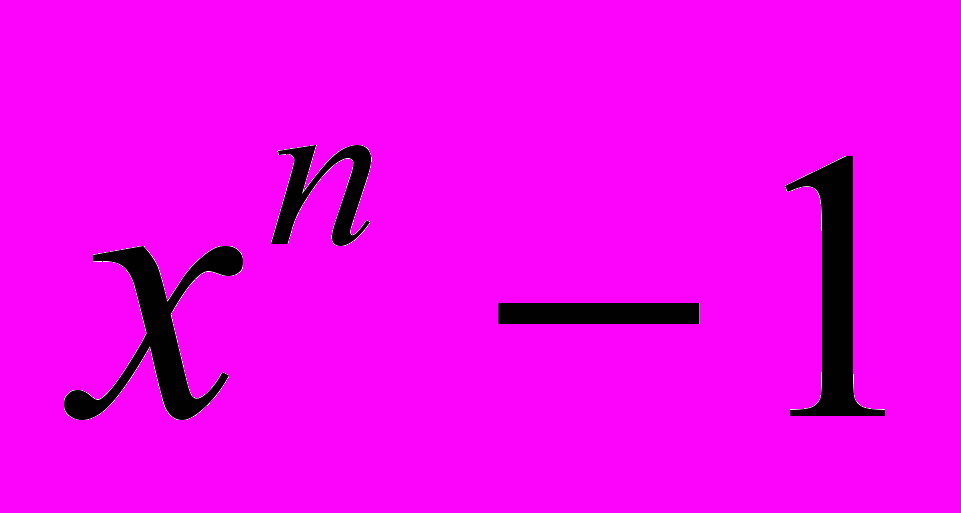18.2. Циклическое подпространство, циклический код, как идеал.

18.3. Порождающий многочлен. Проверочный многочлен.

18.4. Порождающая и проверочная матрицы циклического кода, их

приведённо-ступенчатые формы и связь между ними.

18.5. Кодирование циклического кода.

18.6. Задание циклического кода корнями его порождающего многочлена.

18.7. Длина и число проверочных символов циклического кода.

19. Коды Боуза-Чоудхури-Хоквингема (коды БЧХ).

19.1. Определение кода БЧХ. Длина кода.

19.2. Гарантированное и истинное кодовое расстояние кода БЧХ.

19.3. Число информационных символов кода БЧХ.

19.4. Двоичные коды БЧХ.

19.5. Декодирование двоичного кода БЧХ, исправляющего две ошибки. Общий случай декодирования двоичного кода.

19.6. Многочлен локаторов ошибок.

19.7. Алгоритм декодирования Питерсона-Цирлера.

19.8. Тождества Ньютона.

19.9. Основная теорема декодирования.

19.10. Сложность декодирования.

19.11. Декодирование недвоичных кодов БЧХ.

20. Коды с максимально достижимым кодовым расстоянием (МДР-коды).

20.1. Информационные совокупности кода.

20.2. Связь между информационными совокупностями кода и кодовым расстоянием МДР-кода.

20.3. Дуальный код МДР-кода.

20.4. Укорочение и выкалывание МДР-кода.

20.5. Миноры порождающей матрицы.

20.6. Коды Рида-Соломона.

20.7. Удлинение кодов Рида-Соломона.

20.8. Проверочные матрицы удлиненных кодов.

20.9. Информационный многочлен и компоненты кодового вектора.

20.10. Декодирование кодов Рида-Соломона.

20.11. Исправление пачек ошибок.

20.12. Каскадные коды.

21. Линейные переключательные схемы.

21.1. Умножение и деление многочленов посредством регистров сдвига с линейными обратными связями.

21.2. Применение для кодирования и декодирования.

21.3. Схемы умножения на константу поля Галуа и сопровождающая матрица.

21.4. Мажоритарное декодирование посредством регистра сдвига с линейными обратными связями.

21.5. Основные сведения о методах диагностики посредством переключательных схем.

СПИСОК ЛИТЕРАТУРЫ

1. Сагалович Ю.Л. Введение в алгебраические коды. М.: Минобразования РФ, Агентство по печати; МФТИ; ИППИ РАН, 2007.

2. Блейхут Р. Теория и практика кодов, контролирующих ошибки. М.: Мир. 1986.

3. Мак-Альянс Ф.Дж., Слоям Н.Дж. Теория кодов, исправляющих ошибки. М.: Связь. 1979.

4. Ван дер Бардам Б.Л. Алгебра. М.: Наука. 1976.

5. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.: Мир. 1976.

6. Виноградов И.М. Основы теории чисел. М.: Наука, 1972.

7. Бухштаб А.А. Теория чисел. М.: Просвещение, 1966.

Blog