Geum.ru

В. М. Фомичёв дискретная математика и криптология курс лекций

Вид материалаКурс лекций
6.6. Аффинные преобразования максимального периода
6.7. Задачи и упражнения
Подобный материал:
1   2   3   4

6.5. Линейные регистры сдвига


Линейное преобразование пространства Р(n) над полем Р не является п.ц. при п>0. Это следует из того, что нулевой вектор является неподвижным элементом всякого линейного преобразования. Тем не менее, длина цикла в графе линейного преобразования пространства Р(n) может быть «весьма большой» и достигать величины kn1, где k – порядок поля Р. Такие линейные преобразования называют преобразованиями максимального периода.

Рассмотрим условия максимальности периода преобразования  пространства Р(n) линейным регистром сдвига (ЛРС) с функцией обратной связи an-1хn+...+a1х2+a0х1, где a0,a1,…,an-1Р. Матрица А преобразования  имеет вид:


А = .


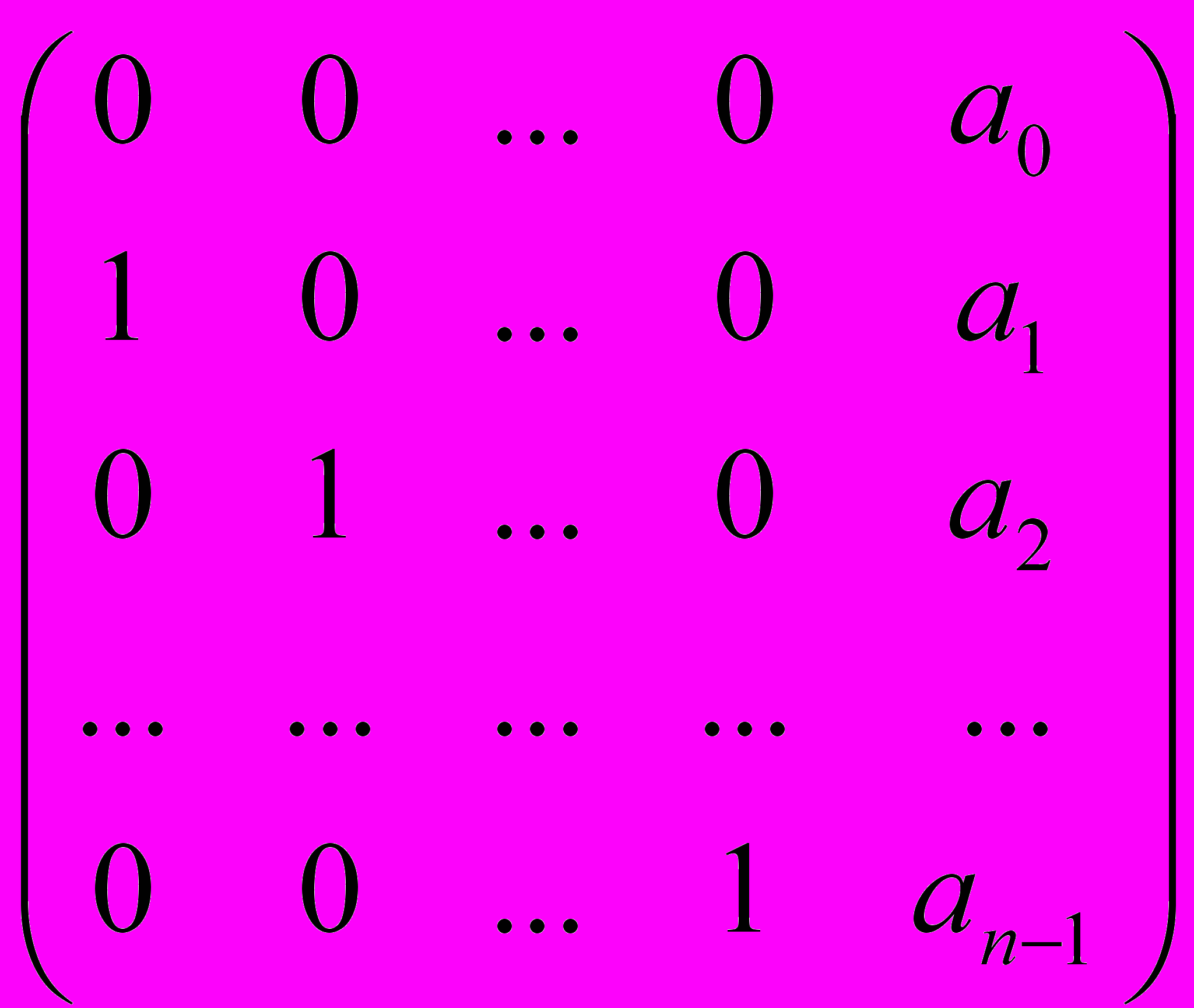Матрица А называется сопровождающей матрицей данного ЛРС. Для реализации преобразования регистра левого сдвига вектор (х1,х2,…,хп) умножается на матрицу А слева.

ЛРС длины п максимального периода обозначим ЛРСmax-п. Особый интерес в криптологии к ЛРСmax-п объясняется удобством их реализации и доказуемостью их высоких периодов (при подходящих п) в отличие от многих нелинейных преобразований. Ведь непосредственное вычисление периода преобразования (см. пример 6.1) может быть выполнено лишь для множеств небольшой мощности.

Преобразование  ЛРС имеет максимальный период в том и только в том случае, если циклическая группа  имеет порядок kn1, или иначе, матрица А имеет порядок kn1 как элемент группы линейных преобразований множества Р(n). Выразим эти условия через характеристики обратной связи.

Функции обратной связи f(x1,x2,…,xn) ЛРС однозначно соответствует многочлен F() степени n над полем Р:


F()=n- an-1n-1- an-2n-2-...- a1- a0,


называемый характеристическим многочленом этого ЛРС. Матрица А является корнем многочлена F(), и если F() неприводим над Р, её порядок совпадает с порядком многочлена F(). Поэтому преобразование  имеет максимальный период тогда и только тогда, когда F() - примитивный многочлен, то есть:

1) F() неприводим над полем Р;

2) F() делит многочлен 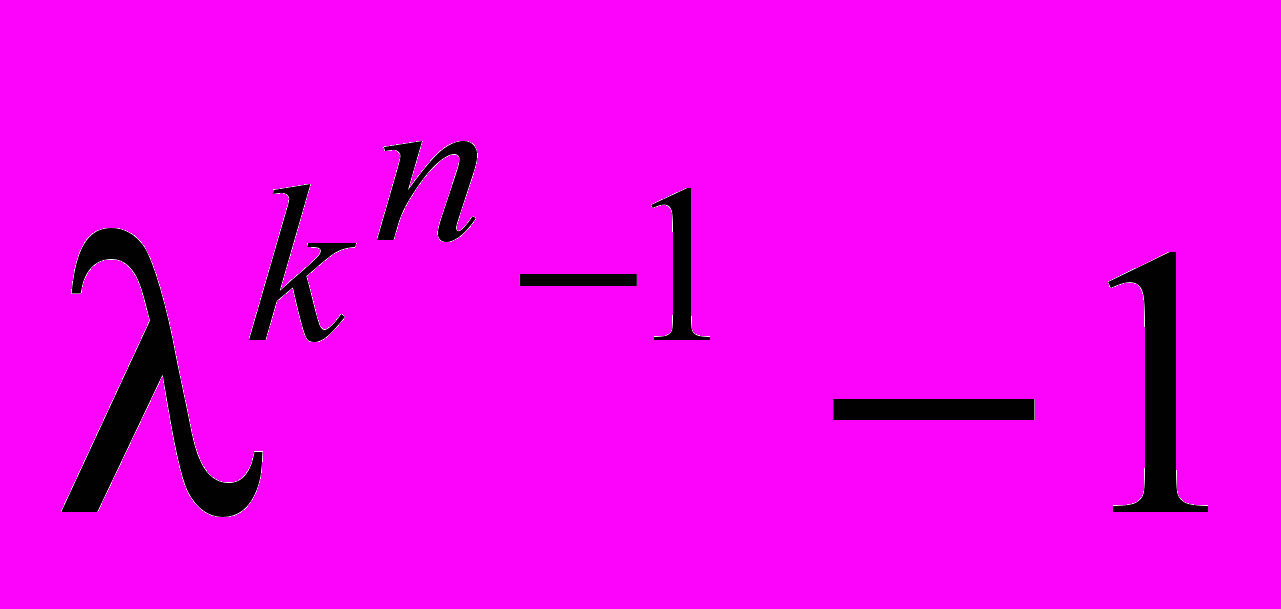и не делит ни один из многочленов вида d-1, где d/kn-1 и dkn-1.

Построение примитивных многочленов в общем случае связано со сложными вычислениями. На практике используются таблицы примитивных многочленов.

Для двоичных ЛРС из условий примитивности многочлена F() вытекает следующее утверждение.

Утверждение 6.5. Если многочлен F() степени n>1 неприводим над полем GF(2), и 2n-1 – простое число, то преобразование ЛРС множества Vn c характеристическим многочленом F() имеет максимальный период.

Доказательство. Из простоты числа 2n-1 следует, что имеется лишь один делитель d числа 2n-1, отличный от 2n-1, а именно, d=1. Осталось заметить, что F() не делит многочлен -1 и делит многочлен 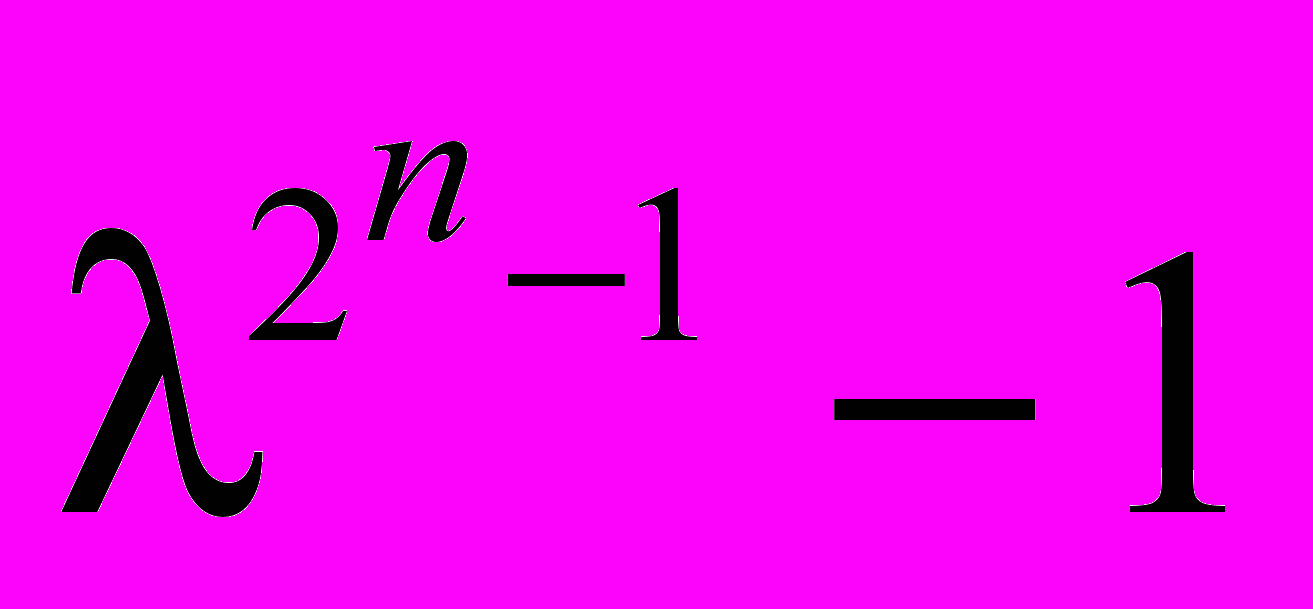, так как все элементы поля GF(2п), кроме единицы, имеют в мультипликативной группе этого поля порядок 2n-1. Следовательно, F() примитивен. 

Утверждение 6.6. Примитивный многочлен F() над полем GF(2) содержит нечётное число членов.

Доказательство. В противном случае единица поля GF(2) является его корнем. 

Утверждение 6.7. Если многочлен F() над полем GF(2) примитивен, то примитивен и многочлен nF(1/).

Последнее утверждение позволяет сократить в два раза таблицы примитивных многочленов над полем GF(2).


6.6. Аффинные преобразования максимального периода

Биективное аффинное преобразование  пространства Р(n) над полем Р порядка k, граф которого содержит цикл длины kn1, назовём преобразованием максимального периода. Определим условия максимальности периода аффинного преобразования.

Утверждение 6.8. Пусть  - линейное преобразование пространства Р(n) и элемент х множества Р(n) имеет предпериод т и период t относительно преобразования . Тогда вектор х, определяемый выражением


х=т(х)+т+1(х)+…+т+t-1(х), (6.5)


есть неподвижный элемент преобразования .

Доказательство. Так как преобразование  линейно, то


(х)=т+1(х)+т+2(х)+…+т+t-1(х)+т+t(х).


По утверждению 6.3 вершины i(х) графа G() при iт являются циклическими и лежат на цикле длины t, поэтому т+t(х)=т(х). Следовательно, (х)=х.

Таким образом, каждому элементу хP(n) соответствует неподвижный элемент линейного преобразования , определяемый выражением (6.5), обозначим его х,.

Аффинные преобразования 1 и 2 пространства P(n) назовём а-параллельными, где а - ненулевой вектор пространства P(n), если 1(х)-2(х)=а для всех хP(n). Заметим, что а-параллельные преобразования 1 и 2 либо оба биективны, либо оба небиективны.

Теорема 6.9. Пусть  - биективное линейное преобразование пространства P(n) над полем Р характеристики p, и  есть а-параллельное ему аффинное преобразование. Тогда  и  оба либо являются, либо не являются преобразованиями максимального периода.

Доказательство. По условиям теоремы (х)=(х)+а для всех хP(n), где аи, и - нулевой вектор пространства P(n). Отсюда с использованием индукции по i несложно вывести равенство, верное для любого хP(n) и любого натурального i:


i(х) = i(х)+i-1(а)+i-2(а)+…+(а)+а. (6.6)


По утверждению 6.3, последовательность {i(а)}, i=1,2,…, является периодической с периодом tа,, равным длине цикла, которому принадлежит вектор а. Тогда по утверждению 6.8 неподвижным элементом преобразования  является элемент а,=l-1(а)+…+(а)+а при l=tа,.

По теореме 6.1 последовательность {i(а)+…+(а)+а}, i=0,1,2,…, является периодической с периодом t, где


t/d(а,)tа, (6.7)


и d(х) есть порядок элемента х как элемента аддитивной группы пространства Р(n). Очевидно, d(х)=1 при х=0 и d(х)=р в противном случае.

Из равенства (6.6) имеем, что последовательность {i(х)} есть сумма периодических последовательностей {i(х)} и {i(а)+…+(а)+а}, i=1,2,…, с периодами соответственно tх, и t. Значит, по теореме 6.2 с учётом равенства (6.7) для периода tх, последовательности {i(х)} выполнено:


tх, /НОК(tх,,d(а,)tа,). (6.8)

Если  - преобразование максимального периода, то оно имеет единственный неподвижный элемент – вектор и, и его порядок равен 1. Поэтому d(а,)=1 и из (6.8) при х=а имеем:


tа,/tа, . (6.9)


С другой стороны, из равенства (6.6) следует, что i(х)=i(х)-i(u) для всех хP(n) и любого натурального i. Значит, по теореме 6.2 tх,/НОК(tх,,tu,). Учитывая, что векторы а и u принадлежат одному циклу преобразования , из последнего соотношения получаем при х=а, что tа,/tа,.

Отсюда и из (6.9) заключаем: tа,=tа,= kn-1.

Пусть теперь биективное аффинное преобразование  пространства Р(n) есть преобразование периода kn-1. Вектор а не является неподвижной точкой преобразования , так как его прообраз есть вектор и, поэтому tа,=kn-1. Тогда из равенства (6.8) при х=а следует, что


(kn-1)/d(а,)tа, .


Так как величина d(а,) равна либо 1, либо характеристике р поля Р, то (kn-1,dа,)=1, поэтому из последнего соотношения получаем, что (kn-1)/tа,. То есть, tа,=kn-1, и  - преобразование максимального периода. 


6.7. Задачи и упражнения


6.1. Пусть {xi} и {yi} - периодические последовательности над кольцом вычетов по модулю k с периодами t1 и t2 соответственно, где НОД(t1,t2)=1.

1) Докажите, что период t последовательности {(xi+yi)modk} равен t1t2. Каково наименьшее значение t, если условие НОД(t1,t2)=1 не выполнено? Чему оно равно?

2) При каких а и b период  последовательности {(аxi+byi)modk} равен t1t2?

6.2. Пусть {xi} - периодическая последовательность над множеством Х с периодом t.

1) Каков период последовательности {xri}, где r – натуральное?

2) Каков период последовательности, полученной из {xi} изъятием подпоследовательности {xri}, где r – натуральное?

3) Каковы периоды последовательностей из пунктов 1),2), если {xi} не содержит одинаковых членов?

6.3. Пусть  - преобразование регистра левого сдвига множества Vn с обратной связью f. Постройте граф преобразования , определите предпериоды и периоды нулевого вектора и преобразования , если:

а) n=4, f(x1,x2,..., x4) = x1x2x4;

б) n=4, f(x1,x2,..., x4) = x1x3 x2x41;

в) n=5, f(x1,x2,..., x5) = x2x3x5x3x4x2x4x2x11;

г) n=5, f(x1,x2,..., x5) = x2x3x4x5x1x3x4x2x4x3x2x11.

6.4. Какова цикловая структура и период аффинного преобразования  множества Vn, где (x)=Exa, E – единичная матрица, а0.

6.5. Какова цикловая структура и период преобразования k, если  - полноцикловое преобразование множества Vn?

6.6. Является ли полноцикловым преобразование (х)=ах+b кольца вычетов по модулю 2n, реализуемое линейным конгруэнтным генератором, если:

а) n=10, a=10, b=7;

б) n=10, a=9, b=6;

в) n=10, a=9, b=9.

6.7. Является ли полноцикловым преобразование  множества Vn:

а) n=3, ={x11, x1x2, x1x2x3};

б) n=3, ={x1, x1x21, x1x2x3};

в) n=4, ={x1, x1x2, x1x2x3, x1x2x2x3x4}.

6.8. Пусть f(x1,x2,…,xn) – функция обратной связи двоичного ЛРСmax-п. Докажите, что регистр сдвига с обратной связью f(x1,x2,…,xn)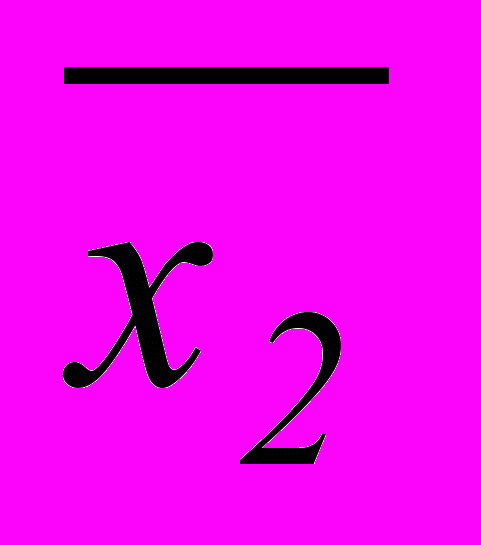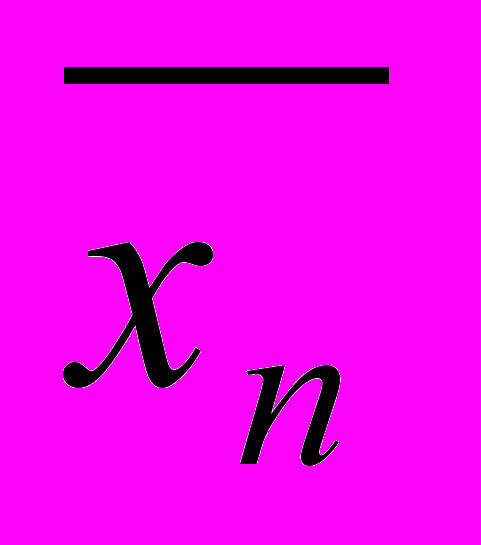… является полноцикловым.

6.9. Пусть f(x1,x2,…,xn)=anхn...a2х2х1 – функция обратной связи биективного преобразования двоичного (левого) ЛРС. Докажите, что преобразование регистра сдвига с обратной связью f(x1,x2,…,xn)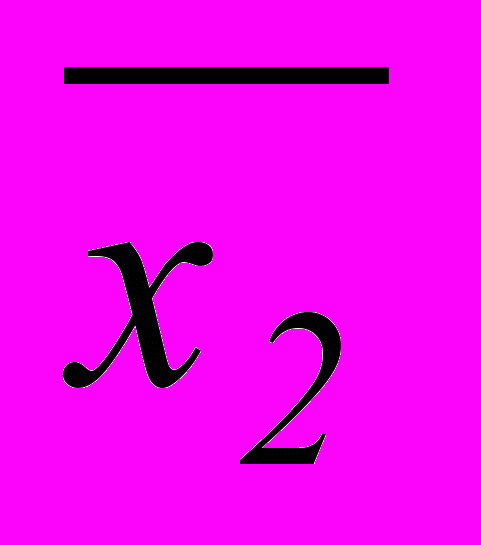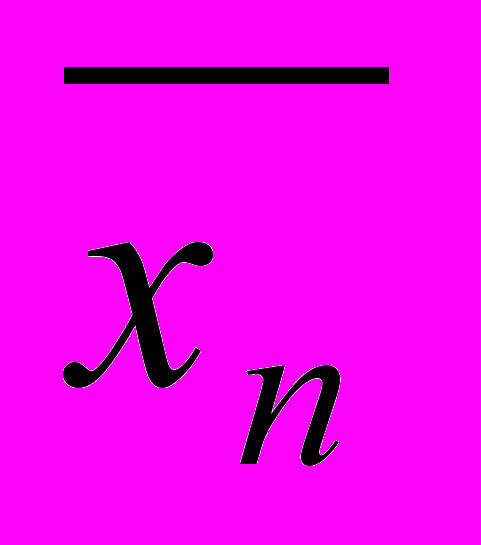… не имеет неподвижных элементов тогда и только тогда, когда an...a2=1.

6.10. Пусть  - преобразование двоичного ЛРСmax-п, =ха - аффинное преобразование множества Vn. Определите неподвижные элементы преобразования .

6.11. Пусть  - преобразование множества Vn,  - инволюция на множестве Vn. Докажите, что t=t.

6.12. Каков период аффинного преобразования множества Vn =a, где  - линейная инволюция и a – ненулевой вектор?

6.13. Пусть  - преобразование двоичного ЛРСmax-п. Каков период преобразования =r, где r – целое; степень числа 2?

6.14. Докажите, что многочлен над полем GF(2), не содержащий нечётных степеней переменной, не является примитивным.

6.15. Является ли примитивным многочлен f() над полем GF(2):

а) f() = 52;

б) f() = 521;

в) f() = 641;

г) f() = 1110976521.