Geum.ru

В. М. Фомичёв дискретная математика и криптология курс лекций

Вид материалаКурс лекций
18.7. Задачи и упражнения
19.4.2. Описание алгоритма
6.1. Периоды последовательностей
6.2. Граф отображения
6.3. Характеристики периодичности преобразования
X и периода вектора x
6.4. Полноцикловые преобразования
Подобный материал:
1   2   3   4

18.7. Задачи и упражнения



Глава 19. ПРИЛОЖЕНИЯ


19.1. Алгоритм шифрования DES

19.2. Алгоритм ГОСТ 28147-89

19.3. Блочный шифр IDEA

19.4. RIJNDAEL

19.4.1. Математические операции алгоритма

19.4.2. Описание алгоритма


19.4.2.1. Состояния, ключи и число циклов шифрования

19.4.2.2. Цикловое преобразование

19.4.2.3. Ключевое расписание

19.5. Стандарт генерации ключей ANSI Х9.17

19.6. Алгоритм А5/1

19.7. Американский стандарт хэш-функции (SHS)

19.8. Криптосистема RSA

19.9. Шифрсистема Эль Гамаля

19.10. Схема цифровой подписи Эль Гамаля


Словарь терминов

Ответы и решения

Литература


Глава 6. СТРУКТУРА И ПЕРИОДЫ ПРЕОБРАЗОВАНИЙ


Многие криптографические системы используют для шифрования информации псевдослучайные последовательности, генерируемые программным способом. Качество шифрования определяется определёнными свойствами псевдослучайных последовательностей, в частности, их периодами. Так как порождение последовательностей большого периода основано на реализации многократных итераций преобразований, то для криптологии представляет интерес изучение структурных и периодических свойств преобразований конечных множеств.


6.1. Периоды последовательностей


Последовательность элементов множества X назовём последовательностью над X и обозначим X.

Последовательность X={x1,x2,…,xi,…} над X называется периодической с предпериодом N и периодом T, если N+1 и T – наименьшие из натуральных чисел, при которых xi=xi+T для всех i>N. Заметим, что если для всех i>N в xi=xi+, то T/.

Если N=0, то последовательность X называется чисто периодической с периодом T.

Утверждение 6.1. Если последовательность Y={(xi)} над Y получена с помощью отображения :ХY из периодической последовательности X={xi} над Х с предпериодом N и периодом T, то Y - периодическая с предпериодом N’ и периодом T’, где N’N, T’ делит T.

Доказательство. Если xi=xi+Т, то и (xi)=(xi+Т), следовательно, N’N и T’/T. 

Теорема 6.1. Для последовательностей X={xi} и Y={yi} над конечной аддитивной группой X, где yi=x1+x2+…+xi, i=1,2,…, верны утверждения:

1. Если X - периодическая с предпериодом N>0 и периодом T, то Y – периодическая с предпериодом N-1 и периодом T’, где T’/dT и d есть порядок элемента yN+T-yN группы X.

2. Если X - чисто периодическая с периодом T, то Y – чисто периодическая с периодом T’, где T’/dT и d есть порядок элемента yT группы X, при этом yrdT=0 при r=1,2,…

Доказательство. Из соотношения между членами последовательностей X и Y имеем:


yi+dT = yi+xi+1+xi+2+…+xi+dT.


В условиях утверждения 1 в силу периодичности X при всех iN выполнено xi+1+xi+2+…+xi+T=yN+T -yN, и как следствие


yi+dT = yi+d(yN+T-yN) = yi.


Значит, N’<N и T’/dT. Если N’<N-1, то yN-1+dT=yN-1 и, следовательно, хN-1+dT=хN-1, что противоречит условию.

В условиях утверждения 2 порядок d элемента yT совпадает при всех i с порядками элементов xi+1+xi+2+…+xi+T. Поэтому при всех i выполнено yi+dT=yi, значит T’/dT. При натуральных r имеем


yrdT = rd(x1+x2+…+xT) = rdyT = 0. 


Рассмотрим последовательность X над X=Х1…Xп, в которой каждый член состоит из п компонент. Выделим в X последовательность (над Хj) j-х компонент её членов. Обозначим её Xj и назовём j-й координатной последовательностью последовательности X, j=1,2,…,n.

С другой стороны, из последовательностей Xj={xij} - над Хj, j=1,2,…,n, можно образовать последовательность X={xi} над Х1…Xп, где xi=(xi1,…,xin), i=1,2,… Последовательность X назовём сопряжением последовательностей Х1,…,Xп (обозначается X=Х1*…*Xп).

Очевидно, любая последовательность X над X=Х1…Xп является сопряжением п координатных последовательностей. Из данных определений следует утверждение.

Утверждение 6.2. Последовательность X над X=Х1…Xп является периодической с предпериодом N и периодом T тогда и только тогда, когда Xj – периодическая последовательность с предпериодом Nj и периодом Tj, где N=max{N1,…,Nn}, T=НОК(T1,…,Tn).

Теорема 6.2. Если последовательность Y={(xi,1,…,xi,n)} периода T получена с помощью отображения :Х1…XпY из периодических последовательностей Xj={xij} над Хj с периодами Tj, j=1,…,n, то T делит НОК(T1,…,Tn). Если при этом отображение  биективно по всем переменным, то

TНОК(T1,…,Tn)/НОД(T1,…,Tn).


Доказательство. Делимость НОК(T1,…,Tn) на T следует из утверждений 6.1 и 6.2. Без ущерба для общности докажем нижнюю оценку для п=2.

Пусть T1=t, T2=, НОД(t,)=d. Тогда t=pd, =qd, НОК(t,)=pqd, где (p,q)=1.

Предположим, что (xi,1,xi,2)=(xi+T,1,xi+T,2) для всех i, где T<pq. Так как T/pqd, то при сделанном предположении T=, где /p, /q, /d, причём, равенства =p и =q не выполнены одновременно, иначе было бы Tpq.

Пусть для определённости . Тогда в последовательности Y имеют место повторы через каждые  членов, где =qd (так как T/). Следовательно, для всех натуральных i

(xi,1,xi,2)=(xi+,1,xi+,2).


Так как /, то для всех i верно xi+,2=xi,2, и последнее равенство принимает вид:

(xi,1,xi,2)=(xi+,1,xi,2). (6.1)


По условию (p,q)=1, значит и (,q)=1. Поэтому t не делит , то есть, xi,1xi+,1 для некоторых i. Последнее неравенство несовместимо с (6.1) при биективности отображения  по первой переменной. Следовательно, Tpq. 


6.2. Граф отображения


Пусть имеется отображение :XY, где X и Y - конечные множества мощности n и m соответственно, n,m>1. Отображению  поставим в соответствие ориентированный двудольный граф G()=(XY,U), где XY - множество вершин, U - множество дуг, и пара (x,y)UxX, y=(x)Y. Граф G() называют графом отображения.

Из однозначности отображения  следует, то полустепень исхода любой вершины xX равна 1 и U=X=n. Полустепень захода py вершины y графа G() равна числу прообразов элемента y относительно отображения , 0pyп. При этом 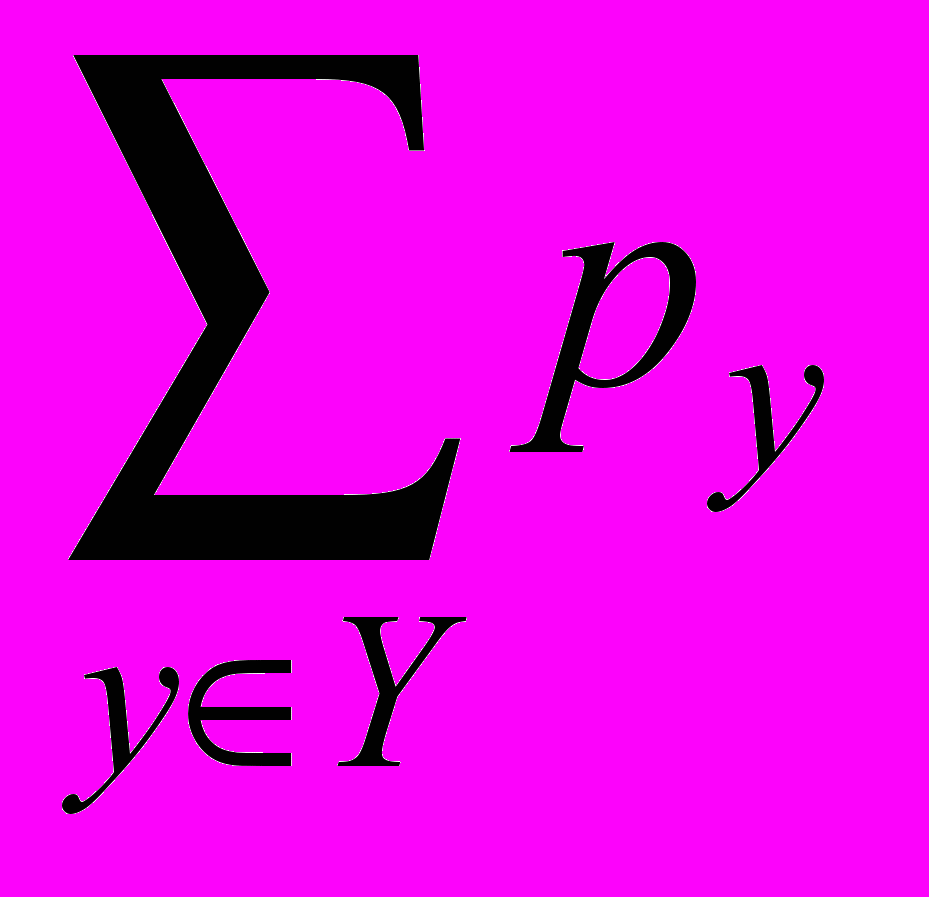=п.

Если  - преобразование п-множества X, то графом преобразования  называют ориентированный граф G()=(X,U) с множеством вершин X и множеством дуг U, где (x,y)Uy=(x).

Полустепень захода px равна 1 для всех xX тогда и только тогда, когда  биективно.

Граф G() преобразования  состоит из r компонент связности, 1r<n, каждая из которых представляет собой простой цикл и, в случае небиективного преобразования, возможно, несколько подходов к этому циклу.

Структурными характеристиками графа G() являются число компонент связности, число циклических вершин, число циклов и число подходов к циклам заданной длины и др. Неподвижный элемент преобразования  образует петлю в графе G().

Граф G() биективного преобразования  (подстановки на множестве Х) состоит из r независимых циклов, 1rn. Если ki - число циклов длины i в графе G(), i{1,2,...,n}, то:


,


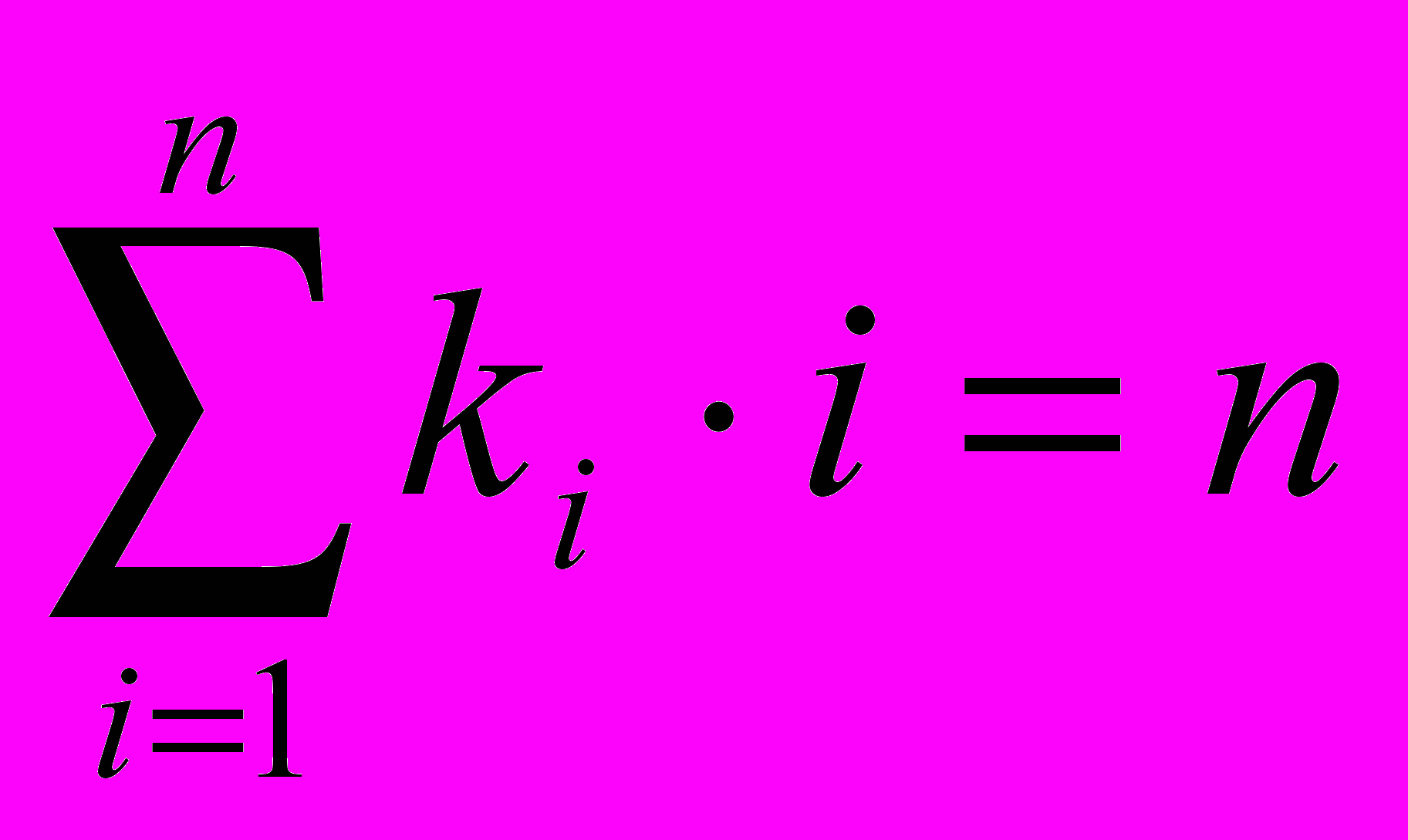где 0kin. Цикловая структура такого графа записывается в виде набора символов , в котором опускаются все компоненты 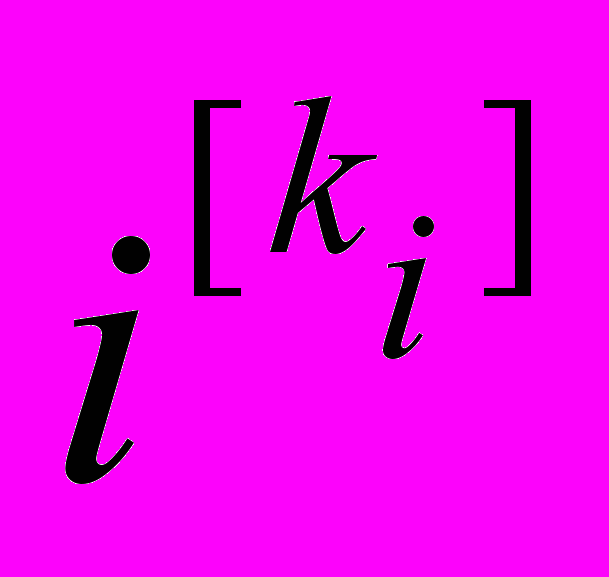, для которых ki=0.

Преобразования  и  множества X называются подобными, если найдётся биективное преобразование  того же множества, при котором  = -1.

Отношение подобия на множестве преобразований есть отношение эквивалентности.

Теорема 6.3. Преобразования  и  множества X подобны тогда и только тогда, когда графы G() и G() изоморфны.

Доказательство. Если преобразования  и  множества X подобны, то у=(х) тогда и только тогда, когда (у)=((х)). Следовательно, графы G() и G() изоморфны, так как отличаются лишь переобозначением вершин с помощью подстановки . Обратное утверждение доказывается рассуждениями в обратном порядке. 


6.3. Характеристики периодичности преобразования


Преобразованию  конечного множества X и элементу xX поставим в соответствие последовательность ={i} i=0,1,2,… над полугруппой всех преобразований множества X и последовательность х над X:


х = {i(х)} i=0,1,2,…


В силу конечности множества X обе последовательности содержат конечное число элементов, при этом если i–й и j–й члены любой из этих последовательностей совпадают, i<j, то совпадают их (i+r)–й и (j+r)–й члены, r=1,2,… Следовательно, обе эти последовательности являются периодическими.

Периодом (предпериодом) элемента x относительно преобразования  называется период (предпериод) последовательности х. Обозначим их tx, и пx, соответственно (или tx и пx, если преобразование  фиксировано).

Утверждение 6.3. 1) Если x – циклическая вершина графа G(), то пx=0 и tx равен длине цикла, которому принадлежит вершина x.

2) Если x – ациклическая вершина графа G(), то пx равен длине подхода к циклу в графе G(), начинающегося из вершины x, и tx равен длине цикла той компоненты связности, которой принадлежит вершина x.

Доказательство. Из определения предпериода пx следует, что повторы в последовательности х имеют место лишь для членов с порядковым номером пx+1 и больше. Следовательно, первые пx членов не могут быть циклическими вершинами графа G().

Из определения периода tx следует, что периодический отрезок последовательности х образует цикл графа G(). 

Периодом (предпериодом) преобразования  называется период (предпериод) последовательности , обозначим их t и п.

Утверждение 6.4. Пусть l1,l2, ... ,lr - все различные длины циклов графа G() преобразования . Тогда


t = НОК(l1,l2, ... ,lm).


Если  - обратимое преобразование, то п=0, в противном случае п равен наибольшей из длин подходов к циклам графа G().

Доказательство. Из определения периода преобразования и утверждения 6.3 следует, что


t=НОК(tx /xX)=НОК(l1,l2, ... ,lm); п=max{пx/xX}.


Если  биективно, то первые t членов последовательности  образуют циклическую группу  порядка t.

Для периода преобразования  п-множества X и периода вектора xX относительно преобразования  верны оценки:


1txп; 1tп!.


Обе нижние оценки достигаются для тождественного преобразования. Первая верхняя оценка достижима при любом множестве X, вторая достигается лишь при множествах X мощности не более 2.

Пример 6.1. Определим период и цикловую структуру преобразования  множества V3 регистра правого сдвига с одной обратной связью f(x1,x2,x3) = x1x2x3.

Из следствия 1 теоремы 5.4. имеем, что  – биективное преобразование. Построим независимые циклы графа G(). При построении очередного цикла выбираем в качестве начальной вершины x ту, которая не фигурировала при предыдущих вычислениях, и вычисляем элементы последовательности х до тех пор, пока впервые не выполнится равенство l(x)=x, означающее, что элемент x принадлежит циклу длины l.

В нашем примере вычисления дают следующие результаты:

1) (0,0,0)=(0,0,0), значит t(0,0,0)=1;

2) (0,0,1)=(1,0,0), (1,0,0)=(1,1,0), (1,1,0)=(0,1,1), (0,1,1)=(0,0,1), значит t(0,0,1)= t(1,0,0)= t(1,1,0)= t(0,1,1)=4;

3) (0,1,0)=(1,0,1),(1,0,1)=(0,1,0), значит t(0,1,0)=t(1,0,1)=2;

4) (1,1,1)=(1,1,1), значит t(1,1,1)=1.

Таким образом, цикловая структура преобразования  имеет вид (1[2],2[1],4[1]); период t преобразования  равен НОК(1,2,4)=4.


6.4. Полноцикловые преобразования


Особый интерес для криптографических приложений представляют преобразования с экстремальными периодическими свойствами.

Преобразование  п-множества называется полноцикловым (п.ц.), если граф G() представляет собой цикл длины п. Всякое п.ц. преобразование  биективно, и tx,=t=п для всех xX.

Теорема 6.4. Число различных п.ц. преобразований n-множества равно (n1)!.

Доказательство. Построение полного цикла из элементов n-множества X можно рассматривать как размещение на n свободных позициях окружности всех n различных элементов множества X. Число различных таких размещений равно числу различных перестановок элементов n-множества, то есть, равно п!.

В то же время, перестановки элементов эквивалентны, если отличаются лишь параллельным сдвигом, так как представляют один и тот же цикл преобразования. Следовательно, множество всех построенных циклов разбивается на классы эквивалентных циклов, где в каждом классе содержится по п циклов. Таким образом, число п.ц. преобразований п-множества равно числу неэквивалентных циклов, то есть (п-1)!.

Пример 6.2. Линейный конгруэнтный генератор (ЛКГ).

Пусть Еk - кольцо вычетов по модулю k,  - преобразование ЛКГ множества Еk, если для любого хЕk:


(x)=(ax+b)modk,


где a, b и k – константы из Еk, называемые множителем, сдвигом, и модулем соответственно.

ЛКГ имеет период не более k. Для любых k и x имеются константы a и b, при которых t=k. Такие генераторы называют ЛКГ полного (или максимального) периода. Приведём без доказательства следующую теорему [61].

Теорема 6.5. Преобразование ЛКГ имеет период k :
  1. (b,k)=1;
  2. a-1 кратно любому простому делителю числа k;
  3. a-1 кратно 4, если k кратно 4.

В частности, если k=2r, то t=2r тогда и только тогда, когда b - нечётное число и а1(mod4).

Теорема 6.6. Биективное преобразование  n-множества X является п.ц. тогда и только тогда, когда для любого отличного от константы отображения :XY, где Y2, отображения  и  различны.

Доказательство. Пусть для п.ц. преобразования  множества X, для любого xX и указанного отображения :


(х)=(х). (6.2)


Тогда для любого натурального t и любого xX:


t(х) =(х),


а это с учётом полноцикловости преобразования  означает, что отображение  - константа. Имеем противоречие, из которого вытекает, что отображения  и  различны.

Пусть теперь  - неполноцикловое биективное преобразование множества X, и X’ – подмножество множества X, образующее некоторый цикл графа G(). Определим отличное от константы отображение :XY, где Y={y1,y2,…}: (х)=y1 для всех хX’ и (х)=y2 для всех хX\X’. При таком  для любого xX выполняется равенство (6.2). Следовательно, отображения  и  совпадают. 

Пусть  и  - преобразования множеств Х(n) и Х(n-1) соответственно, где Х=k и  задано подсистемой системы :


= {f1(x1,x2,...,xn-1),...,fп-1(x1,x2,...,xn-1),fп(x1,x2,...,xn)},


= {f1(x1,x2,...,xn-1),...,fп-1(x1,x2,...,xn-1)}.


Рассмотрим критерий полноцикловости преобразования . Каждому пути s=(s1,s2,…,st) в графе G() поставим в соответствие преобразование (s):


(s)=, (6.3)


где для вершины а=(а1,а2,…,ап-1)Х(n-1) графа G() под fn(a,xn) понимается подфункция fn(а1,а2,…,ап-1,xn), реализующая преобразование множества Х.

Теорема 6.7. Преобразование  является п.ц. тогда и только тогда, когда  - п.ц. преобразование множества Х(n-1) и (s) – п.ц. преобразование множества Х, где s - цикл в G().

Доказательство. Покажем корректность формулировки теоремы, ведь при п.ц. преобразовании  в качестве преобразования (s) множества Х может быть рассмотрено kn-1 различных преобразований в зависимости от начала отсчёта вершин цикла s. Для этого убедимся, что при п.ц. преобразовании  все эти преобразования подобны.

Действительно, если s=(s1,s2,…,st-1,st), s’=(s2,s3,…,st,s1), где t=kn-1, и (s) – п.ц. преобразование множества Х, то из этого следует, что (s) - биективно и в силу (6.3) подфункция fn(a,xn) при любом аХ(n-1) реализует также биективное преобразование. Следовательно, биективно и преобразование (s’) как композиция биективных преобразований, где


(s’) = fn(s2,xn)fn(s3,xn) …fn(st,xn)fn(s1,xn).


Отсюда и из (6.3) следует подобие преобразований (s) и (s’):


(s’) = fn(s1,xn)-1fn(s1,xn)(s’) = fn(s1,xn)-1(s)fn(s1,xn).


То есть, независимо от начала отсчёта вершин цикла s графа G() преобразование (s) является п.ц.

Пусть х[kn] - отрезок последовательности х, состоящий из её первых kn членов, хХ(n). Разобьём х[kn] на k последовательных отрезков х[kn]1, …, х[kn]k по kn-1 членов.

Если преобразования  и (s) п.ц., то, судя по первым п-1 координатам, все члены отрезка х[kn]i различны в силу полноцикловости преобразования , i=1,2,…k. В то же время, судя по п-й координате, последние члены отрезков х[kn]1, …,х[kn]k различны в силу полноцикловости преобразования (s). Следовательно, все члены отрезка х[kn] различны, и  - п.ц. преобразование.

Если  - п.ц. преобразование множества Х(n), то  - п.ц. преобразование множества Х(n-1), так как в этом случае для периодов t и t выполняются соотношения:


tkn-1, kn=t tk.


Далее, если  и  - п.ц. преобразования множеств Х(n) и Х(n-1) соответственно, то для периода t(s) преобразования (s) выполняются равенства:


kn = t = tt(s) = kn-1t(s).


Следовательно, (s) – п.ц. преобразование множества Х. 

Следствие 1. Пусть i - биективное треугольное преобразование множества Х(i), задаваемое системой координатных функций


i = {f1(x1), f2(x1,x2), ... , fi(x1,x2,...,xi)}, i=1,2,… (6.4)


Преобразование п является п.ц. тогда и только тогда, когда для всех i=1,2,…,п преобразования i(si-1) множества Х - п.ц., где при i>1 путь si-1= 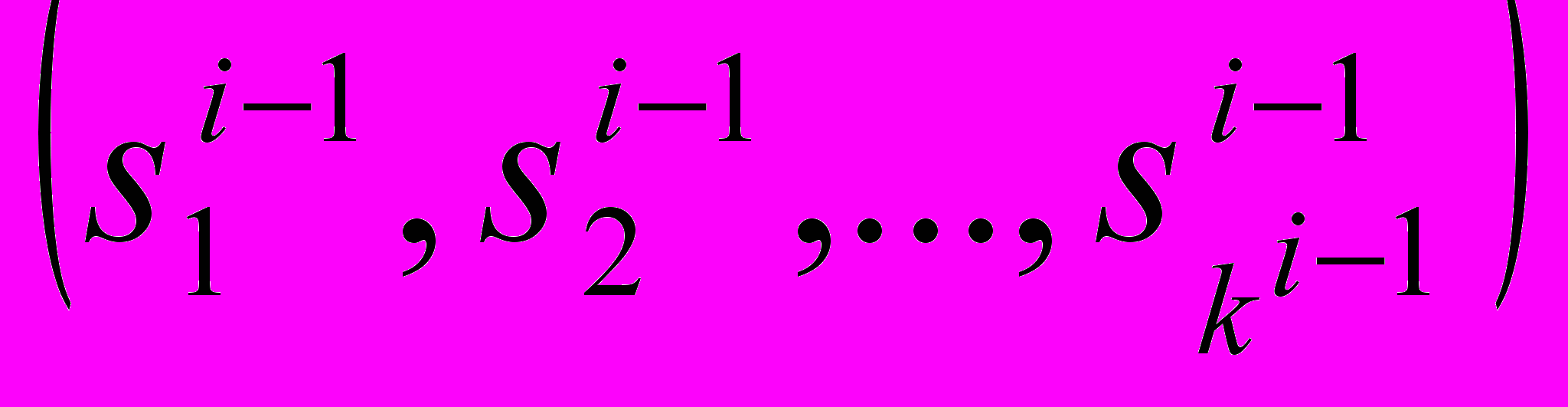- цикл в графе G(i-1) и i(si-1) = 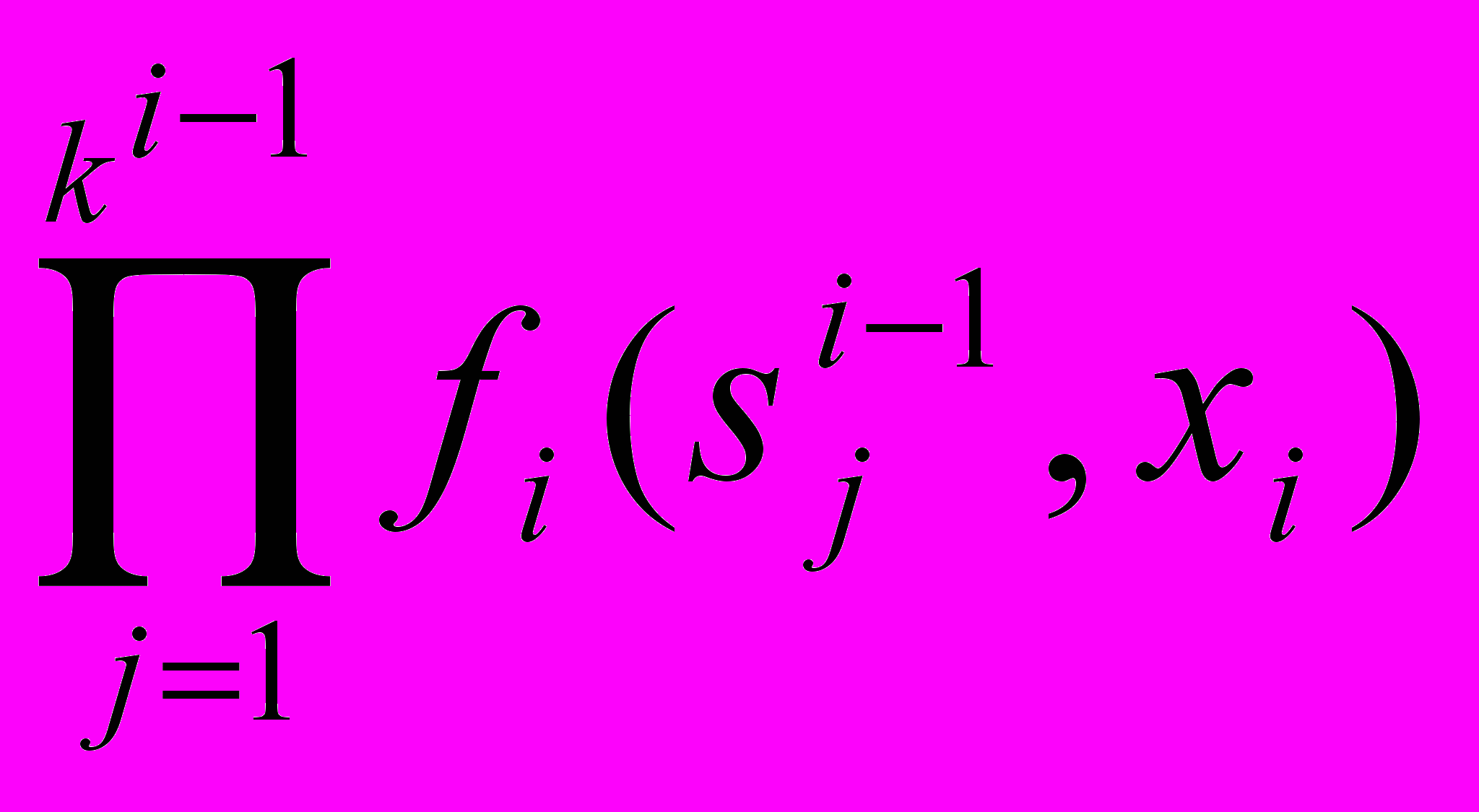, 1(s0)=1=f1(x1).

Доказательство. Если преобразование п множества Х(n) является п.ц., то, применяя п-1 раз прямое утверждение теоремы 6.7 для i=n, n-1,…, 2, получаем, что преобразование i-1 множества Х(i-1) и преобразование i(si-1) множества Х также являются п.ц. Следовательно, для i=1,2,…,п преобразования i(si-1) множества Х являются п.ц.

Если для i=1,2,…,п преобразования i(si-1) множества Х являются п.ц., то, применяя п-1 раз обратное утверждение теоремы 6.7 для i=2, 3,…, n, получаем, что из полноцикловости преобразований i-1 и i(si-1) следует полноцикловость преобразования i множества Х(i). 

Следствие 2. Пусть в условиях теоремы 6.7  и  - преобразования множеств Vn и Vn-1 соответственно. Преобразование  является п.ц. тогда и только тогда, когда  - п.ц. преобразование множества Vn-1 и


fп(x1,x2,...,xn)=g(x1,x2,...,xn-1)xn,


где вес функции g(x1,x2,...,xn-1) нечётен.

Доказательство. В данных условиях (s) есть преобразование множества {0,1}, поэтому если s - цикл в графе G(п-1), то для любого х{0,1}


(s)(х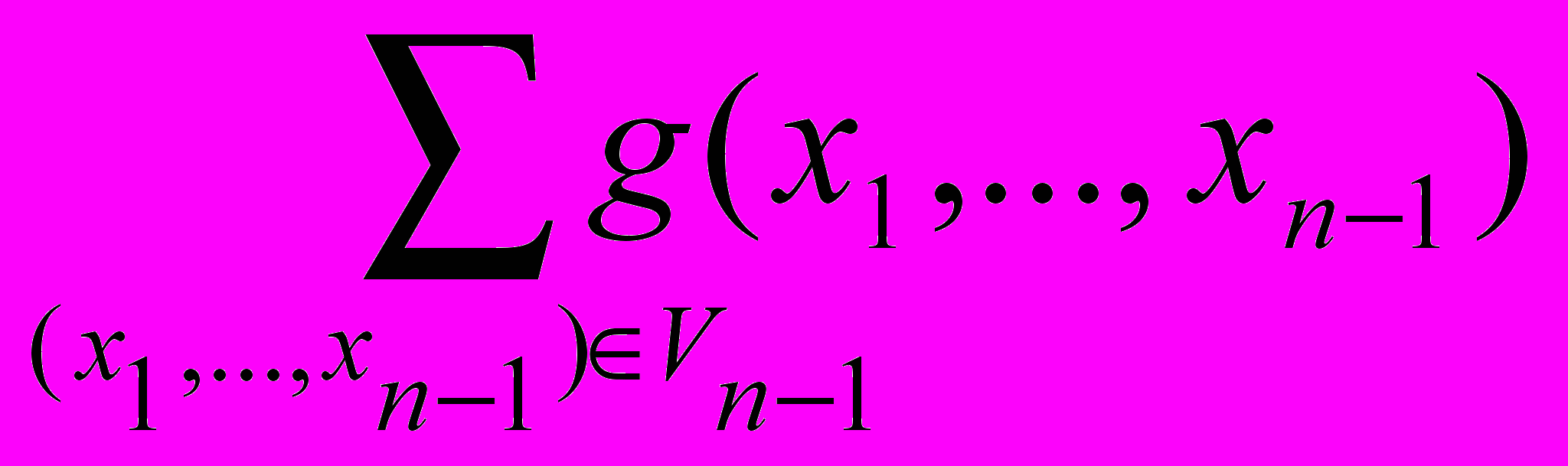) = х = х .


Очевидно, преобразование (s) п.ц  нечётен. 

Следствие 3. Пусть биективное треугольное преобразование п множества Vп задано системой функций (6.4), где fi(x1,x2,...,xi)=gi(x1,x2,...,xi-1)xi, i=1,2,…,п, и g1 =1.

Преобразование п является п.ц. тогда и только тогда, когда вес каждой из функций g2,…,gп нечётен.

Доказательство - индукция по п с использованием следствия 2. 

Известно, что число п.ц. регистров сдвига длины п равно 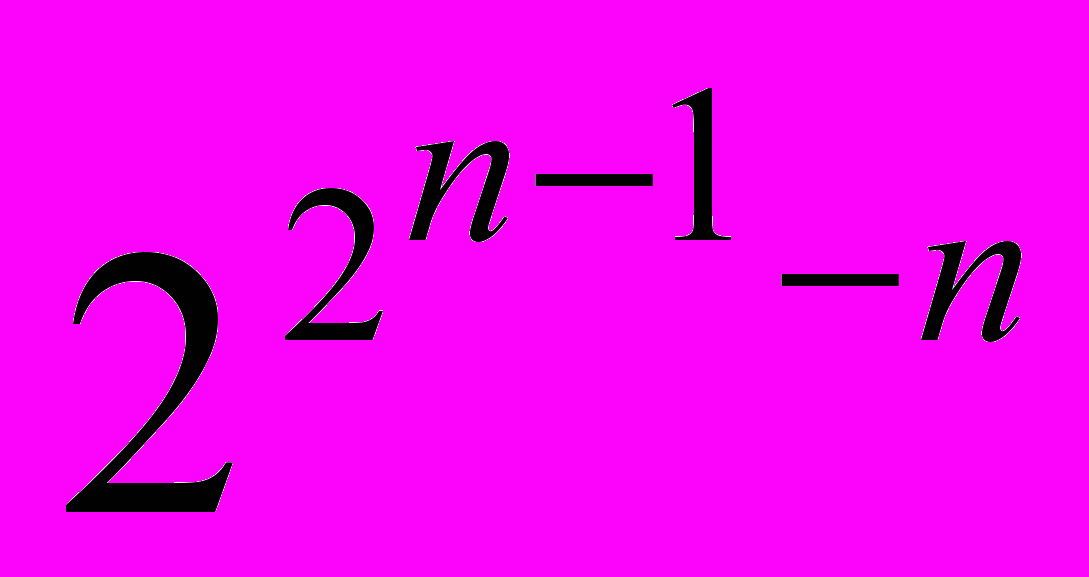, однако удобные критерии полноцикловости для регистровых преобразований не известны. Приведём принцип «склеивания-расклеивания», позволяющий строить п.ц. двоичные регистры сдвига небольших длин.

Теорема 6.8. Пусть  и  - биективные двоичные регистры сдвига длины n с обратными связями f(x1,x2,...,xn) и f(x1,x2,...,xn) соответственно, где а2,…,ап{0,1}. Тогда граф G() отличается от графа G() тем, что либо один цикл графа G() распадается на два цикла графа G(), либо два цикла графа G() объединяются в один цикл графа G().

Доказательство. Так как  и  биективны, то f(x1,x2,...,xn)=x1g(x2,...,xп). Отсюда следует, что


(0,а2,…,ап)=(а2,…,ап,g(а2,…,ап)),


(1,а2,…,ап)=(а2,…,ап,g(а2,…,ап)1),


(0,а2,…,ап)=(а2,…,ап,g(а2,…,ап)1),


(1,а2,…,ап)=(а2,…,ап,g(а2,…,ап)).


Таким образом, если вершины (0,а2,…,ап) и (1,а2,…,ап) лежат на одном цикле графа G(), то в графе G() они лежат на разных циклах. И наоборот, если вершины (0,а2,…,ап) и (1,а2,…,ап) лежат на разных циклах графа G(), то в графе G() они лежат на одном цикле. На остальных вершинах из Vn преобразования  и  совпадают. 

Для построения п.ц. регистрового преобразования из исходного биективного двоичного регистра сдвига путём «склеивания» циклов нужно находить пары соседних по 1-й координате вершин (0,а2,…,ап) и (1,а2,…,ап), лежащих на разных циклах, и изменять функцию обратной связи посредством добавления конъюнкции . Если граф исходного регистра состоит из r циклов, то для построения п.ц. регистра требуется выполнить r-1 таких шагов.