План I введение II основная часть: Многомерное пространство Идея четырехмерного пространства Четырехмерный куб

Вид материала

Документы

Содержание 2.Многомерное пространство 3. Идея четырехмерного пространства 4. Четырехмерный куб Многомерное пространство

Подобный материал:

• Некорректные задачи геофизики. План лекций. Лекция I. Функциональные пространства., 64.34kb.
• План: Введение Знакомство с Африкой Основная часть, 116.44kb.
• Тема 2 Социальное пространство и социальная структура. Понятие социального пространства, 586.13kb.
• План: введение. Основная часть. Культура древней греции. Культура древнего рима. Заключение, 5.14kb.
• План введение Значение внимания в жизни человека Основная часть Свойства внимания, 74.58kb.
• Программа дисциплины «Многомерное шкалирование» для направления 040200. 62 «Социология», 131.59kb.
• План введение. Основная часть: Детство и юность Петра. Рождение, 591.81kb.
• Задачи: формировать умение ориентироваться в новом информационном поле помочь в освоении, 319.12kb.
• План План Введение Связь романа Булгакова с трагедией Гете История создания романа, 412.46kb.
• План I. Введение II. Основная часть Место игры в экологическом воспитании детей., 262.68kb.

ПЛАН


I ВВЕДЕНИЕ

II ОСНОВНАЯ ЧАСТЬ:

1. Многомерное пространство
   
2. Идея четырехмерного пространства
   
3. Четырехмерный куб
   

III ЗАКЛЮЧЕНИЕ

Список используемой литературы


1.ВВЕДЕНИЕ

Многомерность, выход за привычные представления, открывает, казалось бы, новые и многообещающие возможности. Оказывается, наше пространство четырехмерно. Вдобавок ко всем известным трем измерениям - ширине, толщине и высоте, есть еще и четвертое - время.

Представить себе четырехмерное пространство не так-то просто, если учесть, что и в трех измерениях мыслить нелегко. Некоторые искусствоведы утверждали даже в начале века, что без учета многомерности пространства понять современное искусство нельзя. По этому поводу уместно сделать два замечания.

Во-первых, многомерность понимается всегда как четырехмерность, то есть существование наряду с обычными тремя пространственными измерениями (нагляднее всего их можно представить себе как смещения в трех направлениях; вверх-вниз, вперед-назад и влево-вправо) и еще одного, четвертого. За это новое измерение принимали время. Это имело известные основания, поскольку в начале века появилась теория относительности с ее понятием единого пространственно-временного континуума. Однако надо понимать, что если исходить из современной физики, то для нашей обычной жизни, обычных скоростей и расстояний, теория относительности приобретает банальный облик привычного из школьных представлений пространства и независимо от него текущего времени. И это даже в том случае, если за обычные скорости и расстояния взять размеры Солнечной системы и скорости движения планет. Поэтому теория относительности в передаче обычной человеческой жизни, основной темы художников, ничего изменить не должна.

Вторым моментом, который хотелось бы отметить, является то, что значительно более сложное четырехмерное пространство, где четвертой координатой является не время (что себе легко представить), а тоже пространственная координата (что представить себе немыслимо), уже давно привлекло внимание художников. Более того, они даже разработали успешные методы его изображения. Главная трудность в наглядном описании геометрии четырехмерного пространства связана с тем, что представить себе его нельзя. Это невозможно, поскольку требует от нас кроме естественных трех направлений (о них уже говорилось: направления вперед-назад, влево-вправо и вверх-вниз) представить себе движение в "четвертом" направлении, но такое, при котором в трех естественных направлениях движения не происходит. Иными словами, для нас, существ трехмерных, точка будет видна неподвижной, а на самом деле она будет двигаться в "четвертом" направлении. Единственный метод, который может здесь помочь,— это метод аналогий. Будем исходить из того, что наш привычный трехмерный мир "вложен" в четырехмерное пространство, что легко описать словами, но представить себе нельзя. Но зато ничего не стоит представить себе аналогичную, но элементарно простую ситуацию: двухмерный мир, "вложенный" в трехмерный. Хотя бы лист бумаги, находящийся в привычном для нас трехмерном пространстве.

Пусть теперь этот лист бумаги будет тем двухмерным "пространством", на котором живут некие "плоские" существа, могущие ползать по листу; плоские существа, ползающие по плоскому листу, — аналогия нас, трехмерных организмов, перемещающихся в трехмерном пространстве. Пусть этот лист будет безграничным, а по его обеим сторонам ползают эти самые плоские существа: одни с верхней стороны листа, другие — с нижней. Совершенно очевидно, что, сколько бы они ни ползали, верхние никогда не встретятся с нижними, хотя они могут быть бесконечно близки друг к другу — ведь их все равно будет разделять бесконечно тонкая толщина непроницаемого листа. Таким образом, каждую точку листа надо будет считать дважды — как принадлежащую верхней и как принадлежащую нижней стороне. Естественно, что на верхней стороне листа могут происходить одни, а на нижней — другие события, причем эти события не будут мешать друг другу, поскольку они сдвинуты относительно друг друга хотя и на бесконечно малую величину, но в "непостижимом" для плоских существ направлении — перпендикулярно поверхности листа. Эта "непостижимость" обусловлена для плоских существ тем, что последние никогда в своей жизни в таком направлении не перемещались и перемещаться не могут.

2.МНОГОМЕРНОЕ ПРОСТРАНСТВО

Многомерное пространство, пространство, имеющее число измерений (размерность) более трёх. Обычное евклидово пространство, изучаемое в элементарной геометрии, трёхмерно; плоскости — двумерны, прямые — одномерны. Возникновение понятия многомерное пространство связано с процессом обобщения самого предмета геометрии. В основе этого процесса лежит открытие отношений и форм, сходных с пространственными, для многочисленных классов математических объектов (зачастую не имеющих геометрического характера). В ходе этого процесса постепенно выкристаллизовалась идея абстрактного математического пространства как системы элементов любой природы, между которыми установлены отношения, сходные с теми или иными важными отношениями между точками обычного пространства. Наиболее общее выражение эта идея нашла в таких понятиях, как топологическое пространство и, в частности, метрическое пространство.

Простейшими многомерными пространствами являются n-мерные евклидовы пространства, где n может быть любым натуральным числом. Подобно тому, как положение точки обычного евклидова пространства определяется заданием трёх её прямоугольных координат, «точка» n-мерного евклидова пространства задаётся n «координатами» x₁, x₂, ..., x_n (которые могут принимать любые действительные значения); расстояние  между двумя точками M(x₁, x₂, ..., x_n) и М'(у₁, y₂, ..., y_n) определяется формулой



аналогичной формуле расстояния между двумя точками обычного евклидова пространства. С сохранением такой же аналогии обобщаются на случай n-мерного пространства и другие геометрические понятия. Так, в многомерном пространстве рассматриваются не только двумерные плоскости, но и k-мерные плоскости (k < n), которые, как и в обычном евклидовом пространстве, определяются линейными уравнениями (или системами таких уравнений).

Понятие n-мерного евклидова пространства имеет важные применения в теории функций многих переменных, позволяя трактовать функцию n переменных как функцию точки этого пространства и тем самым применять геометрические представления и методы к изучению функций любого числа переменных (а не только одного, двух или трёх). Это и было главным стимулом к оформлению понятия n-мерного евклидова пространства.

Важную роль играют и другие многомерные пространства. Так, при изложении физического принципа относительности пользуются четырёхмерным пространством, элементами которого являются т. н. «мировые точки». При этом в понятии «мировой точки» (в отличие от точки обычного пространства) объединяется определённое положение в пространстве с определённым положением во времени (поэтому «мировые точки» и задаются четырьмя координатами вместо трёх). Квадратом «расстояния» между «мировыми точками» М’(х’, y’, z’, t’) и М’’(х’’, y’’, z’’, t’’) (где первые три «координаты» — пространственные, а четвёртая — временная) естественно считать здесь выражение

(M’ M’’)² = (x’ − x’’)² + (y’ − y’’)² + (z’ −z’’)² − c²(t’ − t’’)²,

где с — скорость света. Отрицательность последнего члена делает это пространство «псевдоевклидовым».

Вообще n-мерным пространством называется топологическое пространство, которое в каждой своей точке имеет размерность n. В наиболее важных случаях это означает, что каждая точка обладает окрестностью, гомеоморфной открытому шару n-мерного евклидова пространства. Мы привыкли оценивать предметы по трём измерениям или параметрам − длине, ширине и высоте. Координатная система этого пространства − это три взаимно перпендикулярные оси, три ребра куба, сходящихся в одной точке.

3. ИДЕЯ ЧЕТЫРЕХМЕРНОГО ПРОСТРАНСТВА

Одна из гипотез о пространстве представляет четвёртое измерение как время. Представить четырехмерное пространство гораздо сложнее. Четвёртая ось системы координат перпендикулярна трём другим − сознание сразу отказывается создать в воображении такую картину. Представим, что надуваем воздушный шар, и с каждым выдохом он становится всё больше и больше. Шар остаётся в трехмерном пространстве, однако он меняется в размерах. Это его изменение можно было бы перераспределить по известным трём измерениям, однако такая тактика приводит к искажению действительности. Шар меняется во времени, с каждым вашим выдохом, приобретая другие размеры и форму − объект перерождается во времени.



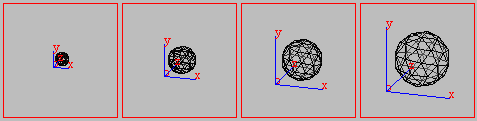
Если заменить изображение шара в трёхмерной системе координат некоторым объёмом, меняющимся от меньшего размера к большему, т.е. движущимся в трехмерной системе координат получится компромисс, удовлетворяющий сознание. На самом деле шар движется во времени и это движение можно искаженно представить движением в трёхмерной системе координат.

4. ЧЕТЫРЕХМЕРНЫЙ КУБ

Нульмерный объект − точка. Одномерный бесконечный объект - линия. Одномерный конечный объект отрезок. Двухмерные объекты плоские. Трехмерный бесконечный объект − пространство Вселенной, (если бы она была евклидова и статична). Трёхмерные конечные объекты − куб, шар, пространство нашей комнаты и так далее. Все эти объекты можно нарисовать на двухмерном листе бумаги. А как быть с четырёхмерным объектом? Существует один метод рисования четырёхмерных объектов на двухмерном листе.

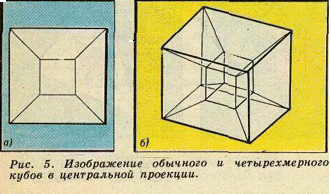
Чтобы представить себе четырехмерный куб, полезно сначала посмотреть на обычный − трехмерный куб, а также на «двухмерный куб» (квадрат) и «одномерный куб» (отрезок) в динамике- так, как они показаны на рисунках 1а, б, в.



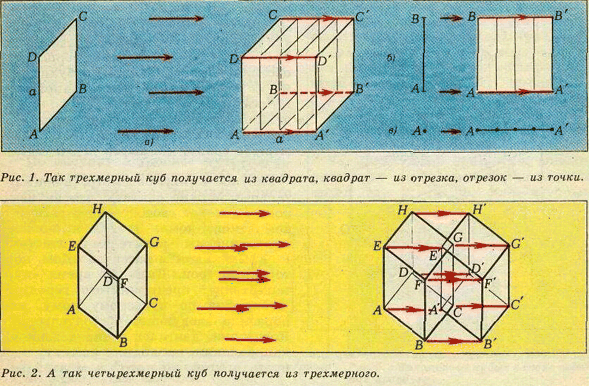
Изучив эти рисунки, можно попытаться понять и рисунок 2, изображающий четырехмерный куб. Так же как (двухмерная) грань ABCD трехмерного куба, двигаясь параллельно самой себе (рис.1а) до положения A’B’C’D’, заметает трехмерный куб, «трехмерная грань» ABCDEFGH, двигаясь параллельно самой себе до положения A’B’…H’, «заметает» четырехмерный куб. Конечно, полученный чертеж четырехмерного куба условен, он дает его искаженное изображение. Но ведь и рисунок 1.а дает искаженное изображение обычного куба на плоскости. На самом деле оба чертежа имеют одинаковую природу: они показывают образы трехмерного и четырехмерного кубов при параллельной проекции на плоскость.

Разница лишь в том, что нам удается «приподнять в пространство» плоское изображение трехмерного куба усилием мысли, а такой способностью представить себе «четырехмерье» мы уже не обладаем.

Попробуем развернуть четырехмерный куб.

Чтобы представить себе развертку четырехмерного куба, сначала посмотрим на развертку трехмерного и двухмерного кубов. Мы видим, что развертка квадрата одномерна и состоит из четырех отрезков; развертка куба двухмерна и состоит из шести квадратов. Аналогично, развертка четырехмерного куба трехмерна и состоит из восьми трехмерных кубов.



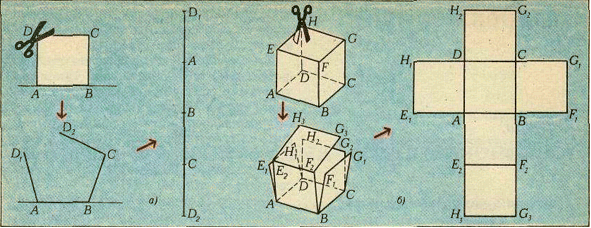
Так же как трехмерный куб можно склеить из развертки, отождествляя вершины G1 =G2 =G3, H1 =H2 =H3, E1 =E2 , F1 =F2 (и соответствующие ребра), четырехмерный куб можно получить из его развертки, «склеивая» вершины, обозначенные одинаковыми буквами, но с разными номерами, например M1 = M2 = M3 = M4 , или I1 = I2; при этом склеиваются не только вершины (и соответствующие ребра), но и двумерные грани, например M3O3P3Q3 =M4O4P4Q4 .

Рисунок 4 стоит рассмотреть внимательнее.



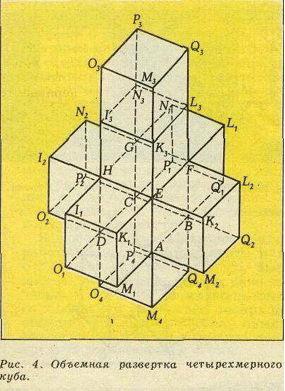
Можно считать, что на нем показан макет своеобразного восьмикомнатного дома. Этот дом описан американским писателем-фантастом Р.Хайнлайном в рассказе «Дом, который построил Тил». Во время «путешествия», предпринятого героями Хайнлайна по чудесному дому, их поразило следующее обстоятельство. Когда они, двигаясь в определенном направлении, проходили комнату одну за другой, то пятой комнатой на их пути оказалась та, из которой они вышли. Например, если, двигаясь «снизу вверх», пройти четыре комнаты, образующие центральную башню развертки, то вновь окажешься в комнате «первого этажа». Действительно, «крыша» дома, как это видно из обозначений вершин, склеена с «полом» нижней комнаты. На самом деле всякий раз при пересечении границ комнат маршрут автоматически поворачивает на 90º, так что, например, ломаная M4AEK3M3 не прямолинейна, но представляет собой контур квадрата. Этот факт легко понять, рассматривая аналогичные пути на развертке трехмерного куба и на поверхности самого куба.

Существует еще один популярный способ изображения четырехмерного куба. Восемь трехмерных граней изображены здесь внутренним (малым) кубом, внешним (большим) кубом и шестью усеченными пирамидами, соединяющими соответственные грани малого и большого кубов. Этот рисунок получается при центральном проектировании четырехмерного куба на некоторую «трехмерную плоскость». Смысл этого рисунка легче понять, если рассмотреть также рисунок 5а, на котором изображена центральная проекция трехмерного куба на плоскость из некоторой точки.

По рисунку 5 удобнее всего сосчитать количество разного рода составляющих элементов четырехмерного куба. А именно, он имеет 16 вершин, 32 ребра, 24 двухмерные грани (в виде квадратов) и 8 «трехмерных граней» (в виде кубов).

Итак, мы получили наглядное представление о четырехмерном кубе. В частности, мы знаем, сколько и каких элементов входит в его состав, и как они соединяются между собой. Мы ознакомились лишь с различными описаниями по аналогии четырехмерного куба, и не дали его строгого математического определения. Между тем сделать это очень просто. Однако прежде чем давать это определение, приведем несколько хорошо известных наблюдений.

Отрезок («одномерный куб») располагается на прямой (в «одномерном пространстве») и в системе координат Ox может быть задан неравенством 0 ≤ х ≤1 (рис.6а).


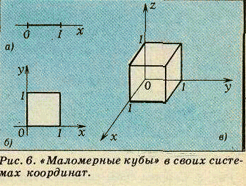Квадрат («двухмерный куб») располагается на плоскости (в «двухмерном пространстве») и в системе координат Oxy может быть задан системой неравенств 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 (рис. 6б.).

Трехмерный куб в системе координат Oxyz трехмерного пространства выделяется системой неравенств 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1 (рис. 6в.).

Эти наблюдения делают естественным такое определение.

Четырехмерный куб − это множество всех четверок действительных чисел (x; y; z; t), для которых 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1, 0 ≤ t ≤ 1. Четырехмерный куб в системе координат x; y; z; t четырехмерного пространства изображен на рисунке 7, где у каждой вершины указаны ее координаты (в целях экономии места без скобок и запятых).



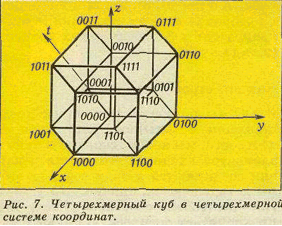
В данный момент необходимо уточнить, что такое трехмерное пространство. Итак, трехмерное пространство- это набор всевозможных троек чисел (x; y; z), где x; y; z − действительные числа (координаты точки), для которых определено расстояние по формуле



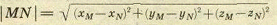
Оказывается, предыдущую фразу можно взять за определение трехмерного пространства: из этого определения можно вывести все основные положения стереометрии с помощью элементарной алгебры. Так, определив плоскость как множество точек, удовлетворяющих линейному уравнению вида Ax + By + Cz + D = 0, (1) несложно доказать, например, что через любую тройку неколлинеарных точек M, N, P проходит одна и только одна плоскость, а именно, плоскость с уравнением



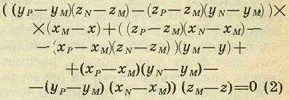
Теперь следующее определение должно прозвучать естественно. Четырехмерным пространством называется множество всех четверок чисел (x; y; z; t), где x, y, z, t − действительные числа, для которых определено расстояние по формуле



С определением плоскости в четырехмерном пространстве дело обстоит не так просто. Дело в том, что здесь бывают как обычные двухмерные плоскости, так и трехмерные «плоскости», называемые гиперплоскостями. С точки зрения задания плоскостей уравнениями, именно гиперплоскость является точным аналогом обычной плоскости в трехмерном пространстве. В уравнении (1) обычной плоскости двум из трех переменных x; y; z можно придавать произвольные значения, и тогда значение третьей переменной будет определяться из уравнения однозначно. Таким образом, множество всех решений этого уравнения описывается двумя произвольными параметрами, то есть оно двумерно. По той же причине множество всех решений одного линейного уравнения в четырехмерном пространстве Ax + By + Cz + Dt + E = 0 само по себе трехмерно. Аналогично трехмерному случаю, вектор с координатами (ABCD) перпендикулярен данной гиперплоскости и называется ее нормальным вектором.

Исходя из вышесказанного, без труда возможно дать определение п-мерного куба для любого п ≥ 1. Для этого он сначала определит п-мерное пространство как множество наборов из п чисел (x1, x2, …xn), расстояние между которыми задается формулой



А затем и п-мерный куб как множество тех точек п-мерного пространства, для которых выполнены неравенства 0 ≤ x1 ≤ 1, 0 ≤ x2 ≤ 1, … 0 ≤ xn ≤ 1.

Как его рассечь?

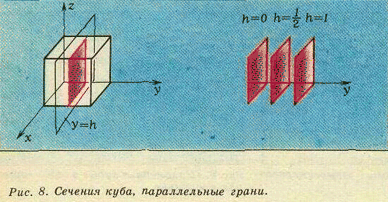
Четырехмерные фигуры удобно представлять себе при помощи их сечений некоторым семейством параллельных друг другу гиперплоскостей (гиперплоскости параллельны между собой, если из нормальные векторы коллинеарные). Смысл этой конструкции можно понять, рассматривая сечения трехмерных тел обычными плоскостями (рис. 8, где показано сечение куба плоскостями y = h). Аналогично выглядят и сечения четырехмерного куба плоскостями t = h.

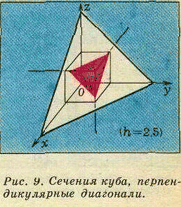
Для лучшего понимания геометрии четырехмерного куба рассмотрим следующую более трудную задачу; изобразить семейство его сечений гиперплоскостями, перпендикулярными главной диагонали. Если взять диагональ, соединяющую вершины (0; 0; 0; 0) и (1; 1; 1; 1), то уравнение этих гиперплоскостей будет иметь вид x + y + z + t = h, где h − некоторая константа.

Разберем сначала аналогичную трехмерную задачу. Трехмерный куб можно представить как пересечение двух октантов, заданных системами неравенств



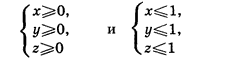
(рис.9). Всякая плоскость вида x + y + z + t = h пересекает каждый из этих двух октантов по правильному треугольнику. Проследим за изменением этой конфигурации при изменении h от 0 до √3. В начальный момент (h = 0) один из треугольников состоит всего из одной точки. Затем его линейные размеры увеличиваются пропорционально h, одновременно с этим второй треугольник постепенно уменьшается, оставаясь гомотетичным первому с отрицательным коэффициентом. Начиная с этого момента, когда вершины меньшего треугольника «протыкают» стороны большего, их пересечение дает шестиугольник. Этот шестиугольник становится правильным, когда размеры треугольников сравниваются. Далее описанный процесс повторяется в обратном порядке.

Подобным образом, четырехмерный куб представляет собой пересечение двух частей четырехмерного пространства, выделяемых системами неравенств x ≥ 0, y ≥ 0, z ≥ 0, t ≥ 0 и x ≤ 1, y ≤ 1, z ≤ 1, t ≤ 1. Нетрудно показать, что гиперплоскость x + y + z + t = h пересекает каждую из этих частей по правильному тетраэдру. Один из этих тетраэдров увеличивается с ростом h, а другой уменьшается. Искомое множество представляет собой пересечение двух таких тетраэдров и может быть точкой, тетраэдром или усеченным тетраэдром (в частности, при совпадении размеров обоих тетраэдров мы получим в пересечении правильный октаэдр).


5. ЗАКЛЮЧЕНИЕ

Оказывается, наше пространство четырехмерно.

Многомерное пространство, пространство, имеющее число измерений (размерность) более трёх. Обычное евклидово пространство, изучаемое в элементарной геометрии, трёхмерно; плоскости — двумерны, прямые — одномерны. Нульмерный объект − точка. Одномерный бесконечный объект − линия. Одномерный конечный объект отрезок. Двухмерные объекты плоские. Трехмерный бесконечный объект − пространство Вселенной, (если бы она была евклидова и статична). Трёхмерные конечные объекты − куб, шар, пространство нашей комнаты и так далее.

Итак, трехмерный куб стоит на нашей плоскости и ждет, когда же мы отправим его в четвертое измерение. Начнем перемещать его перпендикулярно самому себе, то есть в направлении, перпендикулярном всем трем его граням одновременно … Для нас — плоских наблюдателей — и третье-то измерение за пределами воображения, но мы замечаем движение по нашей плоскости тени трехмерного куба, которую он отбрасывает в лучах солнца четвертого измерения. Знакомый рисунок проекции трехмерного куба начал смещаться и остановился, сдвинувшись на некоторое расстояние. И в результате мы получаем четырехмерный куб.




СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1. Болотов В.П. Начертательная геометрия многомерного пространства.
   
2. Дужин С., Рубцов В. Четырехмерный куб// КВАНТ.-1986---№6.
   
3. Зенин Ю.В. Реальная нереальность (Часть 1).
   
4. Гельфанд И.М., Глаголева Е.Г., Кириллов А.А. Метод координат.// Библиотечка физико-математической школы. Метод координат.- М., 1973.-88 стр.