Geum.ru

Рабочая программа и задание на контрольную работу c методическими указаниями для студентов II курса специальности 330200. Инженерная защита

Вид материалаРабочая программа
С – концентрация, кг/м; к
Подобный материал:
1   2   3   4   5
Задачи

69. Найдите ζ-потенциал для суспензии кварца в воде. При электрофорезе частицы перемещаются к аноду; смещение границы составило 5·10-2м за 180 с; Н=10·10-2 В/м; ε=81; ε0=8,85·10-12ф/м; η=1·10-3 Н·с/м2.

70. Вычислить скорость электрофореза коллоидных частиц берлинской лазури в воде, если ζ-потенциал составляет 0,058В, Н=5·10-2В/м; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

71. Вычислите ζ-потенциал коллоидных частиц трехсернистого мышьяка в воде, если при электрофорезе за 180 сек граница сместилась на 5,4·10-2м. Н=8·10-2В/м; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

72. Найдите величину ζ-потенциала на границе кварцевое стекло-водный раствор KCl. Процесс электроосмоса характеризовался следующими показателями: J=4·10-4А; время переноса 0,01·10-6м3 раствора τ=12,4с; χ=1,8·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

73. Вычислите величину ζ-потенциала на границе кварц-водный раствор KCl. Процесс электроосмоса получены следующие данные:

J=2·10-3А; время переноса 0,01·10-6м3 раствора τ=11с; χ=6,2·10-2Ом-1·м-1;

η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

74. При какой силе тока в процессе электроосмоса водного раствора KCl через мембрану из полистирола его объемная скорость будет равна 5,5·10-10м3/сек? χ=9·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

Величина ζ-потенциала равна 10·10-3В.

75. Вычислите величину ζ-потенциала на границе водный раствор KCl-мембрана из полистирола. В процессе электроосмоса объемная скорость равнялась 15·10-10м3/сек; J=7·10-3А; χ=9·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

76. Найдите объемную скорость электроосмоса, наблюдаемого в системе: водный раствор KCl – мембрана из полистирола, окрашенная жировым коричневым красителем. ζ-потенциал = 6·10-3В, J=7·10-3А;

χ=9·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

77. Вычислите величину потенциала Е, если через пленку коллодия продавливается водный раствор KCl при p=20·103 H/м2; χ=1,3·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м; ζ-потенциал=6·10-3В.

78. Вычислите величину ζ-потенциала на границе коллодиевая мембрана-водный раствор KCl, если при продавливании раствора через мембрану под давлением 26,6·103Н/м2 потенциал течения Е оказался равным 8,8·10-3В; χ=1,3·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

79. Найдите величину ζ-потенциала на границе керамический фильтр-водный раствор KCl, если при продавливании раствора при p=13,3·103Н/м2 потенциал течения Е равнялся 2·10-3В; χ=1,3·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

80. Под каким давлением должен продавливаться раствор NaCl через керамическую мембрану, чтобы потенциал течения Е был равен 4·10-3В? ζ- потенциал = 3·10-3В; χ=1,3·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

81. Вычислите величину ζ-потенциала на границе керамической мембраны с водным раствором KCl. Е=6·10-3В, p=39.9·10-3Н/м2, χ=1,3·10-2Ом-1·м-1; η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

82. Найдите величину ζ-потенциала на границе: мембрана из углеуислого бария-96%-ный раствор этилового спирта. Е=0,7В,

χ=1,1·10-4Ом-1·м-1; η=1,2·10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м; p=7,9·10-3Н/м2.

83. Какое давление нужно приложить, продавливая через мембрану из углекислого бария 96% этиловый спирт, чтобы при этом потенциал течения Е оказался равным 1,98В? ζ- потенциал = 54·10-3В; χ=1,1·10-2Ом-1·м-1;

η=1,2·10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м.

84. Вычислите величину потенциала Е на границе: кварцевая диафрагма-водный раствор NaCl, если давление, при котором жидкость продавливается через диафрагму p=200Н/м2; χ=8.0·10-2Ом-1·м-1;

η=10-3Н·с/м2, ε=81; ε0=8,85·10-12ф/м; ζ-потенциал=120·10-3В.


5. Оптические свойства дисперсных систем

Изучение оптических свойств коллоидных систем связано с определением дисперсности или концентрации дисперсной фазы.

Как и молекулярные растворы, коллоидные системы поглощают и преломляют свет. Вместе с этим у них ярко проявляется способность к светорассеянию (опалесценции). Объясняется это соизмеримостью коллоидных частиц с длиной световых волн видимой части спектра: .

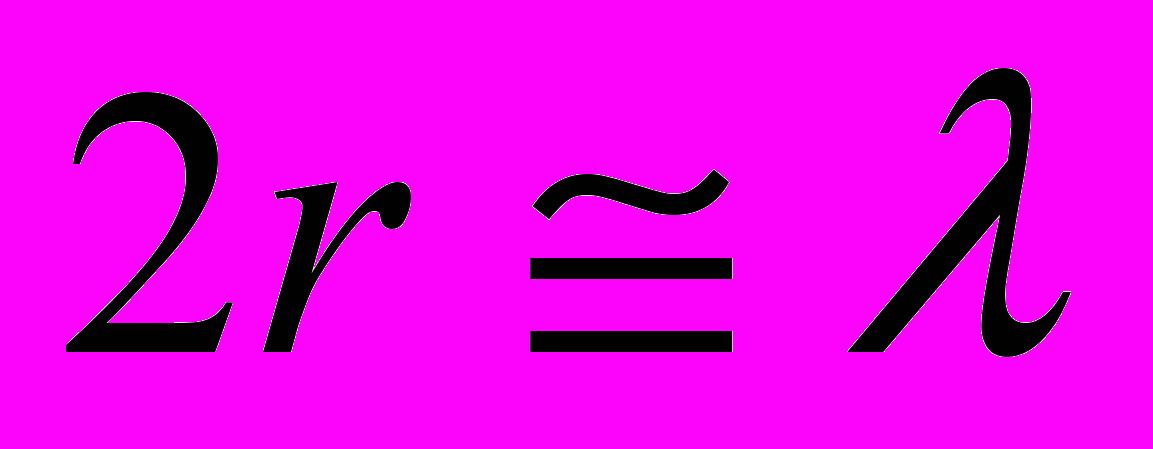Закон Рэлея устанавливает зависимость интенсивности опалесценции от размера частиц, концентрации:

,

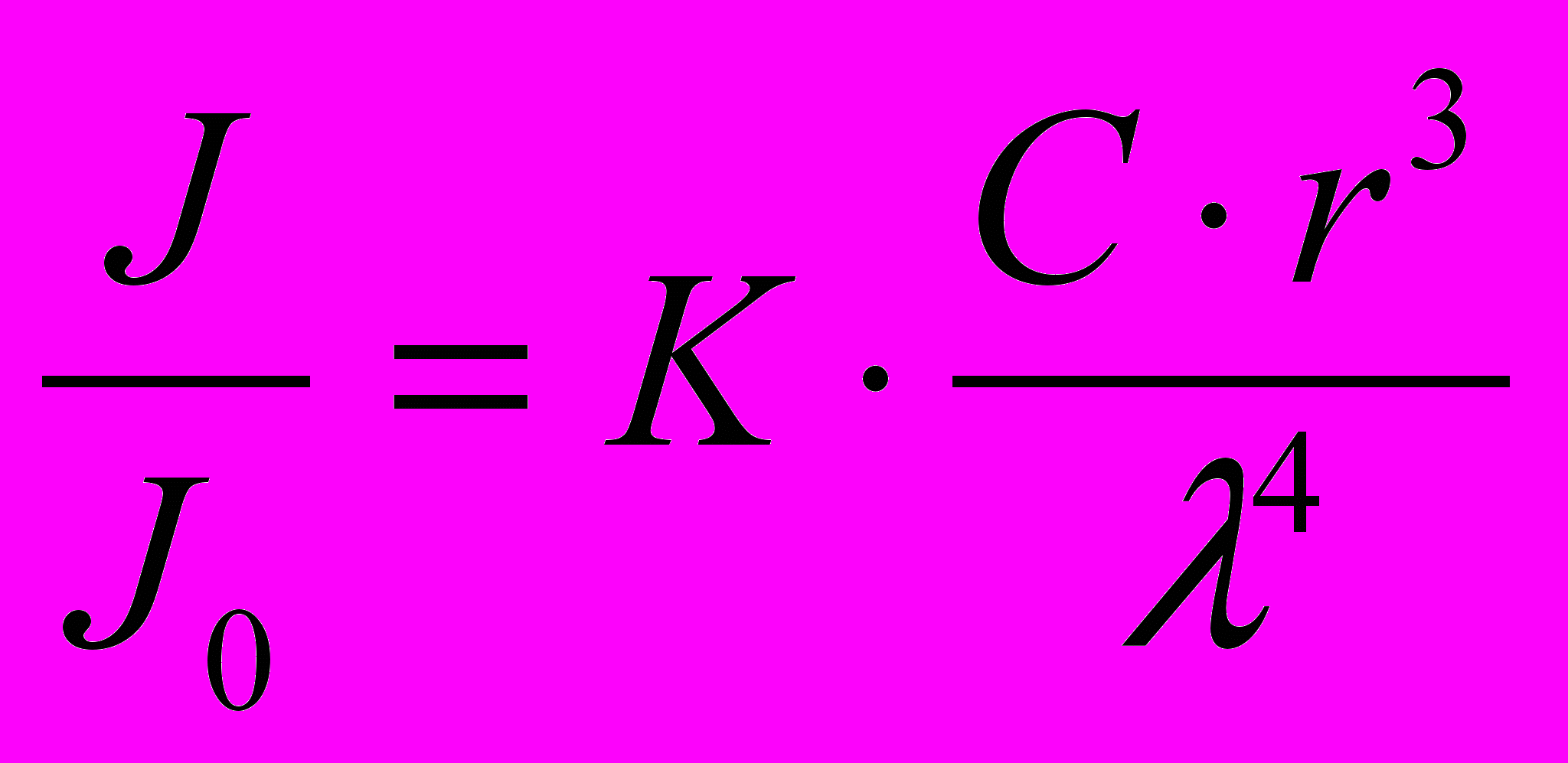где J0 – интенсивность падающего света;

С – концентрация, кг/м3;

к – радиус частицы, м;

λ – длина волны падающего света, м;

К – константа.

Отсюда следует, что отношение интенсивности рассеянного света, получившее название мутности и обозначающееся τ, пропорционально концентрации диспергированного вещества и радиусу его части. В определенной области концентраций зависимость τ = (С) является линейной.

Светорассеяние коллоидных растворов измеряется с помощью нефелометров различных систем. Нефелометрия позволяет определить концентрацию или размеры частиц дисперсной фазы.

Сущность метода заключается в сравнении мутностей τ1 и τ2 двух систем, концентрация (или дисперсность) одной из которых известна.

Освещая куветы с золями равномерно падающим светом и меняя высоту освещенной части золей h1 и h2 добиваются равенства интенсивности света, рассеянного обоими золями. Тогда справедливо равенство:

τ 1· h1 = τ2 · h2 ,

а т.к. мутность τ пропорциональна концентрации С, то С1 · h1 = С2 · h2 .

Дебай предложил формулу, связывающую мутность раствора с размером частиц:

τ =Н · С · М,

где С – концентрация, кг/м3;

Н – обобщенная константа;

М – молекулярная или мицеллярная масса вещества.

Уравнение Дебая справедливо для сильно разбавленных растворов.

Опалесценцию можно наблюдать не только в боковом освещении, но также измеряя интенсивность прошедшего света. При прохождении через систему интенсивность падающего света ослабляется вследствие поглощения или рассеяния, причем, согласно закона Ламберта-Бора:

J=J0 е εСd ,

где J – интенсивность прошедшего света;

d – толщина поглощающего слоя, м;

ε – индивидуальная константа, зависящая от природы вещества, длины световой волны и не зависящая от концентрации раствора.

Логарифм отношения интенсивности падающего света к интенсивности прошедшего света называется оптической плотностью системы Dλ:

.

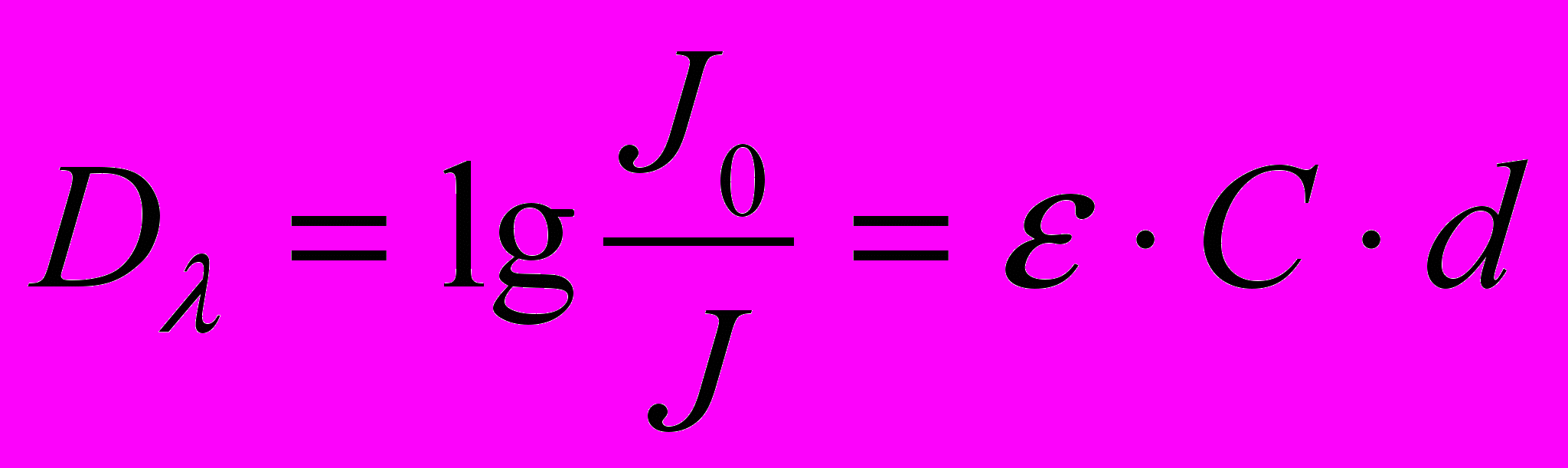Применимость закона Лимберта-Бора проверяется графически: зависимость Dλ от концентрации С должна быть линейной.

В определенной области концентраций уравнение Ламберта-Бора применимо к золям. Для этого одно из оптических явлений (опалесценция или поглощение света) должно доминировать. Например, золи кубовых и зернистых красителей ярко окрашены, но слабо мутны. Наоборот белые золи TiO2, SiO2, Al(OH)3, латексы бесцветны, но мутны. В этом случае Dλ будет расти с концентрацией линейно, что позволяет применить оптический метод для концентрации золей. Для определения Dλ служат разоичные калориметры, фотометры. Для белых золей Геллер установил зависимость общего вида между Dλ и длиной волны:

Dλ = K·λ·α,

где: λ – длина волны падающего света, м;

α – коэффициент, величина которого меняется от 1 до 4 в соответствии с диаметром частиц.

Эта зависимость имеет большое практическое значение для определения размеров частиц золя. Для этого нужно построить прямую в координатах lgDλ=f(lgλ), тангенс угла наклона прямой равен коэффициенту α. Далее по калибровочной кривой Геллера для латексов, построенной в координатах α = f(d), находят средний диаметр частиц.

Показатель α можно определить также по методу Теорелла: пользуясь всего двумя светофильтрами, получают два значения Dλ для двух длин волн (различие в величинах λ должно быть возможно большим), затем по соотношению:



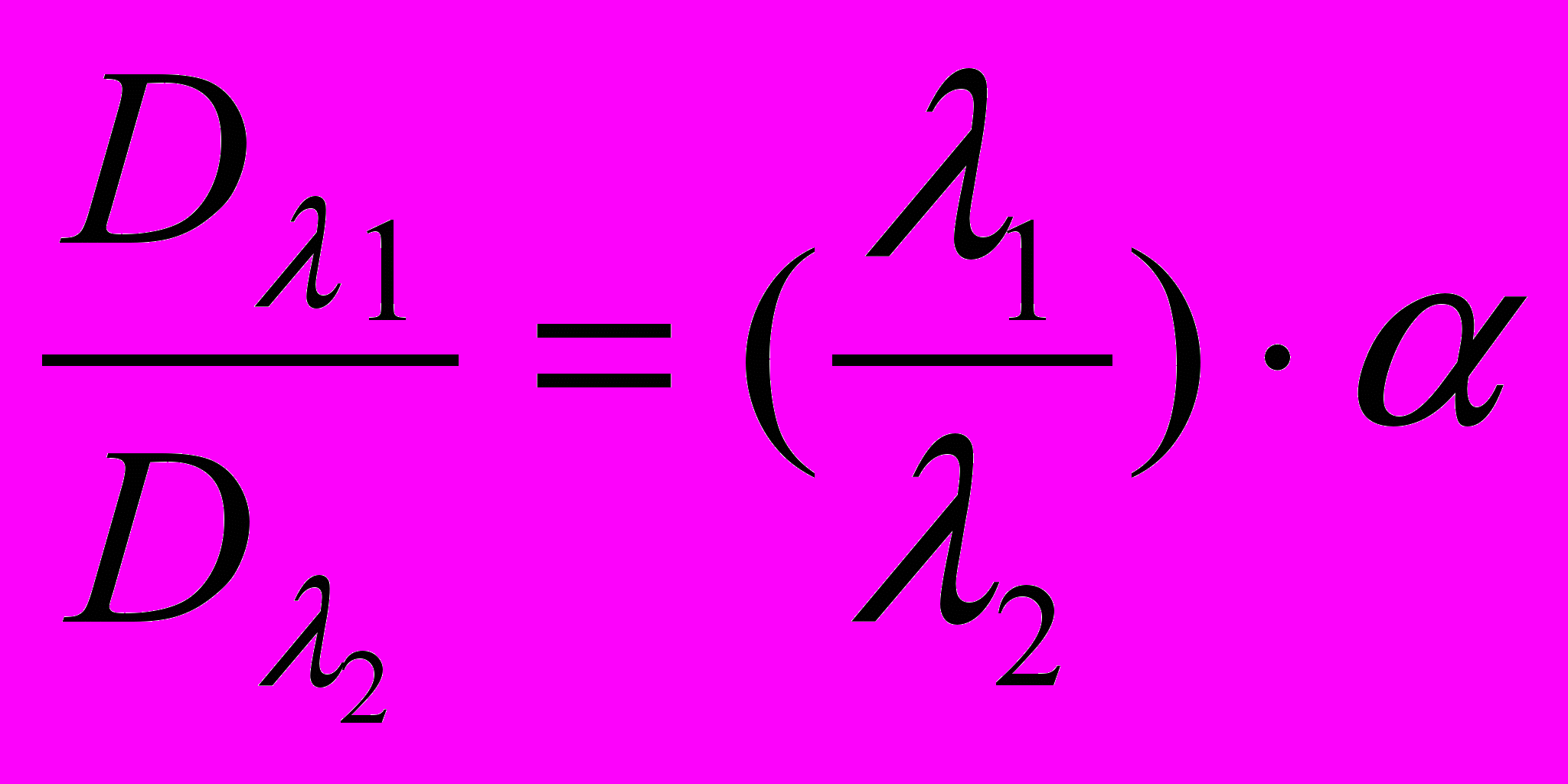
находят α. По α определяют размеры частиц.


Задачи

85. Сравните интенсивности светорассеяния высокодисперсного полистирола, освещенного монохроматическим светом с длиной волны λ1=680·10-9м, а затем с длиной волны λ2=420·10-9м (α=4).

86. В каком случае и во сколько раз интенсивность светорассеяния латекса полистирола больше: при освещении светом λ1=530·10-9м или λ2=680·10-9м?

87. С помощью нефелометра сравнивались мутности двух гидрозолей мастики равных концентраций. Мутности определяемого и стандартного золей стали одинаковыми при высоте освещенности части первовго золя h1=5·10-3м и высоте второго золя h2=19,0·10-3м. Средний радиус частиц второго золя r1=120·10-9м. Определите радиус частиц r2 второго золя.

88. Рассчитайте среднмй радиус частиц гидрозоля латекса полистирола, пользуясь данными нефелометра: высота освещенной части стандартного золя h1=8·10-3м, средний радиус частиц r1=88·10-9м, высота освещенной части неизвестного золя h2=18,0·10-3м. Концентрации стандартного и неизвестного золя равны.

89. Используя экспериментальные значения оптической плотности Dλ для разных длин волн λ, определите средний радиус частиц полистирольного латекса. Указания:

1. При построении логарифмической прямой целесообразно брать логарифмы 100Dλ;

2. Предварительно постройте калибровочную прямую Геллера по следующим данным:

Диаметр частиц латекса d · 109, м
77,0
88,0
95,0
106,7
111,0
119,0

Характеристика дисперсности α
3,82
3,64
3,545
3,30
3,235
3,04

Диаметр частиц латекса d · 109, м
132,0
139,0
143,0
158,0
167,0
189,0

Характеристика дисперсности α
2,82
2,72
2,66
2,45
2,365
2,14


Экспериментальные данные:


Диаметр волны λ · 109, м
415
485
527
685

Оптическая плотность латекса Dλ

0,195
0,127
0,099
0,048


90. То же, что в задаче №89, при экспериментальных данных:


Диаметр волны λ · 109, м
415
485
527
685

Оптическая плотность латекса Dλ

0,474
0,329
0,259
0,133


91. Условие, смотри задачу №89, при экспериментальных данных:


Диаметр волны λ · 109, м
415
485
527
685

Оптическая плотность латекса Dλ

0,324
0,215
0,160
0,084



92. Условие, смотри задачу №89, при экспериментальных данных:


Диаметр волны λ · 109, м
415
485
527
685

Оптическая плотность латекса Dλ

0,189
0,129
0,104
0,050


93. Исходя из значений оптической плотности Dλ1=0,023 и Dλ2=0,135, полученных с помощью ФЭК для длин волн: λ1=680·10-9м и λ2=420·10-9м, и используя калибровочную кривую Геллера (см. задачу №89), найдите средний радиус частиц гидрозоля латекса.

94. Проверьте графически применимость закона Ламберта-Бора к гидрозолю кубового синего красителя, используя данные спектрофотометрического метода:


Концентрация золя С·103, кг/м3
20,0
40,0
60,0
70,0

Оптическая плотность Dλ
0,2
0,38
0,55
0,67


95. Пользуясь экспериментальными данными подтвердите графически применимость закона Ламберта-Бора к гидрозолю сернистого черного красителя и определите конуентрацию золя при Dλ=0,55.


Концентрация золя С·103, кг/м3
20
40
60
80
100
120

Оптическая плотность Dλ
0,15
0,30
0,43
0,60
0,78
0,92



6. Вязкость. Реологические свойства дисперсных систем


Структуры бывают коагуляционные и конденсационные (кристализационные). Первые образуются за счет слабых водородных связей и сил Ван-дер-Ваальса, легко разрушаются при механических воздействиях и через некоторое время могут самопроизвольно восстановиться. Это явление получило название тиксотропии. Примером тиксотропных систем могут служить золи Fe(OH)3 и V2O5, суспензии бентонитовых глин, минеральные краски, растворы некоторых полуколлоидных и высокосолекулярных соединений и др.

Тиксотропные системы обычно проявляют пластичные свойства.

Конденсационные структуры образуются за счет химических связей между частицами, за счет возникающих срастающихся кристаллов. Такие системы не могут обладать тиксотропными свойствами, они не пластичны, а хрупки (цементы, гели кремниевой кислоты).

Закон Пуазейля характеризует ламинарное течение бесструктурной жидкости по капилляру под действием приложенного давления:

,

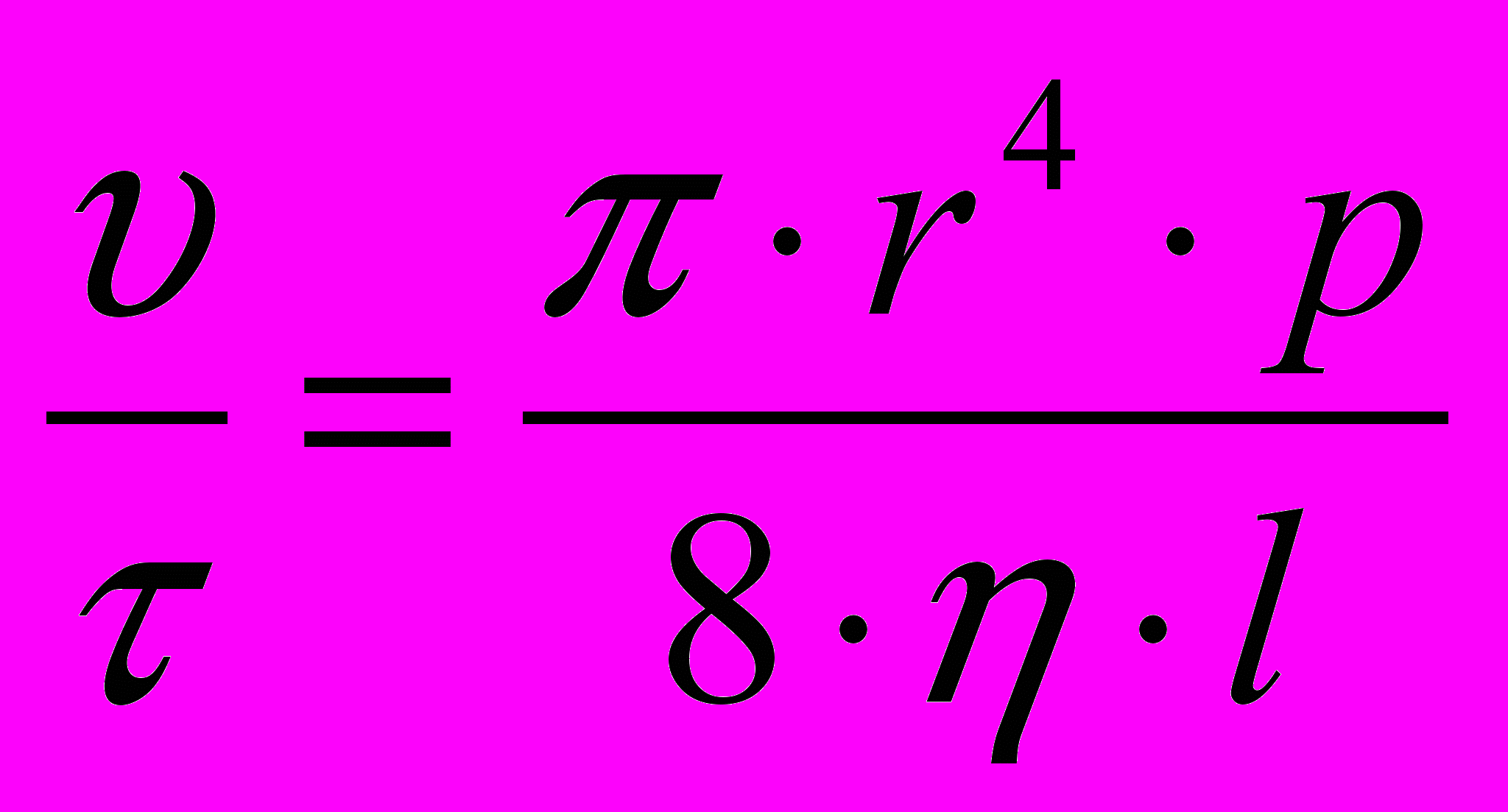где υ/τ – объемная скорость течения, м3/с;

p – приложенное давление (или напряжение на сдвиг), Н/м2;

r – радиус капиляра, м;

l – длина капиляра, м;

η – вязкость жидкости, (H·c)/м2.

Для структурных систем, обладающих структурными свойствами, предполагающее ньютоновское течение системы после разрушения непрочной структуры:

,

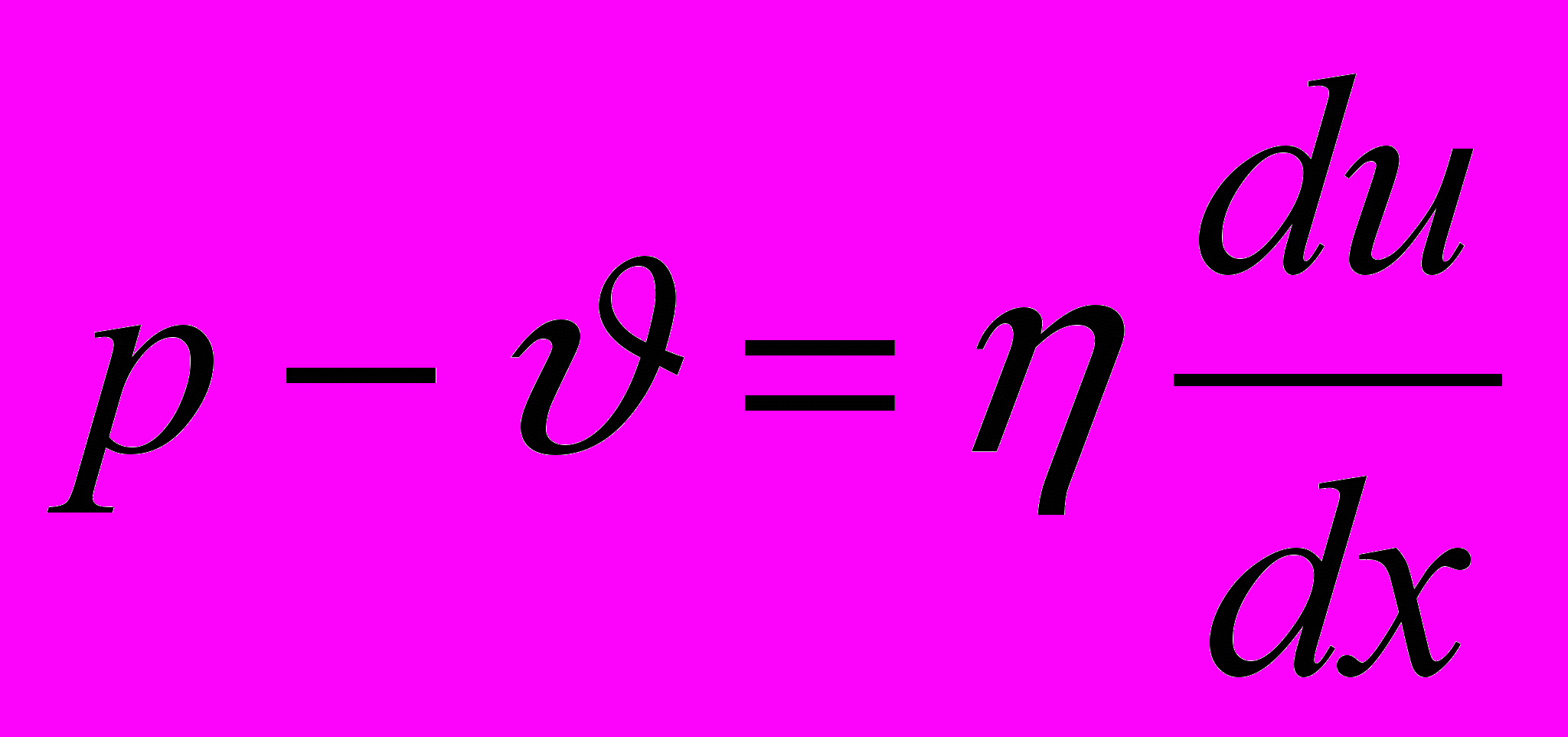где du/dx – градиент скорости;

θ – напряжение на сдвиг, необходимое для начала течения, кг/м2.

Для концентрированных систем используют ротационные вискозиметры типа прибора Волоровича, состоящие из двух коаксиальных цилиндров. Исследуемая система помещается между цилиндрами. Под действием приложенного внешнего напряжения р внутренний цилиндр начинает вращаться, причем число оборотов N (об/с) определяется структурно-механическими свойствами системы. При достижении p=pm (предельное напряжение сдвига) структура полностью разрушена и вязкость системы становится постоянной величиной, близкой к вязкости дисперсной среды.

Для исследования структурированных систем типа паст наиболее прпименимы два метода: конического пластометра и тангенциального смещения пластинки.

Для первого ,

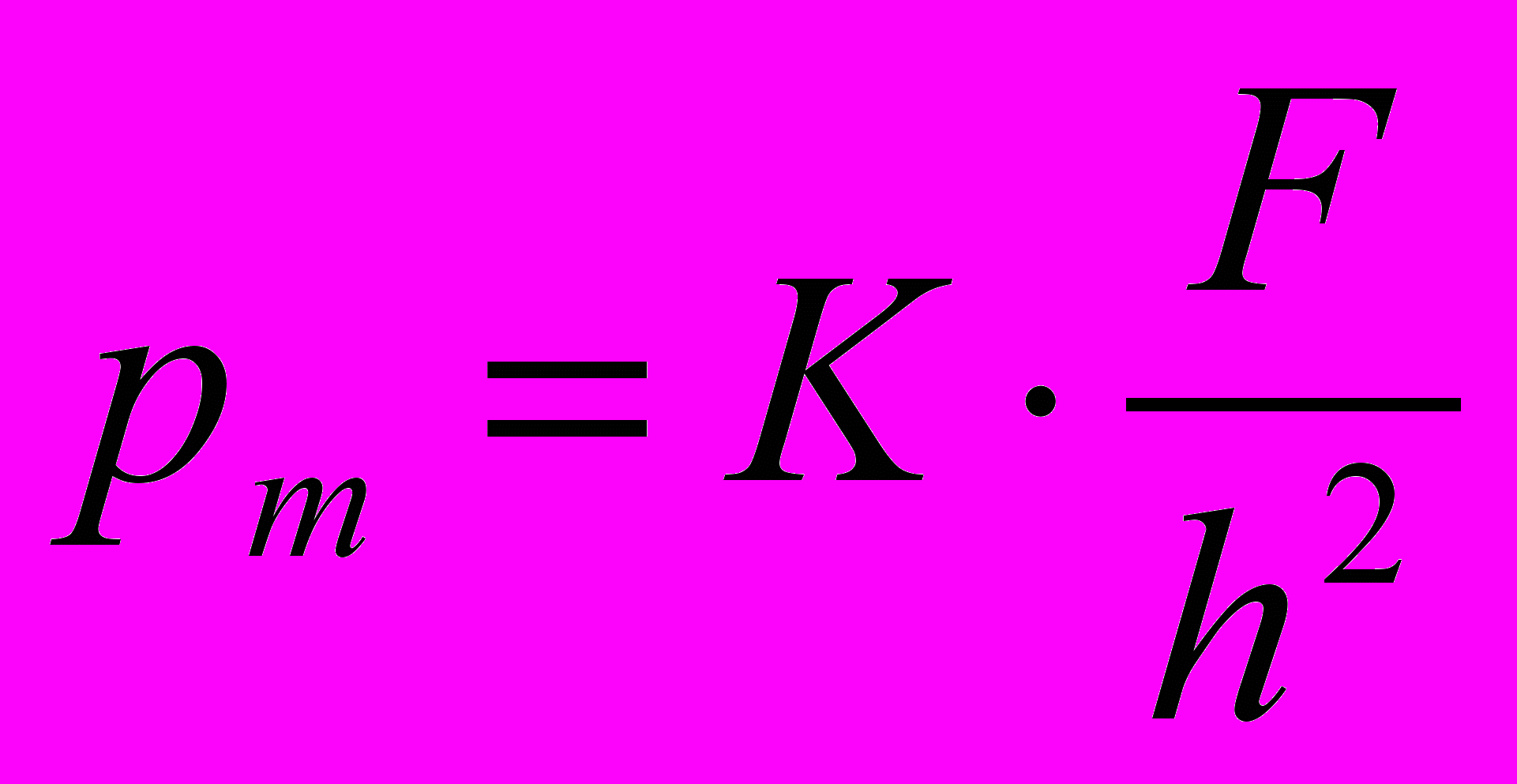где: pm – предельное напряжение сдвига, кг/м2;

К – константа прибора;

F – величина усилия, кг;

h – глубина погружения корпуса, м.

Для второго ,

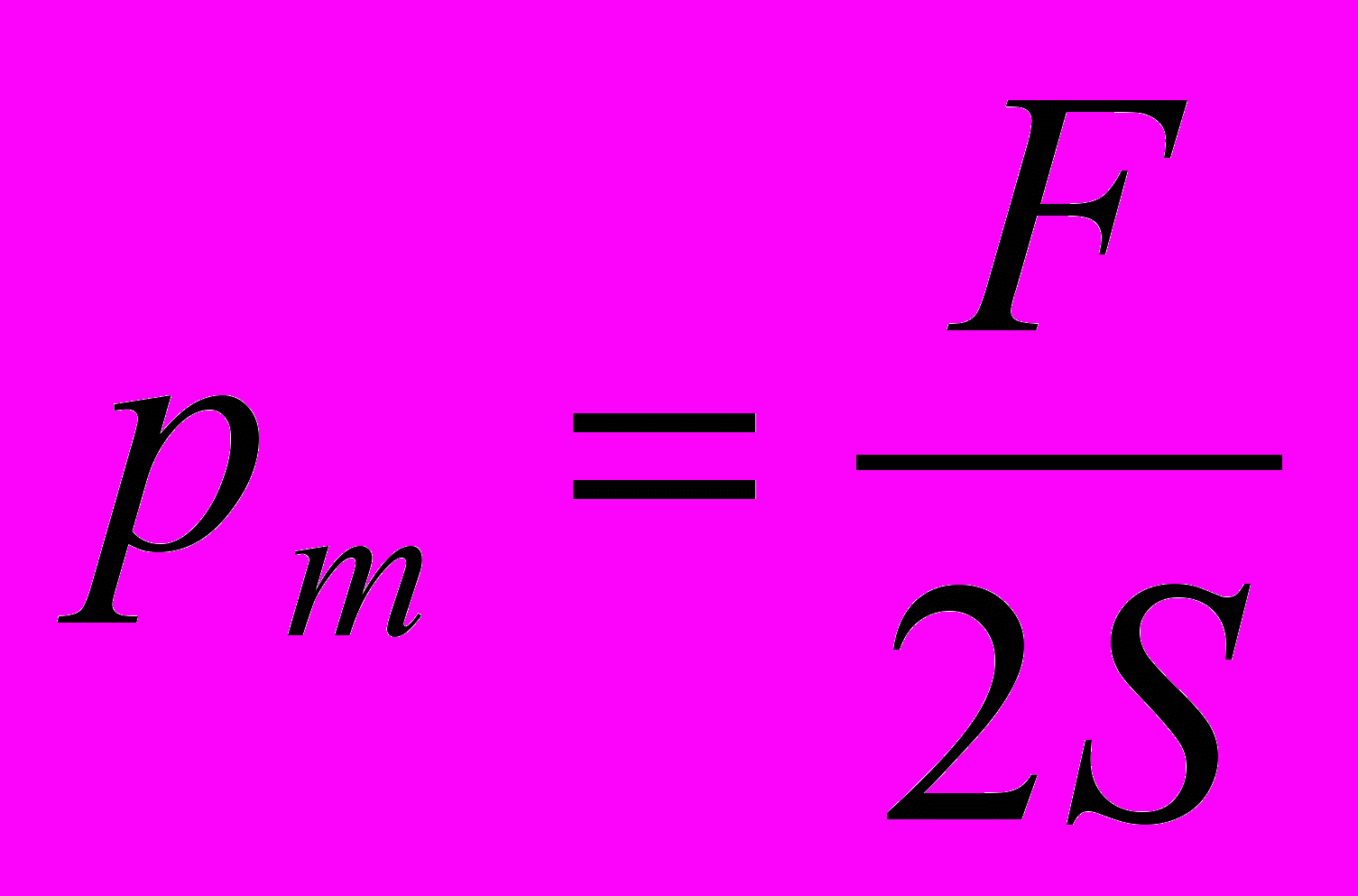Где S – боковая поверхность пластинки, погруженной в исследуемую систему, м2.


Задачи

96. Вычислите скорость истечения жидкости из капилляра длиной l=5·10-2м с радиусом сечения r = 25·10-5м под давлением p=980 Н/м2. Вязкость жидкости η = 2·10-3 Н·с/м2.

97. Какова вязкость глицерина, если из капилляра длиной l=6·10-2м с радиусом сечения r = 1·10-5м он вытекает со скоростью υ/τ=14·10-10м3/с под давлением p=200Н/м2?

98. Определите давление, которое необходимо применить к бесструктурной жидкости при истечении ее из капиляра. Вязкость жидкости η = 1,8·10-3 Н·с/м2. Капилляр имеет длину l=10·10-2м с радиусом сечения r = 2·10-4м.

99. Какова вязкость салициловой кислоты, если из капилляра длиной l=5·10-2м жидкость вытекает со скоростью υ/τ=2·108м3/с под давлением p=150Н/м2?

100. С помощью вискозиметра Волоровича исследована 95%-ная суспензия окиси цинка в органической среде. Постройте реологическую кривую в координатах N=f(p) и определите величину предельного напряжения на сдвиг pm.

Масса груза p·103, кг
40
44
48
52
56
60

Число оборотов N, об/с
0,455
0,566
0,675
0,782
0,89
1,0


101. Определите величину предельного напряжения на сдвиг pm для суспензии TiO2 в органической среде, по данным, полученным с помощью вмскозиметра Волоровича (график строить в координатах N=f(p)).

Масса груза p·103, кг
42
46
50
54
58
62

Число оборотов N, об/с
0,502
0,605
0,708
0,810
0,982
1,036


102. При исследовании реологических свойств олеосуспензий методом тангенциального смещения пластинки напряжения на сдвиг pm=354Н/м2 для 25%-ной суспензии железного сурина. Как будет меняться величина pm в зависимости от концентраций ПА-добавок олеиновой кислоты. Покажите графически.

Концентрация олеиновой кислоты С,%
0,5
2,0
6,0
20,0

Наибольшее усилие Fm·102, Н
2,0
1,2
0,5
0,2


103. Рассчитайте и постройте график изменения величины предельного напряжения сдвига в зависимости от концентрации суспензии железного сурина в параксилоле. При использовании метода тангенциального смещения пластин получены следующие данные:

Концентрация дисперсной фазы С,%
15
20
22
24
27

Наибольшее усилие Fm·102, Н
0,28
1,26
2,10
2,38
2,94

Длина пластинки а=0,7·10-2м, ширина в=0,5·10-2м.

104. Рассчитайте и постройте график зависимости pm агарового студня от концентрации поверхностно-активной добавки – изопропилового спирта. Исследования проводились методом конического пластомера.

Концентрация изопропилового спирта, с·102, кмоль/м3
0,0
3,0
6,0
12,0
30,0

Глубина погружения конуса h·102, м
1,08
1,34
1,54
1,81
2,03

Величина нагрузки F=1·10-2кг, константа конуса K=0,413.

105. При исследовании влияния поверхностно-активных добавок на структурообразование суспензии окиси кальция получены данные (метод конического пластомера):

Концентрация CCБ С,%
0,0
0,14
0,40
0,72
1,44
7,2

Глубина погружения конуса

h·103, м
2,0
1,64
0,95
0,75
0,63
0,59

Величина нагрузки F=1кг, константа конуса К=0,4. Постройте кривую зависимости pm от концентрации добавки.

106. Покажите графически влияние добавки глюкозы на pm концентрированной суспензии CaO (конический пластометр):

Концентрация глюкозы С,%
0,0
0,4
0,8
1,6
4,0
8,0

Глубина погружения конуса

h·103, м
2,14
1,25
1,19
0,95
0,85
0,77

Величина нагрузки F=1,2кг, константа конуса К=0,4.

107. С помощью конического пластометра исследовалось влияние дисперсности пасты красителя кубового зеленого на ее структурообразование. Получены данные:

Время τ, час
Глубина погружения конуса h·103м при радиусе частиц

r1=(0,5+5)·10-6м
r2=(5+10)·10-6м
r3>10·10-6м

1
2,44
3,84
4,21

2
2,09
3,14
4,21

3
1,98
3,05
4,10

4
1,92
2,93
4,10

5
1,88
2,88
4,10

6
1,85
2,88
4,10

Величина нагрузки F=5·10-2кг, константа конуса К=0,5.

Постройте кривые в координатах pm=(τ) и сравните величины pm соответствующие 6 часам.

108. При исследовании реологических свойств нефти получены данные:

Напряжение p·10-2, Н/м2
5,0
10,0
15,0
20,0
25,0
30,0
40,0

Скорость течения (1/τ)·102, 1/с
0,2
1,0
2,2
3,7
5,3
7,0
8,7

Постройте кривую в координатах pτ=(p) и определиие при каком напряжении полностью разрушится структура.

109. Постройте реологическую кривую в координатах dυ/dτ=f(p) для концентрированной суспензии сажи в вазелиновом масле и определите pm.

Напряжение p·10-2,

Н/м2
2,5
3,0
3,5
4,5
6,0
7,0
8,0
9,0
10,0

Градиент скорости dυ/dτ, с-1
10
20
49
120
235
310
360
400
500

110. Рассчитайте и постройте кривую изменениия pm на сдвиг в зависимости от влажности хвалынской глины.

Напряжение p·10-2,

Н/м2
1,0
2,0
8,0
12,8
16,0
24,0
30,0
40,0

Время истечения раствора τ, с
340,0
159,0
39,0
23,4
17,8
10,8
8,7
6,5

Величина нагрузки F=1 кг, константа конуса К=0,66.

111. Постройте реологическую кривую раствора нитроцеллюлозы в ацетоне в координатах pτ=(p).

Влажность глины, %
32
35
40
45
52
60

Глубина погружения конуса

h·103, м
2,45
3,15
3,66
5,12
8,10
11,5

Определите pm.

112. Постройте реологические кривые в координатах pτ=(p) для растворов этилцеллюлозы различной молекулярной массы в толуоле. Сравните величину предельного напряжения сдвига pm.

Напряжение p·10-2, Н/м2
Время истечения растворов τ (c) при молекулярной массе

30,080
46,780
72,160

10,0
735
755
795

20,0
350
360
375

30,0
232
236
246

50,0
138
140
144

70,0
98
99,3
102

80,0
85,7
87,0
89,5

90,0
76,2
77,2
79,3


7. Молекулярно-кинетические свойства коллоидных систем

Молекулярно-кинетические свойства неструктурированных коллоидных систем и обычных истинных растворов принципиального различия не имеют, разница носит лишь количественные характеристики. Как молекулы, так и коллоидные частицы находятся в беспрерывном тепловом движении, которое применительно к коллоидным системам получило название броуновского движения.

Путь частицы не является прямолинейным, т.к. при движении она испытывает толчки со стороны молекул среды, так же находящихся в тепловом движении. Поэтому, не меняя своего направления, частица сдвигается то в одну, то в другую сторону, а ее сложный путь характеризуется так называемым средним сдвигом.

Для вычисления среднего сдвига x, необходимо на произвольно выбранную ось спроектировать все наблюдаемые отклонения частицы, возвести каждую проекцию в квадрат, и взять среднюю величину:

,

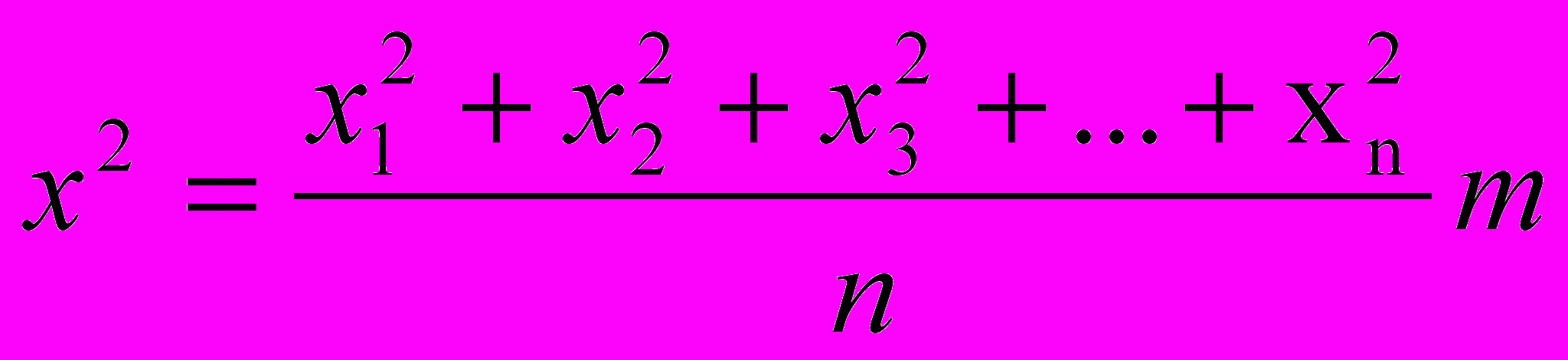где n – число сдвигов.

Согласно уравнению Эйншейна, величина среднего сдвига:

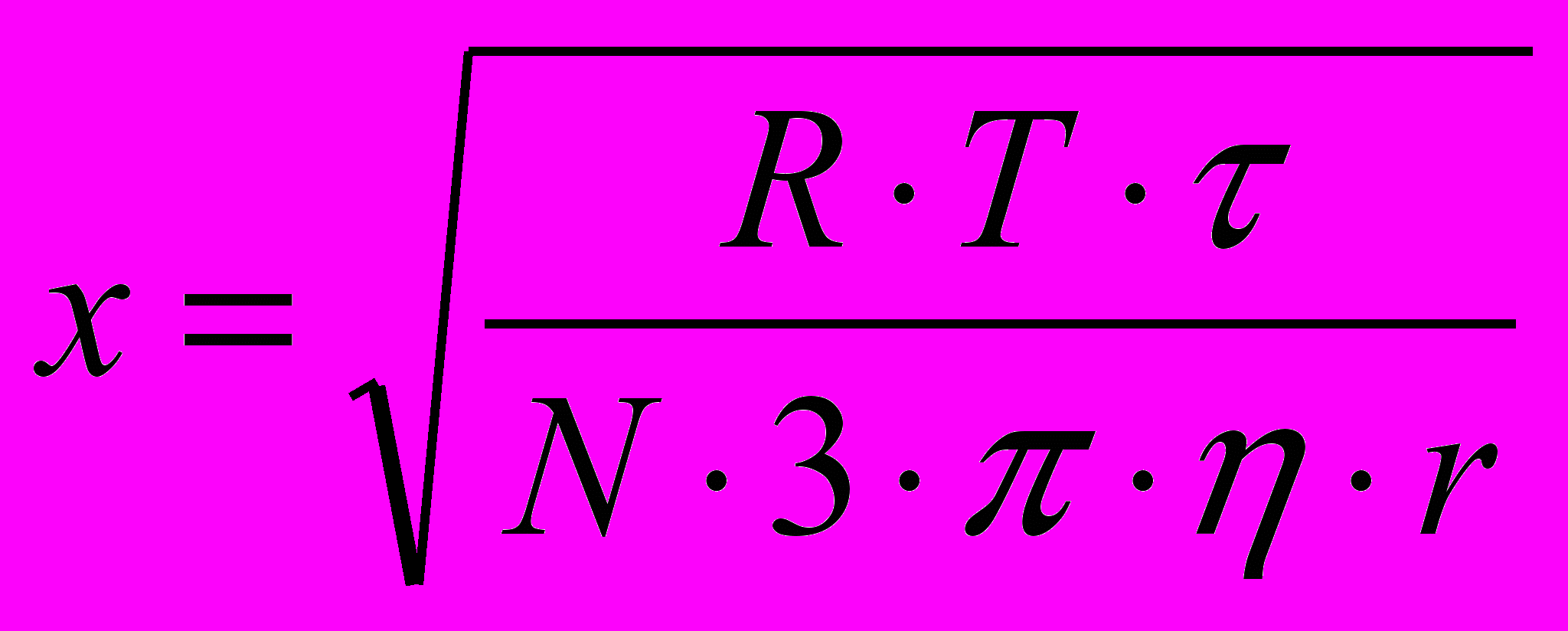,м.

Диффузией называется процесс выравнивания концентраций по всему объему раствора, происходящий под влиянием броуновского движения. Скорость его характеризуется коэффициентом диффузии D, величина которого по Эйнштейну равна:

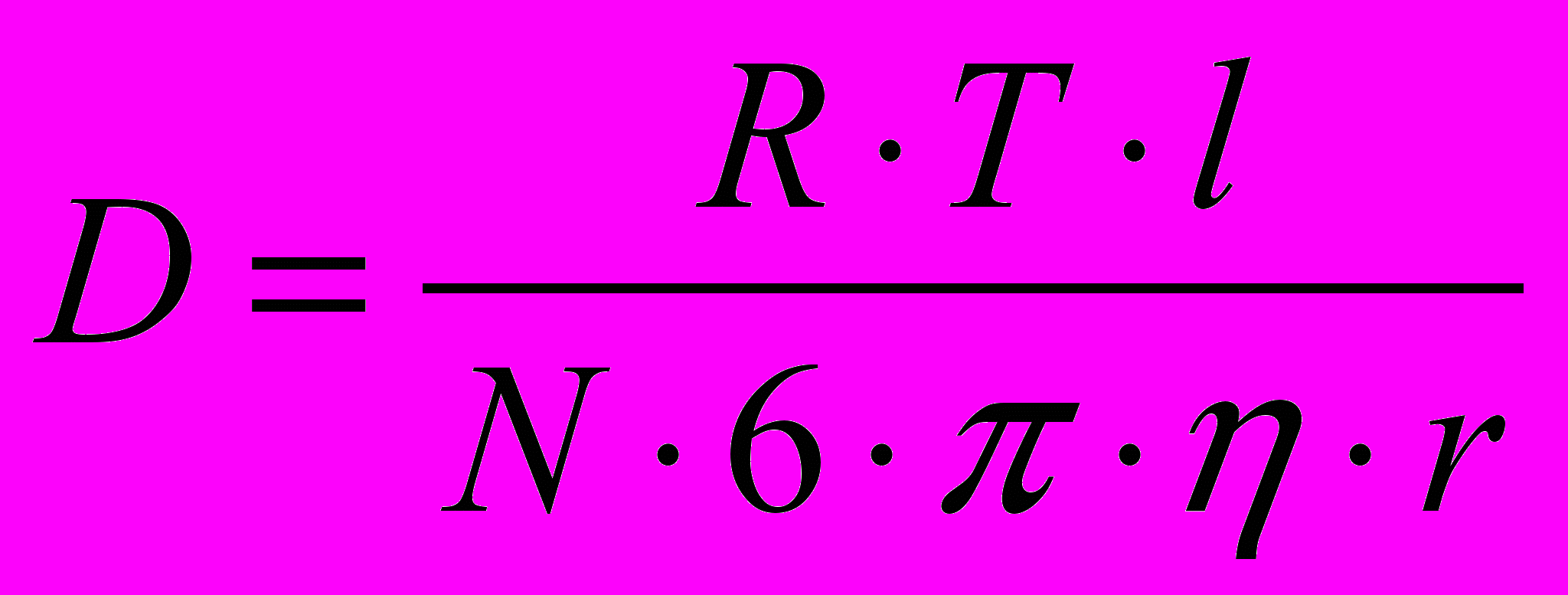(м2/с или м2/сутки),

где R – газовая постоянная;

T – температура, К;

N – число Авогадро;

r – вязкость среды, (Н·с)/м2.

По экспериментальным данным В легко рассчитать средний радиус сферических частиц, отсюда – молекулярная или мицеллярная масса вещества:

М = 4/3 πr3γN, где γ – плотность вещества.

Осмотическое давление p, Н/м2, разбавленных коллоидных растворов можно найти, пользуясь уравнением Вант-Гоффа:

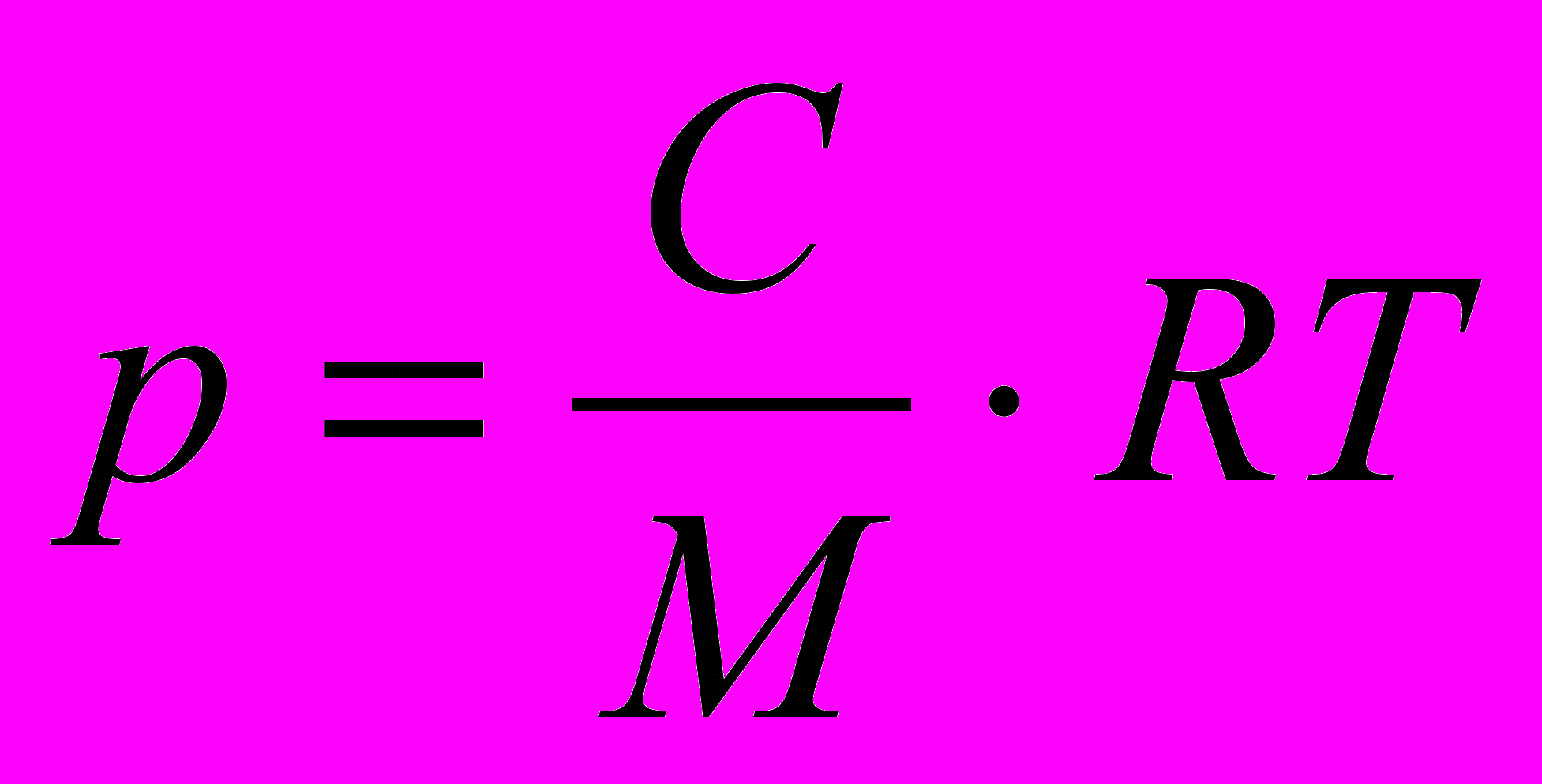или p = nRT Н/м2, т.к. n =С/M,

где С – концентрация раствора, кг/м3;

M – молекулярная масса вещества, кг/моль;

n – частичная концентрация системы;

R – газовая постоянная, Дж/моль;

T – температура, К.

Величина осмотического давления золей значительно меньше осмотического давления истинных растворов. Причиной этого является большая масса коллоидных частиц: при одинаковой массовой концентрации частичная концентрация коллоидной системы всегда меньше, чем у истинного раствора.

Для двух систем одинаковой концентрации и равной плотности, но разных радиусов частиц:

,

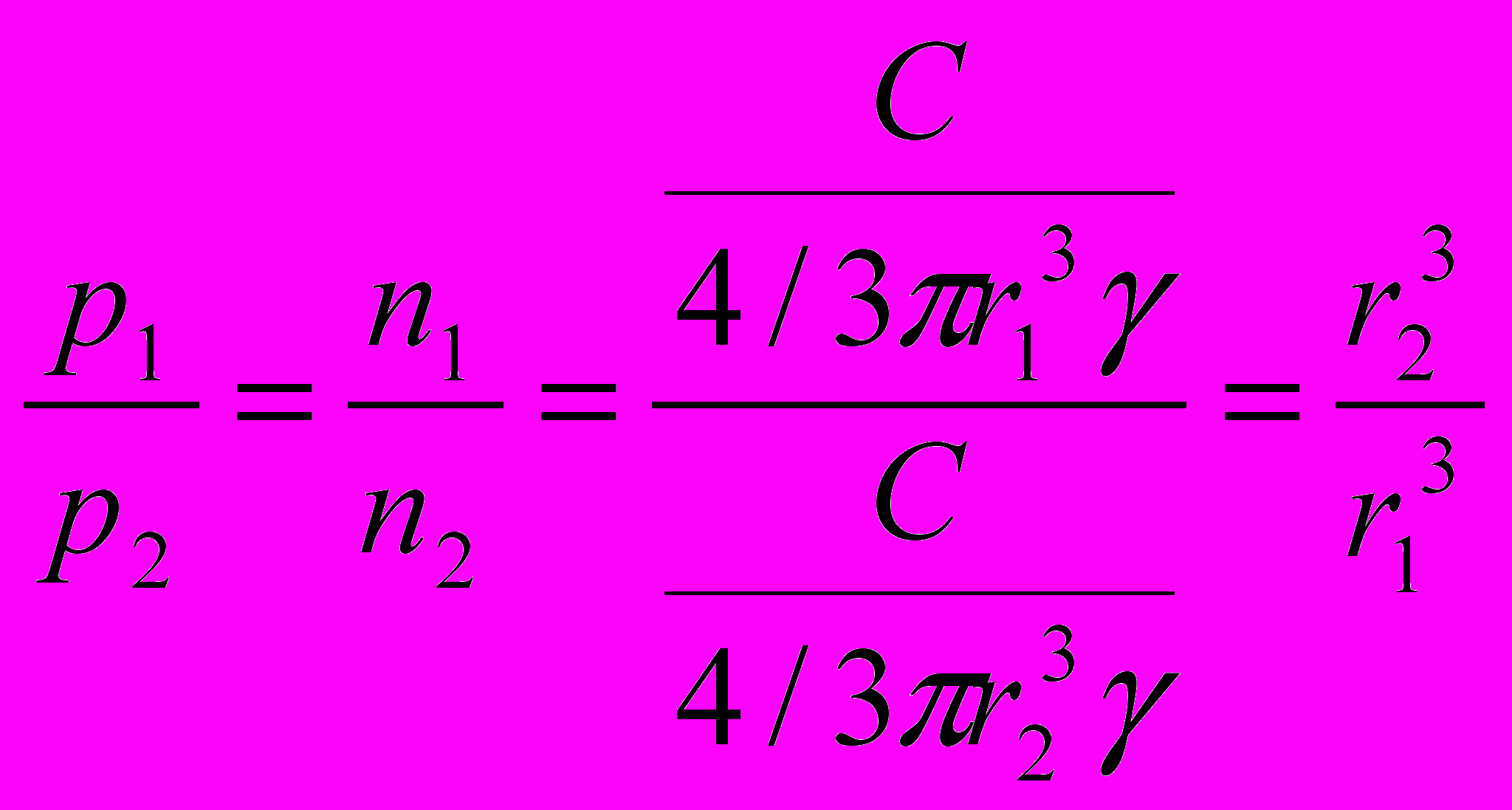где r1 и r2 – радиусы частиц первой и второй системы, м;

p1 и p2 – соответственно величина их осмотического давления;

γ – gплотность вещества, кг/м3;

с – концентрация, кг/м3.

Другой особенностью осмотического давления коллоидных растворов является непостоянство его величины, что объясняется агрегацией, имеющей место в золях. Поэтому метод осмометрии не применяется для определения размера или мицеллярной массы коллоидных частиц.

Если в коллоидной систеие сила тяжести будет превалировать над броуновским движением, то частицы начнут оседать. Скорость оседания (седиментации) по закону Стокса:

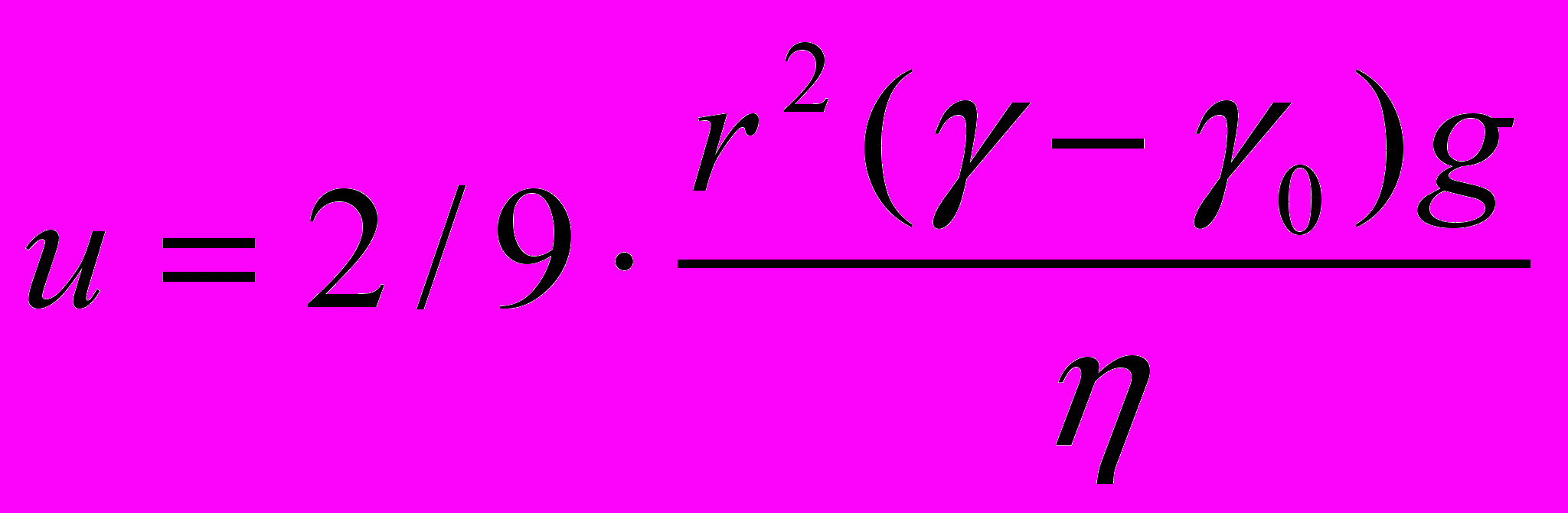м/с,

где r – радиус частицы, м;

γ и γ0 – соответственно плотность дисперсной фазы и дисперсной среды, кг/м3;

g – ускорение силы тяжести, м/с2;

η – вязкость среды, (Н·с)/м2.

Такая зависимость скорости седиментации от размеров частиц положена в основу седиментационного анализа. Заменив скорость оседания u

отношение пути h, пройденного частицей, ко времени τ:

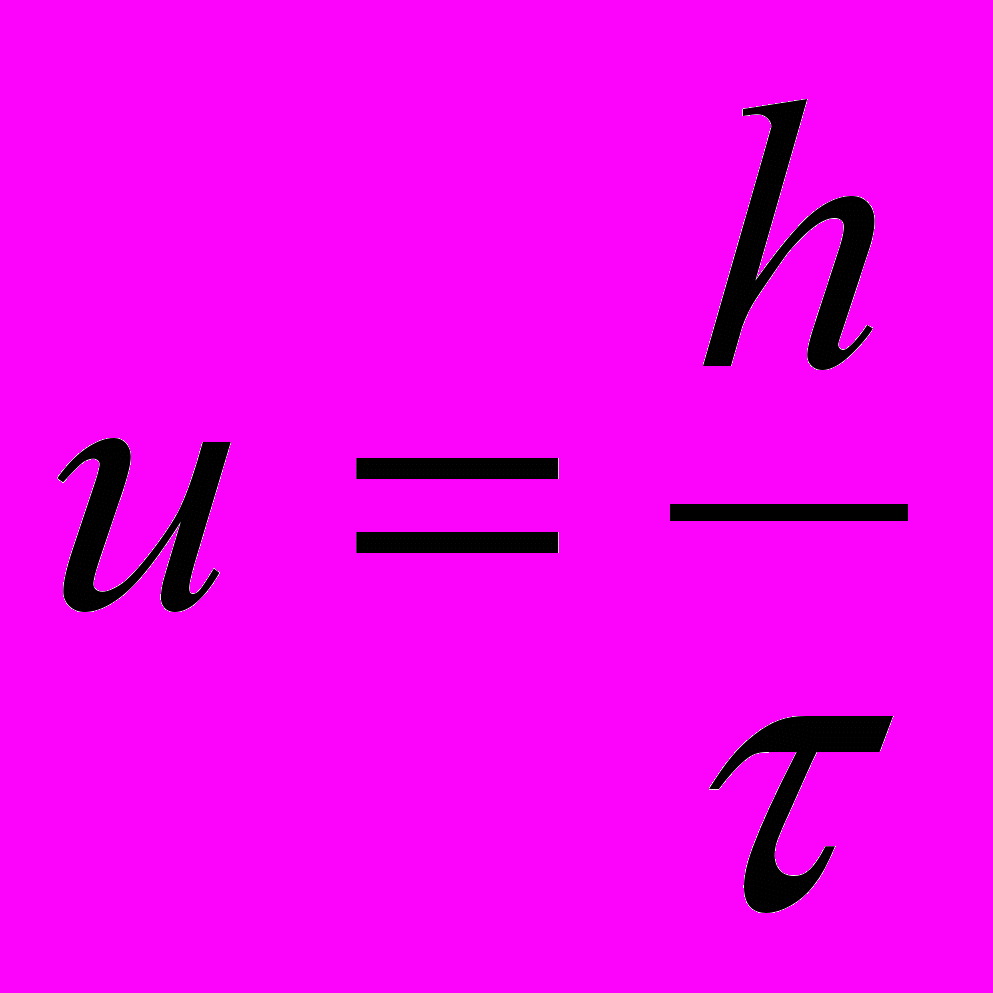(м/с) и объединив постоянные величины в константу К, запишем закон Cтокса в таком виде:

.

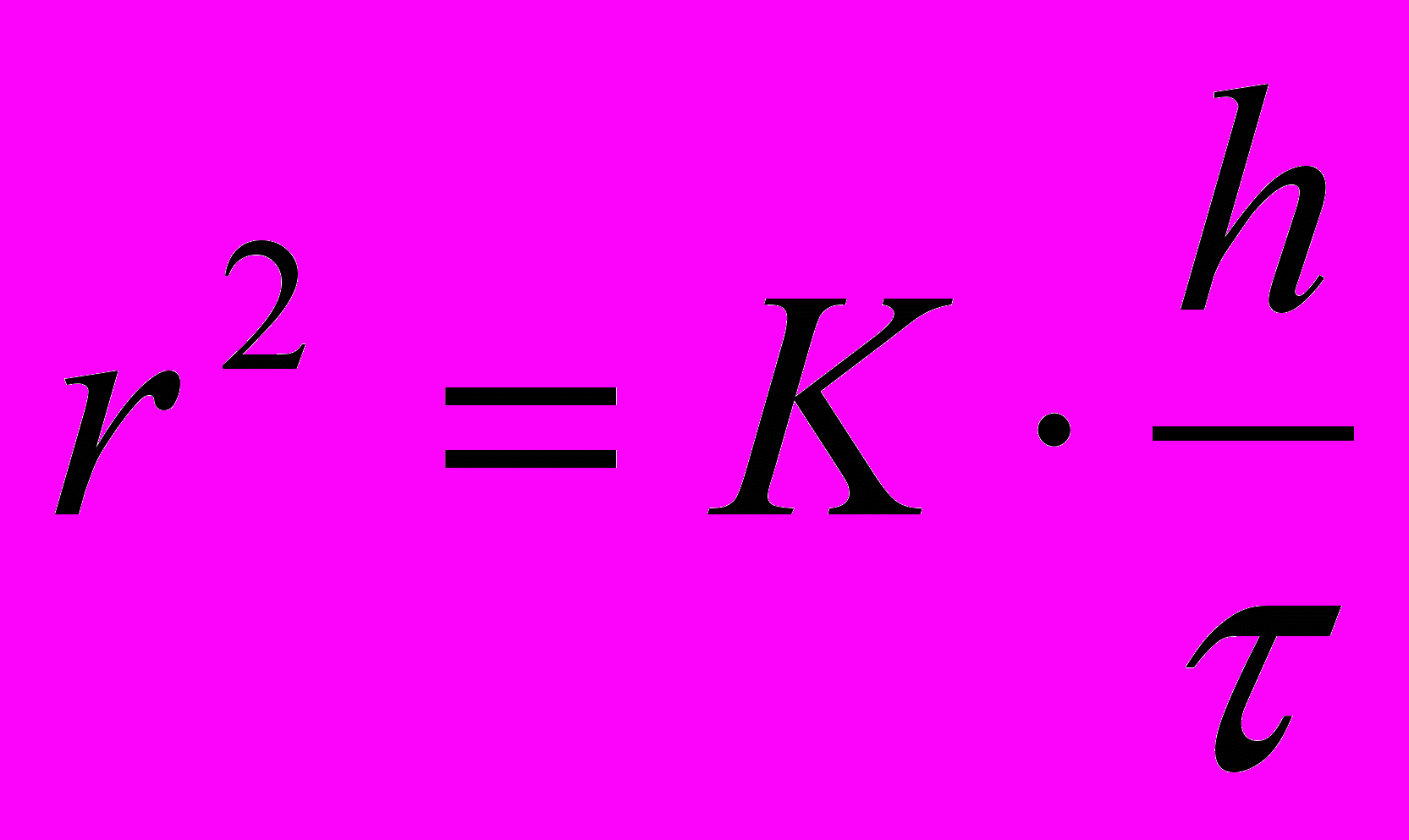Для наблюдения за оседанием суспензии обычно применяют седиментационные или торзиционные весы. На основе экспериментальных данных строят кривую седиментации в координатах Q=f(τ), где Q – количество суспензии (выраженное в процентах к общему количеству порошка), осевшей на время τ. Разбив кривую касательными на несколько участков можно соответственно каждому отрезку времени τ рассчитать радиус частиц:

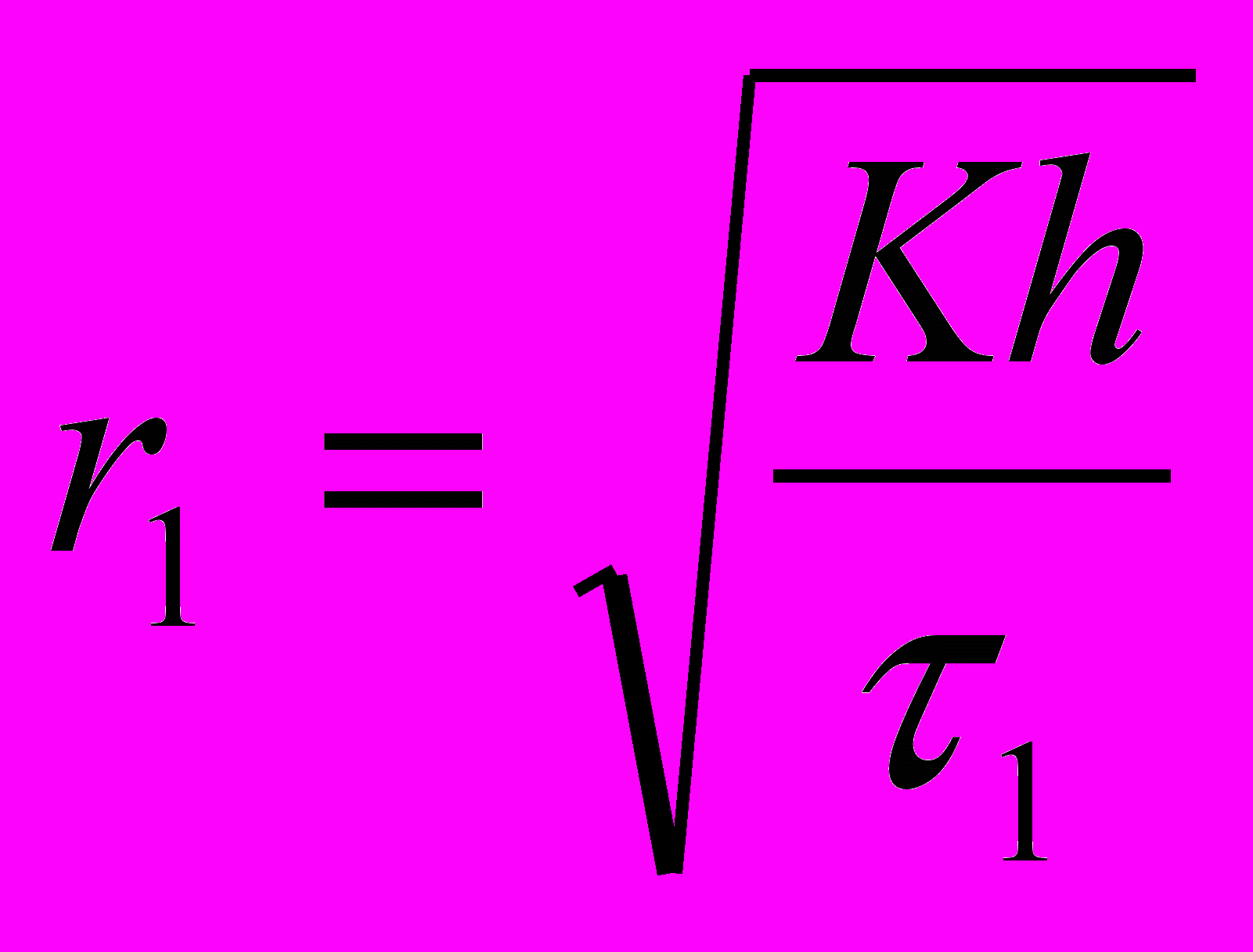
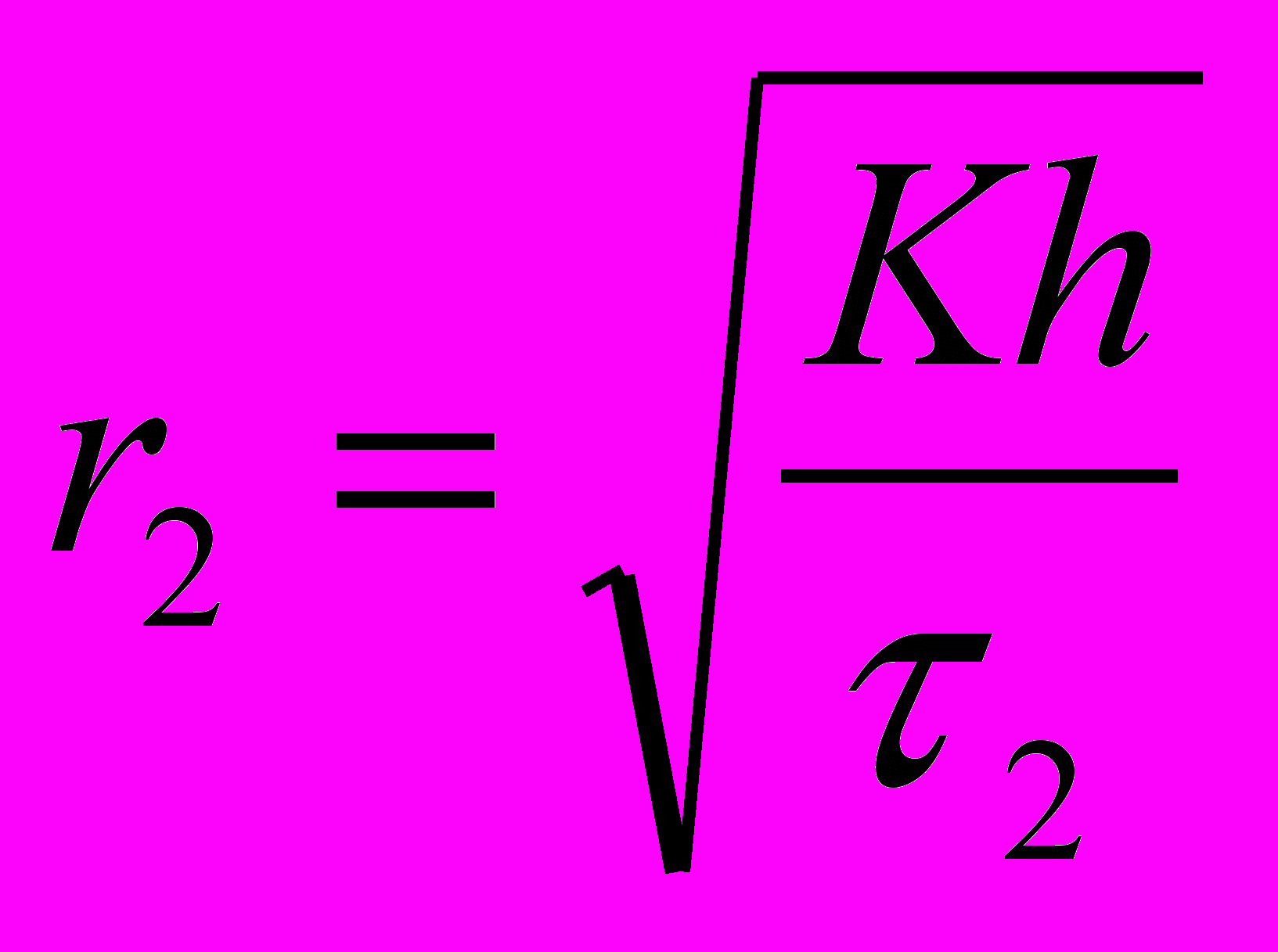и т.д.




Отрезок между касательными 1-2, очевидно, соответствует количеству вещества, осевшему за промежуток времени τ2- τ1 и содержащему радиусы от r1 до r2. Остальные отрезки рассматриваются аналогично. Приняв величину отрезка 0-4 за 100%, находят величину каждого отрезка в процентах: Q1, Q2, Q3 и т.д.

Чтобы построить кривую распределения, нужно на оси ординат отложить отношение 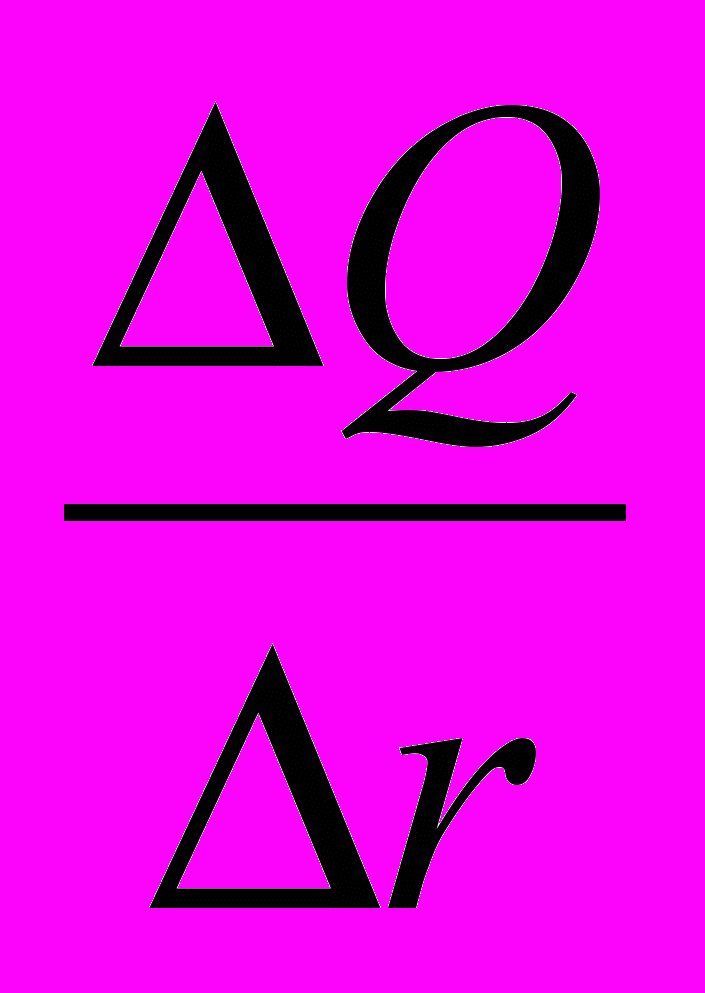(Δr – разность между r2 и r1; r3 и r2 и т.д. )обы построить кривую распределения, нужно на оси ординат отложить отношение 0% находят величину каждого отрезка в процентахей,), а на оси абсцисс средние значения радиусов:

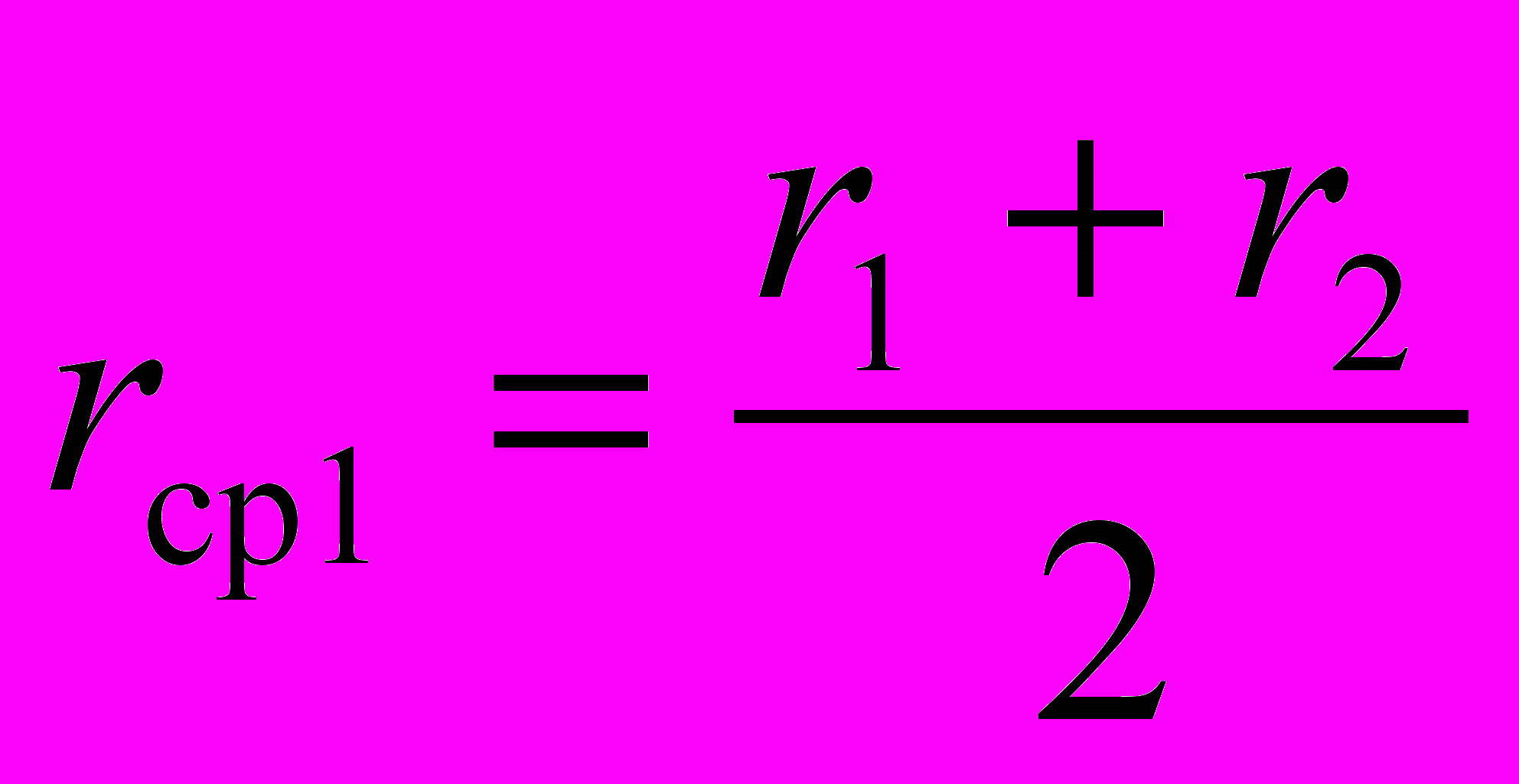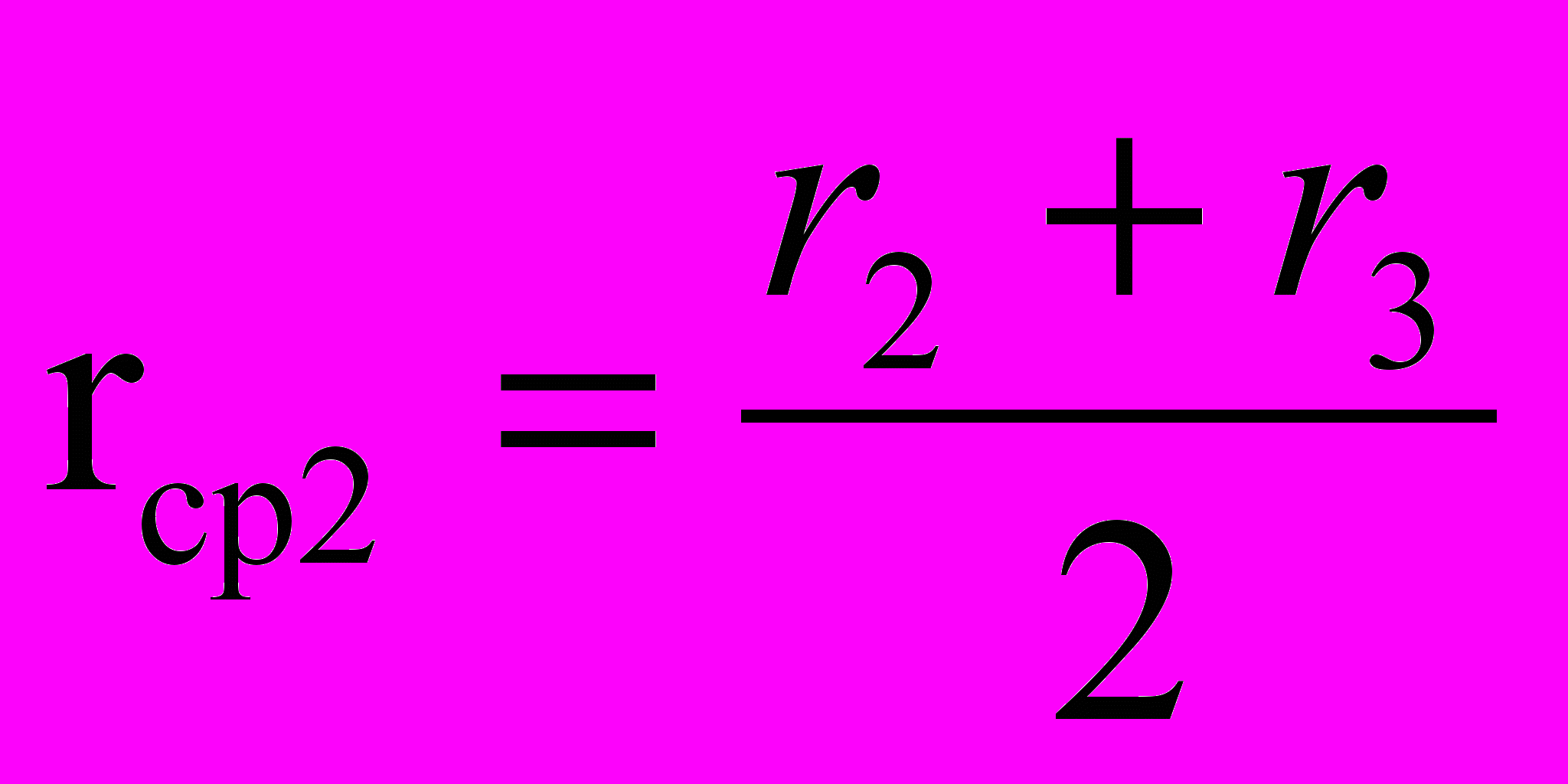; и т.д.

Описанный метод расчета кривых распределения несложен, однако он не всегда может быть применен из-за трудности графического написания касательных.

Более надежным и точным является аналитический метод расчета. В этом методе процесс седиментации описывается уравнением:

,

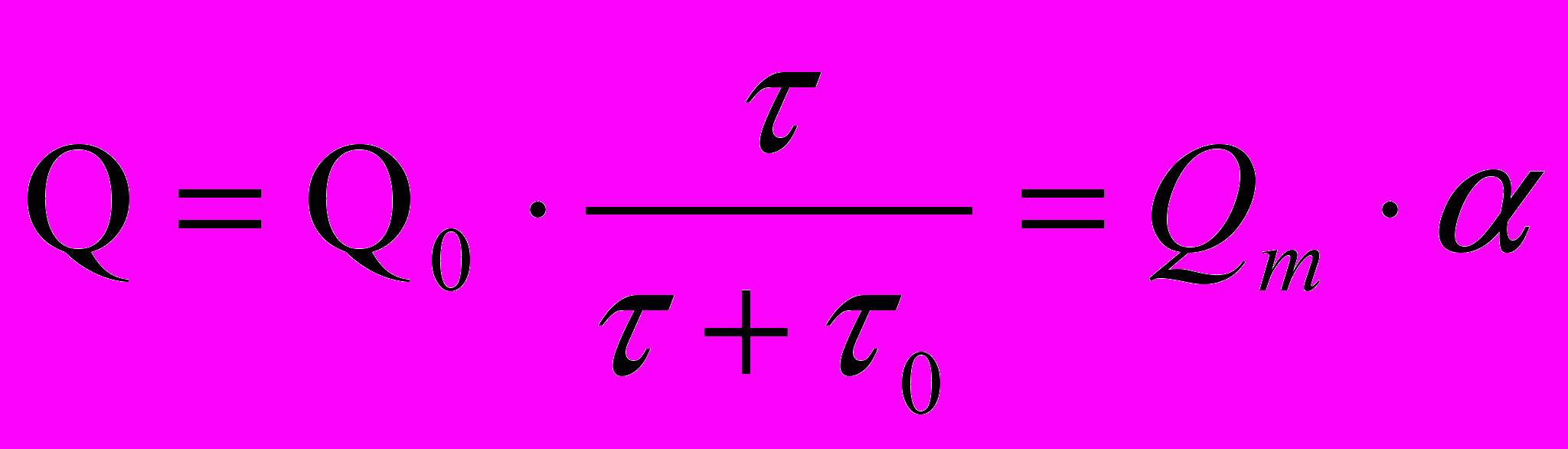где Qm и τ0 – константы (первая выражена в %, вторая – в размерности веремени).

По экспериментальным данным строят кривую оседания Q = f(τ), а затем прямую в координатах [τ/Q]=f(τ), по которой находят τ0 и Qm (где Qm – котангенс угла наклона прямой, а [τ0/Qm]-отрезок, отсекаемый прямой на оси ординат). Затем константу τ0 заменяют, используя закон Стокса, эквивалентной ей константой r0:

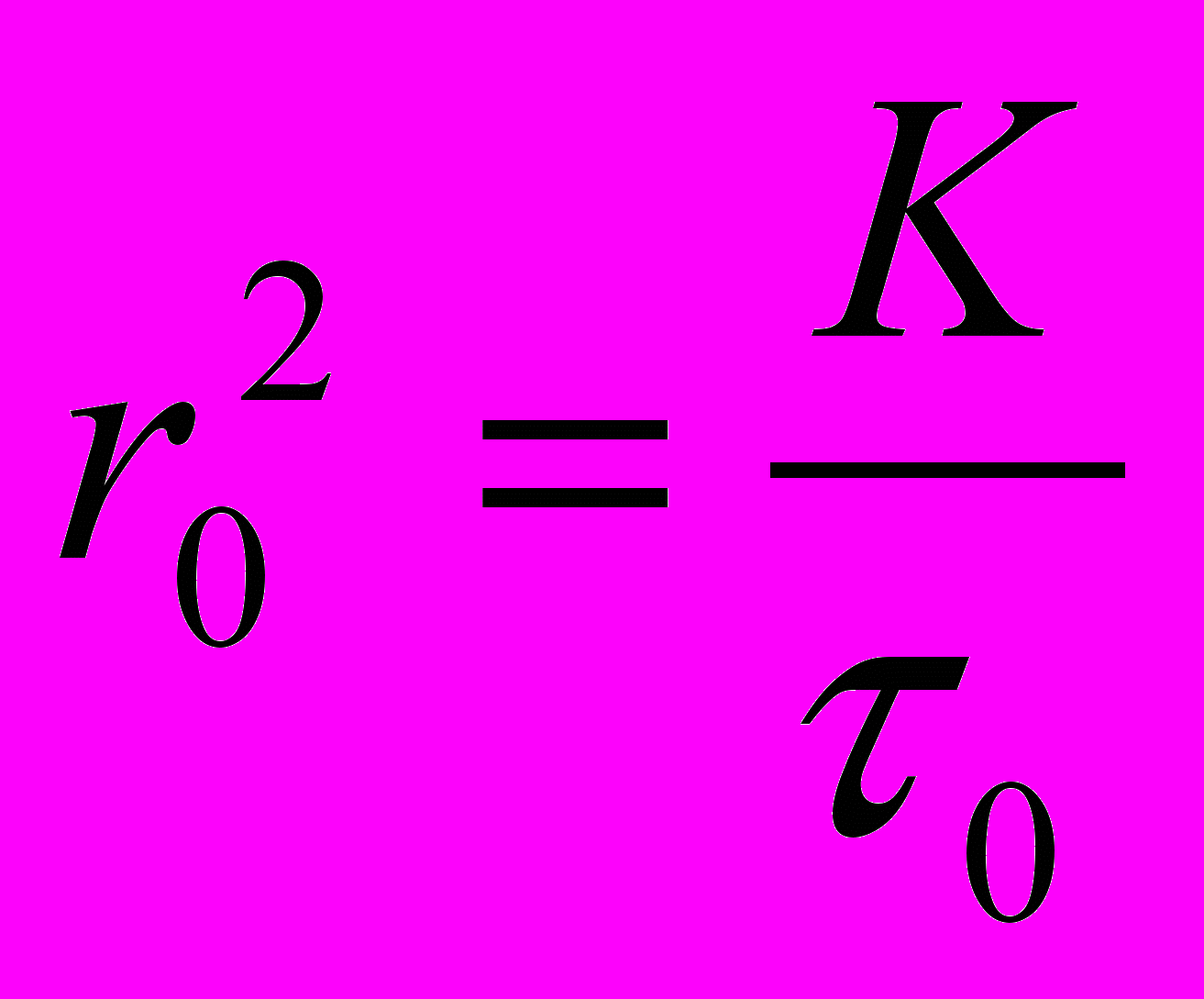, тогда .

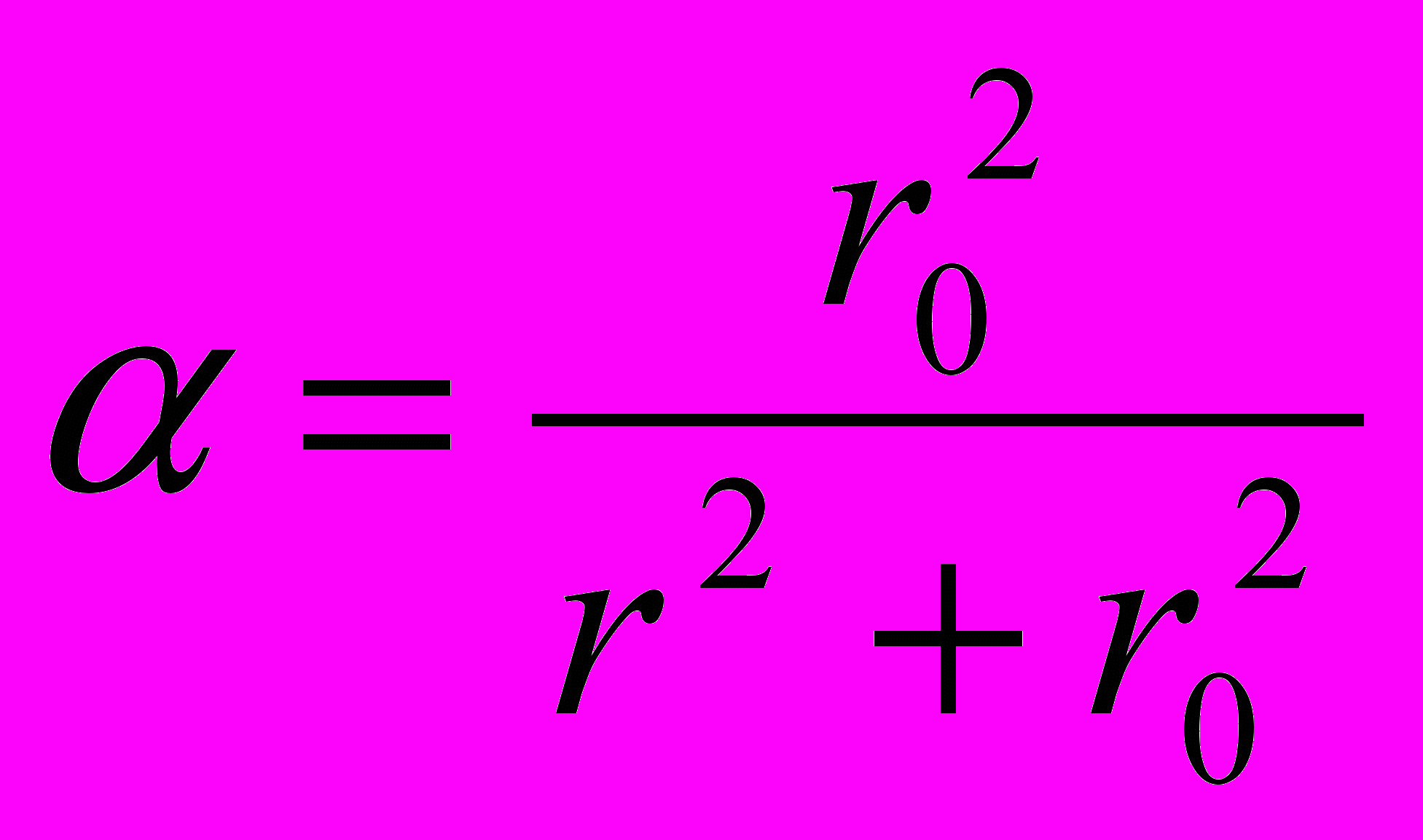Определяют три основных радиуса, характеризующих кривую распределения: rпр – предельный (наименьший); rн – наивероятнейший, отвечающий максимальному значению ΔQ/Δr, и rм – максимальный радиус:



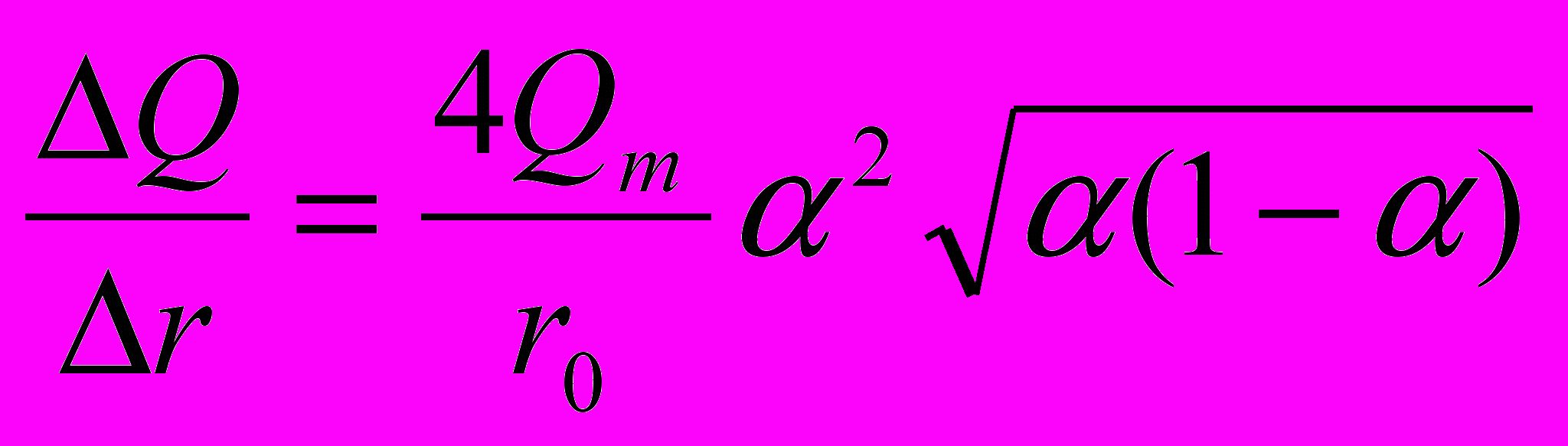
или, заменяя 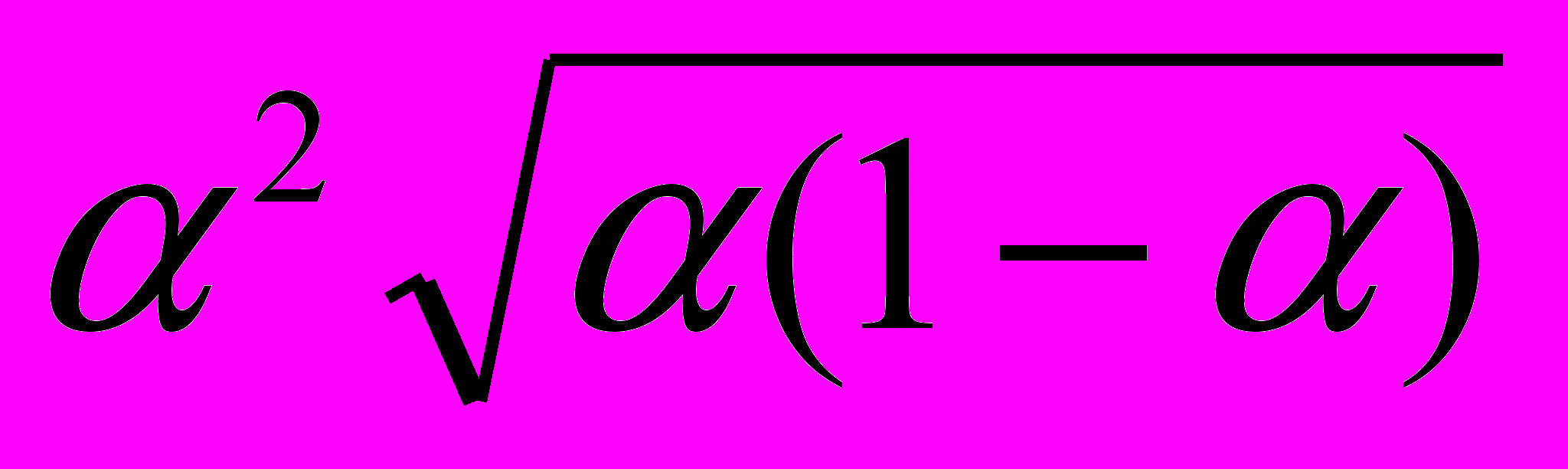через ε:

,

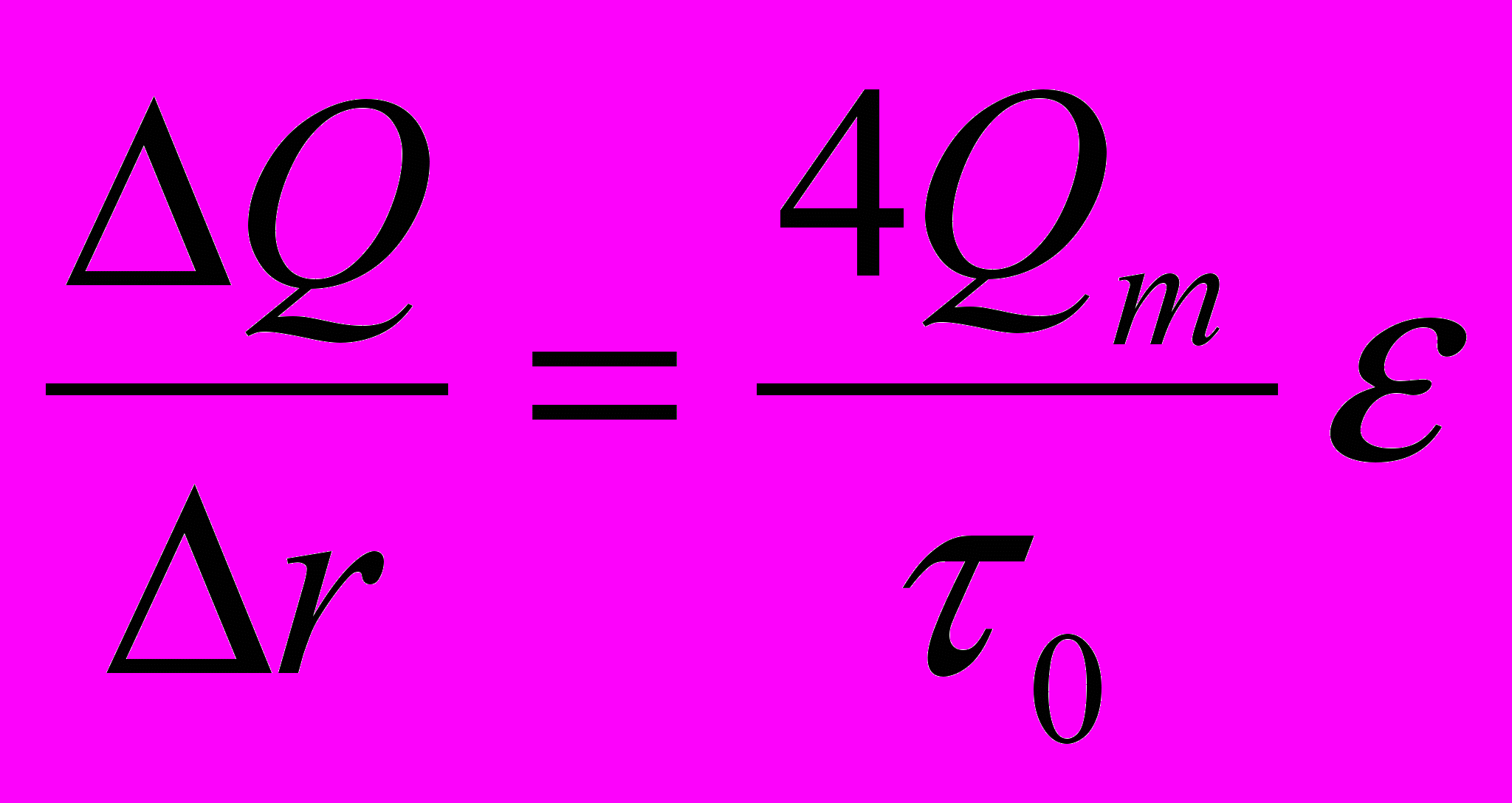т.к. ε зависит только от α, то ее можно найти в табл. 1(см. приложение).

Дифференциальная кривая строится в координатах ΔQ/Δr = f(r).

$_SERVER["DOCUMENT_ROOT"]."/cgi-bin/footer.php"; ?>