Оборин Антон Викторович
| Вид материала | Документы |
- Темникова Наталья Владимировна педагог-психолог 2 степени Бахматов Максим Викторович,, 123.31kb.
- Батурина Анна, 278.65kb.
- Иванов Антон Викторович доцент кафедры уголовного права и процесса Института социальных, 1398.27kb.
- Мальчики и девочки, 161.1kb.
- Юрченко Антон Александрович методические рекомендации, 1030.57kb.
- Прогнозирование потребности в педагогических кадрах в регионе фролов Юрий Викторович, 113.56kb.
- Чехов Антон Павлович. Избранное / Чехов Антон Павлович; предисл. М. П. Громова., 149.56kb.
- Жарков Александр Сергеевич, генеральный директор фгуп «фнпц «Алтай», член-корреспондент;, 137.29kb.
- Номинация «За внедрение новых методик повышения квалификации врачей и провизоров» Номинант:, 68.57kb.
- Номинация «Лучший молодой преподаватель вуза» Номинант Маньков Александр Викторович, 121.54kb.
Оборин Антон Викторович
студент группы СП-2-06
Научный руководитель: Воробьев Анатолий Николаевич
проф., д.т.н.
Московский государственный горный университет
ОПРЕДЕЛЕНИЕ РАЦИОНАЛЬНОГО РАСПОЛОЖЕНИЯ РАССТРЕЛА ПО ВЫСОТЕ КОТЛОВАНА
DEFINITION OF THE RATIONAL ARRANGEMENT OF EXECUTION ON FOUNDATION DITCH HEIGHT
При строительстве подземных сооружений важное место занимает открытый способ ведения работ. Этим способом строятся траншеи и котлованы, предназначенные для тоннелей метрополитена, автомобильные и железнодорожные тоннелей, коллекторные тоннелей и т.д.
При строительстве котлованов наиболее часто применяется способ со свайным креплением и распорками в виде расстрелов, этот способ применяется наиболее часто в городском подземном строительстве с густой застройкой. Примером таких сооружений могут служить приемные и стартовые котлованы для проходческих щитов, установок микротоннелирования и продавливания.
Одним из основных направлений строительной механики является разработка рациональных сооружений, т.е. при их минимальной материалоемкости обеспечение необходимой прочности. Этот критерий реализуется в обеспечении минимальных значений изгибающих моментов в элементах сооружений.
При рассмотрении котлованов со свайным креплением, в которых сваи являются несущими элементами, а расстрелы – промежуточными опорами, задачей рационального крепления является равенство изгибающего момента под опорой в, виде расстрела, и изгибающего момента в пролете сваи.
 q=λγΗ
q=λγΗРассматривая эту задачу с точки зрения строительной механики в виде расчетной схемы можно принять консольную балку с двумя шарнирами, загруженную равномерно распределенной нагрузкой.
В данной задаче неизвестным параметром является расстояние « х » - длина от конца консоли до опоры.


Составляем аналитическое выражение изгибающего момента от координаты « z » и находим его максимальное значение в пролете балки как функцию « х », это значение приравниваем к значению момента на конце консоли qx2/2.
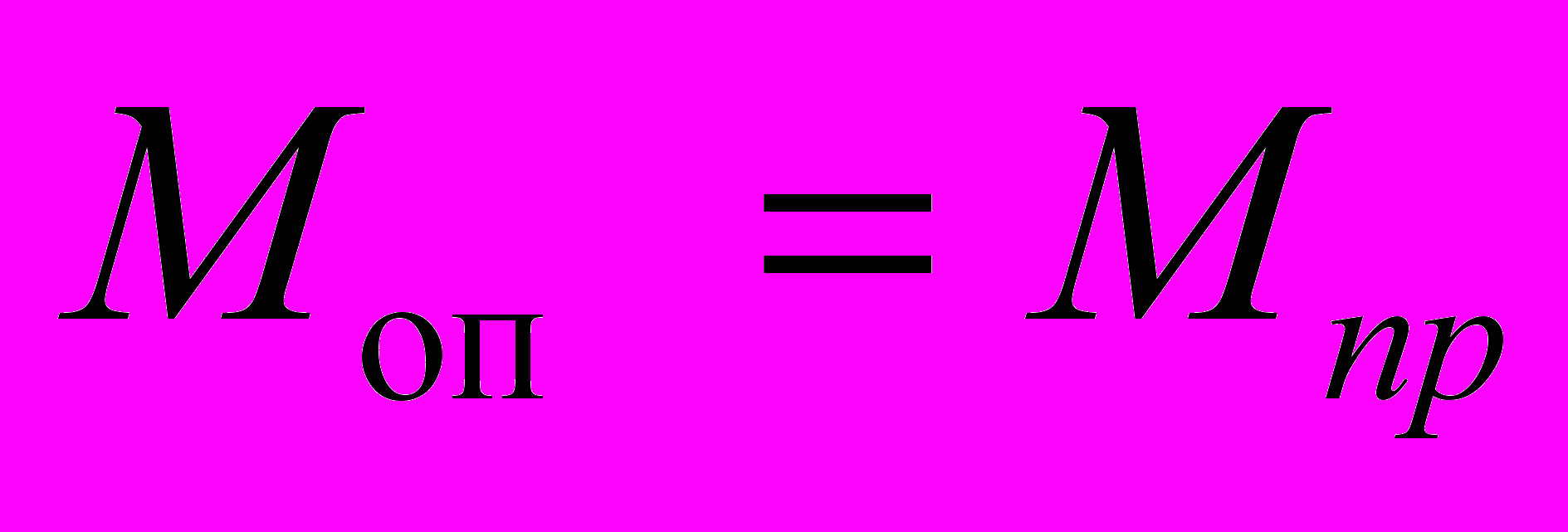
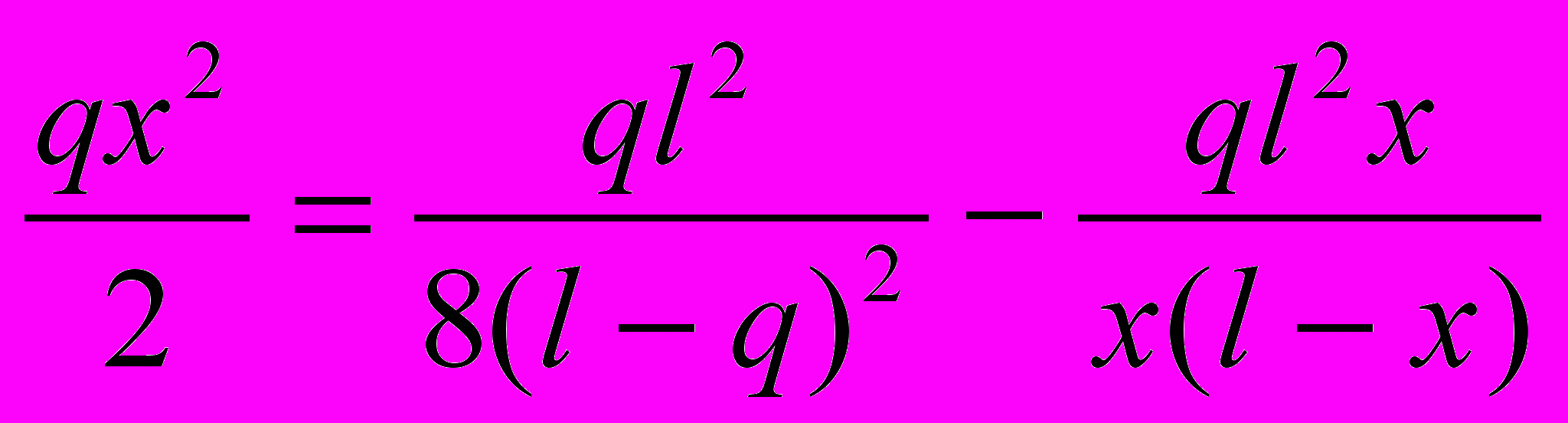
Отсюда получаем степенное уравнение четвертой степени относительно параметра « х » и решаем его с помощью метода последовательных приближений – методом Ньютона
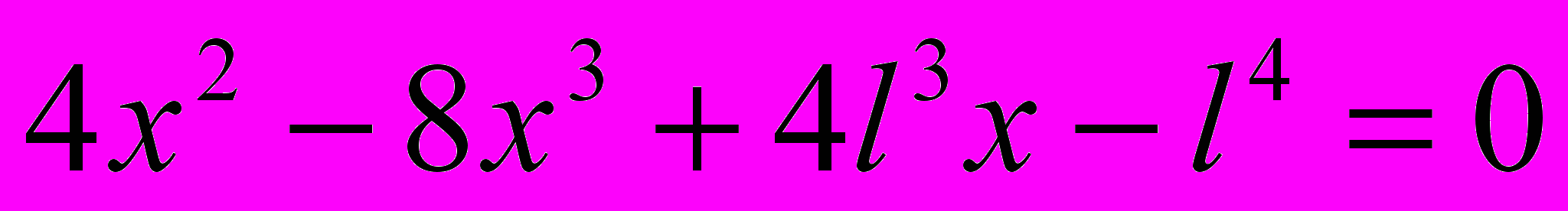





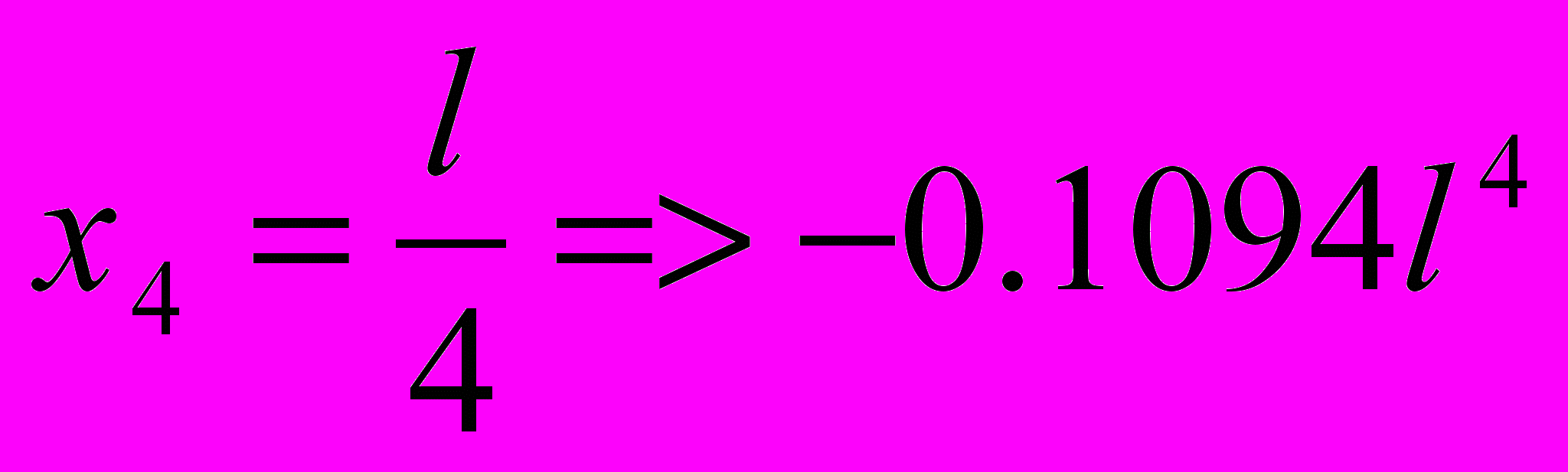
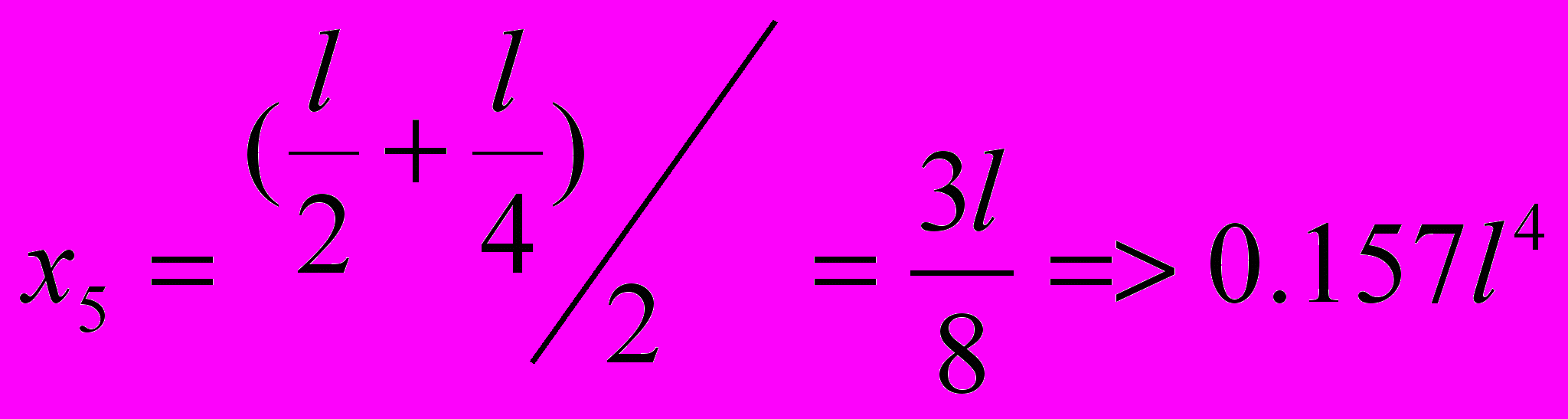
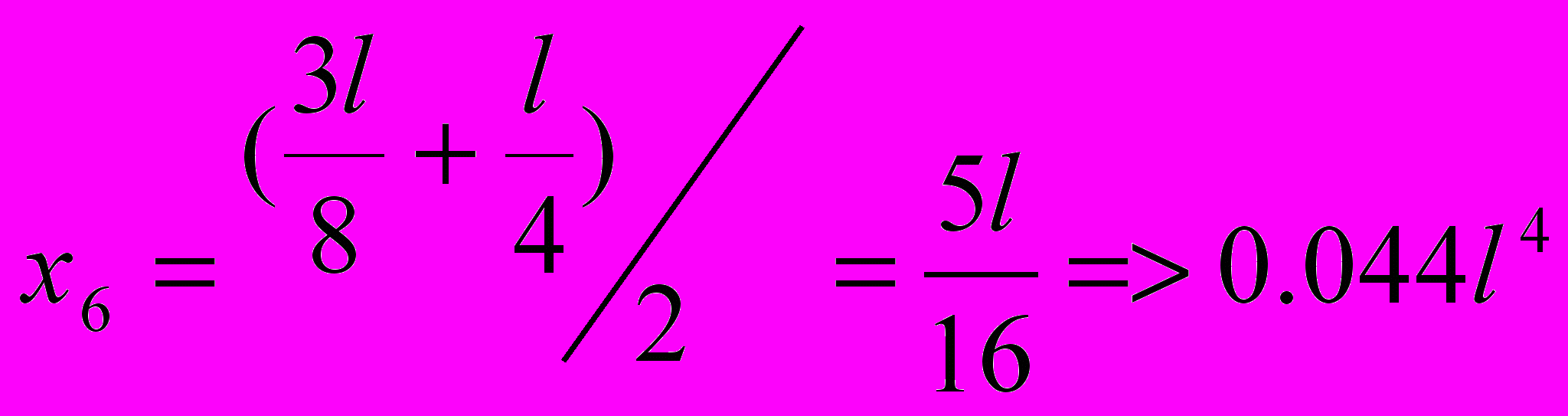
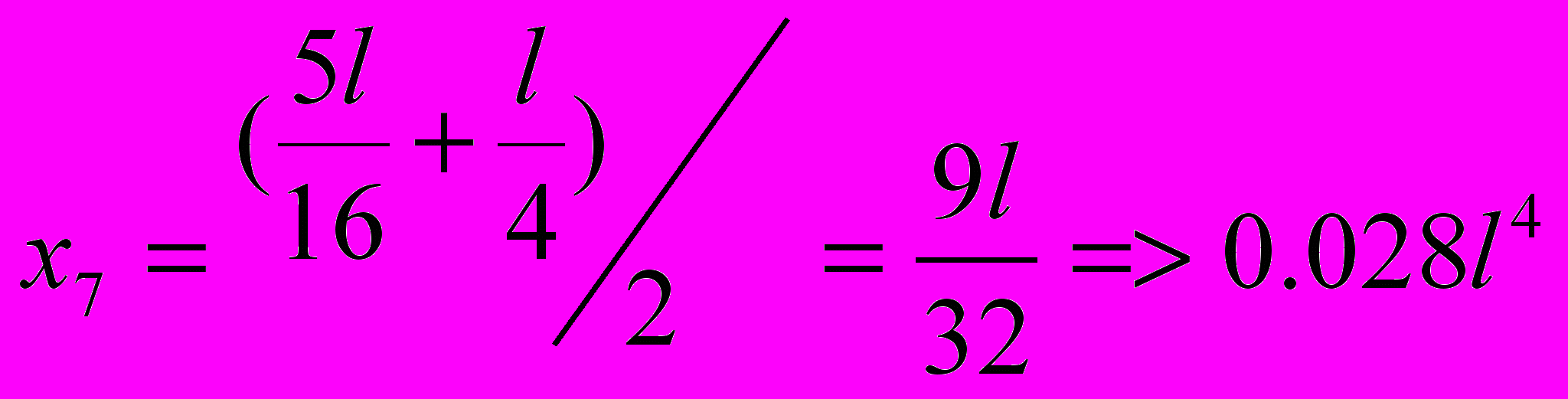
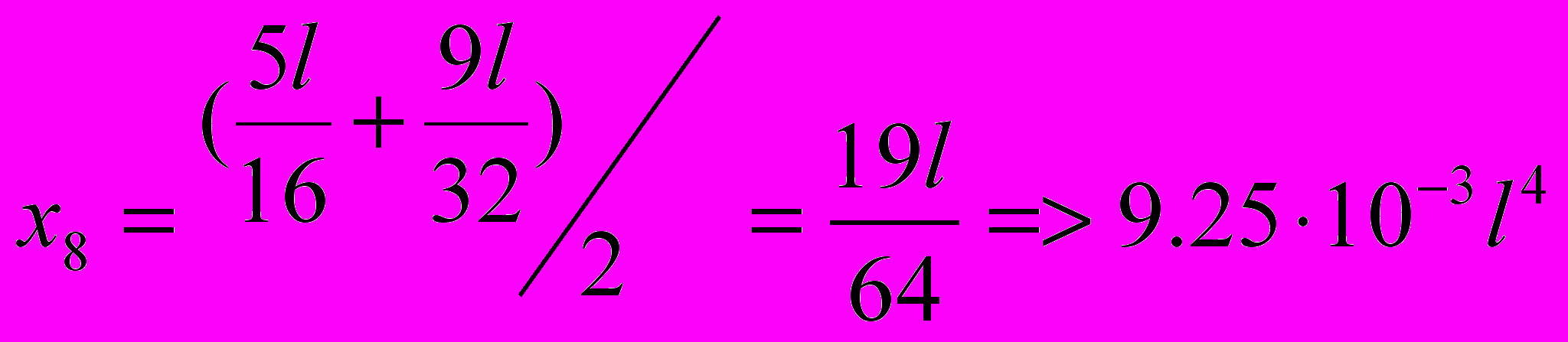

В результате решения данного уравнения получаем то, что рациональная длина консоли « х » равна

В дальнейшем целесообразно усложнить задачу, изменив расчетную схему, считая сваю заделанной в грунте, а нагрузку изменяющейся по линейному треугольному закону. Эта схема наиболее близка к действительной расчетной схеме.
Литература
1. Строительная механика: Учеб. пособие для студентов вузов / Ю.И. Бурчаков, В.Е. Гнедин, В.М. Денисов. – М.: Высш. школа, 1983. – 255с., ил.
2. Сопротивление материалов: Учеб. для вузов / А.В. Александров, В.Д. Потапов, Б.П. Державин; Под ред. А.В. Александрова. – 3-е изд. испр.- М.: Высш. шк., 2003. – 560 с.: ил.
Аннотация
Данный доклад посвящен проблемам рационализации строительных конструкций. Целью доклада является нахождение наиболее выгодного расположения расстрела по высоте котлована. При этом соблюдается равенство изгибающих моментов на опоре и в пролете консоли, расчет ведется методом последовательных приближений
Ключевые слова
расстрел, изгибающие моменты, консоль, котлован, свайное крепление, равномерно распределенная нагрузка, метод Ньютона
