Прогнозирование потребности в педагогических кадрах в регионе фролов Юрий Викторович

Вид материала

Документы

Содержание Постановка задачи и качественное моделирование Пi - потребность в приеме на работу учителей на начало учебного года i, Нi Рi-1 - прогнозное количество работающих учителей в учебном году i-1, Вi-1 Разработка моделей для расчета необходимого количества педагогов Прогнозы рождаемости Модели количества школьников по классам Прогнозы необходимого числа педагогов Рис. 9. Прогнозы выбытияИспользуя полученные значения параметров Нi, Нi-1, Вi-1

Подобный материал:

• И. А. Подковинская Министерство труда, занятости и кадровой политики, 59.37kb.
• Вопросы обеспечения «качества обслуживания» опорной инфраструктуры научно-образовательной, 147.61kb.
• Интерактивного согласования, 87.39kb.
• Прогнозирование, профилактика и упреждающая интенсивная терапия полиорганной недостаточности, 907.95kb.
• Контрольная работа по дисциплине управление персоналом, 297.66kb.
• Методические разработки к практическим занятиям по общественному здоровью, 58.63kb.
• Фролов А. В. Свободная энергия Фролов, 400.6kb.
• Мужицкий Владимир Федорович, д т. н. Федосенко Юрий Кириллович, д т. н. Артемьев Борис, 424.99kb.
• Должностная инструкция 15 контрольные вопросы и задания 17 Глава 3 Определение основных, 1027.03kb.
• Фролов И. Т. и др. 3-е изд, 14108.71kb.

прогнозирование потребности в педагогических кадрах В РЕГИОНЕ


Фролов Юрий Викторович, г. Москва, ГОУ ВПО Московский городской педагогический университет, 129226, 2-й Сельскохозяйственный проезд, д.4, корп.2, jury_frolov@mail.ru
Офицеров Владимир Петрович, г. Москва, ГОУ ВПО Московский городской педагогический университет, 129226, 2-й Сельскохозяйственный проезд, д.4, корп.2, ovp45@mail.ru
Офицеров Михаил Владимирович, г. Москва, ГОУ ВПО Московский городской педагогический университет, 129226, 2-й Сельскохозяйственный проезд, д.4, корп.2, omv8383@mail.ru


При разработке прогнозных моделей использовались модели линейной регрессии, нейросетевые модели и методы динамического моделирования процессов. [1,2]. В ходе выполнения расчетно-экспериментальных исследований показатели, полученные с использованием разных моделей, сопоставлялись и в ряде случаев выполнялось усреднение прогнозов, полученных с помощью разных методов.

По итогам выполненных исследований предложена версия комплексной методологии выполнения прогнозов численности педагогических кадров в Москве, основанная на анализе демографических тенденций и официально зарегистрированных вакансий.

Предложенный методологический подход может быть использован для решения прогнозно-аналитических задач для отраслей социальной сферы на уровне регионов России и в целом по Российской Федерации.

1. Методология построения прогнозов на основе анализа статистических данных

1. Постановка задачи и качественное моделирование

В последнее десятилетие Департамент образования г. Москвы сталкивается с проблемой планирования подготовки необходимого количества педагогов для школьных и дошкольных учреждений.

В связи с относительно длительным периодом подготовки специалистов–педагогов – 5 лет, необходимы среднесрочные и долгосрочные прогнозы потребности необходимого количества педагогов для дошкольных и школьных учреждений.

Прежде чем использовать те или иные технологии прогнозирования, рассмотрим основные факторы, которые предположительно могут влиять на такой показатель, как необходимое количество преподавателей в школе. Очевидно, что в условиях использования относительно стабильных программ обучения одним из ключевых факторов является количество учеников в школах Москвы с разбиением по классам. То есть, если мы будем знать прогнозные значения количества школьников в классах на n лет вперед, то, имея зависимость между количеством учителей в школе и количеством учеников, можно прогнозировать необходимое количество учителей на n лет вперед.

Для принятия управленческих решений по определению объемов подготовки педагогических кадров знание необходимого количества учителей важно, но недостаточно, так как в отрасли уже работает определенный контингент преподавателей. Кроме того, и численность, и состав этого контингента находятся в постоянном движении. Существует постоянный отток из отрасли преподавателей как по возрастной причине (выход на пенсию), так и в связи с переходом к другим видам профессиональной деятельности. Поэтому, помимо прогноза необходимого количества учителей для работы в школах, важно дать прогнозные оценки выбытия педагогических кадров из образовательной отрасли. Тогда уравнение потребности в приеме на работу учителей на начало учебного года i будет иметь вид:


Пi = Нi – Рi-1 + Вi-1, (1)

где

Пi - потребность в приеме на работу учителей на начало учебного года i,

Нi - прогнозное необходимое количество учителей в учебном году i,

Рi-1 - прогнозное количество работающих учителей в учебном году i-1,

Вi-1 - прогнозное количество выбывающих учителей в учебном году i-1.

Если речь идет о текущем годе, то количество работающих учителей известно, известна потребность в учителях (заявленные вакансии от образовательных учреждений). В этом случае можно определить необходимое количество учителей текущего года, которое соответствует известному количеству учеников текущего года. Такое соответствие можно проследить по ретроспективным (историческим) данным.

Предположим, мы хотим спрогнозировать «Потребность в приеме на работу учителей в учебном году, следующем за текущим годом». Тогда мы должны определить «Прогнозное количество выбывающих учителей в текущем учебном году», «Прогнозное необходимое количество учителей в учебном году, следующем за текущим годом» и, применив выражение (1), определить «Потребность в приеме на работу учителей в учебном году, следующем за текущим годом».

Если предположить, что мы полностью удовлетворяем потребность в приеме на работу учителей, то в расчетах по приведенной выше формуле можно принять, что

Рi-1 = Нi-1,

где

Рi-1 - прогнозное количество работающих учителей в учебном году i-1,

Нi-1 - прогнозное необходимое количество учителей в учебном году i-1

Поскольку, так или иначе, потребность в учителях удовлетворяется, то выражение (1) можно упростить:


Пi = Нi – Нi-1 + Вi-1, (2)

где

Пi - потребность в приеме на работу учителей на начало учебного года i,

Нi - прогнозное необходимое количество учителей в учебном году i,

Нi-1 - прогнозное необходимое количество учителей в учебном году i-1,

Вi-1 - прогнозное количество выбывающих учителей в учебном году i-1.

Рассмотрим, от каких параметров зависит величина «Прогнозное количество выбывающих учителей в год». Здесь играют роль несколько ключевых факторов. Во-первых, это количество учителей пенсионного возраста, которые, со временем, уходят, во-вторых, это уровень зарплаты, делающий профессию привлекательной и престижной, в-третьих, это социальный статус учителя, насколько уважительно общество оценивает эту профессию.

«Прогнозное необходимое количество учителей», как предполагается, будет зависеть главным образом от количества учеников. Можно ожидать, что число учеников 2-го класса существенно зависит числа учеников 1 –го класса прошлого года, 3-го класса от числа учеников 2-го класса прошлого года и т.д. В свою очередь, можно предположить, что количество учеников 1-го класса существенно зависит от числа новорожденных 6 , 7 и 8 лет назад. Есть и другие факторы, влияющие на количество учеников, например, миграция населения. Эти факторы, пока в явном виде не учитываются, и будут вносить некоторую погрешность в прогнозы.

Если мы хотим осуществлять прогнозирование более чем на семь лет вперед, то понадобится прогноз числа новорожденных. В настоящей работе сделано предположение, что число новорожденных определяется среднестатистическими коэффициентами рождаемости у женщин разных возрастных категорий и количеством женщин в соответствующих возрастных категориях.

На основе приведенных рассуждений можно построить следующее дерево зависимостей (рис. 1):





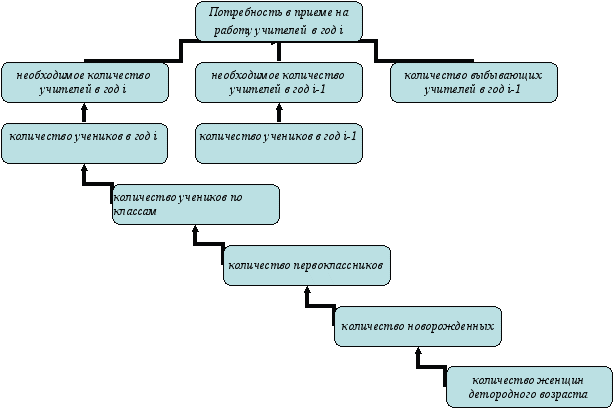
Рис. 1. Взаимосвязь факторов в моделях, прогнозирующих потребность в педагогических кадрах

2. Разработка моделей для расчета необходимого количества педагогов

   1. Регрессионные модели для прогноза количества женщин детородного возраста в г. Москве

При качественном рассмотрении задачи были выделены предполагаемые факторы, влияющие на прогноз необходимого количества учителей и предложена взаимосвязь этих факторов (см. Рис. 1).

Одним из ключевых факторов в предложенном подходе является «Количество женщин детородного возраста». Для получения долгосрочных прогнозов рождаемости разработаны модели, позволяющие оценивать количество женщин на основе известных статистических данных с разбивкой по возрастным группам 0-4 , 5-9, 10-14, 15-19, 20-24, 25-29, 30-34, 35-39, 40-44, 45-49 лет.

В порядке иллюстрации использованного в настоящей работе подхода приведем модель для прогноза числа девочек в возрасте от 5 до 9 лет. Проверим предположение, о том, что количество девочек в возрастной категории 5-9 лет сильно зависит от количества девочек в возрастной категории 0-4 года со сдвигом на пять лет назад. Для этого, с помощью пакета SPSS, получим модель линейной регрессии:

y=0,94867*x + 19,76631,

r =0,99789

r² = 0,99579

где x –количество девочек в возрасте 0-4 года со сдвигом от текущего прогнозного года на пять лет назад; r - коэффициент корреляции Пирсона (показывает связь между независимым фактором х (количеством женщин в возрасте 0-4 года со сдвигом на пять лет назад) и прогнозируемой величиной y - количеством девочек в возрасте 5-9 лет). Величина r близка к единице, что указывает на тесноту связи между зависимой и независимой переменными. Значение r² = 0,99579 показывает, что на 99% совокупное изменение зависимой переменной y описывается выбранной независимой переменной х.

Это говорит о том, что полученная модель линейной регрессии хорошо описывает объективно существующую закономерность.

В результате, исходя из имеющихся данных, получаем прогноз количества девочек в возрасте 5-9 лет до 2011 года включительно. Хотя возраст 5-9 лет и не является детородным, но полученные прогнозные данные можно использовать для прогноза женщин возраста 10-14 лет до 2016 года, а их в свою очередь использовать для прогноза женщин более старшего возраста.

В работе получены аналогичные линейные регрессионные модели для прогноза количества женщин в возрастных группах 10-14 лет, 15-19 лет, 20-24 лет и др. возрастных группах. Результаты прогнозов приведены на рис. 2, при этом до 2006 года показаны фактические данные, а после 2006 года - прогнозные.



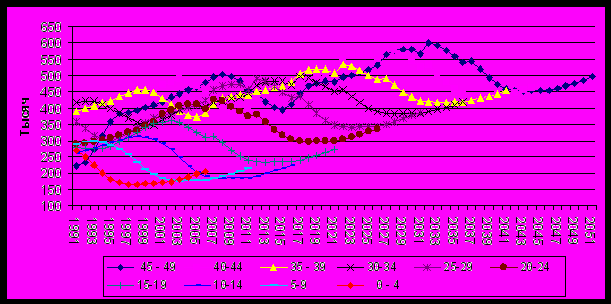
Рис. 2. Сводные значения фактических и прогнозных значений числа женщин от 15-19 до 45-49 лет


Необходимо отметить, что после 2011 года в качестве исходных данных для формирования прогноза используются прогнозные данные, а не реальные статистические данные. Поэтому точность прогноза после 2011 года снижается во всех моделях, а сам прогноз можно рассматривать как качественный.

2. Прогнозы рождаемости

На основе имеющихся данных в работе получены коэффициенты рождаемости у женщин разных возрастных групп в разные годы. Далее были выбраны средние значения коэффициента за последние два года, на основе которых определены прогнозные значения рождаемости. Некоторые полученные результаты представлены на рис. 3.




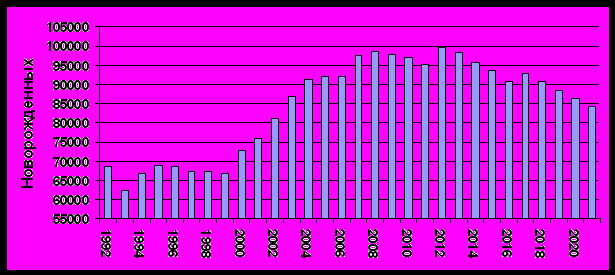
Рис. 3 Фактические данные (по 2006 г.) и прогнозы рождаемости в Москве

3. Модели количества школьников по классам

В результате исследования линейных регрессионных статистических моделей, связывающих первоклассников и новорожденных, получена двухфакторная модель с хорошими статистическими параметрами.

На основании этой модели и предыдущих результатов прогнозов рождаемости получены прогнозы числа первоклассников. Причем, по 2012 год прогнозы получены от значений фактически родившихся детей, а далее от прогнозных значений родившихся. Результаты прогноза приведены на рис. 4.





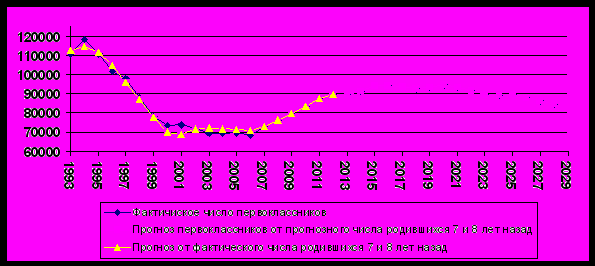
Рис. 4 Прогноз числа первоклассников

Следует отметить, что при исследовании кросскорреляционных связей между родившимися шесть, семь и восемь лет назад и числом первоклассников были обнаружены сильные статистические зависимости. Данные для исследований в рядах для новорожденных брались соответственно временным сдвигам на 6, 7 и 8 лет с 1988г. по 2000г., с 1987г. по 1999г. и с 1986г. по 1998. Соответствующие данные о первоклассниках брались с 1994г. по 2006г. Были получены коэффициенты корреляции между:

- родившимися шесть лет назад и первоклассниками (0,922)

- родившимися семь лет назад и первоклассниками (0,981)

- родившимися восемь лет назад и первоклассниками (0,981),

В предыдущих исследованиях [3] строились три регрессионные модели числа первоклассников по отдельности от родившихся 6, 7 и 8 лет назад, однако сравнение результатов прогнозов с фактическими данными за 2005 и 2006 годы показало завышение прогнозных значений. Более точной оказалась модель прогноза первоклассников в зависимости от числа родившихся 8 лет назад. С учетом новых статистических данных была построена пошаговым методом последовательного исключения переменных регрессионная модель прогноза первоклассников в зависимости от числа родившихся 8 и 7 лет назад. В качестве исходных независимых факторов выступали все три переменные – родившихся 6, 7 и 8 лет назад. Переменная, соответствующая числу родившихся 6 лет назад была автоматически исключена, однако ее влияние на прогноз первоклассников хорошо передает переменная, соответствующая числу родившихся 7 лет назад, так как коэффициент корреляции между этими переменными 0,938.

В зависимости от числа первоклассников на основании найденных линейных регрессионных зависимостей были получены прогнозные значения числа второклассников. В зависимости от числа второклассников (как фактического, так и прогнозного) были найдены прогнозные значения числа третьеклассников и т.д. до 11 класса включительно. На рис. 5 показана предполагаемая динамика общего количества учеников в школе, а на рис. 6 – изменение количества учеников в первых, девятых и одиннадцатых классах школ Москвы.




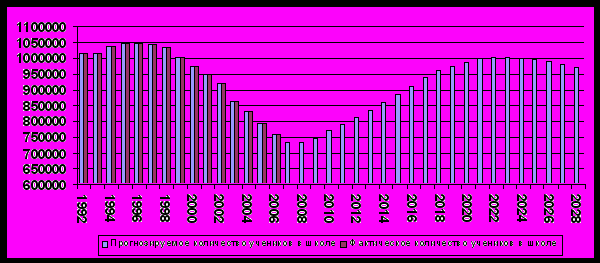
Рис.5 Фактические данные и прогноз общего количества учеников в школах Москвы




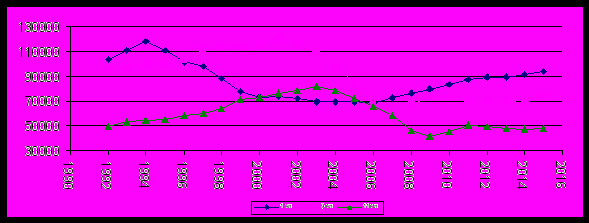
Рис. 6. Фактические данные (по 2006 г.) и прогноз количества обучающихся по классам в школах Москвы

4. Прогнозы необходимого числа педагогов

Для построения прогноза необходимого числа педагогов была разработана регрессионная модель, связывающая общее количество учеников в школе и необходимое количество учителей. Для получения фактических статистических данных о необходимом количестве учителей были использованы данные о работающих педагогах и заявленных вакансиях. На рис. 7 показаны фактические и прогнозные значения необходимого количества учителей. Прогнозные значения получены на основе разработанной регрессионной модели.





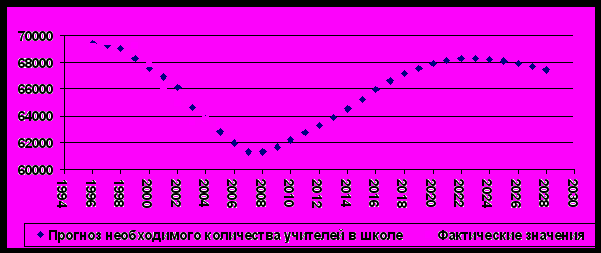
Рис. 7. Прогноз необходимого количества учителей в школе


Следует отметить, что с учетом ежегодного «естественного» выбытия педагогических кадров никакого сокращения потребности не следует ожидать. Далее будут даны прогнозы выбытия педагогических кадров и прогнозы планов приема на работу педагогов по основным предметам.




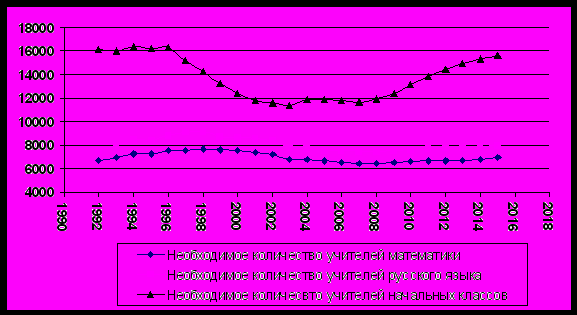
Рис. 8. Фактические данные (по 2006 г.) и прогноз необходимого количества учителей


Анализ имеющихся статистических данных показал, что значения доли выбывающих педагогов в последние годы относительно стабильны. Прогноз этих долей по каждому предмету (педагогической специальности) был выполнен с помощью метода скользящих средних [4]. На рис. 9 показан прогноз выбытия по трем предметам.



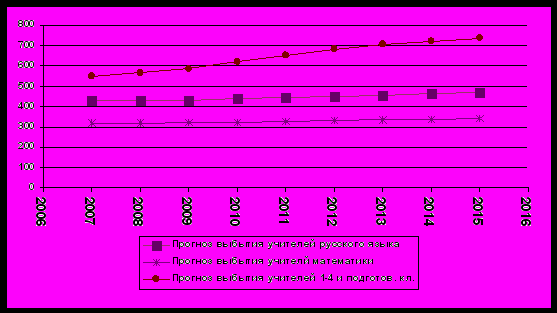
Рис. 9. Прогнозы выбытия


Используя полученные значения параметров Нi, Нi-1, Вi-1 по формуле (2) найдем прогнозные значения Пi - потребности в приеме на работу учителей на начало учебного года i с учетом прогноза количества выбывающих педагогов в год i-1. Результаты вычислений приведены на рис. 10.



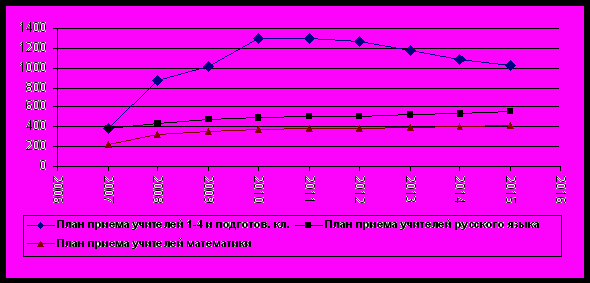
Рис. 10. Прогноз потребности в приеме на работу учителей русского языка, математики, учителей 1-4 и подготовительных классов с учетом прогноза выбытия учителей.

Выводы

1. Выполнен системный анализ проблемы определения потребности в педагогических кадрах и выделены основные качественные факторы, которые влияют на потребность.
   
2. Разработан алгоритм, разбивающий исходную сложную задачу определения потребности в педагогических кадрах на ряд более простых взаимосвязанных подзадач моделирования и прогнозирования:
   

- прогноза количества женщин детородного возраста,

- прогноза рождаемости,

- прогноза числа первоклассников,

-прогноза числа учеников в средних образовательных учреждениях,

- прогноза необходимого числа учителей,

-прогноза выбытия педагогических кадров,

-прогноза плана приема учителей в средние общеобразовательные учреждения.

3. На основе статистических данных разработаны модели для получения перечисленных прогнозов. Модели обладают достаточно хорошими статистическими характеристиками, что подтверждает правомочность их использования.
   
4. Возможно обобщение предложенного методологического подхода для решения прогнозно-аналитических задач для других отраслей социальной сферы Москвы и для других регионов России.
   
5. Приведенные выше результаты по определению потребности носят предварительный характер. Необходимо продолжить исследования и уточнение прогнозных моделей с учетом обновляющихся статистических, социологических данных и результатов обсуждения предложенной методологии в экспертном сообществе.
   

Литература

1. Фролов Ю.В. Интеллектуальные системы и управленческие решения. - М.: МГПУ, 2000. – 294 с.
   
2. Фролов Ю.В., Офицеров В.П., Ануфриев С.В. Моделирование и прогнозирование потребности педагогических кадров в городе Москве. Международный конгресс конференций «Информационные технологии в образовании». XIII Международная конференция «Информационные технологии в образовании»: Сборник трудов участников конференции. Часть V. – М.: Просвещение, 2003, с. 254-255
   
3. Рябов В.В., Пищулин Н.П., Фролов Ю.В. и др. Стратегия образования: основы формирования, методы оценки и прогнозирования. – М.: МГПУ, 2003.
   
4. Ханк Д.Э., Уичерн Д.У., Райтс А.Дж. Бизнес-прогнозирование, М.: Издательский дом «Вильямс», 2003, 656 с.
   
5. Дуброва Т.А. Статистические методы прогнозирования. М.:ЮНИТИ-ДАНА, 2003.- 206 с.